More Is Not Always Better: Local Models Provide Accurate Predictions of Spectral Properties of Porphyrins
Abstract
:1. Introduction
2. Material and Methods
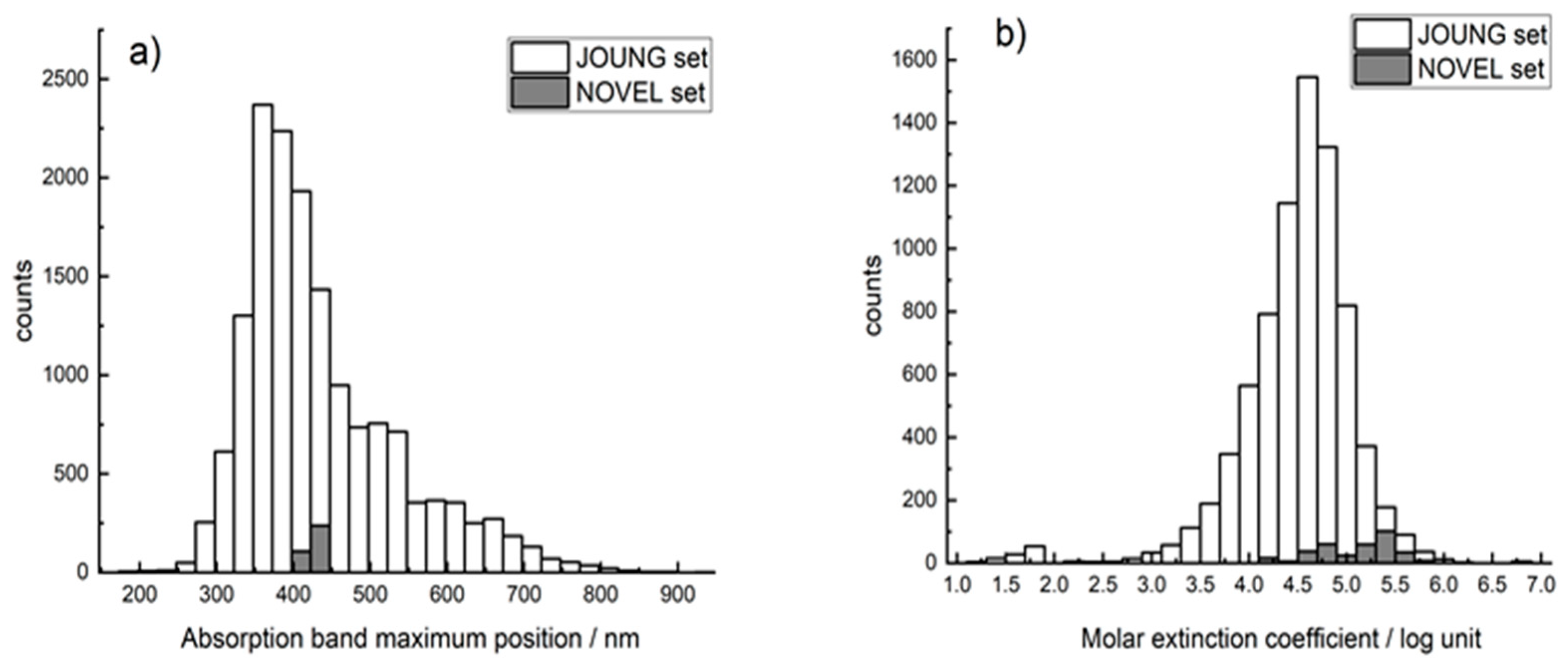
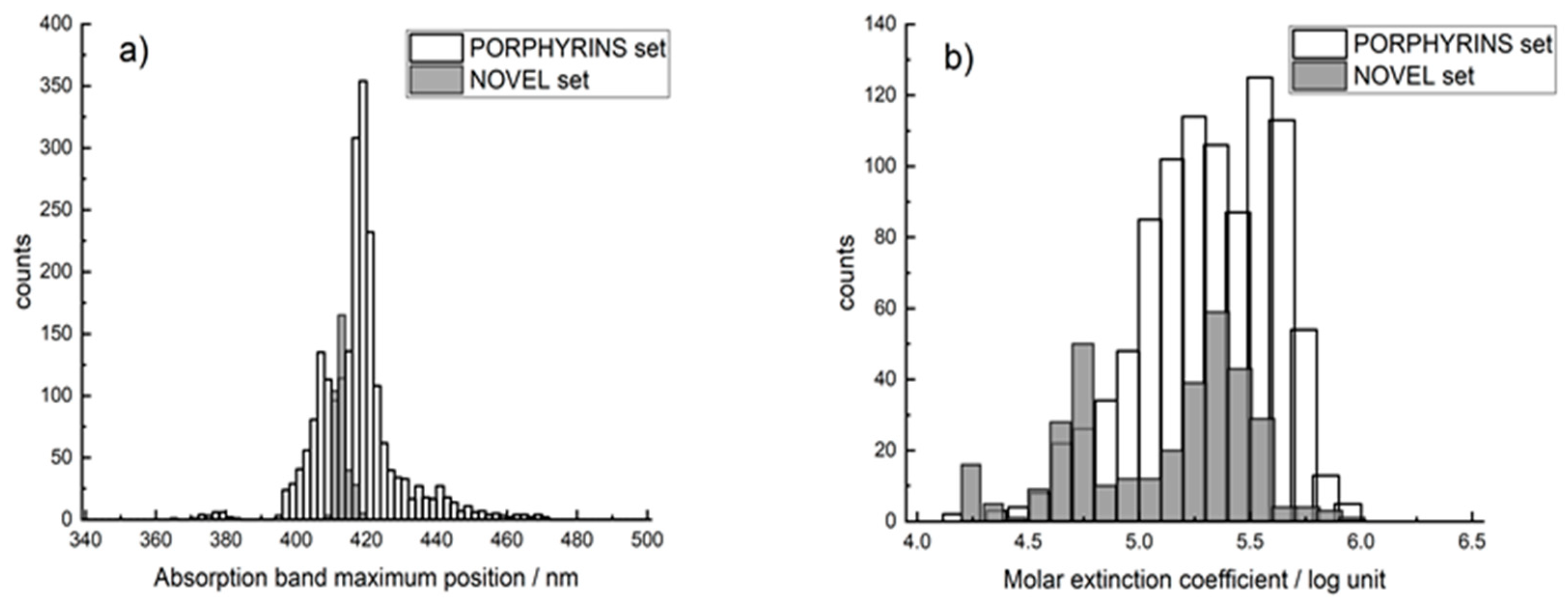
2.1. Datasets
2.2. Methods
2.3. Statistical Parameters
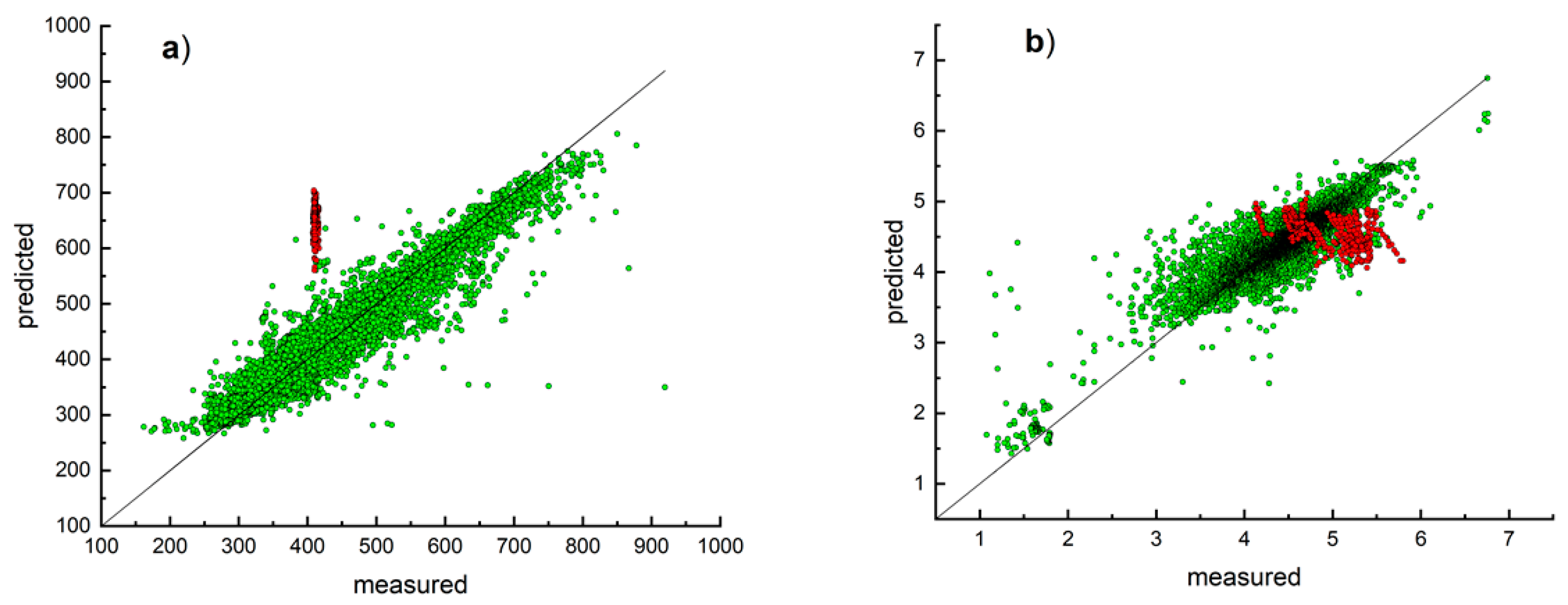
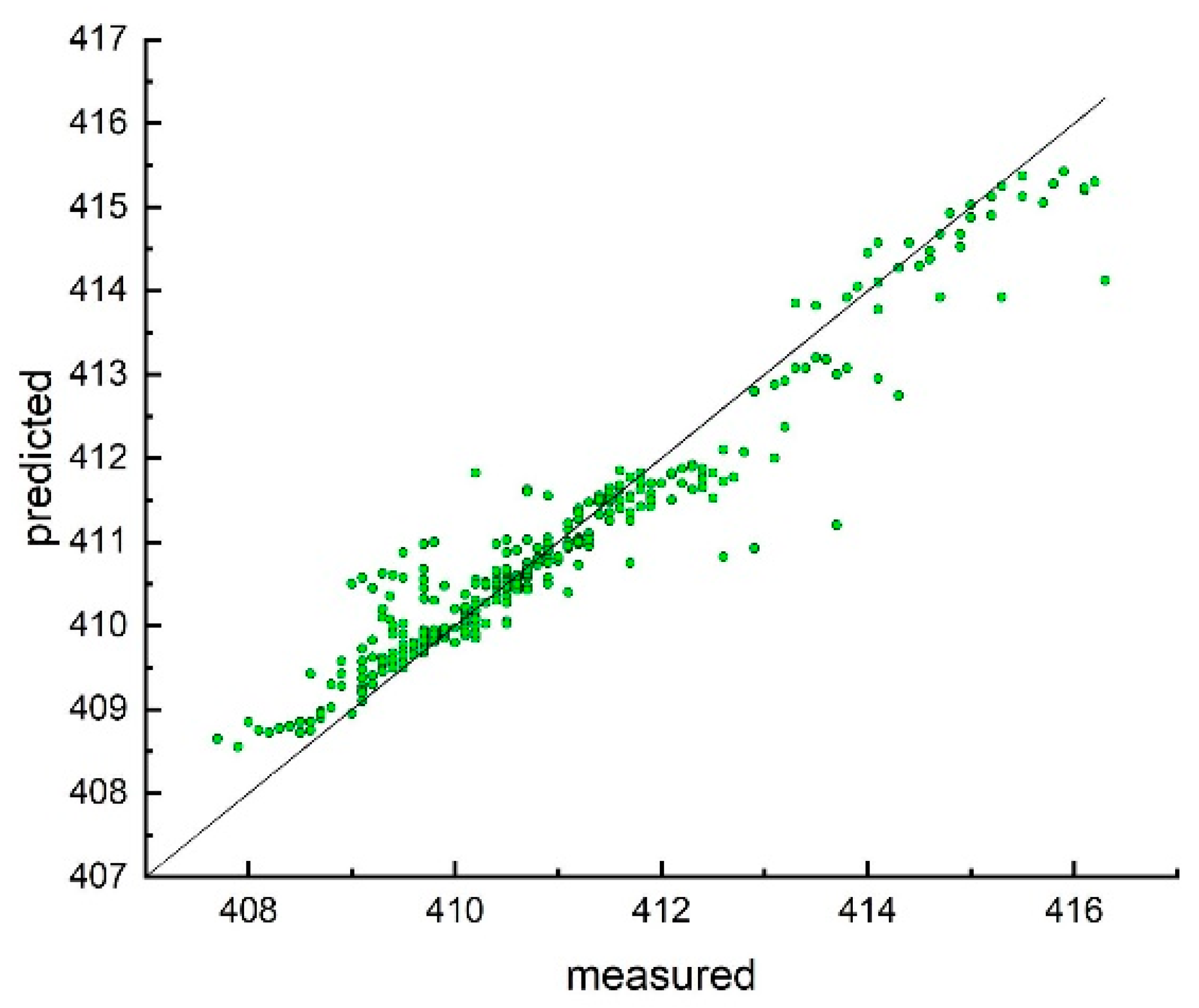
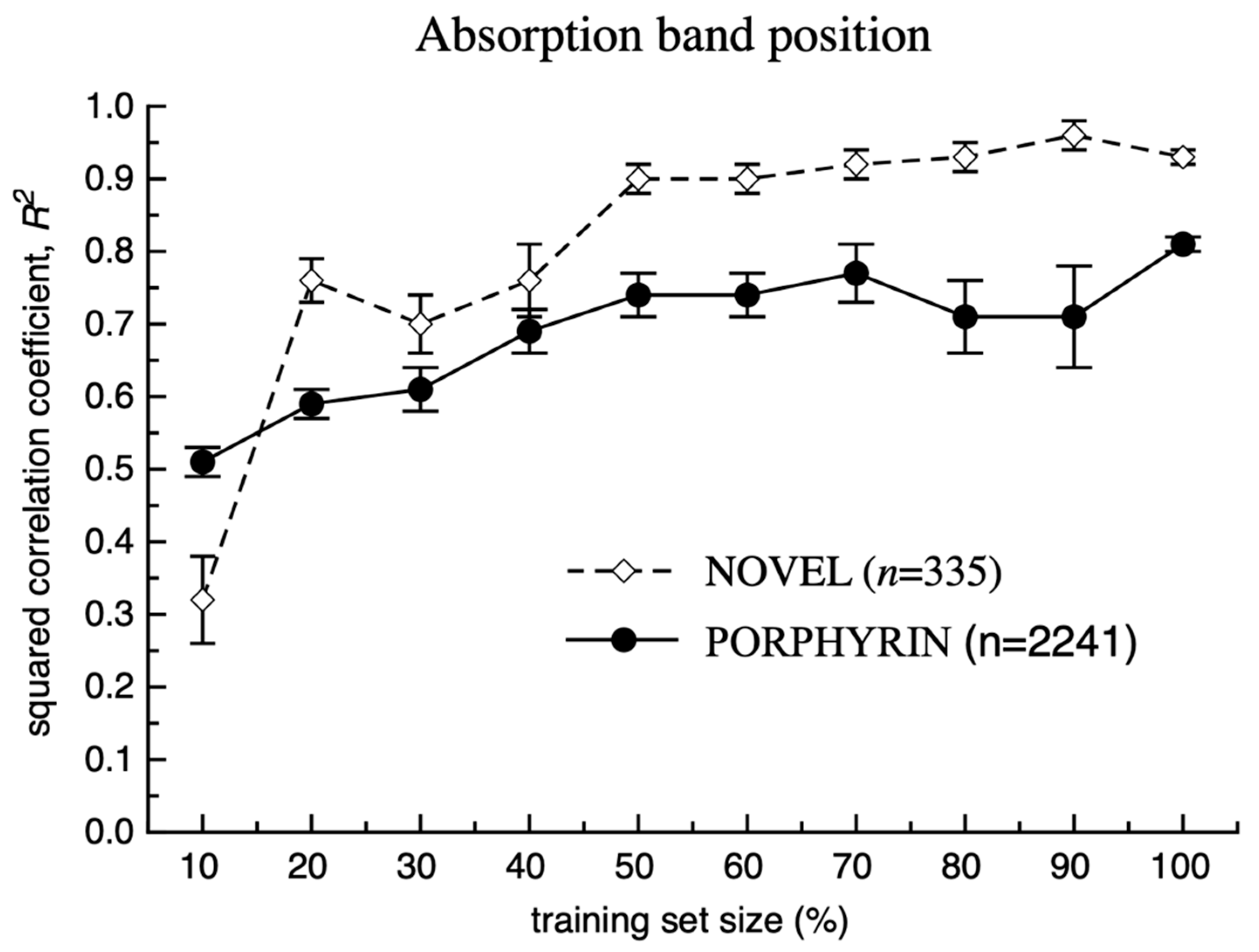
3. Results and Discussion
Model Development and Testing
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ptaszyńska, A.A.; Trytek, M.; Borsuk, G.; Buczek, K.; Rybicka-Jasińska, K.; Gryko, D. Porphyrins Inactivate Nosema Spp. Microsporidia. Sci. Rep. 2018, 8, 5523. [Google Scholar] [CrossRef] [PubMed]
- Varchi, G.; Foglietta, F.; Canaparo, R.; Ballestri, M.; Arena, F.; Sotgiu, G.; Guerrini, A.; Nanni, C.; Cicoria, G.; Cravotto, G.; et al. Engineered Porphyrin Loaded Core-Shell Nanoparticles for Selective Sonodynamic Anticancer Treatment. Nanomedicine 2015, 10, 3483–3494. [Google Scholar] [CrossRef] [PubMed]
- Mamardashvili, G.; Mamardashvili, N.; Koifman, O. Macrocyclic Receptors for Identification and Selective Binding of Substrates of Different Nature. Molecules 2021, 26, 5292. [Google Scholar] [CrossRef]
- Leng, F.; Liu, H.; Ding, M.; Lin, Q.-P.; Jiang, H.-L. Boosting Photocatalytic Hydrogen Production of Porphyrinic MOFs: The Metal Location in Metalloporphyrin Matters. ACS Catal. 2018, 8, 4583–4590. [Google Scholar] [CrossRef]
- Biesaga, M.; Pyrzyńska, K.; Trojanowicz, M. Porphyrins in Analytical Chemistry. A Review. Talanta 2000, 51, 209–224. [Google Scholar] [CrossRef]
- Zucca, P.; Neves, C.; Simões, M.; Neves, M.; Cocco, G.; Sanjust, E. Immobilized Lignin Peroxidase-Like Metalloporphyrins as Reusable Catalysts in Oxidative Bleaching of Industrial Dyes. Molecules 2016, 21, 964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dini, D.; Calvete, M.J.F.; Hanack, M. Nonlinear Optical Materials for the Smart Filtering of Optical Radiation. Chem. Rev. 2016, 116, 13043–13233. [Google Scholar] [CrossRef] [PubMed]
- de la Torre, G.; Bottari, G.; Sekita, M.; Hausmann, A.; Guldi, D.M.; Torres, T. A Voyage into the Synthesis and Photophysics of Homo- and Heterobinuclear Ensembles of Phthalocyanines and Porphyrins. Chem. Soc. Rev. 2013, 42, 8049. [Google Scholar] [CrossRef] [PubMed]
- Saito, S.; Osuka, A. Expanded Porphyrins: Intriguing Structures, Electronic Properties, and Reactivities. Angew. Chem. Int. Ed. 2011, 50, 4342–4373. [Google Scholar] [CrossRef]
- Mamardashvili, N.Z.; Golubchikov, O.A. Spectral Properties of Porphyrins and Their Precursors and Derivatives. Russ. Chem. Rev. 2001, 70, 577–606. [Google Scholar] [CrossRef]
- Nemykin, V.N.; Hadt, R.G. Interpretation of the UV−vis Spectra of the Meso(Ferrocenyl)-Containing Porphyrins Using a TDDFT Approach: Is Gouterman’s Classic Four-Orbital Model Still in Play? J. Phys. Chem. A 2010, 114, 12062–12066. [Google Scholar] [CrossRef] [PubMed]
- Wojciechowski, K.; Szadowski, J. Effect of the Sulphonic Group Position on the Properties of Monoazo Dyes. Dyes Pigments 2000, 44, 137–147. [Google Scholar] [CrossRef]
- Azuma, K.; Suzuki, S.; Uchiyama, S.; Kajiro, T.; Santa, T.; Imai, K. A Study of the Relationship between the Chemical Structures and the Fluorescence Quantum Yields of Coumarins, Quinoxalinones and Benzoxazinones for the Development of Sensitive Fluorescent Derivatization Reagents. Photochem. Photobiol. Sci. 2003, 2, 443. [Google Scholar] [CrossRef] [PubMed]
- Adachi, M.; Nakamura, S. Comparison of the INDO/S and the CNDO/S Method for the Absorption Wavelength Calculation of Organic Dyes. Dyes Pigments 1991, 17, 287–296. [Google Scholar] [CrossRef]
- Sham, L.J.; Kohn, W. One-Particle Properties of an Inhomogeneous Interacting Electron Gas. Phys. Rev. 1966, 145, 561–567. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of Electronic Excitations within the Adiabatic Approximation of Time Dependent Density Functional Theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Adamo, C.; Jacquemin, D. The Calculations of Excited-State Properties with Time-Dependent Density Functional Theory. Chem. Soc. Rev. 2013, 42, 845–856. [Google Scholar] [CrossRef]
- Hahn, D.K.; Callis, P.R. Lowest Triplet State of Indole: An Ab Initio Study. J. Phys. Chem. A 1997, 101, 2686–2691. [Google Scholar] [CrossRef]
- Schüller, A.; Goh, G.B.; Kim, H.; Lee, J.-S.; Chang, Y.-T. Quantitative Structure-Fluorescence Property Relationship Analysis of a Large BODIPY Library. Mol. Inf. 2010, 29, 717–729. [Google Scholar] [CrossRef]
- Grimme, S. A Simplified Tamm-Dancoff Density Functional Approach for the Electronic Excitation Spectra of Very Large Molecules. J. Chem. Phys. 2013, 138, 244104. [Google Scholar] [CrossRef]
- Heil, A. Development and Implementation of New DFT/MRCI Hamiltonians for Odd and Even Numbers of Electrons. Ph.D. Thesis, Henrich Hein University in Düsseldorf, Düsseldorf, Germany, 8 September 2019. [Google Scholar]
- Li, G.-Z.; Yang, J.; Song, H.-F.; Yang, S.-S.; Lu, W.-C.; Chen, N.-Y. Semiempirical Quantum Chemical Method and Artificial Neural Networks Applied for λ m ax Computation of Some Azo Dyes. J. Chem. Inf. Comput. Sci. 2004, 44, 2047–2050. [Google Scholar] [CrossRef] [PubMed]
- Li, H. Quantitative Structure—Property Relationships for Colour Reagents and Their Colour Reactions with Cerium Using Computational Neural Networks. Talanta 1997, 44, 203–211. [Google Scholar] [CrossRef]
- Shi, J.; Luan, F.; Zhang, H.; Liu, M.; Guo, Q.; Hu, Z.; Fan, B. QSPR Study of Fluorescence Wavelengths (Λex/Λem) Based on the Heuristic Method and Radial Basis Function Neural Networks. QSAR Comb. Sci. 2006, 25, 147–155. [Google Scholar] [CrossRef]
- Nantasenamat, C.; Isarankura-Na-Ayudhya, C.; Tansila, N.; Naenna, T.; Prachayasittikul, V. Prediction of GFP Spectral Properties Using Artificial Neural Network. J. Comput. Chem. 2007, 28, 1275–1289. [Google Scholar] [CrossRef]
- Shedden, K.; Brumer, J.; Chang, Y.T.; Rosania, G.R. Chemoinformatic Analysis of a Supertargeted Combinatorial Library of Styryl Molecules. J. Chem. Inf. Comput. Sci. 2003, 43, 2068–2080. [Google Scholar] [CrossRef]
- Joung, J.F.; Han, M.; Hwang, J.; Jeong, M.; Choi, D.H.; Park, S. Deep Learning Optical Spectroscopy Based on Experimental Database: Potential Applications to Molecular Design. JACS Au 2021, 1, 427–438. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, Z.; Chen, B.; Zhang, Q. A Linear QSPR Model for Prediction of Maximum Absorption Wavelength of Second-Order NLO Chromophores. QSAR Comb. Sci. 2006, 25, 372–379. [Google Scholar] [CrossRef]
- Yao, X.; Wang, Y.; Zhang, X.; Zhang, R.; Liu, M.; Hu, Z.; Fan, B. Radial Basis Function Neural Network-Based QSPR for the Prediction of Critical Temperature. Chemom. Intell. Lab. Syst. 2002, 62, 217–225. [Google Scholar] [CrossRef]
- Xia, Z.; Karpov, P.; Popowicz, G.; Tetko, I.V. Focused Library Generator: Case of Mdmx Inhibitors. J. Comput. Aided Mol. Des. 2020, 34, 769–782. [Google Scholar] [CrossRef] [Green Version]
- Joung, J.F.; Han, M.; Jeong, M.; Park, S. Experimental Database of Optical Properties of Organic Compounds. Sci. Data 2020, 7, 295. [Google Scholar] [CrossRef]
- DB for Chromophore. Available online: https://doi.org/10.6084/m9.figshare.12045567.v2 (accessed on 29 December 2021).
- Sushko, I.; Novotarskyi, S.; Körner, R.; Pandey, A.K.; Rupp, M.; Teetz, W.; Brandmaier, S.; Abdelaziz, A.; Prokopenko, V.V.; Tanchuk, V.Y.; et al. Online Chemical Modeling Environment (OCHEM): Web Platform for Data Storage, Model Development and Publishing of Chemical Information. J. Comput. Aided Mol. Des. 2011, 25, 533–554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Varnek, A.; Fourches, D.; Horvath, D.; Klimchuk, O.; Gaudin, C.; Vayer, P.; Solov’ev, V.; Hoonakker, F.; Tetko, I.; Marcou, G. ISIDA—Platform for Virtual Screening Based on Fragment and Pharmacophoric Descriptors. Curr. Comput.-Aided Drug Des. 2008, 4, 191–198. [Google Scholar] [CrossRef]
- Hong, H.; Xie, Q.; Ge, W.; Qian, F.; Fang, H.; Shi, L.; Su, Z.; Perkins, R.; Tong, W. Mold2, Molecular Descriptors from 2D Structures for Chemoinformatics and Toxicoinformatics. J. Chem. Inf. Model. 2008, 48, 1337–1344. [Google Scholar] [CrossRef] [PubMed]
- Mauri, A. AlvaDesc: A Tool to Calculate and Analyze Molecular Descriptors and Fingerprints. In Ecotoxicological QSARs; Roy, K., Ed.; Methods in Pharmacology and Toxicology; Springer: New York, NY, USA, 2020; pp. 801–820. ISBN 978-1-07-160150-1. [Google Scholar]
- Polishchuk, P.; Madzhidov, T.; Gimadiev, T.; Bodrov, A.; Nugmanov, R.; Varnek, A. Structure–Reactivity Modeling Using Mixture-Based Representation of Chemical Reactions. J. Comput. Aided Mol. Des. 2017, 31, 829–839. [Google Scholar] [CrossRef] [PubMed]
- Sadowski, J.; Gasteiger, J. From Atoms and Bonds to Three-Dimensional Atomic Coordinates: Automatic Model Builders. Chem. Rev. 1993, 93, 2567–2581. [Google Scholar] [CrossRef]
- Karpov, P.; Godin, G.; Tetko, I.V. Transformer-CNN: Swiss Knife for QSAR Modeling and Interpretation. J. Cheminf. 2020, 12, 17. [Google Scholar] [CrossRef] [Green Version]
- Weininger, D. SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- OCHEM Materials Home—OCHEM Materials—EADMET. Available online: http://docs.ochem.eu/ (accessed on 28 December 2021).
- Tetko, I.V.; Sushko, I.; Pandey, A.K.; Zhu, H.; Tropsha, A.; Papa, E.; Öberg, T.; Todeschini, R.; Fourches, D.; Varnek, A. Critical Assessment of QSAR Models of Environmental Toxicity against Tetrahymena Pyriformis: Focusing on Applicability Domain and Overfitting by Variable Selection. J. Chem. Inf. Model. 2008, 48, 1733–1746. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, D.; Koch, U.; Hadian, K.; Sattler, M.; Tetko, I.V. Highly Accurate Filters to Flag Frequent Hitters in AlphaScreen Assays by Suggesting Their Mechanism. Mol. Inf. 2021, 41, e2100151. [Google Scholar] [CrossRef]
- Tetko, I.V.; Novotarskyi, S.; Sushko, I.; Ivanov, V.; Petrenko, A.E.; Dieden, R.; Lebon, F.; Mathieu, B. Development of Dimethyl Sulfoxide Solubility Models Using 163,000 Molecules: Using a Domain Applicability Metric to Select More Reliable Predictions. J. Chem. Inf. Model. 2013, 53, 1990–2000. [Google Scholar] [CrossRef] [PubMed]
- Vorberg, S.; Tetko, I.V. Modeling the Biodegradability of Chemical Compounds Using the Online CHEmical Modeling Environment (OCHEM). Mol. Inf. 2014, 33, 73–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ksenofontov, A.A.; Lukanov, M.M.; Bocharov, P.S.; Berezin, M.B.; Tetko, I.V. Deep Neural Network Model for Highly Accurate Prediction of BODIPYs Absorption. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 267, 120577. [Google Scholar] [CrossRef] [PubMed]


| Data Set | Training Set, 5CV | Prediction of NOVEL Set, n = 335 | |||
|---|---|---|---|---|---|
| n | R2 | RMSE | R2 | RMSE | |
| Published model of Joung et al. [27] | 26,098 | 0.926 a | 31.6 a | 0.01 | 200 |
| JOUNG | 15,380 | 0.904 ± 0.003 | 31.5 ± 0.5 | 0.12 ± 0.02 | 204 ± 2 |
| COMBINED | 17,621 | 0.9 ± 0.003 | 30.1 ± 0.5 | 0.03 ± 0.01 | 21 ± 1 |
| COMBINED: JOUNG subset a | 15,380 | 0.902 ± 0.003 | 31.9 ± 0.5 | ||
| COMBINED: PORPHYRINS subset ab | 2241 | 0.43 ± 0.05 | 10.3 ± 0.7 | ||
| PORPHYRINS | 2241 | 0.8 ± 0.01 | 5.4 ± 0.2 | 0 ± 0.005 | 2.61 ± 0.1 |
| NOVEL set | 335 | 0.93 ± 0.01 | 0.5 ± 0.03 | ||
| Data Set | Training Set, 5CV | Prediction of NOVEL Set, n = 335 | |||
|---|---|---|---|---|---|
| n | R2 | RMSE | R2 | RMSE | |
| Published model of Joung et al. [27] | 12,159 | 0.795 a | 0.24 a | 0.10 | 0.89 |
| JOUNG | 7654 | 0.767 ± 0.009 | 0.286 ± 0.005 | 0.62 ± 0.02 | 0.84 ± 0.02 |
| COMBINED | 8600 | 0.806 ± 0.007 | 0.279 ± 0.005 | 0 ± 0.006 | 0.54 ± 0.02 |
| COMBINED: JOUNG subset a | 7654 | 0.765 ± 0.01 | 0.286 ± 0.005 | ||
| COMBINED: PORPHYRINS subset ab | 946 | 0.49 ± 0.03 | 0.218 ± 0.006 | ||
| PORPHYRINS | 946 | 0.52 ± 0.02 | 0.209 ± 0.006 | 0 ± 0.004 | 0.52 ± 0.02 |
| NOVEL set | 335 | 0.989 ± 0.002 | 0.042 ± 0.004 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusanov, A.I.; Dmitrieva, O.A.; Mamardashvili, N.Z.; Tetko, I.V. More Is Not Always Better: Local Models Provide Accurate Predictions of Spectral Properties of Porphyrins. Int. J. Mol. Sci. 2022, 23, 1201. https://doi.org/10.3390/ijms23031201
Rusanov AI, Dmitrieva OA, Mamardashvili NZ, Tetko IV. More Is Not Always Better: Local Models Provide Accurate Predictions of Spectral Properties of Porphyrins. International Journal of Molecular Sciences. 2022; 23(3):1201. https://doi.org/10.3390/ijms23031201
Chicago/Turabian StyleRusanov, Aleksey I., Olga A. Dmitrieva, Nugzar Zh. Mamardashvili, and Igor V. Tetko. 2022. "More Is Not Always Better: Local Models Provide Accurate Predictions of Spectral Properties of Porphyrins" International Journal of Molecular Sciences 23, no. 3: 1201. https://doi.org/10.3390/ijms23031201
APA StyleRusanov, A. I., Dmitrieva, O. A., Mamardashvili, N. Z., & Tetko, I. V. (2022). More Is Not Always Better: Local Models Provide Accurate Predictions of Spectral Properties of Porphyrins. International Journal of Molecular Sciences, 23(3), 1201. https://doi.org/10.3390/ijms23031201







