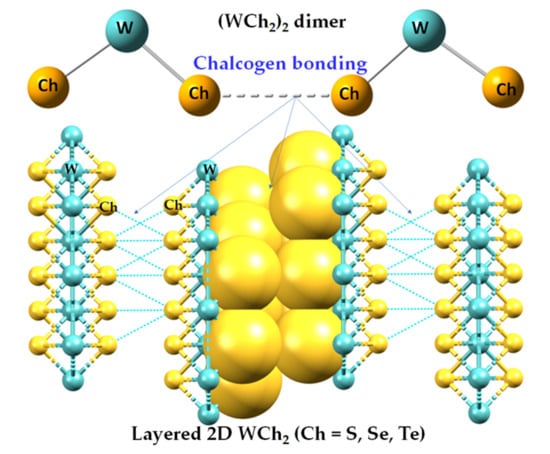
Chalcogen Bonding in the Molecular Dimers of WCh2 (Ch = S, Se, Te): On the Basic Understanding of the Local Interfacial and Interlayer Bonding Environment in 2D Layered Tungsten Dichalcogenides
Abstract
:1. Introduction
2. Results and Discussion
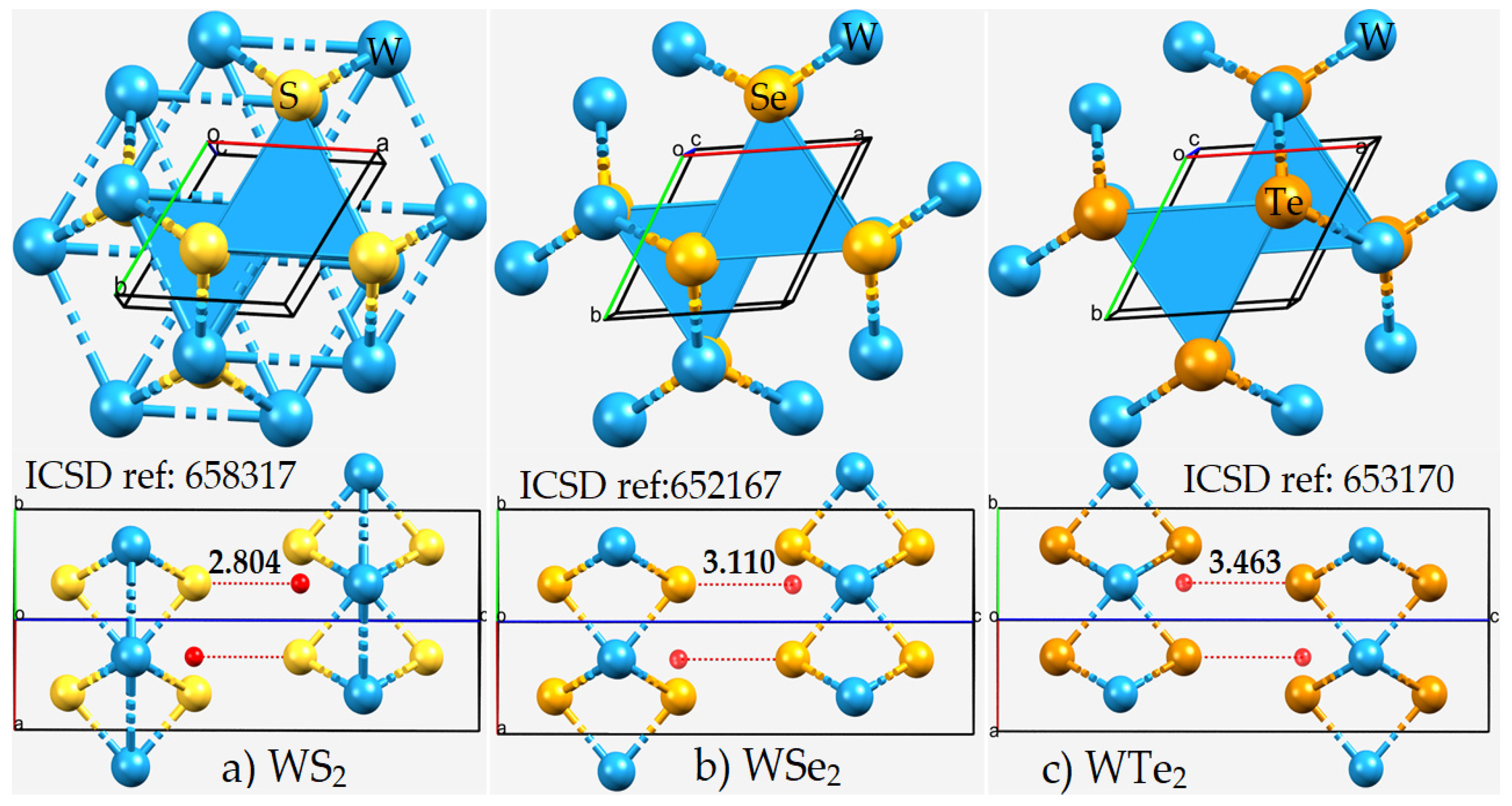
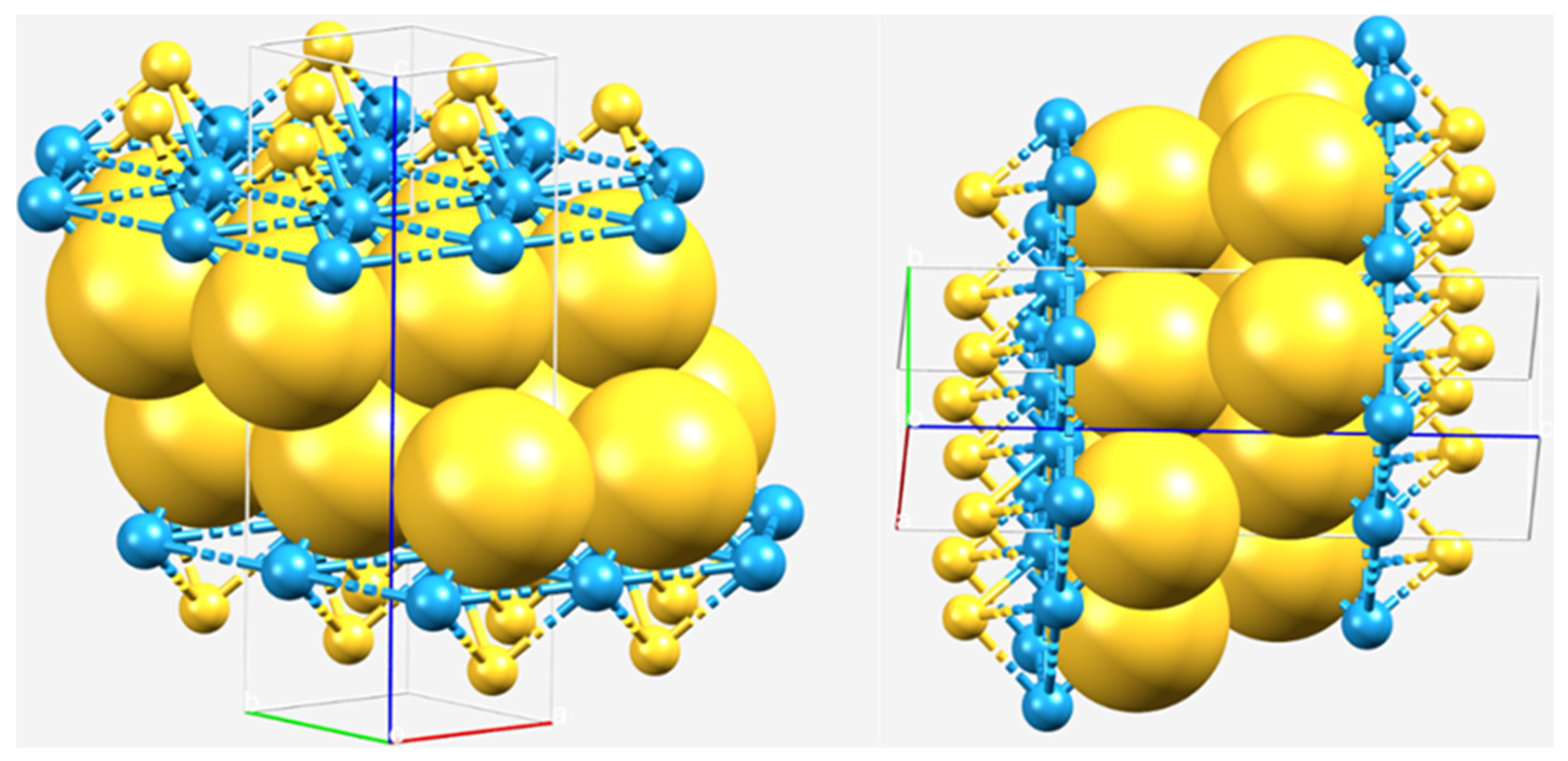
2.1. The Nature of the Interlayer/Interfacial Bonding Interactions in WCh2 Crystals
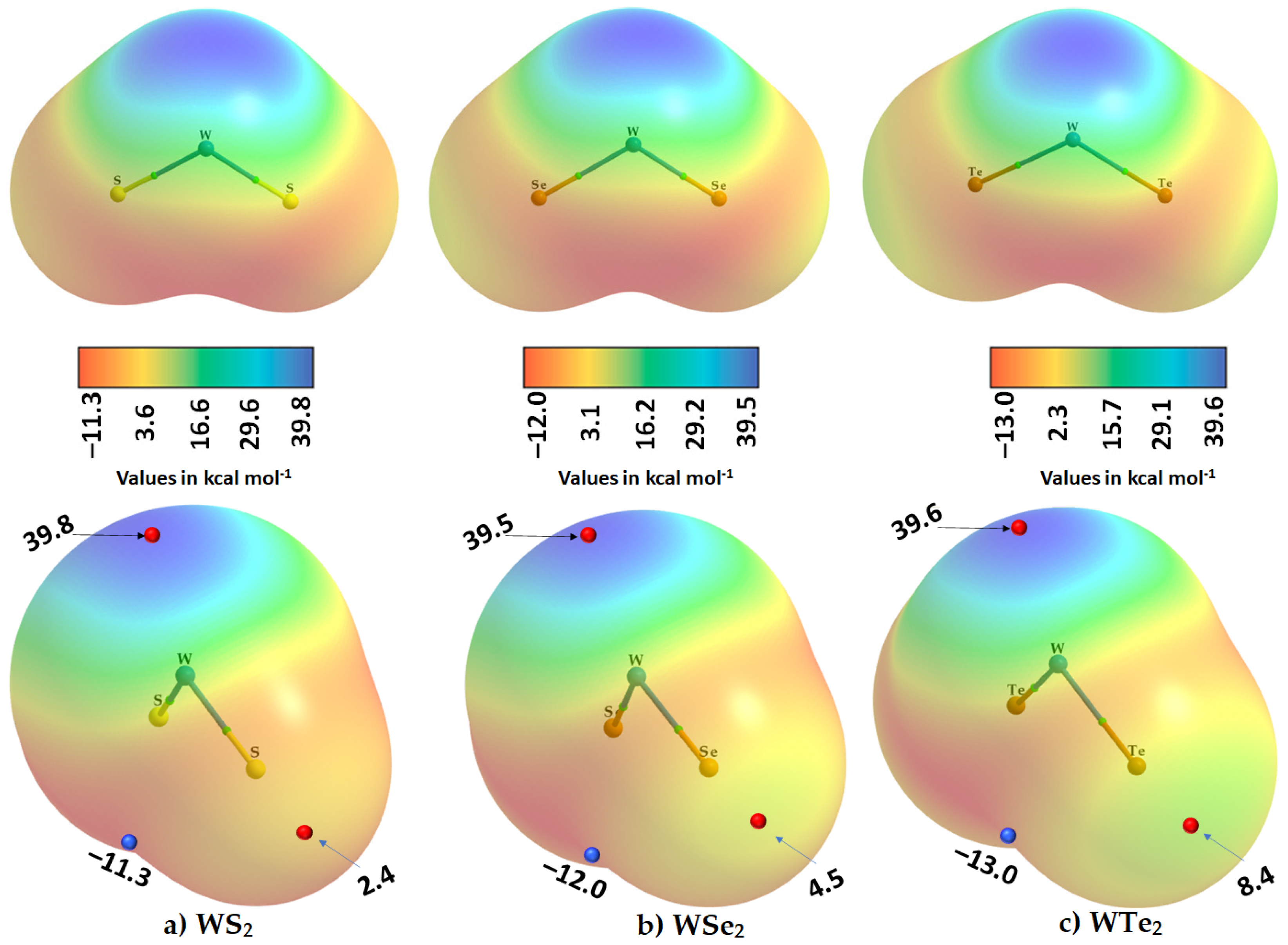
2.2. The Nature of the Potential on the Electrostatic Surfaces of Isolated WCh2 Monomers
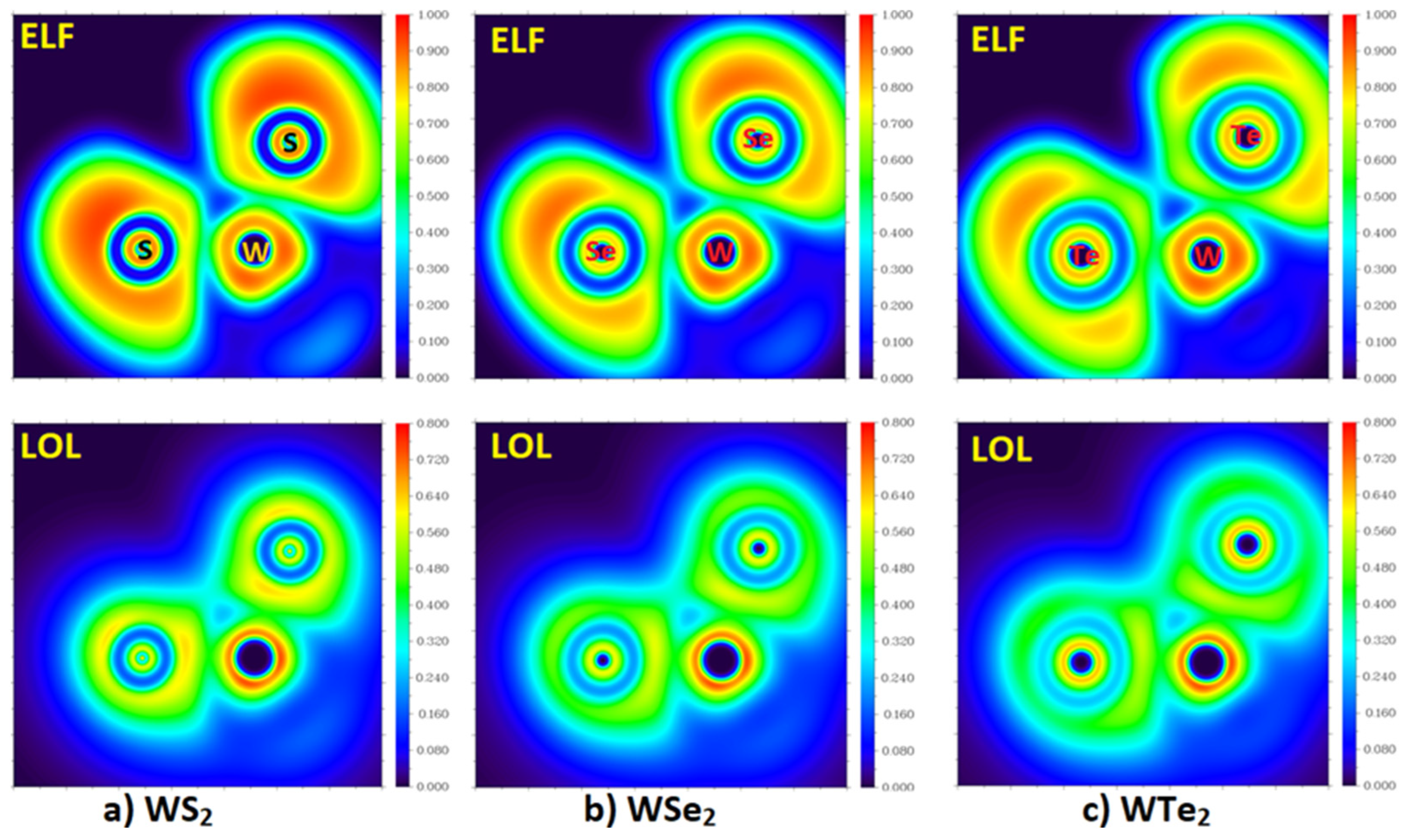
2.3. The Topologies of the Electron Localization and the Local Orbital Locator
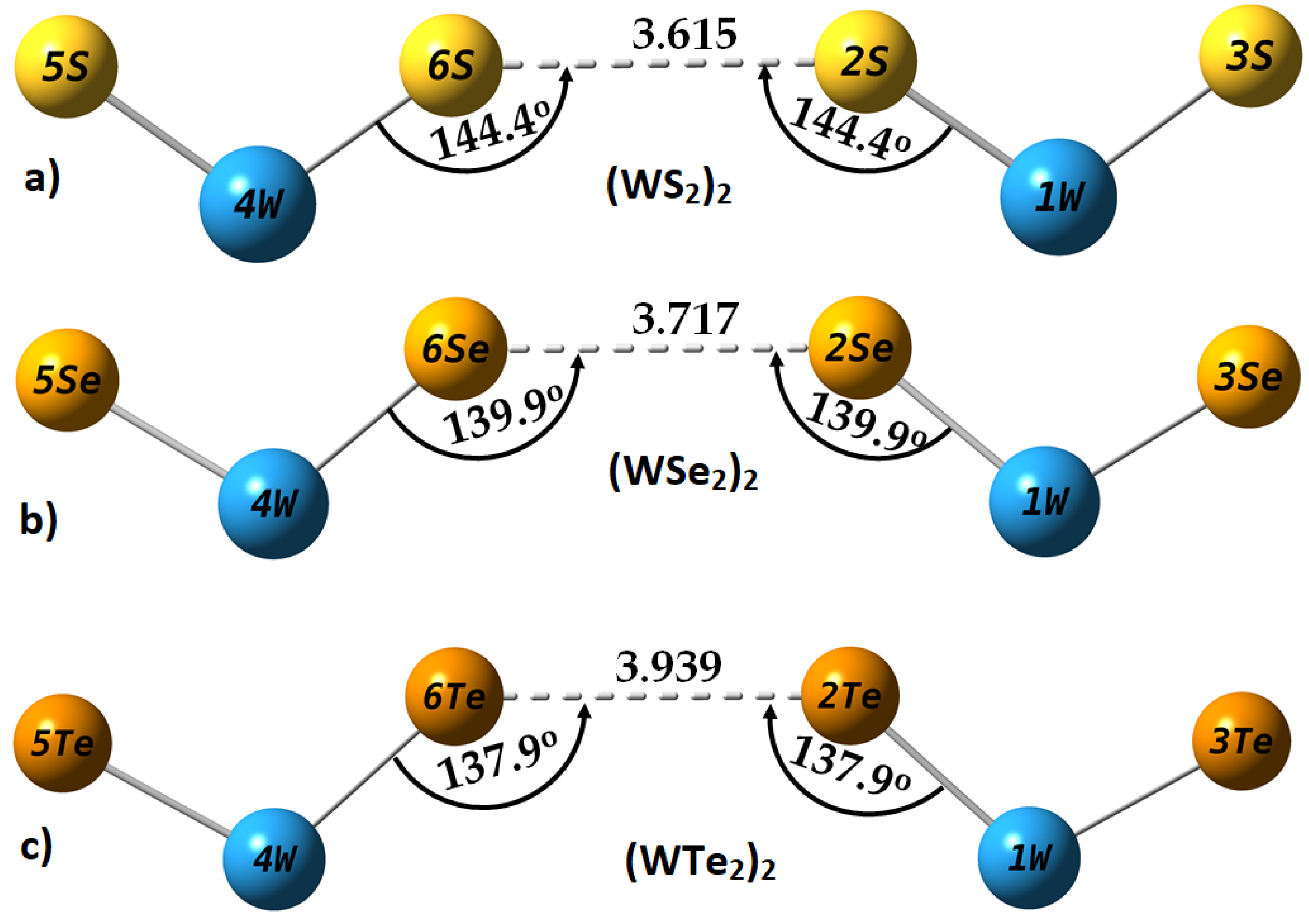
2.4. Intermolecular Properties of (WCh2)2 Dimers, and Comparison with the WCh2 Crystals
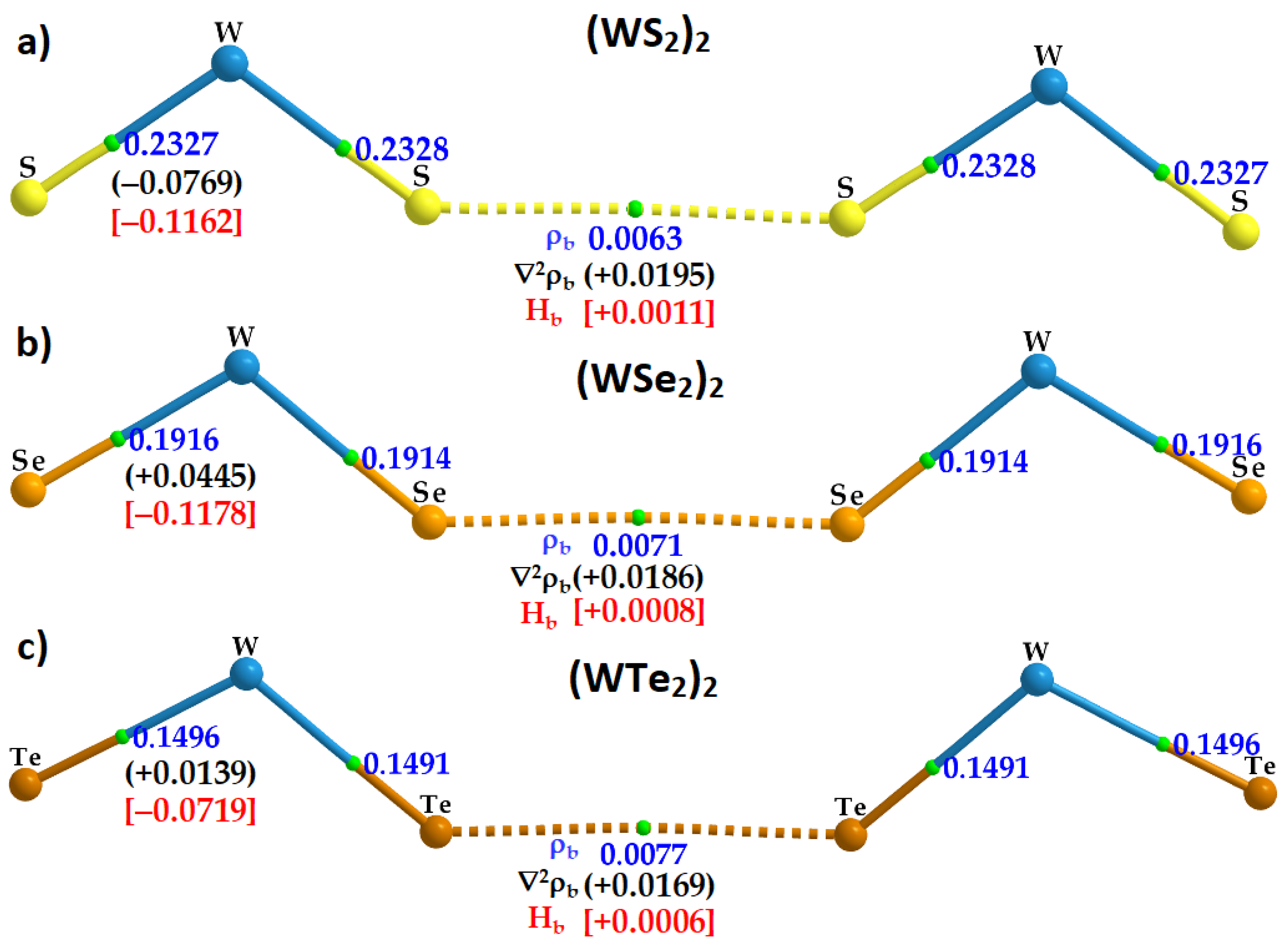
2.5. Charge Density Topological Properties of (WCh2)2 Dimers
2.6. Charge Density Based Isosurface Topologies of (WCh2)2 Dimers
2.7. Second Order Charge Transfer between the Monomers Forming (WCh2)2 Dimers and Bond Order
3. Molecular Models
4. Computational Methodology
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wilson, J.A.; Yoffe, A.D. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Mentzen, B.F.; Sienko, M.J. Preparation and X-ray study of mixed-anion tungsten dichalcogenides. Inorg. Chem. 1976, 15, 2198–2202. [Google Scholar] [CrossRef]
- Ataca, C.; Şahin, H.; Ciraci, S. Stable, Single-Layer MX2 Transition-Metal Oxides and Dichalcogenides in a Honeycomb-Like Structure. J. Phys Chem. C 2012, 116, 8983–8999. [Google Scholar] [CrossRef]
- Oliver, S.M.; Beams, R.; Krylyuk, S.; Kalish, I.; Singh, A.K.; Bruma, A.; Tavazza, F.; Joshi, J.; Stone, I.R.; Stranick, S.J.; et al. The structural phases and vibrational properties of Mo1−x WxTe2 alloys. 2D Mater. 2017, 4, 045008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duerloo, K.-A.N.; Li, Y.; Reed, E.J. Structural phase transitions in two-dimensional Mo- and W-dichalcogenide monolayers. Nat. Commun. 2014, 5, 4214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Güller, F.; Llois, A.M.; Goniakowski, J.; Noguera, C. Prediction of structural and metal-to-semiconductor phase transitions in nanoscale MoS2, WS2 and other transition metal dichalcogenide zigzag ribbons. Phys. Rev. B 2015, 91, 075407. [Google Scholar] [CrossRef]
- Dias, A.C.; Qu, F.; Azevedo, D.L.; Fu, J. Band structure of monolayer transition-metal dichalcogenides and topological properties of their nanoribbons: Next-nearest-neighbor hopping. Phys. Rev. B 2018, 98, 075202. [Google Scholar] [CrossRef]
- Agarwal, V.; Chatterjee, K. Recent advances in the field of transition metal dichalcogenides for biomedical applications. Nanoscale 2018, 10, 16365–16397. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, H.; Bai, X. Two-Dimensional Transition Metal Dichalcogenides: Synthesis, Biomedical Applications and Biosafety Evaluation. Front. Bioeng. Biotech. 2020, 8. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, L.; Chen, Q.; Miao, N.; Si, C.; Zhou, J.; Sun, Z. Quantifying the composition dependency of the ground-state structure, electronic property and phase-transition dynamics in ternary transition-metal-dichalcogenide monolayers. J. Mat. Chem. C 2020, 8, 721–733. [Google Scholar] [CrossRef]
- Fukuda, M.; Zhang, J.; Lee, Y.-T.; Ozaki, T. A structure map for AB2 type 2D materials using high-throughput DFT calculations. Mater. Adv. 2021, 2, 4392–4413. [Google Scholar] [CrossRef]
- Ju, L.; Qin, J.; Shi, L.; Yang, G.; Zhang, J.; Sun, L. Rolling the WSSe Bilayer into Double-Walled Nanotube for the Enhanced Photocatalytic Water-Splitting Performance. Nanomaterials 2021, 11, 705. [Google Scholar] [CrossRef] [PubMed]
- Intercalated Layered Materials; Lévy, F. (Ed.) D. Reidel Publishing: Dordrecht, The Netherlands, 1979. [Google Scholar]
- Inorganic and Metallic Nanotubular Materials; Kijima, T. (Ed.) Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Sokolikova, M.S.; Mattevi, C. Direct synthesis of metastable phases of 2D transition metal dichalcogenides. Chem. Soc. Rev. 2020, 49, 3952–3980. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhu, H. Two-dimensional MoS2: Properties, preparation, and applications. J. Mater. 2015, 1, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Lai, Z.; He, Q.; Tran, T.H.; Repaka, D.V.M.; Zhou, D.-D.; Sun, Y.; Xi, S.; Li, Y.; Chaturvedi, A.; Tan, C.; et al. Metastable 1T′-phase group VIB transition metal dichalcogenide crystals. Nature Mat. 2021, 20, 1113–1120. [Google Scholar] [CrossRef]
- Shi, W.; Ye, J.; Zhang, Y.; Suzuki, R.; Yoshida, M.; Miyazaki, J.; Inoue, N.; Saito, Y.; Iwasa, Y. Superconductivity Series in Transition Metal Dichalcogenides by Ionic Gating. Sci. Rep. 2015, 5, 12534. [Google Scholar] [CrossRef] [Green Version]
- Duong, D.L.; Yun, S.J.; Lee, Y.H. van der Waals Layered Materials: Opportunities and Challenges. ACS Nano 2017, 11, 11803–11830. [Google Scholar] [CrossRef]
- Zhang, X.; Teng, S.Y.; Loy, A.C.M.; How, B.S.; Leong, W.D.; Tao, X. Transition Metal Dichalcogenides for the Application of Pollution Reduction: A Review. Nanomaterials 2020, 10, 1012. [Google Scholar] [CrossRef]
- Constantinescu, G.; Kuc, A.; Heine, T. Stacking in Bulk and Bilayer Hexagonal Boron Nitride. Phys. Rev. Lett. 2013, 111, 036104. [Google Scholar] [CrossRef]
- He, J.; Hummer, K.; Franchini, C. Stacking effects on the electronic and optical properties of bilayer transition metal dichalcogenides MoS2, MoSe2, WS2 and WSe2. Phys. Rev. B 2014, 89, 075409. [Google Scholar] [CrossRef]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Dai, J.; Yao, W.; Xiao, D.; Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotech 2012, 7, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tonndorf, P.; Schmidt, R.; Böttger, P.; Zhang, X.; Börner, J.; Liebig, A.; Albrecht, M.; Kloc, C.; Gordan, O.; Zahn, D.R.T.; et al. Photoluminescence emission and Raman response of monolayer MoS2, MoSe2, and WSe2. Optics Express 2013, 21, 4908–4916. [Google Scholar] [CrossRef] [PubMed]
- Kuc, A.; Zibouche, N.; Heine, T. Influence of quantum confinement on the electronic structure of the transition metal sulfide TS2. Phys. Rev. B 2011, 83, 245213. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.; Yu, K.; Wen, Z.; Chen, J. Semiconducting graphene: Converting graphene from semimetal to semiconductor. Nanoscale 2013, 5, 1353–1368. [Google Scholar] [CrossRef] [PubMed]
- Ravindra, N.M.; Tang, W.; Rassay, S. Transition Metal Dichalcogenides Properties and Applications. In Semiconductors: Synthesis, Properties and Applications; Pech-Canul, M.I., Ravindra, N.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 333–396. [Google Scholar] [CrossRef]
- Liu, M.; Liu, W.; Liu, X.; Wang, Y.; Wei, Z. Application of transition metal dichalcogenides in mid-infrared fiber laser. Nano Select 2021, 2, 37–46. [Google Scholar] [CrossRef]
- Anju, S.; Mohanan, P.V. Biomedical applications of transition metal dichalcogenides (TMDCs). Synth. Met. 2021, 271, 116610. [Google Scholar] [CrossRef]
- Kan, M.; Wang, B.; Lee, Y.H.; Sun, Q. A density functional theory study of the tunable structure, magnetism and metal-insulator phase transition in VS2 monolayers induced by in-plane biaxial strain. Nano Res. 2015, 8, 1348–1356. [Google Scholar] [CrossRef]
- Terrones, H.; López-Urías, F.; Terrones, M. Novel hetero-layered materials with tunable direct band gaps by sandwiching different metal disulfides and diselenides. Sci. Rep. 2013, 3, 1549. [Google Scholar] [CrossRef]
- Bastos, C.M.O.; Besse, R.; Da Silva, J.L.F.; Sipahi, G.M. Ab initio investigation of structural stability and exfoliation energies in transition metal dichalcogenides based on Ti-, V-, and Mo-group elements. Phys. Rev. Mater. 2019, 3, 044002. [Google Scholar] [CrossRef] [Green Version]
- Hsu, W.-T.; Lu, L.-S.; Wang, D.; Huang, J.-K.; Li, M.-Y.; Chang, T.-R.; Chou, Y.-C.; Juang, Z.-Y.; Jeng, H.-T.; Li, L.-J.; et al. Evidence of indirect gap in monolayer WSe2. Nature Commun. 2017, 8, 929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pandey, S.K.; Das, R.; Mahadevan, P. Layer-Dependent Electronic Structure Changes in Transition Metal Dichalcogenides: The Microscopic Origin. ACS Omega 2020, 5, 15169–15176. [Google Scholar] [CrossRef] [PubMed]
- Javaid, M.; Drumm, D.W.; Russo, S.P.; Greentree, A.D. A study of size-dependent properties of MoS2 monolayer nanoflakes using density-functional theory. Sci. Rep. 2017, 7, 9775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva-Guillén, J.Á.; San-Jose, P.; Roldán, R. Electronic Band Structure of Transition Metal Dichalcogenides from Ab Initio and Slater–Koster Tight-Binding Model. Appl. Sci. 2016, 6, 284. [Google Scholar] [CrossRef] [Green Version]
- Khalatbari, H.; Vishkayi, S.I.; Oskouian, M.; Soleimani, H.R. Band structure engineering of NiS2 monolayer by transition metal doping. Sci. Rep. 2021, 11, 5779. [Google Scholar] [CrossRef] [PubMed]
- Förste, J.; Tepliakov, N.V.; Kruchinin, S.Y.; Lindlau, J.; Funk, V.; Förg, M.; Watanabe, K.; Taniguchi, T.; Baimuratov, A.S.; Högele, A. Exciton g-factors in monolayer and bilayer WSe2 from experiment and theory. Nature Commun. 2020, 11, 4539. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Marques, H.M.; Varadwaj, A.; Yamashita, K. Chalcogen···Chalcogen Bonding in Molybdenum Disulfide, Molybdenum Diselenide and Molybdenum Ditelluride Dimers as Prototypes for a Basic Understanding of the Local Interfacial Chemical Bonding Environment in 2D Layered Transition Metal Dichalcogenides. Inorganics 2022, 10, 11. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215. [Google Scholar]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. Available online: https://www.basissetexchange.org/ (accessed on 12 October 2021). [CrossRef]
- Aakeroy, C.B.; Bryce, D.L.; Desiraju, R.G.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the chalcogen bond (IUPAC Recommendations 2019). Pure Appl. Chem. 2019, 91, 1889–1892. [Google Scholar] [CrossRef]
- Glendening, E.E.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO (Natural Bond Orbital), 3.1; as Implemented in GAUSSIAN 03; Gaussian Inc.: Pittsburg, PA, USA, 2004. [Google Scholar]
- Reed, A.E.; Weinhold, F. On the role of d orbitals in sulfur hexafluoride. J. Am. Chem. Soc. 1986, 108, 3586–3593. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Lu, T.; Chen, Q. Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions. Chemistry–Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Lefebvre, C.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations. ChemPhysChem 2018, 19, 724–735. [Google Scholar] [CrossRef]
- Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Hénon, E. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density. Phys. Chem. Chem. Phys. 2017, 19, 17928–17936. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions? Molecules 2019, 24, 379. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Does Chlorine in CH3Cl Behave as a Genuine Halogen Bond Donor? Crystals 2020, 10, 146. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Alvarez, S. A cartography of the van der Waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Murray, J.S. The use and misuse of van der Waals radii. Struct. Chem. 2021, 32, 623–629. [Google Scholar] [CrossRef]
- Trabesinger, A. How many kisses? Nature Phys. 2007, 3, 223. [Google Scholar] [CrossRef]
- Hermann, A.; Lein, M.; Schwerdtfeger, P. The Search for the Species with the Highest Coordination Number. Angew Chem. Int. Edn. 2007, 46, 2444–2447. [Google Scholar] [CrossRef] [PubMed]
- Trombach, L.; Schwerdtfeger, P. Gregory-Newton problem for kissing sticky spheres. Phys. Rev. E 2018, 98, 033311. [Google Scholar] [CrossRef] [Green Version]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. WIREs Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Janjić, G.V.; Zarić, S.D. σ-Hole interactions of covalently-bonded nitrogen, phosphorus and arsenic: A survey of crystal structures. Crystals 2014, 4, 12–31. [Google Scholar] [CrossRef] [Green Version]
- Bauzá, A.; Seth, S.K.; Frontera, A. Molecular electrostatic potential and “atoms-in-molecules” analyses of the interplay between π-hole and lone pair···π/X–H···π/metal···π interactions. J. Comp. Chem. 2018, 39, 458–463. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A. Electrostatically enhanced F•••F interactions through hydrogen bonding, halogen bonding and metal coordination: An ab initio study. Phys. Chem. Chem. Phys. 2016, 18, 20381–20388. [Google Scholar] [CrossRef] [Green Version]
- Ghafouri, R.; Ektefa, F. Exploring the Mechanism of Reactions of SiX3 and CX3 Radicals with Si20X20 Fullerenes (X = H, F): A Density Functional Study. J. Clust. Sci. 2016, 27, 1719–1728. [Google Scholar] [CrossRef]
- Loveday, O.; Echeverría, J. Methyl groups as widespread Lewis bases in noncovalent interactions. Nature Commun. 2021, 12, 5030. [Google Scholar] [CrossRef]
- Zhou, P.-P.; Qiu, W.-Y.; Liu, S.; Jin, N.-Z. Halogen as halogen-bonding donor and hydrogen-bonding acceptor simultaneously in ring-shaped H3N·X(Y)·HF (X = Cl, Br and Y = F, Cl, Br) Complexes. Phys. Chem. Chem. Phys. 2011, 13, 7408–7418. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Do surfaces of positive electrostatic potential on different halogen derivatives in molecules attract? like attracting like! J. Comput. Chem. 2018, 39, 343–350. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. A DFT assessment of some physical properties of iodine-centered halogen bonding and other non-covalent interactions in some experimentally reported crystal geometries. Phys. Chem. Chem. Phys. 2018, 20, 15316–15329. [Google Scholar] [CrossRef]
- McDowell, S.A.C.; Dong, W.; Wang, Y.; Li, Q. Noncovalent Interactions in Complexes Involving the Cyclic C2H2X (X=O, S, Se) Molecules and the Lewis Acids YF (Y=F, Cl, Br, H). ChemistrySelect 2019, 4, 9506–9515. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Halogen bonding interaction of chloromethane withseveral nitrogen donating molecules: Addressing thenature of the chlorine surface σ-hole. Phys. Chem. Chem. Phys. 2014, 16, 19573–19589. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Schmider, H.L.; Becke, A.D. Chemical content of the kinetic energy density. J. Mol. Str. THEOCHEM 2000, 527, 51–61. [Google Scholar] [CrossRef]
- Schmider, H.L.; Becke, A.D. Two functions of the density matrix and their relation to the chemical bond. J. Chem. Phys. 2002, 116, 3184–3193. [Google Scholar] [CrossRef]
- Ruedenberg, K. The Physical Nature of the Chemical Bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
- Bacskay, G.B.; Nordholm, S.; Ruedenberg, K. The Virial Theorem and Covalent Bonding. J. Phys. Chem. A 2018, 122, 7880–7893. [Google Scholar] [CrossRef]
- Carpio-Martínez, P.; Barquera-Lozada, J.E.; Pendás, A.M.; Cortés-Guzmán, F. Laplacian of the Hamiltonian Kinetic Energy Density as an Indicator of Binding and Weak Interactions. ChemPhysChem 2020, 21, 194–203. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, C.; Wen, C.; Zhang, M.; Geng, Y.; Liu, X.; Su, Z. The Al≡Al triple bond in Al2X5+ and Al2X62+ (X = Li, Na) clusters with multiple alkali metal coordination. New J. Chem. 2020, 44, 21119–21124. [Google Scholar] [CrossRef]
- Gatti, C. Chemical bonding in crystals: New directions. Z. Kristall. Cryst. Mater. 2005, 220, 399–457. [Google Scholar] [CrossRef]
- Savin, A.; Jepsen, O.; Flad, J.; Andersen, O.K.; Preuss, H.; von Schnering, H.G. Electron Localization in Solid-State Structures of the Elements: The Diamond Structure. Angew. Chem. Intl. Ed. Eng. 1992, 31, 187–188. [Google Scholar] [CrossRef]
- Jacobsen, H. Localized-orbital locator (LOL) profiles of chemical bonding. Can. J. Chem. 2008, 86, 695–702. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Johnson, S.; Tang, T.H.; Popelier, P.L.A. The Electron Pair. J. Phys. Chem. 1996, 100, 15398–15415. [Google Scholar] [CrossRef]
- Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer: Berlin, Germany, 1994. [Google Scholar]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond: In Structural Chemistry and Biology; Oxford University Press: Oxford, UK, 2001; Volume 19. [Google Scholar]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Hybrid organic–inorganic CH3NH3PbI3 perovskite building blocks: Revealing ultra-strong hydrogen bonding and mulliken inner complexes and their implications in materials design. J. Comput. Chem. 2017, 38, 2802–2818. [Google Scholar] [CrossRef]
- Cossard, A.; Desmarais, J.K.; Casassa, S.; Gatti, C.; Erba, A. Charge Density Analysis of Actinide Compounds from the Quantum Theory of Atoms in Molecules and Crystals. J. Phys. Chem. Lett. 2021, 12, 1862–1868. [Google Scholar] [CrossRef]
- Saleh , G.; Gatti , C.; Lo Presti, L.; Contreras-García, J. Revealing Non-covalent Interactions in Molecular Crystals through Their Experimental Electron Densities. Chem. Eur. J. 2012, 18, 15523–15536. [Google Scholar] [CrossRef]
- Hathwar, V.R.; Guru Row, T.N. Charge Density Analysis of Heterohalogen (Cl···F) and Homohalogen (F···F) Intermolecular Interactions in Molecular Crystals: Importance of the Extent of Polarizability. Cryst. Growth Des. 2011, 11, 1338–1346. [Google Scholar] [CrossRef]
- Thomas, S.P.; Pavan, M.S.; Guru Row, T.N. Experimental evidence for ‘carbon bonding’ in the solid state from charge density analysis. Chem. Commun. 2014, 50, 49–51. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Matta, C.F. Bonding to titanium. Inorg. Chem. 2001, 40, 5603–5611. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Otaki, H.; Ando, K. Atoms-in-molecules analysis of the effect of intermolecular interactions on dielectric properties in hydrogen-bonded material 5-bromo-9-hydroxyphenalenone. Int. J. Quant. Chem. 2013, 113, 386–392. [Google Scholar] [CrossRef] [Green Version]
- Aljameedi, K.; Karton, A.; Jayatilaka, D.; Thomas, S.P. Bond orders for intermolecular interactions in crystals: Charge transfer, ionicity and the effect on intramolecular bonds. IUCrJ 2018, 5, 635–646. [Google Scholar] [CrossRef]
- Koch, U.; Popelier, P.L.A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Pyykkö, P. Strong Closed-Shell Interactions in Inorganic Chemistry. Chem. Rev. 1997, 97, 597–636. [Google Scholar] [CrossRef]
- Love, I. An AIM analysis of S,O bonds. J. Phys. Chem. A 2009, 113, 2640–2646. [Google Scholar] [CrossRef]
- Love, I. Characteristics of Multiple N,O Bonds. J. Phys. Chem. A 2006, 110, 10507–10512. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, J.; Zhu, C.; Miao, J.; Huang, Y.; Heinz, H. Interpretable molecular models for molybdenum disulfide and insight into selective peptide recognition. Chem. Sci. 2020, 11, 8708–8722. [Google Scholar] [CrossRef]
- Neal, S.N.; Li, S.; Birol, T.; Musfeldt, J.L. Chemical bonding and Born charge in 1T-HfS2. npj 2D Mater. Appl. 2021, 5, 45. [Google Scholar] [CrossRef]
- Ghorbani-Asl, M.; Zibouche, N.; Wahiduzzaman, M.; Oliveira, A.F.; Kuc, A.; Heine, T. Electromechanics in MoS2 and WS2: Nanotubes vs. monolayers. Sci. Rep. 2013, 3, 2961. [Google Scholar] [CrossRef] [Green Version]
- Ghorbani-Asl, M.; Borini, S.; Kuc, A.; Heine, T. Strain-dependent modulation of conductivity in single-layer transition-metal dichalcogenides. Phys. Rev. B 2013, 87, 235434. [Google Scholar] [CrossRef] [Green Version]
- Vera-Hidalgo, M.; Giovanelli, E.; Navío, C.; Pérez, E.M. Mild Covalent Functionalization of Transition Metal Dichalcogenides with Maleimides: A “Click” Reaction for 2H-MoS2 and WS2. J. Am. Chem. Soc. 2019, 141, 3767–3771. [Google Scholar] [CrossRef]
- Ghatak, K.; Kang, K.N.; Yang, E.-H.; Datta, D. Controlled edge dependent stacking of WS2-WS2 Homo- and WS2-WSe2 Hetero-structures: A Computational Study. Sci. Rep. 2020, 10, 1648. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Unusual bonding modes of perfluorobenzene in its polymeric (dimeric, trimeric and tetrameric) forms: Entirely negative fluorine interacting cooperatively with entirely negative fluorine. Phys. Chem. Chem. Phys. 2015, 17, 31624–31645. [Google Scholar] [CrossRef]
- Zhao, T.; Zhou, J.; Wang, Q.; Jena, P. Like charges attract? J. Phys. Chem. Lett. 2016, 7, 2689–2695. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Jin, B.-Y. Can an entirely negative fluorine in a molecule, viz. perfluorobenzene, interact attractively with the entirely negative site(s) on another molecule(s)? Like liking like! RSC Adv. 2016, 6, 19098–19110. [Google Scholar] [CrossRef]
- Klein, J.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. New Way for Probing Bond Strength. J. Phys. Chem. A 2020, 124, 1850–1860. [Google Scholar] [CrossRef]
- de Silva, P.; Corminboeuf, C. Simultaneous Visualization of Covalent and Noncovalent Interactions Using Regions of Density Overlap. J. Chem. Theory Comput. 2014, 10, 3745–3756. [Google Scholar] [CrossRef]
- Zupan, A.; Perdew, J.P.; Burke, K.; Causà, M. Density-gradient analysis for density functional theory: Application to atoms. Int. J. Quant. Chem. 1997, 61, 835–845. [Google Scholar] [CrossRef]
- Zupan, A.; Burke, K.; Ernzerhof, M.; Perdew, J.P. Distributions and averages of electron density parameters: Explaining the effects of gradient corrections. J. Chem. Phys. 1997, 106, 10184–10193. [Google Scholar] [CrossRef] [Green Version]
- Lu, T.; Chen, F. A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Matito, E.; Poater, J.; Solà, M.; Duran, M.; Salvador, P. Comparison of the AIM delocalization index and the Mayer and Fuzzy atom bond orders. J. Phys. Chem. A 2005, 109, 9904–9910. [Google Scholar] [CrossRef]
- Mayer, I.; Salvador, P. Overlap populations, bond orders and valences for ‘fuzzy’ atoms. Chem. Phys. Lett. 2004, 383, 368–375. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Stephens, M.E. Spatial localization of the electronic pair and number distributions in molecules. J. Am. Chem. Soc. 1975, 97, 7391–7399. [Google Scholar] [CrossRef]
- Wang, Y.-G.; Werstiuk, N.H. A practical and efficient method to calculate AIM localization and delocalization indices at post-HF levels of theory. J. Comp. Chem. 2003, 24, 379–385. [Google Scholar] [CrossRef]
- Mayer, I. Charge, bond order and valence in the AB initio SCF theory. Chem. Phys. Lett. 1983, 97, 270–274. [Google Scholar] [CrossRef]
- Outeiral, C.; Vincent, M.A.; Martín Pendás, Á.; Popelier, P.L.A. Revitalizing the concept of bond order through delocalization measures in real space. Chem. Sci. 2018, 9, 5517–5529. [Google Scholar] [CrossRef] [Green Version]
- Brixner, L.H. Preparation and properties of the single crystalline AB2-type selenides and tellurides of niobium, tantalum, molybdenum and tungsten. J. Inorg. Nucl. Chem. 1962, 24, 257–263. [Google Scholar] [CrossRef]
- Yanaki, A.A.; Obolonchik, V.A. Preparation of transition-metal tellurides by means of hydrogen telluride. Inorg. Mater. 1973, 9, 1855–1858. [Google Scholar]
- Perrozzi, F.; Emamjomeh, S.M.; Paolucci, V.; Taglieri, G.; Ottaviano, L.; Cantalini, C. Thermal stability of WS2 flakes and gas sensing properties of WS2/WO3 composite to H2, NH3 and NO2. Sens. Actuators B Chem. 2017, 243, 812–822. [Google Scholar] [CrossRef]
- Carlson, R.K.; Truhlar, D.G.; Gagliardi, L. Multiconfiguration Pair-Density Functional Theory: A Fully Translated Gradient Approximation and Its Performance for Transition Metal Dimers and the Spectroscopy of Re2Cl82−. J. Chem. Theory Comp. 2015, 11, 4077–4085. [Google Scholar] [CrossRef]
- Duan, C.; Chen, S.; Taylor, M.G.; Liu, F.; Kulik, H.J. Machine learning to tame divergent density functional approximations: A new path to consensus materials design principles. Chem. Sci. 2021, 12, 13021–13036. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Verma, P.; Jin, X.; Truhlar, D.G.; He, X. Revised M06 density functional for main-group and transition-metal chemistry. Proc. Nail. Acad. Sci. USA 2018, 115, 10257–10262. [Google Scholar] [CrossRef] [Green Version]
- Kepp, K.P. Accuracy of theoretical catalysis from a model of iron-catalyzed ammonia synthesis. Commun. Chem. 2018, 1, 63. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Pople, J.A. The Lennard-Jones lecture. Intermolecular binding. Faraday Discuss. 1982, 73, 7–17. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef] [Green Version]
- Santra, G.; Martin, J.M.L. What Types of Chemical Problems Benefit from Density-Corrected DFT? A Probe Using an Extensive and Chemically Diverse Test Suite. J. Chem. Theory Comp. 2021, 17, 1368–1379. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, J.F.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154119. [Google Scholar] [CrossRef] [Green Version]
- Keith, T.A. AIMAll (Version 19.10.12); TK Gristmill Software: Overland Park, KS, USA, 2016; Available online: https://aim.tkgristmill.com (accessed on 20 October 2021).
- Humphrey, W.; Dalke, A.; Schulten, K. VMD-Visual Molecular Dynamics. J. Molec. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]





| Method/Basis-Set | Dimer | r(Ch2···Ch6) | ∠W1–Ch2···Ch6 | ∠W4–Ch6··Ch2 | μ | ∆E | ∆E(BSSE) |
|---|---|---|---|---|---|---|---|
| M06-2X/LANL08 | (WTe2)2 | 4.033 | 125.2 | 125.2 | 3.4 | −1.07 | −0.72 |
| (WSe2)2 | 3.766 | 136.4 | 136.4 | 5.3 | −0.73 | −0.43 | |
| (WS2)2 | 3.603 | 147.6 | 147.6 | 6.6 | −0.31 | −0.09 | |
| M06-2X-D3 c/LANL08 | (WTe2)2 | 4.034 | 125.4 | 125.4 | 3.4 | −1.18 | −0.83 |
| (WSe2)2 | 3.769 | 136.6 | 136.6 | 5.3 | −0.83 | −0.53 | |
| (WS2)2 | 3.602 | 147.6 | 147.6 | 6.6 | −0.38 | −0.17 | |
| M06-2X/def2-TZVPPD | (WTe2)2 | 3.939 | 138.0 | 138 | 4.2 | −0.98 | −0.85 |
| (WSe2)2 | 3.786 | 139.9 | 139.9 | 5.0 | −0.47 | −0.37 | |
| (WS2)2 | 3.621 | 144.4 | 144.4 | 5.3 | −0.23 | −0.12 | |
| M06-2X/Aug-cc-pVTZ(-PP) | (WTe2)2 | 3.938 | 137.9 | 137.9 | 4.1 | −0.98 | −0.90 |
| (WSe2)2 | 3.717 | 139.9 | 139.9 | 4.7 | −0.55 | −0.43 | |
| (WS2)2 | 3.615 | 144.4 | 144.4 | 5.3 | −0.24 | −0.12 |
| Dimer | M06-2X | M062X-D3 b | MP2(Full) | B97-D3(BJ) c | PW6B95-D3(BJ) c | B3LYP-D3(BJ) c | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ∆E | ∆E(BSSE) | ∆E | ∆E(BSSE) | ∆E | ∆E(BSSE) | ∆E | ∆E(BSSE) | ∆E | ∆E(BSSE) | ∆E | ∆E(BSSE) | |
| (WTe2)2 | −0.98 | −0.90 | −1.09 | −1.01 | −5.63 | −3.32 | −2.17 | −2.00 | −2.05 | −1.94 | −2.65 | −2.52 |
| (WSe2)2 | −0.55 | −0.43 | −0.65 | −0.54 | −5.85 | −3.66 | −1.48 | −1.37 | −1.26 | −1.16 | −1.82 | −1.73 |
| (WS2)2 | −0.24 | −0.12 | −0.32 | −0.20 | −4.16 | −2.95 | −0.92 | −0.80 | −0.81 | −0.70 | −1.25 | −1.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Chalcogen Bonding in the Molecular Dimers of WCh2 (Ch = S, Se, Te): On the Basic Understanding of the Local Interfacial and Interlayer Bonding Environment in 2D Layered Tungsten Dichalcogenides. Int. J. Mol. Sci. 2022, 23, 1263. https://doi.org/10.3390/ijms23031263
Varadwaj PR, Varadwaj A, Marques HM, Yamashita K. Chalcogen Bonding in the Molecular Dimers of WCh2 (Ch = S, Se, Te): On the Basic Understanding of the Local Interfacial and Interlayer Bonding Environment in 2D Layered Tungsten Dichalcogenides. International Journal of Molecular Sciences. 2022; 23(3):1263. https://doi.org/10.3390/ijms23031263
Chicago/Turabian StyleVaradwaj, Pradeep R., Arpita Varadwaj, Helder M. Marques, and Koichi Yamashita. 2022. "Chalcogen Bonding in the Molecular Dimers of WCh2 (Ch = S, Se, Te): On the Basic Understanding of the Local Interfacial and Interlayer Bonding Environment in 2D Layered Tungsten Dichalcogenides" International Journal of Molecular Sciences 23, no. 3: 1263. https://doi.org/10.3390/ijms23031263
APA StyleVaradwaj, P. R., Varadwaj, A., Marques, H. M., & Yamashita, K. (2022). Chalcogen Bonding in the Molecular Dimers of WCh2 (Ch = S, Se, Te): On the Basic Understanding of the Local Interfacial and Interlayer Bonding Environment in 2D Layered Tungsten Dichalcogenides. International Journal of Molecular Sciences, 23(3), 1263. https://doi.org/10.3390/ijms23031263