Molecular Dynamics Simulations of Transmembrane Cyclic Peptide Nanotubes Using Classical Force Fields, Hydrogen Mass Repartitioning, and Hydrogen Isotope Exchange Methods: A Critical Comparison
Abstract
:1. Introduction
2. Materials and Methods
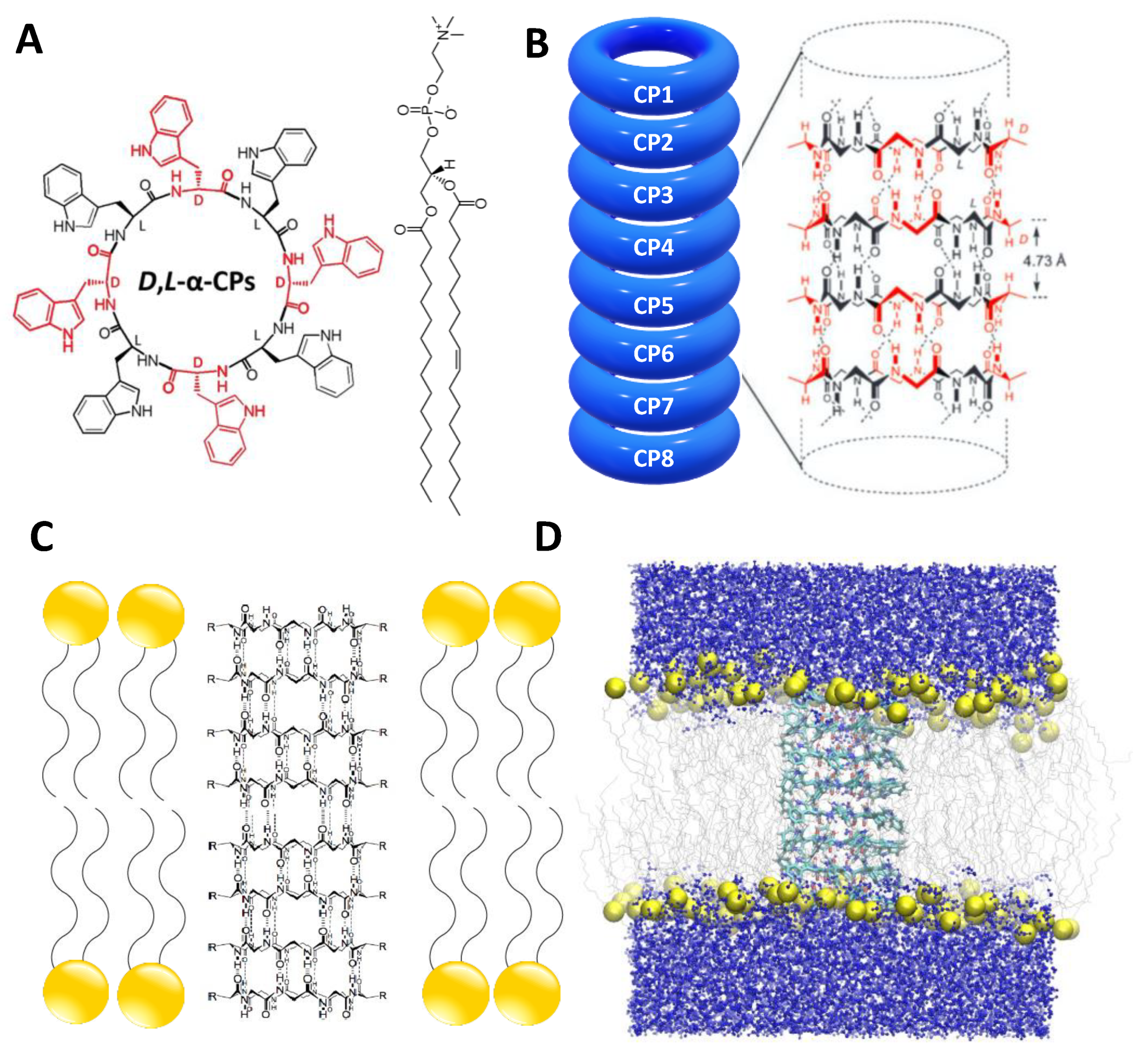
2.1. Simulation Systems and Parameters
2.2. Analysis of the Trajectories
3. Results and Discussion
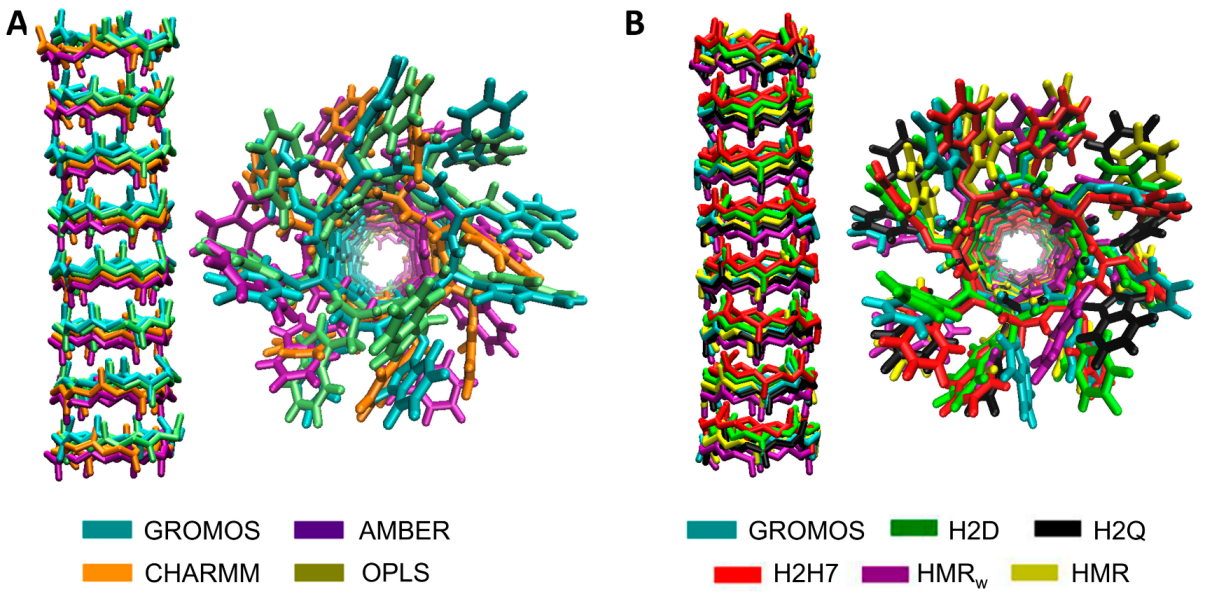
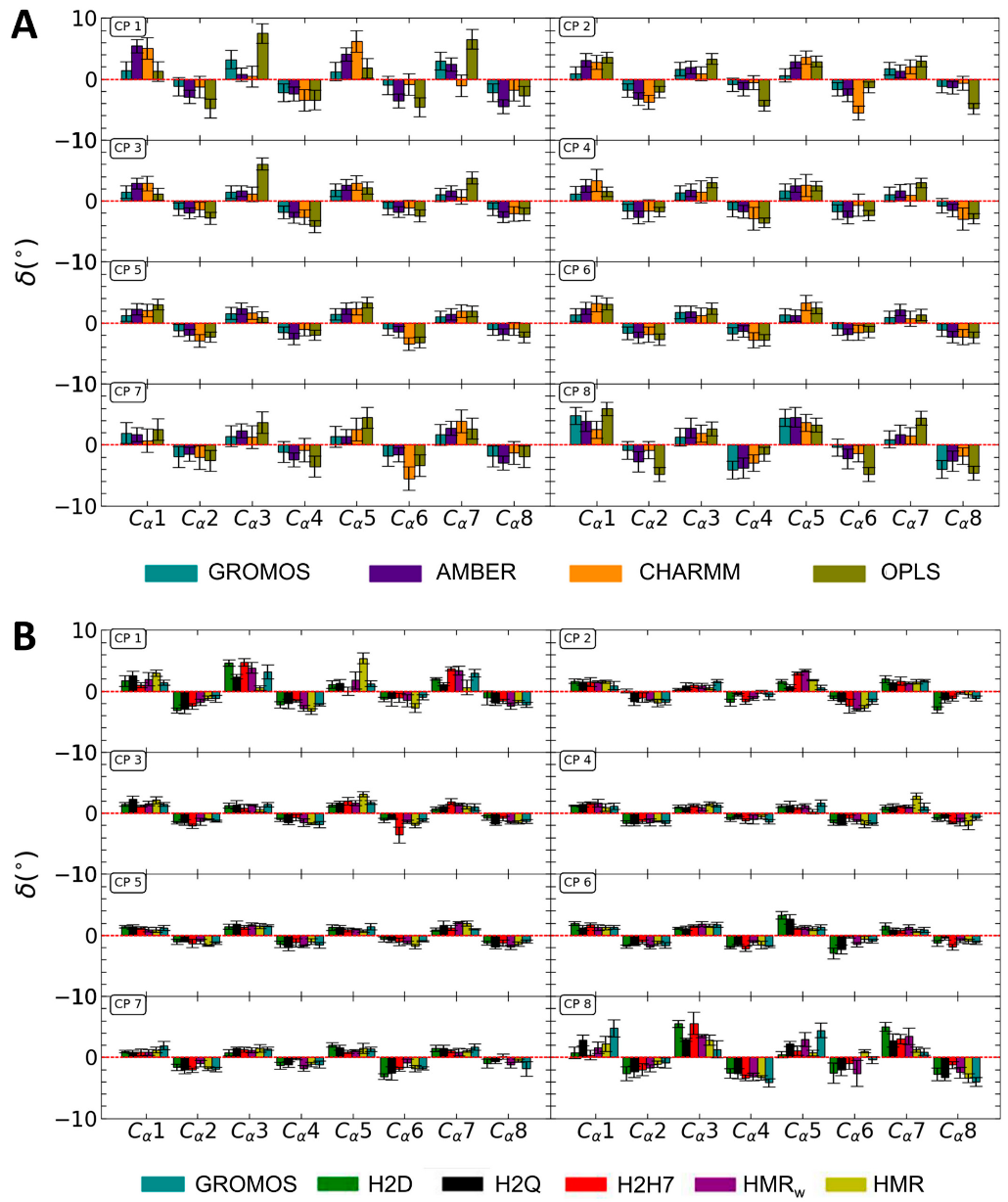
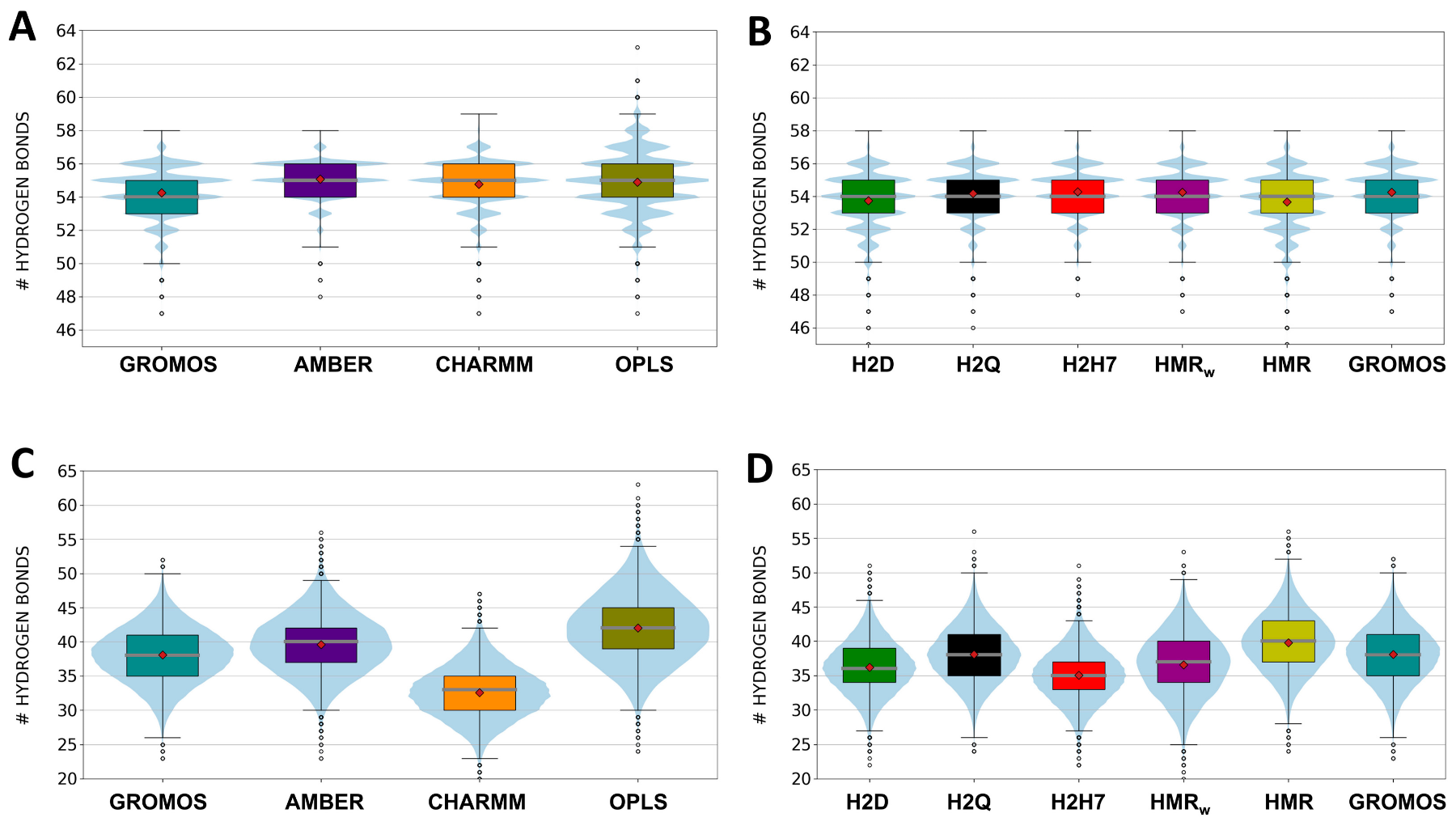
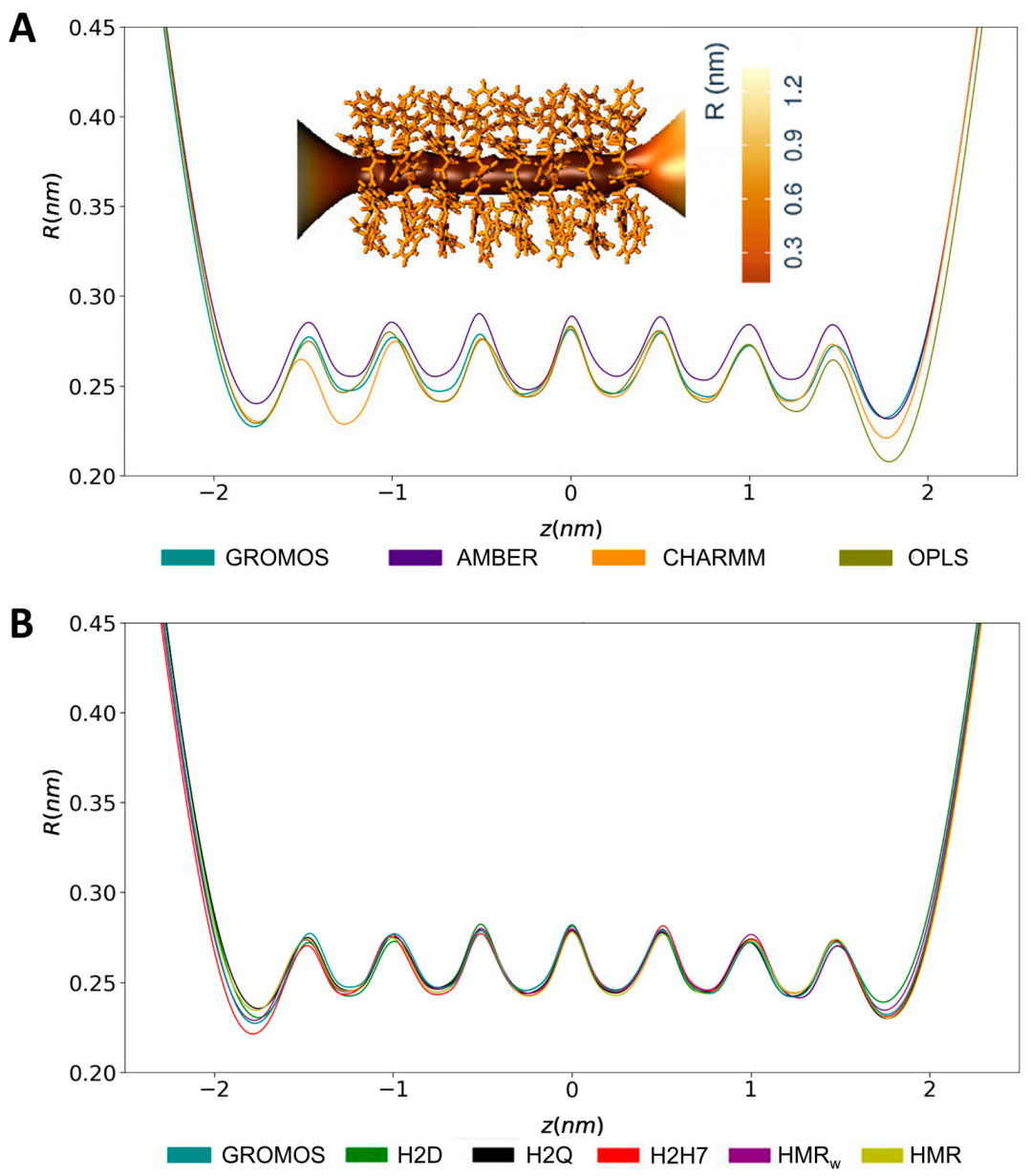
3.1. Force Field Dependence of the Structural Stability of the D,L-α-SCPN
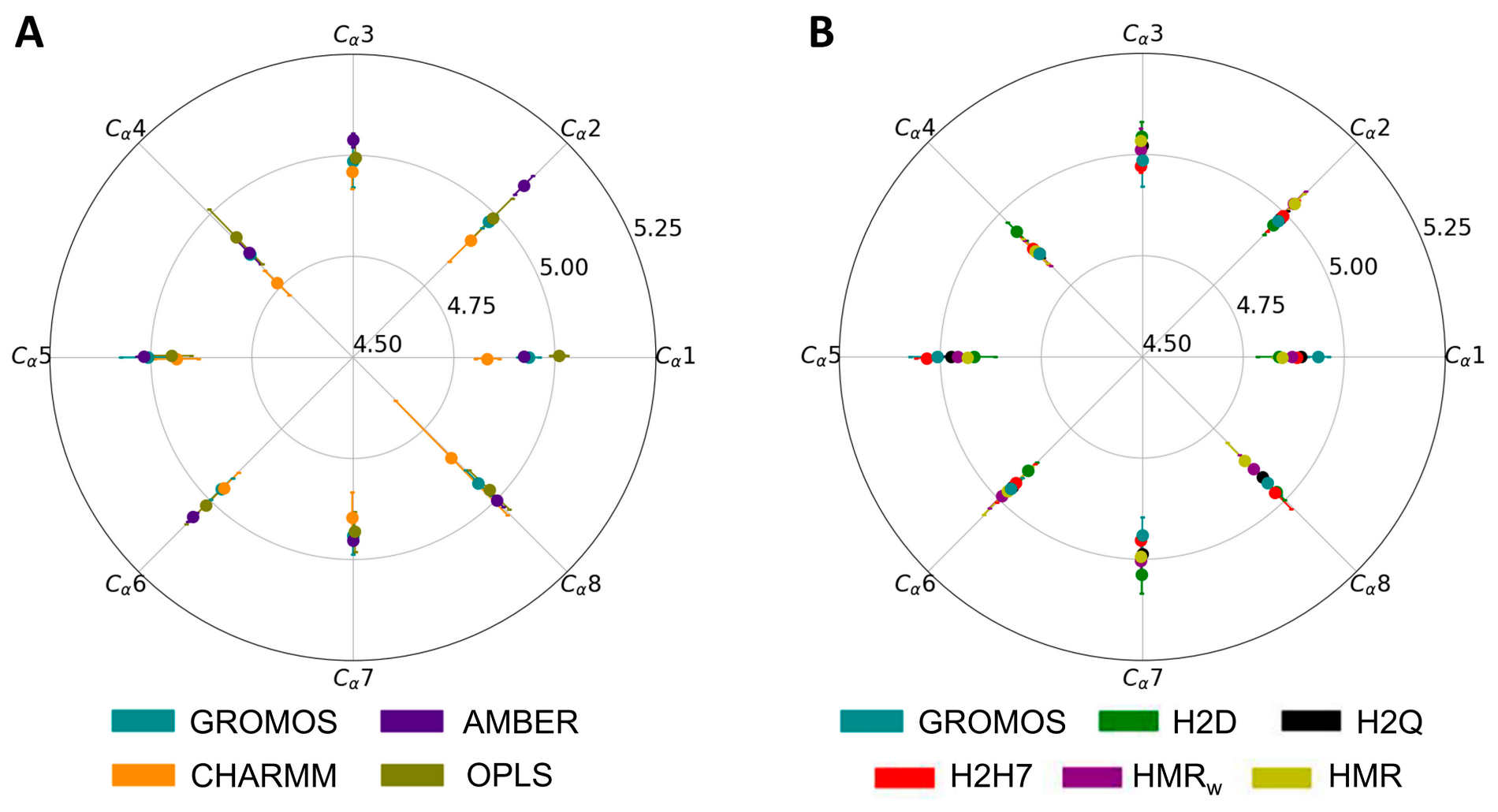
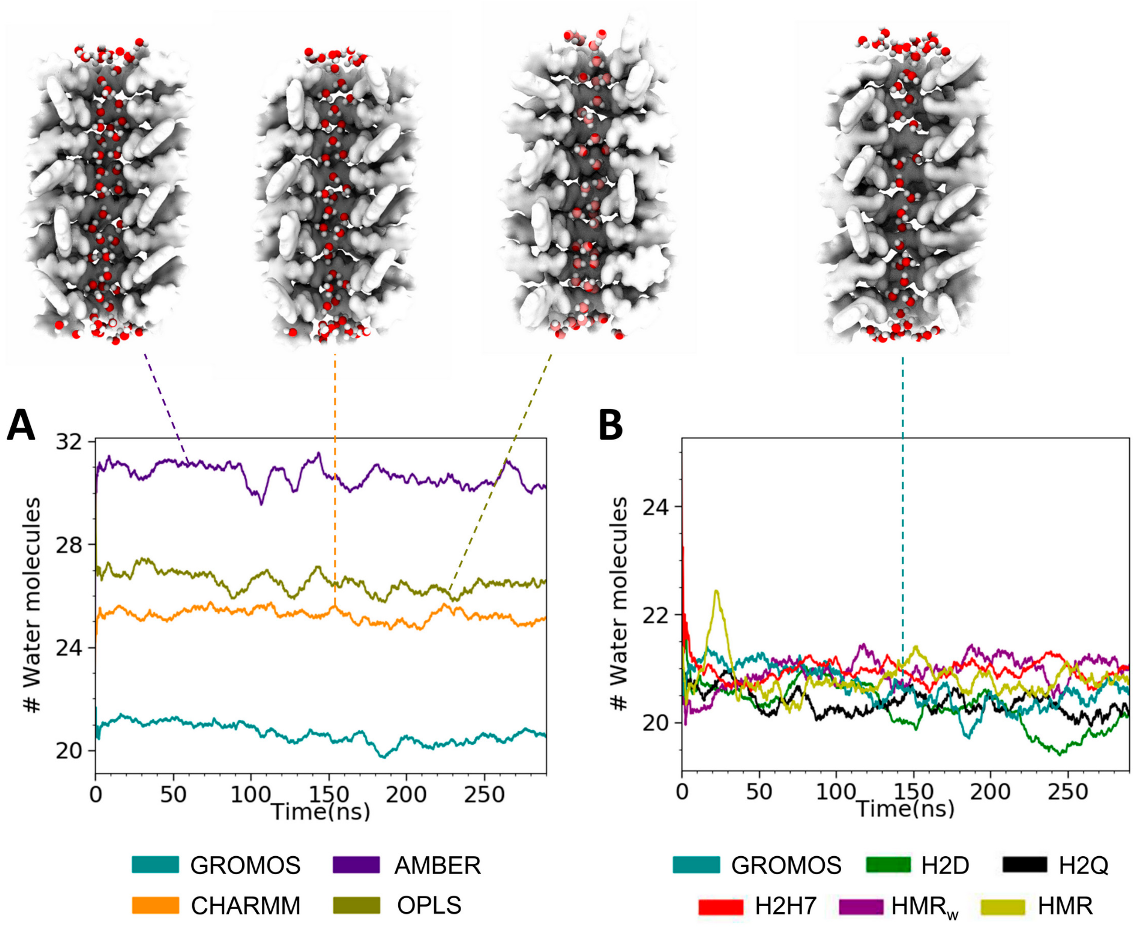
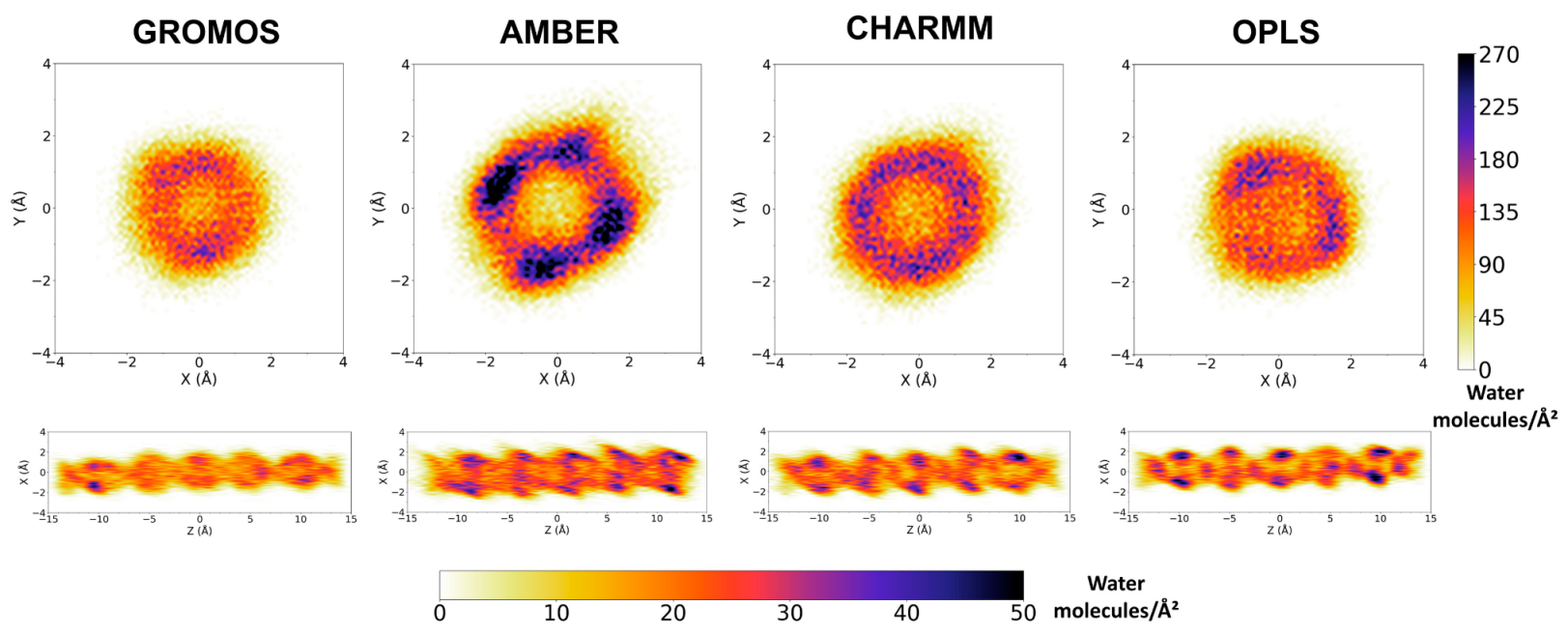
3.2. Force Field Dependence of the Structure of the Nanopores Formed by the D,L-α-SCPN
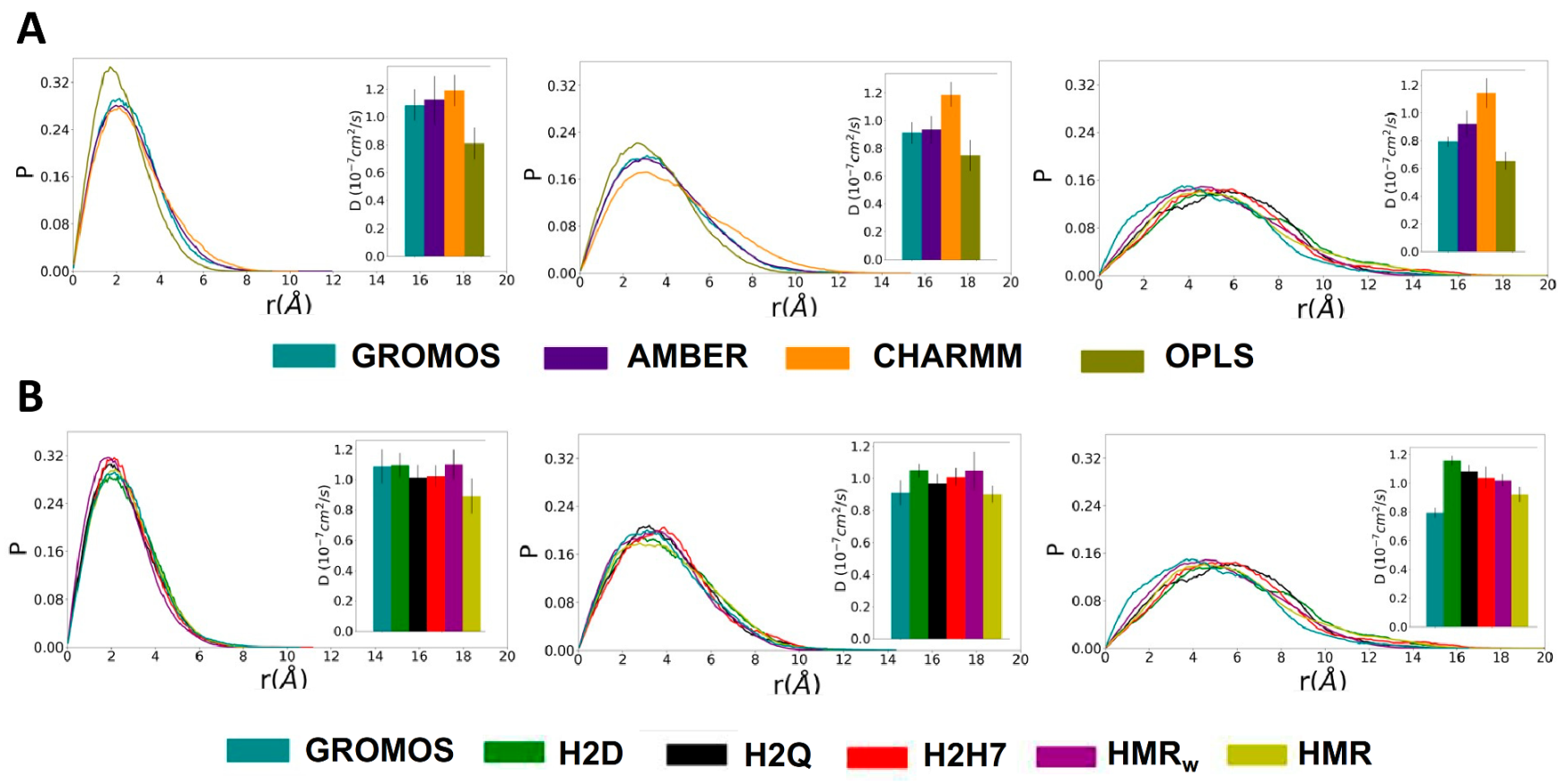
3.3. Force Field Dependence of D,L-α-SCPN Diffusion Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Claro, B.; Bastos, M.; Garcia-Fandino, R. Design and Applications of Cyclic Peptides. In Peptide Applications in Biomedicine, Biotechnology and Bioengineering; Elsevier Inc.: Amsterdam, The Netherlands, 2018; pp. 87–129. [Google Scholar] [CrossRef]
- Garcia-Fandiño, R.; Calvelo, M.; Granja, J.R. Pore- and Channel-Forming Peptides and Their Mimetics. In Comprehensive Supramolecular Chemistry II; Elsevier Inc.: Amsterdam, The Netherlands, 2017; Volume 4, pp. 539–573. [Google Scholar] [CrossRef]
- De Santis, P.; Morosetti, S.; Rizzo, R. Conformational Analysis of Regular Enantiomeric Sequences; UTC: Chattanooga, TN, USA, 1974; Volume 7. [Google Scholar]
- Ghadiri, M.R.; Granja, J.R.; Milligan, R.A.; McRee, D.E.; Khazanovich, N. Self-Assembling Organic Nanotubes Based on a Cyclic Peptide Architecture. Nature 1993, 366, 324–327. [Google Scholar] [CrossRef] [PubMed]
- Bong, D.T.; Clark, T.D.; Granja, J.R.; Ghadiri, M.R. Self-Assembling Organic Nanotubes. Angew. Chem. Int. Ed. 2001, 40, 988–1011. [Google Scholar] [CrossRef]
- García-Fandiño, R.; Amorín, M.; Granja, J.R. Synthesis of Supramolecular Nanotubes. In Supramolecular Chemistry; John Wiley & Sons, Ltd.: Chichester, UK, 2012. [Google Scholar] [CrossRef]
- Rodriguez-Vazquez, N.; Ozores, H.; Guerra, A.; Gonzalez-Freire, E.; Fuertes, A.; Panciera, M.; Priegue, J.; Outeiral, J.; Montenegro, J.; Garcia-Fandino, R.; et al. Membrane-Targeted Self-Assembling Cyclic Peptide Nanotubes. Curr. Top. Med. Chem. 2015, 14, 2647–2661. [Google Scholar] [CrossRef]
- Rodríguez-Vázquez, N.; Amorín, M.; Granja, J.R. Recent Advances in Controlling the Internal and External Properties of Self-Assembling Cyclic Peptide Nanotubes and Dimers. Org. Biomol. Chem. 2017, 15, 4490–4505. [Google Scholar] [CrossRef] [PubMed]
- Ghadiri, M.R.; Granja, J.R.; Buehler, L.K. Artificial Transmembrane Ion Channels from Self-Assembling Peptide Nanotubes. Nature 1994, 369, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Huang, L.; Sun, Z.; Barboiu, M. Self-Assembled Artificial Ion-Channels toward Natural Selection of Functions. Angew. Chem. Int. Ed. 2021, 60, 566–597. [Google Scholar] [CrossRef] [PubMed]
- Hartgerink, J.D.; Granja, J.R.; Milligan, R.A.; Ghadiri, M.R. Self-Assembling Peptide Nanotubes. J. Am. Chem. Soc. 1996, 118, 43–50. [Google Scholar] [CrossRef]
- Zhu, J.; Cheng, J.; Liao, Z.; Lai, Z.; Liu, B. Investigation of Structures and Properties of Cyclic Peptide Nanotubes by Experiment and Molecular Dynamics. J. Comput.-Aided. Mol. Des. 2008, 22, 773–781. [Google Scholar] [CrossRef]
- Lynch, C.I.; Rao, S.; Sansom, M.S.P. Water in Nanopores and Biological Channels: A Molecular Simulation Perspective. Chem. Rev. 2020, 120, 10298–10335. [Google Scholar] [CrossRef]
- Dauber-Osguthorpe, P.; Hagler, A.T. Biomolecular Force Fields: Where Have We Been, Where Are We Now, Where Do We Need to Go and How Do We Get There? J. Comput.-Aided Mol. Des. 2019, 33, 133–203. [Google Scholar] [CrossRef]
- Lopes, P.E.M.; Guvench, O.; Mackerell, A.D. Current Status of Protein Force Fields for Molecular Dynamics Simulations. Methods Mol. Biol. 2015, 1215, 47–71. [Google Scholar] [CrossRef] [Green Version]
- Rosenberger, D.; Smith, J.S.; Garcia, A.E. Modeling of Peptides with Classical and Novel Machine Learning Force Fields: A Comparison. J. Phys. Chem. B 2021, 125, 3598–3612. [Google Scholar] [CrossRef]
- Beauchamp, K.A.; Lin, Y.S.; Das, R.; Pande, V.S. Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements. J. Chem. Theory Comput. 2012, 8, 1409–1414. [Google Scholar] [CrossRef] [Green Version]
- Lindorff-Larsen, K.; Maragakis, P.; Piana, S.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Systematic Validation of Protein Force Fields against Experimental Data. PLoS ONE 2012, 7, e0032131. [Google Scholar] [CrossRef] [Green Version]
- Lange, O.F.; Van Der Spoel, D.; De Groot, B.L. Scrutinizing Molecular Mechanics Force Fields on the Submicrosecond Timescale with NMR Data. Biophys. J. 2010, 99, 647–655. [Google Scholar] [CrossRef] [Green Version]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [Green Version]
- Paissoni, C.; Nardelli, F.; Zanella, S.; Curnis, F.; Belvisi, L.; Musco, G.; Ghitti, M. A Critical Assessment of Force Field Accuracy against NMR Data for Cyclic Peptides Containing β-Amino Acids. Phys. Chem. Chem. Phys. 2018, 20, 15807–15816. [Google Scholar] [CrossRef]
- McHugh, S.M.; Rogers, J.R.; Solomon, S.A.; Yu, H.; Lin, Y.S. Computational Methods to Design Cyclic Peptides. Curr. Opin. Chem. Biol. 2016, 34, 95–102. [Google Scholar] [CrossRef]
- Yu, H.; Lin, Y.S. Toward Structure Prediction of Cyclic Peptides. Phys. Chem. Chem. Phys. 2015, 17, 4210–4219. [Google Scholar] [CrossRef]
- Lin, H.; Fan, J.; Weng, P.; Si, X.; Zhao, X. Molecular Dynamics Simulations on the Behaviors of Hydrophilic/Hydrophobic Cyclic Peptide Nanotubes at the Water/Hexane Interface. J. Phys. Chem. A 2017, 121, 6863–6873. [Google Scholar] [CrossRef]
- Maroli, N.; Kolandaivel, P. Comparative Study of Stability and Transport of Molecules through Cyclic Peptide Nanotube and Aquaporin: A Molecular Dynamics Simulation Approach. J. Biomol. Struct. Dyn. 2020, 38, 186–199. [Google Scholar] [CrossRef] [PubMed]
- Tarek, M.; Maigret, B.; Chipot, C. Molecular Dynamics Investigation of an Oriented Cyclic Peptide Nanotube in DMPC Bilayers. Biophys. J. 2003, 85, 2287–2298. [Google Scholar] [CrossRef] [Green Version]
- Hwang, H.; Schatz, G.C.; Ratner, M.A. Steered Molecular Dynamics Studies of the Potential of Mean Force of a Na+ or K+ Ion in a Cyclic Peptide Nanotube. J. Phys. Chem. B 2006, 110, 26448–26460. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Fan, J.; Tang, M.; Zhou, W. Molecular Dynamics Simulation for the Structure of the Water Chain in a Transmembrane Peptide Nanotube. J. Phys. Chem. A 2010, 114, 2376–2383. [Google Scholar] [CrossRef]
- Vijayaraj, R.; Van Damme, S.; Bultinck, P.; Subramanian, V. Structure and Stability of Cyclic Peptide Based Nanotubes: A Molecular Dynamics Study of the Influence of Amino Acid Composition. Phys. Chem. Chem. Phys. 2012, 14, 15135–15144. [Google Scholar] [CrossRef] [Green Version]
- Bertran, O.; Curcó, D.; Zanuy, D.; Alemán, C. Atomistic Organization and Characterization of Tube-like Assemblies Comprising Peptide-Polymer Conjugates: Computer Simulation Studies. Faraday Discuss. 2013, 166, 59–82. [Google Scholar] [CrossRef] [Green Version]
- Vijayakumar, V.; Vijayaraj, R.; Peters, G.H. In Silico Study of Amphiphilic Nanotubes Based on Cyclic Peptides in Polar and Non-Polar Solvent. J. Mol. Model. 2016, 22, 264. [Google Scholar] [CrossRef]
- Götz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef]
- Páll, S.; Zhmurov, A.; Bauer, P.; Abraham, M.; Lundborg, M.; Gray, A.; Hess, B.; Lindahl, E. Heterogeneous Parallelization and Acceleration of Molecular Dynamics Simulations in GROMACS. J. Chem. Phys. 2020, 153, 44130. [Google Scholar] [CrossRef]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.C.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Hénin, J.; Jiang, W.; et al. Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Stone, J.E.; Hardy, D.J.; Ufimtsev, I.S.; Schulten, K. GPU-Accelerated Molecular Modeling Coming of Age. J. Mol. Graph. Model. 2010, 29, 116–125. [Google Scholar] [CrossRef] [Green Version]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [Green Version]
- Claro, B.; González-Freire, E.; Calvelo, M.; Bessa, L.J.; Goormaghtigh, E.; Amorín, M.; Granja, J.R.; Garcia-Fandiño, R.; Bastos, M. Membrane Targeting Antimicrobial Cyclic Peptide Nanotubes—An Experimental and Computational Study. Colloids Surf. B Biointerfaces 2020, 196, 111349. [Google Scholar] [CrossRef]
- Khalfa, A.; Tarek, M. On the Antibacterial Action of Cyclic Peptides: Insights from Coarse-Grained MD Simulations. J. Phys. Chem. B 2010, 114, 2676–2684. [Google Scholar] [CrossRef]
- Lazim, R.; Suh, D.; Choi, S. Advances in Molecular Dynamics Simulations and Enhanced Sampling Methods for the Study of Protein Systems. Int. J. Mol. Sci. 2020, 21, 6339. [Google Scholar] [CrossRef]
- Yang, Y.I.; Shao, Q.; Zhang, J.; Yang, L.; Gao, Y.Q. Enhanced Sampling in Molecular Dynamics. J. Chem. Phys. 2019, 151, 70902. [Google Scholar] [CrossRef] [Green Version]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Kräutler, V.; Van Gunsteren, W.F.; Hünenberger, P.H. A Fast SHAKE Algorithm to Solve Distance Constraint Equations for Small Molecules in Molecular Dynamics Simulations. J. Comput. Chem. 2001, 22, 501–508. [Google Scholar] [CrossRef]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef]
- Feenstra, K.A.; Hess, B.; Berendsen, H.J.C. Improving Efficiency of Large Time-Scale Molecular Dynamics Simulations of Hydrogen-Rich Systems. J. Comput. Chem. 1999, 20, 786–798. [Google Scholar] [CrossRef]
- Hopkins, C.W.; Le Grand, S.; Walker, R.C.; Roitberg, A.E. Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. [Google Scholar] [CrossRef]
- Beyer, H.; Tukey, J.W. Exploratory Data Analysis. Addison-Wesley Publishing Company Reading, Mass.—Menlo Park, Cal., London, Amsterdam, Don Mills, Ontario, Sydney 1977, XVI, 688 S. Biom. J. 1981, 23, 413–414. [Google Scholar] [CrossRef]
- Garrido, P.F.; Calvelo, M.; Garcia-Fandiño, R.; Piñeiro, Á. Rings, Hexagons, Petals, and Dipolar Moment Sink-Sources: The Fanciful Behavior of Water around Cyclodextrin Complexes. Biomolecules 2020, 10, 431. [Google Scholar] [CrossRef] [Green Version]
- De Laeter, J.R.; Böhlke, J.K.; De Bièvre, P.; Hidaka, H.; Peiser, H.S.; Rosman, K.J.R.; Taylor, P.D.P. Atomic Weights of the Elements: Review 2000 (IUPAC Technical Report). Pure Appl. Chem. 2003, 75, 683–800. [Google Scholar] [CrossRef]
- Korsheninnikov, A.A.; Nikolskii, E.Y.; Kuzmin, E.A.; Ozawa, A.; Morimoto, K.; Tokanai, F.; Kanungo, R.; Tanihata, I.; Timofeyuk, N.K.; Golovkov, M.S.; et al. Experimental Evidence for the Existence of [Formula Presented] and for a Specific Structure of [Formula Presented]. Phys. Rev. Lett. 2003, 90, 082501. [Google Scholar] [CrossRef]
- Silk, M.R.; Newman, J.; Ratcliffe, J.C.; White, J.F.; Caradoc-Davies, T.; Price, J.R.; Perrier, S.; Thompson, P.E.; Chalmers, D.K. Parallel and Antiparallel Cyclic d/l Peptide Nanotubes. Chem. Commun. 2017, 53, 6613–6616. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved Side-Chain Torsion Potentials for the Amber Ff99SB Protein Force Field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; De Groot, B.L.; Grubmüller, H.; MacKerell, A.D. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2016, 14, 71–73. [Google Scholar] [CrossRef] [Green Version]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; Van Gunsteren, W.F. Definition and Testing of the GROMOS Force-Field Versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D. Temperature and Size Dependence for Monte Carlo Simulations of TIP4P Water. Mol. Phys. 1985, 56, 1381–1392. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J. Interaction Models for Water in Relation to Protein Hydration; Springer: Dordrecht, The Netherlands, 1981; pp. 331–342. [Google Scholar] [CrossRef]
- Domański, J.; Stansfeld, P.J.; Sansom, M.S.P.; Beckstein, O. Lipidbook: A Public Repository for Force-Field Parameters Used in Membrane Simulations. J. Membr. Biol. 2010, 236, 255–258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jämbeck, J.P.M.; Lyubartsev, A.P. An Extension and Further Validation of an All-Atomistic Force Field for Biological Membranes. J. Chem. Theory Comput. 2012, 8, 2938–2948. [Google Scholar] [CrossRef]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D.; Pastor, R.W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef] [Green Version]
- Nencini, R. Simulation Data for CHARMM36 POPC Bilayer, 100 Lipids/Leaflet, 310K, GROMACS 5.1.4. 2018. Available online: https://doi.org/10.5281/ZENODO.1198158 (accessed on 10 February 2022).
- Mykhailo, G.; Samuli, O.O.H. POPC_Ulmschneider_OPLS_NaCl_015Mol. 2015. Available online: https://doi.org/10.5281/ZENODO.30892 (accessed on 10 February 2022).
- Ulmschneider, J.P.; Ulmschneider, M.B. United Atom Lipid Parameters for Combination with the Optimized Potentials for Liquid Simulations All-Atom Force Field. J. Chem. Theory Comput. 2009, 5, 1803–1813. [Google Scholar] [CrossRef]
- Poger, D.; Van Gunsteren, W.F.; Mark, A.E. A New Force Field for Simulating Phosphatidylcholine Bilayers. J. Comput. Chem. 2010, 31, 1117–1125. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Piggot, T.J.; Piñeiro, Á.; Khalid, S. Molecular Dynamics Simulations of Phosphatidylcholine Membranes: A Comparative Force Field Study. J. Chem. Theory Comput. 2012, 8, 4593–4609. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Klesse, G.; Rao, S.; Sansom, M.S.P.; Tucker, S.J. CHAP: A Versatile Tool for the Structural and Functional Annotation of Ion Channel Pores. J. Mol. Biol. 2019, 431, 3353–3365. [Google Scholar] [CrossRef]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef] [Green Version]
- Gowers, R.J.; Linke, M.; Barnoud, J.; Reddy, T.J.E.; Melo, M.N.; Seyler, S.L.; Domá nski, J.; Dotson, D.L.; Buchoux, S.; Kenney, I.M.; et al. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. In Proceedings of the 15th Python in Science Conference, Austin, TX, USA, 11–17 July 2016; pp. 98–105. [Google Scholar] [CrossRef] [Green Version]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Mckinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar] [CrossRef] [Green Version]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Garcia-Fandiño, R.; Piñeiro, Á.; Trick, J.L.; Sansom, M.S.P. Lipid Bilayer Membrane Perturbation by Embedded Nanopores: A Simulation Study. ACS Nano 2016, 10, 3693–3701. [Google Scholar] [CrossRef]
- Tiangtrong, P.; Thamwattana, N.; Baowan, D. Modelling Water Molecules inside Cyclic Peptide Nanotubes. Appl. Nanosci. 2016, 6, 345–357. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Pascacio, J.; Piñeiro, Á.; Ruso, J.M.; Hassan, N.; Campbell, R.A.; Campos-Terán, J.; Costas, M. Complex Behavior of Aqueous α-Cyclodextrin Solutions. Interfacial Morphologies Resulting from Bulk Aggregation. Langmuir 2016, 32, 6682–6690. [Google Scholar] [CrossRef]
- Luviano, A.S.; Hernández-Pascacio, J.; Ondo, D.; Campbell, R.A.; Piñeiro, Á.; Campos-Terán, J.; Costas, M. Highly Viscoelastic Films at the Water/Air Interface: α-Cyclodextrin with Anionic Surfactants. J. Colloid Interface Sci. 2020, 565, 601–613. [Google Scholar] [CrossRef]
- Siu, S.W.I.; Vácha, R.; Jungwirth, P.; Böckmann, R.A. Biomolecular Simulations of Membranes: Physical Properties from Different Force Fields. J. Chem. Phys. 2008, 128, 125103. [Google Scholar] [CrossRef]
- Sandoval-Perez, A.; Pluhackova, K.; Böckmann, R.A. Critical Comparison of Biomembrane Force Fields: Protein–Lipid Interactions at the Membrane Interface. J. Chem. Theory Comput. 2017, 13, 2310–2321. [Google Scholar] [CrossRef]
- Guvench, O.; MacKerell, A.D. Comparison of Protein Force Fields for Molecular Dynamics Simulations. Methods Mol. Biol. 2008, 443, 63–88. [Google Scholar] [CrossRef]

| AMBER | CHARMM | OPLS | GROMOS | H2D | H2Q | H2H7 | HMR | HMRw | |
|---|---|---|---|---|---|---|---|---|---|
| Time step/fs | 2 | 2 | 2 | 2 | 5 | 6 | 6 | 6 | 7 |
| Water model | TIP3P | TIP3P | TIP4P | SPC | SPC | SPC | SPC | SPC | SPC |
| Polar H/Da | 1.008 | 1.008 | 1.008 | 1.008 | 2.014 | 4.026 | 7.053 | 4.032 | 4.032 |
| Polar C/Da | 12.010 | 12.011 | 12.011 | 12.011 | 12.011 | 12.011 | 12.011 | 8.987 | 8.987 |
| Water O/Da | 16.000 | 16.000 | 16.000 | 15.999 | 15.999 | 15.999 | 15.999 | 15.999 | 9.951 |
| Water H/Da | 1.008 | 1.008 | 1.008 | 1.008 | 1.008 | 1.008 | 1.008 | 1.008 | 4.032 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conde, D.; Garrido, P.F.; Calvelo, M.; Piñeiro, Á.; Garcia-Fandino, R. Molecular Dynamics Simulations of Transmembrane Cyclic Peptide Nanotubes Using Classical Force Fields, Hydrogen Mass Repartitioning, and Hydrogen Isotope Exchange Methods: A Critical Comparison. Int. J. Mol. Sci. 2022, 23, 3158. https://doi.org/10.3390/ijms23063158
Conde D, Garrido PF, Calvelo M, Piñeiro Á, Garcia-Fandino R. Molecular Dynamics Simulations of Transmembrane Cyclic Peptide Nanotubes Using Classical Force Fields, Hydrogen Mass Repartitioning, and Hydrogen Isotope Exchange Methods: A Critical Comparison. International Journal of Molecular Sciences. 2022; 23(6):3158. https://doi.org/10.3390/ijms23063158
Chicago/Turabian StyleConde, Daniel, Pablo F. Garrido, Martín Calvelo, Ángel Piñeiro, and Rebeca Garcia-Fandino. 2022. "Molecular Dynamics Simulations of Transmembrane Cyclic Peptide Nanotubes Using Classical Force Fields, Hydrogen Mass Repartitioning, and Hydrogen Isotope Exchange Methods: A Critical Comparison" International Journal of Molecular Sciences 23, no. 6: 3158. https://doi.org/10.3390/ijms23063158
APA StyleConde, D., Garrido, P. F., Calvelo, M., Piñeiro, Á., & Garcia-Fandino, R. (2022). Molecular Dynamics Simulations of Transmembrane Cyclic Peptide Nanotubes Using Classical Force Fields, Hydrogen Mass Repartitioning, and Hydrogen Isotope Exchange Methods: A Critical Comparison. International Journal of Molecular Sciences, 23(6), 3158. https://doi.org/10.3390/ijms23063158






