Uranium: The Nuclear Fuel Cycle and Beyond
Abstract
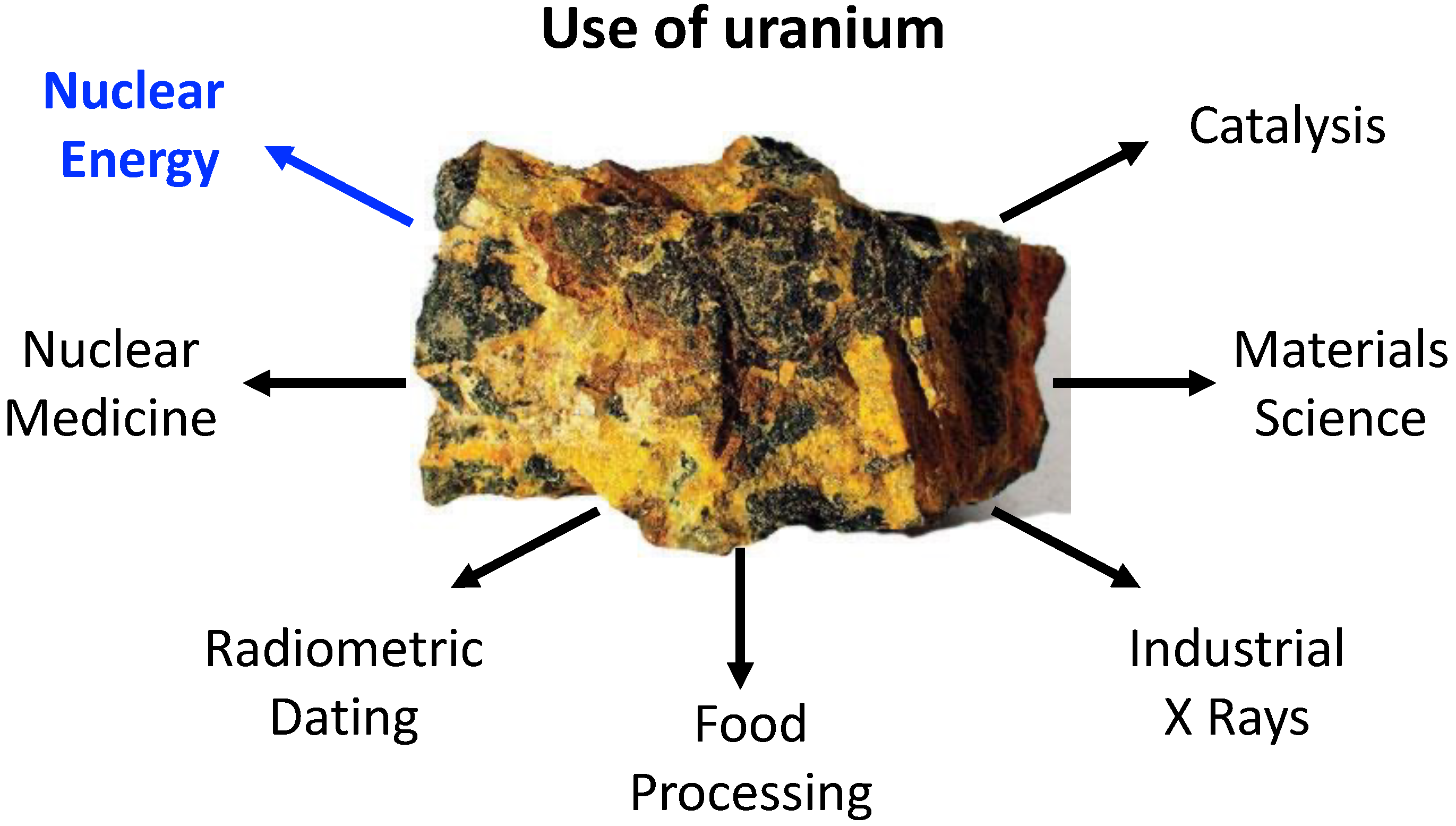
:1. Introduction
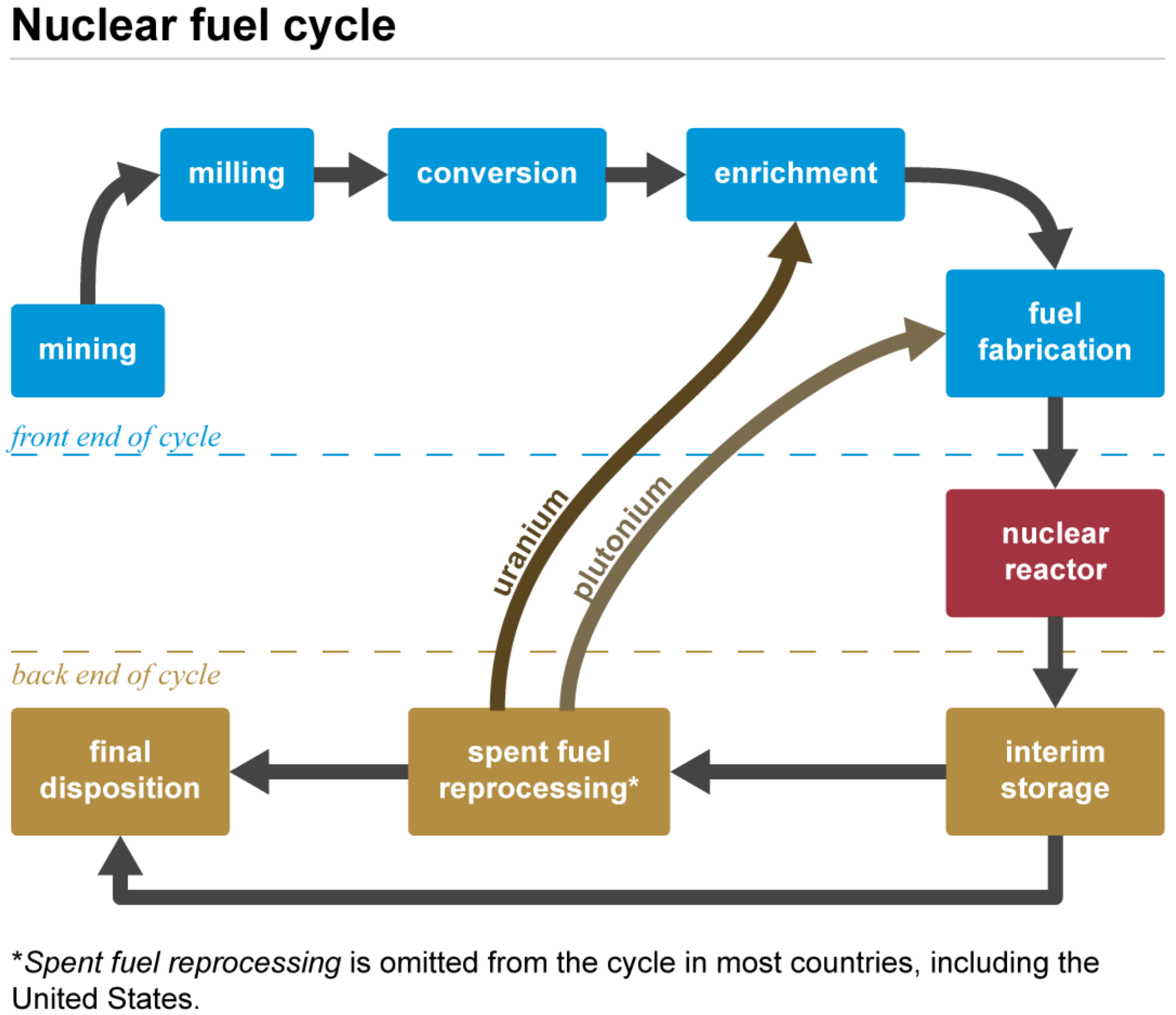
2. Role of Uranium in the Nuclear Fuel Cycle
3. Spent Fuel Recycling
4. Coordination Chemistry of Uranium
5. Uranium and Human Health
6. UN Bond Strength in Uranium Nitrides
7. Conclusions and Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cotton, S. Introduction to the Actinides. In Lanthanide and Actinide Chemistry; John Wiley & Sons, Ltd.: West Sussex, UK, 2006; Chapter 9; pp. 145–153. [Google Scholar]
- Xin, X.; Douair, I.; Zhao, Y.; Wang, S.; Maron, L.; Zhu, C. Dinitrogen Cleavage by a Heterometallic Cluster Featuring Multiple Uranium-Rhodium Bonds. J. Am. Chem. Soc. 2020, 142, 15004–15011. [Google Scholar] [CrossRef] [PubMed]
- Tsoureas, N.; Mansikkamäki, A.; Layfield, R.A. Uranium(IV) cyclobutadienyl sandwich compounds: Synthesis, structure and chemical bonding. Chem. Commun. 2020, 56, 944–947. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.S.; Tsoureas, N.; Huang, G.Z.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. Isolation of a Perfectly Linear Uranium(II) Metallocene. Angew. Chem. Int. Ed. 2020, 59, 2299–2303. [Google Scholar] [CrossRef] [PubMed]
- Boreen, M.A.; McCabe, K.N.; Lohrey, T.D.; Watt, F.A.; Maron, L.; Hohloch, S.; Arnold, J. Uranium Metallocene Azides, Isocyanates, and Their Borane-Capped Lewis Adducts. Inorg. Chem. 2020, 591, 8580–8588. [Google Scholar] [CrossRef]
- Boreen, M.A.; Lohrey, T.D.; Rao, G.; Britt, R.D.; Maron, L.; Arnold, J. A Uranium Tri-Rhenium Triple Inverse Sandwich Compound. J. Am. Chem. Soc. 2019, 141, 5144–5148. [Google Scholar] [CrossRef]
- Boronski, J.T.; Doyle, L.R.; Seed, J.A.; Wooles, A.J.; Liddle, S.T. f-Element Half-Sandwich Complexes: A Tetrasilylcyclobutadienyl-Uranium(IV)-Tris(tetrahydroborate) Anion Pianostool Complex. Angew. Chem. Int. Ed. 2019, 59, 295–299. [Google Scholar] [CrossRef]
- Terrani, K.A.; Jolly, B.C.; Harp, J.M. Uranium nitride tristructural-isotropic fuel particle. J. Nucl. Mater. 2020, 531, 152034. [Google Scholar] [CrossRef]
- Hartline, D.R.; Meyer, K. From chemical curiosities and trophy molecules to uranium-based catalysis: Developments for uranium catalysis as a new facet in molecular uranium chemistry. JACS Au 2021, 1, 698–709. [Google Scholar] [CrossRef]
- Feng, G.; Zhang, M.; Shao, D.; Wang, X.; Wang, S.; Maron, L.; Zhu, C. Transition-metal-bridged bimetallic clusters with multiple uranium–metal bonds. Nat. Chem. 2019, 11, 248–253. [Google Scholar] [CrossRef]
- Das, D.; Joshi, M.; Kannan, S.; Kumar, M.; Ghanty, T.K.; Vincent, T.; Manohar, S.; Kaushik, C. A Combined Experimental and Quantum Chemical Studies on the Structure and Binding Preferences of Picolinamide Based Ligands with Uranyl Nitrate. Polyhedron 2019, 171, 486–492. [Google Scholar] [CrossRef]
- Lu, G.; Haes, A.J.; Forbes, T.Z. Detection and Identification of Solids, Surfaces, and Solutions of Uranium Using Vibrational Spectroscopy. Coord. Chem. Rev. 2018, 374, 314–344. [Google Scholar] [CrossRef] [PubMed]
- Palumbo, C.T.; Scopelliti, R.; Zivkovic, I.; Mazzanti, M. C-H Bond Activation by an Isolated Dinuclear U(III)/U(IV) Nitride. J. Am. Chem. Soc. 2020, 142, 3149–3157. [Google Scholar] [CrossRef] [PubMed]
- Loveland, W.D.; Morrissey, D.J.; Seaborg, G.T. Modern Nuclear Chemistry; John Wiley & Sons: New York, NY, USA, 2017. [Google Scholar]
- Navrotsky, A.; Shvareva, T.; Guo, X.; Burns, P. Thermodynamics of uranium minerals and related materials. In Uranium: Cradle to Grave; Burns, P.C., Sigmin, G.E., Eds.; Mineralogical Association of Canada: Winnipeg, MB, Canada, 2013; pp. 147–164. [Google Scholar]
- Olander, D.R. The theory of uranium enrichment by the gas centrifuge. Prog. Nucl. Energy 1981, 8, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Mazher, A.K. A review of uranium economics. Int. J. Nucl. Gov. Econ. Ecol. 2009, 2, 337–361. [Google Scholar] [CrossRef]
- Edwards, C.; Oliver, A. Uranium processing: A review of current methods and technology. JOM 2000, 52, 12–20. [Google Scholar] [CrossRef]
- Ho, M.; Obbard, E.; Burr, P.A.; Yeoh, G. A review on the development of nuclear power reactors. Energy Procedia 2019, 160, 459–466. [Google Scholar] [CrossRef]
- Gorman-Lewis, D.; Burns, P.C.; Fein, J.B. Review of uranyl mineral solubility measurements. J. Chem. Thermodyn. 2008, 40, 335–352. [Google Scholar] [CrossRef]
- Krivovichev, S.V.; Plášil, J. Mineralogy and crystallography of uranium. In Uranium: From Cradle to Grave; Burns, P.C., Sigmon, G.E., Eds.; Mineralogical Association of Canada Short Courses: Quebec, QC, Canada, 2013; Volume 43, pp. 15–119. [Google Scholar]
- Seyferth, D. Uranocene: The first member of a new class of organometallic derivatives of the f elements. Organometallics 2004, 23, 3562–3583. [Google Scholar] [CrossRef] [Green Version]
- Boronski, J.T.; Liddle, S.T. The Emergence of Actinide Cyclobutadienyl Chemistry. Eur. J. Inorg. Chem. 2020, 2020, 2851–2861. [Google Scholar] [CrossRef]
- Sessler, J.L.; Melfi, P.J.; Pantos, G.D. Uranium complexes of multidentate N-donor ligands. Coord. Chem. Rev. 2006, 250, 816–843. [Google Scholar] [CrossRef]
- Van Horn, J.D.; Huang, H. Uranium (VI) bio-coordination chemistry from biochemical, solution and protein structural data. Coord. Chem. Rev. 2006, 250, 765–775. [Google Scholar] [CrossRef]
- Yang, W.; Parker, T.G.; Sun, Z.M. Structural chemistry of uranium phosphonates. Coord. Chem. Rev. 2015, 303, 86–109. [Google Scholar] [CrossRef]
- Dam, H.H.; Reinhoudt, D.N.; Verboom, W. Multicoordinate ligands for actinide/lanthanide separations. Chem. Soc. Rev. 2007, 36, 367–377. [Google Scholar] [CrossRef]
- Nash, K.L.; Nilsson, M. Introduction to the reprocessing and recycling of spent nuclear fuels. In Reprocessing and Recycling of Spent Nuclear Fuel; Taylor, R., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Oxford, UK, 2015; pp. 3–25. [Google Scholar]
- Geist, A.; Adnet, J.M.; Bourg, S.; Ekberg, C.; Galan, H.; Guilbaud, P.; Miguirditchian, M.; Modolo, G.; Rhodes, C.; Taylor, R. An overview of solvent extraction processes developed in Europe for advanced nuclear fuel recycling, part 1—Heterogeneous recycling. Sep. Sci. Technol. 2021, 56, 1866–1881. [Google Scholar] [CrossRef]
- Taylor, R.; Bodel, W.; Stamford, L.; Butler, G. A Review of Environmental and Economic Implications of Closing the Nuclear Fuel Cycle—Part One: Wastes and Environmental Impacts. Energies 2022, 15, 1433. [Google Scholar] [CrossRef]
- Ewing, R.C.; Weber, W.J.; Clinard, F.W., Jr. Radiation effects in nuclear waste forms for high-level radioactive waste. Prog. Nucl. Energy 1995, 29, 63–127. [Google Scholar] [CrossRef]
- Ewing, R.C.; Weber, W.J.; Lian, J. Nuclear waste disposal—Pyrochlore (A2B2O7): Nuclear waste form for the immobilization of plutonium and “minor” actinides. J. Appl. Phys. 2004, 95, 5949–5971. [Google Scholar] [CrossRef] [Green Version]
- McEachern, R.J.; Taylor, P. A review of the oxidation of uranium dioxide at temperatures below 400 °C. J. Nucl. Mater. 1998, 254, 87–121. [Google Scholar] [CrossRef]
- Belle, J. Oxygen and uranium diffusion in uranium dioxide (a review). J. Nucl. Mater. 1969, 30, 3–15. [Google Scholar] [CrossRef]
- Yoo, T.S.; Herrmann, S.D.; Yoon, S.J.; Marsden, K.C. Analysis and Modeling of Oxide Reduction Processes for Uranium Oxides. J. Nucl. Mater. 2021, 545, 152625. [Google Scholar] [CrossRef]
- Chen, X.; Li, Q.; Gong, Y. Coordination Structures of the Uranyl(VI)-Diamide Complexes: A Combined Mass Spectrometric, EXAFS Spectroscopic, and Theoretical Study. Inorg. Chem. 2019, 58, 5695–5702. [Google Scholar] [CrossRef] [PubMed]
- Klamm, B.E.; Windorff, C.J.; Celis-Barros, C.; Marsh, M.L.; Albrecht-Schmitt, T.E. Synthesis, Spectroscopy, and Theoretical Details of Uranyl Schiff-Base Coordination Complexes. Inorg. Chem. 2020, 59, 23–31. [Google Scholar] [CrossRef]
- King, D.M.; Liddle, S.T. Progress in molecular uranium-nitride chemistry. Coord. Chem. Rev. 2014, 266, 2–15. [Google Scholar] [CrossRef]
- Makoś, M.Z.; Zou, W.; Freindorf, M.; Kraka, E. Metal-Ring Interactions in Actinide Sandwich Compounds: A Combined Normalized Elimination of the Small Component and Local Vibrational Mode Study. Mol. Phys. 2020, 118, e1768314. [Google Scholar] [CrossRef]
- Arfsten, D.P.; Still, K.R.; Ritchie, G.D. A review of the effects of uranium and depleted uranium exposure on reproduction and fetal development. Toxicol. Ind. Health 2001, 17, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Domingo, J.L. Reproductive and developmental toxicity of natural and depleted uranium: A review. Reprod. Toxicol. 2001, 15, 603–609. [Google Scholar] [CrossRef]
- Aly, M.M.; Hamza, M.F. A Review: Studies on Uranium Removal Using Different Techniques. Overview. J. Dispers. Sci. Technol. 2013, 34, 182–213. [Google Scholar] [CrossRef]
- Wang, S.; Ran, Y.; Lu, B.; Li, J.; Kuang, H.; Gong, L.; Hao, Y. A review of uranium-induced reproductive toxicity. Biol. Trace Elem. Res. 2020, 196, 204–213. [Google Scholar] [CrossRef]
- Liddle Kelley, M.P.; Popov, I.A.; Jung, J.; Batista, E.R.; Yang, P. δ and ϕ back-donation in An(IV) metallacycles. Nat. Commun. 2020, 11, 1558. [Google Scholar] [CrossRef]
- Rice, N.T.; McCabe, K.; Bacsa, J.; Maron, L.; Pierre, H.S.L. Two-Electron Oxidative Atom Transfer at a Homoleptic, Tetravalent Uranium Complex. J. Am. Chem. Soc. 2020, 142, 7368–7373. [Google Scholar] [CrossRef]
- Chatelain, L.; Louyriac, E.; Douair, I.; Lu, E.; Tuna, F.; Wooles, A.J.; Gardner, B.M.; Maron, L.; Liddle, S.T. Terminal uranium(V)-nitride hydrogenations involving direct addition or Frustrated Lewis Pair mechanisms. Nat. Chem. 2020, 11, 337. [Google Scholar] [CrossRef] [PubMed]
- Wooles, A.J.; Mills, D.P.; Tuna, F.; McInnes, E.J.L.; Law, G.T.W.; Fuller, A.J.; Kremer, F.; Ridgway, M.; Lewis, W.; Gagliardi, L.; et al. Uranium(III)-carbon multiple bonding supported by arene δ-bonding in mixed-valence hexauranium nanometre-scale rings. Nat. Commun. 2018, 9, 2097–2108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rudel, S.S.; Deubner, H.L.; Müller, M.; Karttunen, A.J.; Kraus, F. Complexes featuring a linear [N≡U≡N] core isoelectronic to the uranyl cation. Nat. Chem. 2020, 12, 962–967. [Google Scholar] [CrossRef] [PubMed]
- Platts, J.A.; Baker, R.J. A computational investigation of orbital overlap versus energy degeneracy covalency in [UE2]2+ (E = O, S, Se, Te) complexes. Dalton Trans. 2020, 49, 1077–1088. [Google Scholar] [CrossRef] [PubMed]
- Degueldre, C.; Goddard, D.; Berhane, G.; Simpson, A.; Boxall, C. Simulation of uranium mononitride spent fuel: A crystallographic approach. J. Nucl. Mater. 2022, 562, 153612. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Neese, F. All-Electron Scalar Relativistic Basis Sets for the Actinides. J. Chem. Theory Comput. 2011, 7, 677–684. [Google Scholar] [CrossRef]
- Kirkegaard, M.C.; Spano, T.L.; Ambrogio, M.W.; Niedziela, J.L.; Miskowiec, A.; Shields, A.E.; Anderson, B.B. Formation of a Uranyl Hydroxide Hydrate via Hydration of [(UO2F2)(H2O)]74H2O. Dalton Trans. 2019, 48, 13685–13698. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Quantum Theory of the Electron. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 1928, 117, 610–624. [Google Scholar]
- Dirac, P.A.M. The Quantum Theory of the Electron. Part II. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 1928, 118, 351–361. [Google Scholar]
- Cremer, D.; Zou, W.; Filatov, M. Dirac-Exact Relativistic Methods: The Normalized Elimination of the Small Component Method. WIREs Comput. Mol. Sci. 2014, 4, 436–467. [Google Scholar] [CrossRef]
- Pyykkö, P. Relativistic Effects in Structural Chemistry. Chem. Rev. 1988, 88, 563–594. [Google Scholar] [CrossRef]
- Pyykkö, P. Relativistic Effects in Chemistry: More Common than You Thought. Ann. Rev. Phys. Chem. 2012, 63, 45–64. [Google Scholar] [CrossRef] [PubMed]
- Dirac, P.A.M. A Theory of Electrons and Protons. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 1930, 126, 360–365. [Google Scholar]
- Liu, W. Advances in Relativistic Molecular Quantum Mechanics. Phys. Rep. 2014, 537, 59–89. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Liu, W. Quasirelativistic Theory Equivalent to Fully Relativistic Theory. J. Chem. Phys. 2005, 123, 241102. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Regular Two-Component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Dirac, P.A. Forms of relativistic dynamics. Rev. Mod. Phys. 1949, 21, 392. [Google Scholar] [CrossRef] [Green Version]
- Liu, W. Essentials of relativistic quantum chemistry. J. Chem. Phys. 2020, 152, 180901. [Google Scholar] [CrossRef]
- Zou, W.; Guo, G.; Suo, B.; Liu, W. Analytic Energy Gradients and Hessians of Exact Two-Component Relativistic Methods: Efficient Implementation and Extensive Applications. J. Chem. Theory Comput. 2020, 16, 1541–1554. [Google Scholar] [CrossRef]
- Peng, D.; Reiher, M. Exact decoupling of the relativistic Fock operator. Theor. Chem. Acc. 2012, 131, 1081. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Liu, W.; Xiao, Y.; Cheng, L. Making Four- and Two-Component Relativistic Density Functional Methods Fully Equivalent Based on the Idea of “From Atoms to Molecule”. J. Chem. Phys. 2007, 127, 104106. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Peng, D. Exact Two-Component Hamiltonians Revisited. J. Chem. Phys. 2009, 131, 031104. [Google Scholar] [CrossRef] [PubMed]
- Iliaš, M.; Saue, T. An Infinite-Order Two-Component Relativistic Hamiltonian by a Simple One-Step Transformation. J. Chem. Phys. 2007, 126, 064102. [Google Scholar] [CrossRef] [PubMed]
- Barysz, M.; Mentel, L.; Leszczynski, J. Recovering four-component solutions by the inverse transformation of the infinite-order two-component wave functions. J. Chem. Phys. 2009, 130, 164114. [Google Scholar] [CrossRef]
- Oyama, T.; Ikabata, Y.; Seino, J.; Nakai, H. Relativistic density functional theory with picture-change corrected electron density based on infinite-order Douglas–Kroll–Hess method. Chem. Phys. Lett. 2017, 680, 37–43. [Google Scholar] [CrossRef]
- Barysz, M.; Sadlej, A.J.; Snijders, J.G. Nonsingular two/one-component relativistic Hamiltonians accurate through arbitrary high order in α2. Int. J. Quantum Chem. 1997, 65, 225–239. [Google Scholar] [CrossRef]
- Douglas, M.; Kroll, N.M. Quantum Electrodynamical Corrections to the Fine Structure of Helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Hess, B.A. Applicability of the no-pair equation with free-particle projection operators to atomic and molecular structure calculations. Phys. Rev. A 1985, 32, 756. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Dyall, K.G. Interfacing relativistic and nonrelativistic methods. I. Normalized elimination of the small component in the modified Dirac equation. J. Chem. Phys. 1997, 106, 9618–9626. [Google Scholar] [CrossRef]
- Zou, W.; Filatov, M.; Cremer, D. Analytical Energy Gradient for the Two-Component Normalized Elimination of the Small Component Method. J. Chem. Phys. 2015, 142, 214106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoshizawa, T.; Zou, W.; Cremer, D. Calculations of Electric Dipole Moments and Static Dipole Polarizabilities Based on the Two-Component Normalized Elimination of the Small Component Method. J. Chem. Phys. 2016, 145, 184104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoshizawa, T.; Zou, W.; Cremer, D. Calculations of Atomic Magnetic Nuclear Shielding Constants Based on the Two-Component Normalized Elimination of the Small Component Method. J. Chem. Phys. 2017, 146, 134109. [Google Scholar] [CrossRef] [PubMed]
- Yoshizawa, T.; Filatov, M.; Cremer, D.; Zou, W. Calculation of contact densities and Mössbauer isomer shifts utilising the Dirac-exact two-component normalised elimination of the small component (2c-NESC) method. Mol. Phys. 2019, 117, 1164–1171. [Google Scholar] [CrossRef]
- Zou, W.; Filatov, M.; Cremer, D. Analytic Calculation of Second-Order Electric Response Properties with the Normalized Elimination of the Small Component (NESC) Method. J. Chem. Phys. 2012, 137, 084108. [Google Scholar] [CrossRef] [Green Version]
- Filatov, M.; Zou, W.; Cremer, D. Relativistically Corrected Electric Field Gradients Calculated with the Normalized Elimination of the Small Component Formalism. J. Chem. Phys. 2012, 137, 054113. [Google Scholar] [CrossRef]
- Zou, W.; Filatov, M.; Cremer, D. Development, Implementation, and Application of an Analytic Second Derivative Formalism for the Normalized Elimination of the Small Component Method. J. Chem. Theory Comput. 2012, 8, 2617–2629. [Google Scholar] [CrossRef]
- Filatov, M.; Zou, W.; Cremer, D. Analytic Calculation of Contact Densities and Mössbauer Isomer Shifts Using the Normalized Elimination of the Small-Component Formalism. J. Chem. Theory Comput. 2012, 8, 875–882. [Google Scholar] [CrossRef]
- Filatov, M.; Zou, W.; Cremer, D. Analytic Calculation of Isotropic Hyperfine Structure Constants Using the Normalized Elimination of the Small Component Formalism. J. Chem. Phys. A 2012, 116, 3481–3486. [Google Scholar] [CrossRef]
- Filatov, M.; Zou, W.; Cremer, D. Calculation of Response Properties with the Normalized Elimination of the Small Component Method. Int. J. Quantum Chem. 2013, 114, 993–1005. [Google Scholar] [CrossRef]
- Russo, T.V.; Martin, R.L.; Hay, P.J. Effective Core Potentials for DFT Calculations. J. Phys. Chem. 1995, 99, 17085–17087. [Google Scholar] [CrossRef]
- Noro, T.; Sekiya, M.; Osanai, Y.; Miyoshi, E.; Koga, T. Relativistic Correlating Basis Sets for the Main Group Elements from Cs to Ra. J. Chem. Phys. 2003, 119, 5142–5148. [Google Scholar] [CrossRef]
- Konkoli, Z.; Cremer, D. A New Way of Analyzing Vibrational Spectra. I. Derivation of Adiabatic Internal Modes. Int. J. Quantum Chem. 1998, 67, 1–9. [Google Scholar] [CrossRef]
- Konkoli, Z.; Larsson, J.A.; Cremer, D. A New Way of Analyzing Vibrational Spectra. II. Comparison of Internal Mode Frequencies. Int. J. Quantum Chem. 1998, 67, 11–27. [Google Scholar] [CrossRef]
- Konkoli, Z.; Cremer, D. A New Way of Analyzing Vibrational Spectra. III. Characterization of Normal Vibrational Modes in terms of Internal Vibrational Modes. Int. J. Quantum Chem. 1998, 67, 29–40. [Google Scholar] [CrossRef]
- Konkoli, Z.; Larsson, J.A.; Cremer, D. A New Way of Analyzing Vibrational Spectra. IV. Application and Testing of Adiabatic Modes within the Concept of the Characterization of Normal Modes. Int. J. Quantum Chem. 1998, 67, 41–55. [Google Scholar] [CrossRef]
- Cremer, D.; Larsson, J.A.; Kraka, E. New Developments in the Analysis of Vibrational Spectra on the Use of Adiabatic Internal Vibrational Modes. In Theoretical and Computational Chemistry; Parkanyi, C., Ed.; Elsevier: Amsterdam, The Netherlands, 1998; pp. 259–327. [Google Scholar]
- Crossland, I. Nuclear Fuel Cycle Science and Engineering; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Wilson, P.D. The Nuclear Fuel Cycle from Ore to Wastes; Oxford Science Publications: Oxford, UK, 1996. [Google Scholar]
- Leybros, A.; Hung, L.; Hertz, A.; Hartmann, D.; Grandjean, A.; Boutin, O. Supercritical CO2 extraction of uranium from natural ore using organophosphorus extractants. Chem. Eng. J. 2017, 316, 196–203. [Google Scholar] [CrossRef]
- Prabhat, P.; Rao, A.; Mishra, V.G.; Shah, D.J.; Kumar, P.; Tomar, B.S. Direct extraction of uranium from yellow cake and ore matrices using supercritical carbon dioxide. Radiochim. Acta 2020, 108, 769–777. [Google Scholar] [CrossRef]
- Zachariasen, W. The Crystal Structure of U2F9. J. Chem. Phys. 1948, 16, 425. [Google Scholar] [CrossRef]
- Zachariasen, W. Crystal Chemical Studies of the 5f-Series of Elements. XI. The Crystal Structure of α-UF5 and of β-UF5. Acta Crystallogr. 1949, 2, 296–298. [Google Scholar] [CrossRef]
- Cotton, S. Binary Compounds of the Actinides. In Lanthanide and Actinide Chemistry; John Wiley & Sons, Ltd.: West Sussex, UK, 2006; Chapter 10; pp. 155–172. [Google Scholar]
- Peluzo, B.M.; Galvão, B.R. Theoretical study on the structure and reactions of uranium fluorides. J. Mol. Model. 2018, 24, 197. [Google Scholar] [CrossRef] [PubMed]
- Krass, A.S. Uranium Enrichment and Nuclear Weapon Proliferation; Oxford University Press: Oxford, UK, 1983. [Google Scholar]
- Katoh, Y.; Vasudevamurthy, G.; Nozawa, T.; Snead, L.L. Properties of zirconium carbide for nuclear fuel applications. J. Nucl. Mater. 2013, 441, 718–742. [Google Scholar] [CrossRef]
- McDeavitt, S.; Abraham, D.; Park, J. Evaluation of stainless steel–zirconium alloys as high-level nuclear waste forms. J. Nucl. Mater. 1998, 257, 21–34. [Google Scholar] [CrossRef]
- Ali, K.; Ghosh, P.; Arya, A. A DFT study of structural, elastic and lattice dynamical properties of Fe2Zr and FeZr2 intermetallics. J. Alloys Compd. 2017, 723, 611–619. [Google Scholar] [CrossRef]
- Basdevant, J.L.; Rich, J. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- Streit, M.; Ingold, F. Nitrides as a nuclear fuel option. J. Eur. Ceram. Soc. 2005, 25, 2687–2692. [Google Scholar] [CrossRef]
- Hunt, R.D.; Yustein, J.T.; Andrews, L. Matrix infrared spectra of NUN formed by the insertion of uranium atoms into molecular nitrogen. J. Chem. Phys. 1993, 98, 6070–6074. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, C.; Ciborowski, S.M.; Asthana, A.; Cheng, L.; Bowen, K.H. Mapping the electronic structure of the uranium (VI) dinitride molecule, UN2. J. Phys. Chem. A 2020, 124, 6486–6492. [Google Scholar] [CrossRef] [PubMed]
- Kushto, G.P.; Souter, P.F.; Andrews, L.; Neurock, M. A matrix isolation FT–IR and quasirelativistic density functional theory investigation of the reaction products of laser-ablated uranium atoms with NO, NO2 and N2O. J. Chem. Phys. 1998, 106, 5894–5903. [Google Scholar] [CrossRef]
- Zhou, M.; Andrews, L. Infrared spectra and pseudopotential calculations for NUO+, NUO, and NThO in solid neon. J. Chem. Phys. 1999, 111, 11044–11049. [Google Scholar] [CrossRef]
- Wang, X.; Andrews, L.; Vlaisavljevich, B.; Gagliardi, L. Combined Triple and Double Bonds to Uranium: The N≡U=N-H Uranimine Nitride Molecule Prepared in Solid Argon. Inorg. Chem. 2011, 50, 3826–3831. [Google Scholar] [CrossRef]
- Cotton, S. Coordination Chemistry of the Actinides. In Lanthanide and Actinide Chemistry; John Wiley & Sons, Ltd.: West Sussex, UK, 2006; Chapter 11; pp. 173–199. [Google Scholar]
- Baldwin, A.G.; Bridges, N.J.; Braley, J.C. Distribution of Fission Products into Tributyl Phosphate under Applied Nuclear Fuel Recycling Conditions. Ind. Eng. Chem. Res. 2016, 55, 13114–13119. [Google Scholar] [CrossRef]
- Malin, S.A.; Alexis-Martin, B. Assessing the state of uranium research: Environmental justice, health, and extraction. Extr. Ind. Soc. 2020, 7, 512–516. [Google Scholar] [CrossRef]
- Mathuthu, M.; Mokhine, N.D.; Stassen, E. Organic solvent extraction of uranium from alkaline nuclear waste. J. Radioanal. Nucl. Chem. 2019, 319, 687–693. [Google Scholar] [CrossRef]
- Kim, C.J.; Kumar, J.R.; Kim, J.S.; Lee, J.Y.; Yoon, H.S. Solvent extraction studies on uranium using amine based extractants and recovery from low grade ore leach liquors. J. Braz. Chem. Soc. 2012, 23, 1254–1264. [Google Scholar] [CrossRef] [Green Version]
- De Jesus, K.; Rodriguez, R.; Baek, D.L.; Fox, R.V.; Pashikanti, S.; Sharma, K. Extraction of lanthanides and actinides present in spent nuclear fuel and in electronic waste. J. Mol. Liq. 2021, 336, 116006. [Google Scholar] [CrossRef]
- Veliscek-Carolan, J. Separation of actinides from spent nuclear fuel: A review. J. Hazard. Mater. 2016, 318, 266–281. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Mohapatra, P.K. Separation of trivalent actinides and lanthanides using various ‘N’,‘S’and mixed ‘N, O’donor ligands: A review. Radiochim. Acta 2019, 107, 931–949. [Google Scholar] [CrossRef]
- Farnaby, J.H.; Chowdhury, T.; Horsewill, S.J.; Wilson, B.; Jaroschik, F. Lanthanides and actinides: Annual survey of their organometallic chemistry covering the year 2019. Coord. Chem. Rev. 2021, 437, 213830. [Google Scholar] [CrossRef]
- Bart, S.C.; Meyer, K. Highlights in Uranium Coordination Chemistry. In Organometallic and Coordination Chemistry of the Actinides; Albrecht-Schmitt, T.E., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 119–176. [Google Scholar]
- Yeon, J.; Smith, M.D.; Sefat, A.S.; Tran, T.T.; Halasyamani, P.S.; Zur Loye, H.C. U3F12 (H2O), a noncentrosymmetric uranium (IV) fluoride prepared via a convenient in situ route that creates U4+ under mild hydrothermal conditions. Inorg. Chem. 2013, 52, 8303–8305. [Google Scholar] [CrossRef]
- Klepov, V.V.; Felder, J.B.; Zur Loye, H.C. Synthetic strategies for the synthesis of ternary uranium (IV) and thorium (IV) fluorides. Inorg. Chem. 2018, 57, 5597–5606. [Google Scholar] [CrossRef]
- Ilton, E.S.; Haiduc, A.; Cahill, C.L.; Felmy, A.R. Mica surfaces stabilize pentavalent uranium. Inorg. Chem. 2005, 44, 2986–2988. [Google Scholar] [CrossRef] [PubMed]
- Vasiliu, M.; Peterson, K.A.; Gibson, J.K.; Dixon, D.A. Reliable potential energy surfaces for the reactions of H2O with ThO2, PaO2+, UO22+, and UO2+. J. Phys. Chem. A 2015, 119, 11422–11431. [Google Scholar] [CrossRef] [Green Version]
- Lucena, A.F.; Odoh, S.O.; Zhao, J.; Marcalo, J.; Schreckenbach, G.; Gibson, J.K. Oxo-exchange of gas-phase uranyl, neptunyl, and plutonyl with water and methanol. Inorg. Chem. 2014, 53, 2163–2170. [Google Scholar] [CrossRef]
- Cowie, B.E.; Purkis, J.M.; Austin, J.; Love, J.B.; Arnold, P.L. Thermal and photochemical reduction and functionalization chemistry of the uranyl dication, [UVIO2]2+. Chem. Rev. 2019, 119, 10595–10637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Windorff, C.J.; MacDonald, M.R.; Meihaus, K.R.; Ziller, J.W.; Long, J.R.; Evans, W.J. Expanding the Chemistry of Molecular U(2+) Complexes: Synthesis, Characterization, and Reactivity of the {[C5H3(SiMe3)2]3U}(-) Anion. Chem. Eur. J. 2016, 22, 772–782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- MacDonald, M.R.; Fieser, M.E.; Bates, J.E.; Ziller, J.W.; Furche, F.; Evans, W.J. Identification of the +2 Oxidation State for Uranium in a Crystalline Molecular Complex, [K(2.2.2-Cryptand)][(C5H4SiMe3)3U]. J. Am. Chem. Soc. 2013, 135, 13310–13313. [Google Scholar] [CrossRef]
- Wu, Q.Y.; Lan, J.H.; Wang, C.Z.; Cheng, Z.P.; Chai, Z.F.; Gibson, J.K.; Shi, W.Q. Paving the way for the synthesis of a series of divalent actinide complexes: A theoretical perspective. Dalton Trans. 2016, 45, 3102–3110. [Google Scholar] [CrossRef] [PubMed]
- Ryan, A.J.; Angadol, M.A.; Ziller, J.W.; Evans, W.J. Isolation of U(ii) compounds using strong donor ligands, C5Me4H and N(SiMe3)2, including a three-coordinate U(ii) complex. Chem. Commun. 2019, 55, 2325–2327. [Google Scholar] [CrossRef]
- Straub, M.D.; Ouellette, E.T.; Boreen, M.A.; Britt, R.D.; Chakarawet, K.; Douair, I.; Gould, C.A.; Maron, L.; Del Rosal, I.; Villarreal, D.; et al. A Uranium(II) Arene Complex That Acts as a Uranium(I) Synthon. J. Am. Chem. Soc. 2021, 143, 19748–19760. [Google Scholar] [CrossRef]
- Yamasaki, S.; Utsunomiya, S. A review of efforts for volume reduction of contaminated soil in the ten years after the accident at the Fukushima Daiichi Nuclear Power Plant. J. Nucl. Sci. Technol. 2022, 59, 135–147. [Google Scholar] [CrossRef]
- Högberg, L. Root Causes and Impacts of Severe Accidents at Large Nuclear Power Plants. AMBIO 2013, 42, 267–284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burns, P.C.; Ewing, R.C.; Navrotsky, A. Nuclear fuel in a reactor accident. Science 2012, 335, 1184–1188. [Google Scholar] [CrossRef] [PubMed]
- Kortov, V.; Ustyantsev, Y. Chernobyl accident: Causes, consequences and problems of radiation measurements. Radiat. Meas. 2013, 55, 12–16. [Google Scholar] [CrossRef] [Green Version]
- Hatch, M.; Ron, E.; Bouville, A.; Zablotska, L.; Howe, G. The Chernobyl Disaster: Cancer following the Accident at the Chernobyl Nuclear Power Plant. Epidemiol. Rev. 2005, 27, 56–66. [Google Scholar] [CrossRef]
- Korsakov, A.V.; Geger, E.V.; Lagerev, D.G.; Pugach, L.I.; Mousseau, T.A. De novo congenital malformation frequencies in children from the Bryansk region following the Chernobyl disaster (2000–2017). Heliyon 2020, 6, e04616. [Google Scholar] [CrossRef]
- Funabashi, Y.; Kitazawa, K. Fukushima in review: A complex disaster, a disastrous response. Bull. At. Sci. 2012, 68, 9–21. [Google Scholar] [CrossRef]
- Steinhauser, G.; Brandl, A.; Johnson, T.E. Comparison of the Chernobyl and Fukushima nuclear accidents: A review of the environmental impacts. Sci. Total Environ. 2014, 470, 800–817. [Google Scholar] [CrossRef]
- Ran, Y.; Wang, S.; Zhao, Y.; Li, J.; Ran, X.; Hao, Y. A review of biological effects and treatments of inhaled depleted uranium aerosol. J. Environ. Radioact. 2020, 222, 106357. [Google Scholar]
- El Hayek, E.; Medina, S.; Guo, J.; Noureddine, A.; Zychowski, K.E.; Hunter, R.; Velasco, C.A.; Wiesse, M.; Maestas-Olguin, A.; Brinker, C.J.; et al. Uptake and toxicity of respirable carbon-rich uranium-bearing particles: Insights into the role of particulates in uranium toxicity. Environ. Sci. Technol. 2021, 55, 9949–9957. [Google Scholar] [CrossRef]
- Yue, Y.C.; Li, M.H.; Wang, H.B.; Zhang, B.L.; He, W. The toxicological mechanisms and detoxification of depleted uranium exposure. Environ. Health Prev. Med. 2018, 23, 18. [Google Scholar] [CrossRef]
- Ma, M.; Wang, R.; Xu, L.; Xu, M.; Liu, S. Emerging health risks and underlying toxicological mechanisms of uranium contamination: Lessons from the past two decades. Environ. Int. 2020, 145, 106107. [Google Scholar] [CrossRef]
- Tsai, H.J.; Wu, P.Y.; Huang, J.C.; Chen, S.C. Environmental Pollution and Chronic Kidney Disease. Int. J. Med. Sci. 2021, 18, 1121–1129. [Google Scholar] [CrossRef] [PubMed]
- Prat, O.; Vercouter, T.; Ansoborlo, E.; Fichet, P.; Perret, P.; Kurttio, P.; Salonen, L. Uranium Speciation in Drinking Water from Drilled Wells in Southern Finland and Its Potential Links to Health Effects. Environ. Sci. Technol. 2009, 43, 3941–3946. [Google Scholar] [CrossRef] [PubMed]
- WHO Team. Guidelines for Drinking-Water Quality, 4th ed.; Incorporating the 1st Addendum; World Health Organization: New York, NY, USA, 2011. [Google Scholar]
- Nelson, B.J.; Andersson, J.D.; Wuest, F. Targeted Alpha Therapy: Progress in Radionuclide Production, Radiochemistry, and Applications. Pharmaceutics 2021, 13, 49. [Google Scholar] [CrossRef] [PubMed]
- Morgenstern, A.; Apostolidis, C.; Kratochwil, C.; Sathekge, M.; Krolicki, L.; Bruchertseifer, F. An Overview of Targeted Alpha Therapy with 225Actinium and 213Bismuth. Curr. Radiopharm. 2018, 11, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Liem, P.H.; Tran, H.N.; Sembiring, T.M. Design optimization of a new homogeneous reactor for medical radioisotope Mo-99/Tc-99m production. Prog. Nucl. Energy 2015, 82, 191–196. [Google Scholar] [CrossRef]
- Kraka, E.; Zou, W.; Tao, Y. Decoding Chemical Information from Vibrational Spectroscopy Data: Local Vibrational Mode Theory. WIREs Comput. Mol. Sci. 2020, 10, 1480. [Google Scholar] [CrossRef]
- Badger, R.M. A Relation between Internuclear Distances and Bond Force Constants. J. Chem. Phys. 1934, 2, 128–131. [Google Scholar] [CrossRef] [Green Version]
- Kraka, E.; Larsson, J.A.; Cremer, D. Generalization of the Badger Rule Based on the Use of Adiabatic Vibrational Modes. In Computational Spectroscopy; Grunenberg, J., Ed.; Wiley: New York, NY, USA, 2010; pp. 105–149. [Google Scholar]
- Wilson, E.B.; Decius, J.C.; Cross, P.C.M. Molecular Vibrations. The Theory of Infrared and Raman Vibrational Spectra; McGraw-Hill: New York, NY, USA, 1955; pp. 59–136. [Google Scholar]
- Wilson, E.B.; Decius, J.C.; Cross, P.C.; Sundheim, B.R. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra. J. Electrochem. Soc. 1955, 102, 235C. [Google Scholar] [CrossRef]
- Zou, W.; Kalescky, R.; Kraka, E.; Cremer, D. Relating Normal Vibrational Modes to Local Vibrational Modes with the Help of an Adiabatic Connection Scheme. J. Chem. Phys. 2012, 137, 084114. [Google Scholar] [CrossRef] [Green Version]
- Zou, W.; Cremer, D. Properties of Local Vibrational Modes: The Infrared Intensity. Theor. Chem. Acc. 2014, 133, 1451–1466. [Google Scholar] [CrossRef]
- Zou, W.; Cremer, D. C2 in a Box: Determining its Intrinsic Bond Strength for the X1Σ+g Ground State. Chem. Eur. J. 2016, 22, 4087–4097. [Google Scholar] [CrossRef] [PubMed]
- Delgado, A.A.A.; Sethio, D.; Munar, I.; Aviyente, V.; Kraka, E. Local Vibrational Mode Analysis of Ion–Solvent and Solvent–Solvent Interactions for Hydrated Ca2+ Clusters. J. Chem. Phys. 2020, 153, 224303. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, R.; Verma, N.; Kraka, E.; Larson, E.C. Deep Learning-Based Ligand Design Using Shared Latent Implicit Fingerprints from Collaborative Filtering. J. Chem. Inf. Model. 2021, 61, 2159–2174. [Google Scholar] [CrossRef]
- Freindorf, M.; Kraka, E. Critical Assessment of the FeC and CO Bond strength in Carboxymyoglobin—A QM/MM Local Vibrational Mode Study. J. Mol. Model. 2020, 26, 281. [Google Scholar] [CrossRef]
- Verma, N.; Tao, Y.; Kraka, E. Systematic Detection and Characterization of Hydrogen Bonding in Proteins via Local Vibrational Modes. J. Phys. Chem. B 2021, 125, 2551–2565. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Identification of the Strongest Bonds in Chemistry. J. Phys. Chem. A 2013, 117, 8981–8995. [Google Scholar] [CrossRef]
- Setiawan, D.; Sethio, D.; Cremer, D.; Kraka, E. From Strong to Weak NF Bonds: On the Design of a New Class of Fluorinating Agents. Phys. Chem. Chem. Phys. 2018, 20, 23913–23927. [Google Scholar] [CrossRef]
- Humason, A.; Zou, W.; Cremer, D. 11,11-Dimethyl-1,6-methano[10]annulene—An Annulene with an Ultralong CC Bond or a Fluxional Molecule? J. Phys. Chem. A 2014, 119, 1666–1682. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Are Carbon-Halogen Double and Triple Bonds Possible? Int. J. Quantum Chem. 2014, 114, 1060–1072. [Google Scholar] [CrossRef]
- Kalescky, R.; Zou, W.; Kraka, E.; Cremer, D. Quantitative Assessment of the Multiplicity of Carbon-Halogen Bonds: Carbenium and Halonium Ions with F, Cl, Br, and I. J. Phys. Chem. A 2014, 118, 1948–1963. [Google Scholar] [CrossRef] [PubMed]
- Larsson, J.A.; Cremer, D. Theoretical Verification and Extension of the Mckean Relationship between Bond Lengths and Stretching Frequencies. J. Mol. Struct. 1999, 485–486, 385–407. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. From Molecular Vibrations to Bonding, Chemical Reactions, and Reaction Mechanism. Curr. Org. Chem. 2010, 14, 1524–1560. [Google Scholar] [CrossRef]
- Cremer, D.; Wu, A.; Larsson, J.A.; Kraka, E. Some Thoughts about Bond Energies, Bond Lengths, and Force Constants. J. Mol. Model. 2000, 6, 396–412. [Google Scholar] [CrossRef]
- Kraka, E.; Cremer, D. Weaker Bonds with Shorter Bond Lengths. Rev. Proc. Quim. 2012, 6, 31–34. [Google Scholar] [CrossRef]
- Setiawan, D.; Kraka, E.; Cremer, D. Hidden Bond Anomalies: The Peculiar Case of the Fluorinated Amine Chalcogenides. J. Phys. Chem. A 2015, 119, 9541–9556. [Google Scholar] [CrossRef]
- Kraka, E.; Setiawan, D.; Cremer, D. Re-Evaluation of the Bond Length-Bond Strength Rule: The Stronger Bond Is not Always the Shorter Bond. J. Comp. Chem. 2015, 37, 130–142. [Google Scholar] [CrossRef]
- Delgado, A.A.A.; Humason, A.; Kalescky, R.; Freindorf, M.; Kraka, E. Exceptionally Long Covalent CC Bonds—A Local Vibrational Mode Study. Molecules 2021, 26, 950. [Google Scholar] [CrossRef]
- Zhao, L.; Zhi, M.; Frenking, G. The strength of a chemical bond. Int. J. Quantum Chem. 2021, 122, e26773. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. The Intrinsic Strength of the Halogen Bond: Electrostatic and Covalent Contributions Described by Coupled Cluster Theory. Phys. Chem. Chem. Phys. 2016, 18, 33031–33046. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. Quantitative Assessment of Halogen Bonding Utilizing Vibrational Spectroscopy. Inorg. Chem. 2016, 56, 488–502. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, V.; Cremer, D. Transition from Metal-Ligand Bonding to Halogen Bonding Involving a Metal as Halogen Acceptor: A Study of Cu, Ag, Au, Pt, and Hg Complexes. Chem. Phys. Lett. 2017, 681, 56–63. [Google Scholar] [CrossRef]
- Yannacone, S.; Oliveira, V.; Verma, N.; Kraka, E. A Continuum from Halogen Bonds to Covalent Bonds: Where Do λ3 Iodanes Fit? Inorganics 2019, 7, 47. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, V.P.; Kraka, E.; Machado, F.B.C. Pushing 3c-4e Bonds to the Limit: A Coupled Cluster Study of Stepwise Fluorination of First-Row Atoms. Inorg. Chem. 2019, 58, 14777–14789. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, V.P.; Marcial, B.L.; Machado, F.B.C.; Kraka, E. Metal-Halogen Bonding Seen through the Eyes of Vibrational Spectroscopy. Materials 2020, 13, 55. [Google Scholar] [CrossRef] [Green Version]
- Setiawan, D.; Kraka, E.; Cremer, D. Description of Pnicogen Bonding with the help of Vibrational Spectroscopy—The Missing Link between Theory and Experiment. Chem. Phys. Lett. 2014, 614, 136–142. [Google Scholar] [CrossRef]
- Setiawan, D.; Kraka, E.; Cremer, D. Strength of the Pnicogen Bond in Complexes Involving Group VA Elements N, P, and As. J. Phys. Chem. A 2014, 119, 1642–1656. [Google Scholar] [CrossRef]
- Setiawan, D.; Cremer, D. Super-Pnicogen Bonding in the Radical Anion of the Fluorophosphine Dimer. Chem. Phys. Lett. 2016, 662, 182–187. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, V.; Cremer, D.; Kraka, E. The Many Facets of Chalcogen Bonding: Described by Vibrational Spectroscopy. J. Phys. Chem. A 2017, 121, 6845–6862. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E. Systematic Coupled Cluster Study of Noncovalent Interactions Involving Halogens, Chalcogens, and Pnicogens. J. Phys. Chem. A 2017, 121, 9544–9556. [Google Scholar] [CrossRef]
- Sethio, D.; Oliveira, V.; Kraka, E. Quantitative Assessment of Tetrel Bonding Utilizing Vibrational Spectroscopy. Molecules 2018, 23, 2763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Dai, H.; Yan, H.; Zou, W.; Cremer, D. B-H π Interaction: A New Type of Nonclassical Hydrogen Bonding. J. Am. Chem. Soc. 2016, 138, 4334–4337. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Zhang, X.; Dai, H.; Yan, H.; Cremer, D.; Kraka, E. Description of an Unusual Hydrogen Bond between Carborane and a Phenyl Group. J. Organometal. Chem. 2018, 856, 114–127. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, Y.; Zou, W.; Nanayakkara, S.; Yannacone, S.; Kraka, E. In Situ Assessment of Intrinsic Strength of X-I⋯OA Type Halogen Bonds in Molecular Crystals with Periodic Local Vibrational Mode Theory. Molecules 2020, 25, 1589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalescky, R.; Zou, W.; Kraka, E.; Cremer, D. Local Vibrational Modes of the Water Dimer—Comparison of Theory and Experiment. Chem. Phys. Lett. 2012, 554, 243–247. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Local Vibrational Modes of the Formic Acid Dimer—The Strength of the Double H-Bond. Mol. Phys. 2013, 111, 1497–1510. [Google Scholar] [CrossRef]
- Freindorf, M.; Kraka, E.; Cremer, D. A Comprehensive Analysis of Hydrogen Bond Interactions Based on Local Vibrational Modes. Int. J. Quantum Chem. 2012, 112, 3174–3187. [Google Scholar] [CrossRef]
- Kalescky, R.; Zou, W.; Kraka, E.; Cremer, D. Vibrational Properties of the Isotopomers of the Water Dimer Derived from Experiment and Computations. Aust. J. Chem. 2014, 67, 426. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.; Zou, W.; Jia, J.; Li, W.; Cremer, D. Different Ways of Hydrogen Bonding in Water—Why Does Warm Water Freeze Faster than Cold Water? J. Chem. Theory Comput. 2017, 13, 55–76. [Google Scholar] [CrossRef]
- Tao, Y.; Zou, W.; Kraka, E. Strengthening of Hydrogen Bonding With the Push-Pull Effect. Chem. Phys. Lett. 2017, 685, 251–258. [Google Scholar] [CrossRef]
- Freindorf, M.; Tao, Y.; Sethio, D.; Cremer, D.; Kraka, E. New Mechanistic Insights into the Claisen Rearrangement of Chorismate—A Unified Reaction Valley Approach Study. Mol. Phys. 2018, 117, 1172–1192. [Google Scholar] [CrossRef]
- Makoś, M.Z.; Freindorf, M.; Sethio, D.; Kraka, E. New Insights into Fe–H2 and Fe–H- Bonding of a [NiFe] Hydrogenase Mimic—A Local Vibrational Mode Study. Theor. Chem. Acc. 2019, 138, 76. [Google Scholar] [CrossRef]
- Lyu, S.; Beiranvand, N.; Freindorf, M.; Kraka, E. Interplay of Ring Puckering and Hydrogen Bonding in Deoxyribonucleosides. J. Phys. Chem. A 2019, 123, 7087–7103. [Google Scholar] [CrossRef] [PubMed]
- Yannacone, S.; Sethio, D.; Kraka, E. Quantitative Assessment of Intramolecular Hydrogen Bonds in Neutral Histidine. Theor. Chem. Acc. 2020, 139, 125. [Google Scholar] [CrossRef]
- Beiranvand, N.; Freindorf, M.; Kraka, E. Hydrogen Bonding in Natural and Unnatural Base Pairs—Explored with Vibrational Spectroscopy. Molecules 2021, 26, 2268. [Google Scholar] [CrossRef]
- Tao, Y.; Zou, W.; Sethio, D.; Verma, N.; Qiu, Y.; Tian, C.; Cremer, D.; Kraka, E. In Situ Measure of Intrinsic Bond Strength in Crystalline Structures: Local Vibrational Mode Theory for Periodic Systems. J. Chem. Theory Comput. 2019, 15, 1761–1776. [Google Scholar] [CrossRef]
- Nanayakkara, S.; Tao, Y.; Kraka, E. Capturing Individual Hydrogen Bond Strengths in Ices via Periodic Local Vibrational Mode Theory: Beyond the Lattice Energy Picture. J. Chem. Theory Comput. 2022, 18, 562–579. [Google Scholar] [CrossRef]
- Delgado, A.A.A.; Humason, A.; Kraka, E. Pancake bonding seen through the eyes of spectroscopy. In Density Functional Theory—Recent Advances, New Perspectives and Applications; IntechOpen: London, UK, 2021; pp. 1–21. [Google Scholar] [CrossRef]
- Mayer, I. Charge, bond brder an valence in the ab initio theory. Chem. Phys. Lett. 1983, 97, 270–274. [Google Scholar] [CrossRef]
- Mayer, I. Bond orders and valences from ab initio wave functions. Int. J. Quantum Chem. 1986, 29, 477–483. [Google Scholar] [CrossRef]
- Mayer, I. Bond order and valence indices: A personal account. J. Comput. Chem. 2007, 28, 204–221. [Google Scholar] [CrossRef]
- Kraka, E.; Freindorf, M. Characterizing the Metal Ligand Bond Strength via Vibrational Spectroscopy: The Metal Ligand Electronic Parameter (MLEP). In Topics in Organometallic Chemistry—New Directions in the Modeling of Organometallic Reactions; Lledós, A., Ujaque, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 67, pp. 1–43. [Google Scholar]
- Wang, X.; Andrews, L.; Marsden, C.J. Reactions of Uranium Atoms with Ammonia: Infrared Spectra and Quasi-Relativistic Calculations of the U:NH3, H2N-UH, and HN=UH2 Complexes. Chem. Eur. J. 2008, 14, 9192–9201. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Bader, R. Atoms in Molecules: A Quantum Theory; Clarendron Press: Oxford, UK, 1995. [Google Scholar]
- Popelier, P. Atoms in Molecules: An Introduction; Prentice-Hall: Harlow, UK, 2000. [Google Scholar]
- Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density? Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. 1984, 23, 627–628. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
- Kraka, E.; Cremer, D. Chemical Implication of Local Features of the Electron Density Distribution. In Theoretical Models of Chemical Bonding. The Concept of the Chemical Bond; Maksic, Z.B., Ed.; Springer: Heidelberg, Germany, 1990; Volume 2, pp. 453–542. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
- Feng, R.; Peterson, K.A. Correlation consistent basis sets for actinides. II. The atoms Ac and Np-Lr. J. Chem. Phys. 2017, 147, 084108. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibsom, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kraka, E.; Cremer, D.; Zou, W.; Filatov, M.; Gräfenstein, J.; Izotov, D.; Gauss, J.; He, Y.; Wu, A.; Konkoli, Z.; et al. COLOGNE2020; Computational and Theoretical Chemistry Group (CATCO), Southern Methodist University: Dallas, TX, USA, 2020. [Google Scholar]
- Zou, W.; Tao, Y.; Freindorf, M.; Makoś, M.Z.; Verma, N.; Cremer, D.; Kraka, E. Local Vibrational Mode Analysis (LModeA); Computational and Theoretical Chemistry Group (CATCO), Southern Methodist University: Dallas, TX, USA, 2021. [Google Scholar]
- Keith, T.A. AIMALL; TK Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]



| U≡N | U=L; L=N,O | U State | |||||||
|---|---|---|---|---|---|---|---|---|---|
| r | k | BSO | H(r) | r | k | BSO | H(r) | ||
| N≡U≡N | 1.713 | 8.085 | 3.081 | −0.437 | - | - | - | - | —U(VI) |
| N≡U | 1.732 | 7.772 | 2.976 | −0.398 | - | - | - | - | —U(III) |
| N≡U=NH | 1.695 | 8.077 | 3.078 | −0.474 | 1.828 | 4.918 | 1.989 | −0.222 | —U(V) |
| N≡U=O | 1.697 | 8.554 | 3.238 | −0.470 | 1.761 | 7.824 | 2.066 | −0.319 | —U(V) |
| UO | - | - | - | - | 1.836 | 5.883 | 1.689 | −0.239 | —U(IV) |
| UO | - | - | - | - | 1.775 | 7.288 | 1.966 | −0.310 | —U(IV) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa Peluzo, B.M.T.; Kraka, E. Uranium: The Nuclear Fuel Cycle and Beyond. Int. J. Mol. Sci. 2022, 23, 4655. https://doi.org/10.3390/ijms23094655
Costa Peluzo BMT, Kraka E. Uranium: The Nuclear Fuel Cycle and Beyond. International Journal of Molecular Sciences. 2022; 23(9):4655. https://doi.org/10.3390/ijms23094655
Chicago/Turabian StyleCosta Peluzo, Bárbara Maria Teixeira, and Elfi Kraka. 2022. "Uranium: The Nuclear Fuel Cycle and Beyond" International Journal of Molecular Sciences 23, no. 9: 4655. https://doi.org/10.3390/ijms23094655
APA StyleCosta Peluzo, B. M. T., & Kraka, E. (2022). Uranium: The Nuclear Fuel Cycle and Beyond. International Journal of Molecular Sciences, 23(9), 4655. https://doi.org/10.3390/ijms23094655







