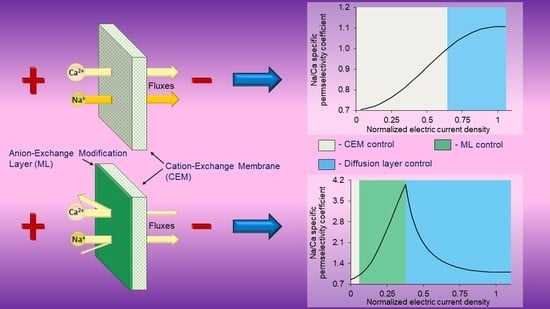
Mathematical Modeling of Monovalent Permselectivity of a Bilayer Ion-Exchange Membrane as a Function of Current Density
Abstract
1. Introduction
2. Theoretical Part
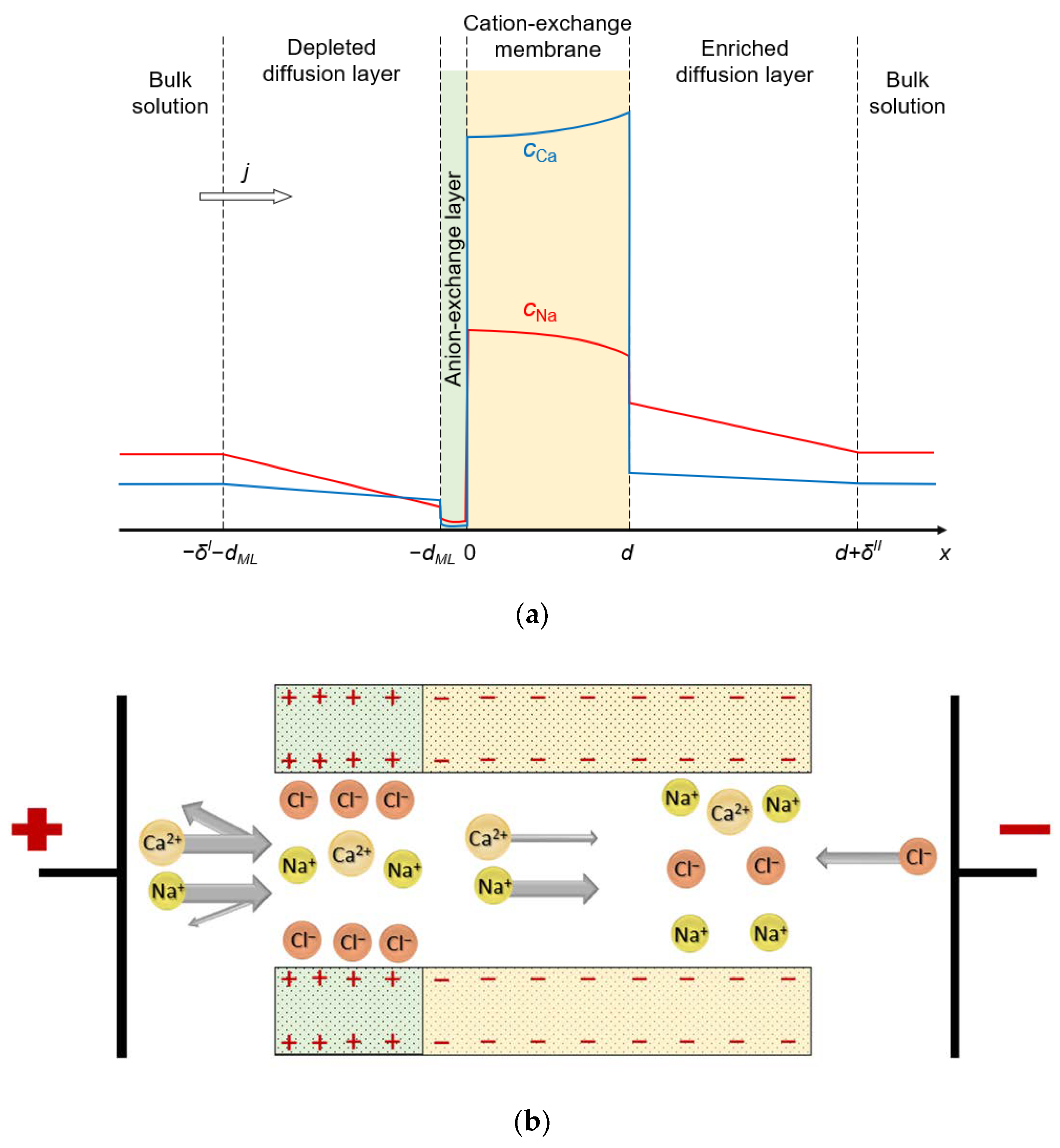
2.1. Mathematical Model
- The substrate and modification layers are considered as a homogeneous medium in which fixed charged groups are uniformly distributed;
- It is assumed that the solvent flux through the membrane is negligible, and therefore the phenomena of osmosis and electroosmosis are not taken into account;
- The impact of convection transport in solution is taken into account implicitly through the diffusion layer thickness, which is considered independent of the voltage applied;
- The gradients of temperature, pressure and solution density are ignored;
- Water splitting and electroconvection are not taken into account.
2.2. Input Parameters
3. Results and Discussions
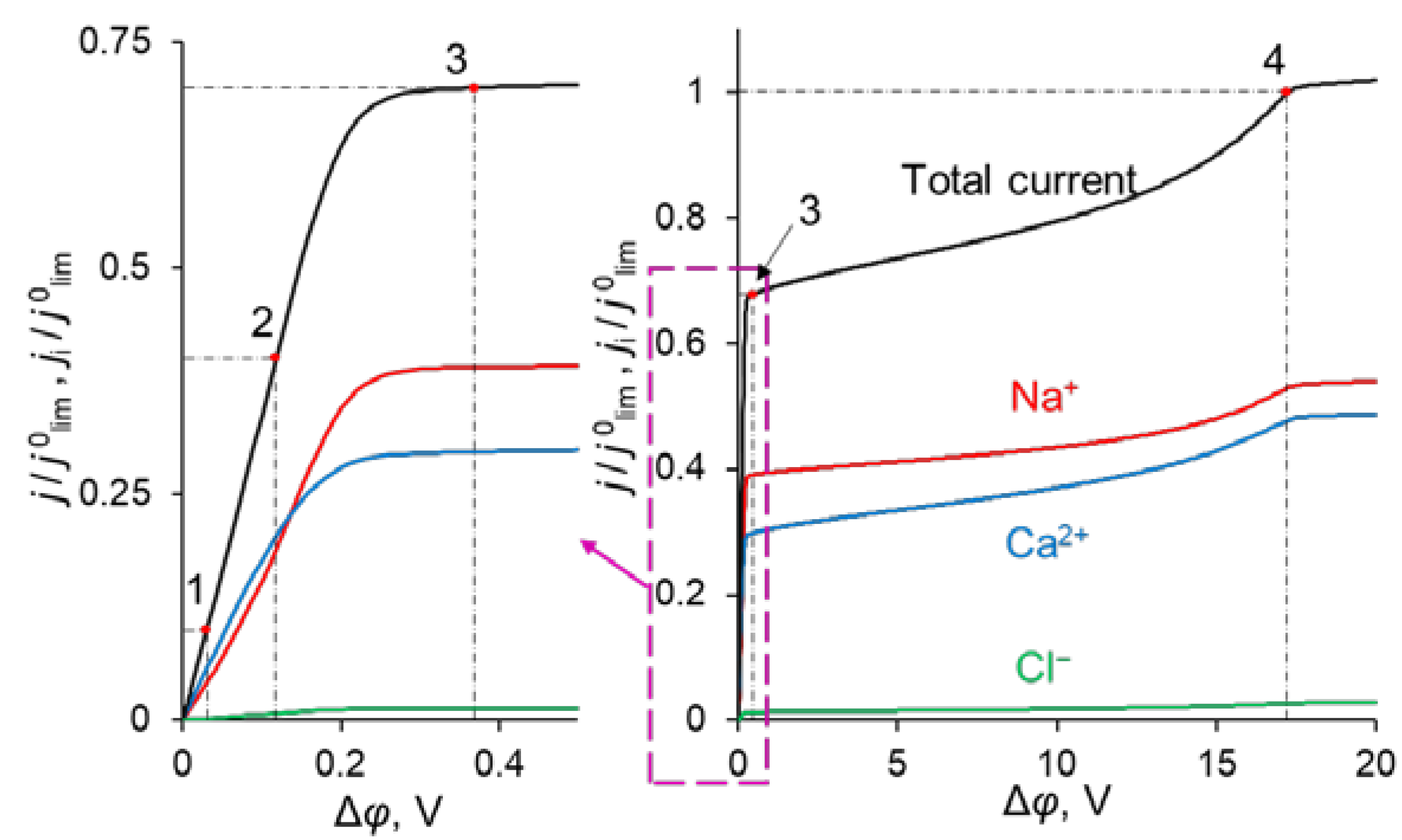
3.1. Limiting Current Density
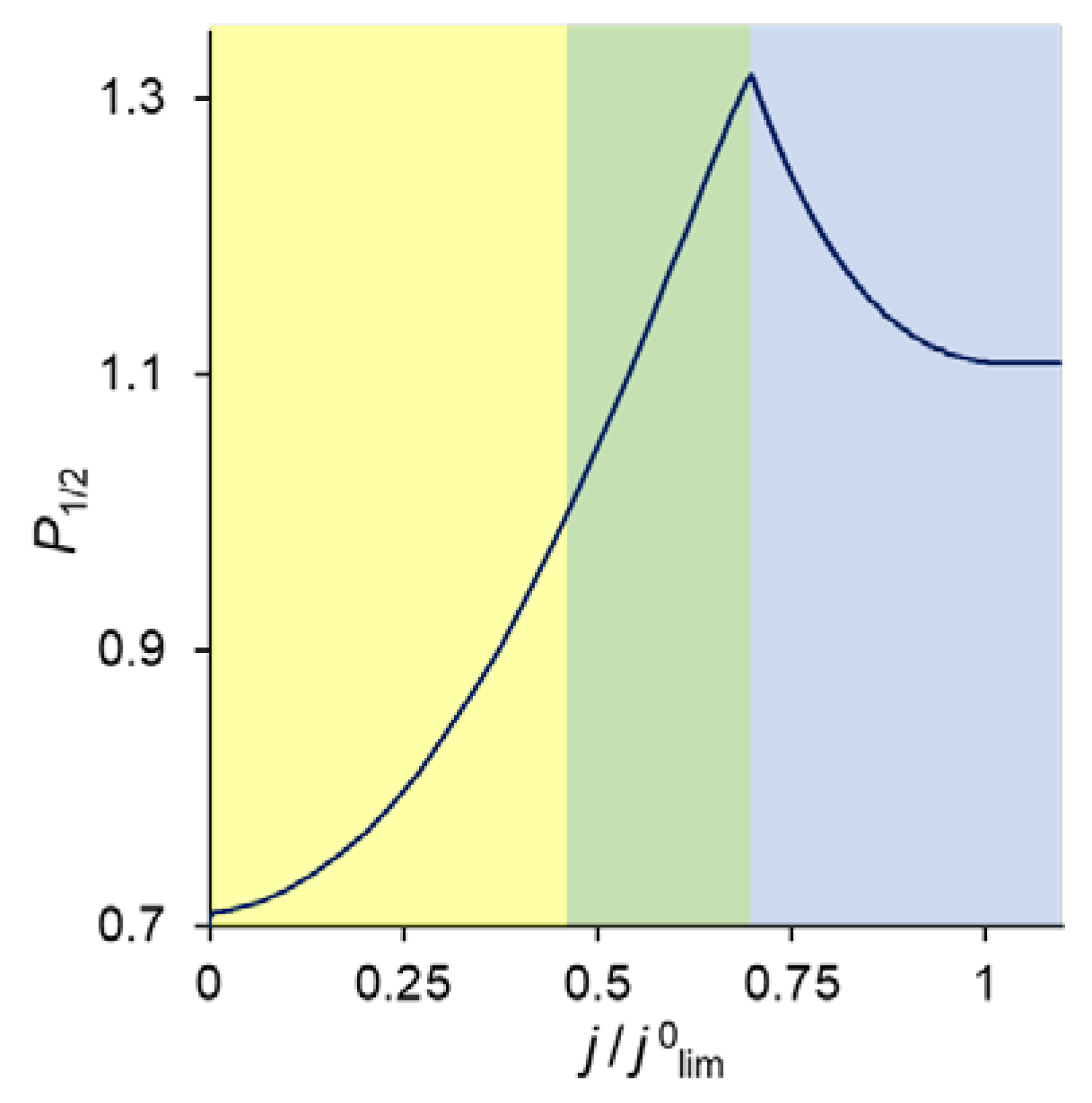
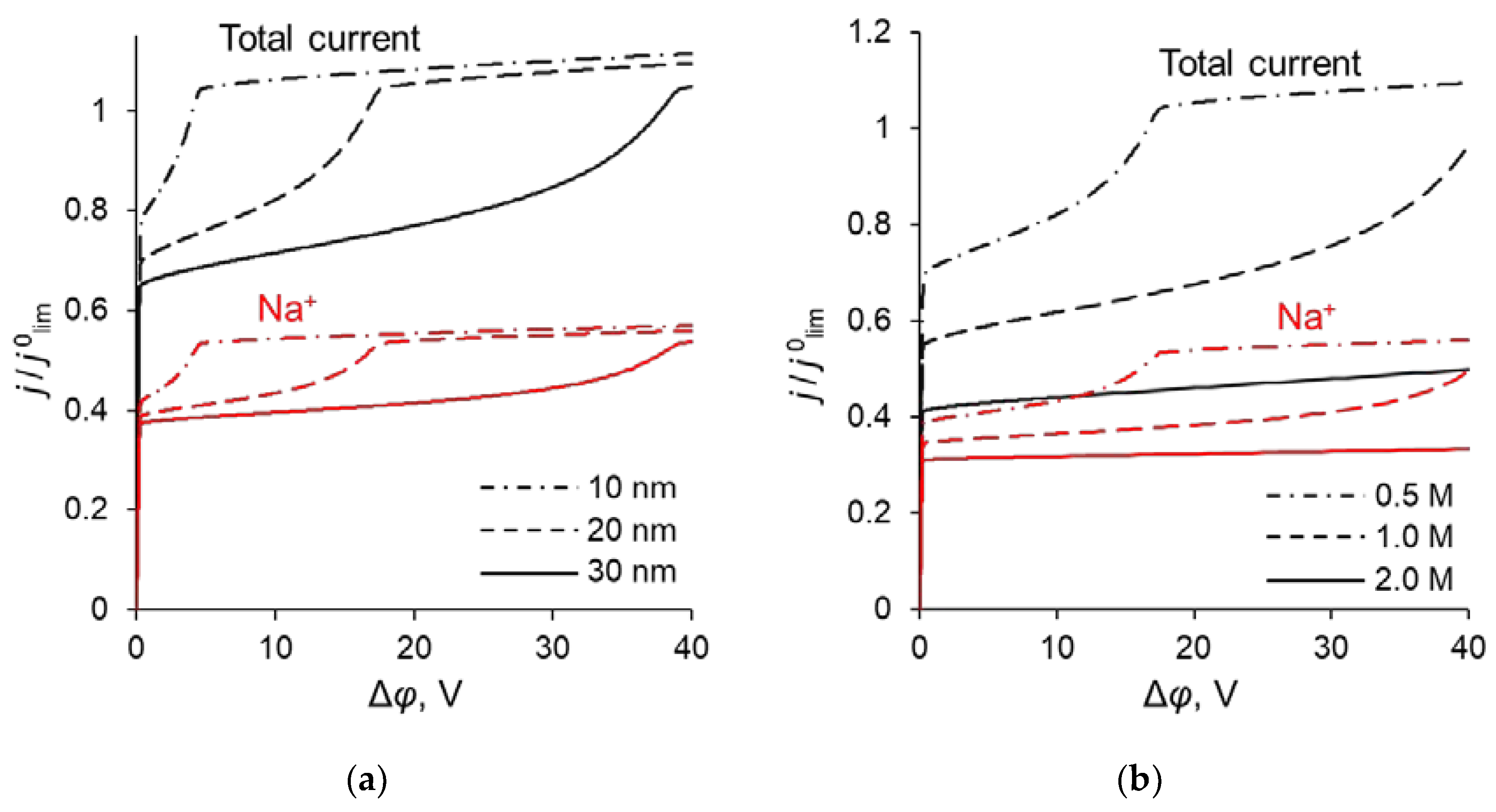
3.2. Specific Permselectivity and CVC
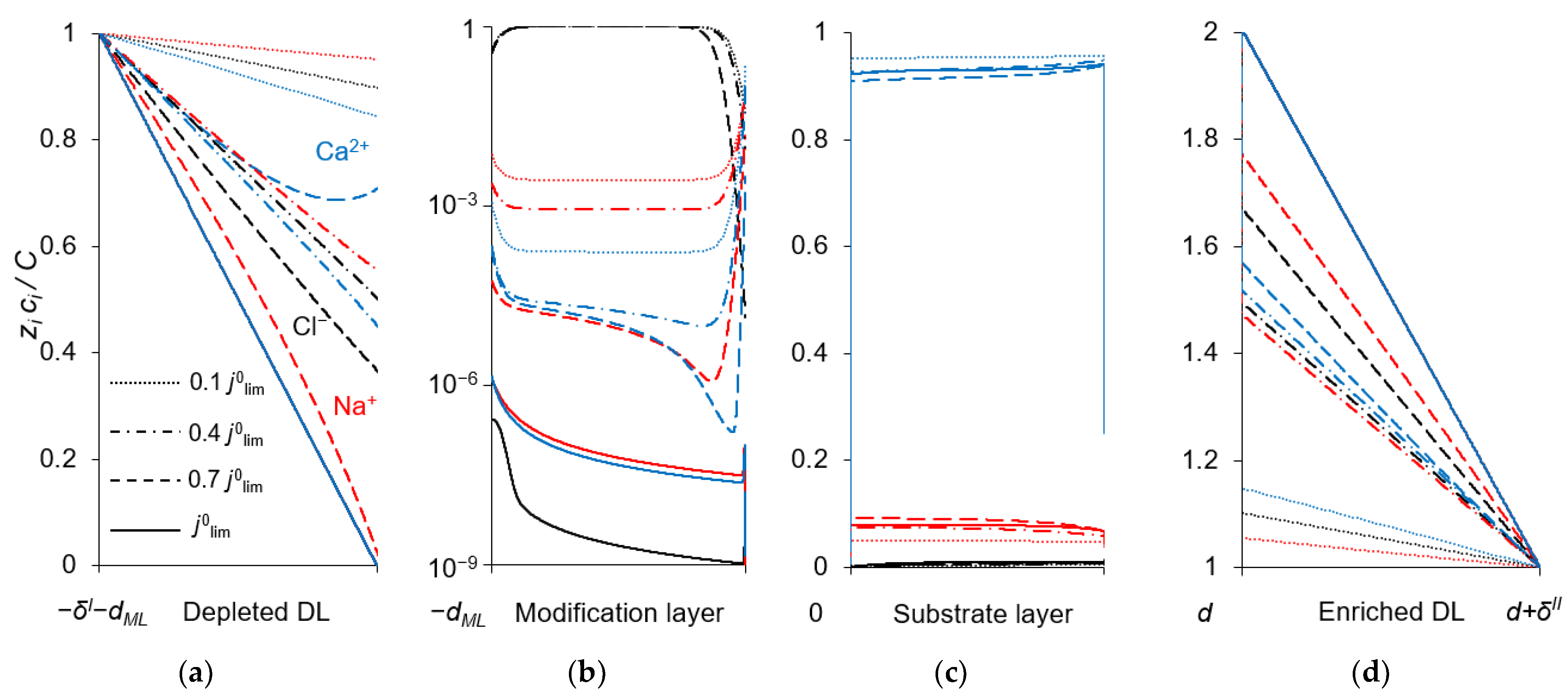
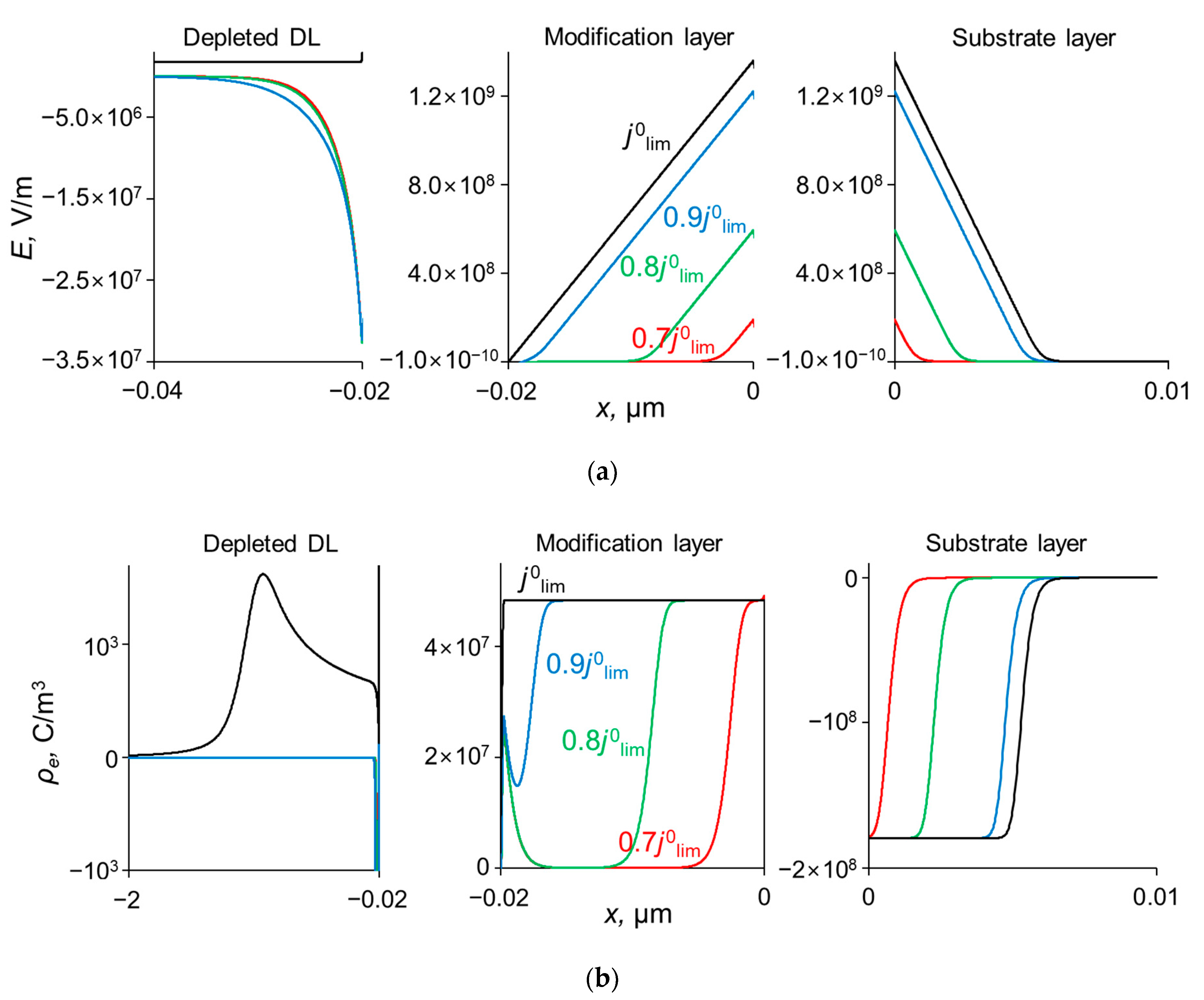
3.3. Concentration Profiles
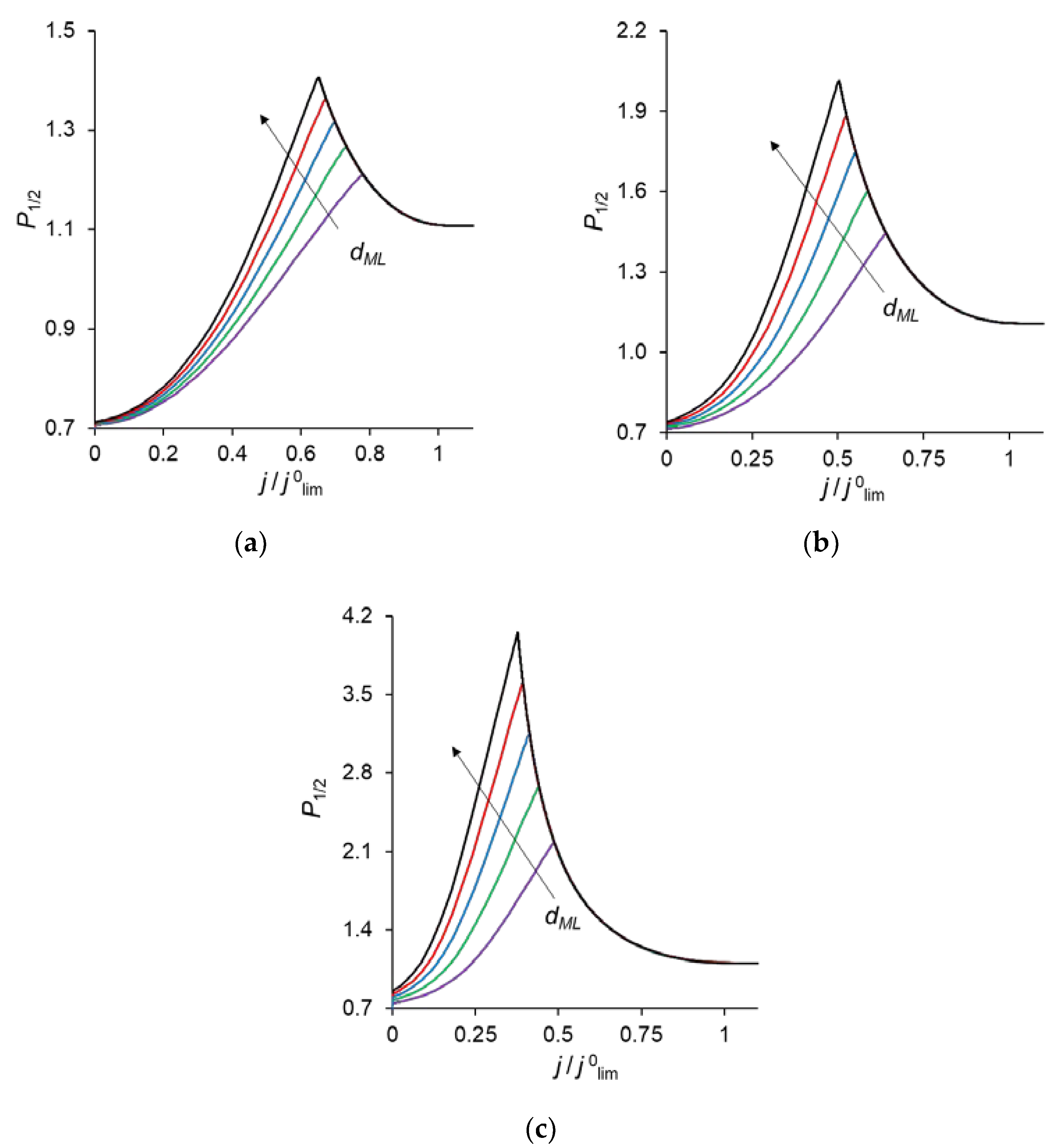
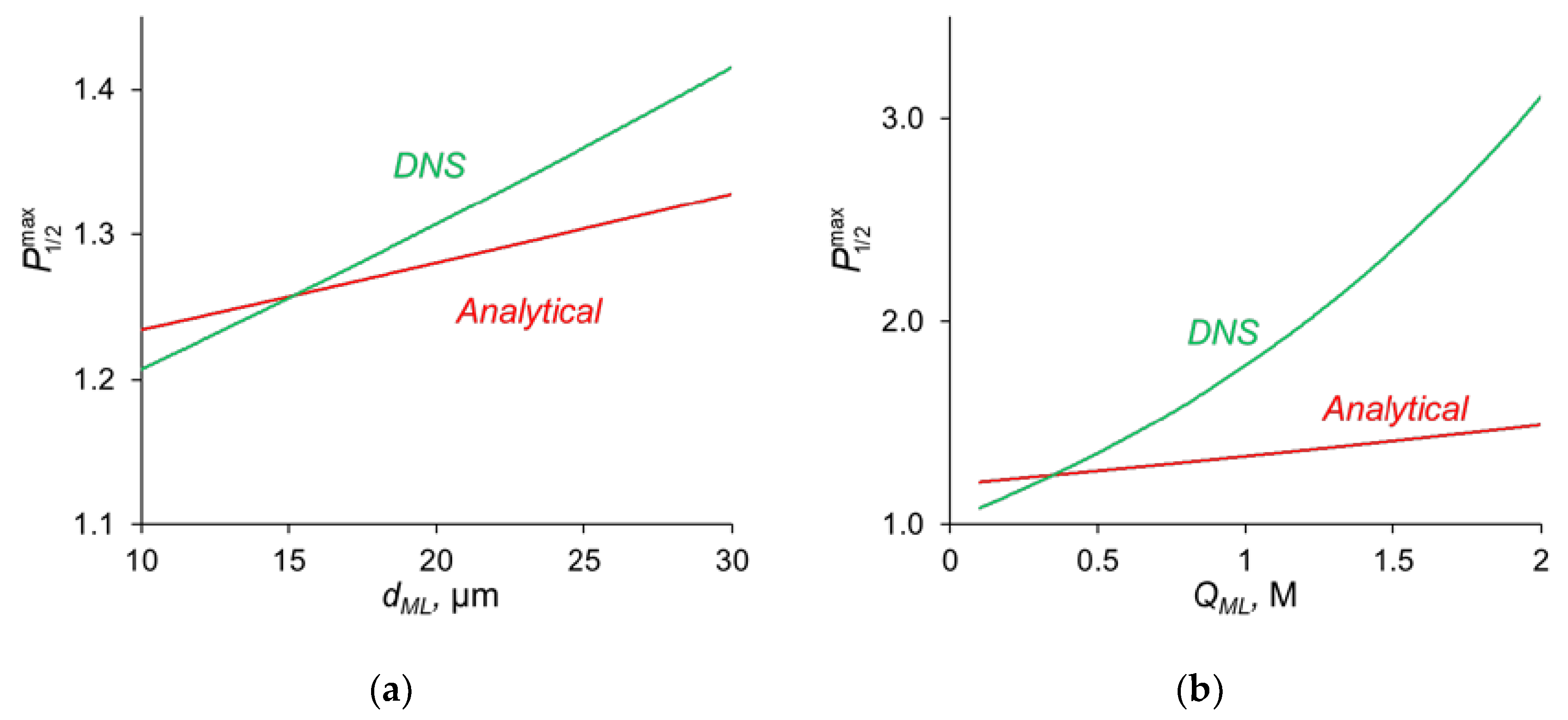
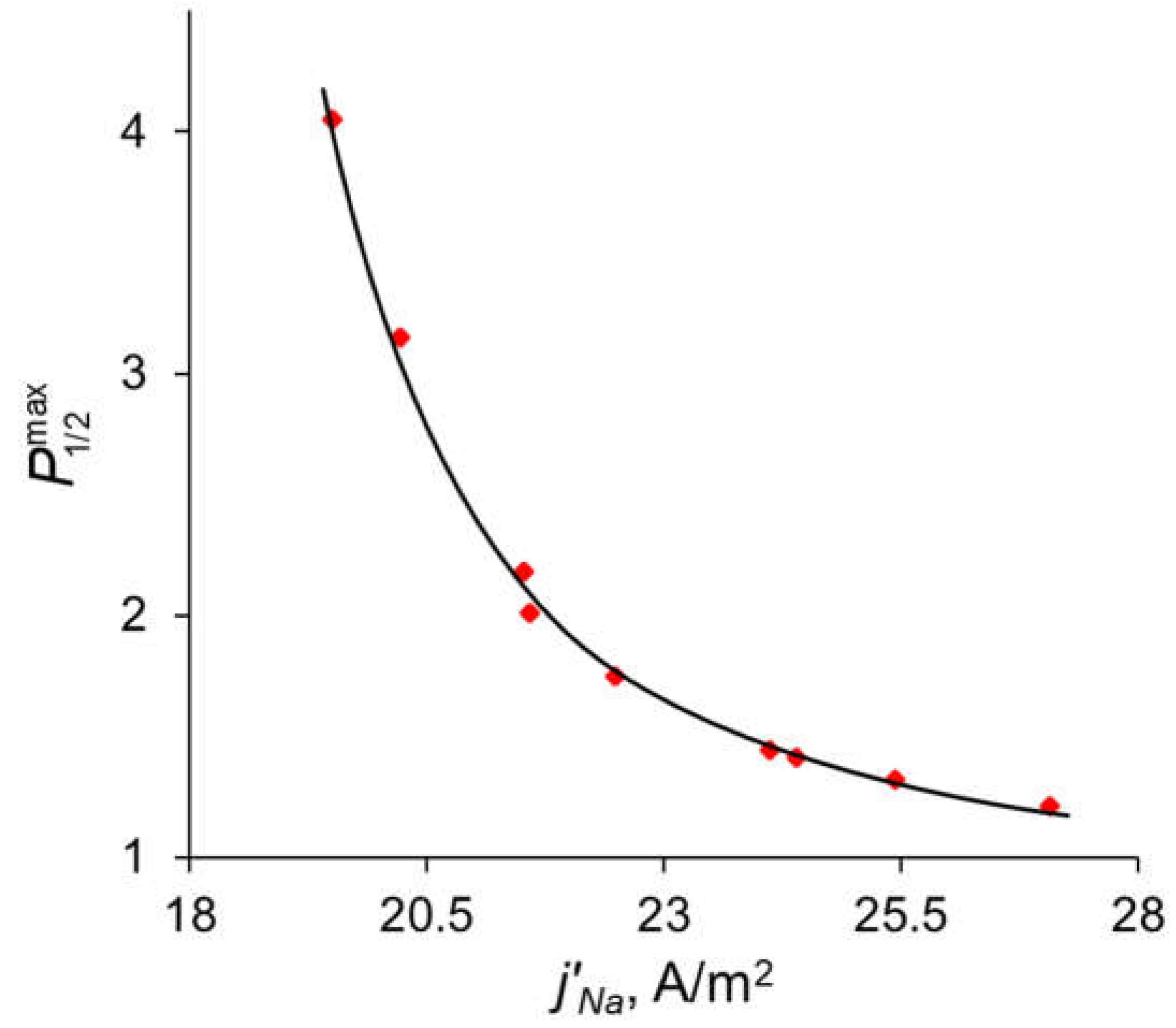
3.4. Analytical Assessement of the Maximum Value of P1/2
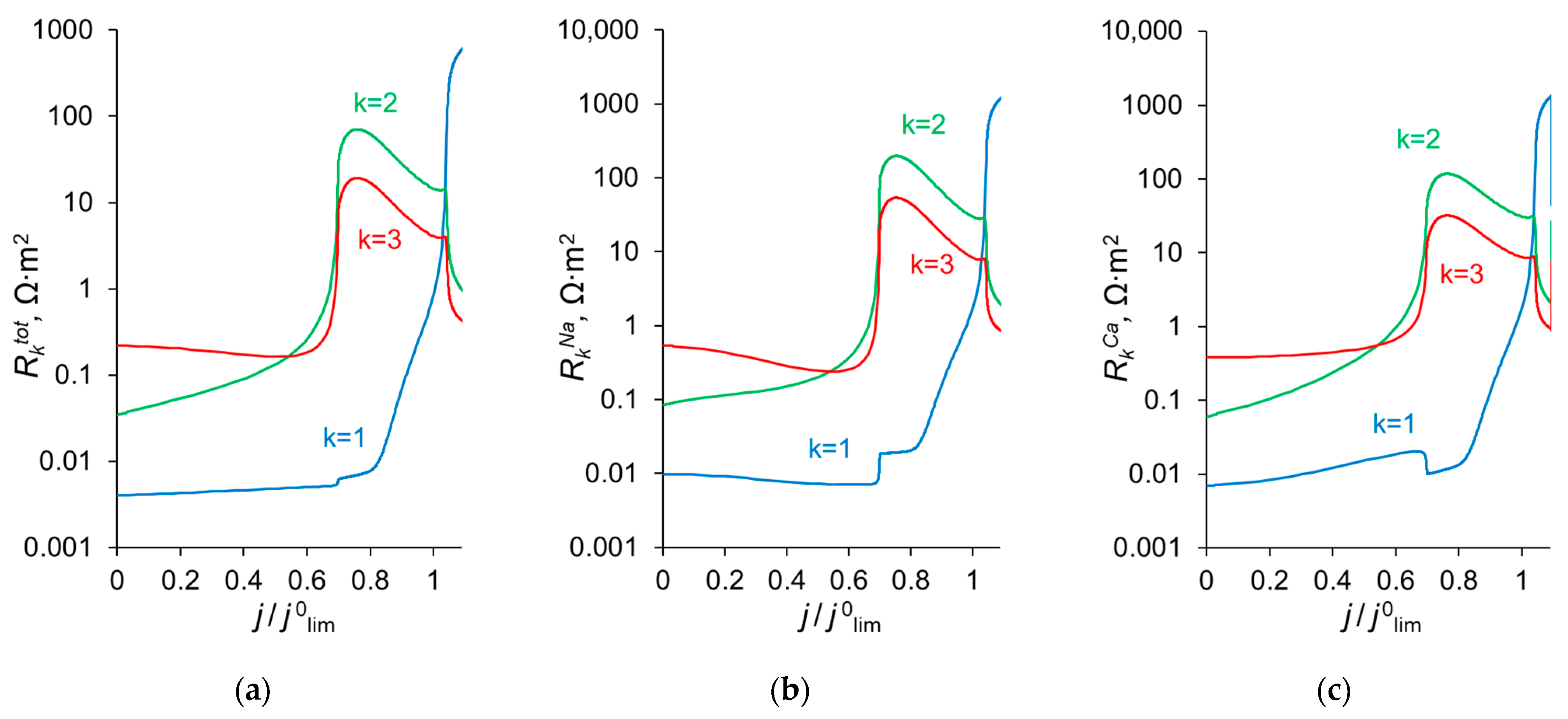
3.5. Change in the Kinetic Control with Increasing Current Density
3.6. Trade-Off Curve between Membrane Permselectivity and Permeability. The Effect of the Concentration of Fixed Groups in the Modification Layer and Its Thickness
3.7. Discussion
4. Determination of the Model Input Parameters
4.1. Parameters of the Substrate Membrane and Modification Layer
4.2. Determination of Activity Coefficients
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion exchange membranes: New developments and applications. J. Memb. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Al-Amshawee, S.; Yunus, M.Y.B.M.; Azoddein, A.A.M.; Hassell, D.G.; Dakhil, I.H.; Hasan, H.A. Electrodialysis desalination for water and wastewater: A review. Chem. Eng. J. 2020, 380, 122231. [Google Scholar] [CrossRef]
- Scarazzato, T.; Panossian, Z.; Tenório, J.A.S.; Pérez-Herranz, V.; Espinosa, D.C.R. A review of cleaner production in electroplating industries using electrodialysis. J. Clean. Prod. 2017, 168, 1590–1602. [Google Scholar] [CrossRef]
- Peng, H.; Guo, J. Removal of chromium from wastewater by membrane filtration, chemical precipitation, ion exchange, adsorption electrocoagulation, electrochemical reduction, electrodialysis, electrodeionization, photocatalysis and nanotechnology: A review. Environ. Chem. Lett. 2020, 18, 2055–2068. [Google Scholar] [CrossRef]
- Daufin, G.; Escudier, J.P.; Carrère, H.; Bérot, S.; Fillaudeau, L.; Decloux, M. Recent and Emerging Applications of Membrane Processes in the Food and Dairy Industry. Food Bioprod. Process. 2001, 79, 89–102. [Google Scholar] [CrossRef]
- Bazinet, L.; Geoffroy, T.R. Electrodialytic processes: Market overview, membrane phenomena, recent developments and sustainable strategies. Membranes 2020, 10, 221. [Google Scholar] [CrossRef]
- Cohen, B.; Lazarovitch, N.; Gilron, J. Upgrading groundwater for irrigation using monovalent selective electrodialysis. Desalination 2018, 431, 126–139. [Google Scholar] [CrossRef]
- Zhang, Y.; Paepen, S.; Pinoy, L.; Meesschaert, B.; Van Der Bruggen, B. Selectrodialysis: Fractionation of divalent ions from monovalent ions in a novel electrodialysis stack. Sep. Purif. Technol. 2012, 88, 191–201. [Google Scholar] [CrossRef]
- Zhang, Y.; Desmidt, E.; Van Looveren, A.; Pinoy, L.; Meesschaert, B.; Van Der Bruggen, B. Phosphate separation and recovery from wastewater by novel electrodialysis. Environ. Sci. Technol. 2013, 47, 5888–5895. [Google Scholar] [CrossRef]
- Reig, M.; Valderrama, C.; Gibert, O.; Cortina, J.L. Selectrodialysis and bipolar membrane electrodialysis combination for industrial process brines treatment: Monovalent-divalent ions separation and acid and base production. Desalination 2016, 399, 88–95. [Google Scholar] [CrossRef]
- Van Soestbergen, M.; Biesheuvel, P.M.; Bazant, M.Z. Diffuse-charge effects on the transient response of electrochemical cells. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 81, 021503. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.; Wu, B.; Yu, D.; Mondal, A.N.; Hou, L.; Afsar, N.U.; Li, Q.; Xu, T.; Miao, J.; Xu, T. Monovalent cation perm-selective membranes (MCPMs): New developments and perspectives. Chin. J. Chem. Eng. 2017, 25, 1606–1615. [Google Scholar] [CrossRef]
- Van der Bruggen, B. Ion-Exchange Membrane Systems—Electrodialysis and Other Electromembrane Processes. In Fundamental Modeling of Membrane Systems; Luis, P., Ed.; Elsevier, Inc.: Amsterdam, The Netherlands, 2018; ISBN 9780128134849. [Google Scholar]
- Nir, O.; Sengpiel, R.; Wessling, M. Closing the cycle: Phosphorus removal and recovery from diluted effluents using acid resistive membranes. Chem. Eng. J. 2018, 346, 640–648. [Google Scholar] [CrossRef]
- Lemay, N.; Mikhaylin, S.; Mareev, S.; Pismenskaya, N.; Nikonenko, V.; Bazinet, L. How demineralization duration by electrodialysis under high frequency pulsed electric field can be the same as in continuous current condition and that for better performances? J. Memb. Sci. 2020, 603, 117878. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Memb. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Stenina, I.; Golubenko, D.; Nikonenko, V.; Yaroslavtsev, A. Selectivity of transport processes in ion-exchange membranes: Relationship with the structure and methods for its improvement. Int. J. Mol. Sci. 2020, 21, 5517. [Google Scholar] [CrossRef]
- Park, H.B.; Kamcev, J.; Robeson, L.M.; Elimelech, M.; Freeman, B.D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science 2017, 356, 1138–1148. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Luo, H.; Geise, G.M. Specific co-ion sorption and diffusion properties influence membrane permselectivity. J. Memb. Sci. 2018, 563, 492–504. [Google Scholar] [CrossRef]
- Dong, T.; Yao, J.; Wang, Y.; Luo, T.; Han, L. On the permselectivity of di- and mono-valent cations: Influence of applied current density and ionic species concentration. Desalination 2020, 488, 114521. [Google Scholar] [CrossRef]
- Golubenko, D.V.; Yaroslavtsev, A.B. Effect of current density, concentration of ternary electrolyte and type of cations on the monovalent ion selectivity of surface-sulfonated graft anion-exchange membranes: Modelling and experiment. J. Memb. Sci. 2021, 635, 119466. [Google Scholar] [CrossRef]
- Sata, T. Studies on anion exchange membranes having permselectivity for specific anions in electrodialysis—Effect of hydrophilicity of anion exchange membranes on permselectivity of anions. J. Memb. Sci. 2000, 167, 1–31. [Google Scholar] [CrossRef]
- Glueckauf, E.; Kitt, G.P. A new electrolytic separation technique using semi-permeable membranes. J. Appl. Chem. 1956, 6, 511–516. [Google Scholar] [CrossRef]
- Di Benedetto, A.T.; Lightfoot, E.N. Ion Fractionation by Permselective Membranes. Factors Affecting Relative Transfer of Glycine and Chloride Ions. Ind. Eng. Chem. 1958, 50, 691–696. [Google Scholar] [CrossRef]
- Sata, T.; Izuo, R.; Mizutani, Y.; Yamane, R. Transport properties of ion-exchange membranes in the presence of surface active agents. J. Colloid Interface Sci. 1972, 40, 317–328. [Google Scholar] [CrossRef]
- Oren, Y.; Litan, A. State of the solution-membrane interface during ion transport across an ion-exchange membrane. J. Phys. Chem. 1974, 78, 1805–1811. [Google Scholar] [CrossRef]
- Rubinstein, I. Effect of concentration polarization upon the valency-induced counterion selectivity of ion-exchange membranes. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1984, 80, 335–344. [Google Scholar] [CrossRef]
- Vaselbehagh, M.; Karkhanechi, H.; Takagi, R.; Matsuyama, H. Surface modification of an anion exchange membrane to improve the selectivity for monovalent anions in electrodialysis—Experimental verification of theoretical predictions. J. Memb. Sci. 2015, 490, 301–310. [Google Scholar] [CrossRef]
- Golubenko, D.V.; Karavanova, Y.A.; Melnikov, S.S.; Achoh, A.R.; Pourcelly, G.; Yaroslavtsev, A.B. An approach to increase the permselectivity and mono-valent ion selectivity of cation-exchange membranes by introduction of amorphous zirconium phosphate nanoparticles. J. Memb. Sci. 2018, 563, 777–784. [Google Scholar] [CrossRef]
- Afsar, N.U.; Shehzad, M.A.; Irfan, M.; Emmanuel, K.; Sheng, F.; Xu, T.; Ren, X.; Ge, L.; Xu, T. Cation exchange membrane integrated with cationic and anionic layers for selective ion separation via electrodialysis. Desalination 2019, 458, 25–33. [Google Scholar] [CrossRef]
- Tang, C.; Bruening, M.L. Ion separations with membranes. J. Polym. Sci. 2020, 58, 2831–2856. [Google Scholar] [CrossRef]
- Achoh, A.; Petriev, I.; Melnikov, S. Removal of Excess Alkali from Sodium Naphthenate Solution by Electrodialysis Using Bilayer Membranes for Subsequent Conversion to Naphthenic Acids. Membranes 2021, 11, 980. [Google Scholar] [CrossRef] [PubMed]
- Sata, T. Modification of Properties of Ion-Exchange Membranes—4. Change of Transport Properties of Cation-Exchange Membranes by Various Polyelectrolytes. J. Polym. Sci. Polym. Chem. Ed. 1978, 16, 1063–1080. [Google Scholar] [CrossRef]
- Pang, X.; Yu, X.; He, Y.; Dong, S.; Zhao, X.; Pan, J.; Zhang, R.; Liu, L. Preparation of monovalent cation perm-selective membranes by controlling surface hydration energy barrier. Sep. Purif. Technol. 2021, 270, 118768. [Google Scholar] [CrossRef]
- Roghmans, F.; Evdochenko, E.; Martí-Calatayud, M.C.; Garthe, M.; Tiwari, R.; Walther, A.; Wessling, M. On the permselectivity of cation-exchange membranes bearing an ion selective coating. J. Memb. Sci. 2020, 600, 117854. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Achoh, A.R.; Lebedev, K.A.; Melnikov, S.S. Permselectivity of bilayered ion-exchange membranes in ternary electrolyte. J. Memb. Sci. 2020, 608, 118152. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, D.; Muhammad, A.S.; Hossain, M.M.; Ge, Z.; He, Y.; Feng, H.; Xu, T. Fouling deposition as an effective approach for preparing monovalent selective membranes. J. Memb. Sci. 2019, 580, 327–335. [Google Scholar] [CrossRef]
- Evdochenko, E.; Kamp, J.; Femmer, R.; Xu, Y.; Nikonenko, V.V.; Wessling, M. Unraveling the effect of charge distribution in a polyelectrolyte multilayer nanofiltration membrane on its ion transport properties. J. Memb. Sci. 2020, 611, 118045. [Google Scholar] [CrossRef]
- Tsygurina, K.; Rybalkina, O.; Sabbatovskiy, K.; Kirichenko, E.; Sobolev, V.; Kirichenko, K. Layer-by-layer coating of mk-40 heterogeneous membrane with polyelectrolytes creates samples with low electrical resistance and weak generation of H+ and OH− ions. Membranes 2021, 11, 145. [Google Scholar] [CrossRef] [PubMed]
- Rijnaarts, T.; Reurink, D.M.; Radmanesh, F.; de Vos, W.M.; Nijmeijer, K. Layer-by-layer coatings on ion exchange membranes: Effect of multilayer charge and hydration on monovalent ion selectivities. J. Memb. Sci. 2019, 570–571, 513–521. [Google Scholar] [CrossRef]
- Abdu, S.; Martí-Calatayud, M.C.; Wong, J.E.; García-Gabaldón, M.; Wessling, M. Layer-by-layer modification of cation exchange membranes controls ion selectivity and water splitting. ACS Appl. Mater. Interfaces 2014, 6, 1843–1854. [Google Scholar] [CrossRef] [PubMed]
- Sata, T.T.; Sata, T.T.; Yang, W. Studies on cation-exchange membranes having permselectivity between cations in electrodialysis. J. Memb. Sci. 2002, 206, 31–60. [Google Scholar] [CrossRef]
- Gorobchenko, A.; Mareev, S.; Nikonenko, V. Mathematical modeling of the effect of pulsed electric field on the specific permselectivity of ion-exchange membranes. Membranes 2021, 11, 115. [Google Scholar] [CrossRef] [PubMed]
- Helfferich, F. Ion. Exchange; McGraw-Hil: London, UK; New York, NY, USA, 1962. [Google Scholar]
- Nikonenko, V.V.; Zabolotskii, V.I.; Gnusin, N.P. Effect of stationary external electric fields on ion-exchange-membrane selectivity. Sov. Electrochem. 1980, 16, 472–479. [Google Scholar]
- Kim, Y.; Walker, W.S.; Lawler, D.F. Competitive separation of di- vs. mono-valent cations in electrodialysis: Effects of the boundary layer properties. Water Res. 2012, 46, 2042–2056. [Google Scholar] [CrossRef]
- Danielli, F.J.; Cadenhead, D.A.; Rosenberg, M.D. Progress in Surface and Membrane Science; Academic Press: New York, NY, USA, 1973; Volume 7, ISBN 9781483219752. [Google Scholar]
- Sarapulova, V.; Shkorkina, I.; Mareev, S.; Pismenskaya, N.; Kononenko, N.; Larchet, C.; Dammak, L.; Nikonenko, V. Transport characteristics of fujifilm ion-exchange membranes as compared to homogeneous membranes AMX and CMX and to heterogeneous membranes MK-40 and MA-41. Membranes 2019, 9, 84. [Google Scholar] [CrossRef]
- Titorova, V.D.; Mareev, S.A.; Gorobchenko, A.D.; Gil, V.V.; Nikonenko, V.V.; Sabbatovskii, K.G.; Pismenskaya, N.D. Effect of current-induced coion transfer on the shape of chronopotentiograms of cation-exchange membranes. J. Memb. Sci. 2021, 624, 119036. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics; CRC Press, LLC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Urtenov, M.A.K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst−Planck and Poisson Equations. Application to a Membrane System at Overlimiting Currents. J. Phys. Chem. B 2007, 111, 14208–14222. [Google Scholar] [CrossRef]
- Hill, T.L.; Scatchard, G.; Pethica, B.A.; Straub, I.J.; Schlögl, R.; Manecke, G.; Schlögl, R.; Nagasawa, M.; Kagawa, I.; Meares, P.; et al. General discussion. Discuss. Faraday Soc. 1956, 21, 117–140. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Kontturi, K. Transport Numbers of Ions in Charged Membrane Systems. In Surface Chemistry and Electrochemistry of Membranes; CRC Press: Boca Raton, FL, USA, 1999; pp. 419–456. ISBN 9780429177682. [Google Scholar]
- Kharkats, Y.I. Theory of the exaltation effect and the effect of correlation exaltation of migration current. J. Electroanal. Chem. Interfacial Electrochem. 1979, 105, 97–114. [Google Scholar] [CrossRef]
- Mareev, S.A.; Evdochenko, E.; Wessling, M.; Kozaderova, O.A.; Niftaliev, S.I.; Pismenskaya, N.D.; Nikonenko, V.V. A comprehensive mathematical model of water splitting in bipolar membranes: Impact of the spatial distribution of fixed charges and catalyst at bipolar junction. J. Memb. Sci. 2020, 603, 118010. [Google Scholar] [CrossRef]
- Strathmann, H.; Krol, J.J.; Rapp, H.J.; Eigenberger, G. Limiting current density and water dissociation in bipolar membranes. J. Memb. Sci. 1997, 125, 123–142. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Memb. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Yaroslavtsev, A.B.; Pourcelly, G. Ion Transfer in and Through Charged Membranes: Structure, Properties, and Theory. In Ionic Interactions in Natural and Synthetic Macromolecules; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 267–335. ISBN 9780470529270. [Google Scholar]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef] [PubMed]
- Ahmadian Yazdi, A.; Sadeghi, A.; Saidi, M.H. Steric effects on electrokinetic flow of non-linear biofluids. Colloids Surf. A Physicochem. Eng. Asp. 2015, 484, 394–401. [Google Scholar] [CrossRef]
- Yu, A.S.L.; Cheng, M.H.; Angelow, S.; Günzel, D.; Kanzawa, S.A.; Schneeberger, E.; Fromm, M.; Coalson, R.D. Molecular Basis for Cation Selectivity in Claudin-2–based Paracellular Pores: Identification of an Electrostatic Interaction Site. J. Gen. Physiol. 2009, 133, 111–127. [Google Scholar] [CrossRef]
- Pifferi, S.; Boccaccio, A.; Menini, A. Cyclic nucleotide-gated ion channels in sensory transduction. FEBS Lett. 2006, 580, 2853–2859. [Google Scholar] [CrossRef]
- Marchesi, A.; Mazzolini, M.; Torre, V. Gating of cyclic nucleotide-gated channels is voltage dependent. Nat. Commun. 2012, 3, 973. [Google Scholar] [CrossRef][Green Version]
- Arcangeletti, M.; Marchesi, A.; Mazzolini, M.; Torre, V. Multiple mechanisms underlying rectification in retinal cyclic nucleotide-gated (CNGA1) channels. Physiol. Rep. 2013, 1, e00148. [Google Scholar] [CrossRef]
- Napolitano, L.M.R.; Torre, V.; Marchesi, A. CNG channel structure, function, and gating: A tale of conformational flexibility. Pflügers Arch. Eur. J. Physiol. 2021, 473, 1423–1435. [Google Scholar] [CrossRef]
- Gliozzi, A.; Rolandi, R.; De Rosa, M.; Gambacorta, A. Monolayer black membranes from bipolar lipids of archaebacteria and their temperature-induced structural changes. J. Membr. Biol. 1983, 75, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wu, Y.; Voth, G.A. Origins of Proton Transport Behavior from Selectivity Domain Mutations of the Aquaporin-1 Channel. Biophys. J. 2006, 90, L73–L75. [Google Scholar] [CrossRef] [PubMed]
- Scholz, F. Nikolsky’s ion exchange theory versus Baucke’s dissociation mechanism of the glass electrode. J. Solid State Electrochem. 2011, 15, 67–68. [Google Scholar] [CrossRef]
- Sonin, A.A.; Grossman, G. Ion transport through layered ion exchange membranes. J. Phys. Chem. 1972, 76, 3996–4006. [Google Scholar] [CrossRef]

| Parameter | Value | Description | Reference |
|---|---|---|---|
| C0 | 0.02 eq/L | Bulk solution concentration | [16] |
| Qm | 1.86 mol/L | Concentration of fixed ion groups in the substrate layer | [50] |
| QML | 0.5 mol/L 1 mol/L 2 mol/L | Concentration of fixed ion groups in the thin modification layer | * |
| 1.33·10–9 m2/s | Ion diffusion coefficients in the solution | [51] | |
| 7.96·10−10 m2/s | |||
| 2.04·10−9 m2/s | |||
| 6.57·10−11 m2/s | Ion diffusion coefficients in the substrate layer | [50] | |
| 2.50·10−12 m2/s | |||
| 2.89·10−11 m2/s | |||
| 3 | “Tortuosity factor” in modification layer | ** | |
| 1.5 | Ion activity coefficients in the substrate layer | Equation (18) | |
| 0.5 | |||
| 1 | |||
| δ | 150 μm | Diffusion layer thickness | [16] |
| d | 183 μm | Substrate layer thickness | [50] |
| 10–30 nm | Modification layer thickness | * | |
| 20 | Ion-exchange equilibrium coefficient | [45] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorobchenko, A.; Mareev, S.; Nikonenko, V. Mathematical Modeling of Monovalent Permselectivity of a Bilayer Ion-Exchange Membrane as a Function of Current Density. Int. J. Mol. Sci. 2022, 23, 4711. https://doi.org/10.3390/ijms23094711
Gorobchenko A, Mareev S, Nikonenko V. Mathematical Modeling of Monovalent Permselectivity of a Bilayer Ion-Exchange Membrane as a Function of Current Density. International Journal of Molecular Sciences. 2022; 23(9):4711. https://doi.org/10.3390/ijms23094711
Chicago/Turabian StyleGorobchenko, Andrey, Semyon Mareev, and Victor Nikonenko. 2022. "Mathematical Modeling of Monovalent Permselectivity of a Bilayer Ion-Exchange Membrane as a Function of Current Density" International Journal of Molecular Sciences 23, no. 9: 4711. https://doi.org/10.3390/ijms23094711
APA StyleGorobchenko, A., Mareev, S., & Nikonenko, V. (2022). Mathematical Modeling of Monovalent Permselectivity of a Bilayer Ion-Exchange Membrane as a Function of Current Density. International Journal of Molecular Sciences, 23(9), 4711. https://doi.org/10.3390/ijms23094711