1. Introduction
Studying acoustic plasmons (APs) in single-layer [
1,
2,
3,
4,
5], double-layer [
3,
6,
7,
8,
9] and multi-layer [
10,
11,
12,
13] graphene or in metal/dielectric/graphene superstructures [
14] is a very active field of research. Recently, an AP was detected in a graphene–dielectric–metal structure using near-field scattering microscopy [
2]. That experiment demonstrated a very robust character of the AP with small propagation loss, which enables its efficient coupling to the electromagnetic field at infra-red frequencies. The graphene/graphene-nanoribbon superstructure also supports a strong AP which can be excited by light and provide strong field enhancement inside the nano-gap, allowing efficient biosensing [
6]. In this work, we focus on the AP in graphene doped by alkali metals.
As alkali atoms are added to graphene deposited on various substrates, they intercalate between the graphene layer and the substrate and metalize, i.e., they arrange in a two-dimensional (2D) crystal lattice, which supports a partially filled parabolic band [
15,
16,
17,
18,
19,
20,
21]. The alkali atoms then usually donate electrons to the graphene
band, lifting the Fermi level above the Dirac point and transforming the graphene from a gapless semiconductor into a metal. Therefore, the alkali adlayer results in the formation of two thin, i.e., quasi two-dimensional (q2D), plasmas able to support a variety of different plasmonic modes, which do not exist in pristine or electrostatically doped graphene. Our previous theoretical research of electronic excitations in graphene doped by alkali atoms (AC
) showed that this system supports two kinds of intraband or 2D plasmons: the Dirac plasmon (DP) and the acoustic plasmon (AP). The intensity of these modes depends on the type of the dielectric substrate, as well as on electrostatic or natural doping [
22,
23,
24,
25]. Moreover, these theoretical studies suggest the possibility of simple manipulation of the DP and AP intensities (they can be switched ‘on’ and ‘off’ in a controlled way) [
25], thereby opening new possibilities for their application in various fields, such as plasmonics, photonics, transformation optics, optoelectronics, light emitters, detectors and photovoltaic devices [
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36]. Additionally, these ‘tunable’ 2D plasmons could be very useful in the area of chemical or biological sensing [
27,
37,
38,
39,
40].
In this paper, we focus on the AP, firstly because of its linear dispersion, but also because of the still rather unclear mechanism of its occurrence in the AC
. The mechanism of formation of the AP on a metal surface was resolved a long time ago [
41,
42,
43]. In that case, a partially filled surface state supports a 2D plasmon, which hybridizes with the ordinary surface plasmon, resulting in the transformation of the usual 2D plasmon with square-root 2D dispersion into a linear AP [
41]. However, our previous studies of plasmons in AC
systems show that the AP is very sensitive and strongly dependent on several parameters: the type of the alkali metal atom (A), the coverage (
x) and the electrostatic doping. In other words, it is substantially unstable, and the aim of this research is to explore the mechanism of the (in)stability of the AP in the AC
.
In order to do that, we investigate two model systems of doped graphene, KC and CsC, which are isostructural, but the first system does support the AP, while the second one does not. Moreover, the DP in the KC is very sharp, while in the CsC it is quite broad, even though the occupancies of the graphene band and the alkali atom band in these two systems are almost identical. We shall show that the AP in the AC is not, as previously believed, just a consequence of the hybridization between the intraband 2D plasmons in the and bands, but rather a very subtle interplay between these plasmons and the background screening caused by the interlayer interband transitions. We shall also demonstrate that the electronic screening coming from the high-energy interband transitions significantly reduces the intensity of the AP in both systems.
We study electronic excitations in the AC
using two complementary methods: the ab initio random phase approximation (RPA) approach [
24] and a reduced model. In the reduced model, the electrons in the alkali atom layer are approximated by a parabolic band with parameters (the effective mass
and the Fermi energy
) taken from the ab initio calculations. We refer to this approximation as the “massive” 2D electron gas (m2DEG). The graphene band structure is approximated by the conical
bands with the occupation corresponding to the occupation of the
band (Fermi energy
) in the ab initio AC
sample. This approximation is also known as the ’massless’ Dirac fermion (MDF) approximation [
44,
45]. The polarization effects coming from the high-energy interband transitions are included through the polarizability parameters
and
deduced from the ab initio calculations.
The paper is organized as follows. In
Section 2, we present the geometry of the system, a derivation of the ab initio ground state and the RPA spectra of the electronic excitations
in the AC
deposited on a dielectric substrate. We also present a theoretical formulation of the reduced model. In
Section 3, we show the band structures of the KC
and CsC
, as well as the intensities of the electronic excitations in these systems. After that, using a detailed analysis, which combines the ab initio RPA method and the reduced model, we resolve the mechanism of the AP instability. The conclusions are presented in
Section 4.
2. Theoretical Formulation
In this section, we derive the spectral function of the electronic excitations in the self-standing KC
and CsC
. However, to demonstrate the robustness of these electronic excitations, we show how a dielectric substrate can be included in our expressions for the spectral function, to enable the calculation of the electronic excitation spectra for systems consisting of crystals (CsC
and KC
) deposited on Al
O
substrate described by a local dielectric function
. Additionally, we make use of the plausible assumption [
25] that the Al
O
substrate does not affect the ground state electronic structure (Kohn–Sham (KS) wave functions and energies) of the AC
crystal, but it can influence its dielectric properties.
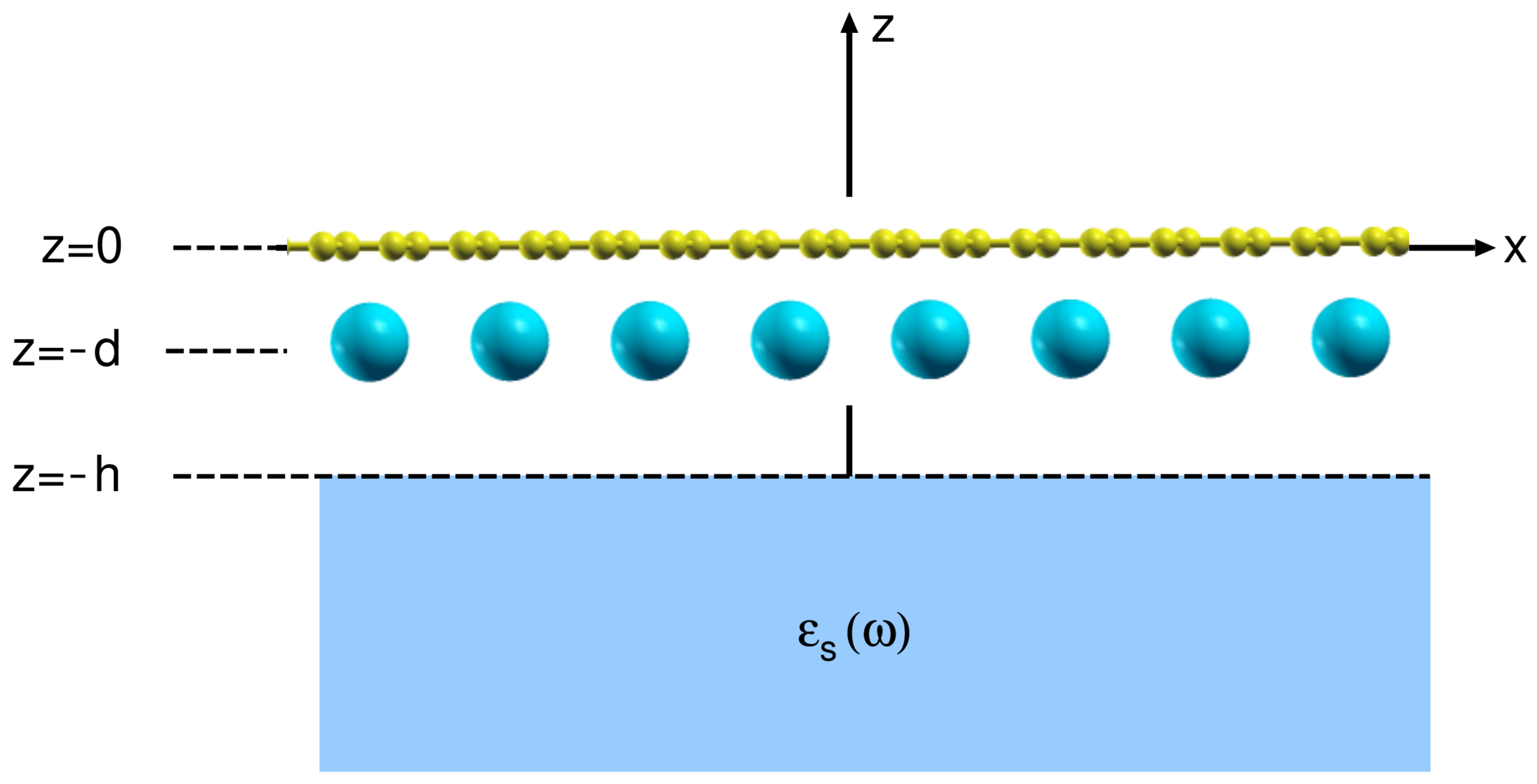
Figure 1 shows the geometry of the studied system. The coordinates are oriented so that the AC
crystal is positioned in the
plane, the
z direction is perpendicular to the crystal plane, the graphene layer occupies the
plane, the alkali atom layer occupies the
plane and the dielectric substrate occupies the
half-space.
2.1. Calculation of the Surface Electronic Excitations Spectra
We shall briefly describe the method of calculation of the surface electronic excitation spectra at the arbitrary position
, previously used in several studies of electronic excitations in 2D crystals [
22,
23,,
46,
47,
48,
49,
50].
We start from the 3D Fourier transform of the noninteracting (free) electron response function
where
is the normalization volume and
is the Fermi–Dirac distribution at temperature
T. The matrix elements (or the charge vertices) are
where
is the 2D wave vector,
is the momentum transfer vector parallel to the
plane,
are the
reciprocal lattice vectors and
is the
position vector. The integration is performed over the normalization volume
. The plane wave expansion of the wave function has the form
where the coefficients
are obtained by solving the KS equations within the local density approximation (LDA) self-consistently.
The Fourier expansion of the free electron response function in the
z and
coordinates is:
where we assume that our system is periodical in the
z and
direction as well, i.e., that it repeats periodically from supercell to supercell, and the supercells are q2D crystals separated by the distance
L. We now need to determine the screened response function
of one supercell without including the polarization of the surrounding supercells. This spurious interaction with the replicas of the q2D crystal can be eliminated easily, by using the RPA Dyson equation
where the matrix of the bare Coulomb interaction is
and the 2D Fourier transform of the bare Coulomb interaction is
Since the integrations in (
4) are performed from
to
, the interaction between the density fluctuations, via the Coulomb propagator
, is limited to one supercell located at
. After inserting the Fourier expansion (
3), and a similar one for
, in RPA Dyson Equation (
4), it again becomes a matrix equation
where the matrix of the bare Coulomb interaction is
with
,
,
, and
.
The solution of Equation (
7) has the form
where the dielectric matrix is
After solving Equation (
7), the nonlocal screened response function in the
z and
direction becomes:
The propagator of the induced dynamically screened Coulomb interaction can be calculated from the response function (
9) as [
50]
where the index zero means that
. After using the expansion (
11) and Equation (
6), the integrations over
and
can be performed analytically, and the induced dynamically screened interaction at
can be written as
where the propagator of the surface excitations is
and the form factors
F are
The spectral function, which defines the intensity of the energy loss by an external perturbation to the excitation of the
modes, can now be calculated as
Up to this point, we derived the expressions for the self-standing q2D systems, but including a dielectric substrate polarization is now straightforward. It is obtained simply by replacing the bare Coulomb interaction (
6) with the Coulomb interaction screened by the substrate
where the dielectric surface response function is
This also means that the matrix (
8) used in matrix Dyson Equation (
7) should be modified as
2.2. Calculation of the 2D Dynamical Polarizability Function
In the long-wavelength or optical limit (
), the in-plane dielectric function of a 2D crystal can be approximated as
The 2D polarizability
can be divided into intraband and interband contributions
where
and
or
y. The intraband optical conductivity is [
51]
where the effective number of charge carriers is
The interband optical conductivity is determined from the optical limit of the nonlocal interband conductivity
The nonlocal interband conductivity is [
51]
where the current vertices are
and the current produced by the transitions between the Bloch states
is defined as
Figure 2 shows the interband contribution to the dynamical polarizability
in the KC
(black), CsC
(orange) and doped graphene (red dashed). The graphene is doped so that the Fermi level is 1eV above the Dirac point, which corresponds to the doping of the
bands in the KC
and CsC
. All three systems show qualitatively equal behavior; the peak at about
eV, indicating the onset for the
interband transitions, and the dip at
eV is a consequence of the high density of the
interband transitions at the M point of the Brillouin zone. Even though the
bands in all three systems are almost equally doped, we can see a substantial difference in the KC
and CsC
statical polarizabilities which are
Å and
Å, respectively. This difference probably comes from the difference in the intensities of the
interlayer (interband) excitations in the two systems. These excitations are manifested as the peak at
eV for the CsC
, which does not exist for the KC
. Finally, we can see that the agreement between the dynamical polarizabilities in the KC
and the equivalently doped graphene is almost perfect. As we shall demonstrate later, this small deviation in the low-energy part of the dynamical polarizability is responsible for the disappearance of the AP in the CsC
, but only if we take into account that these transitions represent a perpendicular polarization.
2.3. Calculation of the Substrate Dielectric Function
We assume that the dielectric media is vacuum (i.e.,
), and that the substrate is aluminium oxide Al
O
described by the macroscopic dielectric function
. To calculate the
, we start from the 3D Fourier transform of the independent electron response function
where
indicates that the summation is performed within the first Brillouin zone. The charge vertices are defined as
where
,
and
are the 3D wave vector, the transfer wave vector and the reciprocal lattice vector, respectively. The integration is performed over the normalization volume
. We use the response matrix (
26) to determine the dielectric matrix as
where the bare Coulomb interaction is
. Finally, the macroscopic dielectric function is determined by inverting the dielectric matrix
2.4. Reduced Model
Analytical modeling of the energy loss spectra is achieved by representing each of the systems, CsC
and KC
, by a two-layer structure consisting of a single sheet of doped graphene and an m2DEG, placed in vacuum at a distance
d apart, as shown in
Figure 3. In the reduced model, the substrate is neglected, i.e., we assume
, and the energy loss function
is then obtained from the effective 2D dielectric permittivity for this two-layer structure, in the RPA given by [
44,
52]
where
is the Coulomb interaction, while
and
are the response functions of the noninteracting electrons in the graphene and the m2DEG layers, respectively.
For the doped graphene, we follow the method proposed by Gjerding et al. [
53], and write the response function as
, where
is the response function given in Refs. [
54,
55], which describes both intraband and low-energy interband electron transitions within the
electron bands approximated by the Dirac cones with the Fermi energy
, while
is the phenomenological parameter providing the correction due to the high-energy interband transitions. For the m2DEG, we similarly write
, where
is the polarization function given in Ref. [
56], describing the intraband transitions in the 2DEG which occupies a single parabolic energy band with the effective mass
and the Fermi energy
, while
is a phenomenological parameter taking into account interband transitions in the m2DEG. The expressions used for both response functions,
and
, are formulated for zero temperature, but they are corrected by the Mermin procedure to take into account a finite damping parameter
in both graphene and m2DEG layers [
53]. We use
meV as in the ab initio calculations, as well as
meV to take into account the additional smearing at room temperature.
We note that the relevant parameters for the KC
(
Å,
eV,
eV,
) and CsC
(
Å,
eV,
eV,
) are obtained from the electronic band structure calculation for these two systems, shown in
Figure 4a,b, respectively. The parameters
are obtained from the static limit (
) of the ab initio results for the corresponding dynamic polarizability functions
in the optical limit. In particular, the value
Å for high-energy interband transitions is deduced from the data for the intrinsic graphene [
53], and by adding the value for the low-energy
interband transitions, estimated from the Dirac model in the optical limit at zero temperature [
57] as
Å, we obtain that the total contribution of the interband transitions in the doped graphene is around 2.45 Å. This is close to the result
Å shown in
Figure 2 for the KC
, which indicates that
for that system. On the other hand, the result
Å shown in
Figure 2 for CsC
indicates that
Å for that system.
2.5. Computational Details
The KC
, CsC
and graphene KS wave functions
and energies
are determined using the plane-wave self-consistent field DFT code (PWSCF) within the QUANTUM ESPRESSO (QE) package [
58]. The core–electron interaction is approximated by the norm-conserving pseudopotentials [
59,
60]. For the KC
and CsC
, the exchange correlation (XC) potential is approximated by the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional [
61]. The ground state electronic densities are calculated using the
Monkhorst–Pack K-mesh [
62] and the plane-wave cut-off energy is 60Ry. For both AC
crystals, we used the hexagonal Bravais lattice, where
Å and the separation between the AC
layers is
. The atomic and the unit cell relaxations were performed until maximum force below
Ry/a.u. was obtained. After performing the structural optimization, the obtained separations between the K and Cs layers and the graphene layer are d = 2.92 Å and d = 3.13 Å respectively. The graphene XC potential is approximated by the Perdew–Zunger (PZ) LDA [
63]. The ground state electronic density is determined using
K-point mesh, and for the plane-wave cut-off energy we choose 50 Ry. For the graphene unit-cell constant we use the experimental value
Å [
64], while for the superlattice unit-cell constant we take
.
The AC
response functions (
1) and conductivities (
22)–(
25) are evaluated from the wave functions
and energies
calculated for the
Monkhorst–Pack K-point mesh. The band summation (
) is performed over 60 bands, the damping parameters are
meV and the temperature is
meV. Due to the large spatial dispersivity of the dielectric response in the perpendicular (
z) direction, the crystal local field effects are taken into account only in the
z direction and neglected in the
plane, i.e., we set the
to zero. To calculate the matrix
we set the energy cut-off to 10Ry, which corresponds to a
matrix. Graphene conductivity (
22)–(
25) is calculated by performing the summation over
K-point mesh, the band summations (
) are performed over 20 bands, the damping parameters are
meV and
meV and the temperature is
meV. The conductivity of the doped graphene is calculated using the rigid band approximation, i.e., the occupation parameter (the Fermi energy relative to the Dirac point) is adjusted a posteriori.
The ground state electronic density of the bulk Al
O
is calculated using
K-mesh, the plane-wave cut-off energy is 50Ry and the Bravais lattice is hexagonal (12 Al and 18 O atoms in the unit cell) with the lattice constants
Å and
Å. The response function (
26) of the Al
O
is calculated using the
k-point mesh and the band summations
are performed over 120 bands. The damping parameter is
meV and the temperature is
meV. For the optically small wave vectors
, the crystal local field effects are negligible, so the crystal local field effect cut-off energy is set to zero. Using this approach, the Al
O
dielectric function is estimated to be
for
eV, which is in good agreement with the experimental value
[
65]. However, in the calculations we used the full dynamical
.
3. Results and Discussion
Figure 4 shows (a) KC
and (b) CsC
band structures, respectively, along the high symmetry
directions. The blue circles represent the parabolic fit
for the alkali atom
bands. In both figures, we can see that the graphene
band and the alkali atom
band are significantly doped by the electrons, so the Fermi level is around 1eV above the Dirac point and the
band bottom. It is also evident that the
bands behave almost as an ideal 2D free electron gas. They are parabolic (described by effective masses
and
, respectively) up to the Fermi energy, especially in
Figure 4a where the
band is parabolic almost through the entire Brillouin zone. Finally, the most important feature is the obvious similarity between the two band structures, which both fulfill conditions for the occurrence of the AP (two bands of different effective masses crossing the Fermi energy) [
22,
41]. However, as we shall see, the spectra of the low-energy electronic excitations in these two systems are quite different. In both systems, we can identify the lowest band that remains above the Fermi lever for all wave-vectors, and we call it the lowest unoccupied band (LUCB), even though for some wave-vectors there is another unoccupied band below that one, since this one turns out to be of particular importance, as explained below.
Figure 5 shows the intensities of the electronic excitations in the (a) KC
and (b) CsC
deposited on the dielectric Al
O
surface. Since the graphene
bands are abundantly doped by the electrons, both systems support a strong DP. However, although the occupancies of both
bands are almost identical (
eV for the KC
and
eV for the CsC
), the intensities of the DP are quite different. We can see that the DP in the CsC
is broader and much more efficiently damped by the interband
electron hole excitations than the DP in the KC
. Moreover, we can see that the DP in the KC
is very sharp and it extends deep into the interband
continuum while the DP in the CsC
decays immediately upon entering the interband
continuum. The most interesting difference between the two systems is that, even though the occupancies of their
bands are very similar (
eV in the KC
and
eV in the CsC
), the KC
does support the AP while the CsC
does not. Moreover, we can see that the
plasmon (denoted by the blue symbol
) in the KC
is well defined, and it appears to be a very intensive optically active plasmon (its intensity does not vanish for
), while the
plasmon in the CsC
is less intensive, more diffuse and not in optically active mode. It is very interesting that these two very similar band structures lead to very different excitation spectra.
To demonstrate that these effects are not driven by the dielectric substrate, in
Figure 5 we also show the intensities of the electronic excitations in the self-standing (c) KC
and (d) CsC
. The magenta dots in
Figure 5a,b denote the DP and AP dispersion relations in the self-standing samples, for comparison. It is worth noting that the insulator surface does not change the qualitative behavior of the electronic modes. The only quantitative differences are: the dielectric screening slightly reduces the DP energy and slightly reduces the intensities of the AP and
plasmons. However, the AP in the KC
is still clearly visible. Since the substrate does not affect the qualitative behavior of the excitation spectra, it will be omitted from further consideration. Therefore, the fact that one system does and the other does not support the AP, even though the bands crossing the Fermi energy in the two systems are almost identical, suggests that the mechanism responsible for this AP instability is probably in the screening coming from the interband excitations beyond the Fermi energy.
To investigate this mechanism, we take advantage of the reduced model which clearly distinguishes between the different interband contributions to the dynamical response in the two systems. As discussed in
Section 2.4, the statical polarizabilities due to the high-energy interband excitations in the metallic subsystem (characterized by the parameter
) are
in the KC
and
in the CsC
. This difference suggests that this polarization mechanism may be responsible for suppressing the AP.
Figure 5e,f show the energy loss function
in the self-standing KC
and CsC
, respectively, obtained using the reduced model. We can see that the agreement between the ab initio and the reduced model intensities for the KC
for
eV and
a.u. is almost perfect. Beyond these values, the plasmons in the reduced model appear at higher energies, which is reasonable since the reduced model neglects the dynamical effects of the high-energy interband transitions. For example, one can notice the absence of the
plasmon in the reduced model. In the case of the CsC
, the agreement is no longer so good, and the most important difference is that the reduced model (at this level of approximation) is obviously not able to reproduce the disappearance of the AP. The stronger metallic interband screening in the CsC
is still not sufficient to suppress the AP. Moreover, even the implementation of the ab initio dynamic polarizability
in the reduced model (taking into account that the low-energy interband excitations in the
and
need to be extracted) fails to cause the disappearance of the AP. This means that the mechanism of the AP disappearance is more complex and obviously the explanation requires more accurate treatment of the spatial dispersivity of the interband dynamical response, beyond the 2D model. Therefore, we shall again exploit the ab initio method, which incorporates the effects of the local crystal field (the spatial dispersivity of the dynamical response in the
z direction), where the interband screening will be modified by changing the number of valence bands participating in the interband screening.
Resolving the Mechanism of the AP Instability
To explore how the screening coming from the interband excitations beyond the Fermi energy influences the AP, we omit one or more unoccupied bands from the calculation, to determine exactly how each band influences the excitation spectra. As we can see from the band structures shown in
Figure 4a,b, in both systems, CsC
and KC
, there is one band crossing the Fermi level, i.e., for some wave-vectors that band is the highest occupied valence band (HOVB), while for other wave-vectors that same band is the lowest unoccupied band. Therefore, to avoid confusion, we use the expression lowest unoccupied band for the next one, i.e., the first band above the Fermi level at the
point (magenta line in
Figure 4a,b), since that one remains above the Fermi level for all wave-vectors. That particular band is the one that has to be omitted from the calculation to achieve a qualitative difference with respect to the complete calculation (the one taking into account all bands). However, the difference becomes much more significant if we omit more bands. To keep track of the bands omitted from the calculation, we introduce the integer
n which denotes the number of omitted bands. For example,
denotes that no bands are omitted,
denotes that only the lowest unoccupied band is omitted,
denotes that the first two unoccupied bands are omitted, etc.
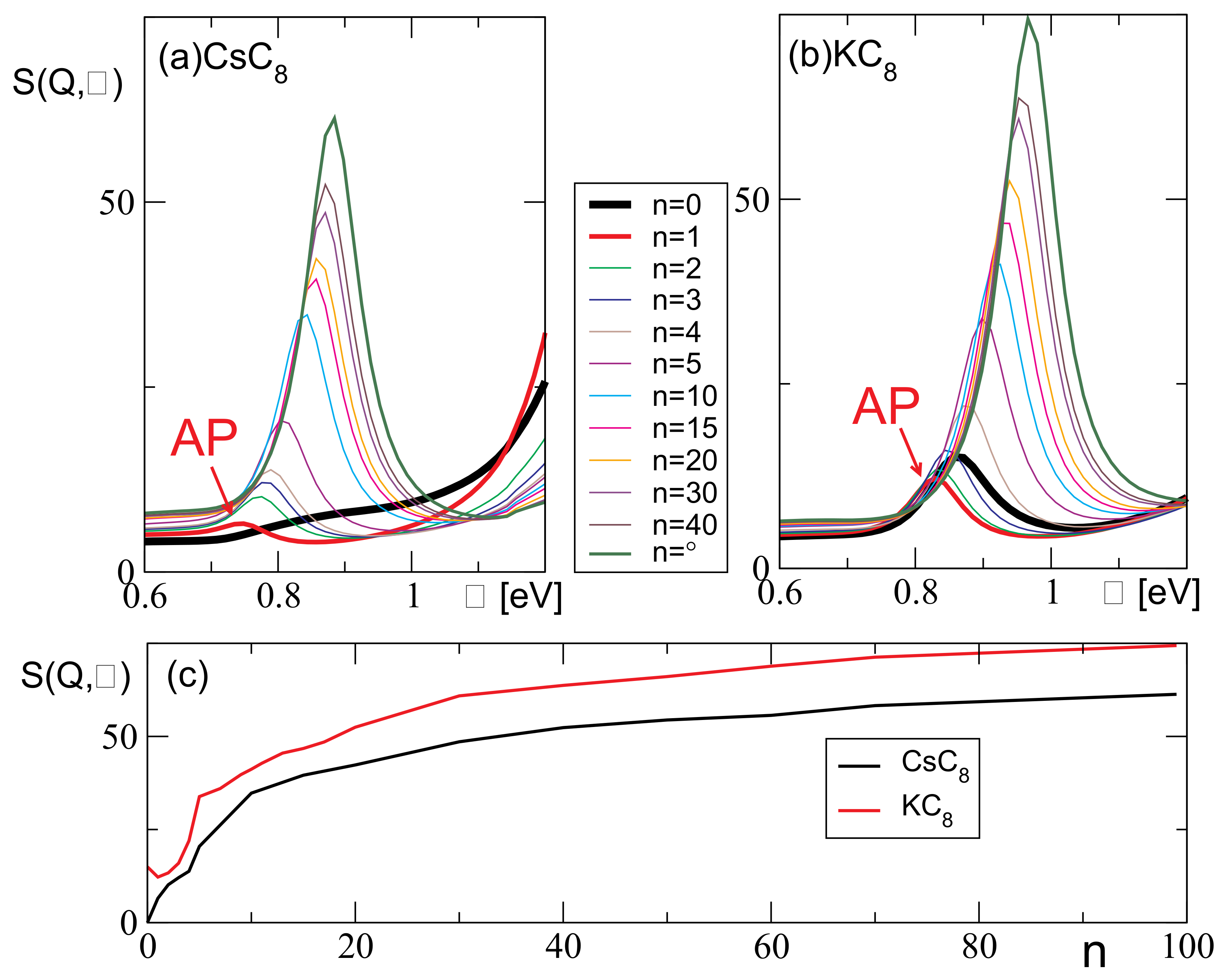
Figure 6a,b show how the AP peak changes as we omit the unoccupied bands from the calculation, for
a.u. and for the CsC
and KC
, respectively. The thick black lines show the actual spectra, i.e., the ones obtained without omitting any bands (
), and we can see that for the selected wave-vector the AP in the KC
is clearly present (though not very strong), while in the CsC
it does not exist. On the other hand, the red line shows that the AP peak exists in both systems if we omit the LUCB from the calculation (
). In the CsC
, that peak is very weak but it exists, while in the KC
it is, surprisingly, lower than the actual (
) peak. The other lines show that the intensity of the peak increases as we omit more and more bands, in both systems, and it is the strongest when all the unoccupied bands are omitted (
). The same can be seen in
Figure 6c, which shows how the intensity of the peak changes with
n. It is important to point out that we also attempted to keep the lowest unoccupied band in the calculation while omitting any number of the other unoccupied bands, above that one, and that did not lead to the occurrence of the AP in the CsC
. This means that omitting the lowest unoccupied band (
) is crucial for the occurrence of the AP, while omitting the higher bands as well (
) only enhances its intensity. This leads to the conclusion that the mechanism responsible for the disappearance of the AP in the CsC
is the small difference in the ‘out-of-plane’ polarization coming from the interband (interlayer) transitions between the graphene
band and the lowest unoccupied alkali atom
band (denoted by red arrows in
Figure 4). This difference is also manifested as the small peak at
eV in the CsC
dynamical polarizability
shown in
Figure 2, which is missing for the KC
. However, even if we include this difference in the dynamical polarizability in the reduced model, that still fails to reproduce the disappearance of the AP. This is because the reduced model is inherently a 2D model, i.e., it allows only the ‘in-plane’ polarization, while the
transitions induce the ‘out-of-plane’ polarization.
Another interesting point is that the difference in the intensities of the transitions is obviously correlated with the strength of the hybridization of the and bands at the crossing point. We can see that the and bands in the KC intersect without any distortion while in the CsC we notice a significant avoided crossing. In other words, the and in the CsC hybridize significantly while this is not the case in the KC. This leads to one very unusual conclusion; the intensity of the AP, which was to date believed to be a consequence of various long-range screening mechanisms, can be significantly affected by the short-range electronic correlations occurring between the atomic orbitals (i.e., by the chemical bonding between the alkaline atoms and graphene).