Morphology of Polymer Brushes in the Presence of Attractive Nanoparticles: Effects of Temperature
Abstract
1. Introduction
2. Results
2.1. Pure Brush
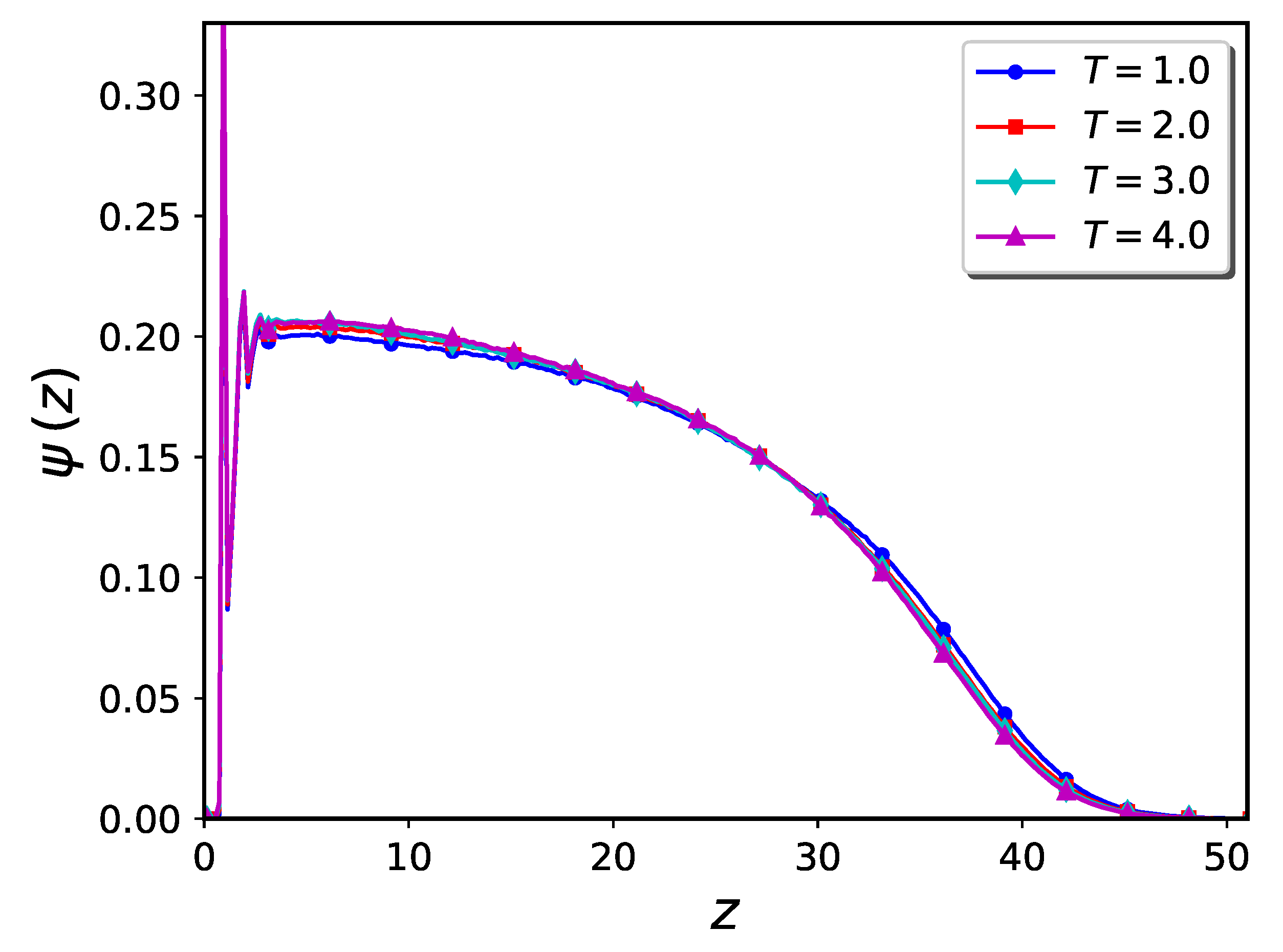
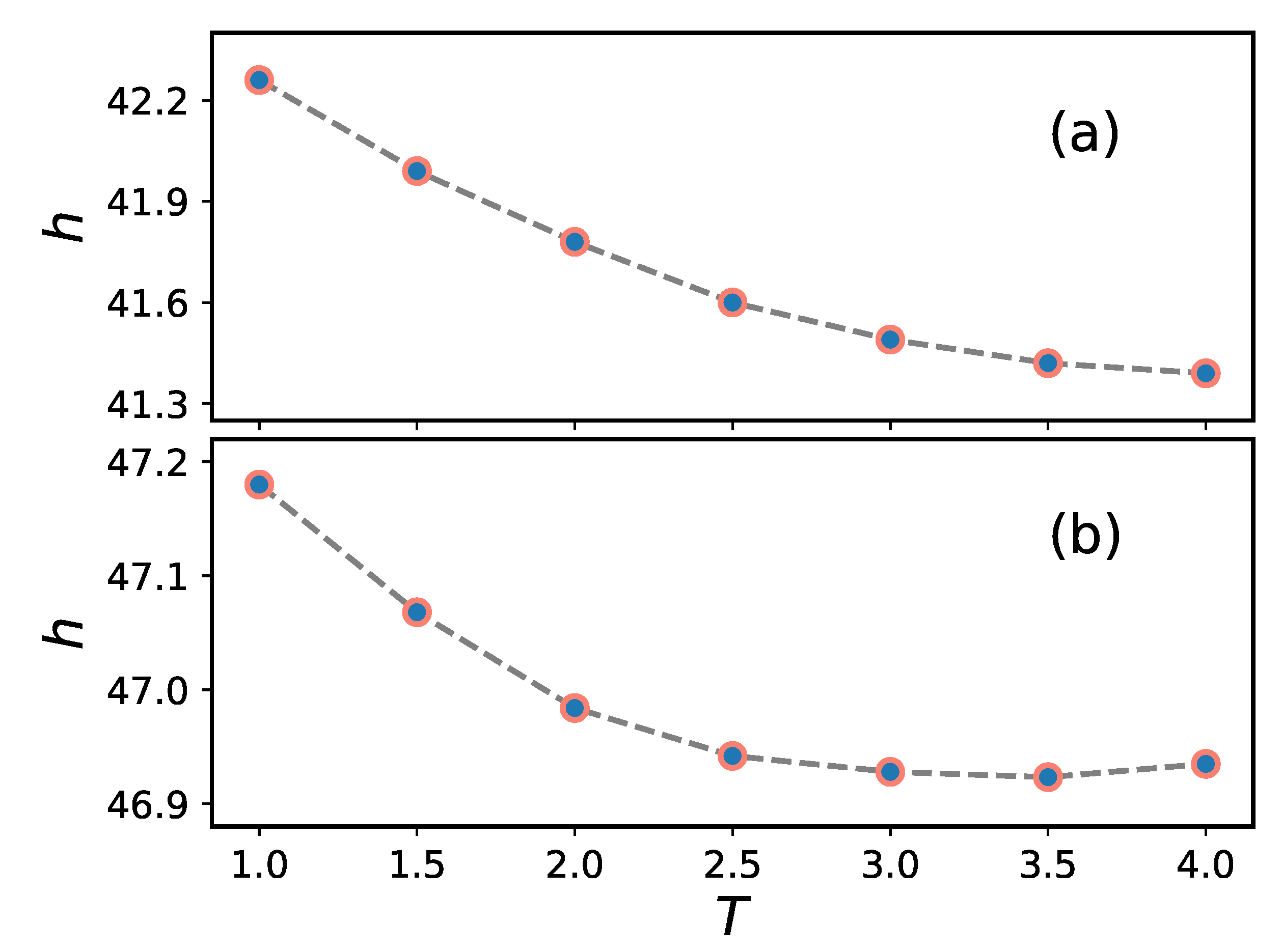
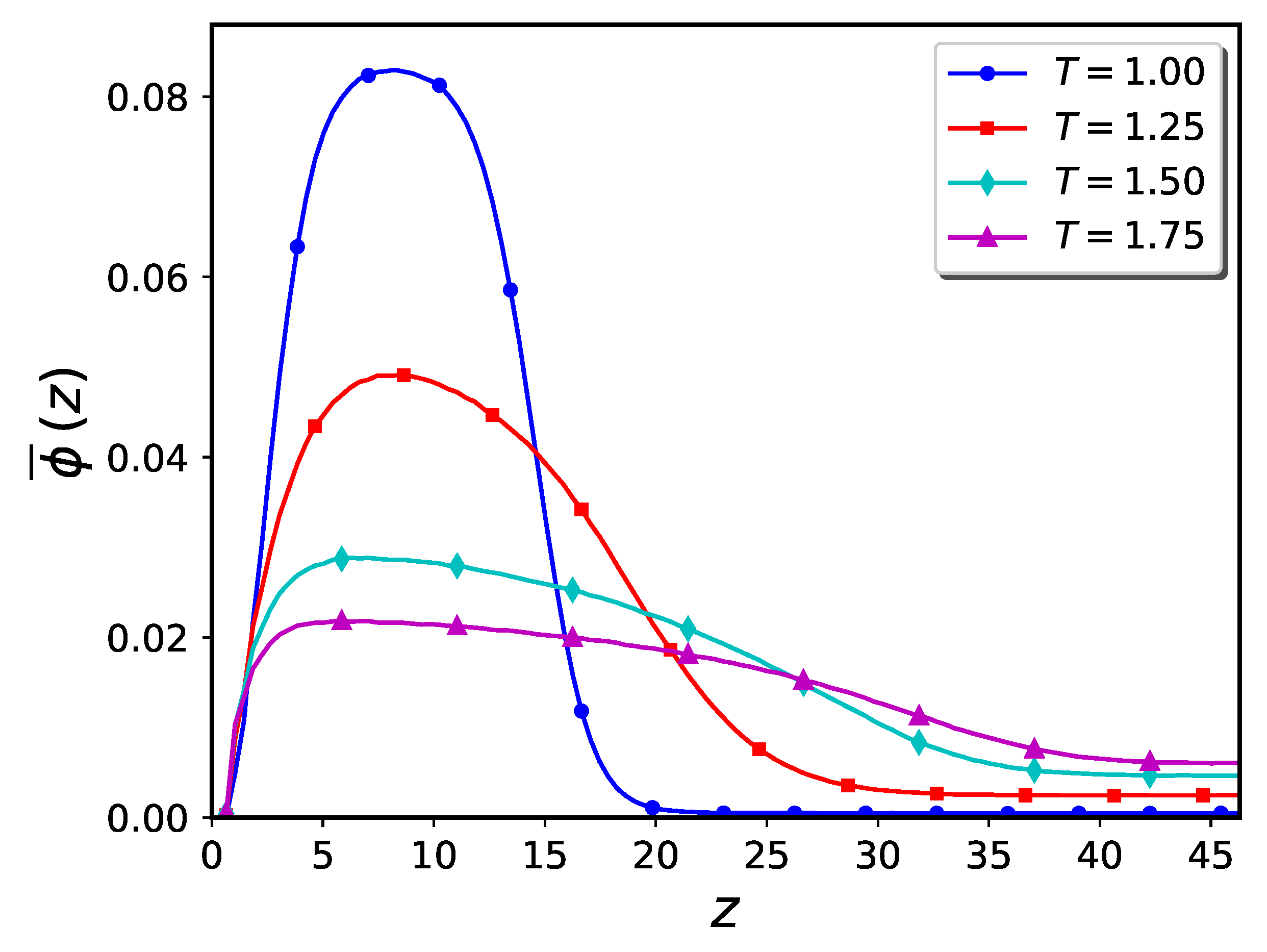
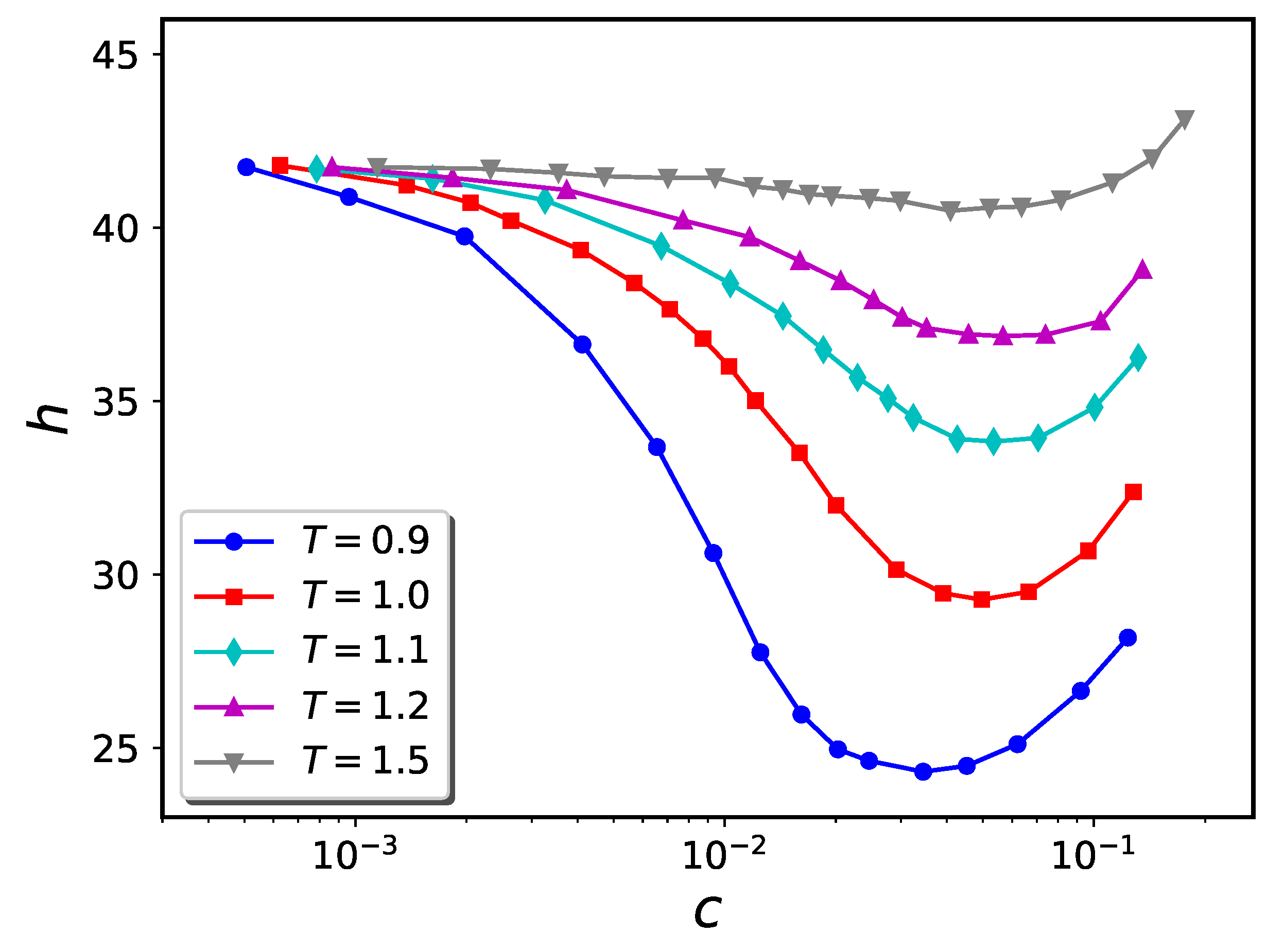
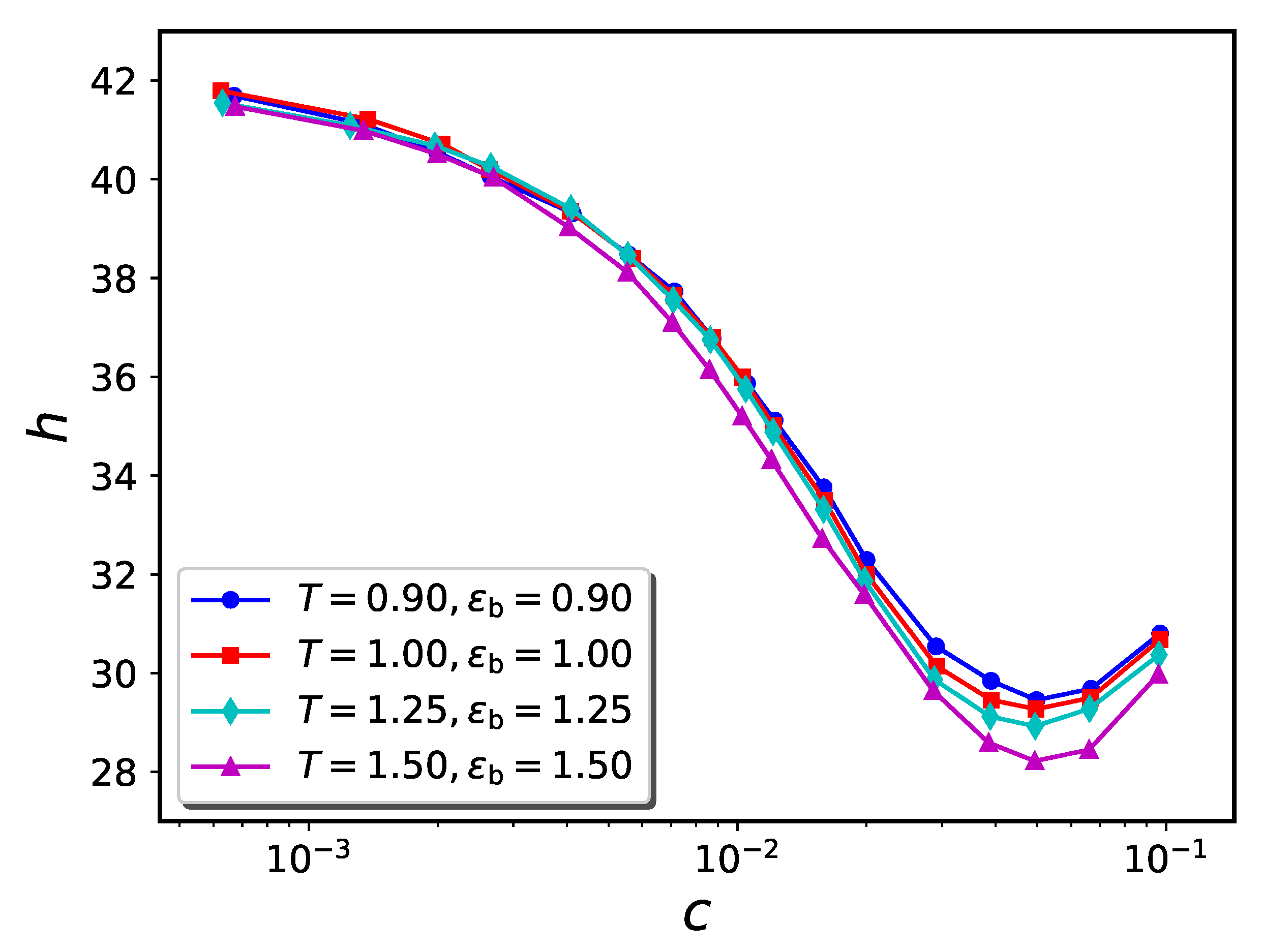
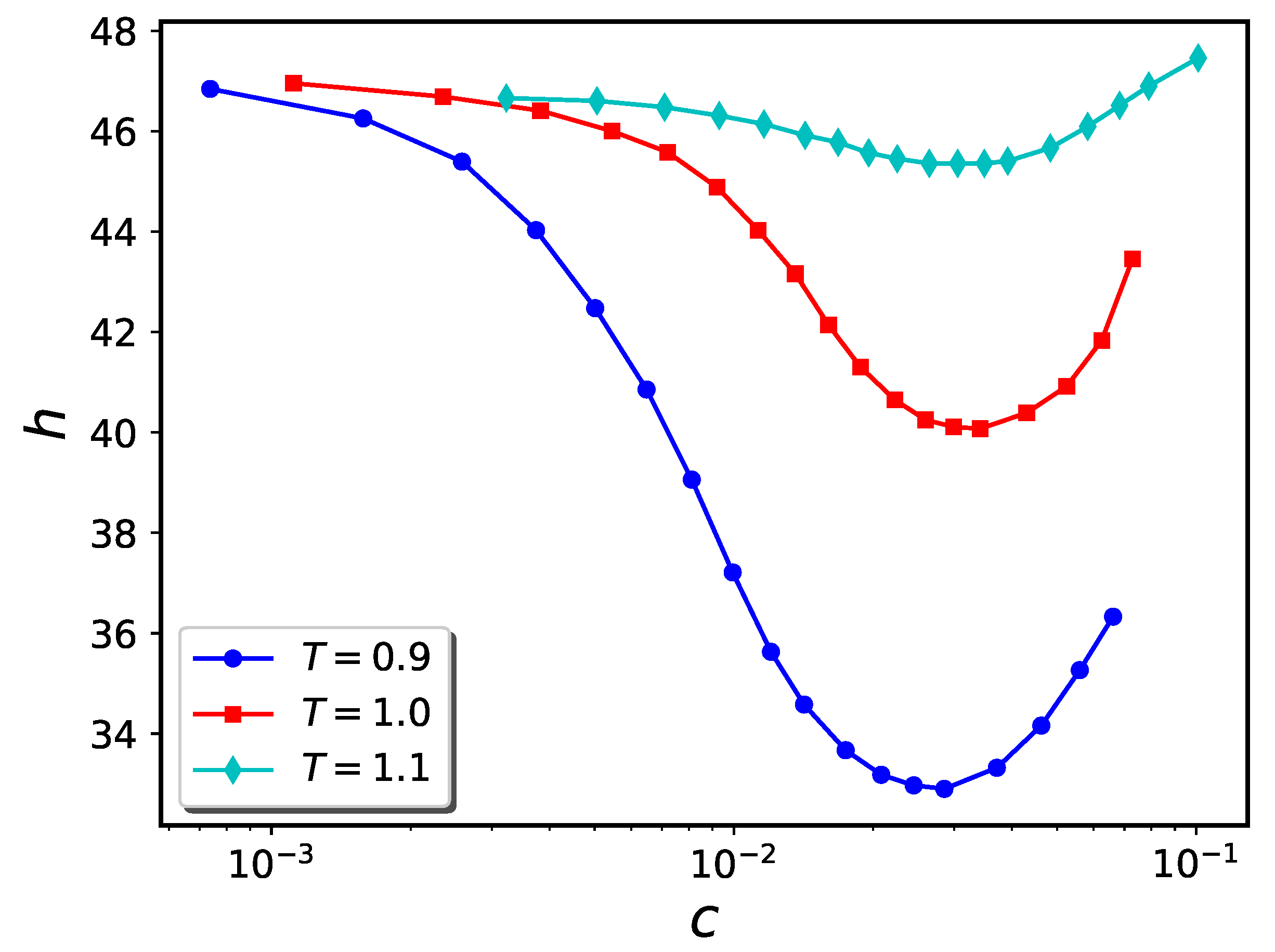
2.2. Brush plus Nanoparticles—Flat Geometry
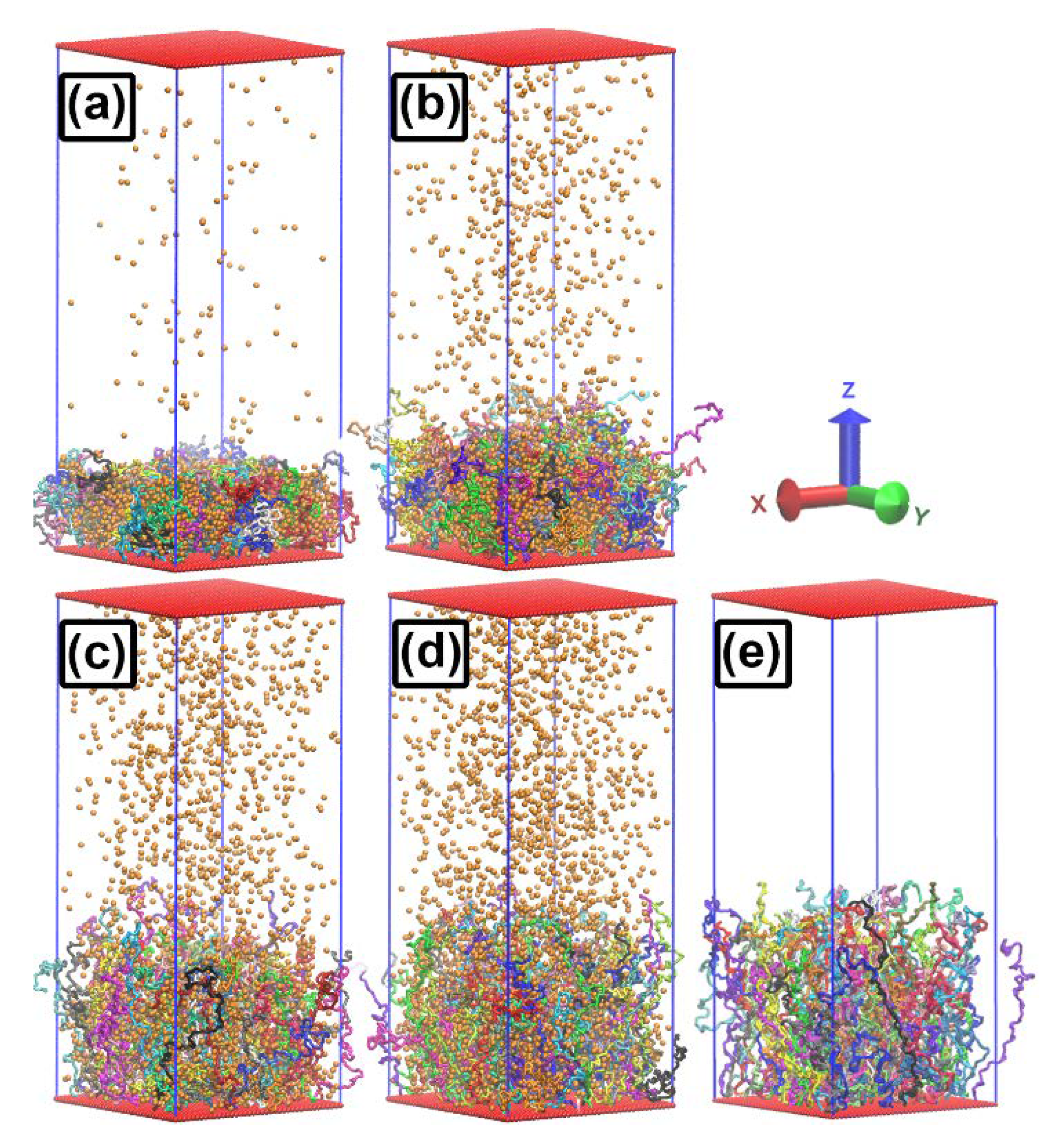
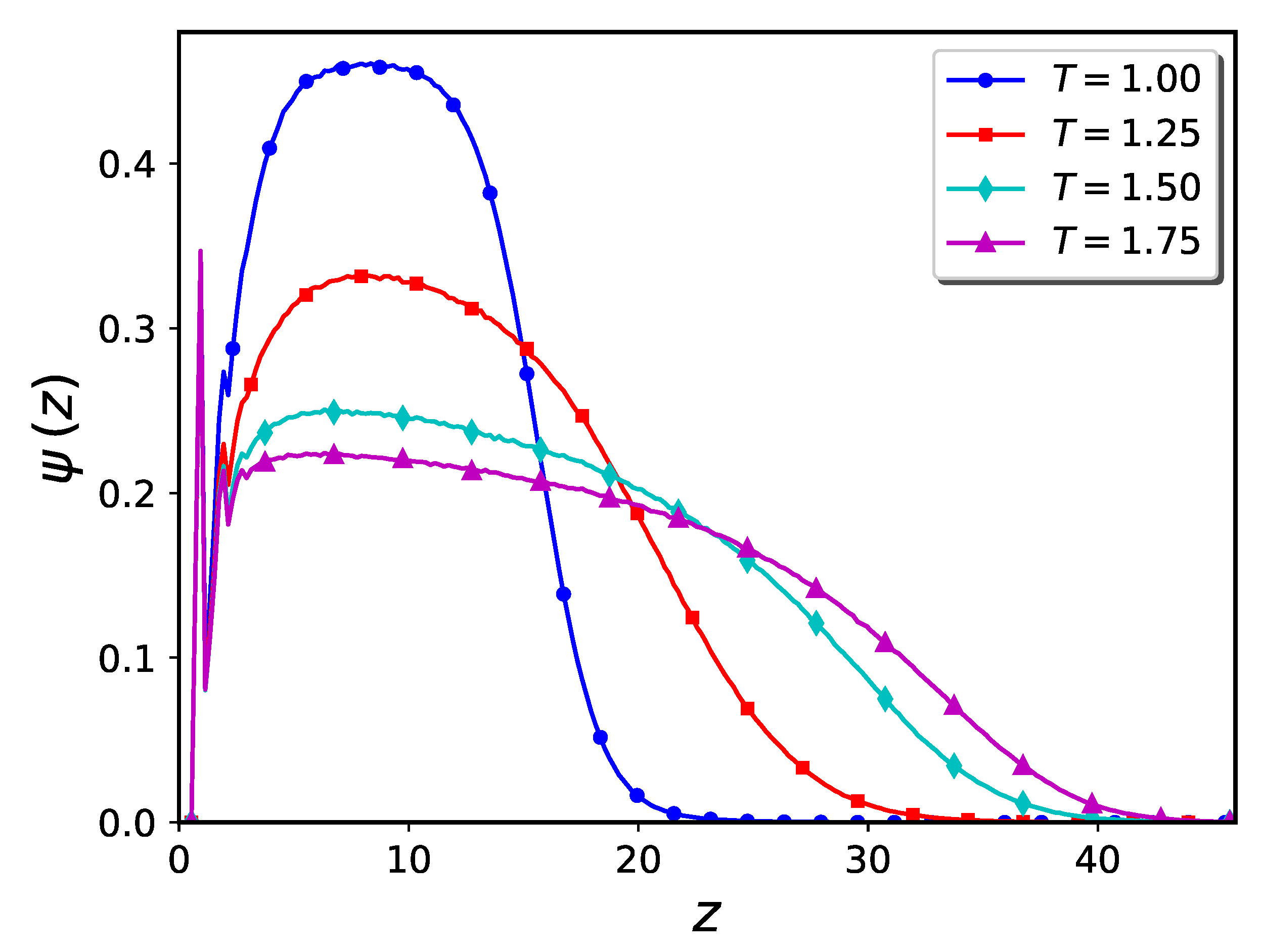
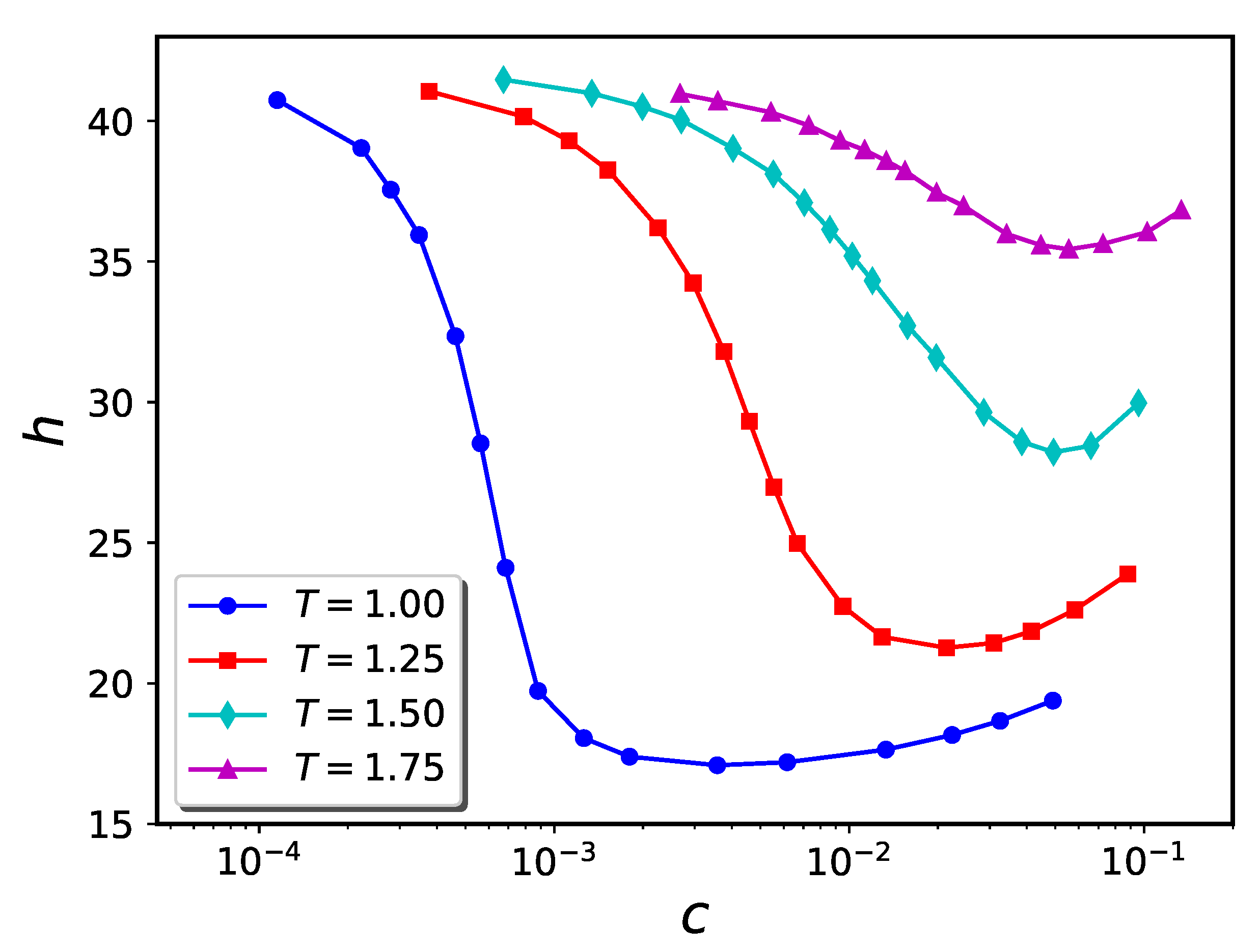
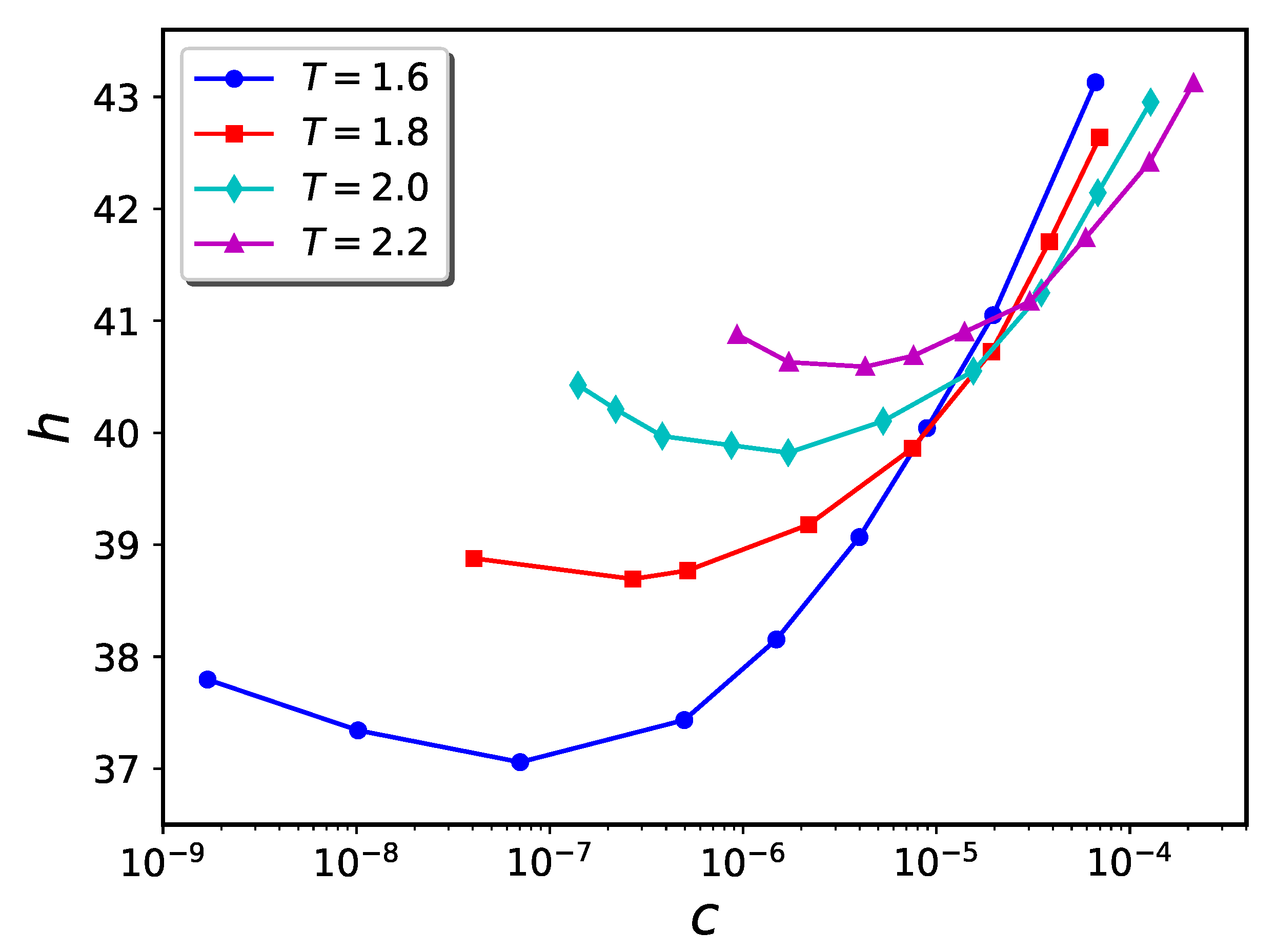
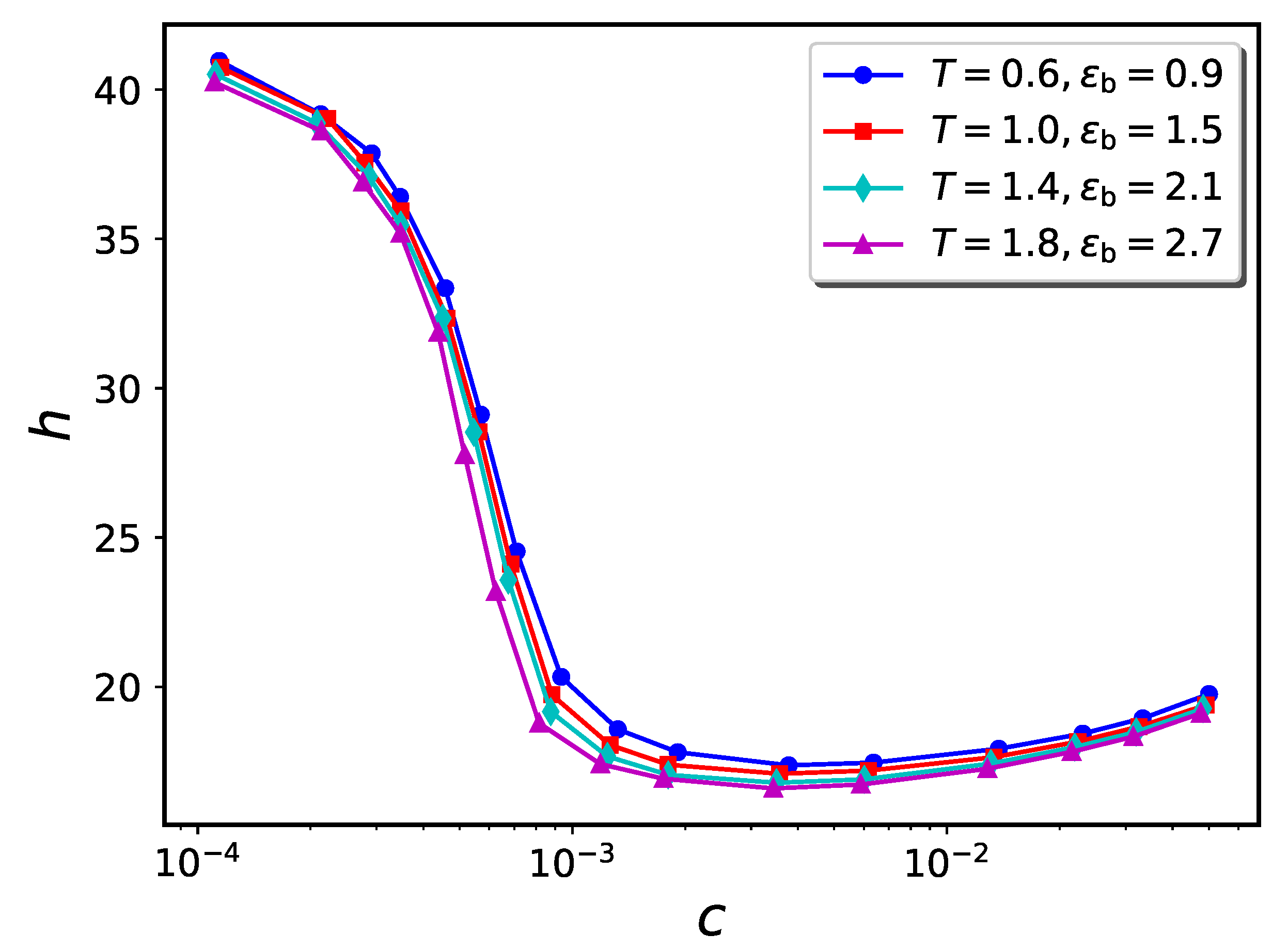
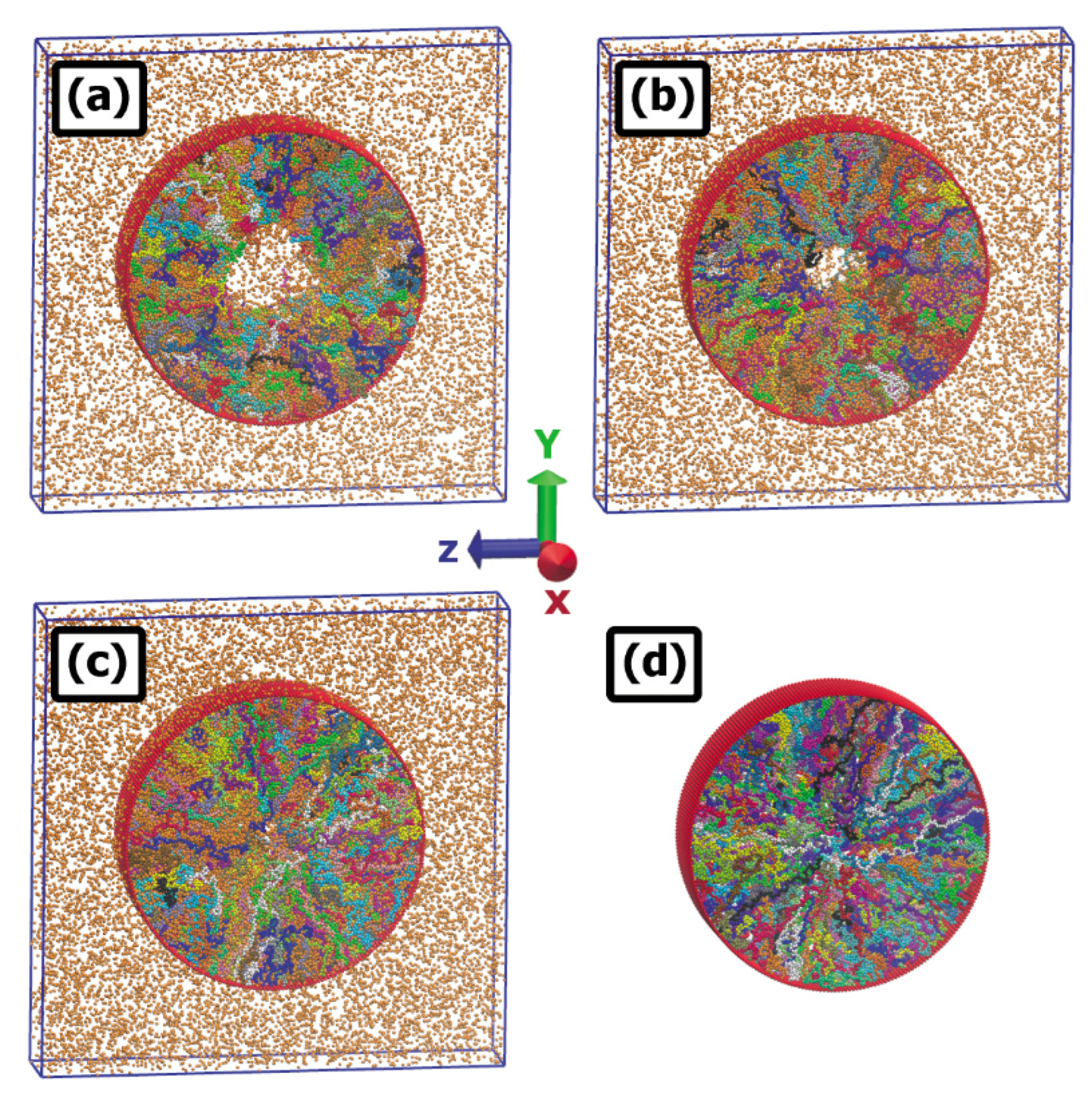
2.3. Brush plus Nanoparticles—Cylindrical Geometry
3. Discussion
4. Methods and Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Opferman, M.G.; Coalson, R.D.; Jasnow, D.; Zilman, A. Morphological control of grafted polymer films via attraction to small nanoparticle inclusions. Phys. Rev. E 2012, 86, 031806. [Google Scholar] [CrossRef] [PubMed]
- Opferman, M.G.; Coalson, R.D.; Jasnow, D.; Zilman, A. Morphology of polymer brushes infiltrated by attractive nanoinclusions of various sizes. Langmuir 2013, 29, 8584–8591. [Google Scholar] [CrossRef] [PubMed]
- Coalson, R.D.; Eskandari Nasrabad, A.; Jasnow, D.; Zilman, A. A polymer-brush-based nanovalve controlled by nanoparticle additives: Design principles. J. Phys. Chem. B 2015, 119, 11858–11866. [Google Scholar] [CrossRef] [PubMed]
- Eskandari Nasrabad, A.; Jasnow, D.; Zilman, A.; Coalson, R.D. Precise control of polymer coated nanopores by nanoparticle additives: Insights from computational modeling. J. Chem. Phys. 2016, 145, 64901. [Google Scholar] [CrossRef]
- Ozmaian, M.; Jasnow, D.; Eskandari Nasrabad, A.; Zilman, A.; Coalson, R.D. Effects of cross-linking on partitioning of nanoparticles into a polymer brush: Coarse-grained simulations test simple approximate theories. J. Chem. Phys. 2018, 148, 024902. [Google Scholar] [CrossRef]
- Patel, S.S.; Belmont, B.J.; Santé, J.M.; Rexach, M.F. Natively Unfolded Nucleoporins Gate Protein Diffusion across the Nuclear Pore Complex. Cell 2007, 129, 83–96. [Google Scholar] [CrossRef]
- Stewart, M. Molecular mechanism of the nuclear protein import cycle. Nat. Rev. Mol. Cell Biol. 2007, 8, 195–208. [Google Scholar] [CrossRef]
- Hoogenboom, B.W.; Hough, L.E.; Lemke, E.A.; Lim, R.Y.H.; Onck, P.R.; Zilman, A. Physics of the Nuclear Pore Complex: Theory, Modeling and Experiment. Phys. Rep. 2021, 921, 1–53. [Google Scholar] [CrossRef]
- Terry, L.J.; Shows, E.; Wente, S.R. Crossing the Nuclear Envelope: Hierarchical Regulation of Nucleocytoplasmic Transport. Science 2007, 318, 1412–1416. [Google Scholar] [CrossRef]
- Isgro, T.A.; Schulten, K. Binding dynamics of isolated nucleoporin repeat regions to importin-beta. Structure 2005, 13, 1869–1879. [Google Scholar] [CrossRef]
- Peters, R. Translocation through the nuclear pore: Kaps pave the way. BioEssays 2009, 31, 466–477. [Google Scholar] [CrossRef] [PubMed]
- Kapinos, L.E.; Schoch, R.L.; Wagner, R.S.; Schleicher, K.D.; Lim, R.Y.H. Karyopherin-centric control of nuclear pores based on molecular occupancy and kinetic analysis of multivalent binding with FG nucleoporins. Biophys. J. 2014, 106, 1751–1762. [Google Scholar] [CrossRef] [PubMed]
- Vovk, A.; Gu, C.; Opferman, M.G.; Kapinos, L.E.; Lim, R.Y.; Coalson, R.D.; Jasnow, D.; Zilman, A. Simple biophysics underpins collective conformations of the intrinsically disordered proteins of the Nuclear Pore Complex. eLife 2016, 5, 10785. [Google Scholar] [CrossRef] [PubMed]
- Wagner, R.S.; Kapinos, L.E.; Marshall, N.J.; Stewart, M.; Lim, R.Y.H. Promiscuous Binding of Karyopherinβ1 Modulates FG Nucleoporin Barrier Function and Expedites NTF2 Transport Kinetics. Biophys. J. 2015, 108, 918–927. [Google Scholar] [CrossRef]
- Zahn, R.; Osmanovic, D.; Ehret, S.; Callis, C.A.; Frey, S.; Stewart, M.; You, C.; Görlich, D.; Hoogenboom, B.W. A physical model describing the interaction of nuclear transport receptors with FG nucleoporin domain assemblies. eLife 2016, 5, 14119. [Google Scholar] [CrossRef]
- Kim, J.; Izadyar, A.; Shen, M.; Ishimatsu, R.; Amemiya, S. Ion Permeability of the Nuclear Pore Complex and Ion-Induced Macromolecular Permeation as Studied by Scanning Electrochemical and Fluorescence Microscopy. Anal. Chem. 2014, 86, 2090–2098. [Google Scholar] [CrossRef]
- Emilsson, G.; Sakiyama, Y.; Malekian, B.; Xiong, K.; Adali-Kaya, Z.; Lim, R.Y.H.; Dahlin, A.B. Gating Protein Transport in Solid State Nanopores by Single Molecule Recognition. ACS Cent. Sci. 2018, 4, 1007–1014. [Google Scholar] [CrossRef]
- Osmanovic, D.; Ford, I.J.; Hoogenboom, B.W. Model Inspired by Nuclear Pore Complex Suggests Possible Roles for Nuclear Transport Receptors in Determining Its Structure. Biophys. J. 2013, 105, 2781. [Google Scholar] [CrossRef]
- Sirkin, Y.; Tagliazucchi, M.; Szleifer, I. Nanopore gates via reversible crosslinking of polymer brushes: A theoretical study. Soft Matter 2021, 17, 2791–2802. [Google Scholar] [CrossRef]
- Ananth, A.; Mishra, A.; Frey, S.; Dwarkasing, A.; Versloot, R.C.A.; van der Giessen, E.; Görlich, D.; Onck, P.R.; Dekker, C. Spatial structure of disordered proteins dictates conductance and selectivity in nuclear pore complex mimics. eLife 2018, 7, e31510. [Google Scholar] [CrossRef]
- Li, C.W.; Merlitz, H.; Wu, C.X.; Sommer, J.U. Nanopores as Switchable Gates for Nanoparticles: A Molecular Dynamics Study. Macromolecules 2018, 51, 6238–6247. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A.; Cates, M.E. A Parabolic Density Profile for Grafted Polymers. Europhys. Lett. 1988, 5, 413. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G. Interaction between grafted polymeric brushes: A molecular dynamics study. Phys. Rev. Lett. 1989, 63, 1074. [Google Scholar] [CrossRef]
- Muthukumar, M.; Ho, J.S. Self-consistent field theory of surfaces with terminally attached chains. Macromolecules 1989, 22, 965–973. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V.; Priamitsyn, V.A. Theory of steric stabilization of colloid dispersions by grafted polymers. J. Colloid Interface Sci. 1990, 137, 495. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Singh, C.; Balazs, A.C. Forming Patterned Films with Tethered Diblock Copolymers. Macromolecules 1996, 29, 6338–6348. [Google Scholar] [CrossRef]
- Schmid, F. Self-consistent-field theories for complex fluids. J. Phys. Condens. Matter 1998, 10, 8105–8138. [Google Scholar] [CrossRef]
- Matsen, M.W. Corrections to the strong-stretching theory of polymer brushes due to the entropy of the free ends. J. Chem. Phys. 2002, 117, 2351–2358. [Google Scholar] [CrossRef]
- Müller, M. Phase diagram of a mixed polymer brush. Phys. Rev. E 2002, 65, 030802. [Google Scholar] [CrossRef]
- Ye, Y.; McCoy, J.D.; Curro, J.G. Application of density functional theory to tethered polymer chains: Effect of intermolecular attractions. J. Chem. Phys. 2003, 119, 555–564. [Google Scholar] [CrossRef]
- Adiga, S.P.; Brenner, D.W. Flow Control through Polymer-Grafted Smart Nanofluidic Channels: Molecular Dynamics Simulations. Nano Lett. 2005, 5, 2509–2514. [Google Scholar] [CrossRef] [PubMed]
- Minko, S. Responsive Polymer Brushes. J. Macromol. Sci. C 2006, 46, 397–420. [Google Scholar] [CrossRef]
- Dimitrov, D.I.; Milchev, A.; Binder, K.; Heermann, D.W. Structure of Polymer Brushes in Cylindrical Tubes: A Molecular Dynamics Simulation. Macromol. Theory Sim. 2006, 15, 573. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. B Polym. Phys. 2012, 50, 1515. [Google Scholar] [CrossRef]
- Tagliazucchi, M.; Szleifer, I. Stimuli-responsive polymers grafted to nanopores and other nano-curved surfaces: Structure, chemical equilibrium and transport. Soft Matter 2012, 8, 7292–7305. [Google Scholar] [CrossRef]
- Suo, T.; Whitmore, M.D. Controlling microtube permeability via grafted polymers and solvent quality. J. Chem. Phys. 2014, 140, 114902. [Google Scholar] [CrossRef]
- Sommer, J.-U. Adsorption-attraction model for co-nonsolvency in polymer brushes. Macromolecules 2017, 50, 2219. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Theory of the grafted polymer brush. Macromolecules 1988, 21, 2610–2619. [Google Scholar] [CrossRef]
- Semenov, A.N. Contribution to the theory of microphase layering in block-copolymer melts. J. Exp. Theor. Phys. 1985, 61, 733. [Google Scholar]
- Alexander, S. Polymer adsorption on small spheres. A scaling approach. J. Phys. 1977, 38, 977–981. [Google Scholar] [CrossRef]
- de Gennes, P.G. Conformations of Polymers Attached to an Interface. Macromolecules 1980, 13, 1069–1075. [Google Scholar] [CrossRef]
- Yameen, B.; Ali, M.; Neumann, R.; Ensinger, W.; Knoll, W.; Azzaroni, O. Ionic Transport Through Single Solid-State Nanopores Controlled with Thermally Nanoactuated Macromolecular Gates. Small 2009, 5, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Bittrich, E.; Kuntzsch, M.; Eichhorn, K.; Uhlmann, P. Complex pH- and temperature-sensitive swelling behavior of mixed polymer brushes. J. Polym. Sci. B 2010, 48, 1606–1615. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G. Dynamics of entangled linear polymer melts: A molecular dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- McQuarrie, D. Statistical Mechanics; Harper & Row: Pittsburgh, PA, USA, 1976. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G. Structure of a grafted polymer brush: A molecular dynamics simulation. Macromolecule 1989, 22, 4054. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eskandari Nasrabad, A.; Laghaei, R.; Coalson, R.D. Morphology of Polymer Brushes in the Presence of Attractive Nanoparticles: Effects of Temperature. Int. J. Mol. Sci. 2023, 24, 832. https://doi.org/10.3390/ijms24010832
Eskandari Nasrabad A, Laghaei R, Coalson RD. Morphology of Polymer Brushes in the Presence of Attractive Nanoparticles: Effects of Temperature. International Journal of Molecular Sciences. 2023; 24(1):832. https://doi.org/10.3390/ijms24010832
Chicago/Turabian StyleEskandari Nasrabad, Afshin, Rozita Laghaei, and Rob D. Coalson. 2023. "Morphology of Polymer Brushes in the Presence of Attractive Nanoparticles: Effects of Temperature" International Journal of Molecular Sciences 24, no. 1: 832. https://doi.org/10.3390/ijms24010832
APA StyleEskandari Nasrabad, A., Laghaei, R., & Coalson, R. D. (2023). Morphology of Polymer Brushes in the Presence of Attractive Nanoparticles: Effects of Temperature. International Journal of Molecular Sciences, 24(1), 832. https://doi.org/10.3390/ijms24010832





