Electron Scattering from 1-Methyl-5-Nitroimidazole: Cross-Sections for Modeling Electron Transport through Potential Radiosensitizers
Abstract
:1. Introduction
2. Results
2.1. Total Electron Scattering Cross-Sections
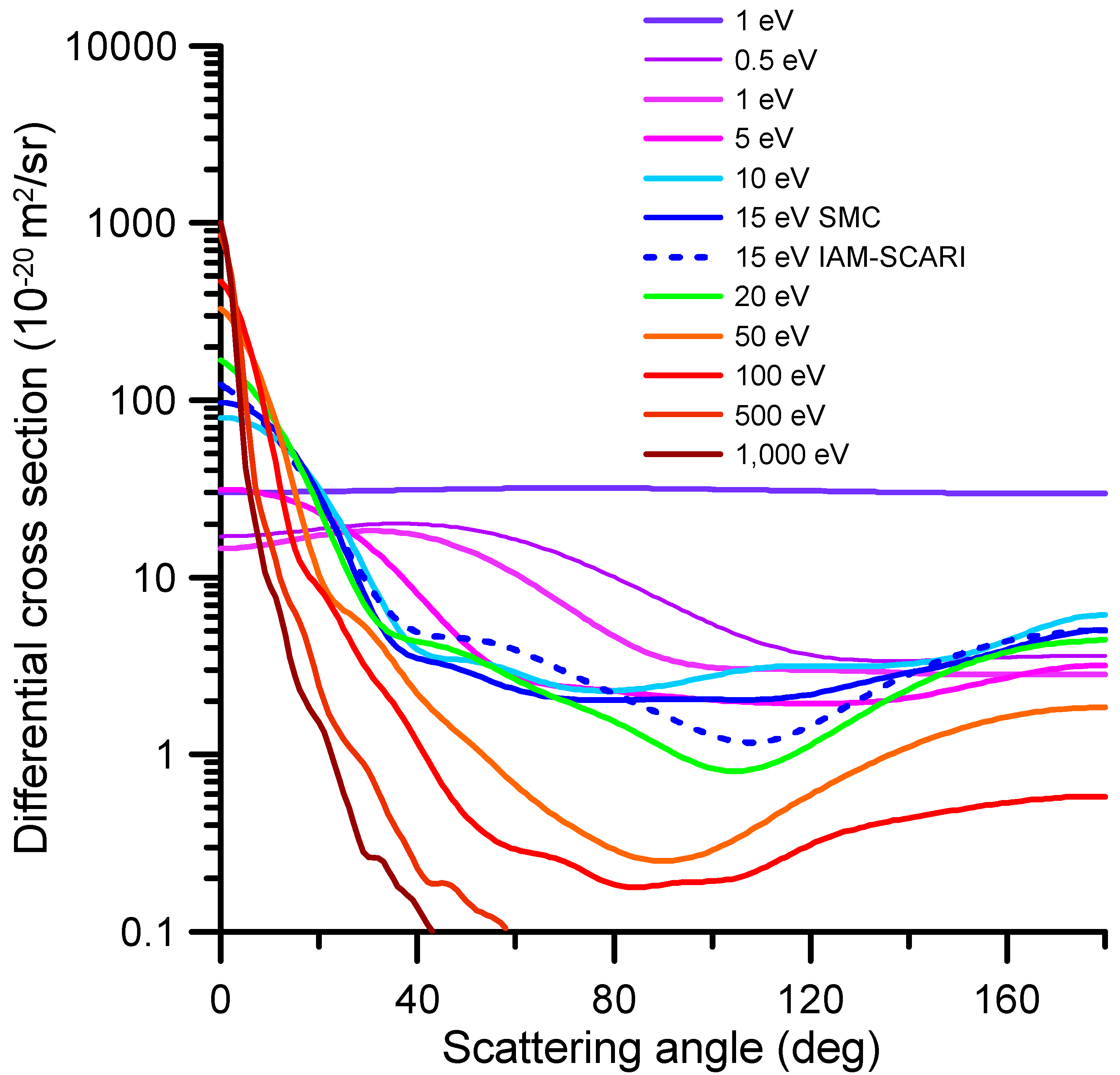
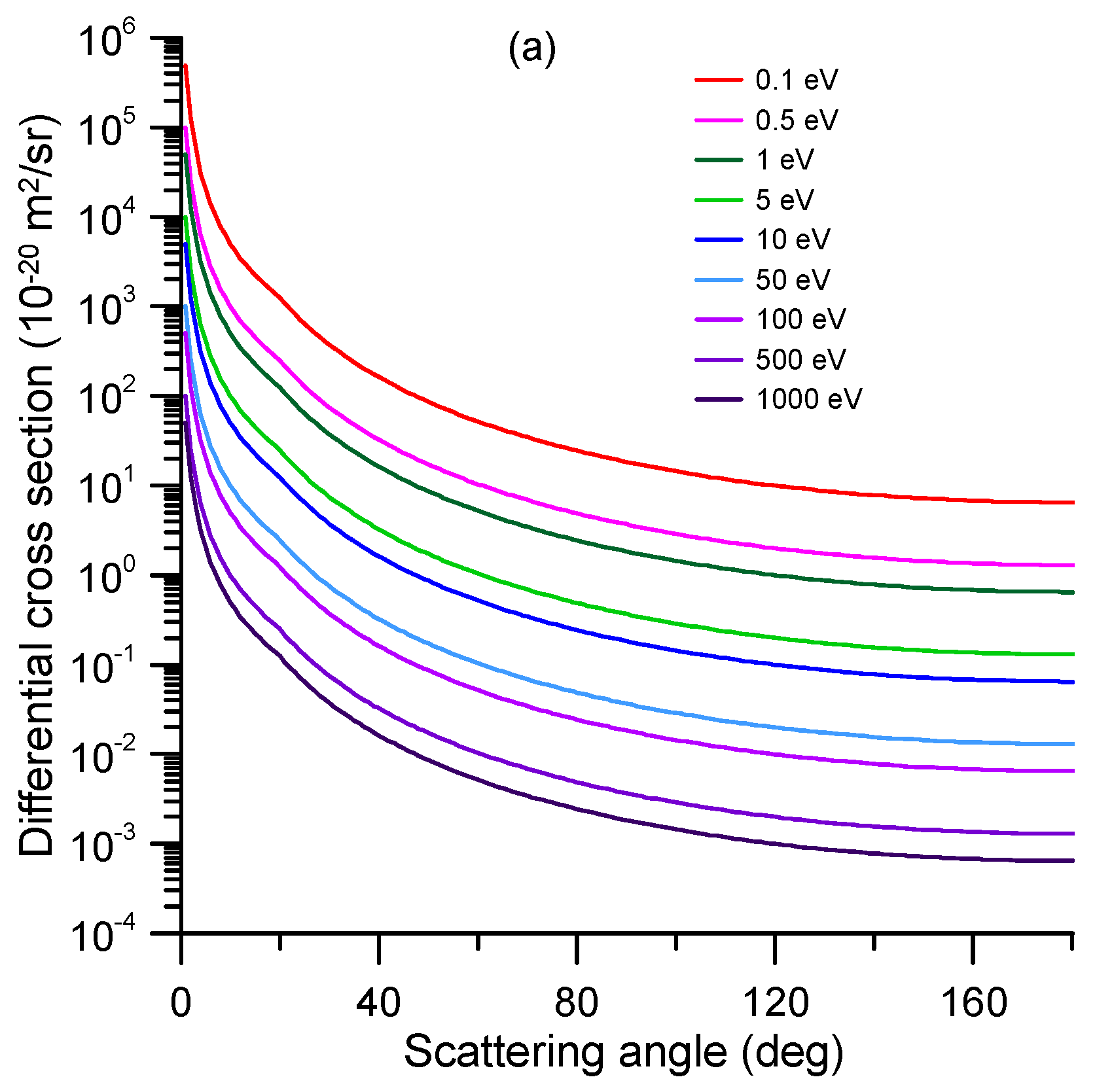
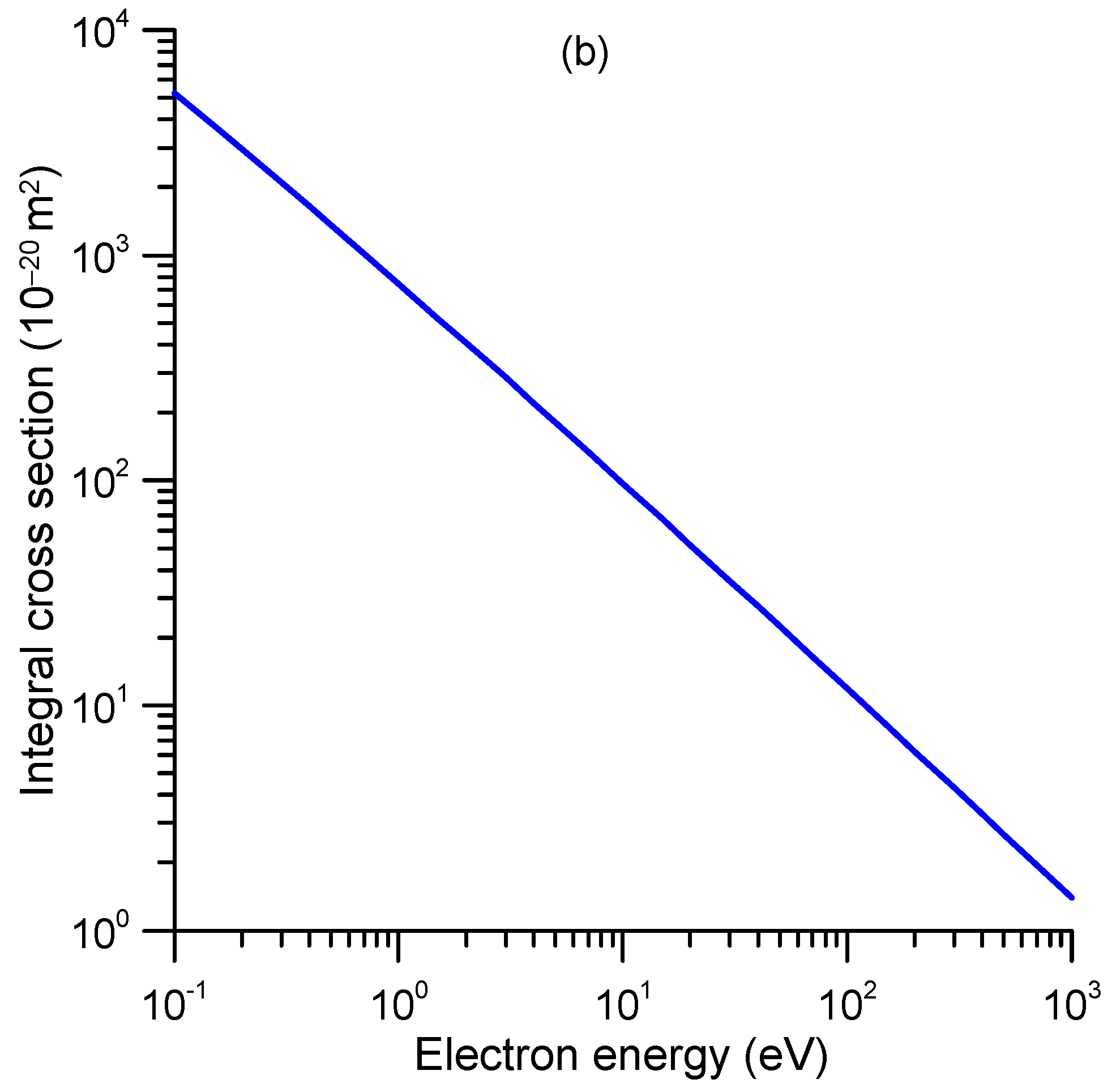
2.2. Differential and Integral Elastic Cross-Sections
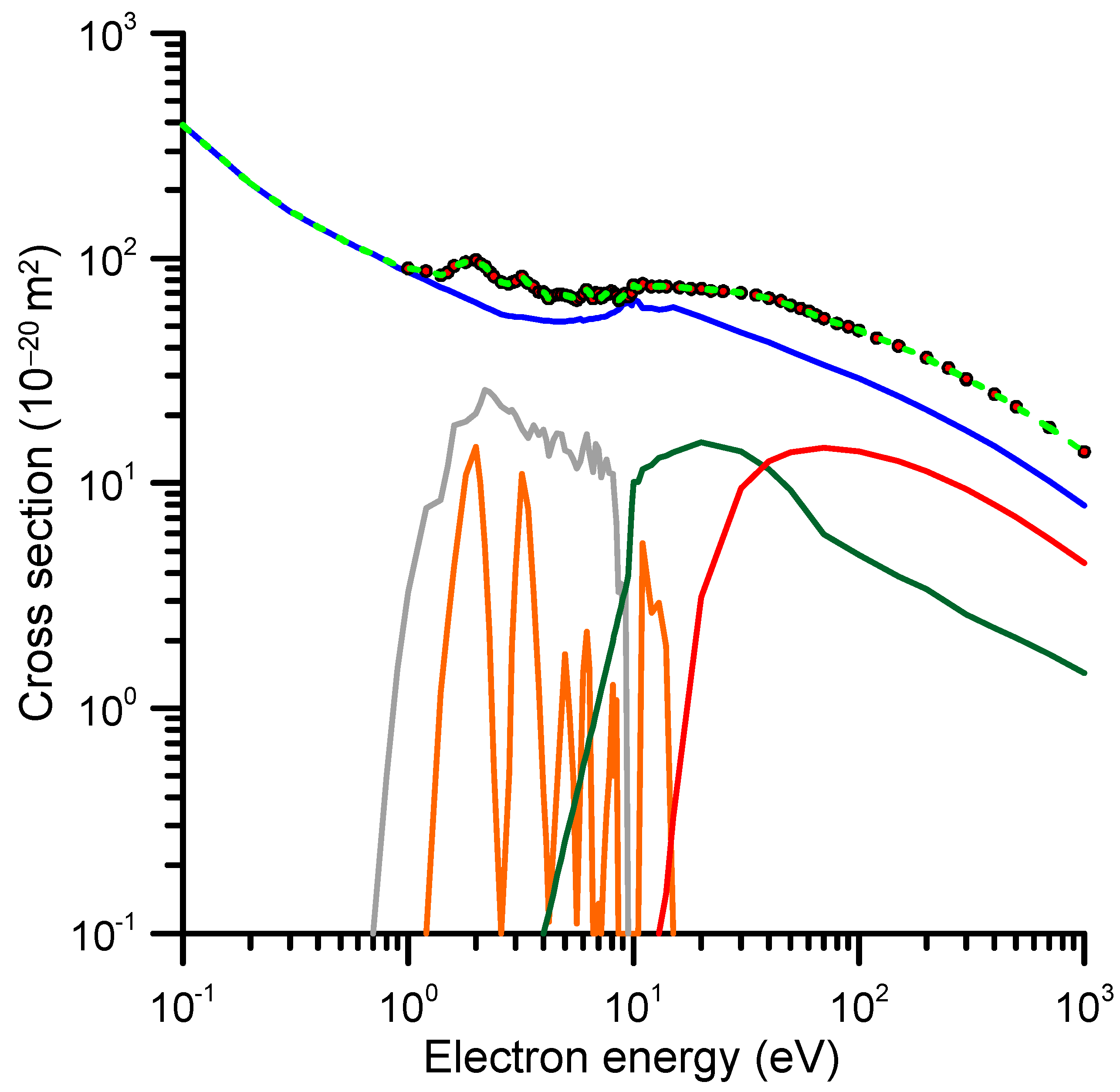
2.3. Differential and Integral Inelastic Cross-Sections
2.3.1. Electron Attachment Cross-Sections
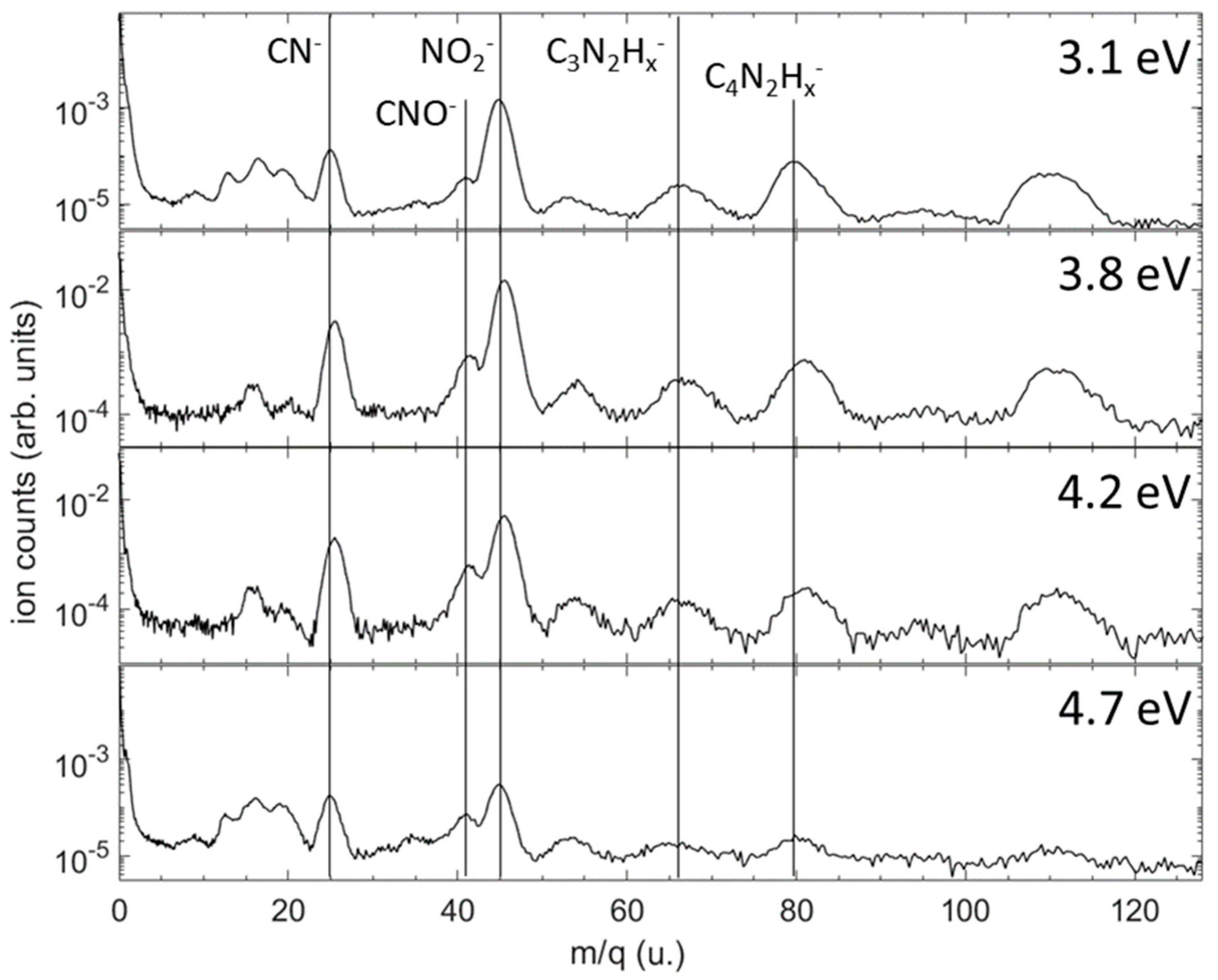
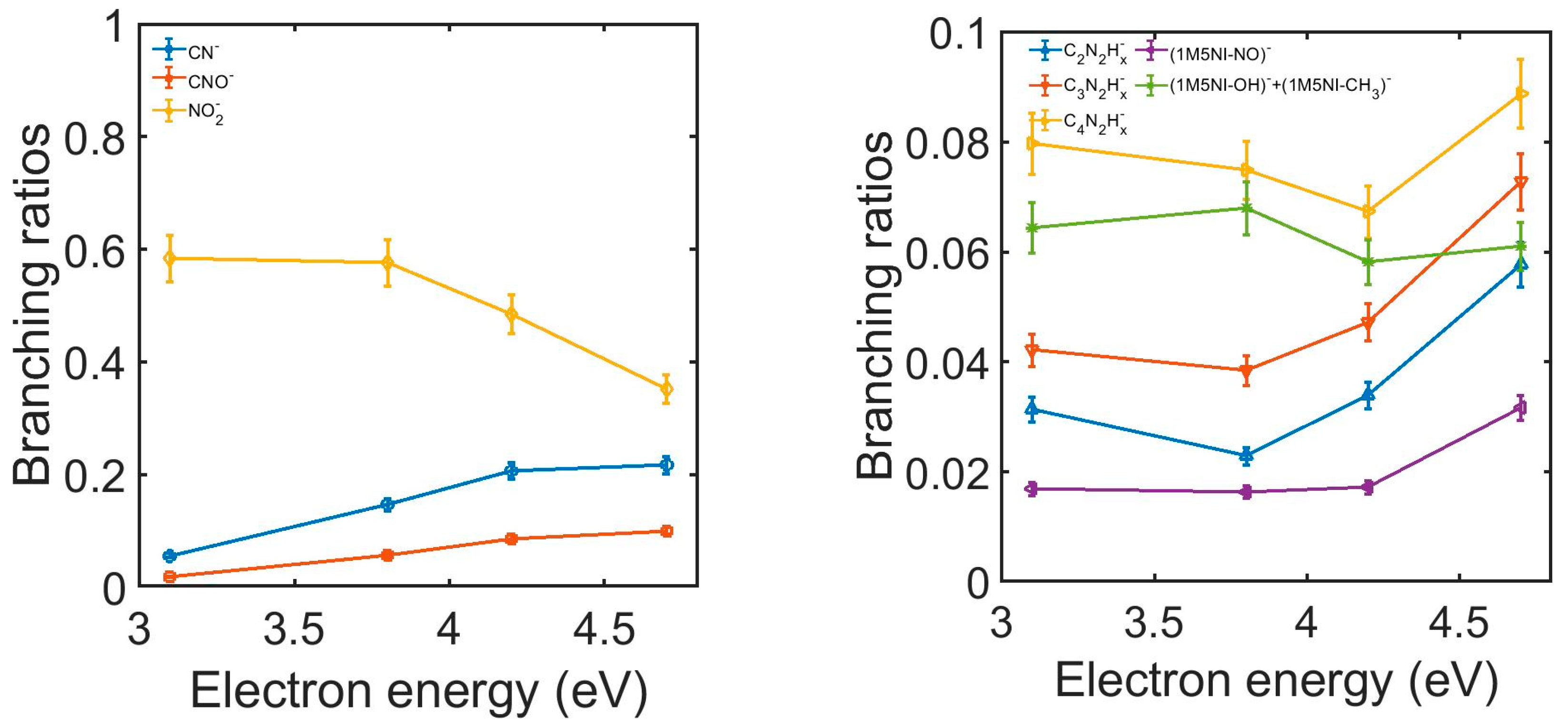
2.3.2. Anion Yield Analysis
2.3.3. Total Ionization Cross-Sections and Cation Formation by Electron Impact
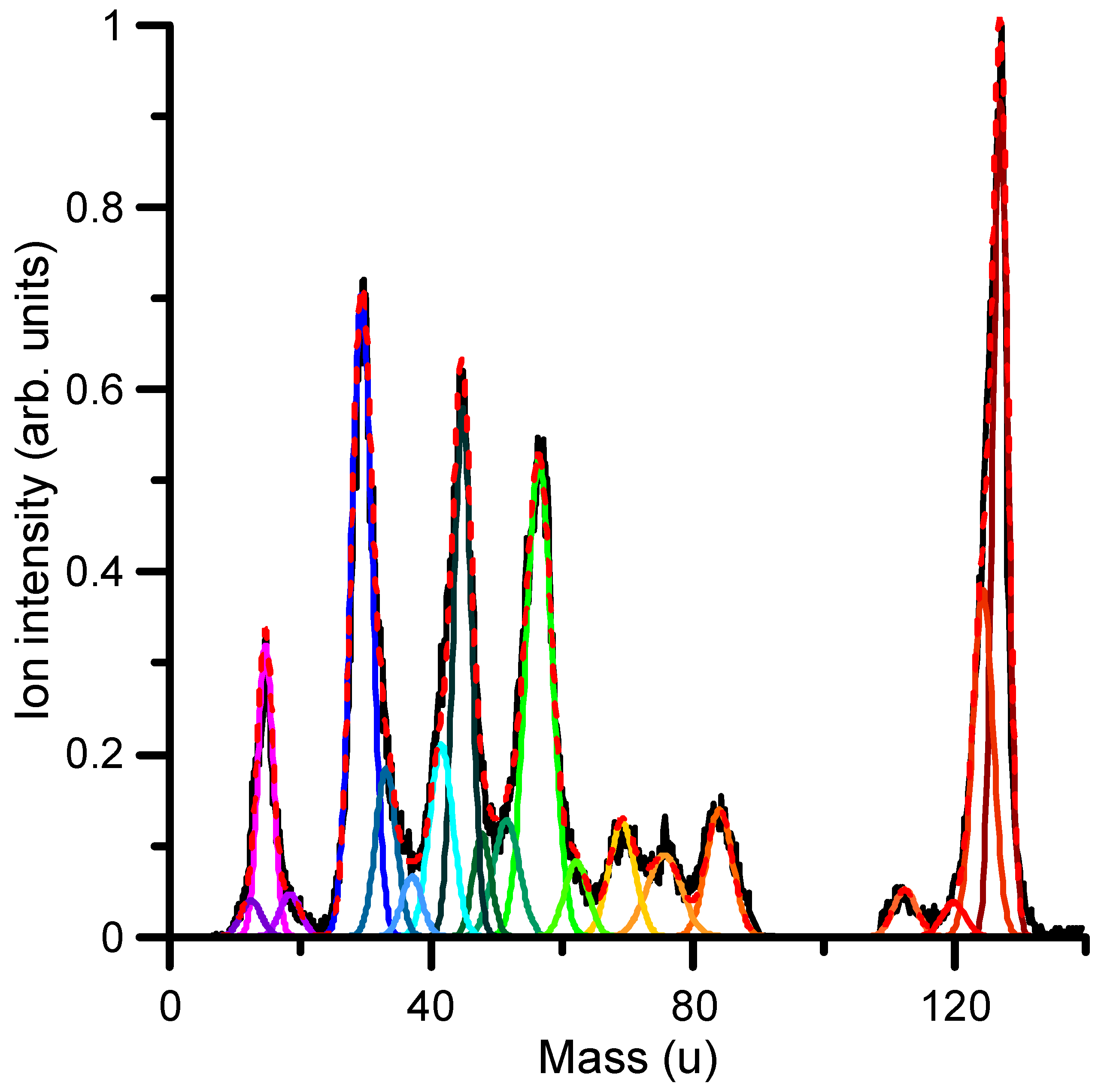
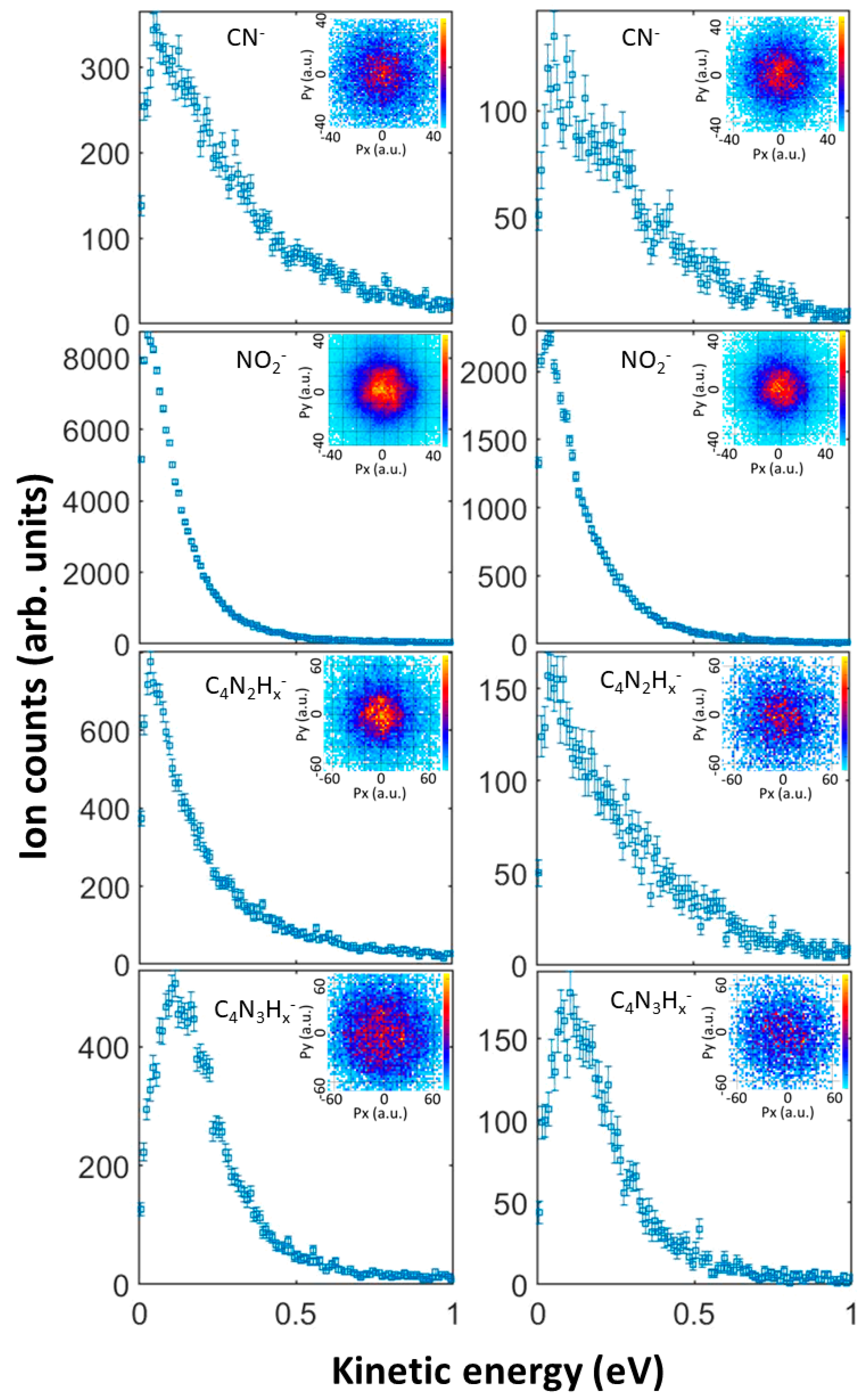
2.3.4. Differential Inelastic Cross-Sections
2.3.5. Rotational, Vibrational and Electronic Excitation Cross-Sections
3. Discussion
4. Materials and Methods
4.1. Calculation Methods
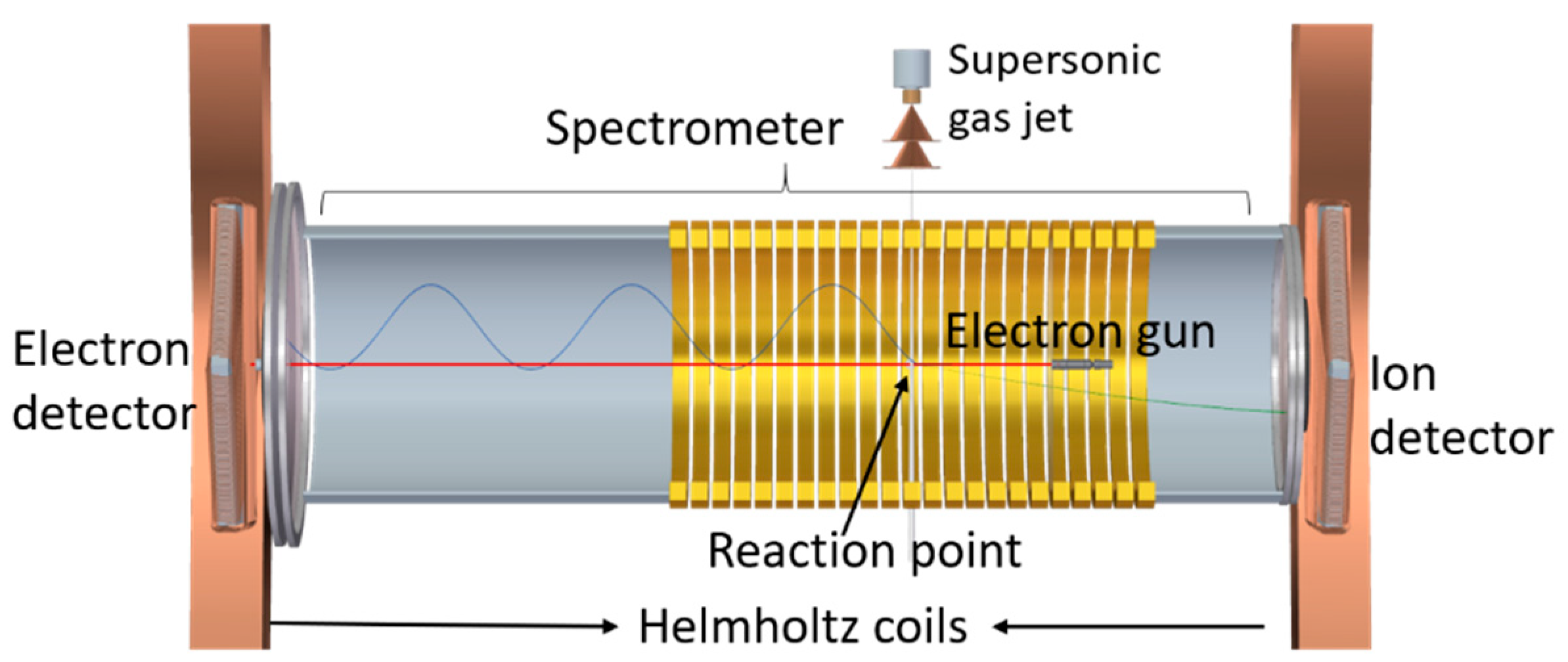
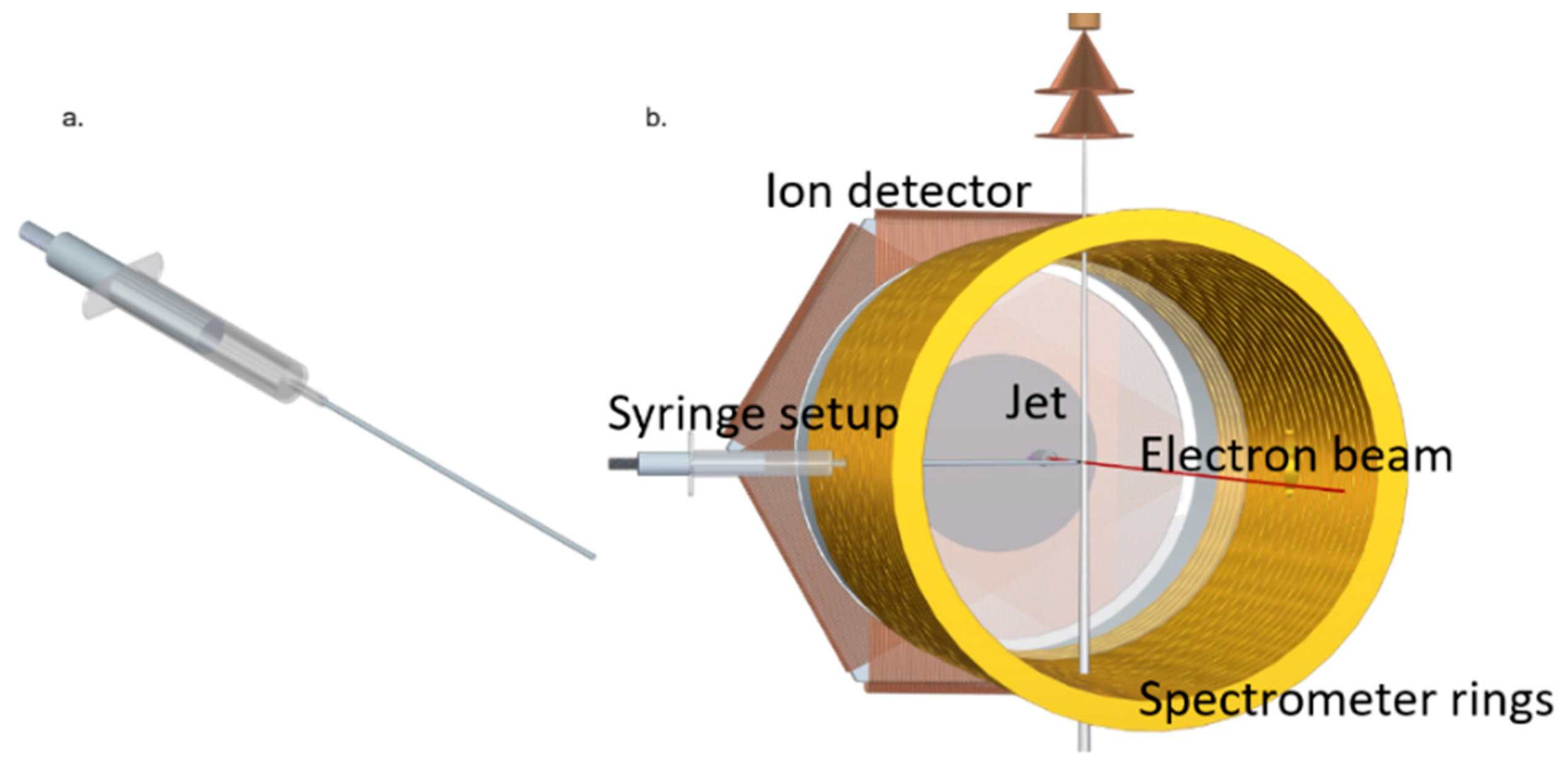
4.2. Experimental Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spiers, F.W. The Influence of Energy Absorption and Electron Range on Dosage in Irradiated Bone. Br. J. Radiol. 1949, 22, 521–533. [Google Scholar] [CrossRef] [PubMed]
- Haume, K.; Rosa, S.; Grellet, S.; Śmiałek, M.A.; Butterworth, K.T.; Solov’yov, A.; Prise, K.M.; Golding, J.; Mason, N.J. Gold nanoparticles for cancer radiotherapy: A review. Cancer Nanotechnol. 2016, 7, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Yun, K.-H.; Lee, H.; Goh, S.-H.; Suh, Y.-G.; Choi, Y. Porous platinum nanoparticles as a high-Z and oxygen generating nano-zyme for enhanced radiotherapy in vivo. Biomaterials 2019, 197, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Yang, M.; Pang, B.; Vara, M.; Xia, Y. Gold nanomaterials at work in biomedicine. Chem. Rev. 2015, 115, 10410–10488. [Google Scholar] [CrossRef]
- Gong, L.; Zhang, Y.; Chengcheng, L.; Ahang, M.; Han, S. Application of Radiosensitizers in Cancer Radiotherapy. Int. J. Nanomed. 2021, 16, 1083–1102. [Google Scholar] [CrossRef]
- Pradhan, A.K.; Nahar, S.N.; Montenegro, M.; Yu, Y.; Zhang, H.L.; Sur, C.; Mrozik, M.; Pitzer, R.M. Resonant X-ray Enhancement of the Auger Effect in High-Z Atoms, Molecules, and Nanoparticles: Potential Biomedical Applications. J. Phys. Chem. A 2009, 113, 12356–12363. [Google Scholar] [CrossRef]
- Calvo, F.A.; Serrano, J.; Cambeiro, M.; Aristu, J.; Asencio, J.M.; Rubio, I.; Delgado, J.M.; Ferrer, C.; Pascau, J. Intra-Operative Electron Radiation Therapy: An Update of the Evidence Collected in 40 Years to Search for Models for Electron-FLASH Studies. Cancers 2022, 14, 3693. [Google Scholar] [CrossRef]
- Mohan, R. A review of proton-therapy–Current status and future directions. Prec. Radiat. Oncol. 2022, 6, 164–176. [Google Scholar] [CrossRef]
- Mairani, A.; Mein, S.; Blakely, E.; Debus, J.; Durante, M.; Ferrari, A.; Fuchs, H.; Georg, D.; Grosshans, D.R.; Guan, F.; et al. Roadmap: Helium ion therapy. Phys. Med. Biol. 2022, 67, 15TR02. [Google Scholar] [CrossRef]
- Seneviratne, D.; Ishikawa, H.; Mao, J.; Dougherty, J.M.; Bush, A.; Thomas, M.; Manochakian, R.; Lou, Y.; Owen, D.; Sio, T.T.; et al. Carbon ion radiotherapy in the management of non-small cell lung cancer. Prec. Radiat. Oncol. 2022, 6, 69–74. [Google Scholar] [CrossRef]
- Sokol, O.; Scifoni, E.; Tinganelli, W.; Kraft-Weyrather, W.; Wiedemann, J.; Maier, A.; Boscolo, D.; Friedrich, T.; Brons, S.; Durante, M.; et al. Oxygen beams for therapy: Advanced biological treatment planning and experimental verification. Phys. Med. Biol. 2017, 62, 7798. [Google Scholar] [CrossRef]
- Schlathölter, T.; Eustache, O.; Porcel, E.; Salado, D.; Stefancikova, L.; Tillement, O.; Lux, F.; Mowat, P.; Biegun, A.K.; van Goethem, M.-J.; et al. Improving proton therapy by metal-containing nanoparticles: Nanoscale insights. Int. J. Nanomed. 2016, 11, 1549–1556. [Google Scholar] [CrossRef] [Green Version]
- Meißner, R.; Kočišek, J.; Feketeová, L.; Fedor, J.; Fárník, M.; Limão-Vieira, P.; Illenberger, E.; Denifl, S. Low-energy electrons transform the nimorazole molecule into a radiosensitizer. Nat. Commun. 2019, 10, 2388. [Google Scholar] [CrossRef] [Green Version]
- Meißner, R.; Feketeová, L.; Illenberger, E.; Denifl, S. Reactions in the Radiosensitizer Misonidazole Induced by Low-Energy (0–10 eV) Electrons. Int. J. Mol. Sci. 2019, 20, 3496. [Google Scholar] [CrossRef] [Green Version]
- Benej, M.; Hong, X.; Vibhute, S.; Scott, S.; Wu, J.; Graves, E.; Le, Q.-T.; Koong, A.C.; Giaccia, A.J.; Yu, B.; et al. Papaverine and its derivatives radiosensitize solid tumors by inhibiting mitochondrial metabolism. Proc. Natl. Acad. Sci. USA 2018, 115, 10756–10761. [Google Scholar] [CrossRef] [Green Version]
- Tanzer, K.; Feketeová, L.; Puschnigg, B.; Scheier, P.; Illenberger, E.; Denifl, S. Reactions in Nitroimidazole Triggered by Low-Energy (0–2 eV) Electrons: Methylation at N1-H Completely Blocks Reactivity. Angew. Chem. Int. Ed. 2014, 53, 12240–12243. [Google Scholar] [CrossRef] [Green Version]
- Lozano, A.I.; García-Abenza, A.; Blanco, F.; Hasan, M.; Slaughter, D.S.; Weber, T.; McEachran, R.P.; White, R.D.; Brunger, M.J.; Limão-Vieira, P.; et al. Electron and Positron Scattering Cross Sections from CO2: A Comparative Study over a Broad Energy Range (0.1–5000 eV). J. Phys. Chem. A 2022, 126, 6032–6046. [Google Scholar] [CrossRef]
- Lozano, A.I.; Kossoski, F.; Blanco, F.; Limão-Vieira, P.; Varella, M.T.d.N.; García, G. Observation of Transient Anions That Do Not Decay through Dissociative Electron Attachment: New Pathways for Radiosensitization. J. Phys. Chem. Lett. 2022, 13, 7001–7008. [Google Scholar] [CrossRef]
- Lozano, A.I.; Oller, J.C.; Krupa, K.; Ferreira da Silva, F.; Limão-Vieira, P.; Blanco, F.; Muloz, A.; Colmenares, R.; García, G. Magnetically confined electron beam system for high resolution electron transmission-beam experiments. Rev. Sci. Instrum. 2018, 89, 063105. [Google Scholar] [CrossRef] [Green Version]
- Blanco, F.; García, G. Screening Corrections for Calculation of Electron Scattering Differential Cross Sections from Polyatomic Molecules. Phys. Lett. A 2004, 330, 230–237. [Google Scholar] [CrossRef]
- Blanco, F.; Ellis-Gibbings, L.; García, G. Screening corrections for the interference contributions to the electron and positron scattering cross sections from polyatomic molecules. Chem. Phys. Lett. 2016, 645, 71–75. [Google Scholar] [CrossRef]
- Lozano, A.I.; Oller, J.C.; Jones, D.B.; Da Costa, R.F.; do Varella, M.T.N.; Bettega, M.H.; Da Silva, F.F.; Limão-Vieira, P.; Lima, M.A.P.; White, R.D.; et al. Total electron scattering cross sections from para-benzoquinone in the energy range 1–200 eV. Phys. Chem. Chem. Phys. 2018, 20, 22368. [Google Scholar] [CrossRef] [PubMed]
- Takatsuka, K.; McKoy, V. Extension of the Schwinger Variational Principle beyond the Static-Exchange Approximation. Phys. Rev. A 1981, 24, 2473–2480. [Google Scholar] [CrossRef] [Green Version]
- da Costa, R.F.; do Varella, M.T.N.; Bettega, M.H.F.; Lima, M.A.P. Recent Advances in the Application of the Schwinger Multichannel Method with Pseudopotentials to Electron-Molecule Collisions. Eur. Phys. J. D 2015, 69, 159. [Google Scholar] [CrossRef] [Green Version]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comput. Phys. Commun. 1998, 142, 142–167. [Google Scholar] [CrossRef]
- Modelli, A.; Venuti, M. Empty level structure and dissociative electron attachment in gas-phase nitro derivatives. Int. J. Mass Spectrom. 2001, 205, 7–16. [Google Scholar] [CrossRef]
- Álvarez, L.; Costa, F.; Lozano, A.I.; Oller, J.C.; Munoz, A.; Blanco, F.; Limão-Vieira, P.; White, R.D.; Brunger, M.J.; García, G. Electron scattering cross sections from nitrobenzene in the energy range 0.4–1000 eV: The role of dipole interactions in measurements and calculations. Phys. Chem. Chem. Phys. 2020, 22, 13505. [Google Scholar] [CrossRef]
- Adaniya, H.; Slaughter, D.S.; Osipov, T.; Weber, T.; Belkacem, A. A momentum imaging microscope for dissociative electron attachment. Rev. Sci. Instrum. 2012, 83, 023106. [Google Scholar] [CrossRef]
- Tanzer, K.; Feketeová, L.; Puschnigg, B.; Scheier, P.; Illenberger, E.; Denifl, S. Reactions in Nitroimidazole and Methylnitroimidazole Triggered by Low-Energy (0–8 eV) Electrons. J. Phys. Chem. A 2015, 119, 6668–6675. [Google Scholar] [CrossRef] [Green Version]
- Inokuti, M. Inelastic Collisions of Fast Charged Particles with Atoms and Molecules—The Bethe Theory Revisited. Rev. Mod. Phys. 1971, 43, 297–347. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954–3967. [Google Scholar] [CrossRef] [Green Version]
- Torres, I.; Martínez, R.; Sánchez Rayo, M.N.; Castaño, F. Evaluation of the computational methods for electron-impact total ionization cross sections: Fluoromethanes as benchmarks. J. Chem. Phys. 2001, 115, 4041–4050. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Nixon, K.L.; Pires, W.A.D.; Amorim, R.A.A.; Neves, R.F.C.; Duque, H.V.; da Silva, D.G.M.; Jones, D.B.; Blanco, F.; García, G.; et al. Electron impact ionization of 1-butanol: II. Total ionization cross sections and appearance energies. Int. J. Mass. Spectrom. 2018, 430, 44–51. [Google Scholar] [CrossRef] [Green Version]
- Bartschat, K.; Burke, P.G. The R-matrix method for electron impact ionization. J. Phys. B 1987, 20, 3191–3200. [Google Scholar] [CrossRef]
- Bray, I.; Fursa, D.V.; Röder, J.; Ehrhardt, H. Low-energy electron-impact ionization of helium. Phys. Rev. A 1998, 57, R3161–R3164. [Google Scholar] [CrossRef] [Green Version]
- Itälä, E.; Tanzer, K.; Granroth, S.; Kooser, K.; Denifl, S.; Kukk, E. Fragmentation patterns of 4(5)-nitroimidazole and 1-methyl-5-nitroimidazole—The effect of the methylation. J. Mass. Spectrom. 2017, 52, 770–776. [Google Scholar] [CrossRef]
- Yu, Z.; Bernstein, E. Experimental and theoretical studies of the decomposition of new imidazole based energetic materials: Model systems. J. Chem. Phys. 2012, 137, 114303. [Google Scholar] [CrossRef] [Green Version]
- Feketová, L.; Postler, J.; Savras, A.; Scheier, P.; Denifl, S.; O’Hair, R.A.J. Decomposition of nitroimidazole ions: Experiment and theory. Phys. Chem. Chem. Phys. 2015, 17, 12598. [Google Scholar] [CrossRef] [Green Version]
- Kuśmierek, J.T.; Singer, B. Reaction of diazoalkanes with 1-substituted 2, 4-dioxopyrimidines. Formation of O2, N-3 and O4-alkyl products. Nucleic Acids Res. 1976, 3, 989–1000. [Google Scholar] [CrossRef] [Green Version]
- Yadav, H.; Vinodkumar, M.; Limbachiya, C.; Vinodkumar, P.C. Scattering of electrons with formyl radical. Mol. Phys. 2017, 115, 952–961. [Google Scholar] [CrossRef]
- Li, X.; Lu, B.; Jiang, J.; Wang, L.; Trabelsi, T.; Francisco, J.S.; Fang, W.; Zhou, M.; Zeng, X. Water Complex of Imidogen. J. Am. Chem. Soc. 2023, 145, 1982–1987. [Google Scholar] [CrossRef] [PubMed]
- Kingston, A.E.; Walters, H.R.J. Electron scattering by atomic hydrogen: The distorted-wave second Born approximation. J. Phys. B 1980, 13, 4633–4662. [Google Scholar] [CrossRef]
- Champion, C.; Dal Cappello, C.; Houamer, S.; Mansouri, A. Single ionization of the water molecule by electron impact: Angular distributions at low incident energy. Phys. Rev. A 2006, 73, 012717. [Google Scholar] [CrossRef]
- De Sanctis, M.L.; Politis, M.-F.; Vuilleumier, R.; Stia, C.R.; Fojón, O.A. Double differential cross sections for liquid water ionization by fast electron impact. Eur. Phys. J. D. 2017, 71, 125. [Google Scholar] [CrossRef]
- Costa, F.; Traoré-Dubuis, A.; Álvarez, L.; Lozano, A.I.; Ren, X.; Dorn, A.; Limão-Vieira, P.; Blanco, F.; Oller, J.C.; Muñoz, A.; et al. A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV. Int. J. Mol. Sci. 2020, 21, 6947. [Google Scholar] [CrossRef]
- Loupas, A.; Lozano, A.I.; Blanco, F.; Gorfinkiel, J.; García, G. Cross sections for electron scattering from thiophene for a broad energy range. J. Chem. Phys. 2018, 149, 034304. [Google Scholar] [CrossRef] [Green Version]
- Sieradzka, A.; Blanco, F.; Fuss, M.C.; Mašín, Z.; Gorfinkiel, J.D.; García, G. Electron Scattering from Pyridine. J. Phys. Chem. A 2014, 118, 6657–6663. [Google Scholar] [CrossRef]
- Colmenares, R.; Carrión-Marchante, R.; Martín, M.E.; Salinas-Muñoz, L.; García-Bermejo, M.L.; Oller, J.C.; Muñoz, A.; Blanco, F.; Rosado, J.; Lozano, A.I.; et al. Dependence of the induced biological damage on the energy distribution and intensity of intra-operative radiotherapy elec-tron beams. Int. J. Mol. Sci. 2023, 24, 10816. [Google Scholar] [CrossRef]
- García-Abenza, A.; Lozano, A.I.; Oller, J.C.; Blanco, F.; Gorfinkiel, J.D.; Limão-Vieira, P.; García, G. Evaluation of Recommended Cross Sections for the Simulation of Electron Tracks in Water. Atoms 2021, 9, 98. [Google Scholar] [CrossRef]
- García-Abenza, A.; Lozano, A.I.; Alvarez, L.; Oller, J.C.; Rosado, J.; Blanco, F.; Limao-Vieira, P.; Garcia, G. Evaluated electron scattering cross section dataset for gaseous benzene in the energy range 0.1–1000 eV. Phys. Chem. Chem. Phys. 2023. submitted. [Google Scholar] [CrossRef]
- Kossoski, F.; Bettega, M.H.F. Low-Energy Electron Scattering from the Aza-Derivatives of Pyrrole, Furan, and Thiophene. J. Chem. Phys. 2013, 138, 234311. [Google Scholar] [CrossRef]
- Kossoski, F.; Varella, M.T.d.N. How Does Methylation Suppress the Electron Induced Decomposition of 1-Methyl-Nitroimidazoles? J. Chem. Phys. 2017, 147, 164310. [Google Scholar] [CrossRef]
- Rescigno, T.N.; Schneider, B.I. Electron-Impact Excitation of the T and V States of Ethylene: An Ab Initio Study. Phys. Rev. A 1992, 45, 2894–2902. [Google Scholar] [CrossRef]
- Szalay, P.G.; Müller, T.; Gidofalvi, G.; Lischka, H.; Shepard, R. Multiconfiguration Self-Consistent Field and Multireference Configuration Interaction Methods and Applications. Chem. Rev. 2012, 112, 108–181. [Google Scholar] [CrossRef]
- Pople, J.A.; Seeger, R.; Krishnan, R. Variational Configuration Interaction Methods and Comparison with Perturbation Theory. Int. J. Quantum Chem. 1977, 12, 149–163. [Google Scholar] [CrossRef]
- Lischka, H.; Shepard, R.; Müller, T.; Szalay, P.G.; Pitzer, R.M.; Aquino, A.J.A.; Araújo do Nascimento, M.M.; Barbatti, M.; Belcher, L.T.; Blaudeau, J.-P.; et al. The Generality of the GUGA MRCI Approach in COLUMBUS for Treating Complex Quantum Chemistry. J. Chem. Phys. 2020, 152, 134110. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Guassian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- García-Abenza, A.; Lozano, A.I.; Álvarez, L.; Oller, J.C.; Blanco, F.; Stokes, P.; White, R.D.; de Urquijo, J.; Limão-Vieira, P.; Jones, D.B.; et al. A Complete Data Set for the Simulation of Electron Transport through Gaseous Tetrahydrofuran in the Energy Range 1–100 eV. Eur. Phys. J. D 2021, 75, 303. [Google Scholar] [CrossRef]
- Fuss, M.C.; Sanz, A.G.; Blanco, F.; Oller, J.C.; Lim, P.; Brunger, M.J.; Garc, G. Total Electron-Scattering Cross Sections from Pyrimidine as Measured Using a Magnetically Confined Experimental System. Phys. Rev. A 2013, 88, 042702. [Google Scholar] [CrossRef] [Green Version]
- Lozano, A.I.; da Silva, F.F.; Blanco, F.; Limão-Vieira, P.; García, G. Total Electron Scattering Cross Section from Sevoflurane by 1–300 eV Energy Electron Impact. Chem. Phys. Lett. 2018, 706, 533–537. [Google Scholar] [CrossRef]
- Ullrich, J.; Moshammer, R.; Dorn, A.; Dörner, R.; Schmidt, L.; Schmidt-Böcking, H. Recoil-ion and electron momentum spectroscopy: Reaction-microscopes. Rep. Prog. Phys. 2003, 66, 1463–1545. [Google Scholar] [CrossRef]
- Ren, X.; Pflüger, T.; Weyland, M.; Baek, W.Y.; Rabus, H.; Ullrich, J.; Dorn, A. An (e, 2e + ion) study of low-energy electron-impact ionization and fragmentation of tetrahydrofuran with high mass and energy resolutions. J. Chem. Phys. 2014, 141, 134314. [Google Scholar] [CrossRef] [PubMed]


| E (eV) | TCS_exp (10−20 m2) | TCS + MA (10−20 m2) | E (eV) | TCS_exp (10−20 m2) | TCS + MA (10−20 m2) |
|---|---|---|---|---|---|
| 1 | 84.4 | 90.13 | 7.8 | 67.8 | 69.47 |
| 1.2 | 81.8 | 87.77 | 8 | 69.7 | 71.47 |
| 1.4 | 78 | 84.10 | 8.2 | 67.6 | 69.46 |
| 1.5 | 80.4 | 86.52 | 8.4 | 66.4 | 68.34 |
| 1.6 | 86.3 | 92.40 | 8.6 | 62.9 | 64.93 |
| 1.8 | 90.2 | 96.13 | 8.8 | 64.8 | 66.92 |
| 2 | 92.6 | 98.16 | 9 | 65.7 | 67.93 |
| 2.1 | 89.2 | 94.49 | 9.2 | 67.3 | 69.66 |
| 2.2 | 86.8 | 91.77 | 9.5 | 64.7 | 67.26 |
| 2.3 | 82.3 | 86.93 | 9.8 | 67.2 | 69.93 |
| 2.4 | 78.8 | 83.06 | 10 | 73.2 | 75.99 |
| 2.6 | 74.7 | 78.23 | 10.5 | 71.4 | 74.13 |
| 2.8 | 74 | 76.85 | 11 | 74.2 | 76.86 |
| 2.9 | 75.7 | 78.27 | 12 | 71.8 | 74.77 |
| 3 | 76.7 | 79.06 | 13 | 72 | 74.90 |
| 3.2 | 76.1 | 78.20 | 14 | 71.6 | 74.84 |
| 3.4 | 75.5 | 77.57 | 16 | 71.5 | 74.12 |
| 3.6 | 72.8 | 74.97 | 18 | 70.5 | 73.05 |
| 3.8 | 68.5 | 70.88 | 20 | 70.7 | 73.18 |
| 4 | 68.1 | 70.72 | 22 | 69.1 | 71.52 |
| 4.1 | 66 | 68.72 | 25 | 69 | 71.34 |
| 4.2 | 63.2 | 66.02 | 30 | 67.9 | 70.13 |
| 4.4 | 65 | 67.98 | 35 | 66.4 | 68.55 |
| 4.6 | 65.9 | 69.00 | 40 | 64.3 | 66.37 |
| 4.8 | 65.9 | 69.06 | 45 | 62.7 | 64.71 |
| 5 | 65.3 | 68.46 | 50 | 59.7 | 61.65 |
| 5.2 | 64.6 | 67.68 | 55 | 57.9 | 59.80 |
| 5.4 | 63.5 | 66.46 | 60 | 56.3 | 58.16 |
| 5.6 | 62.4 | 65.17 | 65 | 53.9 | 55.72 |
| 5.8 | 64.5 | 67.07 | 70 | 52.1 | 53.88 |
| 6 | 66.9 | 69.24 | 80 | 49.6 | 51.32 |
| 6.2 | 70.4 | 72.51 | 90 | 47.9 | 49.56 |
| 6.4 | 67.6 | 69.51 | 100 | 46.2 | 47.81 |
| 6.6 | 64.4 | 66.12 | 120 | 42.6 | 44.13 |
| 6.8 | 68.6 | 70.18 | 150 | 39.3 | 40.74 |
| 7 | 68.3 | 69.80 | 200 | 34.8 | 36.12 |
| 7.2 | 65.1 | 66.57 | 250 | 31.3 | 32.54 |
| 7.4 | 66.8 | 68.31 | 300 | 27.6 | 28.78 |
| 7.6 | 68.4 | 69.98 |
| Mass (u) | Chemical Composition | Relative Intensity |
|---|---|---|
| 127 | C4H5N3O2+ (1M5NI ion) | 1 |
| 124 | C4H2N3O2+ (1M5NI-3H) | 0.415 |
| 112 | C4H4N2O2+ (1M5NI-NH) | 0.0564 |
| 84 | C4HNO (Acrylonitrile-ketone) | 0.152 |
| 75 | C2H5NO2 (Glycine) | 0.0978 |
| 69 | C2H3N3 (Triazole) | 0.137 |
| 62 | CH4NO (Hydroxymethyl-amino-oxy radical) | 0.0900 |
| 56 | C2H4N2 (Diazoethane) | 0.571 |
| 51 | C3HN (Cyanoacetylene) | 0.139 |
| 48 | H2NO2+ (Nitronium) | 0.124 |
| 45 | CH3NO+ (Formaldoxime) | 0.633 |
| 42 | C2OH2+ (Ketene) | 0.230 |
| 38 | C2N (Carbon Cyanide radical) | 0.0720 |
| 33 | H3NO (Hydroxylamine) | 0.201 |
| 29 | CHO (Formyl radical) | 0.768 |
| 18 | H2O+ (Water) | 0.0512 |
| 15 | NH (Imidogen) | 0.349 |
| 12 | C (Carbon) | 0.0435 |
| Energy (eV) | Elastic | Electron Attachment | Vibrational Excitation | Electronic Excitation | Ionization | SUM |
|---|---|---|---|---|---|---|
| 0.1 | 390 | 390 | ||||
| 0.2 | 214 | 214 | ||||
| 0.3 | 162 | 162 | ||||
| 0.4 | 138 | 138 | ||||
| 0.5 | 122 | 122 | ||||
| 0.7 | 104 | 0.1 | 104 | |||
| 1.0 | 86.8 | 3.28 | 90.1 | |||
| 1.5 | 72.2 | 2.39 | 11.9 | 86.5 | ||
| 2.0 | 63.3 | 14.5 | 20.3 | 98.2 | ||
| 3.0 | 55.0 | 4.12 | 20.0 | 79.1 | ||
| 4.0 | 52.9 | 0.425 | 17.3 | 0.1 | 70.7 | |
| 5.0 | 52.5 | 1.74 | 13.9 | 0.257 | 68.5 | |
| 7.0 | 54.4 | 0.136 | 14.2 | 1.07 | 69.8 | |
| 10 | 65.8 | 0.1 | 10.1 | 76.0 | ||
| 15 | 60.5 | 0.1 | 13.7 | 0.328 | 74.5 | |
| 20 | 54.9 | 15.2 | 3.11 | 73.2 | ||
| 30 | 46.8 | 13.8 | 9.52 | 70.1 | ||
| 40 | 42.3 | 11.5 | 12.6 | 66.4 | ||
| 50 | 38.6 | 9.29 | 13.7 | 61.6 | ||
| 70 | 33.6 | 11.5 | 12.5 | 66.4 | ||
| 100 | 29.1 | 4.78 | 13.9 | 47.8 | ||
| 150 | 24.3 | 3.83 | 12.6 | 40.7 | ||
| 200 | 21.2 | 3.38 | 11.3 | 35.9 | ||
| 300 | 17.1 | 2.62 | 9.41 | 29.2 | ||
| 400 | 14.6 | 2.27 | 8.04 | 24.89 | ||
| 500 | 12.7 | 2.04 | 7.06 | 21.8 | ||
| 700 | 10.2 | 1.74 | 5.68 | 17.7 | ||
| 1000 | 7.95 | 1.43 | 4.42 | 13.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozano, A.I.; Álvarez, L.; García-Abenza, A.; Guerra, C.; Kossoski, F.; Rosado, J.; Blanco, F.; Oller, J.C.; Hasan, M.; Centurion, M.; et al. Electron Scattering from 1-Methyl-5-Nitroimidazole: Cross-Sections for Modeling Electron Transport through Potential Radiosensitizers. Int. J. Mol. Sci. 2023, 24, 12182. https://doi.org/10.3390/ijms241512182
Lozano AI, Álvarez L, García-Abenza A, Guerra C, Kossoski F, Rosado J, Blanco F, Oller JC, Hasan M, Centurion M, et al. Electron Scattering from 1-Methyl-5-Nitroimidazole: Cross-Sections for Modeling Electron Transport through Potential Radiosensitizers. International Journal of Molecular Sciences. 2023; 24(15):12182. https://doi.org/10.3390/ijms241512182
Chicago/Turabian StyleLozano, Ana I., Lidia Álvarez, Adrián García-Abenza, Carlos Guerra, Fábris Kossoski, Jaime Rosado, Francisco Blanco, Juan Carlos Oller, Mahmudul Hasan, Martin Centurion, and et al. 2023. "Electron Scattering from 1-Methyl-5-Nitroimidazole: Cross-Sections for Modeling Electron Transport through Potential Radiosensitizers" International Journal of Molecular Sciences 24, no. 15: 12182. https://doi.org/10.3390/ijms241512182
APA StyleLozano, A. I., Álvarez, L., García-Abenza, A., Guerra, C., Kossoski, F., Rosado, J., Blanco, F., Oller, J. C., Hasan, M., Centurion, M., Weber, T., Slaughter, D. S., Mootheril, D. M., Dorn, A., Kumar, S., Limão-Vieira, P., Colmenares, R., & García, G. (2023). Electron Scattering from 1-Methyl-5-Nitroimidazole: Cross-Sections for Modeling Electron Transport through Potential Radiosensitizers. International Journal of Molecular Sciences, 24(15), 12182. https://doi.org/10.3390/ijms241512182