Next Article in Journal
Role of the Nrf2 Signaling Pathway in Ovarian Aging: Potential Mechanism and Protective Strategies
Next Article in Special Issue
Porous and Close Packed Supramolecular Assemblies from 2,4-Difluoronitrobenzene with Three Different Linkers and an n-Butylamine Cap
Previous Article in Journal
DHA-Provoked Reduction in Adipogenesis and Glucose Uptake Could Be Mediated by Gps2 Upregulation in Immature 3T3-L1 Cells
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 24
Issue 17
10.3390/ijms241713324
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Halogen Bonding Involving Isomeric Isocyanide/Nitrile Groups

by
Andrey S. Smirnov
1,
Eugene A. Katlenok
1,
Alexander S. Mikherdov
1,
Mariya A. Kryukova
1,
Nadezhda A. Bokach
1 and
Vadim Yu. Kukushkin
1,2,*
1
Institute of Chemistry, Saint Petersburg State University, Universitetskaya Nab. 7/9, 199034 Saint Petersburg, Russia
2
Laboratory of Crystal Engineering of Functional Materials, South Ural State University, 76, Lenin Av., 454080 Chelyabinsk, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2023, 24(17), 13324; https://doi.org/10.3390/ijms241713324
Submission received: 26 July 2023 / Revised: 24 August 2023 / Accepted: 25 August 2023 / Published: 28 August 2023
(This article belongs to the Special Issue Bonding in Supramolecular Organic Assemblies)
Browse Figures
Review Reports Versions Notes

Abstract

:
2,3,5,6-Tetramethyl-1,4-diisocyanobenzene (1), 1,4-diisocyanobenzene (2), and 1,4-dicyanobenzene (3) were co-crystallized with 1,3,5-triiodotrifluorobenzene (1,3,5-FIB) to give three cocrystals, 1·1,3,5-FIB, 2·2(1,3,5-FIB), and 3·2(1,3,5-FIB), which were studied by X-ray diffraction. A common feature of the three structures is the presence of I···Cisocyanide or I···Nnitrile halogen bonds (HaBs), which occurs between an iodine σ-hole and the isocyanide C-(or the nitrile N-) atom. The diisocyanide and dinitrile cocrystals 2·2(1,3,5-FIB) and 3·2(1,3,5-FIB) are isostructural, thus providing a basis for accurate comparison of the two types of noncovalent linkages of C≡N/N≡C groups in the composition of structurally similar entities and in one crystal environment. The bonding situation was studied by a set of theoretical methods. Diisocyanides are more nucleophilic than the dinitrile and they exhibit stronger binding to 1,3,5-FIB. In all structures, the HaBs are mostly determined by the electrostatic interactions, but the dispersion and induction components also provide a noticeable contribution and make the HaBs attractive. Charge transfer has a small contribution (<5%) to the HaB and it is higher for the diisocyanide than for the dinitrile systems. At the same time, diisocyanide and dinitrile structures exhibit typical electron-donor and π-acceptor properties in relation to the HaB donor.

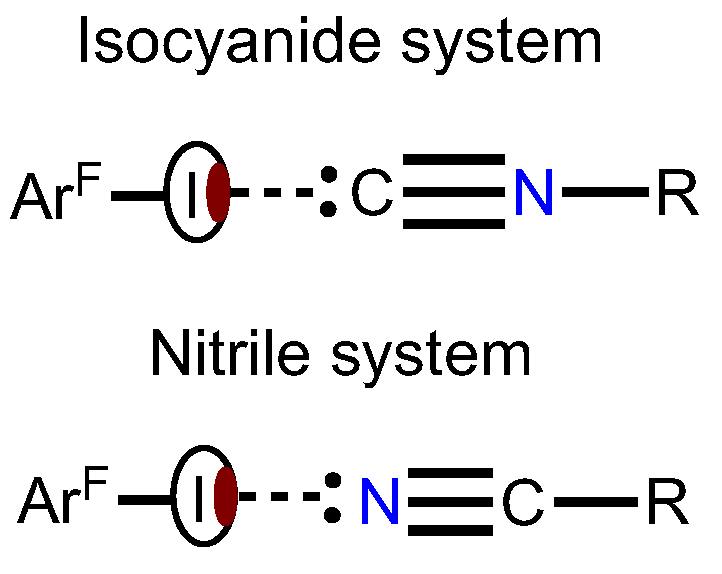
1. Introduction

Halogen bonding (abbreviated as HaB) is currently among the most actively studied forces in the palette of noncovalent interactions [1,2,3,4,5,6,7,8]. This interest is determined by impressive applications of HaB in various fields of science. Recently published reviews focus on general aspects of HaB [9,10,11,12,13] and also more specific topics such as HaB-based crystal engineering [14,15,16,17,18], sensoring [19,20], molecular [9,20] and anion [11,21] recognition, noncovalent catalysis [11,20,22,23,24,25,26], synthetic organometallic and coordination chemistry [27], polymer chemistry [28], and drug design [29,30,31,32]. It is noteworthy that HaB is involved in human physiology [33,34], in particular in the functioning of thyroid hormones [33].
The great diversity of the studied HaB systems, in many respects, is associated with a significant variety of accepting centers, which act as the nucleophilic components of Hal···Nu contacts. In the overwhelming majority of instances, HaB acceptors are represented by electronegative heteroatoms bearing a lone pair (abbreviated as LP). Owing to the lower electronegativity of C-atoms compared to N, O, S, halogens etc., noncovalent interactions including LP of a carbon site are rare. They have been only identified in some cocrystals of iodoperfluoroarenes with aryl isocyanides [35,36,37] or highly nucleophilic persistent carbenes [38].
In view of our interest in crystal engineering of noncovalent systems with C- or N-nucleophilic coformers, we attempted to compare HaBs, which include the acceptor centers of a different nature in the composition of structurally similar entities and in one crystal environment. For this study, we addressed the isomeric isocyanide and nitrile species and the goal was to establish how the C≡N/N≡C isomerism affects the HaB (Figure 1).
As HaB acceptors, we chose homoditopic 2,3,5,6-tetramethyl-1,4-diisocyanobenzene (1), 1,4-diisocyanobenzene (2), 1,4-dicyanobenzene (3) and, as HaB donor, potentially trifunctional 1,3,5-triiodotrifluorobenzene (1,3,5-FIB) (Figure 2). We found that cocrystallization of diisocyanides 1 and 2 and also dinitrile 3 with 1,3,5-FIB afford cocrystals 1·1,3,5-FIB, 2·2(1,3,5-FIB), and 3·2(1,3,5-FIB), exhibiting halogen-bonded supramolecular architecture. These cocrystals were studied by single-crystal X-ray diffraction (XRD) followed by theoretical calculations to closely interrogate the HaB systems. Our findings—uncovering common features and differences in the two types of noncovalent linkages of isomeric C≡N/N≡C groups (Figure 1)—are detailed in the following sections.

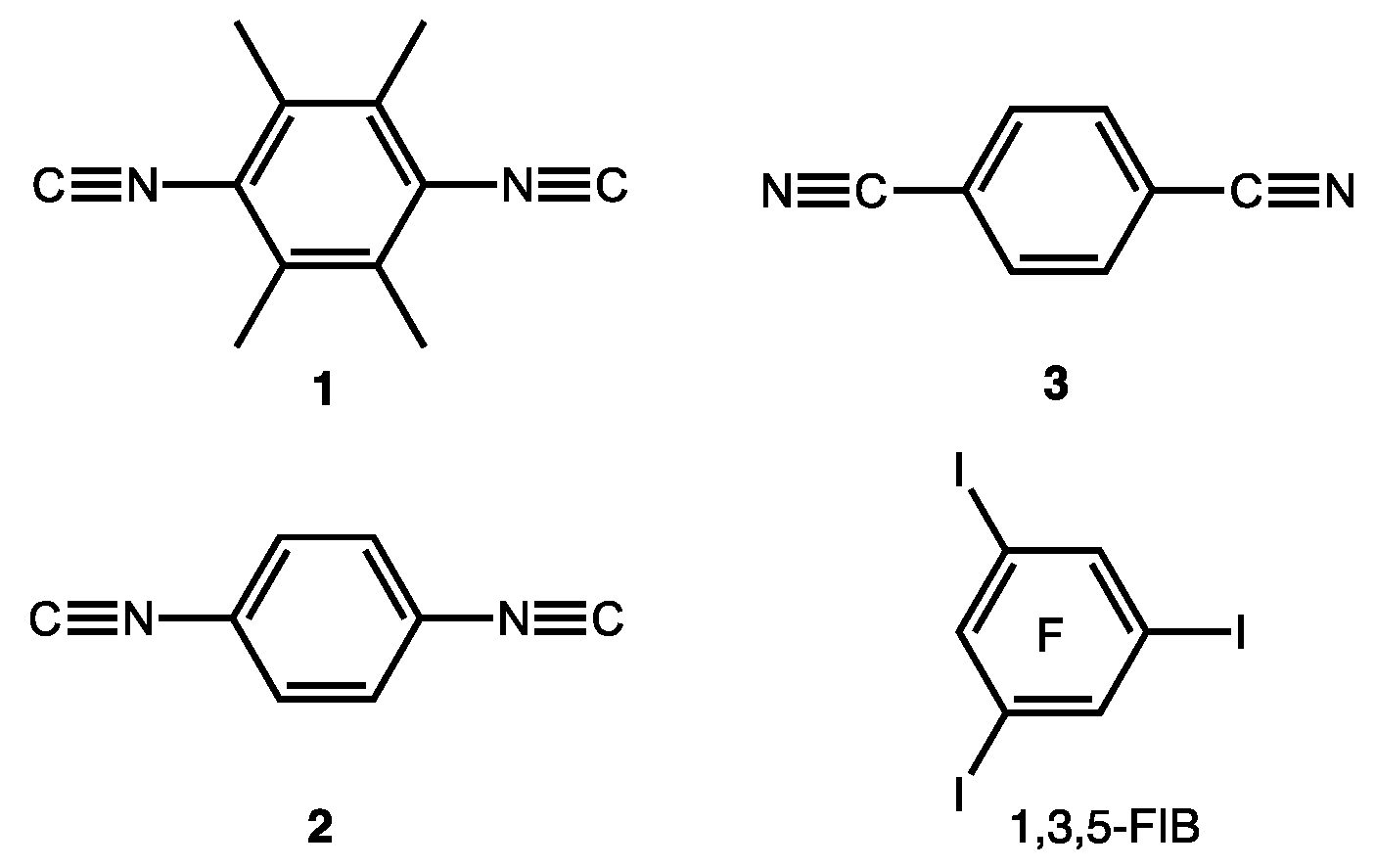
2. Results

2.1. Crystal Growth and Structural Motifs of the XRD Structures

Diisocyanides 1 and 2 and dinitrile 3 were co-crystallized with 1,3,5-FIB (1:1 molar ratio between the components) on slow evaporation of their solutions at 20–23 °C. This procedure provided three cocrystals, 1·1,3,5-FIB, 2·2(1,3,5-FIB), and 3·2(1,3,5-FIB), which were studied by XRD (Table S1, the Supplementary Materials). The homogeneity of the samples was confirmed by powder diffraction X-ray experiments (Figures S8–S10, the Supplementary Materials).
The structures exhibit different molar ratios between the coformers, namely 1:2 for 2·2(1,3,5-FIB) and 3·2(1,3,5-FIB), and 1:1 for 1·1,3,5-FIB; for TG characterization see Figures S11–S13 and Table S5, the Supplementary Materials. In all structures, 1,3,5-FIB acts as a trifunctional 120°-orienting HaB donor, whereas the diisocyanides (1 and 2) and the dinitrile (3) function as homoditopic 180°-orienting HaB acceptors. In the structures of 1·1,3,5-FIB and 2·2(1,3,5-FIB), we observed several types of HaBs, namely I···C, σ-(I)-hole···iodine electron-belt, and I···F. In 3·2(1,3,5-FIB), I···N and σ-(I)-hole···iodine electron-belt contacts.
Although the crystal structures exhibit different supramolecular architectures, their common feature is the presence of I···Cisocyanide or I···Nnitrile HaBs occurring between an iodine σ-hole and the isocyanide C- or the nitrile N- atom (Table 1). These HaBs are characterized by rather short interatomic distances. For the diisocyanide cocrystals, the I···N distances are comparable with those previously observed in cocrystals of iodo(perfluoro)arenes with CNMes [35] or with 1 and 2 [37]. For the dinitrile cocrystal, the I···N distance is similar to those found in C6F5I·NCMes (3.092(4) Å, EBIHEF) [39] and (2,3,5,6-tetramethyl-1,4-dicyanobenzene)·1,4-I2C6F4 (3.061(3) Å, HUMLOQ) [40]. In addition, weak σ-(I)-hole···iodine electron-belt HaB was observed in the structures of 2·2(1,3,5-FIB) and 3·2(1,3,5-FIB) and σ-(I)-hole···fluorine, I···F HaB in 1·1,3,5-FIB (Table 1 and Table S2 in the Supplementary Materials).
The diisocyanide and dinitrile cocrystals 2·2(1,3,5-FIB) and 3·2(1,3,5-FIB) are isostructural, they exhibit similar cell parameters, and display the same supramolecular organization. In these structures, the I-atoms of the I···C contact (in 2·2(1,3,5-FIB)) or the I···N contact (in 3·2(1,3,5-FIB)) function as HaB acceptor sites and are involved in two additional I···I HaBs (Figure 3). In these two cases, two relatively short contacts, which are different in 2·2(1,3,5-FIB) and 3·2(1,3,5-FIB), namely I···C and I···N, exist in a very similar environment; this provides a basis for an accurate comparison between the isocyanide and the isomeric nitrile groups. For this comparison, we performed the appropriate quantum chemical calculations detailed in Section 2.2.
In the structure of 1·1,3,5-FIB, a rather strong HaB is formed, apparently because of an enhanced σ-hole acceptor ability of the isocyano C-atom in 1 due to the combined effect of four electron-donating methyl groups (Figure 4); tri(poly)-center HaBs were not observed.
We measured FTIR-ATR spectra for pure 1–3 and their cocrystals (Figures S1–S7, the Supplementary Materials). The isocyanide-based cocrystals 1·1,3,5-FIB and 2·2(1,3,5-FIB) demonstrate a high-frequency shift of the ν(NC) band (18 and 13 cm–1) relative to 1 and 2, while the difference between the dinitrile-involving structures, 3·2(1,3,5-FIB) and 3, is small (1 cm–1). This trend in experimental ν(NC) band shifts is in a good agreement with theoretical data (Table S4). Small changes in ν(NC) frequency for a dinitrile-based system may indicate a weakening of the charge transfer (CT) for dinitrile as compared to isocyanides; this correlates well with the calculation of the CT by NBO method (Section 2.2.4).
The high-frequency shift induced by the HaB resembles the situation with C-isocyanide/N-nitrile coordination to Lewis acidic centers. Siginficant ν(NC) increase (150 cm–1) was observed for the H3B·CNMe associate and this blue shift was rationalized by an appropriate increase of CN force constant upon coordination [41]. A high-frequency shift of the ν(NC) band in IR and Raman spectra was observed for the homoleptic copper(I) [Cu(CNMe)4]+ and [Cu(NCMe)4]+ complexes as compared to the corresponding uncomplexed isocyanide and nitrile species [42]. This shift is greater for the isocyanide ligand (40–60 cm–1) and smaller for the nitrile (~15 cm–1) [42].

2.2. Theoretical Calculations

The nature of C–I···C/N contacts occurring between the diisocyanides or the dinitrile and 1,3,5-FIB were studied by a set of computational methods including Molecular electrostatic potential (MEP), Quantum theory of atoms in molecules (QTAIM), Independent gradient model based on Hirshfeld partition (IGMH), Electron localization function (ELF), Natural Bond Orbital (NBO), The domain based local pair-natural orbital coupled-cluster (DLPNO-CCSD(T)), and Symmetry Adapted Perturbation Theory (SAPT). We also performed a comparative analysis of HaB in the cocrystals to verify common features and differences of these noncovalent interactions.
To study HaB in our systems, geometry optimization was carried out for all bimolecular fragments, [(1–3)‧1,3,5-FIB]. The optimized structures are shown in Figure 5 and the relevant main geometric parameters are collected in Table S3. In all structures, the geometry optimization led to a reduction of N≡C (isocyanide) or C≡N (nitrile) and C–I distances (Table S3), and a slight decrease (by ~6°) of ∠(C–I···C/N). The lengths of the I···C/N HaBs increase by 0.03, 0.08, and 0.10 Å, respectively, for the two diisocyanide structures and one dinitrile structure. In general, the obtained optimized structures are consistent with the experimental XRD data.

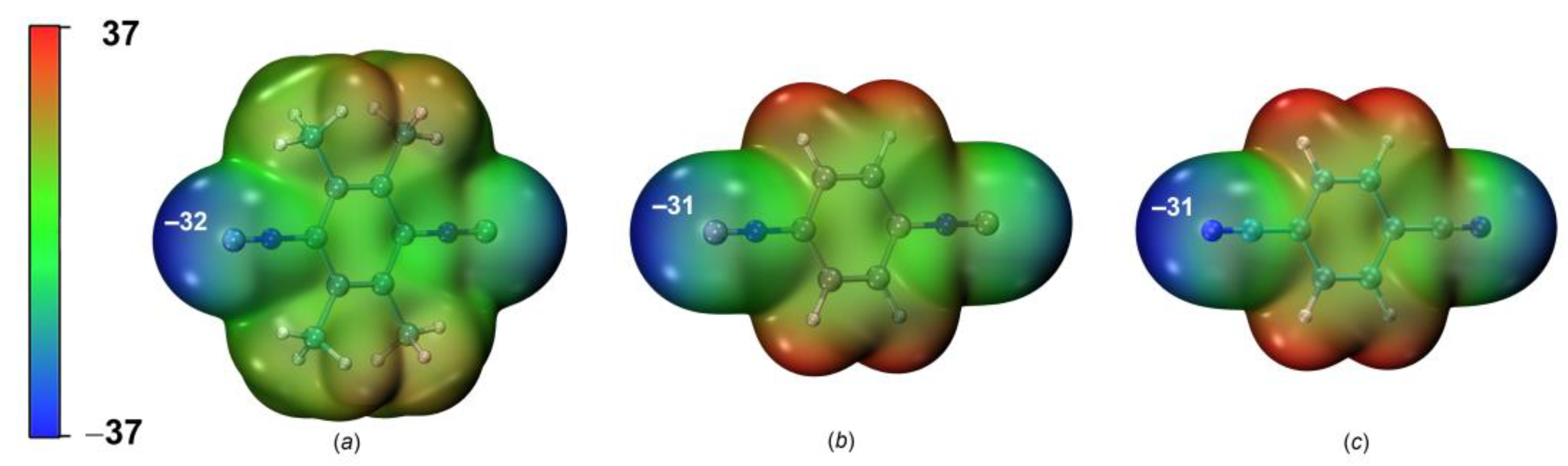
2.2.1. Nucleophilicity and Molecular Electrostatic Potential

We determined the global (NNu) and local (NNuloc) nucleophilicity indexes and found that NNu decreases in the following order: 1 (2.35 eV) > 2 (1.80 eV) > 3 (1.40 eV). This order correlates well with Mayr’s experimental nucleophilicity N+ indexes [43]. At the same time, the analysis of local nucleophilicity showed that the NNuloc of the C-atom of the isocyanide group in 1 is approximately equal to the NNuloc of the C-atom in 2. This observation suggests that the interaction energy of HaB should be approximately the same for 1 and 2. The NNuloc at the N-atom of the nitrile group in 3 is slightly lower than that at any one of the C-atoms of the isocyanide groups (Table 2).
The molecular electrostatic potential (MEP) is also an important descriptor in studies of noncovalent interactions [44,45]. Its analysis reveals the areas of interaction involved in the occurrence of HaB. The calculated MEP isosurfaces for HaB acceptors and their negative potentials (Vs,min) for HaB acceptors are shown in Figure 6. Its consideration clearly demonstrates the involvement of C- and N-atoms in the HaB. The Vs,min value for 3 is slightly larger than those for 2 and 1; this is in agreement with NNuloc indexes of the HaB acceptors.

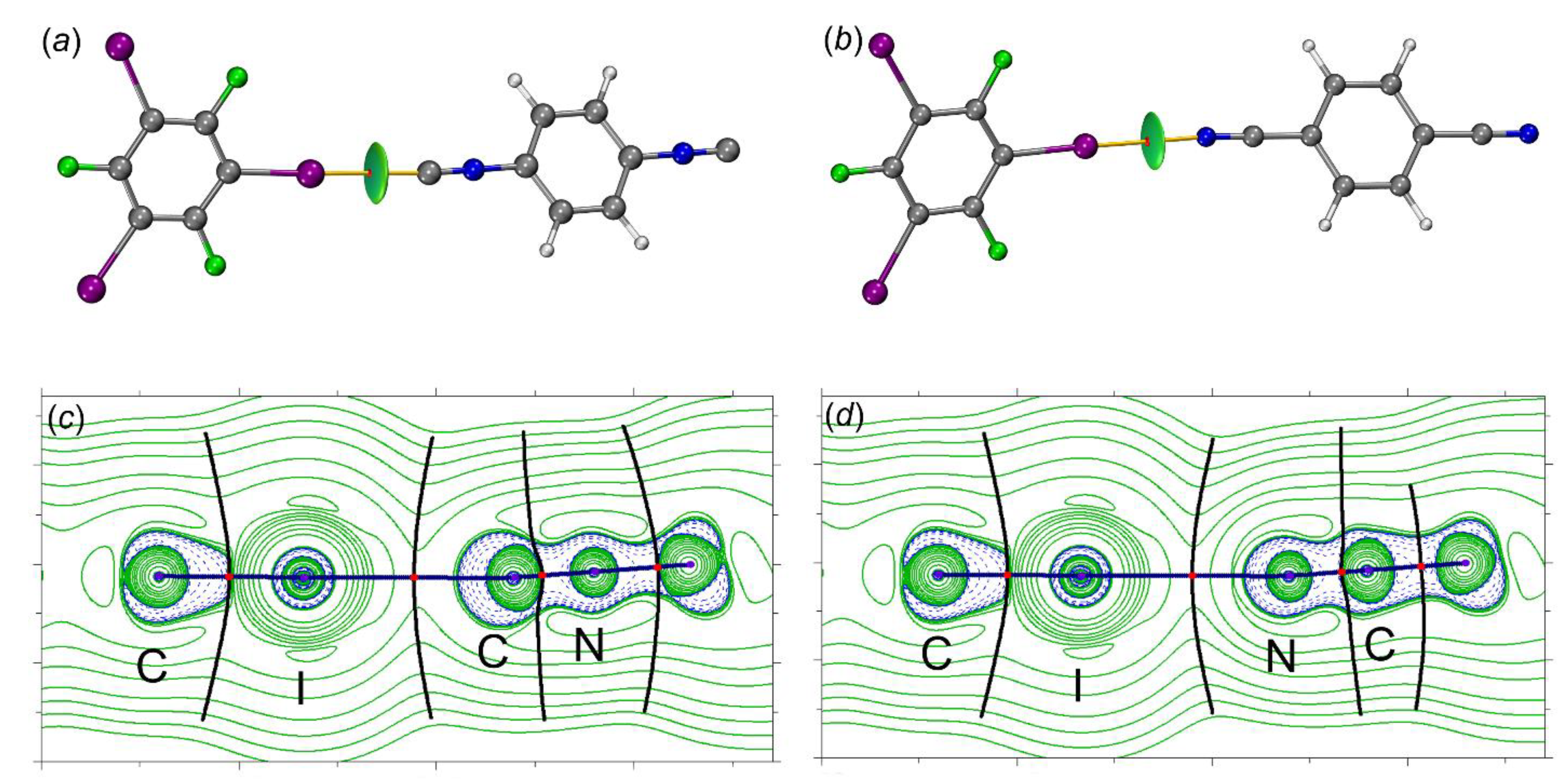
2.2.2. QTAIM-IGMH

The QTAIM [46,47] analysis (recommended by IUPAC [48] for studies of HaB) for all contact types revealed the presence of bond critical points (BCPs) and a bond path through the BCP. This bond path indicates the accumulation of the maximum electron density between the interacting nuclear attractors. The most important topological parameters at BCPs (namely, electron density (ρb), Laplacian (∇2ρb), and total energy density (Hb = Vb + Gb), potential and kinetic energy densities (Vb and Gb), and second eigenvalues of the Hessian matrix (λ2) are listed in Table 3 [49]. The molecular graphs for [(1–3)‧1,3,5-FIB] are given in Figure 7. Low values of ρb (0.015–0.019 a.u.), positive values of ∇2ρb (0.047–0.050 a.u.), and virtually zero values of Hb are typical for noncovalent interactions and their consideration confirms the presence of the closed-shell HaB. The ρb values for the HaB involving the nitrile are slightly lower than those found for the isocyanides; this indicates a weakening of the interaction energy in the nitrile system. The negative value of λ2 ranges from –0.012 to –0.010 a.u., showing that these interactions are attractive. Furthermore, the computed value of the electron localization function (ELF) at the BCP is slightly higher for both (diisocyanide)·1,3,5-FIB systems (Table 3), probably because of a higher contribution of the covalent component in the HaB (for detailed ELF consideration, see Section 2.2.3).
In addition to QTAIM, the HaBs were also explored and visualized using an independent gradient model (IGMH) method [50,51,52,53,54,55]. This method is based on hybrid QM/promolecular atomic separation based on Hirschfeld electron density gradient [56]. The IGMH method also allows for the calculation of IBSI indices, which are useful for the evaluation of HaB strength [57,58].
This IGMH isosurface (Figure 7a,b) is represented by a drop-shaped green surface located between the HaB-donating I- and the HaB-accepting C- or N-atoms. Analysis of the calculated intrinsic bond strength index (IBSI [58], the local stretching force constant) indices, similar to QTAIM, favors the weakening of HaB between 1,3,5-FIB and the dinitrile than that for diisocyanides. In all adducts, no auxiliary interactions were found, which means that HaB is the main attractive interaction in the studied systems.

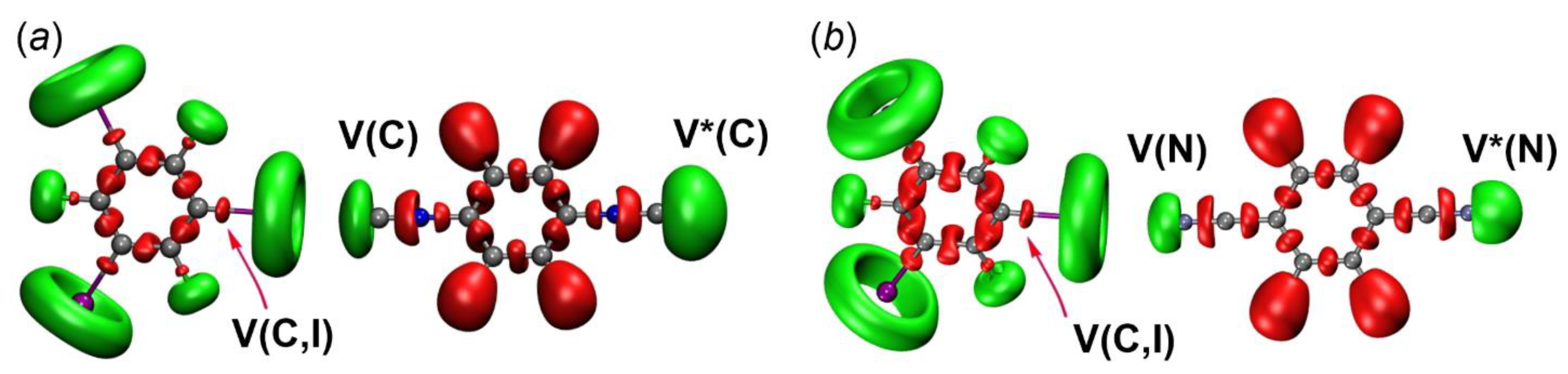
2.2.3. Electron Localization Function

To understand why the isocyanide systems are characterized by a larger contribution of the covalent component, we additionally performed an ELF analysis [59] for [(1–3)‧1,3,5-FIB]. This analysis allows us to measure the excess kinetic energy caused by Pauli repulsion and also to visualize the localization of electrons. The values of the ELF function at high electron localization (the localization can be interpreted either as LPs, or chemical bonds) should exhibit a value close to 1, while for low electron localization, the value of the ELF function tends to 0 [60].
The topological analysis of the gradient field of the ELF function is also very useful because this analysis leads to the division of the molecular space into non-overlapping basins of attractors [61]. These basins can be classified as basic (C(X), concentrated on atoms) and valence (V(X) or V(X,Y), concentrated between atoms). The basins could have a synaptic order indicating the number of basins linked together. Figure 8 shows that in all cases, the disynaptic basins between the I-atom of the HaB donor and the C- or N-atoms of the HaB acceptors were not observed; this fact additionally favors the noncovalent nature of the HaB.
Hence, primary attention was paid to the electron population and volume of the monosynaptic V(C) or V(N) and the dinosynaptic V(C,I) basins. The monosynaptic basins can be attributed to LPs on the C- or N- atoms, while the disynaptic basin V(C,I) is related to the localization of the electron density of the C–I bond; these basins are directly involved in the HaBs. The population of the V(C,I) basin for [(1 and 2)‧1,3,5-FIB], involved in the HaB is higher (by 0.08 e) than the basins that are not involved in the HaB (Table 4).
The population of the monosynaptic basin V(C) is reduced by 0.01 e compared to the unbound C-atoms of the isocyanides. We also found that the interaction of the isocyanides with 1,3,5-FIB leads to a decrease in the local volume of the basin V(C) for LP(C), from 280 to 100 Å3 for [1‧1,3,5-FIB], and from 440 to 170 Å3 for [2‧1,3, 5-FIB]. Remarkably, the basin V(C) volume for LP(C) is also decreased from 280 to 100 Å3 for [1‧1,3,5-FIB] and 440 to 170 Å3 for [2‧1,3,5-FIB]. The analysis of the ELF basin for [3‧1,3,5-FIB] also shows an increase in the population of the V(C,I) basin, but the population of the monosynaptic V(N) basin remains unchanged. All these features are coherent with the weakening of the charge transfer (CT) for the dinitrile system in comparison with the diisocyanide systems.
The ELF data clearly indicate that the covalent component is caused by the outflow of electrons as a result of CT from the diisocyanides (or the dinitrile) to 1,3,5-FIB. However, the HaB with the dinitrile, in contrast to those for both diisocyanides, is characterized by a very weak CT.

2.2.4. Natural Bond Orbital Approach

Since the examination of the ELF results revealed the presence of CT, we performed an NBO analysis to characterize orbital interactions [62] between the HaB donors and acceptors; NBO data are collected in Table 5. We found that two most important donor–acceptor interactions are associated with CT and they are responsible for stabilizing HaB by the HaB acceptors.
The first type is related to the donor–acceptor interaction with LP(C/N) to σ*-orbital (I–C) of 1,3,5-FIB (Figure 9). The second order perturbation energies E(2) for the transitions LP(C/N)→σ*(I–C) follow the order [1‧1,3,5-FIB] (9.6)~[2‧1,3,5-FIB] (10.2) > [3‧1,3,5-FIB] (5.2 kcal/mol). The second interaction type is associated with the LP(I)⟶σ*/π*(C–N)isocyanide and σ*/π*(N–C)nitrile bond orbitals. On the whole, the E(2) values also follow the general trend of the first type interaction, but are characterized by smaller E(2) values (Table 5). To study the directions of the charge flow, we analyzed the occupancy of the σ*(I–C) orbital of 1,3,5-FIB and also the total population of the orbitals associated with the (C–N)isocyanide or (N–C)nitrile bonds (Table 5). As can be inferred from consideration of the data gathered in Table 5, the population of the σ*(I–C) site increases by 50 me.
This increase is associated with the CT from the LP(C or N) orbitals of the diisocyanides (or the dinitrile) to the σ*(I–C) orbital of 1,3,5-FIB. At the same time, the population of the orbitals of the HaB acceptors and σ*(N≡C) and σ*(C≡N) bonds is increased by 16 me. This increase favors the presence of a reverse CT from LP(I)⟶σ*/π*(C≡N)isocyanide and σ*/π*(N≡C)nitrile bond orbitals. In these cases, the first effect prevails over the second one and it leads to an increase (by 0.01 Å) of the I–C bond length (Table S3). This observation indicates that for the isocyanides, the direct CT is 3-fold higher than the reverse CT due to the more pronounced σ-donor properties of the diisocyanides compared to the dinitrile. The direct CT decreases in a series [1‧1,3,5-FIB] ~ [2‧1,3,5-FIB] > [3‧1,3,5-FIB]. The latter trend is consistent with the weakening of the nucleophilicity in the order 1~2 > 3 (Section 2.2.1; calculated indices are given in Table 2). Thus, the diisocyanides and the dinitrile exhibit typical electron-donor and π-acceptor properties with respect to the HaB donor.

2.2.5. Energy

The interaction (EintSM) and binding (EbSM) energy data—obtained using the supramolecular approach and calculated at the DLPNO-CCSD(T)) [63,64] level—are collected in Table 6. In general, EintSM values do not exceed –4 kcal/mol; this energy corresponds to weak noncovalent interactions. The values of EbSM are comparable to those of EintSM. This is due to the fact that the deformation energy of the HaB acceptors has a positive sign, while the deformation energy of the HaB donor is negative. Thus, the resultant energy responsible for the deformation of the monomers in the dimer geometry becomes low.
Finally, to closely interrogate the physical nature of the HaBs, we performed the decomposition of the interaction energy by the SAPT [65,66,67,68,69] method into electrostatic (Eelec), induction (Eind), dispersion (Edis), and exchange (Eexch) components (Figure 10). In general, the total interaction energies SAPT(0) (EintSAPT) correlate with the corresponding energies of the supramolecular interaction (Table 6), although the energies calculated using the DLPNO-CCSD(T) method are 18% lower in absolute values than those calculated at the SAPT(0) level.
According to the obtained SAPT data (Table 6), HaBs are characterized by the predominance of electrostatic energy, which comprise approx. 60% of Σ(Eelec, Eind, and Edis). The dispersive attractive energy provides a significant contribution (~30%), while the repulsive Pauli energy has a 70% fraction. It has been proved [70,71] that the high directionality of HaB is determined by electrostatic and exchange-repulsion interactions and therefore we carefully analyzed the Eexch energy. Ongoing from [1‧1,3,5-FIB] (66%) to [2‧1,3,5-FIB] (71%), the contribution of the repulsion Pauli energy increases, and then it decreases in [3‧1,3,5-FIB] (43%). This trend is in a good agreement with the weakening of orbital interactions on the transition from the diisocyanide to the dinitrile systems. The highest value of Eexch for [2‧1,3,5-FIB] is probably associated with an increase in the basin volume LP(C) for [2‧1,3,5-FIB] than that for [1‧1,3,5-FIB]. As a result of the increase in the LP(C) volume, the Eexch energy also increases (Table 4). The inductive effect also makes some contribution to the HaB but it does not exceed 15%. In particular, the induction term includes both polarization and CT. However, the SAPT method allows for an estimate of the contribution of CT to the induction energy [72]. An analysis of the obtained Ect data shows that the contribution of CT to the HaB interaction energy is relatively small (<30% and 6% of the induction energy for the diisocyanides and the dinitrile, respectively).

3. Discussion

In this work, we obtained cocrystals of two diisocyanides, 1 and 2, and one dinitrile, 3, with HaB-donating 1,3,5-FIB. A characteristic feature of all three structures is the occurrence of C···I or N···I HaB, correspondingly. Two cocrystals, 2·2(1,3,5-FIB) and 3·2(1,3,5-FIB), are isostructural, which facilitates the comparison of HaBs with two different acceptors (the terminal C- or N-atoms) under similar crystal environments. The results of our theoretical studies allowed us to identify common features and to verify differences in these two types of interactions (Table 7).
In summary, the examination of the obtained results revealed that the diisocyanides are more nucleophilic than the dinitrile, and they exhibit stronger binding to 1,3,5-FIB. The HaBs in all structures are mostly determined by the electrostatic interactions, which is not, however, sufficient to compensate the repulsion Pauli energy. Considering all these, we led to the conclusion that the dispersion and induction components also provide a noticeable contribution to the HaB and make this interaction attractive. Charge transfer has a small contribution (<5%) to the HaB, but it is higher for the diisocyanide than for the dinitrile systems. At the same time, diisocyanide and dinitrile structures exhibit typical electron-donor and π-acceptor properties in relation to the HaB donor.
The obtained data help enhance the cognition of noncovalent interactions for HaB-involving crystal engineering and provide new perspectives for the targeted design of extended supramolecular architectures utilizing highly directional HaB. The results of this study, in addition, highlight the importance of ditopic 180°-directing HaB acceptors for the construction of linear supramolecular assemblies. Comparison of the isocyanide and nitrile systems shows the significance of using halogen-bonded assembly, which includes C-nucleophilic isocyanide components of noncovalent interactions, for those systems in which strengthening of the HaB due to charge transfer can be expected.

4. Materials and Methods

4.1. Materials and Instruments

Solvents, compounds 2 and 3, and 1,3,5-FIB were obtained from commercial sources and used as received. Diisocyanide 1 was prepared from commercial durene according to the known four-step procedure [37]. FTIR-ATR spectra were obtained on Schimadzu IRAffinity-1 instrument (Shimadzu, Kyoto, Japan). The TG studies were performed on a NETZSCH TG 209 F1 Libra thermoanalyzer (NETZSCH, Selb, Germany); MnO2 powder was used as a standard. The initial weights of the samples were in the range 1.2–3.9 mg. The experiments were run in an open aluminum crucible in a stream of argon at a heating rate of 10 °/min. The final temperature was 450 °C. Processing of the thermal data was performed with NETZSCH Proteus Thermal Analysis software version 6.1.0 [73]. The samples were examined by XRD phase analysis using Bruker “D8 DISCOVER” high resolution diffractometer (Bruker AXS, Karlsruhe, Germany) with monochromated CuKα long focus source. Background correction and full-profile analyzes of powder diffraction patterns were carried out using the diffractometer software (TOPAS, 4.2).

4.2. Cocrystal Growth

1,3,5-FIB (82 mg, 0.16 mmol) and any one of 1–3 (0.16 mmol) were mixed in 1:1 molar ratio in hexane/methylene chloride mixture (2 mL; 1:1 v/v), and the obtained solution was left for 2 d at 20–23 °C in a vial with poorly closed lid. During this time, the solvent was completely evaporated and the released crystals of 1·1,3,5-FIB, 2·2(1,3,5-FIB), and 3·2(1,3,5-FIB) were mechanically separated and studied by XRD.

4.3. XRD Studies

XRD experiments were performed using SuperNova (Rigaku Oxford Diffraction, Oxford, UK), Single source at offset/far, HyPix3000 (for 1·1,3,5-FIB and 2·2(1,3,5-FIB)) and XtaLAB Synergy (Rigaku Oxford Diffraction, Oxford, UK), Single source at home/near, HyPix (for 3·2(1,3,5-FIB)) diffractometers with monochromated CuKα radiation. All crystals were kept at 100 K during data collection. The structures were solved using ShelXT [74] structure solution program and refined by means using ShelXL [74] incorporated in Olex2 version 1.5 [75] program package. Empirical absorption correction was accounted for using spherical harmonics implemented in SCALE3 ABSPACK scaling algorithm (CrysAlisPro 1.171.41.122a; Rigaku Oxford Diffraction, 2021). The structures can be obtained free of charge via CCDC database (CCDC numbers 2280076, 2280077, and 2281032).

4.4. Computational Details

Full geometry optimization of the model clusters was carried out at the DFT level of theory using the PBE0 [76,77] functional with the atom-pairwise dispersion correction with the Becke–Johnson damping scheme (D3BJ) [78,79]. The ORCA package (version 5.0.3) was used for the calculation [80,81]. Zero-order regular approximation (ZORA) [82] was employed to account the relativistic effects. The optimization calculations based on the X-ray geometries were performed at the PBE0-D3BJ level with the ZORA-def2-TZVP(–f) [82] (for H, C, N, and F) and the SARC-ZORA-TZVP (for I) basis sets [83]. The Hessian matrix was calculated analytically for the optimized structures to prove the location of correct minima (no imaginary frequencies). Combination of the “resolution of identity” and the “chain of spheres exchange” algorithms (RIJCOSX) [84] in conjunction with the auxiliary basis sets SARC/J were used [85]. The SCF calculations were tightly converged “TightSCF”. This level of theory was used the QTAIM, ELF, IGMH, MEP, CDF, NBO, and ETS-NOCV analyses. The natural bond orbital analysis was performed using the NBO 7.0 program [86]. The DLPNO-CCSD(T) method was applied to calculate single-point energy with the ZORA-def2-TZVP(–f) (for H, C, N, and F) and the SARC-ZORA-TZVP (for I) basis. The approach DLPNO-CCSD(T) used the level of accuracy “TightPNO”.
The QTAIM, ELF, IGMH, and MEP calculations were carried out using the Multiwfn 3.8 software [87,88,89] and results were visualized using the VMD program [90]. The SAPT calculations at the SAPT0 level were performed with the recommended basis sets aug-cc-pVTZ (for H, C, N, and F) and aug-cc-pVTZ-PP (for I) for the bimolecular clusters using the Psi4 package (version 1.7.1) [91]. The CDF and ETS-NOCV analyses were carried out according to the methodology described in refs [92,93,94] using the Multiwfn (version 3.8) software.
The interaction and binding energies (Eint and Eb) were calculated for bimolecular clusters as
Eint(A···B) = E(AB) − E{A} − E{B}
Eb(A···B) = E(AB) − E(A) − E(B),
where A and B are molecules, E(AB), E(A), and E(B) are total energies of the corresponding optimized structures, E{A} and E{B} are total energies of A and B in the geometry of the optimized AB.
The global nucleophilicity index was calculated as NNu = EHOMO(1–3) − EHOMO(TCE) where EHOMO(TCE) energy HOMO tetracyanoethylene (TCE) molecule [95]. The local nucleophilicity index NNuloc where calculated as NNuloc = fx − NNu were fx− is Fukui function of atom x in a molecule [96].

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms241713324/s1.

Author Contributions

Conceptualization, A.S.S., E.A.K. and V.Y.K.; methodology, A.S.S., A.S.M. and E.A.K.; investigation, A.S.S., E.A.K., M.A.K. and A.S.M.; resources, A.S.S. and E.A.K.; writing—original draft preparation, A.S.S., E.A.K. and N.A.B.; writing—review and editing, V.Y.K.; visualization, E.A.K. and N.A.B.; supervision, V.Y.K.; funding acquisition, A.S.S. All authors have read and agreed to the published version of the manuscript.

Funding

Support from the Russian Science Foundation (project 22-23-00307) is greatly appreciated.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in the article and Supplementary Materials. Also CIFs are openly available in www.ccdc.cam.ac.uk/data_request/cif (accessed on 23 May 2023; version 5.44).

Acknowledgments

The article is in commemoration of the 300th anniversary of St. Petersburg State University’s founding. Physicochemical studies were performed at the Center for X-ray Diffraction Studies and Center for Chemical Analysis and Materials Research, Center for Thermogravimetric and Calorimetric Research, Center for Magnetic Resonance while theoretical calculations were performed at Computational Center, liquid nitrogen for research was obtained from Cryogenic Department (all belonging to Saint Petersburg State University).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cornaton, Y.; Djukic, J.-P. Noncovalent Interactions in Organometallic Chemistry: From Cohesion to Reactivity, a New Chapter. Acc. Chem. Res. 2021, 54, 3828–3840. [Google Scholar] [CrossRef]
  2. Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef]
  3. Frontera, A.; Bauzá, A. On the Importance of σ–Hole Interactions in Crystal Structures. Crystals 2021, 11, 1205. [Google Scholar] [CrossRef]
  4. Shukla, R.; Chopra, D. Chalcogen and pnictogen bonds: Insights and relevance. Curr. Sci. 2021, 120, 1848–1853. [Google Scholar] [CrossRef]
  5. Miller, D.K.; Chernyshov, I.Y.; Torubaev, Y.V.; Rosokha, S.V. From weak to strong interactions: Structural and electron topology analysis of the continuum from the supramolecular chalcogen bonding to covalent bonds. Phys. Chem. Chem. Phys. 2022, 24, 8251–8259. [Google Scholar] [CrossRef] [PubMed]
  6. Resnati, G.; Metrangolo, P. Celebrating 150 years from Mendeleev: The Periodic Table of Chemical Interactions. Coord. Chem. Rev. 2020, 420, 213409. [Google Scholar] [CrossRef]
  7. Brammer, L. Halogen bonding, chalcogen bonding, pnictogen bonding, tetrel bonding: Origins, current status and discussion. Faraday Discuss. 2017, 203, 485–507. [Google Scholar] [CrossRef]
  8. Brammer, L.; Peuronen, A.; Roseveare, T.M. Halogen bonds, chalcogen bonds, pnictogen bonds, tetrel bonds and other [sigma]-hole interactions: A snapshot of current progress. Acta Crystallogr. Sect. C 2023, 79, 204–216. [Google Scholar] [CrossRef]
  9. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
  10. Li, B.; Zang, S.-Q.; Wang, L.-Y.; Mak, T.C.W. Halogen bonding: A powerful, emerging tool for constructing high-dimensional metal-containing supramolecular networks. Coord. Chem. Rev. 2016, 308, 1–21. [Google Scholar] [CrossRef]
  11. Tepper, R.; Schubert, U.S. Halogen Bonding in Solution: Anion Recognition, Templated Self-Assembly, and Organocatalysis. Angew. Chem. Int. Ed. Engl. 2018, 57, 6004–6016. [Google Scholar] [CrossRef] [PubMed]
  12. Maharramov, A.M.; Mahmudov, K.T.; Kopylovich, M.N.; Pombeiro, A.J.L. (Eds.) Non-Covalent Interactions in the Synthesis and Design of New Compounds; Wiley Online Library: Hoboken, NJ, USA, 2016. [Google Scholar]
  13. Saha, B.K.; Veluthaparambath, R.V.P.; Krishna, G.V. Halogen⋯Halogen Interactions: Nature, Directionality and Applications. Chem. Asian J. 2023, 18, e202300067. [Google Scholar] [CrossRef] [PubMed]
  14. Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef] [PubMed]
  15. Mukherjee, A.; Tothadi, S.; Desiraju, G.R. Halogen Bonds in Crystal Engineering: Like Hydrogen Bonds yet Different. Acc. Chem. Res. 2014, 47, 2514–2524. [Google Scholar] [CrossRef]
  16. Xin, D.; Matti, T.; Matti, H. Halogen Bonding in Crystal Engineering. In Recent Advances in Crystallography; Jason, B.B., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 7. [Google Scholar]
  17. Teyssandier, J.; Mali, K.S.; De Feyter, S. Halogen Bonding in Two-Dimensional Crystal Engineering. ChemistryOpen 2020, 9, 225–241. [Google Scholar] [CrossRef]
  18. Ivanov, D.M.; Bokach, N.A.; Yu. Kukushkin, V.; Frontera, A. Metal Centers as Nucleophiles: Oxymoron of Halogen Bond-Involving Crystal Engineering. Chem. Eur. J. 2022, 28, e202103173. [Google Scholar]
  19. Hein, R.; Beer, P.D. Halogen bonding and chalcogen bonding mediated sensing. Chem. Sci. 2022, 13, 7098–7125. [Google Scholar] [CrossRef] [PubMed]
  20. Zheng, J.; Suwardi, A.; Wong, C.J.E.; Loh, X.J.; Li, Z. Halogen bonding regulated functional nanomaterials. Nanoscale Adv. 2021, 3, 6342–6357. [Google Scholar] [CrossRef]
  21. Pancholi, J.; Beer, P.D. Halogen bonding motifs for anion recognition. Coord. Chem. Rev. 2020, 416, 213281. [Google Scholar] [CrossRef]
  22. Mahmudov, K.T.; Kopylovich, M.N.; da Silva, M.F.C.G.; Pombeiro, A.J. Noncovalent Interactions in Catalysis; Royal Society of Chemistry: London, UK, 2019. [Google Scholar]
  23. Mahmudov, K.T.; Gurbanov, A.V.; Guseinov, F.I.; Guedes da Silva, M.F.C. Noncovalent interactions in metal complex catalysis. Coord. Chem. Rev. 2019, 387, 32–46. [Google Scholar] [CrossRef]
  24. Breugst, M.; von der Heiden, D.; Schmauck, J. Novel Noncovalent Interactions in Catalysis: A Focus on Halogen, Chalcogen, and Anion-π Bonding. Synthesis 2017, 49, 3224–3236. [Google Scholar] [CrossRef]
  25. Benz, S.; Poblador-Bahamonde, A.I.; Low-Ders, N.; Matile, S. Catalysis with Pnictogen, Chalcogen, and Halogen Bonds. Angew. Chem. Int. Ed. 2018, 57, 5408–5412. [Google Scholar] [CrossRef]
  26. Bulfield, D.; Huber, S.M. Halogen Bonding in Organic Synthesis and Organocatalysis. Chem. Eur. J. 2016, 22, 14434–14450. [Google Scholar] [CrossRef]
  27. Mahmudov, K.T.; Kopylovich, M.N.; Guedes da Silva, M.F.C.; Pombeiro, A.J.L. Non-covalent interactions in the synthesis of coordination compounds: Recent advances. Coord. Chem. Rev. 2017, 345, 54–72. [Google Scholar] [CrossRef]
  28. Berger, G.; Soubhye, J.; Meyer, F. Halogen bonding in polymer science: From crystal engineering to functional supramolecular polymers and materials. Polym. Chem. 2015, 6, 3559–3580. [Google Scholar] [CrossRef]
  29. Mendez, L.; Henriquez, G.; Sirimulla, S.; Narayan, M. Looking Back, Looking Forward at Halogen Bonding in Drug Discovery. Molecules 2017, 22, 1397. [Google Scholar] [CrossRef]
  30. Ho, P.S. Halogen bonding in medicinal chemistry: From observation to prediction. Future Med. Chem. 2017, 9, 637–640. [Google Scholar] [CrossRef] [PubMed]
  31. Dalpiaz, A.; Pavan, B.; Ferretti, V. Can pharmaceutical co-crystals provide an opportunity to modify the biological properties of drugs? Drug Discov Today 2017, 22, 1134–1138. [Google Scholar] [CrossRef]
  32. Lu, Y.; Liu, Y.; Xu, Z.; Li, H.; Liu, H.; Zhu, W. Halogen bonding for rational drug design and new drug discovery. Expert Opin. Drug Discov 2012, 7, 375–383. [Google Scholar] [CrossRef] [PubMed]
  33. Bayse, C.A. Halogen bonding from the bonding perspective with considerations for mechanisms of thyroid hormone activation and inhibition. New J. Chem. 2018, 42, 10623–10632. [Google Scholar] [CrossRef]
  34. Marsan, E.S.; Bayse, C.A. A Halogen Bonding Perspective on Iodothyronine Deiodinase Activity. Molecules 2020, 25, 1328. [Google Scholar] [CrossRef] [PubMed]
  35. Mikherdov, A.S.; Novikov, A.S.; Boyarskiy, V.P.; Kukushkin, V.Y. The halogen bond with isocyano carbon reduces isocyanide odor. Nat. Commun. 2020, 11, 2921. [Google Scholar] [CrossRef] [PubMed]
  36. Mikherdov, A.S.; Popov, R.A.; Smirnov, A.S.; Eliseeva, A.A.; Novikov, A.S.; Boyarskiy, V.P.; Gomila, R.M.; Frontera, A.; Kukushkin, V.Y.; Bokach, N.A. Isocyanide and Cyanide Entities Form Isostructural Halogen Bond-Based Supramolecular Networks Featuring Five-Center Tetrafurcated Halogen···C/N Bonding. Cryst. Growth Des. 2022, 22, 6079–6087. [Google Scholar] [CrossRef]
  37. Smirnov, A.S.; Mikherdov, A.S.; Rozhkov, A.V.; Gomila, R.M.; Frontera, A.; Kukushkin, V.Y.; Bokach, N.A. Halogen Bond-Involving Supramolecular Assembly Utilizing Carbon as a Nucleophilic Partner of I⋅⋅⋅C Non-covalent Interaction. Chem. Asian J. 2023, 18, e202300037. [Google Scholar] [CrossRef]
  38. Arduengo, A.J.; Kline, M.; Calabrese, J.C.; Davidson, F. Synthesis of a reverse ylide from a nucleophilic carbene. J. Am. Chem. Soc. 1991, 113, 9704–9705. [Google Scholar] [CrossRef]
  39. Wasilewska, A.; Gdaniec, M.; Polonski, T. CCDC 618388: Experimental Crystal Structure Determination; Cambridge Crystallographic Data Centre: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
  40. Britton, D.; Gleason, W.B. Dicyanodurene-p-tetrafluorodiiodobenzene (1/1). Acta Crystallogr. Sect. E 2002, 58, o1375–o1377. [Google Scholar] [CrossRef]
  41. Watari, F. Vibrational frequencies, assignments and normal-coordinate analysis for the methyl isocyanide-borane complex. Inorg. Chem. 1982, 21, 1442–1446. [Google Scholar] [CrossRef]
  42. Bell, A.; Walton, R.A.; Edwards, D.A.; Poulter, M.A. Cationic copper(I) isocyanide complexes, [Cu(CNR)4]+ (R = CH3, C(CH3)3 and 2,6-(CH3)2C6H3): Preparations, spectroscopic properties and reactions with neutral ligands. A comparison of the vibrational spectra of [Cu(CNCH3)4]+, [Cu(NCCH3)4]+ and [Cu(NCCD3)4]+. Inorganica Chim. Acta 1985, 104, 171–178. [Google Scholar] [CrossRef]
  43. Tumanov, V.V.; Tishkov, A.A.; Mayr, H. Nucleophilicity Parameters for Alkyl and Aryl Isocyanides. Angew. Chem. Int. Ed. 2007, 46, 3563–3566. [Google Scholar] [CrossRef]
  44. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
  45. Murray, J.S.; Politzer, P. Molecular electrostatic potentials and noncovalent interactions. WIREs Comput. Mol. Sci. 2017, 7, e1326. [Google Scholar] [CrossRef]
  46. Bader, R.F. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  47. Kumar, P.S.V.; Raghavendra, V.; Subramanian, V. Bader’s Theory of Atoms in Molecules (AIM) and its Applications to Chemical Bonding. J. Chem. Sci. 2016, 128, 1527–1536. [Google Scholar] [CrossRef]
  48. Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
  49. Kuznetsov, M.L. Relationships between Interaction Energy and Electron Density Properties for Homo Halogen Bonds of the [(A)nY–X···X–Z(B)m] Type (X = Cl, Br, I). Molecules 2019, 24, 2733. [Google Scholar] [CrossRef]
  50. Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Hénon, E. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density. Phys. Chem. Chem. Phys. 2017, 19, 17928–17936. [Google Scholar] [CrossRef]
  51. Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef]
  52. Zhu, S.; Asim Khan, M.; Wang, F.; Bano, Z.; Xia, M. Rapid removal of toxic metals Cu2+ and Pb2+ by amino trimethylene phosphonic acid intercalated layered double hydroxide: A combined experimental and DFT study. Chem. Eng. J. 2020, 392, 123711. [Google Scholar] [CrossRef]
  53. Huang, W.; Lin, R.; Zhao, X.; Li, Q.; Huang, Y.; Ye, G. How does a weak interaction change from a reactive complex to a saddle point in a reaction? Comput. Theor. Chem. 2020, 1173, 112640. [Google Scholar] [CrossRef]
  54. Lefebvre, C.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations. ChemPhysChem 2018, 19, 724–735. [Google Scholar] [CrossRef] [PubMed]
  55. Lu, T.; Chen, Q. Visualization Analysis of Weak Interactions in Chemical Systems. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
  56. Lefebvre, C.; Klein, J.; Khartabil, H.; Boisson, J.-C.; Hénon, E. IGMPlot: A program to identify, characterize, and quantify molecular interactions. J. Comput. Chem. 2023, 44, 1750–1766. [Google Scholar] [CrossRef]
  57. Šivickytė, O.; Costa, P.J. Intrinsic bond strength index as a halogen bond interaction energy predictor. Phys. Chem. Chem. Phys. 2023, 25, 17535–17546. [Google Scholar] [CrossRef]
  58. Klein, J.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. New Way for Probing Bond Strength. J. Phys. Chem. A 2020, 124, 1850–1860. [Google Scholar] [CrossRef]
  59. Silvi, B.; Gillespie, R.J.; Gatti, C. Electron density analysis. In Comprehensive Inorganic Chemistry II; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 9, pp. 187–226. [Google Scholar]
  60. Fuster, F.; Sevin, A.; Silvi, B. Topological Analysis of the Electron Localization Function (ELF) Applied to the Electrophilic Aromatic Substitution. J. Phys. Chem. A 2000, 104, 852–858. [Google Scholar] [CrossRef]
  61. Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
  62. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  63. Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
  64. Altun, A.; Neese, F.; Bistoni, G. Local energy decomposition analysis of hydrogen-bonded dimers within a domain-based pair natural orbital coupled cluster study. Beilstein J. Org. Chem. 2018, 14, 919–929. [Google Scholar] [CrossRef]
  65. Hohenstein, E.G.; Parrish, R.M.; Sherrill, C.D.; Turney, J.M.; Schaefer, H.F., 3rd. Large-scale symmetry-adapted perturbation theory computations via density fitting and Laplace transformation techniques: Investigating the fundamental forces of DNA-intercalator interactions. J. Chem. Phys. 2011, 135, 174107. [Google Scholar] [CrossRef]
  66. Hohenstein, E.G.; Jaeger, H.M.; Carrell, E.J.; Tschumper, G.S.; Sherrill, C.D. Accurate Interaction Energies for Problematic Dispersion-Bound Complexes: Homogeneous Dimers of NCCN, P2, and PCCP. J. Chem. Theory Comput. 2011, 7, 2842–2851. [Google Scholar] [CrossRef]
  67. Hayes, I.; Stone, A. An intermolecular perturbation theory for the region of moderate overlap. Mol. Phys. 1984, 53, 83–105. [Google Scholar] [CrossRef]
  68. Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation theory approach to intermolecular potential energy surfaces of van der Waals complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
  69. Patkowski, K. Recent developments in symmetry-adapted perturbation theory. WIREs Comput. Mol. Sci. 2020, 10, e1452. [Google Scholar] [CrossRef]
  70. Grant Hill, J.; Legon, A.C. On the directionality and non-linearity of halogen and hydrogen bonds. Phys. Chem. Chem. Phys. 2015, 17, 858–867. [Google Scholar] [CrossRef]
  71. Adhikari, U.; Scheiner, S. Sensitivity of pnicogen, chalcogen, halogen and H-bonds to angular distortions. Chem. Phys. Lett. 2012, 532, 31–35. [Google Scholar] [CrossRef]
  72. Stone, A.J.; Misquitta, A.J. Charge-transfer in Symmetry-Adapted Perturbation Theory. Chem. Phys. Lett. 2009, 473, 201–205. [Google Scholar] [CrossRef]
  73. NETZSCH Proteus Software v.6.1; Netzsch-Gerätebau Bayern: Selb, Germany, 2013.
  74. Sheldrick, G. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
  75. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  76. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
  77. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  78. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  79. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys 2010, 132, 154104. [Google Scholar] [CrossRef]
  80. Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  81. Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
  82. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
  83. Rolfes, J.D.; Neese, F.; Pantazis, D.A. All-electron scalar relativistic basis sets for the elements Rb–Xe. J. Comput. Chem. 2020, 41, 1842–1849. [Google Scholar] [CrossRef]
  84. Neese, F. An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix. J. Comput. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
  85. Pantazis, D.A.; Neese, F. All-Electron Scalar Relativistic Basis Sets for the Actinides. J. Chem. Theory Comput. 2011, 7, 677–684. [Google Scholar] [CrossRef]
  86. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO7; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
  87. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  88. Lu, T.; Chen, F. Quantitative analysis of molecular surface based on improved Marching Tetrahedra algorithm. J. Mol. Graph. Modell. 2012, 38, 314–323. [Google Scholar] [CrossRef] [PubMed]
  89. Lu, T.; Chen, Q. Independent gradient model based on Hirshfeld partition: A new method for visual study of interactions in chemical systems. J. Comput. Chem. 2022, 43, 539–555. [Google Scholar] [CrossRef] [PubMed]
  90. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
  91. Turney, J.M.; Simmonett, A.C.; Parrish, R.M.; Hohenstein, E.G.; Evangelista, F.A.; Fermann, J.T.; Mintz, B.J.; Burns, L.A.; Wilke, J.J.; Abrams, M.L. Psi4: An open-source ab initio electronic structure program. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 556–565. [Google Scholar] [CrossRef]
  92. Nunzi, F.; Cesario, D.; Belpassi, L.; Tarantelli, F.; Roncaratti, L.F.; Falcinelli, S.; Cappelletti, D.; Pirani, F. Insight into the halogen-bond nature of noble gas-chlorine systems by molecular beam scattering experiments, ab initio calculations and charge displacement analysis. Phys. Chem. Chem. Phys. 2019, 21, 7330–7340. [Google Scholar] [CrossRef] [PubMed]
  93. Belpassi, L.; Infante, I.; Tarantelli, F.; Visscher, L. The Chemical Bond between Au(I) and the Noble Gases. Comparative Study of NgAuF and NgAu+ (Ng = Ar, Kr, Xe) by Density Functional and Coupled Cluster Methods. J. Am. Chem. Soc. 2008, 130, 1048–1060. [Google Scholar] [CrossRef]
  94. Liu, Z.; Lu, T.; Chen, Q. Intermolecular interaction characteristics of the all-carboatomic ring, cyclo[18]carbon: Focusing on molecular adsorption and stacking. Carbon 2021, 171, 514–523. [Google Scholar] [CrossRef]
  95. Domingo, L.R.; Pérez, P. The nucleophilicity N index in organic chemistry. Org. Biomol. Chem. 2011, 9, 7168–7175. [Google Scholar] [CrossRef]
  96. Chattaraj, P.K.; Duley, S.; Domingo, L.R. Understanding local electrophilicity/nucleophilicity activation through a single reactivity difference index. Org. Biomol. Chem. 2012, 10, 2855–2861. [Google Scholar] [CrossRef]
Ijms 24 13324 g001
Figure 1. Schematic representation of HaB in the isomeric isocyanide and nitrile systems.
Figure 1. Schematic representation of HaB in the isomeric isocyanide and nitrile systems.
Ijms 24 13324 g001
Ijms 24 13324 g002
Figure 2. Coformers of the HaB-based cocrystals and their numbering.
Figure 2. Coformers of the HaB-based cocrystals and their numbering.
Ijms 24 13324 g002
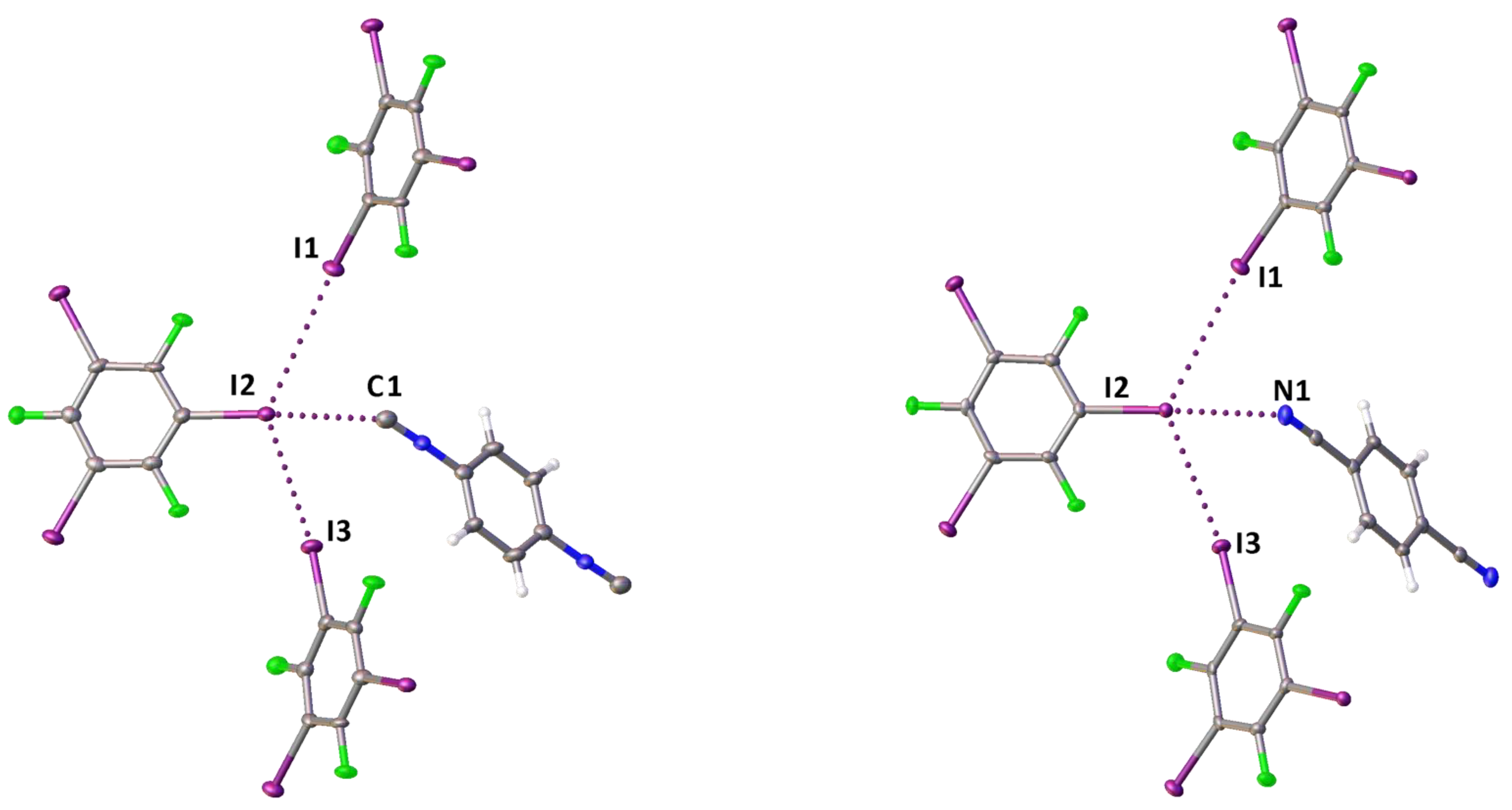
Ijms 24 13324 g003
Figure 3. Fragments of the molecular structures of 2·2(1,3,5-FIB) (left) and 3·2(1,3,5-FIB) (right); HaB is given by dotted lines.
Figure 3. Fragments of the molecular structures of 2·2(1,3,5-FIB) (left) and 3·2(1,3,5-FIB) (right); HaB is given by dotted lines.
Ijms 24 13324 g003
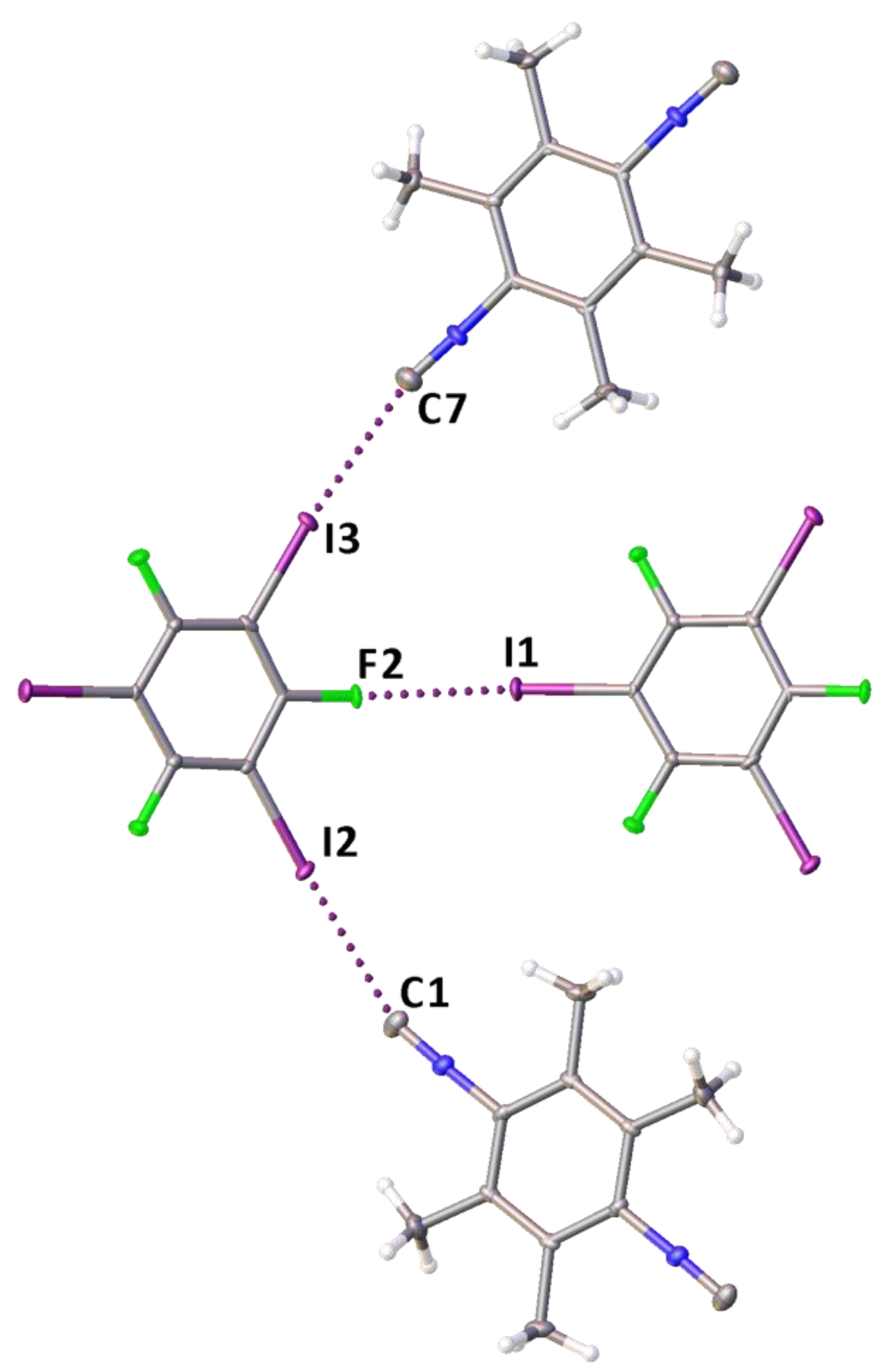
Ijms 24 13324 g004
Figure 4. A fragment of the molecular structure of 1·1,3,5-FIB displaying three two-center HaBs.
Figure 4. A fragment of the molecular structure of 1·1,3,5-FIB displaying three two-center HaBs.
Ijms 24 13324 g004
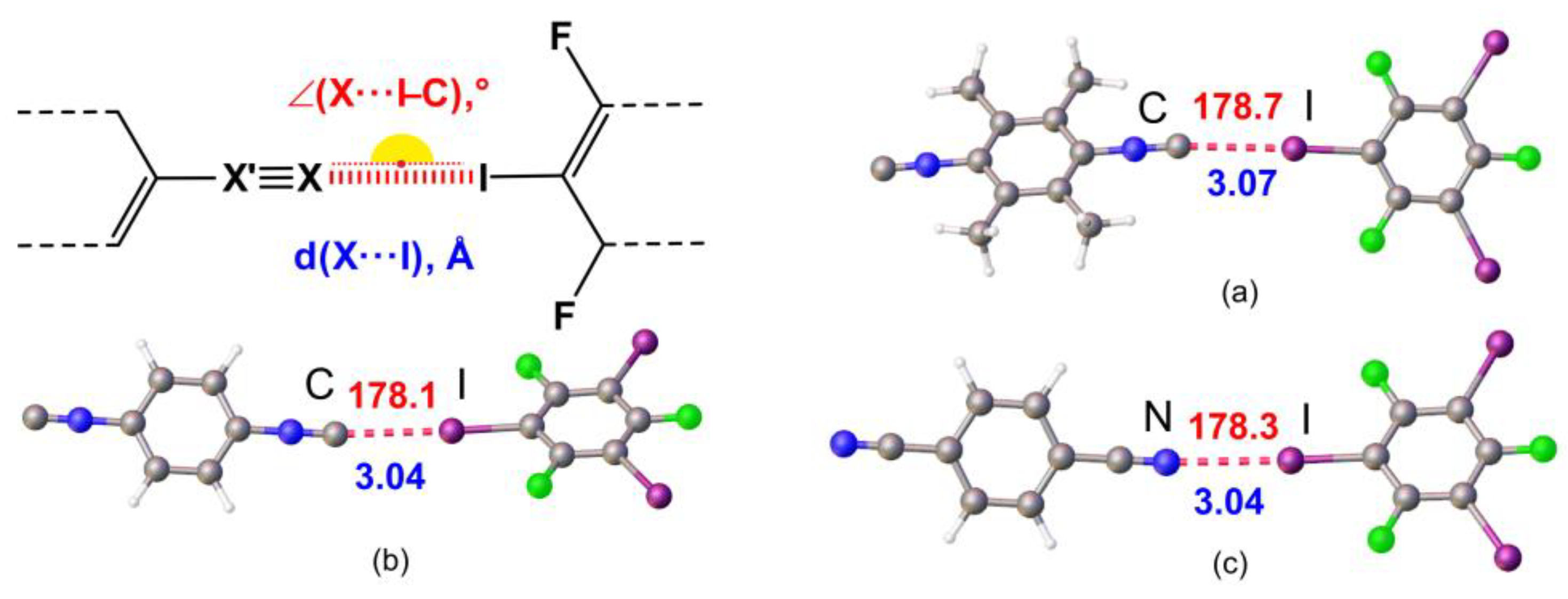
Ijms 24 13324 g005
Figure 5. Optimized structures of (a) [1‧1,3,5-FIB], (b) [2‧1,3,5-FIB], and (c) [3‧1,3,5-FIB].
Figure 5. Optimized structures of (a) [1‧1,3,5-FIB], (b) [2‧1,3,5-FIB], and (c) [3‧1,3,5-FIB].
Ijms 24 13324 g005
Ijms 24 13324 g006
Figure 6. MEP distribution in (a) 1, (b) 2, and (c) 3 calculated for the optimized structures (Vs,min MEP values in kcal/mol).
Figure 6. MEP distribution in (a) 1, (b) 2, and (c) 3 calculated for the optimized structures (Vs,min MEP values in kcal/mol).
Ijms 24 13324 g006
Ijms 24 13324 g007
Figure 7. The molecular graph (BCPs in red and bond paths as orange lines) and δginter isosurface for the structure of (a) [2‧1,3,5-FIB] and (b) [3‧1,3,5-FIB] (δginter = 0.01 a.u. and blue-cyan-green-yellow-red color scale −0.05 < sign(λ2)ρ(r) < 0.05); Contour line diagram of the Laplacian distribution, ∇2ρ(r), zero flux surfaces and bond paths in the C–I–C and C–I–N plane (bond critical points are shown by red dots) for the systems of [2‧1,3,5-FIB] (c) and [3‧1,3,5-FIB] (d).
Figure 7. The molecular graph (BCPs in red and bond paths as orange lines) and δginter isosurface for the structure of (a) [2‧1,3,5-FIB] and (b) [3‧1,3,5-FIB] (δginter = 0.01 a.u. and blue-cyan-green-yellow-red color scale −0.05 < sign(λ2)ρ(r) < 0.05); Contour line diagram of the Laplacian distribution, ∇2ρ(r), zero flux surfaces and bond paths in the C–I–C and C–I–N plane (bond critical points are shown by red dots) for the systems of [2‧1,3,5-FIB] (c) and [3‧1,3,5-FIB] (d).
Ijms 24 13324 g007
Ijms 24 13324 g008
Figure 8. ELF localization domains for the structures of (a) [2‧1,3,5-FIB] and (b) [3‧1,3,5-FIB]. Monosynaptic basins are shown in green, disynaptic basins are shown in red. * Values of the basin V(C or N) that are not involved in the HaB.
Figure 8. ELF localization domains for the structures of (a) [2‧1,3,5-FIB] and (b) [3‧1,3,5-FIB]. Monosynaptic basins are shown in green, disynaptic basins are shown in red. * Values of the basin V(C or N) that are not involved in the HaB.
Ijms 24 13324 g008
Ijms 24 13324 g009
Figure 9. Natural bond orbitals corresponding to the (a) LP(C)→σ*(I−C) transitions; (b) LP(I)→σ*(C−N); (c) LP(I)→π*(C=N) in [2‧1,3,5-FIB]. Green and blue colors indicate the opposite phase of the wave function.
Figure 9. Natural bond orbitals corresponding to the (a) LP(C)→σ*(I−C) transitions; (b) LP(I)→σ*(C−N); (c) LP(I)→π*(C=N) in [2‧1,3,5-FIB]. Green and blue colors indicate the opposite phase of the wave function.
Ijms 24 13324 g009
Ijms 24 13324 g010
Figure 10. Contribution to the sum of the attractive contributions to the interaction energy (%). Energies are in kcal/mol.
Figure 10. Contribution to the sum of the attractive contributions to the interaction energy (%). Energies are in kcal/mol.
Ijms 24 13324 g010
Table 1. Geometrical parameters of HaB.
Table 1. Geometrical parameters of HaB.
CocrystalContact
I···Nu (Nu = C, I, or F)		Interatomic
Distance, Å		Nc 1Angle
C–I···Nu, °		Angle
I···Nu–Y, °
1·1,3,5-FIBI2···C13.084 (5)0.84173.22 (16)153.4 (4)
I3···C73.035 (5)0.82173.38 (16)159.5 (4)
I1···F22.992 (3)0.87171.54 (13)136.9 (3)
2·2(1,3,5-FIB)I2···C12.957 (6)0.80172.0 (2)138.4 (5)
I1···I23.9561 (5)1.00163.51 (14)116.60 (15)
I3···I23.8022 (4)0.96172.52 (14)110.56 (14)
3·2(1,3,5-FIB)I2···N12.935 (5)0.80173.79 (19)135.9 (5)
I1···I23.9625 (6)1.00163.79 (14)116.95 (18)
I3···I23.8122 (5)0.96171.32 (14)111.63 (17)
1 Nc is the normalized contact, which here is the ratio between the observed I···C, I···N, I···F, and I···I distances and the sum of the van der Waals radii of involved atoms.
Table 2. Global and local nucleophilicity of HaB acceptors.
Table 2. Global and local nucleophilicity of HaB acceptors.
123
NNu, eV2.351.801.40
NNuloc (C or N), e*eV0.330.300.23
Table 3. Electron density (ρb), its Laplacian (∇2ρb), potential, kinetic, and total energy densities (Vb, Gb, and Hb), second eigenvalue of the Hessian matrix (λ2), values (in a.u.), ELF at BCPs, IBSI, and δgpair.
Table 3. Electron density (ρb), its Laplacian (∇2ρb), potential, kinetic, and total energy densities (Vb, Gb, and Hb), second eigenvalue of the Hessian matrix (λ2), values (in a.u.), ELF at BCPs, IBSI, and δgpair.
ContactClustersρb∇2ρbVbGbHbλ2ELFIBSIδgpair
I···C[1‧1,3,5-FIB]0.01770.0467–0.01010.01090.0008–0.01150.090.0320.027
I···C[2‧1,3,5-FIB]0.01860.0494–0.01090.01160.0007–0.01230.090.0340.028
I···N[3‧1,3,5-FIB]0.01500.0505–0.00940.01100.0016–0.01030.050.0250.024
Table 4. Values of the basin electron population V(C or N), V(C,I), (in e), and electron volume VELF for basin V(C or N) (in Å3).
Table 4. Values of the basin electron population V(C or N), V(C,I), (in e), and electron volume VELF for basin V(C or N) (in Å3).
ClustersV(C or N), e [VELF, Ǻ3]V(C,I), e
[1‧1,3,5-FIB]2.62 [100]; 2.63 * [380]1.75; 1.67 *; 1.67 *
[2‧1,3,5-FIB]2.60 [170]; 2.61 * [610]1.76, 1.68 *; 1.68 *
[3‧1,3,5-FIB]3.31 [90]; 3.31 * [460]1.74, 1.67 *; 1.67 *
* Values of the basin V(C or N) and V(C,I) electron population that are not involved in the HaB.
Table 5. Second order NBO perturbation energies (E(2), in kcal/mol), change of the occupancy of the σ*(I–C) and σ*/π*(C≡N) or σ*/π*(N≡C) NBO on the occurrence of HaB (Δocc, in me).
Table 5. Second order NBO perturbation energies (E(2), in kcal/mol), change of the occupancy of the σ*(I–C) and σ*/π*(C≡N) or σ*/π*(N≡C) NBO on the occurrence of HaB (Δocc, in me).
ClustersTransitionE(2)Δocc
[1‧1,3,5-FIB]LP(C)⟶σ*(I–C)9.644
LP(I)⟶σ*/π*(C≡N)2.115
[2‧1,3,5-FIB]LP(C)⟶σ*(I–C)10.246
LP(I)⟶σ*/π*(C≡N)2.316
[3‧1,3,5-FIB]LP(N)⟶σ*(I–C)5.216
LP(I)⟶σ*/π*(N≡C)1.812
Table 6. Calculated values of the interaction and binding energies and their decomposition (in kcal/mol).
Table 6. Calculated values of the interaction and binding energies and their decomposition (in kcal/mol).
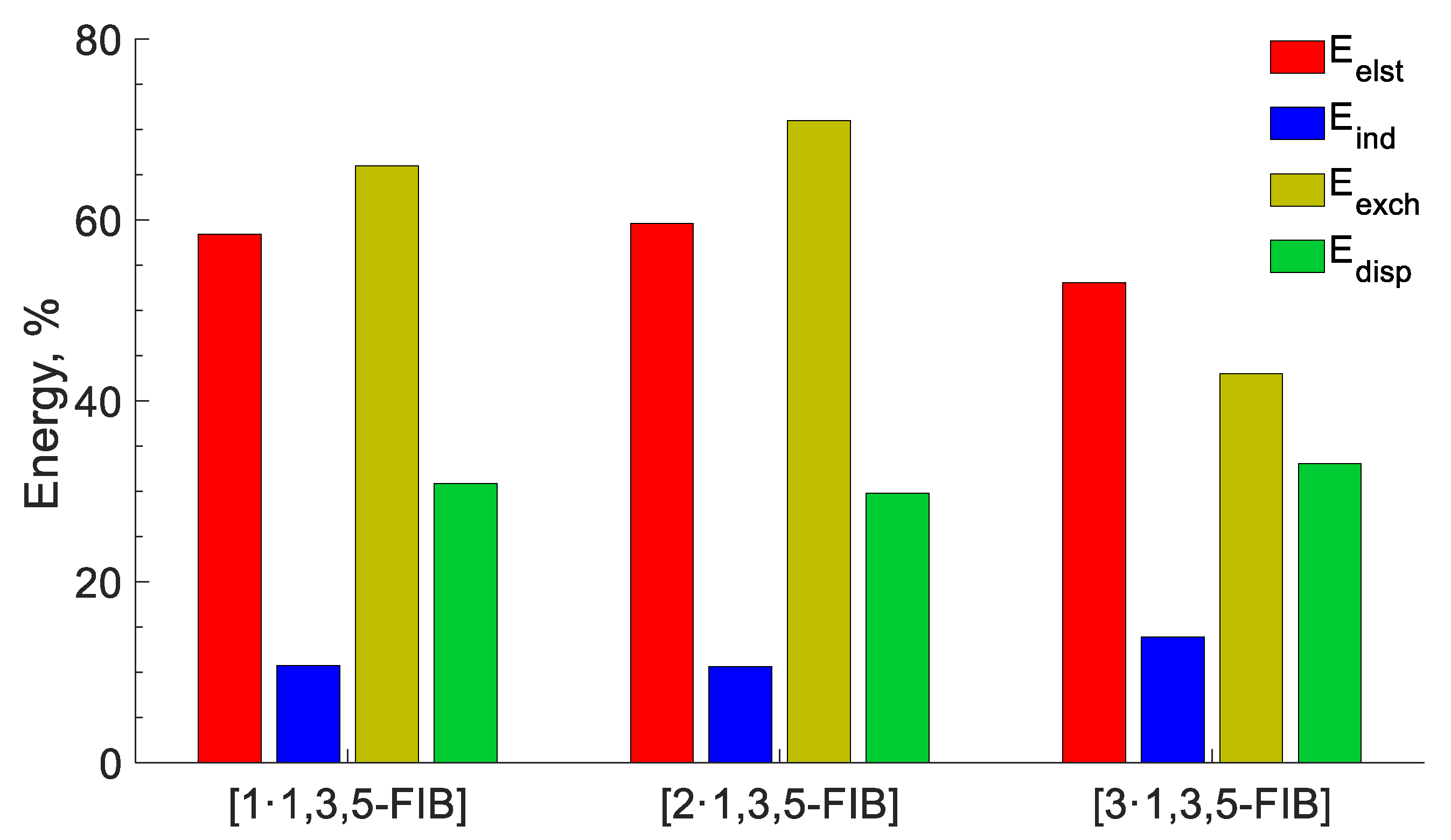
ClusterEelstEind (Ect)EexchEdispEintSAPT *EintSMEbSM
[1‧1,3,5-FIB]–8.7–1.6 (0.5)9.8–4.6–5.1–4.2–4.1
[2‧1,3,5-FIB]–9.0–1.6 (0.5)10.6–4.5–4.6–3.8–3.8
[3‧1,3,5-FIB]–6.1–1.6 (0.1)6.4–3.8–5.0–3.7–3.7
* Eint (SAPT) = Eelst + Eind + Edis + Eexch + δHF.
Table 7. Comparison of the diisocyanides and dinitriles functioning as HaB acceptors.
Table 7. Comparison of the diisocyanides and dinitriles functioning as HaB acceptors.
Methods (Descriptors)HaB I···Ciso vs. I···NnitrComments
Global Nucleophilicity (NNu)NNiso > NNnitrDiisocyanides are more nucleophilic than the dinitrile
Local Nucleophilicity (NNuloc)NNuloc(iso) > NNuloc(nitr)
MEP (Vs,min)Vs,miniso~Vs,minnitrElectrostatic potentials are nearly the same for both systems
QTAIM (ρb)ρbiso > ρbnitrThe electron density values at the BCP of the HaB are slightly higher for the diisocyanide system; this indicates a stronger binding of the diisocyanides to 1,3,5-FIB
IBSIIBSIiso > IBSInitrThe index IBSI indicates a stronger binding of the diisocyanides to 1,3,5-FIB
ELF (V(C,I))V(C,I)iso > V(C,I)nitrCharge transfer effect is higher for the isocyanide systems
NBO (Δocc (σ*(I–C))Δocc iso > Δocc nitr
DLPNO-CCSD(T) (EbSM)Ebiso > EbnitrBinding energy between the coformers is larger for the diisocyanide structures
SAPT (Eexch)Eexchiso > EexchnitrRepulsive Pauli energy for the I···C/N HaBs is higher for the isocyanides. This is in agreement with increased orbital interactions for the diisocyanide systems
SAPT (Eelst)ΔEelstiso~ΔEelstnitrlSAPT results indicate the dominance of Coulomb interactions in the HaB of both systems; they contribute approximately 60% to the sum of negative energy components. The dispersion contribution is no more than 30%
SAPT (Edisp)ΔEdispiso~ΔEdispnitrl
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Smirnov, A.S.; Katlenok, E.A.; Mikherdov, A.S.; Kryukova, M.A.; Bokach, N.A.; Kukushkin, V.Y. Halogen Bonding Involving Isomeric Isocyanide/Nitrile Groups. Int. J. Mol. Sci. 2023, 24, 13324. https://doi.org/10.3390/ijms241713324

AMA Style

Smirnov AS, Katlenok EA, Mikherdov AS, Kryukova MA, Bokach NA, Kukushkin VY. Halogen Bonding Involving Isomeric Isocyanide/Nitrile Groups. International Journal of Molecular Sciences. 2023; 24(17):13324. https://doi.org/10.3390/ijms241713324

Chicago/Turabian Style

Smirnov, Andrey S., Eugene A. Katlenok, Alexander S. Mikherdov, Mariya A. Kryukova, Nadezhda A. Bokach, and Vadim Yu. Kukushkin. 2023. "Halogen Bonding Involving Isomeric Isocyanide/Nitrile Groups" International Journal of Molecular Sciences 24, no. 17: 13324. https://doi.org/10.3390/ijms241713324

APA Style

Smirnov, A. S., Katlenok, E. A., Mikherdov, A. S., Kryukova, M. A., Bokach, N. A., & Kukushkin, V. Y. (2023). Halogen Bonding Involving Isomeric Isocyanide/Nitrile Groups. International Journal of Molecular Sciences, 24(17), 13324. https://doi.org/10.3390/ijms241713324

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop