Exploration of the Conformational Scenario for α-, β-, and γ-Cyclodextrins in Dry and Wet Conditions, from Monomers to Crystal Structures: A Quantum-Mechanical Study
Abstract
:1. Introduction
2. Results and Discussion
2.1. Nomenclature and Workflow
- xTB-CREST for the conformational exploration;
- xTB-GFN2 for semiempirical geometry optimization on all the β-CD conformations derived by CREST;
- Composite DFT functionals for re-optimization on a number of structures selected in the range within 2 kcal/mol with respect to the most stable structure in the CREST energetic ranking;
- Double-hybrid DFT functionals for single-point calculations during the benchmark (see Section 2.2.1);
- r2SCAN-3c composite DFT functional for vibrational frequency calculations on a number of structures selected in the range within 1 kcal/mol with respect to the most stable structure in the r2SCAN-3c energetic ranking.
2.2. The Case of β-Cyclodextrin
2.2.1. Benchmarking Computational Methods
2.2.2. β-CD Monomer in Dry and Wet Conditions
2.2.3. Increasing System Size: β-CD Dimers
2.2.4. Towards Periodicity: β-CD Crystal
2.3. α-Cyclodextrin
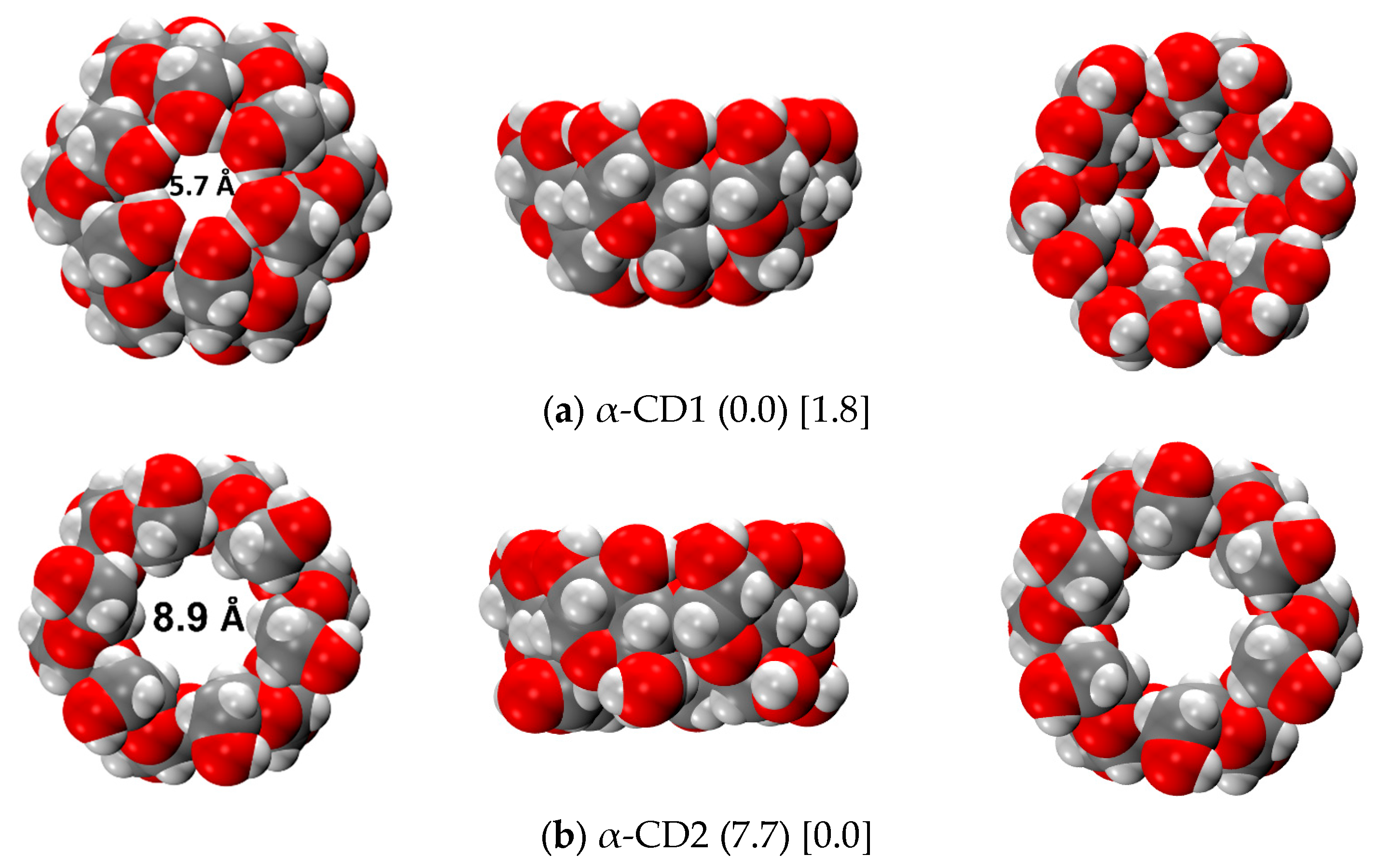
2.3.1. α-CD Monomer
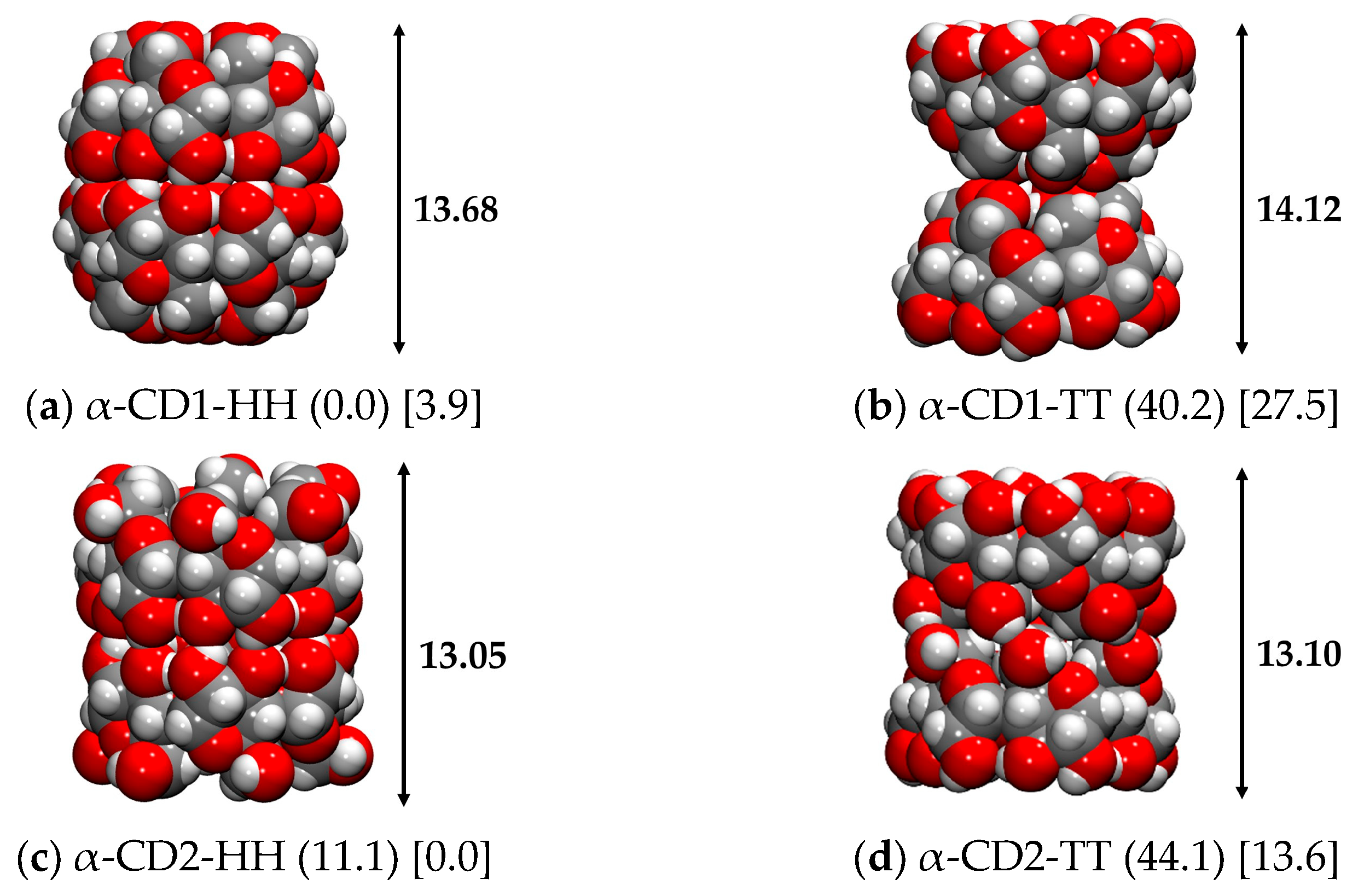
2.3.2. α-CD Dimer
2.4. γ-Cyclodextrin
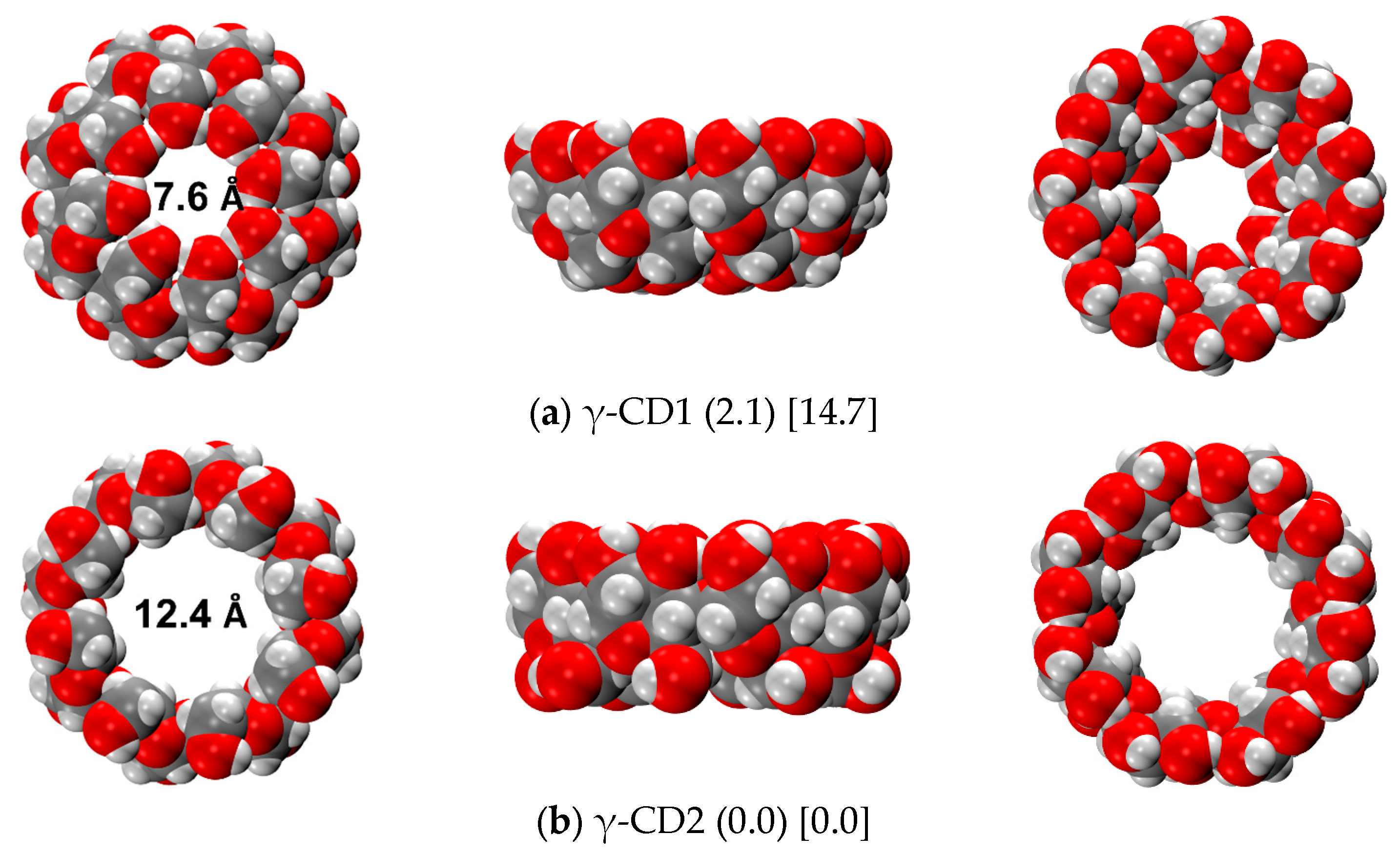
2.4.1. γ-CD Monomer
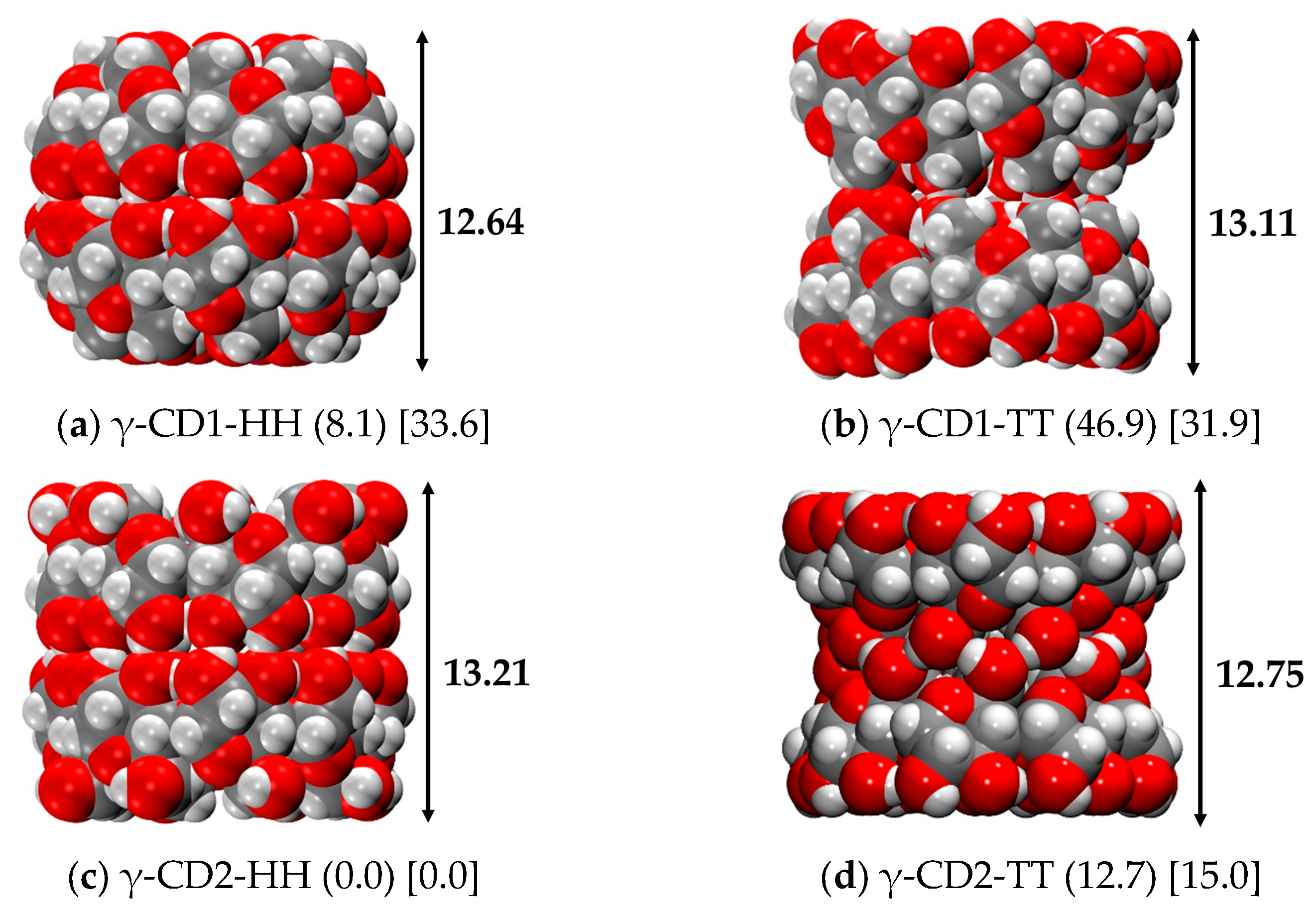
2.4.2. γ-CD Dimer
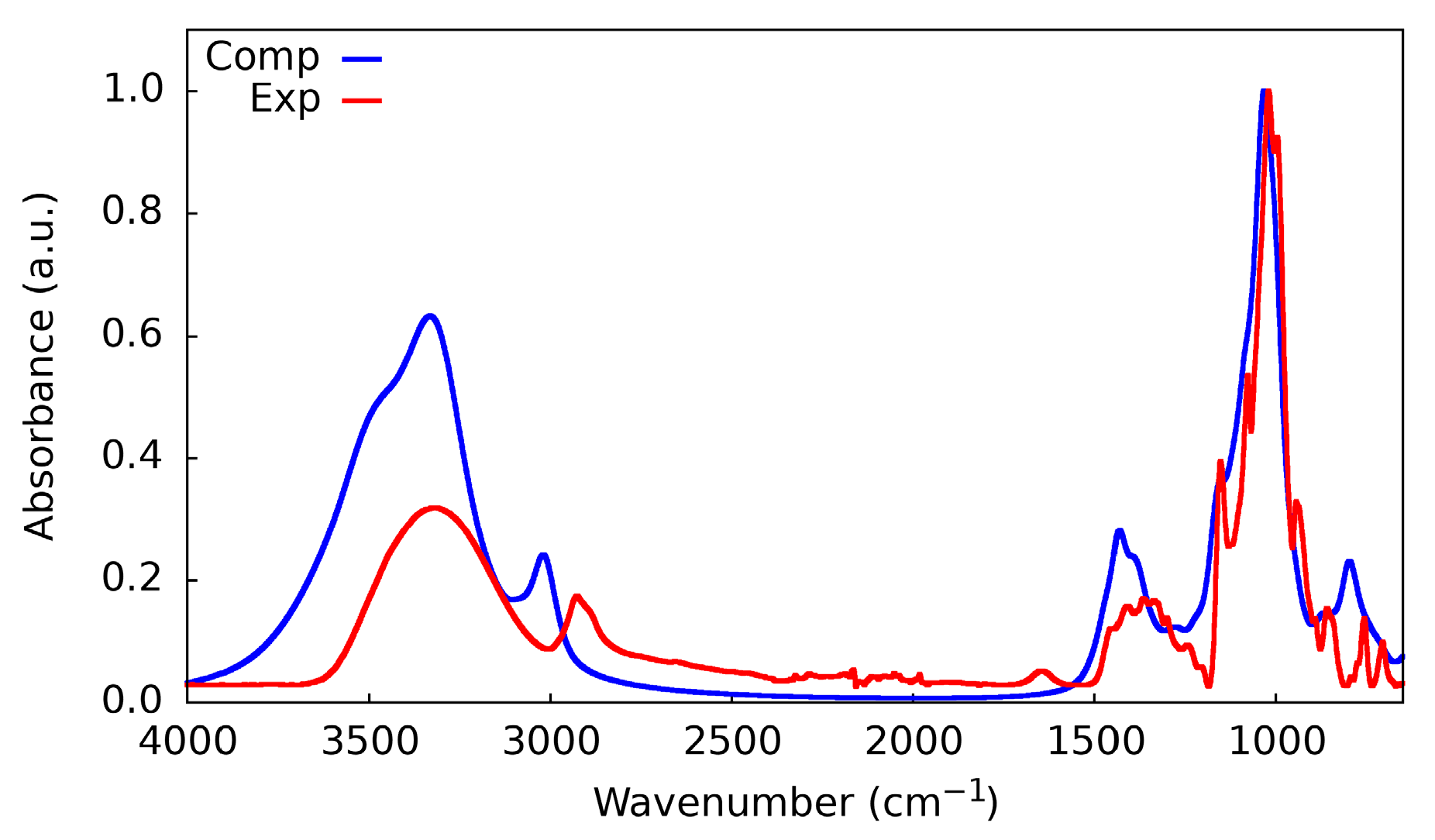
2.5. Cyclodextrin IR-Spectra
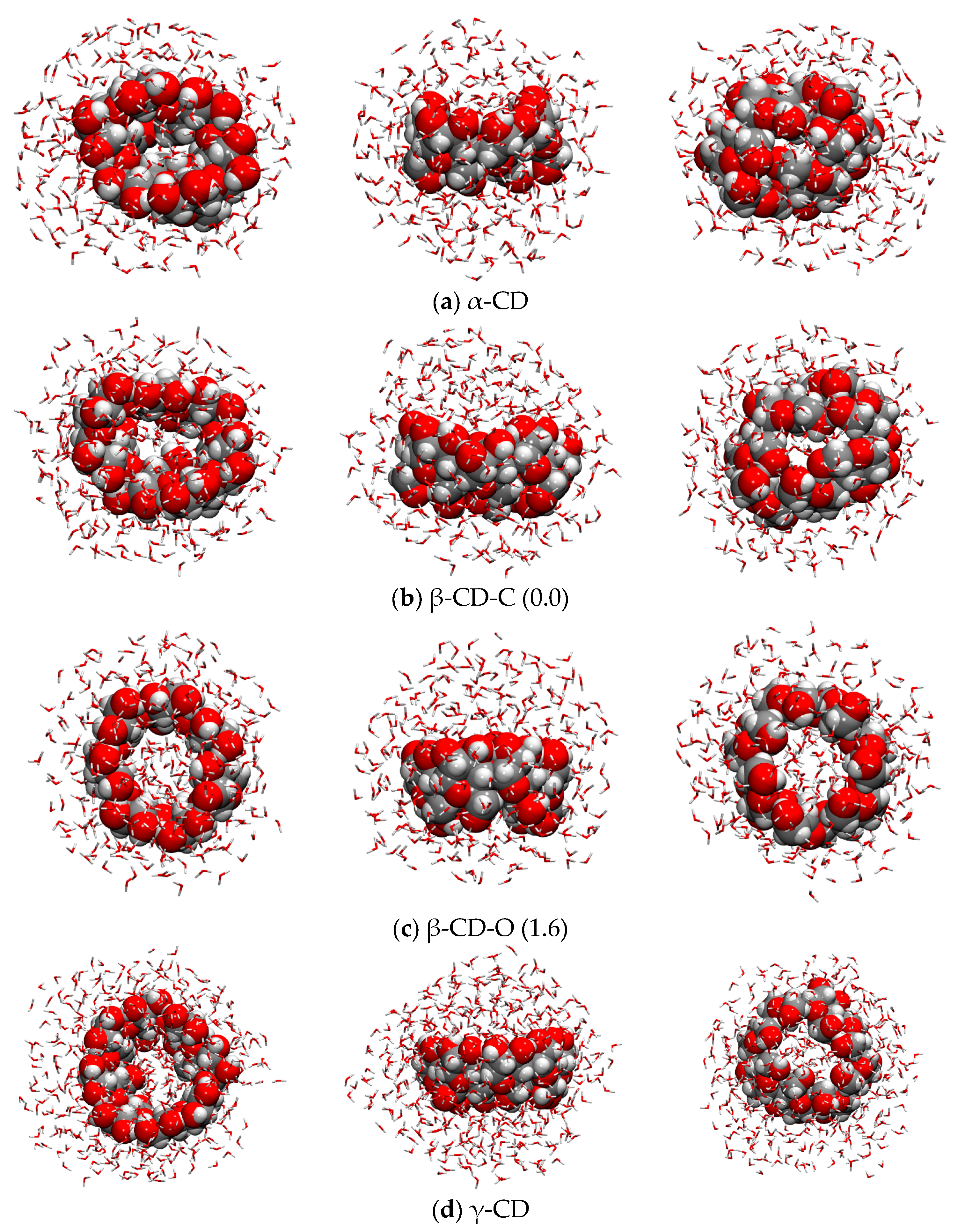
2.6. Explicit Solvation
3. Materials and Methods
3.1. Computational Codes and Associated Parameters
3.1.1. Conformational Search: xTB
3.1.2. DFT Refinement: ORCA
3.1.3. Periodic Simulations: CRYSTAL
3.1.4. Reference Equations for Computing the Energetic Contributions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crini, G. Review: A History of Cyclodextrins. Chem. Rev. 2014, 114, 10940–10975. [Google Scholar] [CrossRef] [PubMed]
- Szejtli, J. Introduction and General Overview of Cyclodextrin Chemistry. Chem. Rev. 1998, 90, 1743–1753. [Google Scholar] [CrossRef] [PubMed]
- Jansook, P.; Ogawa, N.; Loftsson, T. Cyclodextrins: Structure, Physicochemical Properties and Pharmaceutical Applications. Int. J. Pharm. 2018, 535, 272–284. [Google Scholar] [CrossRef] [PubMed]
- Larsen, K.L. Large Cyclodextrins. J. Incl. Phenom. Macrocycl. Chem. 2002, 43, 1–13. [Google Scholar] [CrossRef]
- Braga, S.S. Cyclodextrin Superstructures for Drug Delivery. J. Drug. Deliv. Sci. Technol. 2022, 75, 103650. [Google Scholar] [CrossRef]
- del Valle, E.M.M. Cyclodextrins and Their Uses: A Review. Process Biochem. 2004, 39, 1033–1046. [Google Scholar] [CrossRef]
- Trotta, F.; Zanetti, M.; Cavalli, R. Cyclodextrin-Based Nanosponges as Drug Carriers. Beilstein J. Org. Chem. 2012, 8, 2091–2099. [Google Scholar] [CrossRef]
- Krabicová, I.; Appleton, S.L.; Tannous, M.; Hoti, G.; Caldera, F.; Pedrazzo, A.R.; Cecone, C.; Cavalli, R.; Trotta, F. History of Cyclodextrin Nanosponges. Polymers 2020, 12, 1122. [Google Scholar] [CrossRef]
- Mori, T.; Tsuchiya, R.; Doi, M.; Nagatani, N.; Tanaka, T. Solubilization of Ultraviolet Absorbers by Cyclodextrin and Their Potential Application in Cosmetics. J. Incl. Phenom. Macrocycl. Chem. 2019, 93, 91–96. [Google Scholar] [CrossRef]
- Giovannelli, L.; Milanesi, A.; Ugazio, E.; Fracchia, L.; Segale, L. Effect of Methyl–β–Cyclodextrin and Trehalose on the Freeze–Drying and Spray–Drying of Sericin for Cosmetic Purposes. Pharmaceuticals 2021, 14, 262. [Google Scholar] [CrossRef]
- Dubey, S.K.; Dey, A.; Singhvi, G.; Pandey, M.M.; Singh, V.; Kesharwani, P. Emerging Trends of Nanotechnology in Advanced Cosmetics. Colloids Surf. B 2022, 214, 112440. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, Y.; Gao, X.; Fu, J.; Hu, L. Application of Cyclodextrin in Food Industry. Crit. Rev. Food Sci. Nutr. 2022, 62, 2627–2640. [Google Scholar] [CrossRef] [PubMed]
- Tian, B.; Xiao, D.; Hei, T.; Ping, R.; Hua, S.; Liu, J. The Application and Prospects of Cyclodextrin Inclusion Complexes and Polymers in the Food Industry: A Review. Polym. Int. 2020, 69, 597–603. [Google Scholar] [CrossRef]
- Morin-Crini, N.; Fourmentin, S.; Fenyvesi, É.; Lichtfouse, E.; Torri, G.; Fourmentin, M.; Crini, G. 130 Years of Cyclodextrin Discovery for Health, Food, Agriculture, and the Industry: A Review. Environ. Chem. Lett. 2021, 19, 2581–2617. [Google Scholar] [CrossRef]
- Liu, Y.; Sameen, D.E.; Ahmed, S.; Wang, Y.; Lu, R.; Dai, J.; Li, S.; Qin, W. Recent Advances in Cyclodextrin-Based Films for Food Packaging. Food Chem. 2022, 370, 131026. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Zhang, Y.; Niu, Y.; Ke, Q.; Kou, X. Cyclodextrins as Carriers for Volatile Aroma Compounds: A Review. Carbohydr. Polym. 2021, 269, 118292. [Google Scholar] [CrossRef]
- Pedrazzo, A.R.; Smarra, A.; Caldera, F.; Musso, G.; Dhakar, N.K.; Cecone, C.; Hamedi, A.; Corsi, I.; Trotta, F. Eco-Friendly β-Cyclodextrin and Linecaps Polymers for the Removal of Heavy Metals. Polymers 2019, 11, 1658. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, Y.; Lu, J.; Zhou, Y. Novel Cyclodextrin-Based Adsorbents for Removing Pollutants from Wastewater: A Critical Review. Chemosphere 2020, 241, 125043. [Google Scholar] [CrossRef]
- Tian, B.; Hua, S.; Tian, Y.; Liu, J. Cyclodextrin-Based Adsorbents for the Removal of Pollutants from Wastewater: A Review. Environ. Sci. Pollut. Res. 2021, 28, 1317–1340. [Google Scholar] [CrossRef]
- Verma, M.; Lee, I.; Hong, Y.; Kumar, V.; Kim, H. Multifunctional β-Cyclodextrin-EDTA-Chitosan Polymer Adsorbent Synthesis for Simultaneous Removal of Heavy Metals and Organic Dyes from Wastewater. Environ. Pollut. 2022, 292, 118447. [Google Scholar] [CrossRef]
- Yadav, M.; Thakore, S.; Jadeja, R. A Review on Remediation Technologies Using Functionalized Cyclodextrin. Environ. Sci. Pollut. Res. 2022, 29, 236–250. [Google Scholar] [CrossRef] [PubMed]
- Sivakumar, K.; Parinamachivayam, G. Review on β-Cyclodextrin Inclusion Complex Based Chemosensors for Heavy Metals. J. Incl. Phenom. Macrocycl. Chem. 2022, 102, 603–618. [Google Scholar] [CrossRef]
- Jambhekar, S.S.; Breen, P. Cyclodextrins in Pharmaceutical Formulations I: Structure and Physicochemical Properties, Formation of Complexes, and Types of Complex. Drug. Discov. Today 2016, 21, 356–362. [Google Scholar] [CrossRef] [PubMed]
- Ferrero, R.; Pantaleone, S.; Delle Piane, M.; Caldera, F.; Corno, M.; Trotta, F.; Brunella, V. On the Interactions of Melatonin/β-Cyclodextrin Inclusion Complex: A Novel Approach Combining Efficient Semiempirical Extended Tight-Binding (Xtb) Results with Ab Initio Methods. Molecules 2021, 26, 5881. [Google Scholar] [CrossRef] [PubMed]
- Wankar, J.; Kotla, N.G.; Gera, S.; Rasala, S.; Pandit, A.; Rochev, Y.A. Recent Advances in Host–Guest Self-Assembled Cyclodextrin Carriers: Implications for Responsive Drug Delivery and Biomedical Engineering. Adv. Funct. Mater. 2020, 30, 1909049. [Google Scholar] [CrossRef]
- Tian, B.; Liu, Y.; Liu, J. Smart Stimuli-Responsive Drug Delivery Systems Based on Cyclodextrin: A Review. Carbohydr. Polym. 2021, 251, 116871. [Google Scholar] [CrossRef] [PubMed]
- Fang, G.; Yang, X.; Chen, S.; Wang, Q.; Zhang, A.; Tang, B. Cyclodextrin-Based Host–Guest Supramolecular Hydrogels for Local Drug Delivery. Coord. Chem. Rev. 2022, 454, 214352. [Google Scholar] [CrossRef]
- Allahyari, S.; Zahednezhad, F.; Khatami, M.; Hashemzadeh, N.; Zakeri-Milani, P.; Trotta, F. Cyclodextrin Nanosponges as Potential Anticancer Drug Delivery Systems to Be Introduced into the Market, Compared with Liposomes. J. Drug. Deliv. Sci. Technol. 2022, 67, 102931. [Google Scholar] [CrossRef]
- Mazurek, A.H.; Szeleszczuk, Ł. Current Status of Quantum Chemical Studies of Cyclodextrin Host–Guest Complexes. Molecules 2022, 27, 3874. [Google Scholar] [CrossRef]
- Muzaffar, S.; Imtiaz, S.; Ali, S.M. Demonstrating Accuracy of the Proposed Protocol for Structure Elucidation of Cyclodextrin Inclusion Complexes by Validation Using DFT Studies. J. Mol. Struct. 2020, 1217, 128419. [Google Scholar] [CrossRef]
- Bao, X.; Liu, X.; Dou, R.; Xu, S.; Liu, D.; Luo, J.; Gong, X.; Wong, C.F.; Zhou, B. How Are N-Methylcarbamates Encapsulated by β-Cyclodextrin: Insight into the Binding Mechanism. Phys. Chem. Chem. Phys. 2023, 25, 13923–13932. [Google Scholar] [CrossRef] [PubMed]
- Nie, B.; Yan, J.; Shi, S.; Wang, L.J.; Wu, Y.C.; Li, H.J. Sustainable Corrosion Resistance of Piroxicam-Cyclodextrin Inclusion Complex to Mild Steel and Its Mechanism. J. Mater. Res. Technol. 2023, 23, 3665–3675. [Google Scholar] [CrossRef]
- Aree, T. Atomic-Level Understanding on Conformational Flexibility of Neochlorogenic and Chlorogenic Acids and Their Inclusion Complexation with β-Cyclodextrin. Food Hydrocoll. 2023, 141, 108742. [Google Scholar] [CrossRef]
- Benaïssa, A.; Bouhadiba, A.; Naili, N.; Chekkal, F.; Khelfaoui, M.; Bouras, I.; Madjram, M.S.; Zouchoune, B.; Mogalli, S.; Malfi, N.; et al. Computational Investigation of Dimethoate and β-Cyclodextrin Inclusion Complex: Molecular Structures, Intermolecular Interactions, and Electronic Analysis. Struct. Chem. 2023, 34, 1189–1204. [Google Scholar] [CrossRef]
- Imamura, W.; Yamasaki, T.; Kato, H.; Ishikawa, T. Insights into the Molecular Interaction of Cyclodextran with a Guest Molecule: A Computational Study. Carbohydr. Polym. 2023, 301, 120315. [Google Scholar] [CrossRef] [PubMed]
- Badi, S.; Madi, F.; Nouar, L.; Gheid, A. Effect of Cyclodextrins Inclusion Complexes into Absorption and Emission Spectra of P-Methylaminobenzoate Derivatives: A DFT and TD-DFT Investigation. J. Fluoresc. 2023, 33, 1457–1467. [Google Scholar] [CrossRef] [PubMed]
- Zaboub, A.; Madi, F.; Merdes, R.; Mohamedi, M.; Nouar, L. A Combined DFT and Experimental Study of Proline/β-Cyclodextrin Inclusion Complex. J. Mol. Liq. 2016, 216, 716–723. [Google Scholar] [CrossRef]
- Nora, M.; Ismahan, L.; Abdelkrim, G.; Mouna, C.; Leila, N.; Fatiha, M.; Nada, B.; Brahim, H. Interactions in Inclusion Complex of β-Cyclodextrin/l-Metheonine: DFT Computational Studies. J. Incl. Phenom. Macrocycl. Chem. 2020, 96, 43–54. [Google Scholar] [CrossRef]
- Harris, R.C.; Deng, N.; Levy, R.M.; Ishizuka, R.; Matubayasi, N. Computing Conformational Free Energy Differences in Explicit Solvent: An Efficient Thermodynamic Cycle Using an Auxiliary Potential and a Free Energy Functional Constructed from the End Points. J. Comput. Chem. 2017, 38, 1198–1208. [Google Scholar] [CrossRef]
- Belhouchet, H.R.; Abbaz, T.; Bendjedou, A.; Gouasmia, A.; Villemin, D. A Computational Study of the Inclusion of β-Cyclodextrin and Nicotinic Acid: DFT, DFT-D, NPA, NBO, QTAIM, and NCI-RDG Studies. J. Mol. Model. 2022, 28, 348. [Google Scholar] [CrossRef]
- Liu, R.; Qin, X.; Liu, X.; Wang, Y.; Zhong, J. Host-Guest Interactions between Oleic Acid and β-Cyclodextrin: A Combined Experimental and Theoretical Study. Food Chem. 2022, 387, 132910. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, N.; Poorbagher, N. Host-Guest Inclusion Complexes of Sulfabenzamide with β- and Methyl-β-Cyclodextrins: Characterization, Antioxidant Activity and DFT Calculation. J. Mol. Struct. 2022, 1260, 132809. [Google Scholar] [CrossRef]
- Karoyo, A.H.; Borisov, A.S.; Wilson, L.D.; Hazendonk, P. Formation of Host-Guest Complexes of β-Cyclodextrin and Perfluorooctanoic Acid. J. Phys. Chem. B 2011, 115, 9511–9527. [Google Scholar] [CrossRef]
- Topuz, F.; Uyar, T. Advances in the Development of Cyclodextrin-Based Nanogels/Microgels for Biomedical Applications: Drug Delivery and Beyond. Carbohydr. Polym. 2022, 297, 120033. [Google Scholar] [CrossRef] [PubMed]
- Jicsinszky, L.; Rossi, F.; Solarino, R.; Cravotto, G. Comparison of the Conventional and Mechanochemical Syntheses of Cyclodextrin Derivatives. Molecules 2023, 28, 467. [Google Scholar] [CrossRef] [PubMed]
- Cirri, M.; Nerli, G.; Mennini, N.; Maestrelli, F.; Mura, P. Development and Characterization of Cyclodextrin-Based Nanogels as a New Ibuprofen Cutaneous Delivery System. Pharmaceutics 2022, 14, 2567. [Google Scholar] [CrossRef] [PubMed]
- Peimanfard, S.; Zarrabi, A.; Trotta, F.; Matencio, A.; Cecone, C.; Caldera, F. Developing Novel Hydroxypropyl-β-Cyclodextrin-Based Nanosponges as Carriers for Anticancer Hydrophobic Agents: Overcoming Limitations of Host–Guest Complexes in a Comparative Evaluation. Pharmaceutics 2022, 14, 1059. [Google Scholar] [CrossRef]
- Bonnet, P.; Jaime, C.; Morin-Allory, L. Structure and Thermodynamics of α-, β-, and γ-Cyclodextrin Dimers. Molecular Dynamics Studies of the Solvent Effect and Free Binding Energies. J. Org. Chem. 2002, 67, 8602–8609. [Google Scholar] [CrossRef]
- Stachowicz, A.; Styrcz, A.; Korchowiec, J.; Modaressi, A.; Rogalski, M. DFT Studies of Cation Binding by β-Cyclodextrin. Theor. Chem. Acc. 2011, 130, 939–953. [Google Scholar] [CrossRef]
- Zhang, H.; Tan, T.; van der Spoel, D. Generalized Born and Explicit Solvent Models for Free Energy Calculations in Organic Solvents: Cyclodextrin Dimerization. J. Chem. Theory Comput. 2015, 11, 5103–5113. [Google Scholar] [CrossRef]
- He, P.; Sarkar, S.; Gallicchio, E.; Kurtzman, T.; Wickstrom, L. Role of Displacing Confined Solvent in the Conformational Equilibrium of β-Cyclodextrin. J. Phys. Chem. B 2019, 123, 8378–8386. [Google Scholar] [CrossRef]
- Anconi, C.P.A.; Nascimento, C.S.; De Almeida, W.B.; Santos, H.F.D. Structure and Stability of (α-CD)3 Aggregate and OEG at (α-CD)3 Pseudorotaxane in Aqueous Solution: A Molecular Dynamics Study. J. Phys. Chem. B 2009, 113, 9762–9769. [Google Scholar] [CrossRef] [PubMed]
- de Sousa, S.M.R.; Guimarães, L.; Ferrari, J.L.; de Almeida, W.B.; Nascimento, C.S. A DFT Investigation on the Host/Guest Inclusion Process of Prilocaine into β-Cyclodextrin. Chem. Phys. Lett. 2016, 652, 123–129. [Google Scholar] [CrossRef]
- Bouchemela, H.; Madi, F.; Nouar, L. DFT Investigation of Host–Guest Interactions between α-Terpineol and β-Cyclodextrin. J. Incl. Phenom. Macrocycl. Chem. 2019, 95, 247–258. [Google Scholar] [CrossRef]
- Ignaczak, A.; Orszański, Ł.; Adamiak, M.; Olejniczak, A.B. Comparative DFT Study of Inclusion Complexes of Thymidine-Carborane Conjugate with β-Cyclodextrin and Heptakis(2,6-O-Dimethyl)-β-Cyclodextrin in Water. J. Mol. Liq. 2020, 315, 113767. [Google Scholar] [CrossRef]
- Lopes, J.F.; Nascimento, C.S.; Anconi, C.P.A.; Santos, H.F.D.; Almeida, W.B.D. Inclusion Complex Thermodynamics: The β-Cyclodextrin and Sertraline Complex Example. J. Mol. Graph. Model. 2015, 62, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Passos, J.J.; De Sousa, F.B.; Lula, I.S.; Barreto, E.A.; Lopes, J.F.; De Almeida, W.B.; Sinisterra, R.D. Multi-Equilibrium System Based on Sertraline and β-Cyclodextrin Supramolecular Complex in Aqueous Solution. Int. J. Pharm. 2011, 421, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Anconi, C.P.A.; Nascimento, C.S.; Fedoce-Lopes, J.; Dos Santos, H.F.; De Almeida, W.B. Ab Initio Calculations on Low-Energy Conformers of α-Cyclodextrin. J. Phys. Chem. A 2007, 111, 12127–12135. [Google Scholar] [CrossRef] [PubMed]
- Ramos, A.I.; Braga, T.M.; Silva, P.; Fernandes, J.A.; Ribeiro-Claro, P.; De Fátima Silva Lopes, M.; Paz, F.A.A.; Braga, S.S. Chloramphenicol·cyclodextrin Inclusion Compounds: Co-Dissolution and Mechanochemical Preparations and Antibacterial Action. CrystEngComm 2013, 15, 2822–2834. [Google Scholar] [CrossRef]
- Harata, K. The Structure of the Cyclodextrin Complex. V. Crystal Structures of α-Cyclodextrin Complexes with p-Nitrophenol and p-Hydroxybenzoic Acid. Bull. Chem. Soc. Jpn. 1977, 60, 1416–1424. [Google Scholar] [CrossRef]
- Jiang, Z.G.; Mao, W.T.; Huang, D.P.; Wang, Y.; Wang, X.J.; Zhan, C.H. A Nonconventional Host-Guest Cubic Assembly Based on γ-Cyclodextrin and a Keggin-Type Polyoxometalate. Nanoscale 2020, 12, 10166–10171. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef] [PubMed]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-XTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef]
- Spicher, S.; Grimme, S. Robust Atomistic Modeling of Materials, Organometallic, and Biochemical Systems. Angew. Chem. 2020, 132, 15795–15803. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A Generally Applicable Atomic-Charge Dependent London Dispersion Correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Pracht, P.; Bohle, F.; Grimme, S. Automated Exploration of the Low-Energy Chemical Space with Fast Quantum Chemical Methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef] [PubMed]
- Ehlert, S.; Stahn, M.; Spicher, S.; Grimme, S. A Robust and Efficient Implicit Solvation Model for Fast Semiempirical Methods. J. Chem. Theory Comput. 2021, 17, 4250–4261. [Google Scholar] [CrossRef]
- Spicher, S.; Plett, C.; Pracht, P.; Hansen, A.; Grimme, S. Automated Molecular Cluster Growing for Explicit Solvation by Efficient Force Field and Tight Binding Methods. J. Chem. Theory Comput. 2022, 18, 3174–3189. [Google Scholar] [CrossRef]
- Grimme, S.; Bannwarth, C.; Caldeweyher, E.; Pisarek, J.; Hansen, A. A General Intermolecular Force Field Based on Tight-Binding Quantum Chemical Calculations. J. Chem. Phys. 2017, 147, 161708. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Bannwarth, C.; Hansen, A.; Grimme, S. B97-3c: A Revised Low-Cost Variant of the B97-D Density Functional Method. J. Chem. Phys. 2018, 148, 064104. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Ehlert, S.; Mewes, J.M. r2SCAN-3c: A “Swiss Army Knife” Composite Electronic-Structure Method. J. Chem. Phys. 2021, 154, 064103. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Kruse, H.; Grimme, S. A Geometrical Correction for the Inter- and Intra-Molecular Basis Set Superposition Error in Hartree-Fock and Density Functional Theory Calculations for Large Systems. J. Chem. Phys. 2012, 136, 154101. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
- Kozuch, S.; Gruzman, D.; Martin, J.M.L. DSD-BLYP: A General Purpose Double Hybrid Density Functional Including Spin Component Scaling and Dispersion Correction. J. Phys. Chem. C 2010, 114, 20801–20808. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. DSD-PBEP86: In Search of the Best Double-Hybrid DFT with Spin-Component Scaled MP2 and Dispersion Corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104–20107. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.; Bush, I.; et al. CRYSTAL23 User’s Manual. 2022. Available online: https://www.crystal.unito.it/include/manuals/crystal23.pdf (accessed on 20 June 2023).
- Erba, A.; Desmarais, J.K.; Casassa, S.; Civalleri, B.; Donà, L.; Bush, I.J.; Searle, B.; Maschio, L.; Edith-Daga, L.; Cossard, A.; et al. CRYSTAL23: A Program for Computational Solid State Physics and Chemistry. J. Chem. Theory Comput. 2022, 19, 6891–6932. [Google Scholar] [CrossRef] [PubMed]
- Furness, J.W.; Kaplan, A.D.; Ning, J.; Perdew, J.P.; Sun, J. Accurate and Numerically Efficient r2SCAN Meta-Generalized Gradient Approximation. J. Phys. Chem. Lett. 2020, 11, 8208–8215. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Pascale, F.; Zicovich-Wilson, C.M.; Gejo, F.L.; Civalleri, B.; Orlando, R.; Dovesi, R. The Calculation of the Vibrational Frequencies of Crystalline Compounds and Its Implementation in the CRYSTAL Code. J. Comput. Chem. 2004, 25, 888–897. [Google Scholar] [CrossRef] [PubMed]
- Zicovich-Wilson, C.M.; Pascale, F.; Roetti, C.; Saunders, V.R.; Orlando, R.; Dovesi, R. Calculation of the Vibration Frequencies of α-Quartz: The Effect of Hamiltonian and Basis Set. J. Comput. Chem. 2004, 25, 1873–1881. [Google Scholar] [CrossRef] [PubMed]
- Dall’Olio, S.; Dovesi, R.; Resta, R. Spontaneous Polarization as a Berry Phase of the Hartree-Fock Wave Function: The Case of KNbO3. Phys. Rev. B 1997, 56, 10105–10114. [Google Scholar] [CrossRef]
- Huggins, C.M.; Pimentel, G.C. Systematics of the infrared spectral properties of hydrogen bonding systems: Frequency shift, half width and intensity. J. Phys. Chem. 1956, 60, 1615–1619. [Google Scholar] [CrossRef]
- Ugliengo, P.; Viterbo, D.; Chiari, G. MOLDRAW: Molecular Graphics on a Personal Computer. Z. Krist.—Cryst. Mater. 1993, 207, 9–23. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. Gaussview6; Semichem Inc.: Shawnee, KS, USA, 2016. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
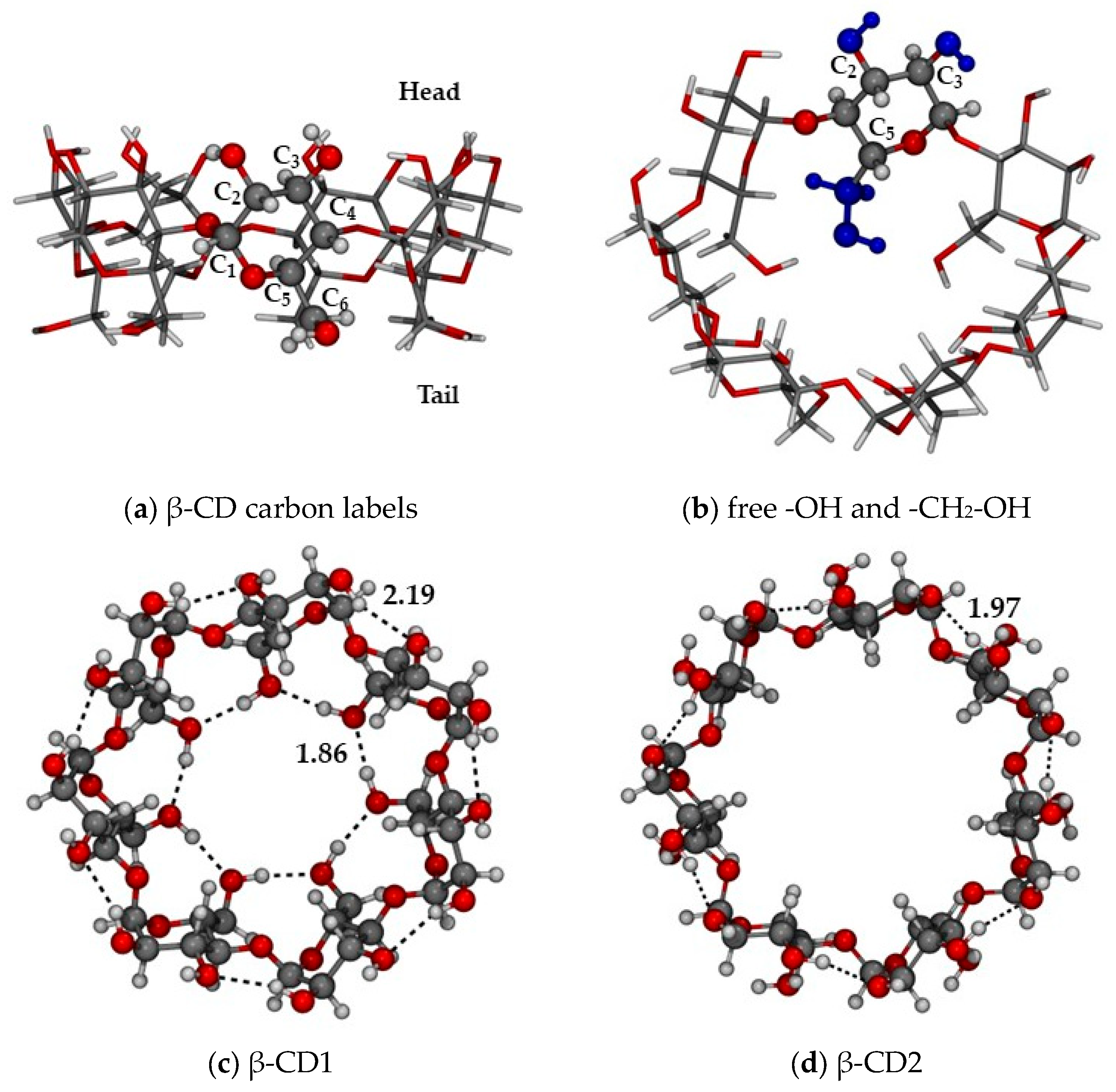
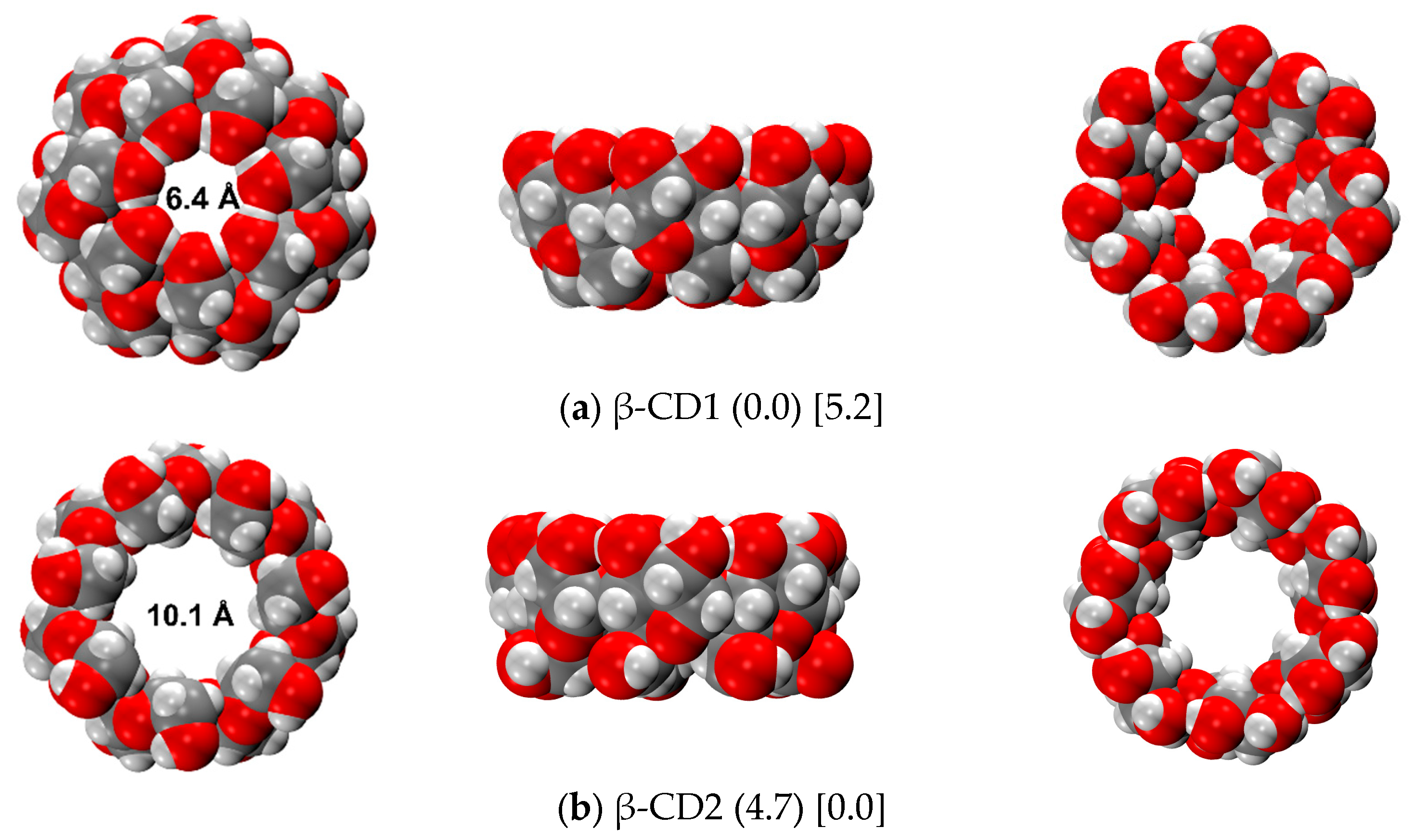
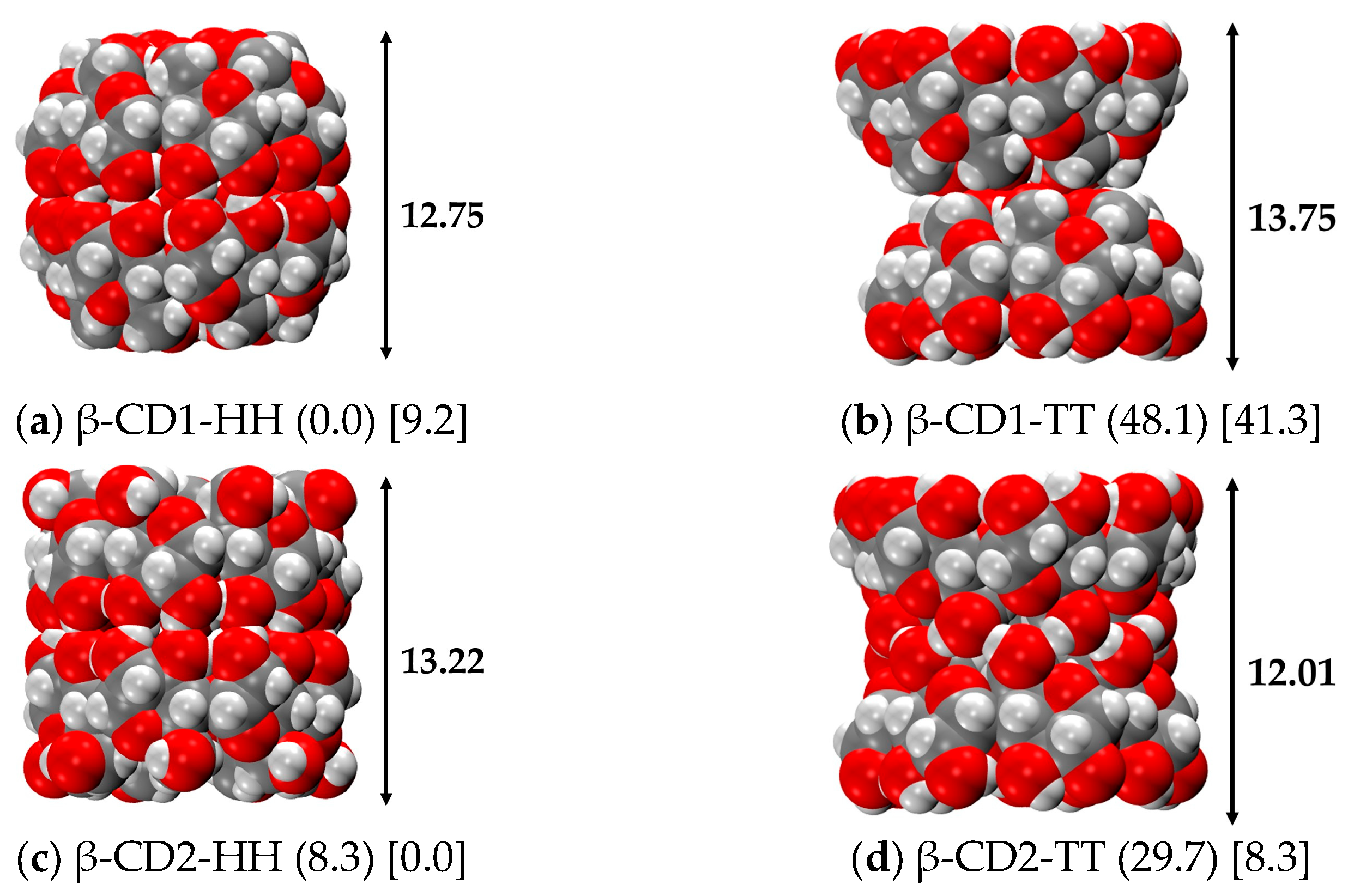
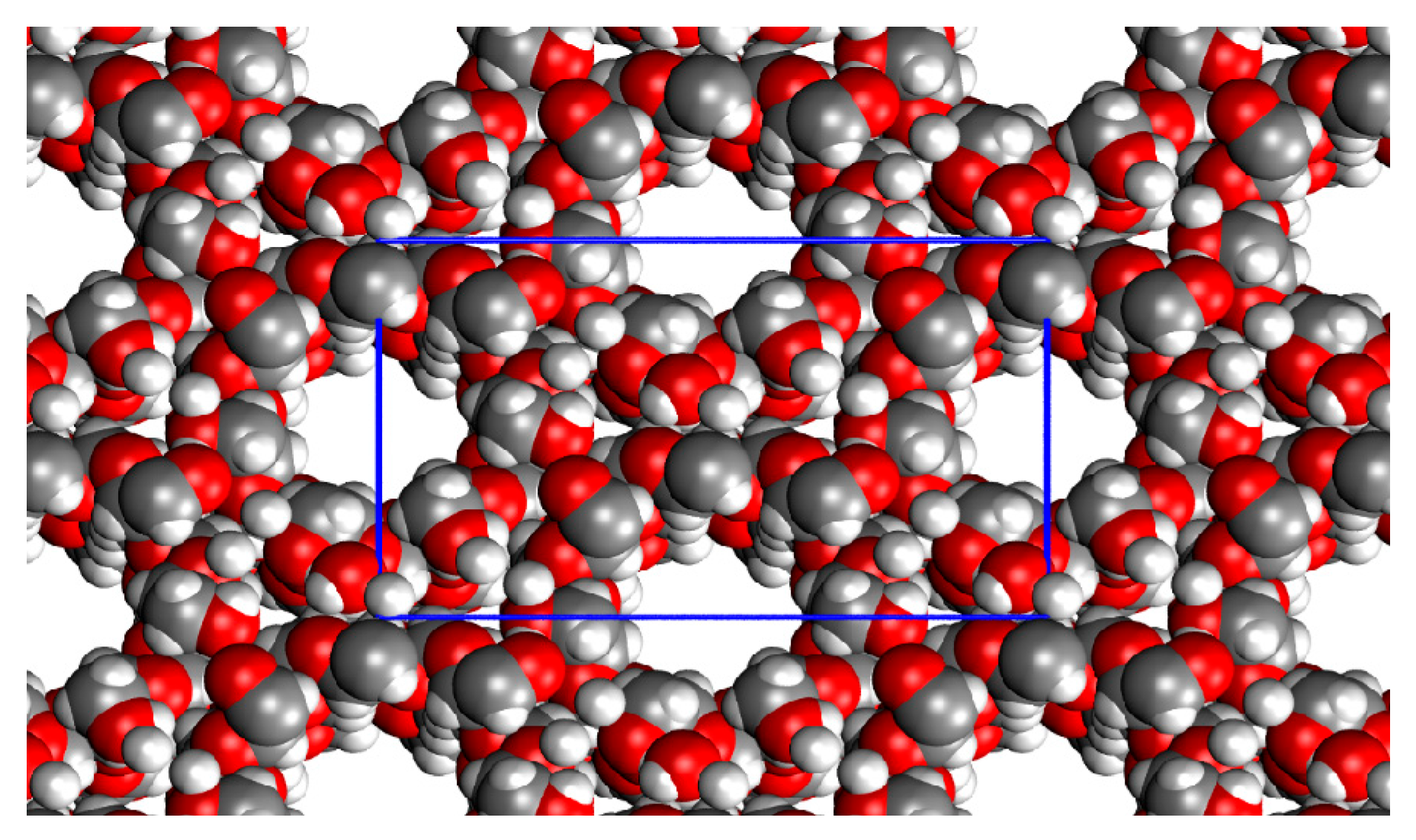
| Structures | ΔErel | |||||||
|---|---|---|---|---|---|---|---|---|
| r2SCAN-3c | B2PLYP | DSD-BLYP | DSD-PBEP86 | r2SCAN-3c | B2PLYP | DSD-BLYP | DSD-PBEP86 | |
| 1. | CD1 (0.000) | CD1 | CD1 | CD1 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2. | CD2 (1.110) | x121 | x121 | x121 | 4.7 | 6.7 | 5.9 | 6.0 |
| 3. | x121 (1.789) | x033 | x026 | x026 | 5.8 | 6.8 | 6.1 | 6.3 |
| 4. | x026 (1.858) | x026 | x033 | x033 | 6.3 | 6.8 | 6.1 | 6.3 |
| 5. | x033 (1.864) | x080 | CD2 | CD2 | 6.4 | 7.6 | 6.3 | 6.5 |
| 6. | x153 (1.820) | x072 | x080 | x080 | 7.3 | 7.6 | 6.8 | 6.8 |
| 7. | x023 (1.820) | CD2 | x072 | x072 | 7.3 | 7.7 | 6.8 | 6.8 |
| 8. | x043 (1.820) | x043 | x043 | x023 | 7.3 | 8.4 | 7.6 | 7.7 |
| 9. | x072 (2.147) | x023 | x023 | x043 | 7.4 | 8.4 | 7.6 | 7.7 |
| 10. | x080 (2.141) | x153 | x153 | x153 | 7.4 | 8.4 | 7.6 | 7.7 |
| B97-3c | B2PLYP | DSD-BLYP | DSD-PBEP86 | B97-3c | B2PLYP | DSD-BLYP | DSD-PBEP86 | |
| 1. | CD1 (0.000) | CD1 | CD1 | CD1 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2. | x026 (1.853) | x033 | x121 | x121 | 8.6 | 6.7 | 6.0 | 6.2 |
| 3. | x033 (1.854) | x026 | x033 | x033 | 8.7 | 6.7 | 6.1 | 6.4 |
| 4. | CD2 (1.166) | x121 | x026 | x026 | 9.1 | 6.8 | 6.1 | 6.4 |
| 5. | x121 (1.788) | x080 | CD2 | CD2 | 9.2 | 7.6 | 6.4 | 6.7 |
| 6. | x023 (1.814) | x072 | x080 | x080 | 10.4 | 7.6 | 6.9 | 7.0 |
| 7. | x043 (1.814) | CD2 | x072 | x072 | 10.4 | 7.7 | 6.9 | 7.0 |
| 8. | x153 (1.822) | x043 | x153 | x153 | 10.5 | 8.4 | 7.7 | 7.9 |
| 9. | x072 (2.150) | x023 | x023 | x023 | 10.5 | 8.4 | 7.7 | 8.0 |
| 10. | x080 (2.150) | x153 | x043 | x043 | 10.6 | 8.4 | 7.7 | 8.0 |
| Structure | ΔErel | Solvation E |
|---|---|---|
| CD2 | 0.0 (0.0) | −49.5 (−60.2) |
| x05 | 0.5 (0.4) | −49.0 (−59.8) |
| x01 | 0.5 (0.6) | −49.0 (−59.6) |
| x03 | 1.0 (1.2) | −48.5 (−59.1) |
| x02 | 1.6 | −47.9 |
| x08 | 3.1 | −46.3 |
| x06 | 3.2 | −46.3 |
| x23 | 3.6 | −45.9 |
| x16 | 4.3 | −45.2 |
| x15 | 4.3 | −45.1 |
| CD1 | 5.2 | −44.3 |
| x76 | 6.0 | −44.0 |
| Structure | Gas Phase | Water (C-PCM) | ||
|---|---|---|---|---|
| ΔErel | ΔEdim | ΔErel | ΔEdim | |
| β-CD1-HH | 0.0 (2.4) | −64.6 (−35.2) | 9.2 | −35.6 |
| β-CD2-HH | 8.3 (0.0) | −56.2 (−37.6) | 0.0 (0.0) | −44.8 (−15.7) |
| β-CD2-TT | 29.7 | −34.8 | 8.3 (7.1) | −36.5 (−8.7) |
| β-CD1-TT | 48.1 | −16.5 | 41.3 | −3.5 |
| a | b | c | β | Volume | Cohesive H | Cohesive G | |
|---|---|---|---|---|---|---|---|
| r2SCAN-D3BJ/ def2-TZVP (gCP) | 16.867 | 25.339 | 15.849 | 113.185 | 6226.575 | −91.4 | −64.2 |
| EXP | 19.056 | 24.415 | 15.698 | 109.463 | 6886.183 | -- | -- |
| Δ% | 12.5 | −4.8 | −2.0 | −3.6 | 8.0 | -- | -- |
| Gas Phase | Water (C-PCM) | |||
|---|---|---|---|---|
| Structure | ΔErel | ΔEdim | ΔErel | ΔEdim |
| α-CD1-HH | 0.0 (0.0) | −52.0 (−26.1) | 3.9 (12.3) | −34.6 (3.1) |
| α-CD2-HH | 11.1 (3.8) | −40.9 (−22.3) | 0.0 (0.0) | −38.5 (−9.2) |
| α-CD1-TT | 40.2 | −11.8 | 27.5 | −11.0 |
| α-CD2-TT | 44.1 | −7.9 | 13.6 | −24.9 |
| Structure | ΔErel | Solvation E |
|---|---|---|
| γ-CD2 | 0.0 (0.0) | −64.5 (−74.7) |
| γ-x08 | 0.5 (1.9) | −64.0 (−72.8) |
| γ-x09 | 0.5 (0.5) | −63.9 (−74.2) |
| γ-x24 | 0.8 (1.3) | −63.6 (−73.4) |
| γ-x42 | 1.3 (1.0) | −63.2 (−73.6) |
| γ-x38 | 1.3 (2.2) | −63.2 (−72.4) |
| γ-x31 | 4.1 | −60.4 |
| Gas Phase | Water (C-PCM) | |||
|---|---|---|---|---|
| Structure | ΔErel | ΔEdim | ΔErel | ΔEdim |
| γ-CD2-HH | 0.0 (0.0) | −78.6 (−56.0) | 0.0 (0.0) | −51.1 (−20.5) |
| γ-CD1-HH | 8.1 (15.5) | −70.5 (−40.5) | 33.6 | −17.6 |
| γ-CD2-TT | 12.7 | −37.2 | 13.9 (15.7) | −37.2 (−4.8) |
| γ-CD1-TT | 46.9 | −31.7 | 31.9 | −19.3 |
| α-CD | β-CD-C | β-CD-O | γ-CD | |
|---|---|---|---|---|
| −37.91 | −49.46 | −64.48 | ||
| SASA (PCM) | 3014.21 | 3486.24 | 3994.49 | |
| Normalized | −1.26 × 10−2 | −1.42 × 10−2 | −1.61 × 10−2 | |
| −36.82 | −48.91 | −41.52 | −190.53 | |
| SASA (explicit) | 2759.61 | 3272.97 | 3438.82 | 3827.84 |
| Normalized | −1.33 × 10−2 | −1.57 × 10−2 | −1.28 × 10−2 | −4.98 × 10−2 |
| 78.30 | 63.51 | 83.39 | 70.34 | |
| 198.13 | 222.91 | 252.90 | 103.42 | |
| Experimental solubility | 145 | 18.5 | 18.5 | 232 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantaleone, S.; Gho, C.I.; Ferrero, R.; Brunella, V.; Corno, M. Exploration of the Conformational Scenario for α-, β-, and γ-Cyclodextrins in Dry and Wet Conditions, from Monomers to Crystal Structures: A Quantum-Mechanical Study. Int. J. Mol. Sci. 2023, 24, 16826. https://doi.org/10.3390/ijms242316826
Pantaleone S, Gho CI, Ferrero R, Brunella V, Corno M. Exploration of the Conformational Scenario for α-, β-, and γ-Cyclodextrins in Dry and Wet Conditions, from Monomers to Crystal Structures: A Quantum-Mechanical Study. International Journal of Molecular Sciences. 2023; 24(23):16826. https://doi.org/10.3390/ijms242316826
Chicago/Turabian StylePantaleone, Stefano, Cecilia Irene Gho, Riccardo Ferrero, Valentina Brunella, and Marta Corno. 2023. "Exploration of the Conformational Scenario for α-, β-, and γ-Cyclodextrins in Dry and Wet Conditions, from Monomers to Crystal Structures: A Quantum-Mechanical Study" International Journal of Molecular Sciences 24, no. 23: 16826. https://doi.org/10.3390/ijms242316826
APA StylePantaleone, S., Gho, C. I., Ferrero, R., Brunella, V., & Corno, M. (2023). Exploration of the Conformational Scenario for α-, β-, and γ-Cyclodextrins in Dry and Wet Conditions, from Monomers to Crystal Structures: A Quantum-Mechanical Study. International Journal of Molecular Sciences, 24(23), 16826. https://doi.org/10.3390/ijms242316826








