Diffusion/Reaction Limited Aggregation Approach for Microstructure Evolution and Condensation Kinetics during Synthesis of Silica-Based Alcogels
Abstract
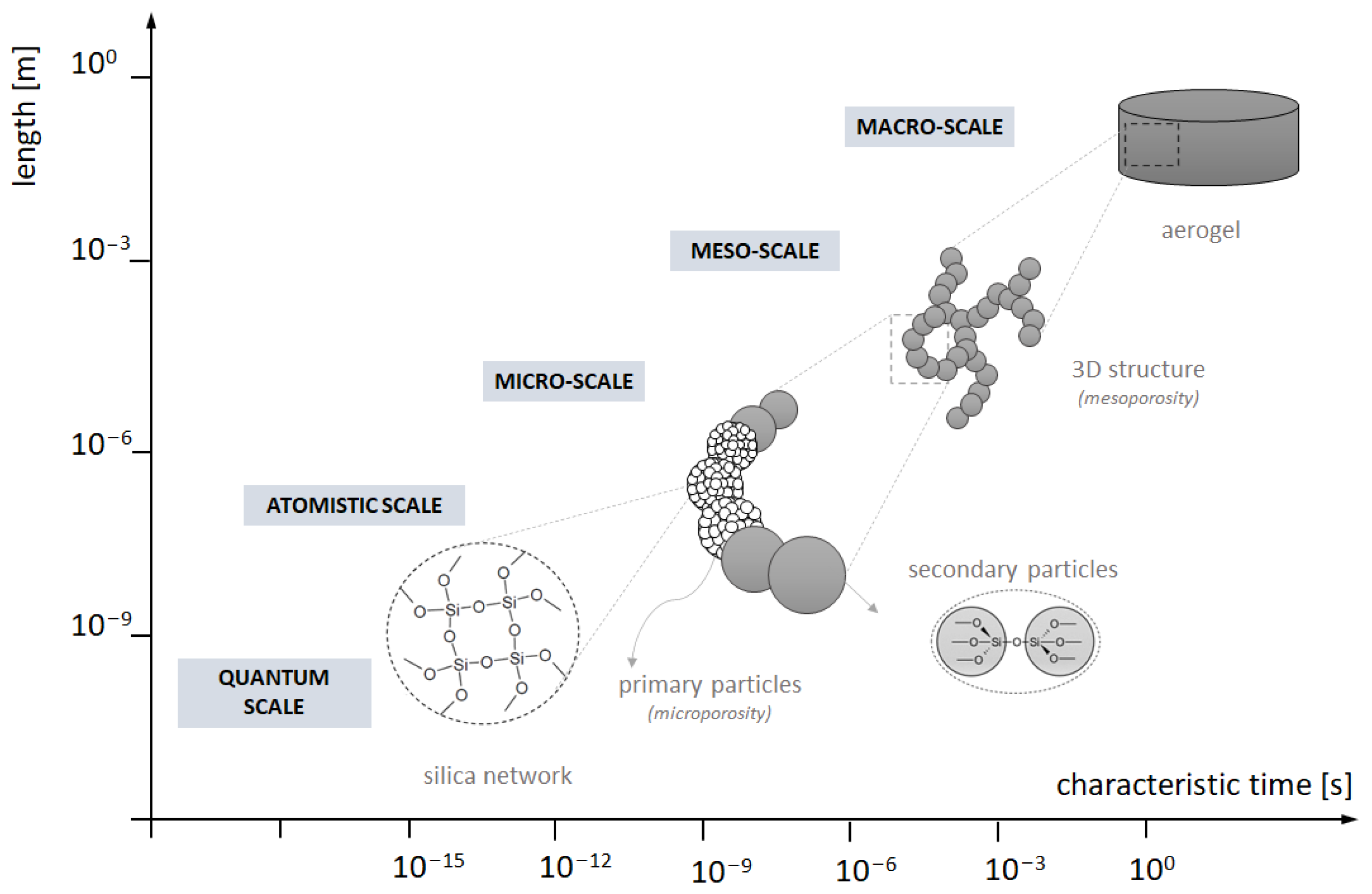
:1. Introduction
2. Results
2.1. Estimation of Model Parameters
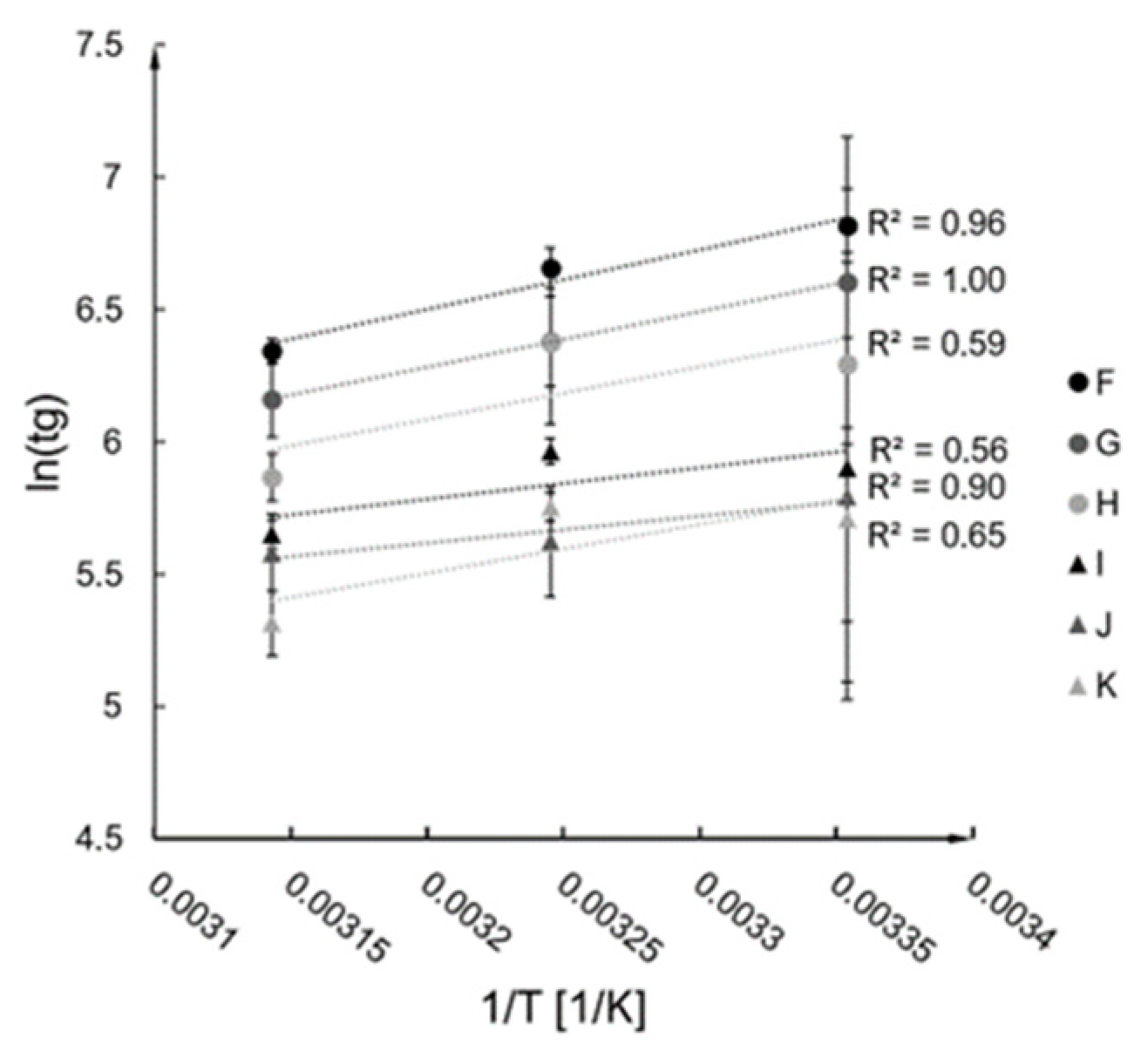
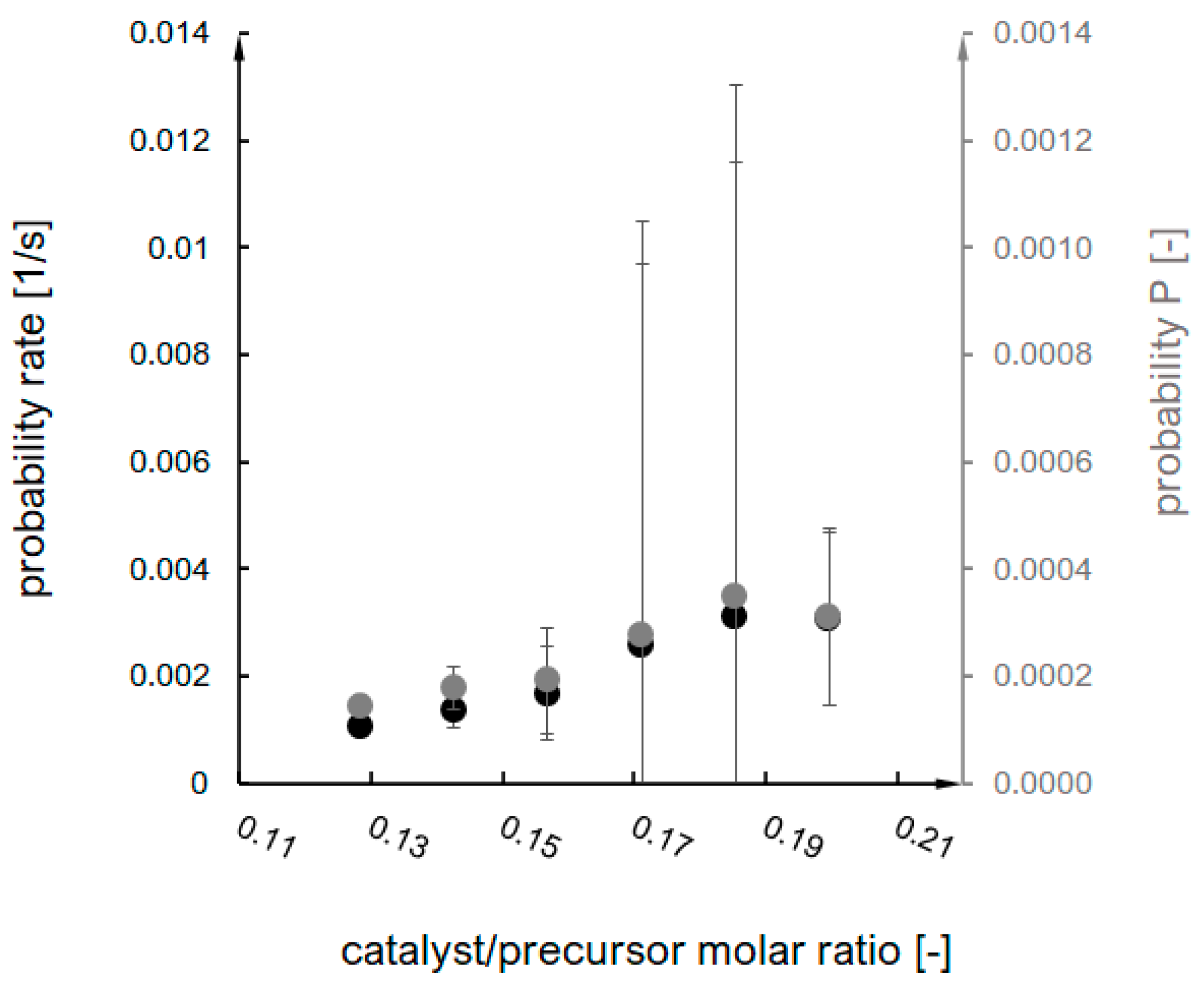
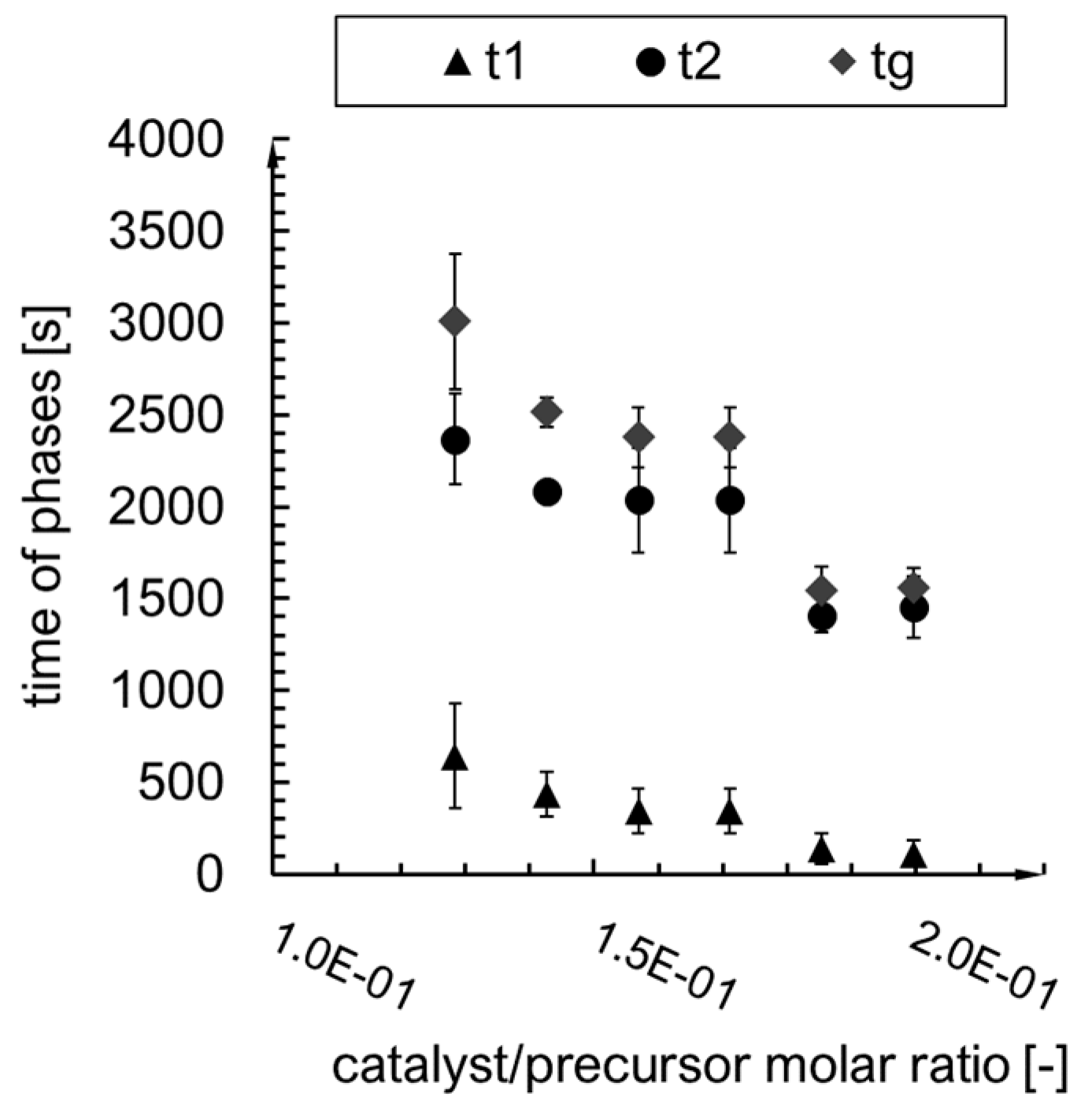
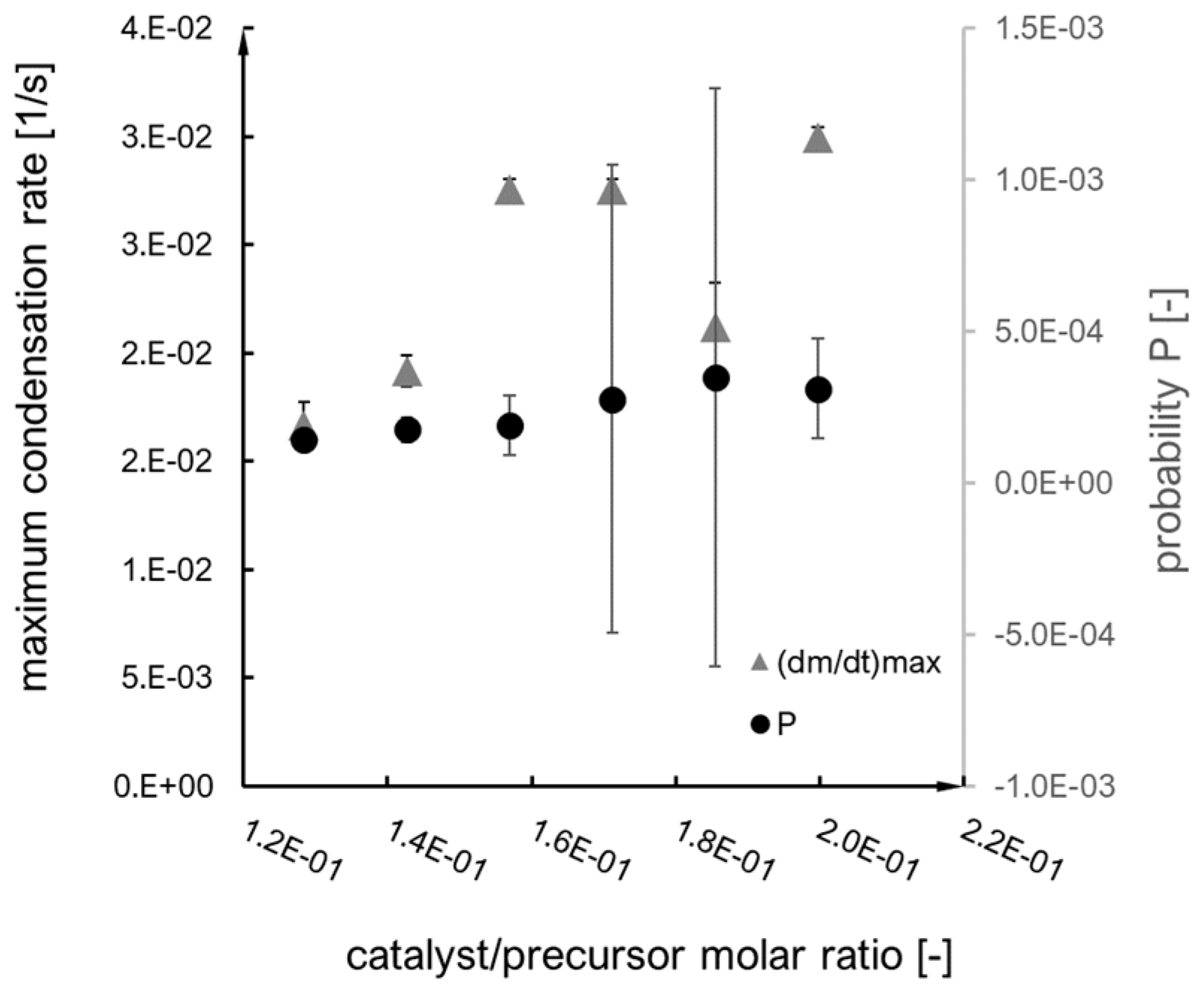
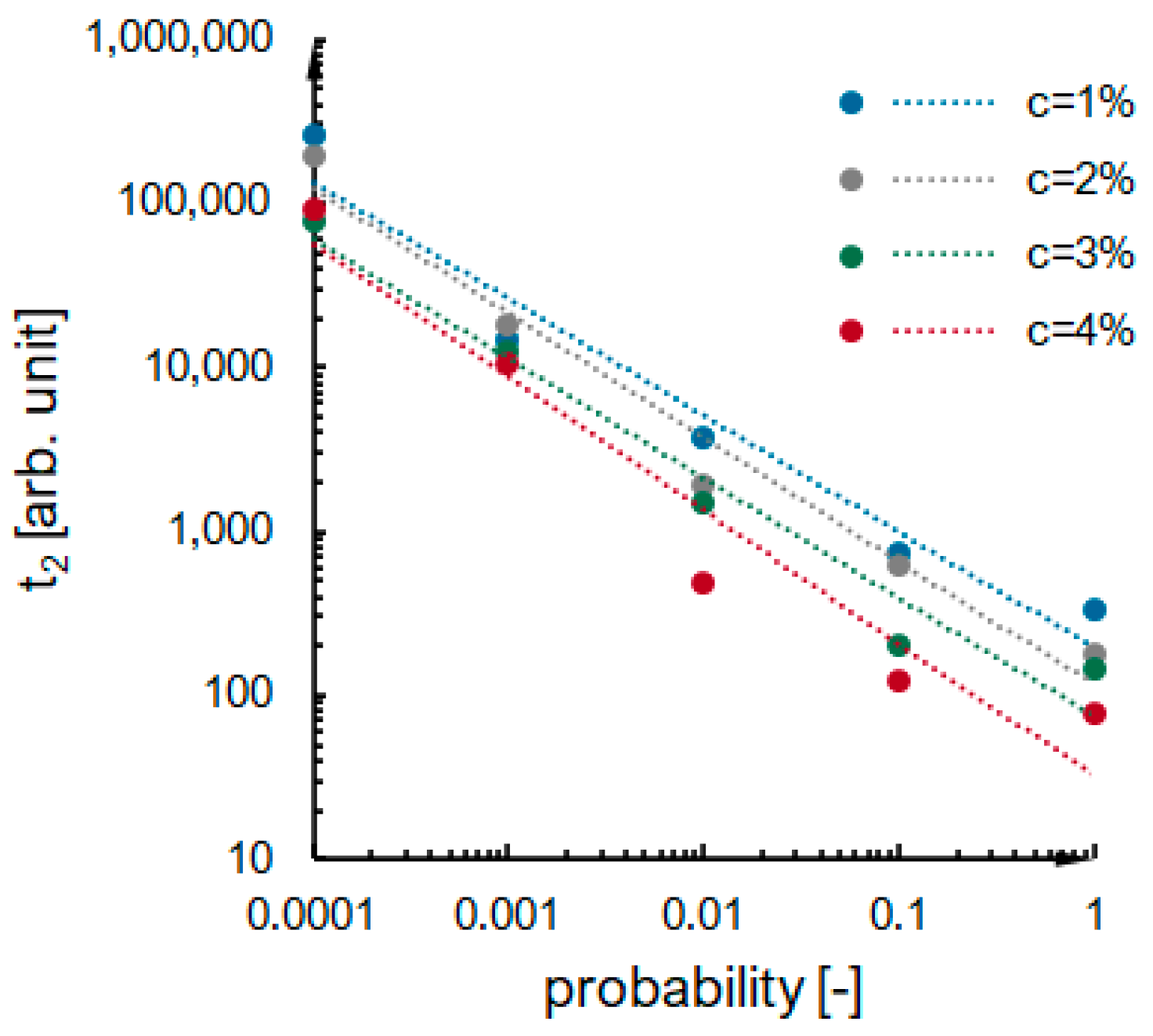
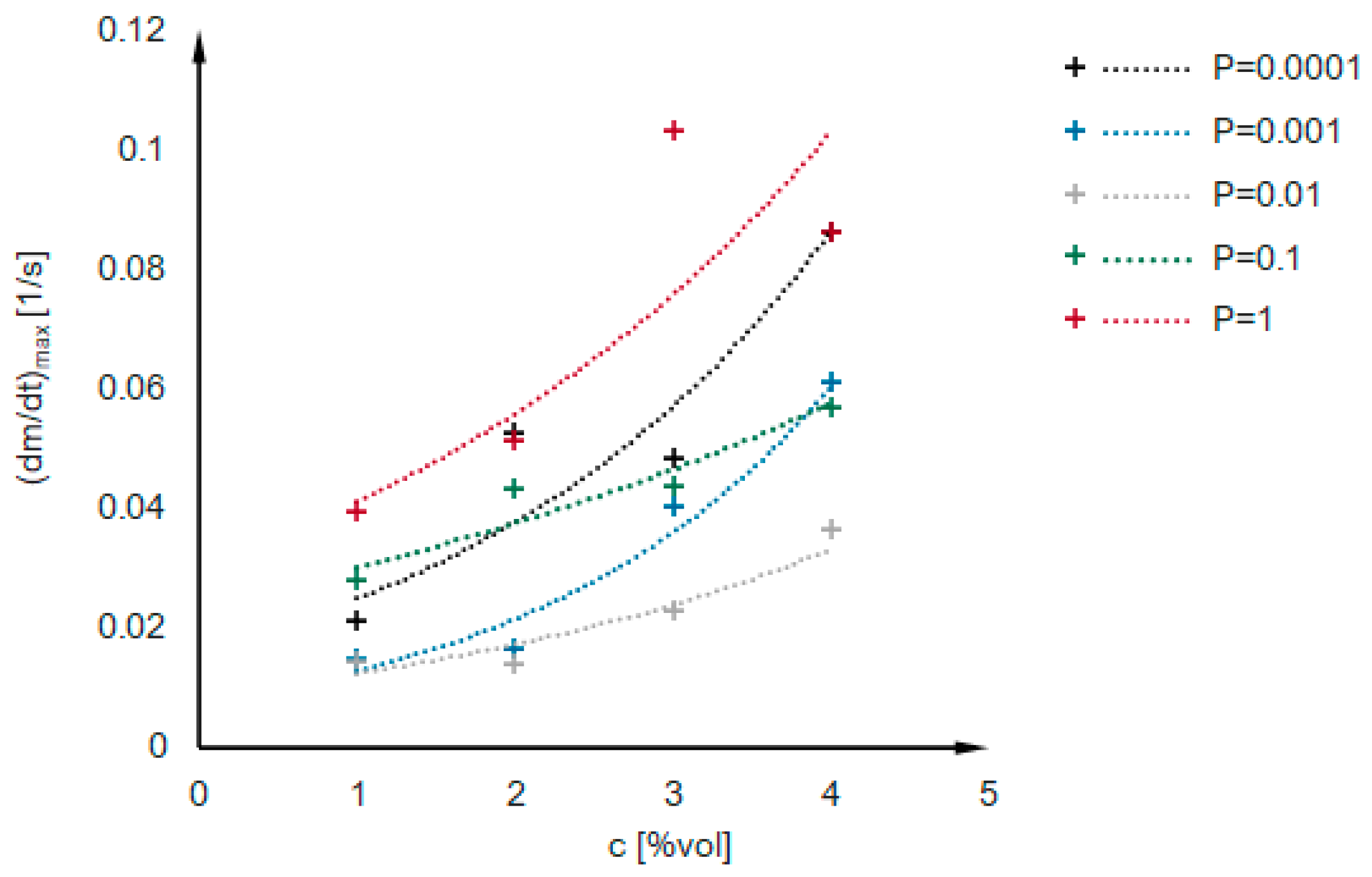
2.2. Kinetics Analysis
- i.
- The value of the maximum condensation rate ;
- ii.
- The time corresponding to the occurrence of the maximum rate;
- iii.
- The “span” of the first derivative’s peak.
- i.
- The probability of an effective collision increases;
- ii.
- The concentration of secondary particles increases.
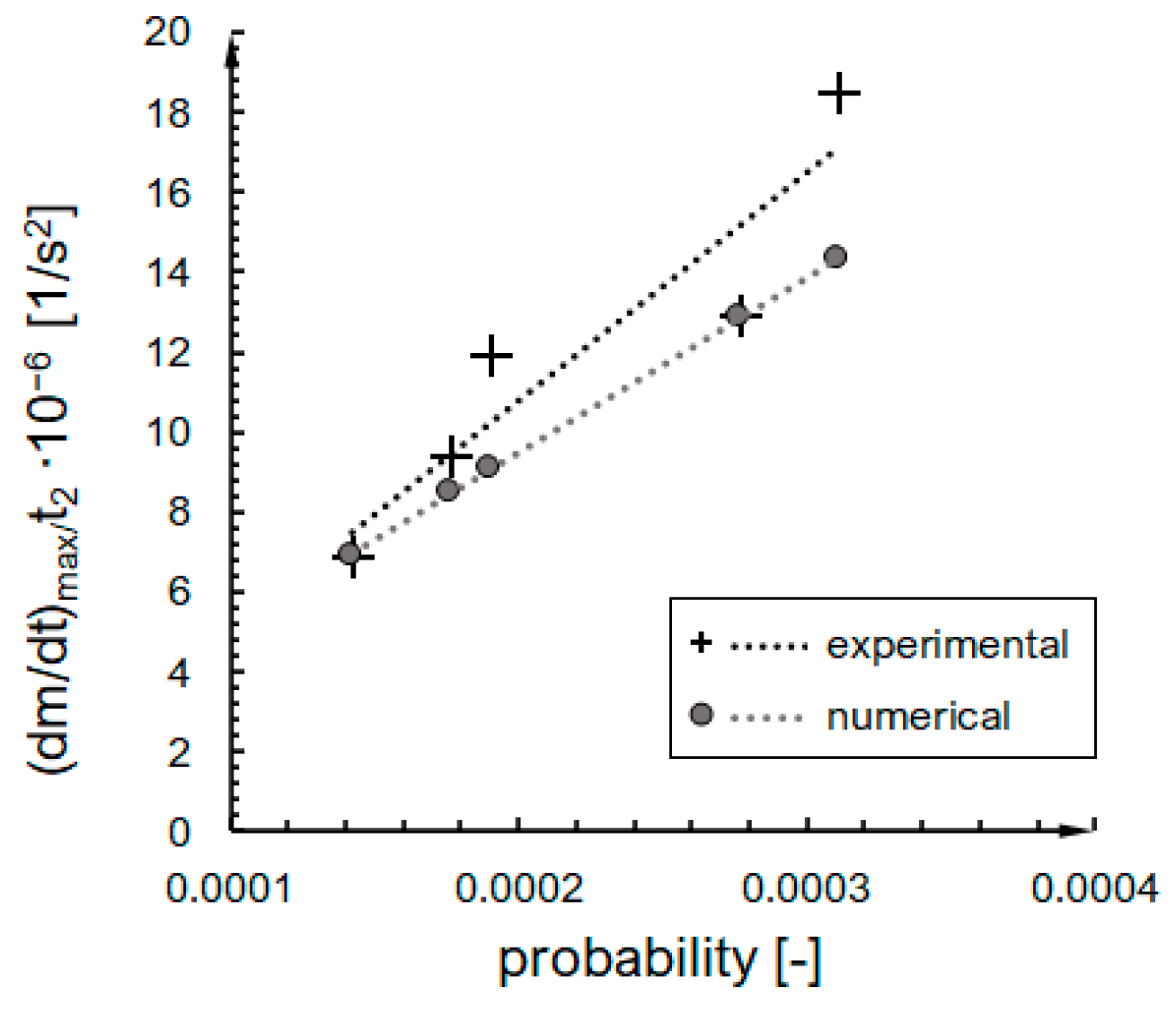
2.3. Verification of Kinetics
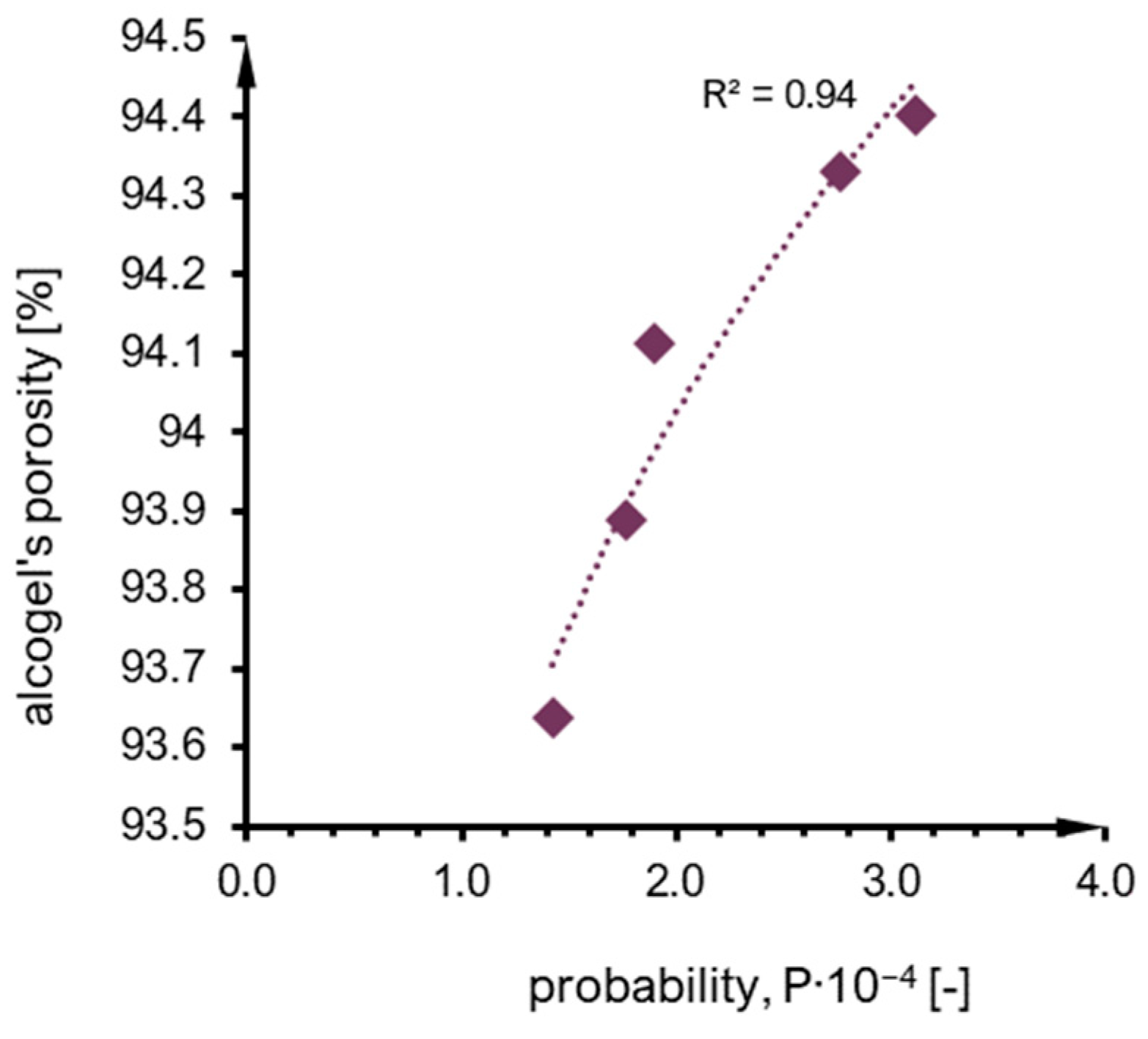
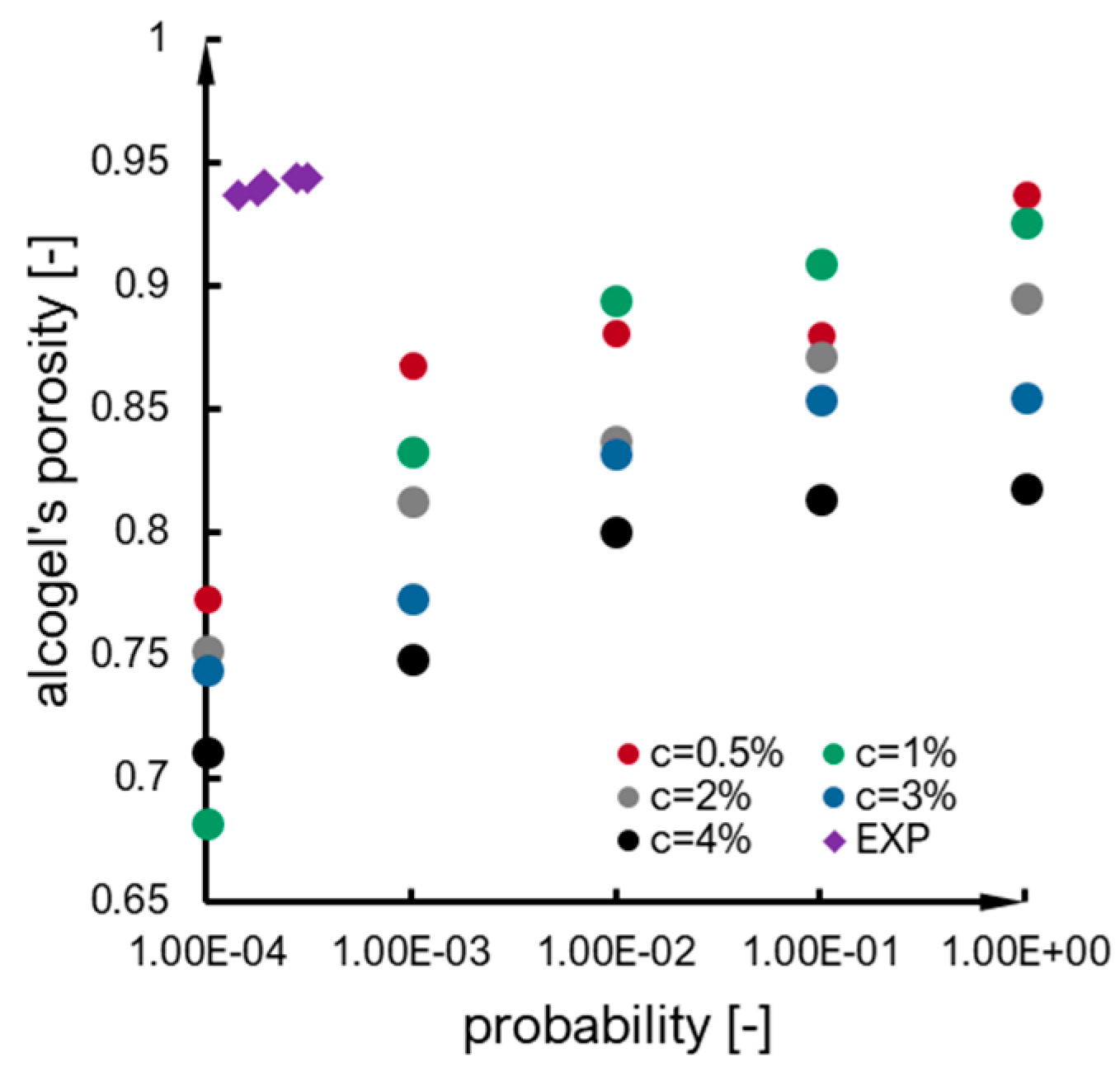
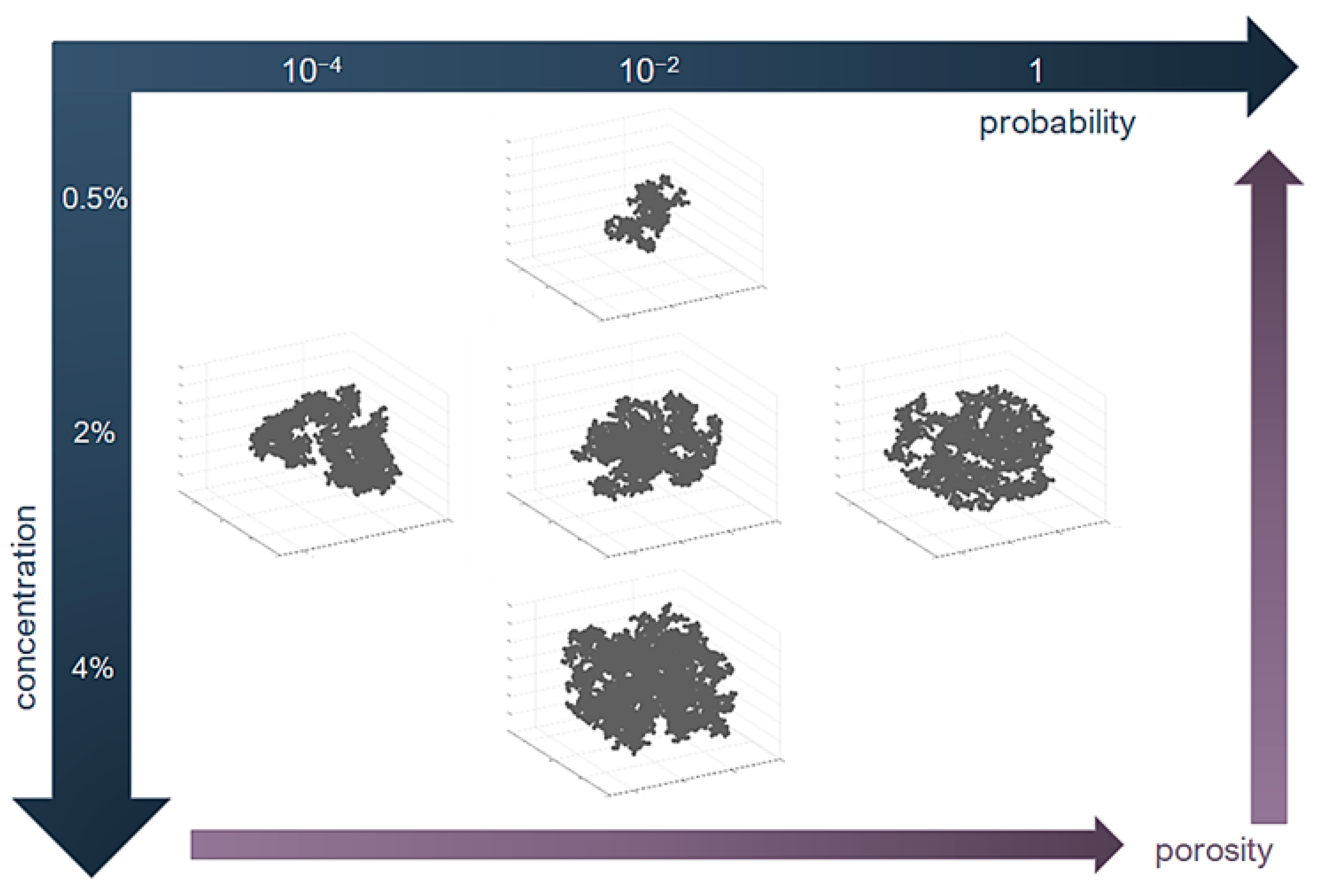
2.4. Structure
3. Discussion
4. Materials and Methods
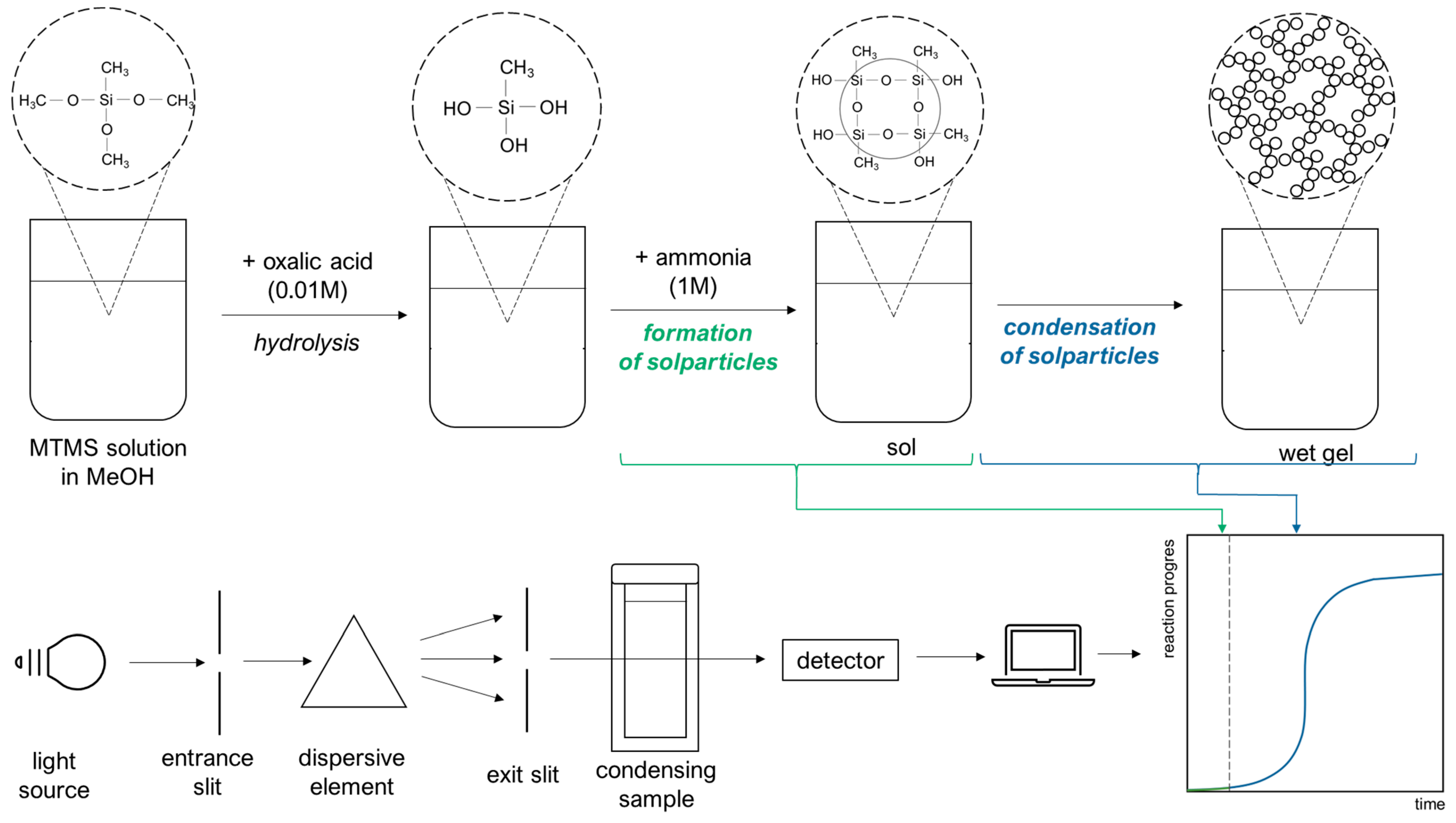
4.1. Experimental
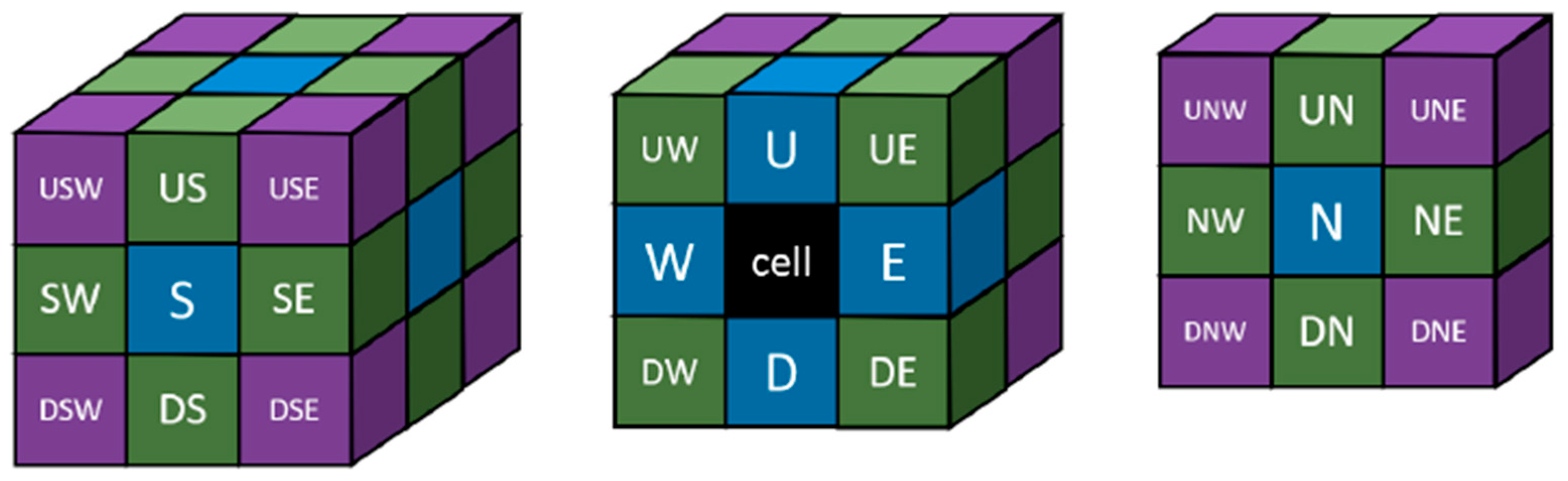
4.2. Numerical Model Description
4.3. Kinetics Simulation
4.4. Structural Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B

References
- Yamahara, K.; Okazaki, K. Molecular Dynamics Simulation of the Structural Development in Sol-Gel Process for Silica Systems. Fluid Phase Equilib. 1998, 144, 449–459. [Google Scholar] [CrossRef]
- Issa, A.A.; Luyt, A.S. Kinetics of Alkoxysilanes and Organoalkoxysilanes Polymerization: A Review. Polymers 2019, 11, 537. [Google Scholar] [CrossRef] [Green Version]
- Innocenzi, P. The Sol-to-Gel Transition; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 9783030200299. [Google Scholar]
- Dong, H.; Brook, M.A.; Brennan, J.D. A New Route to Monolithic Methylsilsesquioxanes: Gelation Behavior of Methyltrimethoxysilane and Morphology of Resulting Methylsilsesquioxanes under One-Step and Two-Step Processing. Chem. Mater. 2005, 17, 2807–2816. [Google Scholar] [CrossRef]
- Hüsing, N.; Schubert, U. Aerogels—Airy Materials: Chemistry, Structure, and Properties. Angew. Chem. Int. Ed. 1998, 37, 22–45. [Google Scholar] [CrossRef]
- Roy, R. Ceramics by the Solution-Sol-Gel Route. Science 1987, 238, 1664–1669. [Google Scholar] [CrossRef]
- Deshmukh, K.; Kovářík, T.; Křenek, T.; Docheva, D.; Stich, T.; Pola, J. Recent Advances and Future Perspectives of Sol-Gel Derived Porous Bioactive Glasses: A Review. RSC Adv. 2020, 10, 33782–33835. [Google Scholar] [CrossRef] [PubMed]
- Brinker, C.J.; Hurd, A.J.; Schunk, P.R.; Frye, G.C.; Ashley, C.S. Review of Sol-Gel Thin Film Formation. J. Non-Cryst. Solids 1992, 147–148, 424–436. [Google Scholar] [CrossRef] [Green Version]
- Minami, T. Advanced Sol-Gel Coatings for Practical Applications. J. Sol-Gel Sci. Technol. 2013, 65, 4–11. [Google Scholar] [CrossRef]
- Kloskowski, A.; Pilarczyk, M.; Chrzanowski, W.; Namieśnik, J. Sol-Gel Technique—A Versatile Tool for Adsorbent Preparation. Crit. Rev. Anal. Chem. 2010, 40, 172–186. [Google Scholar] [CrossRef]
- Jelle, B.P.; Baetens, R.; Gustavsen, A. Aerogel Insulation for Building Applications. In The Sol-Gel Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2015; Volume 3. [Google Scholar]
- Aegerter, M.A.; Leventis, N.; Koebel, M.M. (Eds.) Aerogels Handbook; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Brinker, C.J.; Scherer, G.W. Sol-Gel Science The physics and Chemistry of Sol-Gel Processing; Academic Press, Inc.: San Diego, CA, USA, 1990; p. 462. [Google Scholar]
- Nakanishi, K.; Kanamori, K. Organic-Inorganic Hybrid Poly(Silsesquioxane) Monoliths with Controlled Macro- and Mesopores. J. Mater. Chem. 2005, 15, 3776–3786. [Google Scholar] [CrossRef]
- Itagaki, A.; Nakanishi, K.; Hirao, K. Phase Separation in Sol-Gel System Containing Mixture of 3- and 4-Functional Alkoxysilanes. J. Sol-Gel Sci. Technol. 2003, 26, 153–156. [Google Scholar] [CrossRef]
- Kaji, H.; Nakanishi, K.; Soga, N. Polymerization-Induced Phase Separation in Silica Sol-Gel Systems Containing Formamide. J. Sol-Gel Sci. Technol. 1993, 1, 35–46. [Google Scholar] [CrossRef]
- Chateau, D.; Liotta, A.; Lundén, H.; Lerouge, F.; Chaput, F.; Krein, D.; Cooper, T.; Lopes, C.; El-Amay, A.A.G.; Lindgren, M.; et al. Long Distance Enhancement of Nonlinear Optical Properties Using Low Concentration of Plasmonic Nanostructures in Dye Doped Monolithic Sol–Gel Materials. Adv. Funct. Mater. 2016, 26, 6005–6014. [Google Scholar] [CrossRef]
- Pawlik, N.; Szpikowska-Sroka, B.; Goryczka, T.; Pisarski, W.A. Studies of Sol-Gel Evolution and Distribution of Eu3+ Ions in Glass–Ceramics Containing Laf3 Nanocrystals Depending on Initial Sols Composition. Int. J. Mol. Sci. 2021, 22, 996. [Google Scholar] [CrossRef] [PubMed]
- Barrulas, R.V.; López-Iglesias, C.; Zanatta, M.; Casimiro, T.; Mármol, G.; Carrott, M.R.; García-González, C.A.; Corvo, M.C. The AEROPILs Generation: Novel Poly(Ionic Liquid)-based Aerogels for CO2 Capture. Int. J. Mol. Sci. 2022, 23, 200. [Google Scholar] [CrossRef] [PubMed]
- Kubicka, M.; Bakierska, M.; Chudzik, K.; Świętosławski, M.; Molenda, M. Nitrogen-Doped Carbon Aerogels Derived from Starch Biomass with Improved Electrochemical Properties for Li-Ion Batteries. Int. J. Mol. Sci. 2021, 22, 9918. [Google Scholar] [CrossRef] [PubMed]
- Babiarczuk, B.; Lewandowski, D.; Szczurek, A.; Kierzek, K.; Meffert, M.; Gerthsen, D.; Kaleta, J.; Krzak, J. Novel Approach of Silica-PVA Hybrid Aerogel Synthesis by Simultaneous Sol-Gel Process and Phase Separation. J. Supercrit. Fluids 2020, 166, 104997. [Google Scholar] [CrossRef]
- Pruna, A.; Cárcel, A.; Benedito, A.; Giménez, E. Article Hydrothermal-Freeze-Casting of Poly(Amidoamine)-Modified Graphene Aerogels towards CO2 Adsorption. Int. J. Mol. Sci. 2021, 22, 9333. [Google Scholar] [CrossRef]
- Narayan, R.; Laberty-Robert, C.; Pelta, J.; Tarascon, J.M.; Dominko, R. Self-Healing: An Emerging Technology for Next-Generation Smart Batteries. Adv. Energy Mater. 2022, 12, 2102652. [Google Scholar] [CrossRef]
- Mo, F.; Li, H.; Pei, Z.; Liang, G.; Ma, L.; Yang, Q.; Wang, D.; Huang, Y.; Zhi, C. A Smart Safe Rechargeable Zinc Ion Battery Based on Sol-Gel Transition Electrolytes. Sci. Bull. 2018, 63, 1077–1086. [Google Scholar] [CrossRef]
- Fu, L.J.; Liu, H.; Li, C.; Wu, Y.P.; Rahm, E.; Holze, R.; Wu, H.Q. Electrode Materials for Lithium Secondary Batteries Prepared by Sol-Gel Methods. Prog. Mater. Sci. 2005, 50, 881–928. [Google Scholar] [CrossRef]
- Lim, J.; Malati, P.; Bonet, F.; Dunn, B. Nanostructured Sol-Gel Electrodes for Biofuel Cells. J. Electrochem. Soc. 2007, 154, A140–A145. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, X.; Du, S.; Wang, J.; Dong, J.; Wu, D. Facile Synthesis of Highly Active Ti/Sb-SnO2 Electrode by Sol-Gel Spinning Technique for Landfill Leachate Treatment. Water Sci. Technol. 2021, 84, 1366–1378. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.; Li, D.; Fedorovskaya, E.O.; Kallio, T.; Ren, X. New Insights in Al-Doping Effects on the LiNiO2 Positive Electrode Material by a Sol-Gel Method. Int. J. Energy Res. 2021, 45, 10489–10499. [Google Scholar] [CrossRef]
- Reddy, R.N.; Reddy, R.G. Sol-Gel MnO2 as an Electrode Material for Electrochemical Capacitors. J. Power Sources 2003, 124, 330–337. [Google Scholar] [CrossRef]
- Carvalho, R.N.L.; Cordas, C.M.; da Fonseca, L.J.P. Electrode Kinetics of Ion Jelly and Ion Sol-Gel Redox Materials on Screen-Printed Electrodes. Appl. Sci. 2022, 12, 2087. [Google Scholar] [CrossRef]
- Ratke, L.; Hajduk, A. On the Size Effect of Gelation Kinetics in Rf Aerogels. Gels 2015, 1, 276–290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziff, R.M.; Ernst, M.H.; Hendriks, E.M. Kinetics of Gelation and Universality. J. Phys. A Gen. Phys. 1983, 16, 2293–2320. [Google Scholar] [CrossRef]
- Jiang, Y.; Gang, H.; Benkun, M. Critical Property and Universality in the Generalised Smoluchovski Coagulation Equation. Phys. Rev. B 1990, 41, 9424–9429. [Google Scholar] [CrossRef]
- Mellema, M.; van Opheusden, J.H.J.; van Vliet, T. Relating Colloidal Particle Interactions to Gel Structure Using Brownian Dynamics Simulations and the Fuchs Stability Ratio. J. Chem. Phys. 1999, 111, 6129–6135. [Google Scholar] [CrossRef]
- Whittle, M.; Dickinson, E. Brownian Dynamics Simulation of Gelation in Soft Sphere Systems with Irreversible Bond Formation. Mol. Phys. 1997, 90, 739–758. [Google Scholar] [CrossRef]
- Gelb, L.D. Simulating Silica Aerogels with a Coarse-Grained Flexible Model and Langevin Dynamics. J. Phys. Chem. C 2007, 111, 15792–15802. [Google Scholar] [CrossRef]
- Ferreiro-Rangel, C.A.; Gelb, L.D. Investigation of the Bulk Modulus of Silica Aerogel Using Molecular Dynamics Simulations of a Coarse-Grained Model. J. Phys. Chem. B 2013, 117, 7095–7105. [Google Scholar] [CrossRef]
- Depta, P.N.; Gurikov, P.; Schroeter, B.; Forgács, A.; Kalmár, J.; Paul, G.; Marchese, L.; Heinrich, S.; Dosta, M. DEM-Based Approach for the Modeling of Gelation and Its Application to Alginate. J. Chem. Inf. Model. 2022, 62, 49–70. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.E.; Wilcoxon, J.; Adolf, D. Critical Exponents for the Sol-Gel Transition. Phys. Rev. A 1987, 36, 1803–1810. [Google Scholar] [CrossRef] [PubMed]
- Shibayama, M. Gel Formation Analyses by Dynamic Light Scattering. Bull. Chem. Soc. Jpn. 2002, 75, 641–659. [Google Scholar] [CrossRef]
- Hsieh, K.; Lallet, F.; Olivi-Tran, N. DLCA and Langevin Dynamics Approaches of Sol Gel Transition: A Comparison via the Fractal Dimension during Aggregation. Fractals 2008, 16, 361–365. [Google Scholar] [CrossRef]
- Abdusalamabov, R.; Itskov, M.; Milow, B.; Reichenauer, G.; Rege, A. Investigation of the Fractal Properties of Aerogels by Di Usion-Limited Aggregation Models. In Proceedings of the 8th GACM Colloquium on Computational Mechanics: For Young Scientists from Academia and Industry, Kassel, Germany, 28–30 August 2019. [Google Scholar]
- Weitz, D.A.; Huang, J.S.; Lin, M.Y.; Sung, J. Dynamics of Diffusion-Limited Kinetic Aggregation. Phys. Rev. Lett. 1984, 53, 1657–1660. [Google Scholar] [CrossRef]
- Borzęcka, N.H.; Kozłowska, I.; Gac, J.M.; Bojarska, M. Anti-Fouling Properties of Poly(Acrylic Acid) Grafted Ultrafiltration Membranes—Experimental and Theoretical Study. Appl. Surf. Sci. 2019, 506, 144658. [Google Scholar] [CrossRef]
- Borzęcka, N.H.; Nowak, B.; Pakuła, R.; Przewodzki, R.; Gac, J.M. Cellular Automata Modeling of Silica Aerogel Condensation Kinetics. Gels 2021, 7, 50. [Google Scholar] [CrossRef]
- Morales, R.V.; da Cunha, C.R.; Rambo, C.R. A Complex Network Approach for the Growth of Aerogels. Phys. A Stat. Mech. Its Appl. 2014, 406, 131–138. [Google Scholar] [CrossRef] [Green Version]
- Garofalini, S.H.; Martin, G. Molecular Simulations of the Polymerization of Silicic Acid Molecules and Network Formation. J. Phys. Chem. 1994, 98, 1311–1316. [Google Scholar] [CrossRef]
- Pereira, J.C.G.; Catlow, C.R.A.; Price, G.D. Molecular Dynamics Simulation of Methanolic and Ethanolic Silica-Based Sol-Gel Solutions at Ambient Temperature and Pressure. J. Phys. Chem. A 2002, 106, 130–148. [Google Scholar] [CrossRef]
- Elanany, M.; Selvam, P.; Yokosuka, T.; Takami, S.; Kubo, M.; Imamura, A.; Miyamoto, A. A Quantum Molecular Dynamics Simulation Study of the Initial Hydrolysis Step in Sol-Gel Process. J. Phys. Chem. B 2003, 107, 1518–1524. [Google Scholar] [CrossRef]
- Bałdyga, J.; Tyl, G.; Bouaifi, M. Aggregation Efficiency of Amorphous Silica Nanoparticles. Chem. Eng. Technol. 2019, 42, 1717–1724. [Google Scholar] [CrossRef]
- Aniszewska, D.; Rybaczuk, M. Mechanical Properties of Silica Aerogels Modelled by Movable Cellular Automata Simulations. Mater. Today Commun. 2021, 27, 102432. [Google Scholar] [CrossRef]
- Smolin, A.Y.; Shilko, E.V.; Astafurov, S.V.; Konovalenko, I.S.; Buyakova, S.P.; Psakhie, S.G. Modeling Mechanical Behaviors of Composites with Various Ratios of Matrix–Inclusion Properties Using Movable Cellular Automaton Method. Def. Technol. 2015, 11, 18–34. [Google Scholar] [CrossRef] [Green Version]
- Scalise, D.; Schulman, R. Emulating Cellular Automata in Chemical Reaction–Diffusion Networks. Nat. Comput. 2016, 15, 197–214. [Google Scholar] [CrossRef]
- Davies, C.H.J. Growth of Nuclei in a Cellular Automaton Simulation of Recrystallisation. Scr. Mater. 1997, 36, 35–40. [Google Scholar] [CrossRef]
- Wessling, B. Cellular Automata Simulation of Dissipative Structure Formation in Heterogeneous Polymer Systems, Formation of Networks of a Dispersed Phase by Flocculation. J. Phys. II 1996, 6, 395–404. [Google Scholar] [CrossRef]
- Ponton, A.; Warlus, S.; Griesmar, P. Rheological Study of the Sol-Gel Transition in Silica Alkoxides. J. Colloid Interface Sci. 2002, 249, 209–216. [Google Scholar] [CrossRef] [PubMed]
- Rao, A.V.; Bhagat, S.D.; Hirashima, H.; Pajonk, G. Synthesis of flexible silica aerogels using methyltrimethoxysilane (MTMS) precursor. J. Colloid Interface Sci. 2006, 300, 279–285. [Google Scholar] [CrossRef] [PubMed]
- Boonstra, A.H.; Bernards, T.N.M. The Dependence of the Gelation Time on the Hydrolysis Time in a Two-Step SiO2 Sol-Gel Process. J. Non-Cryst. Solids 1988, 105, 207–213. [Google Scholar] [CrossRef]
- Taylor, S.J.; Haw, M.D.; Sefcik, J.; Fletcher, A.J. Monitoring the Gelation Mechanism of Resorcinol-Formaldehyde Gels by Dynamic Light Scattering. Langmuir 2014, 30, 10231–10240. [Google Scholar] [CrossRef] [Green Version]
- Gaca, K.Z.; Sefcik, J. Mechanism and Kinetics of Nanostructure Evolution during Early Stages of Resorcinol-Formaldehyde Polymerisation. J. Colloid Interface Sci. 2013, 406, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Borzęcka, N.H.; Nowak, B.; Gac, J.M.; Głaz, T.; Bojarska, M. Kinetics of MTMS-Based Aerogel Formation by the Sol-Gel Method—Experimental Results and Theoretical Description. J. Non-Cryst. Solids 2020, 547, 120310. [Google Scholar] [CrossRef]
- Maleki, H. Recent Advances in Aerogels for Environmental Remediation Applications. Chem. Eng. J. 2016, 300, 98–118. [Google Scholar] [CrossRef]
- Kier, L.B.; Seybold, P.G.; Cheng, C.-K. Cellular Automata Modeling of Chemical Systems a Textbook and Laboratory Manual; Springer: Dordrecht, The Netherlands, 2005; ISBN 9781402036576. [Google Scholar]



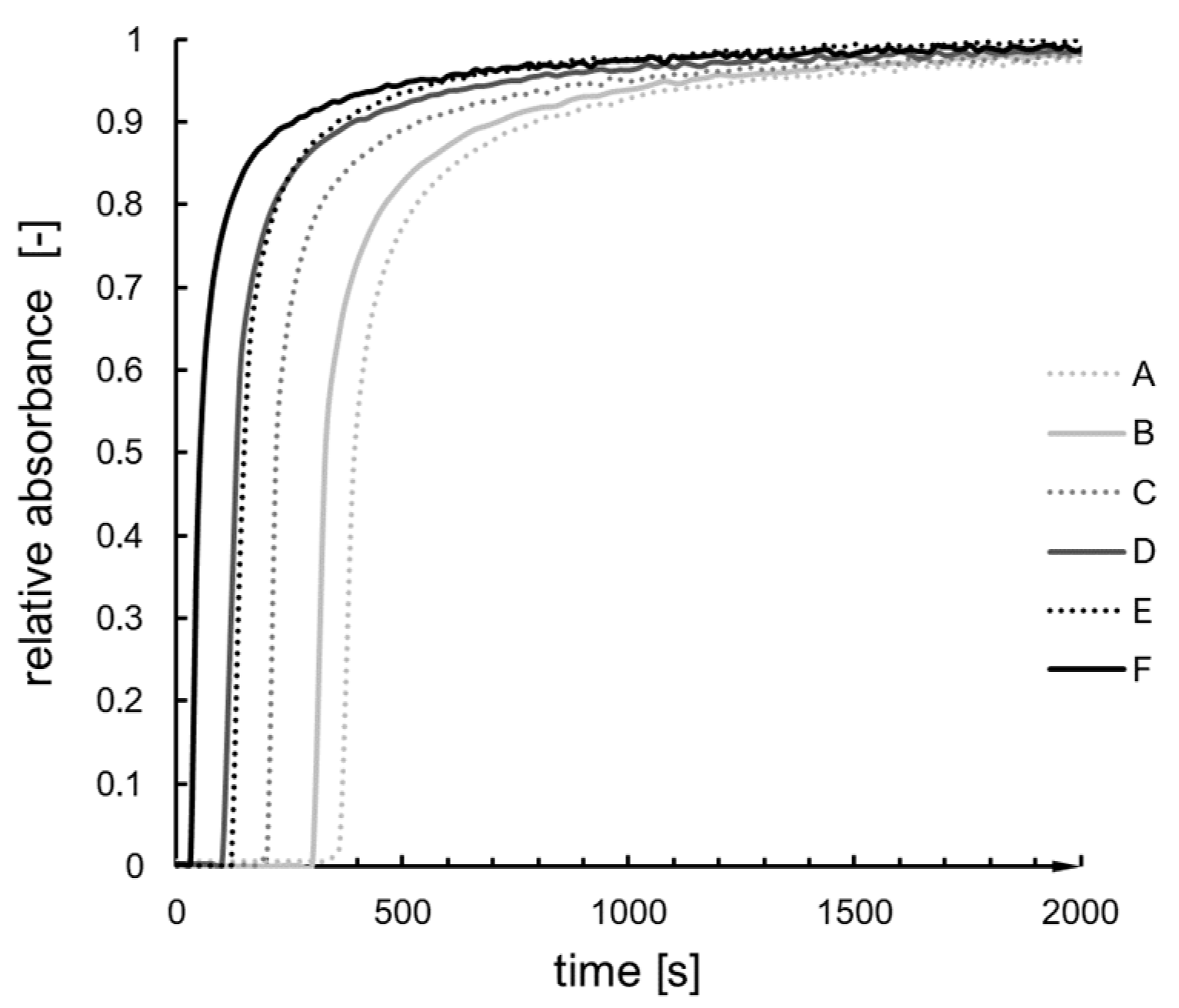
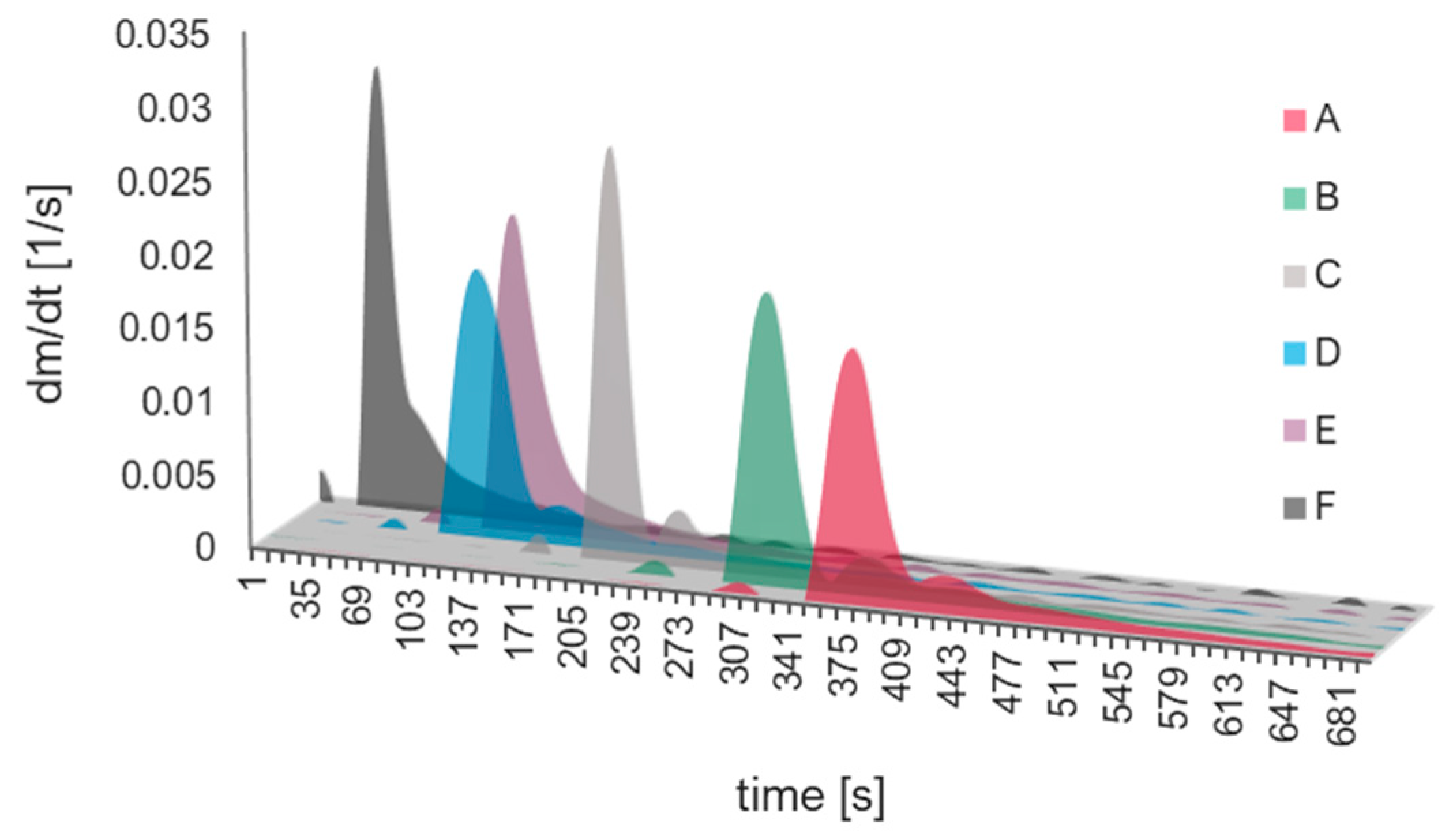


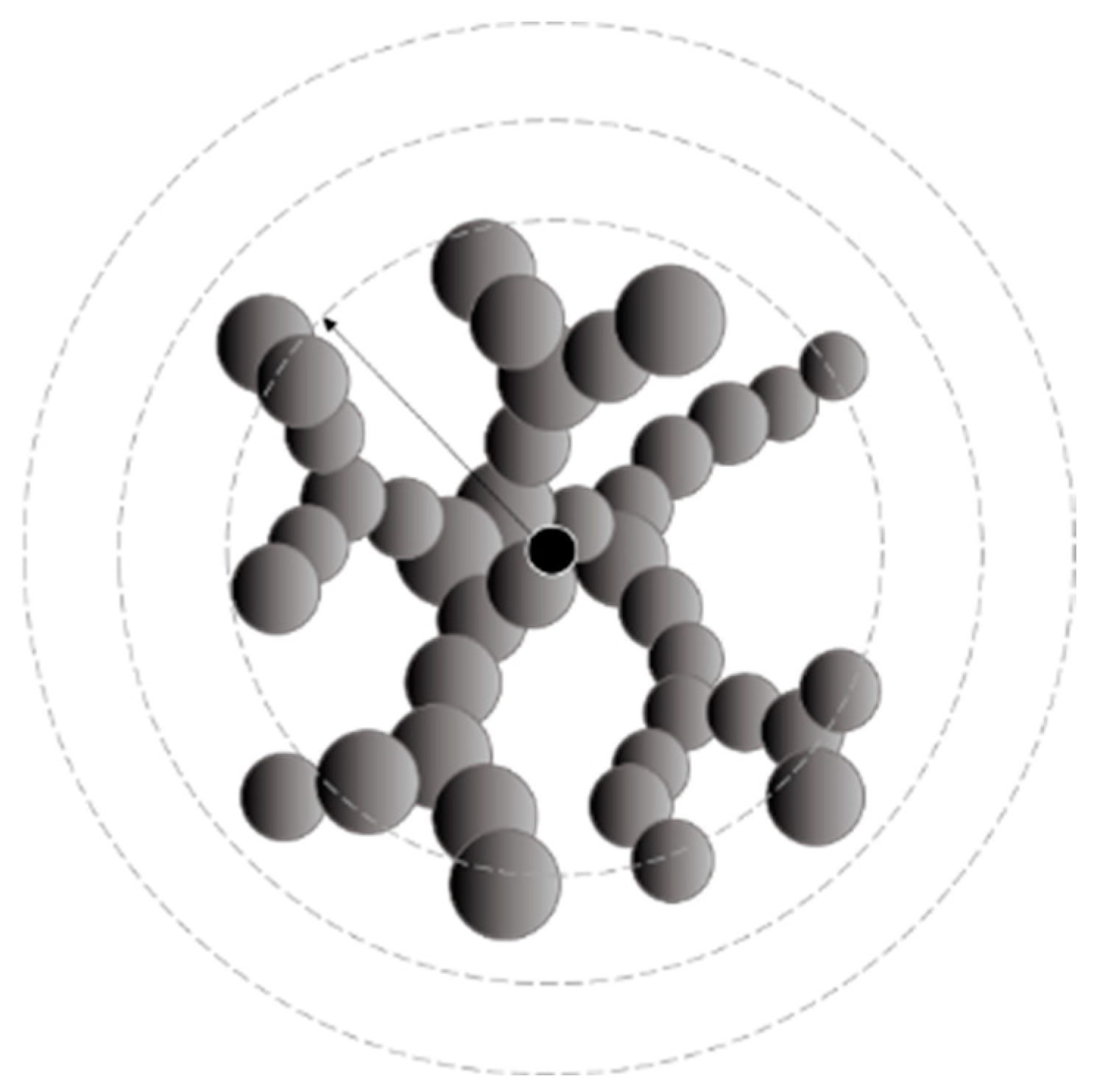
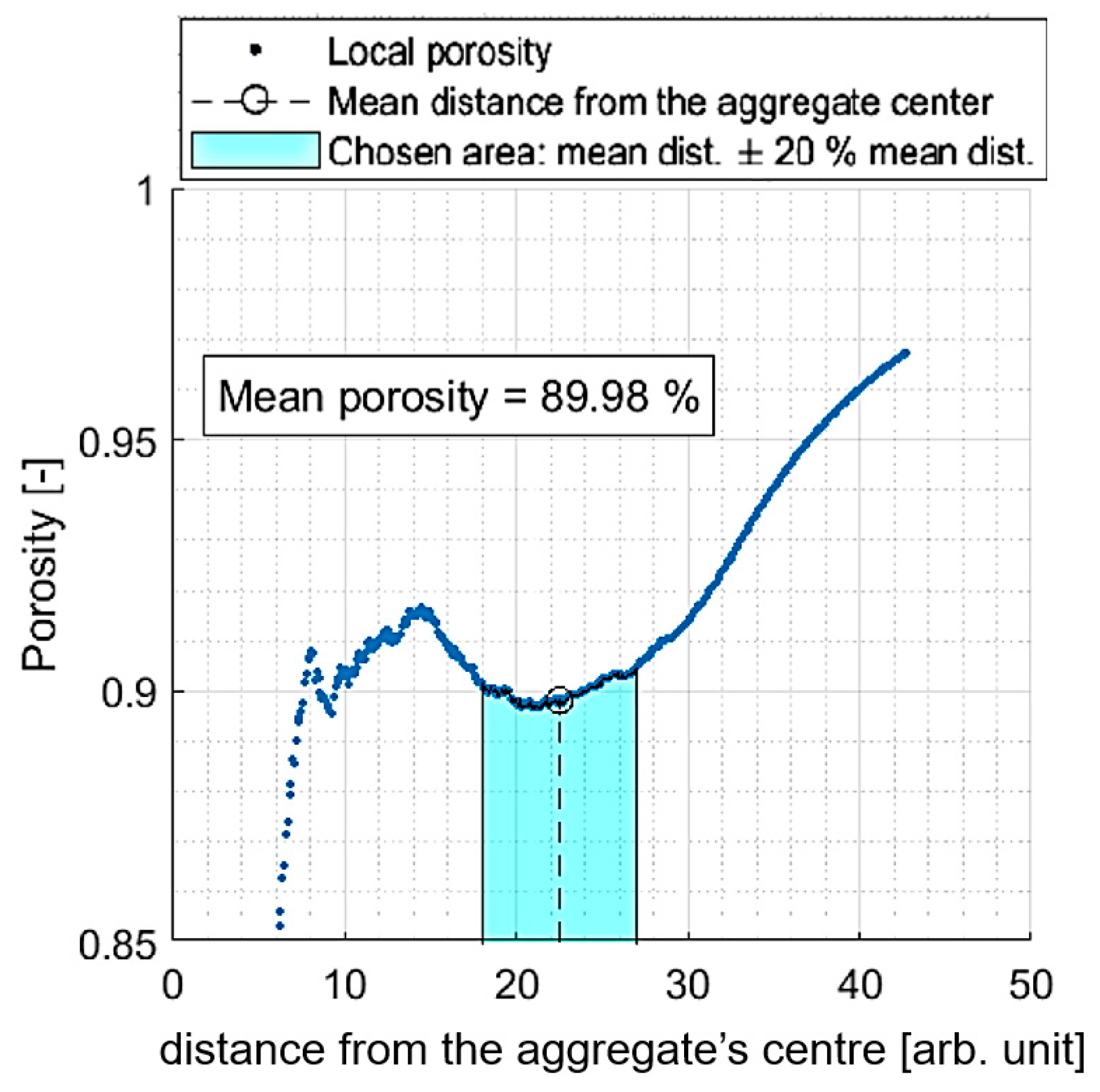
| A (1-2-0.9-0.9) | B (1-2-1-1) | C (1-2-1.1-1.1) | |||
 |  |  | |||
| D (1-2-1.2-1.2) | E (1-2-1.3-1.3) | F (1-2-1.4-1.4) | |||
 |  |  | |||
| Condensation Kinetics Phases | Prevailing Mechanism of Structure Growth | |
|---|---|---|
| Experimental | Numerical | |
| 1 nucleation | mechanism A | - (not considered in the model) |
| 2 intensive mass growth (microscopic phase separation) phase | mechanism B | |
| 3 cluster–cluster gelation (plateau) | mechanism C | |
| Approach | Established Dependence | Coefficient of Determination |
|---|---|---|
| (a) Experimental | ||
| (b) Numerical |
| Source | Precursor | Reference | |
|---|---|---|---|
| This paper | methyltrimethoxysilane (MTMS) | 2.6–37.6 | - |
| A. Ponton et al. (2002) | tetramethoxysilane (TMOS) | 37.1–38.2 | [56] |
| C.J. Brinker and G.W. Scherer (1990) | general data for silica precursors | 42–84 | [13] |
| Parameter | Experimental | Numerical |
|---|---|---|
| RLCA, Narrow Range | RLCA–DLCA, Very Wide Range | |
| Decreases (linearly) with an increase in the molar ratio Decreases with an increase in the probability (estimated based on Arrhenius eq.) | No data | |
| Decreases (most likely in an exponential manner; power and linear functions are also a good approximation) with an increase in both the molar ratio and . | Decrease in power function manner with the increase in probability. | |
| Decreases with an increase in both and P. Exponential and power trendlines are a good fit. However, we use an exponential approximation for the designation of E, | Decrease in power function of . | |
| Increases (but not constantly) with or . | Seems to increase with concentration and P but in an unclear or constant manner. |
| Synthesis Denotation | MTMS/MeOH Vol. Ratio | Acid/MTMS Vol. Ratio | Base/MTMS Vol. Ratio | Moles | ||||
|---|---|---|---|---|---|---|---|---|
| MTMS | MeOH | Water | Acid | Base | ||||
| A | 1:2 | 0.9 | 0.9 | 0.0069 | 0.049 | 0.050 | 1.2 × 10−9 | 5.9 × 10−8 |
| B | 1.0 | 1.0 | 0.055 | 1.2 × 10−9 | 6.3 × 10−8 | |||
| C | 1.1 | 1.1 | 0.061 | 1.3 × 10−9 | 6.7 × 10−8 | |||
| D | 1.2 | 1.2 | 0.066 | 1.4 × 10−9 | 7.0 × 10−8 | |||
| E | 1.3 | 1.3 | 0.072 | 1.4 × 10−9 | 7.4 × 10−8 | |||
| F | 1.4 | 1.4 | 0.077 | 1.5 × 10−9 | 7.7 × 10−8 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borzęcka, N.H.; Nowak, B.; Pakuła, R.; Przewodzki, R.; Gac, J.M. Diffusion/Reaction Limited Aggregation Approach for Microstructure Evolution and Condensation Kinetics during Synthesis of Silica-Based Alcogels. Int. J. Mol. Sci. 2023, 24, 1999. https://doi.org/10.3390/ijms24031999
Borzęcka NH, Nowak B, Pakuła R, Przewodzki R, Gac JM. Diffusion/Reaction Limited Aggregation Approach for Microstructure Evolution and Condensation Kinetics during Synthesis of Silica-Based Alcogels. International Journal of Molecular Sciences. 2023; 24(3):1999. https://doi.org/10.3390/ijms24031999
Chicago/Turabian StyleBorzęcka, Nina Helena, Bartosz Nowak, Rafał Pakuła, Robert Przewodzki, and Jakub Maksymilian Gac. 2023. "Diffusion/Reaction Limited Aggregation Approach for Microstructure Evolution and Condensation Kinetics during Synthesis of Silica-Based Alcogels" International Journal of Molecular Sciences 24, no. 3: 1999. https://doi.org/10.3390/ijms24031999
APA StyleBorzęcka, N. H., Nowak, B., Pakuła, R., Przewodzki, R., & Gac, J. M. (2023). Diffusion/Reaction Limited Aggregation Approach for Microstructure Evolution and Condensation Kinetics during Synthesis of Silica-Based Alcogels. International Journal of Molecular Sciences, 24(3), 1999. https://doi.org/10.3390/ijms24031999








