Factors That Control the Force Needed to Unfold a Membrane Protein in Silico Depend on the Mode of Denaturation
Abstract
:1. Introduction
2. Results
2.1. Membrane Burial Potential
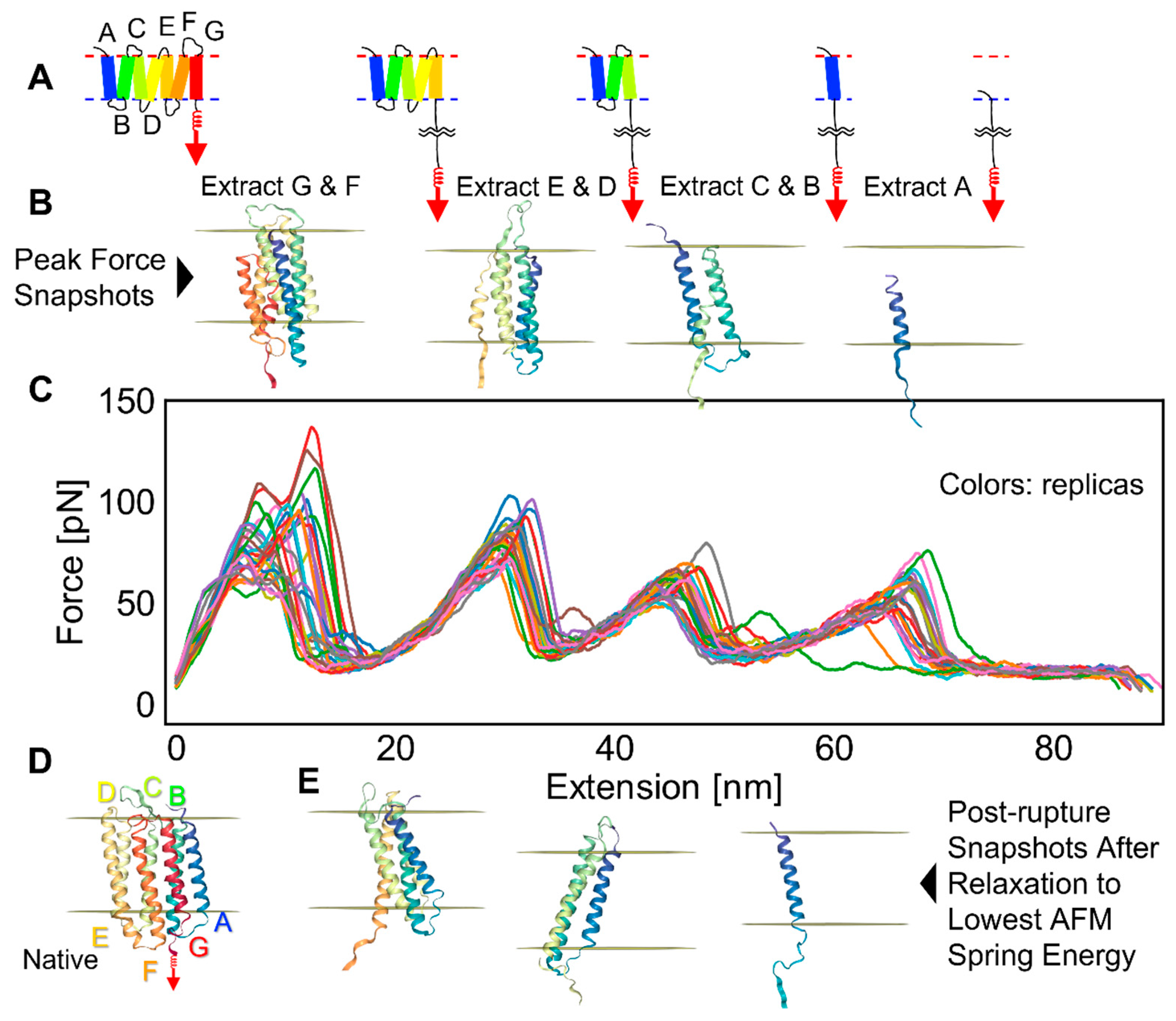
2.2. bR Unfolding
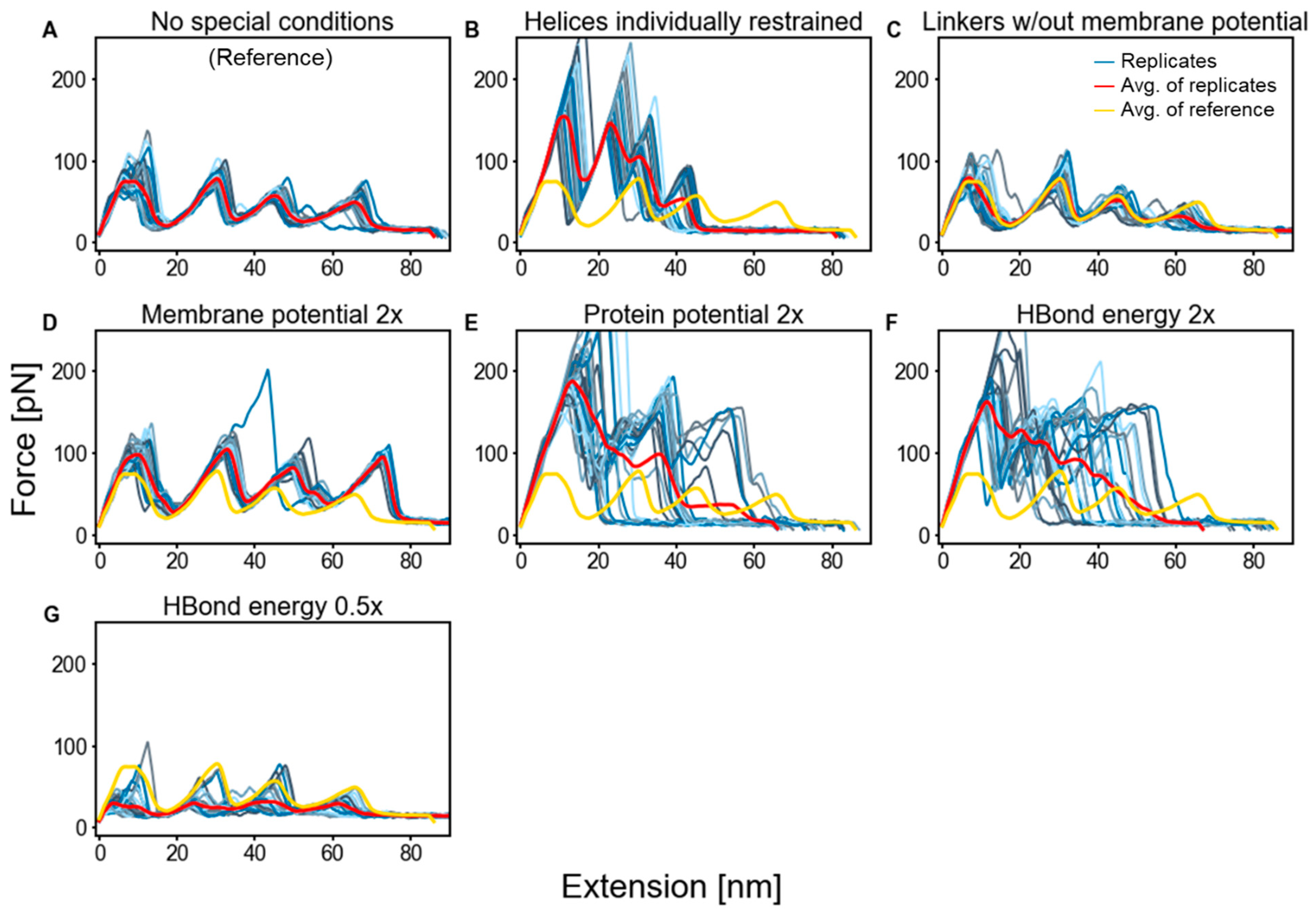
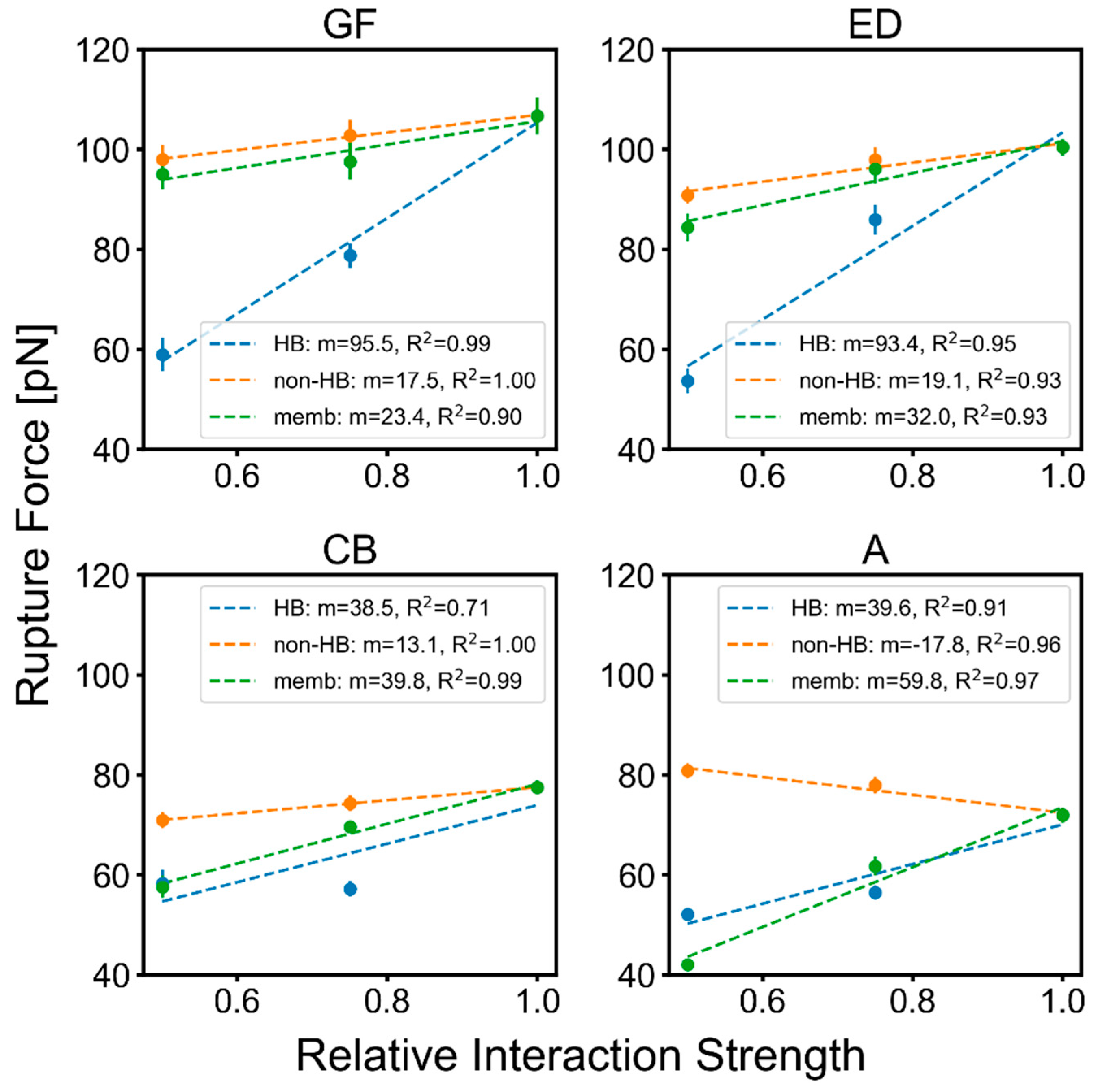
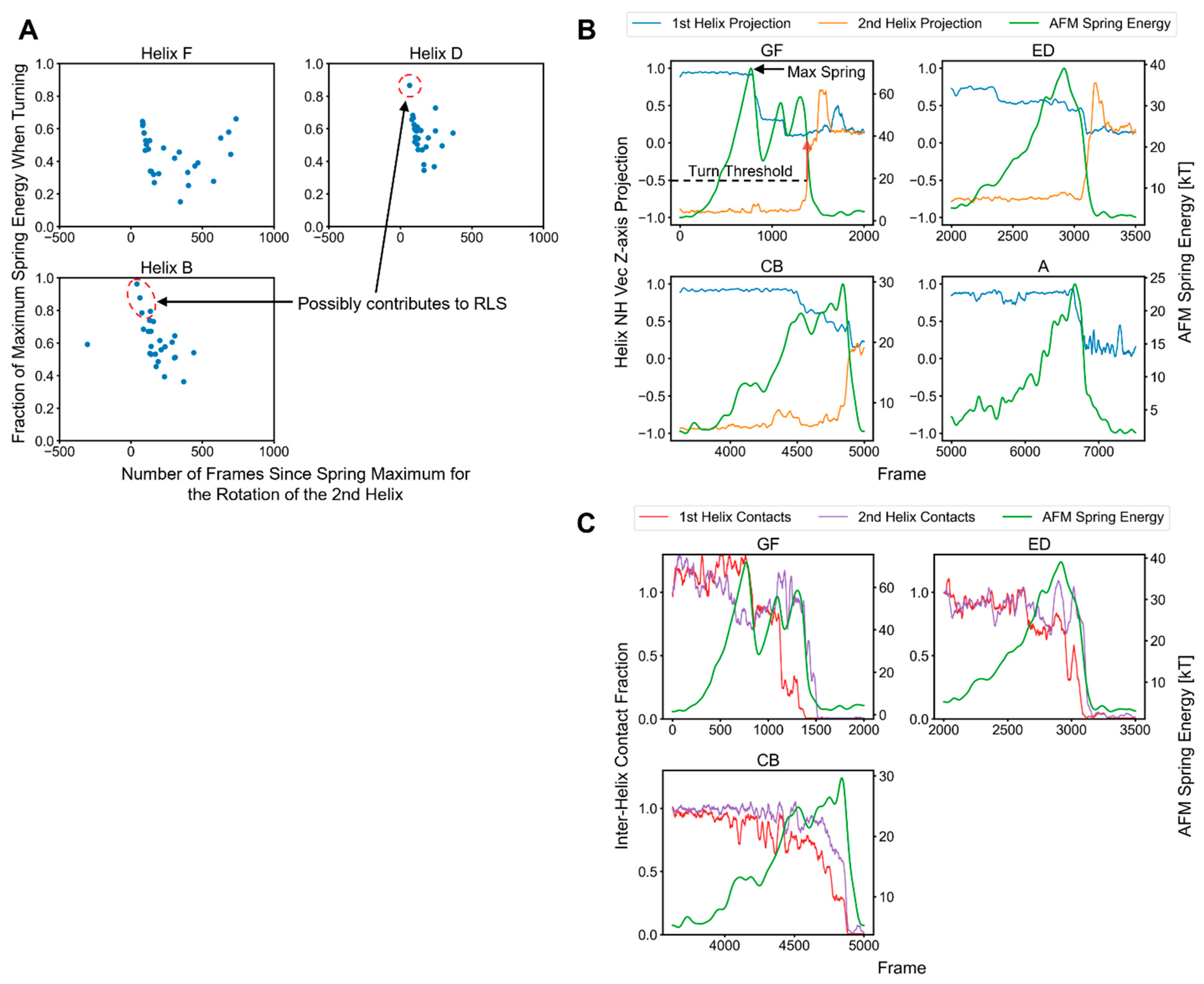
2.3. Factors That Govern Rupture Force Levels
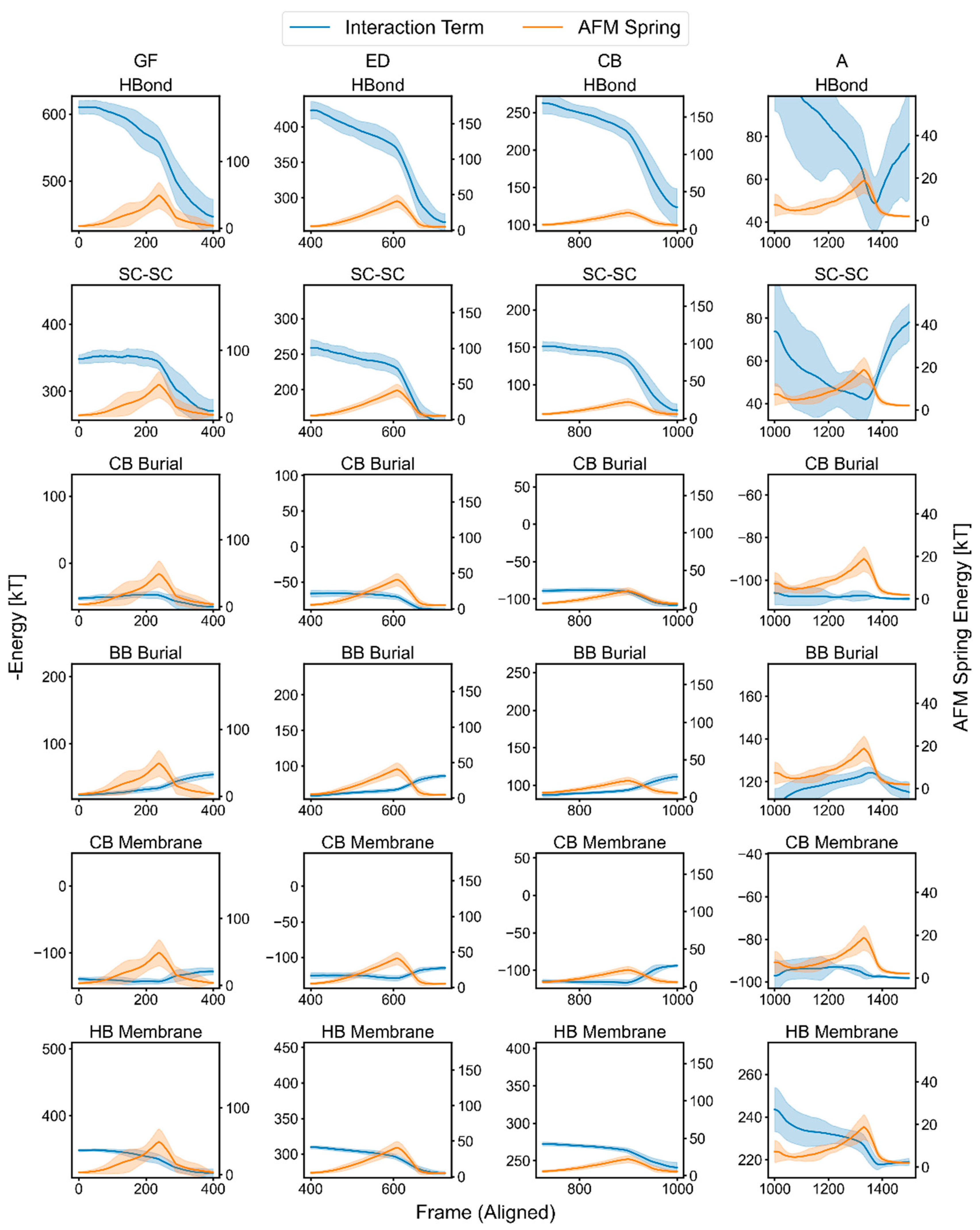
2.4. Characterization of the Rupture Event
2.5. GlpG Lateral Pulling
3. Discussion
- Comparison to previous studies.
| Protein (Reference) | Study | Reference State | Comments |
|---|---|---|---|
| bR (present study) | Vertical pulling with stiff spring from carboxy terminus | Extended with some residual helical structure after release from membrane | Pairwise unfolding of helices, H-bond strength affects rupture event |
| bR [35] | φ analysis conducted in SDS | Helical structure due to the presence of SDS | Stable core, polarized transition with some helices structured |
| bR [14] | AFM studies of point mutant in helices | Extended under tension | ΔΔG for helix to extend under tension, unlike mutational studies with soluble proteins |
| GlpG (present study) | Lateral pulling with stiff spring | Extended under tension | Unfolding can begin from middle, amino, or carboxy terminus, but some helices separate before unfolding |
| GlpG [9] | SDS denaturation from mixed micelles using φ analysis | Helical structure due to SDS | N-terminal nucleus involving helix 1 and 2, but with non-native contact in the loops with 3 C-terminal helices unfolded |
| GlpG [12] | Steric trapping with streptavidin in bicelles and lipid bilayers | Some helix fraying, expanded compared to native state, but still compact | Unfolding and separation at C-terminus or middle with the unfolded or separated helices potentially at membrane–water interface |
| GlpG [16] | Magnetic tweezers pulling laterally in bicelles | Extended under tension | Mostly cooperative unfolding from carboxy-to-amino with two observed intermediates, suggestive of pairwise unfolding of helices, transition state close to native state |
| PagP [36] | Urea denaturation from pure liposomes studied using φ analysis | Chemically denatured | Highly polarized transition state lacking β sheet structure, suggests tilted insertion into membrane, folding pathway and transition state affected by lipid composition |
| KcsA (helical tetramer) [37] | Folding upon transfer from SDS into liposomes | Partially folded monomers | Partially folded monomers rapidly associate, rate-limiting step is unimolecular, possibly relates to formation of the tetramer’s selectivity for filter and pore helices |
4. Methods
4.1. Structure Preparation
4.2. Upside Simulation Settings
4.3. Data Processing
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Plaxco, K.W.; Simons, K.T.; Baker, D. Contact Order, Transition State Placement and the Refolding Rates of Single Domain Proteins. J. Mol. Biol. 1998, 277, 985–994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sosnick, T.R.; Mayne, L.; Englander, S.W. Molecular Collapse: The Rate-Limiting Step in Two-State Cytochrome c Folding. Proteins 1996, 24, 413–426. [Google Scholar] [CrossRef]
- Pandit, A.D.; Jha, A.; Freed, K.F.; Sosnick, T.R. Small Proteins Fold through Transition States with Native-like Topologies. J. Mol. Biol. 2006, 361, 755–770. [Google Scholar] [CrossRef]
- Baxa, M.C.; Sosnick, T.R. Engineered Metal-Binding Sites to Probe Protein Folding Transition States: Psi Analysis. Methods Mol. Biol. 2022, 2376, 31–63. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.W.; Thiyagarajan, P.; Sosnick, T.R.; Pan, T. The Rate-Limiting Step in the Folding of a Large Ribozyme without Kinetic Traps. Proc. Natl. Acad. Sci. USA 2002, 99, 8518–8523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, X.; Pan, T.; Sosnick, T.R. Mg2+-Dependent Folding of a Large Ribozyme without Kinetic Traps. Nat. Struct. Biol. 1999, 6, 1091–1095. [Google Scholar]
- Harris, N.J.; Pellowe, G.A.; Blackholly, L.R.; Gulaidi-Breen, S.; Findlay, H.E.; Booth, P.J. Methods to Study Folding of Alpha-Helical Membrane Proteins in Lipids. Open Biol. 2022, 12, 220054. [Google Scholar] [CrossRef]
- Curnow, P.; Booth, P.J. The Transition State for Integral Membrane Protein Folding. Proc. Natl. Acad. Sci. USA 2009, 106, 773–778. [Google Scholar] [CrossRef] [Green Version]
- Paslawski, W.; Lillelund, O.K.; Kristensen, J.V.; Schafer, N.P.; Baker, R.P.; Urban, S.; Otzen, D.E. Cooperative Folding of a Polytopic α-Helical Membrane Protein Involves a Compact N-Terminal Nucleus and Nonnative Loops. Proc. Natl. Acad. Sci. USA 2015, 112, 7978–7983. [Google Scholar] [CrossRef] [Green Version]
- Huysmans, G.H.; Baldwin, S.A.; Brockwell, D.J.; Radford, S.E. The Transition State for Folding of an Outer Membrane Protein. Proc. Natl. Acad. Sci. USA 2010, 107, 4099–4104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schlebach, J.P.; Woodall, N.B.; Bowie, J.U.; Park, C. Bacteriorhodopsin Folds through a Poorly Organized Transition State. J. Am. Chem. Soc. 2014, 136, 16574–16581. [Google Scholar] [CrossRef] [PubMed]
- Gaffney, K.A.; Guo, R.; Bridges, M.D.; Muhammednazaar, S.; Chen, D.; Kim, M.; Yang, Z.; Schilmiller, A.L.; Faruk, N.F.; Peng, X.; et al. Lipid Bilayer Induces Contraction of the Denatured State Ensemble of a Helical-Bundle Membrane Protein. Proc. Natl. Acad. Sci. USA 2022, 119, e2109169119. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Siewny, M.G.; Edwards, D.T.; Sanders, A.W.; Perkins, T.T. Hidden Dynamics in the Unfolding of Individual Bacteriorhodopsin Proteins. Science 2017, 355, 945–950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jacobson, D.R.; Perkins, T.T. Free-Energy Changes of Bacteriorhodopsin Point Mutants Measured by Single-Molecule Force Spectroscopy. Proc. Natl. Acad. Sci. USA 2021, 118, e2020083118. [Google Scholar] [CrossRef] [PubMed]
- Min, D.; Jefferson, R.E.; Qi, Y.; Wang, J.Y.; Arbing, M.A.; Im, W.; Bowie, J.U. Unfolding of a ClC Chloride Transporter Retains Memory of Its Evolutionary History. Nat. Chem. Biol. 2018, 14, 489–496. [Google Scholar] [CrossRef]
- Min, D.; Jefferson, R.E.; Bowie, J.U.; Yoon, T.Y. Mapping the Energy Landscape for Second-Stage Folding of a Single Membrane Protein. Nat. Chem. Biol. 2015, 11, 981–987. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Jumper, J.M.; Freed, K.F.; Sosnick, T.R. On the Interpretation of Force-Induced Unfolding Studies of Membrane Proteins Using Fast Simulations. Biophys. J. 2019, 117, 1429–1441. [Google Scholar] [CrossRef]
- Kappel, C.; Grubmüller, H. Velocity-Dependent Mechanical Unfolding of Bacteriorhodopsin Is Governed by a Dynamic Interaction Network. Biophys. J. 2011, 100, 1109–1119. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Baxa, M.; Faruk, N.; Sachleben, J.R.; Pintscher, S.; Gagnon, I.A.; Houliston, S.; Arrowsmith, C.H.; Freed, K.F.; Rocklin, G.J.; et al. Prediction and Validation of a Protein’s Free Energy Surface Using Hydrogen Exchange and (Importantly) Its Denaturant Dependence. J. Chem. Theory Comput. 2022, 18, 550–561. [Google Scholar] [CrossRef]
- Jumper, J.M.; Faruk, N.F.; Freed, K.F.; Sosnick, T.R. Trajectory-Based Training Enables Protein Simulations with Accurate Folding and Boltzmann Ensembles in Cpu-Hours. PLoS Comput. Biol. 2018, 14, e1006578. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucl. Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Evans, E. Probing the Relation between Force--Lifetime--and Chemistry in Single Molecular Bonds. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 105–128. [Google Scholar] [CrossRef] [Green Version]
- McDonald, S.K.; Fleming, K.G. Negative Charge Neutralization in the Loops and Turns of Outer Membrane Phospholipase A Impacts Folding Hysteresis at Neutral PH. Biochemistry 2016, 55, 6133–6137. [Google Scholar] [CrossRef] [Green Version]
- Lomize, M.A.; Pogozheva, I.D.; Joo, H.; Mosberg, H.I.; Lomize, A.L. OPM Database and PPM Web Server: Resources for Positioning of Proteins in Membranes. Nucleic Acids Res. 2012, 40, D370–D376. [Google Scholar] [CrossRef] [PubMed]
- Bavi, N.; Nikolaev, Y.A.; Bavi, O.; Ridone, P.; Martinac, A.D.; Nakayama, Y.; Cox, C.D.; Martinac, B. Principles of Mechanosensing at the Membrane Interface. Biophys. Cell Membr. 2017, 19, 85–119. [Google Scholar] [CrossRef]
- Yamada, T.; Yamato, T.; Mitaku, S. Forced Unfolding Mechanism of Bacteriorhodopsin as Revealed by Coarse-Grained Molecular Dynamics. Biophys. J. 2016, 111, 2086–2098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baker, R.P.; Urban, S. Architectural and Thermodynamic Principles Underlying Intramembrane Protease Function. Nat. Chem. Biol. 2012, 8, 759–768. [Google Scholar] [CrossRef] [Green Version]
- Ganchev, D.N.; Rijkers, D.T.S.; Snel, M.M.E.; Killian, J.A.; de Kruijff, B. Strength of Integration of Transmembrane α-Helical Peptides in Lipid Bilayers As Determined by Atomic Force Spectroscopy. Biochemistry 2004, 43, 14987–14993. [Google Scholar] [CrossRef]
- Sapra, K.T.; Balasubramanian, G.P.; Labudde, D.; Bowie, J.U.; Muller, D.J. Point Mutations in Membrane Proteins Reshape Energy Landscape and Populate Different Unfolding Pathways. J. Mol. Biol. 2008, 376, 1076–1090. [Google Scholar] [CrossRef] [Green Version]
- Sundaram, A.; Yamsek, M.; Zhong, F.; Hooda, Y.; Hegde, R.S.; Keenan, R.J. Substrate-Driven Assembly of a Translocon for Multipass Membrane Proteins. Nature 2022, 611, 167–172. [Google Scholar] [CrossRef]
- Cymer, F.; von Heijne, G.; White, S.H. Mechanisms of Integral Membrane Protein Insertion and Folding. J. Mol. Biol. 2015, 427, 999–1022. [Google Scholar] [CrossRef] [PubMed]
- Marx, D.C.; Fleming, K.G. Membrane Proteins Enter the Fold. Curr. Opin. Struct. Biol. 2021, 69, 124–130. [Google Scholar] [CrossRef]
- Lundquist, K.; Billings, E.; Bi, M.; Wellnitz, J.; Noinaj, N. The Assembly of β-Barrel Membrane Proteins by BAM and SAM. Mol. Microbiol. 2021, 115, 425–435. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Bakelar, J.W.; Lundquist, K.; Zhang, Z.; Kuo, K.M.; Ryoo, D.; Pang, Y.T.; Sun, C.; White, T.; Klose, T.; et al. Plasticity within the Barrel Domain of BamA Mediates a Hybrid-Barrel Mechanism by BAM. Nat. Commun. 2021, 12, 7131. [Google Scholar] [CrossRef] [PubMed]
- Curnow, P.; Di Bartolo, N.D.; Moreton, K.M.; Ajoje, O.O.; Saggese, N.P.; Booth, P.J. Stable Folding Core in the Folding Transition State of an Alpha-Helical Integral Membrane Protein. Proc. Natl. Acad. Sci. USA 2011, 108, 14133–14138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huysmans, G.H.M.; Radford, S.E.; Baldwin, S.A.; Brockwell, D.J. Malleability of the Folding Mechanism of the Outer Membrane Protein PagP: Parallel Pathways and the Effect of Membrane Elasticity. J. Mol. Biol. 2012, 416–318, 453–464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, K.C.; Molina, A.V.; Chen, R.; Gagnon, I.A.; Koh, Y.H.; Roux, B.; Sosnick, T.R. Folding and Misfolding of Potassium Channel Monomers during Assembly and Tetramerization. Proc. Natl. Acad. Sci. USA 2021, 118, e2103674118. [Google Scholar] [CrossRef]
- Kopf, A.; Paul, W.; Dünweg, B. Multiple Time Step Integrators and Momentum Conservation. Comput. Phys. Commun. 1997, 101, 1–8. [Google Scholar] [CrossRef]
- Riback, J.A.; Bowman, M.A.; Zmyslowski, A.M.; Plaxco, K.W.; Clark, P.L.; Sosnick, T.R. Commonly Used FRET Fluorophores Promote Collapse of an Otherwise Disordered Protein. Proc. Natl. Acad. Sci. USA 2019, 116, 8889–8894. [Google Scholar] [CrossRef] [Green Version]
- Riback, J.A.; Bowman, M.A.; Zmyslowski, A.M.; Knoverek, C.R.; Jumper, J.M.; Hinshaw, J.R.; Kaye, E.B.; Freed, K.F.; Clark, P.L.; Sosnick, T.R. Innovative Scattering Analysis Shows That Hydrophobic Disordered Proteins Are Expanded in Water. Science 2017, 358, 238–241. [Google Scholar] [CrossRef] [Green Version]
- Bowman, M.A.; Riback, J.A.; Rodriguez, A.; Guo, H.; Li, J.; Sosnick, T.R.; Clark, P.L. Properties of Protein Unfolded States Suggest Broad Selection for Expanded Conformational Ensembles. Proc. Natl. Acad. Sci. USA 2020, 117, 23356–23364. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faruk, N.F.; Peng, X.; Sosnick, T.R. Factors That Control the Force Needed to Unfold a Membrane Protein in Silico Depend on the Mode of Denaturation. Int. J. Mol. Sci. 2023, 24, 2654. https://doi.org/10.3390/ijms24032654
Faruk NF, Peng X, Sosnick TR. Factors That Control the Force Needed to Unfold a Membrane Protein in Silico Depend on the Mode of Denaturation. International Journal of Molecular Sciences. 2023; 24(3):2654. https://doi.org/10.3390/ijms24032654
Chicago/Turabian StyleFaruk, Nabil F., Xiangda Peng, and Tobin R. Sosnick. 2023. "Factors That Control the Force Needed to Unfold a Membrane Protein in Silico Depend on the Mode of Denaturation" International Journal of Molecular Sciences 24, no. 3: 2654. https://doi.org/10.3390/ijms24032654
APA StyleFaruk, N. F., Peng, X., & Sosnick, T. R. (2023). Factors That Control the Force Needed to Unfold a Membrane Protein in Silico Depend on the Mode of Denaturation. International Journal of Molecular Sciences, 24(3), 2654. https://doi.org/10.3390/ijms24032654







