Next Article in Journal
Effects of Oncolytic Vaccinia Viruses Harboring Different Marine Lectins on Hepatocellular Carcinoma Cells
Next Article in Special Issue
Polymorphism and Ligand Binding Modulate Fast Dynamics of Human Telomeric G-Quadruplexes
Previous Article in Journal
Urotensin II Enhances Advanced Aortic Atherosclerosis Formation and Delays Plaque Regression in Hyperlipidemic Rabbits
Previous Article in Special Issue
Evolutionary Dynamics of Avian Influenza Viruses Isolated from Wild Birds in Moscow
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 24
Issue 4
10.3390/ijms24043822
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

cRNAsp12 Web Server for the Prediction of Circular RNA Secondary Structures and Stabilities

by
Fengfei Wang
1,†,
Wei Li
1,†,
Baiyi Li
1,
Liangxu Xie
1,
Yunguang Tong
2 and
Xiaojun Xu
1,*
1
Institute of Bioinformatics and Medical Engineering, Jiangsu University of Technology, Changzhou 213001, China
2
Department of Pharmacy, China Jiliang University, Hangzhou 310000, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Int. J. Mol. Sci. 2023, 24(4), 3822; https://doi.org/10.3390/ijms24043822
Submission received: 26 December 2022 / Revised: 29 January 2023 / Accepted: 7 February 2023 / Published: 14 February 2023
(This article belongs to the Special Issue Structure, Dynamics, and Function of Nucleic Acids)
Browse Figures
Versions Notes

Abstract

:
Circular RNAs (circRNAs) are a novel class of non-coding RNA that, unlike linear RNAs, form a covalently closed loop without the 5′ and 3′ ends. Growing evidence shows that circular RNAs play important roles in life processes and have great potential implications in clinical and research fields. The accurate modeling of circRNAs structure and stability has far-reaching impact on our understanding of their functions and our ability to develop RNA-based therapeutics. The cRNAsp12 server offers a user-friendly web interface to predict circular RNA secondary structures and folding stabilities from the sequence. Through the helix-based landscape partitioning strategy, the server generates distinct ensembles of structures and predicts the minimal free energy structures for each ensemble with the recursive partition function calculation and backtracking algorithms. For structure predictions in the limited structural ensemble, the server also provides users with the option to set the structural constraints of forcing the base pairs and/or forcing the unpaired bases, such that only structures that meet the criteria are enumerated recursively.

1. Introduction

Most RNA molecules are linear. Circular RNAs (circRNAs) are a small but novel class of non-coding RNA that, unlike linear RNAs, form a covalently closed loop without the 5′ and 3′ ends. With the development of high-throughput sequencing technology and promising bioinformatics tools, emerging evidence indicates that circRNAs are stable, widely expressed, and play multifunctional roles in life processes, such as miRNA sponges, regulators of gene splicing and transcription, RNA-binding protein sponges and protein/peptide translators [1,2,3,4,5,6]. In consideration of their association with diseases [7,8,9,10,11,12,13], circRNAs have become a new hotspot in the clinical and research fields. Therefore, the accurate modeling of circRNAs annotation, structure determination and interaction analysis has a far-reaching impact on our understanding of their functions and our ability to develop RNA-based therapeutics [14,15,16,17,18,19,20,21,22].
Computational algorithms for predicting the secondary structures of circRNAs have been implemented in the Mfold [23,24] and Vienna RNA [25,26] package. Mfold predicts circRNA secondary structures from the “internal” and “external” linear subsequences separated by a base pair. It requires twice as much time and computer storage as the linear algorithm for a sequence of the same size. The Vienna RNA algorithm, furthermore, optimizes the memory requirements for the circRNA folding with the proper treatment for the exterior hairpin loops, internal loops, and multiloops within the “external” subsequence. It predicts circular secondary structures without additional memory requirements as a kind of “post-processing” of the linear structures.
Previous studies of the helix-based strategy for RNA folding kinetics prediction [27,28,29,30,31] implies that the landscape partitioning approach has the ability to predict alternative secondary structures for linear RNAs. Since the whole folding landscape is divided into discrete folding partitions through stable helices, each partition defines a structural ensemble mainly featured by the inclusion and exclusion of selected stable helices. Therefore, there is at least one helix difference between any two of them, making it better to address the conformational heterogeneity in RNAs [30,31]. Here, we apply the helix-based landscape partitioning strategy to develop a new model, cRNAsp12 (circular RNA structure prediction, from 1D to 2D), for predicting secondary structures of circRNAs. For a given folding temperature, the model uses the stable helical regions to define the main features of distinct structural ensembles in circular RNA folding landscape and determine the stable secondary structures of each ensemble with the corresponding constraints from the selected stable helices. By adding the structural constraints of forcing base pairs and/or forcing unpaired bases, furthermore, the model has the ability to predict circRNA secondary structures within the limited folding landscape. The cRNAsp12 model is freely accessible at the cRNAsp12 web server (http://xxulab.org.cn/crnasp12 accessed on 15 December 2022) for the prediction of circRNA secondary structures and folding stabilities from the given sequence.

2. Results

The cRNAsp12 web server is a user-friendly platform for the prediction of circular RNA secondary structures and folding stabilities. The computational time scales with the chain length N as O(N3) and the computer memory scales as O(N2). To avoid a long computational time, the current version of the cRNAsp12 server restricts the input sequence length up to 500 nts.

2.1. cRNAsp12 Input

To predict the circular RNA secondary structures, the cRNAsp12 server requires users to input the circRNA sequence in plain text form (see the snapshot of a web server in Figure 1). The default folding temperature is 37 °C. Users have the option to change the temperature to other desired values. Since the model predicts alternative structures with the helix-based landscape partitioning strategy, users have the option to set the maximum number of predicted structures (five in default) from the drop-down list, such that the model selects saturated helices from the most stable to least stable ones until the number of partitions reaches the user-selected value. Once a calculation is submitted, a unique job ID is assigned and a notification page (see the snapshot of web server in Figure 1) containing job information, such as the circRNA name, sequence, folding temperature, e-mail address (if provided), structural constraints (if provided), and the assigned job ID, is displayed. If the e-mail address is provided during job submission, the cRNAsp12 web server automatically sends out an e-mail notification with the results attached once the calculation is completed.
For structure predictions in the limited (not full) structural ensemble, the server also provides users with the option to set the structural constraints of forcing the base pairs (HELIX i j k) and/or forcing the unpaired bases (LOOP i k), as shown in Figure 2a,b. For the forced base pairs (HELIX i j k), i–j is the sequence positions of starting base pair and k (bps) is the length of the forced helix. All forced base pairs should be canonical (A–U, G–C, and G–U). For the unpaired bases (LOOP i k), i is the sequence position of the starting nucleotide and k (nts) is the length of the forced loop. The values of i and j are in the range of (1, N) with N as the length of input circRNA sequence, and the value of k is selected from the drop-down list. As shown in Figure 2c, users can easily use the “add” and “remove” buttons to set constraints properly. It should be noted that improper settings of structural constraints, such as the overlapping or crossing between forced base pairs, may lead to no predictions.

2.2. cRNAsp12 Output

By visiting the “Job Status” page; on the other hand, users have the option to retrieve the job status through the job ID (for one particular calculation) or e-mail address (for calculations submitted with the same e-mail address). There are three types of job status: “submitted”, “completed”, and “error”. For the completed jobs, users can visit the cRNAsp12 results page through the hyperlinks from the corresponding job IDs, as shown in Figure 3. In order to save storage space, the server keeps all the job files for only six months from the date of submission. However, the server may return no predictions for jobs with improper settings of structural constraints, whose statuses are marked as “error”.
The server provides the results of the predicted secondary structures (in dot-bracket notation) in text format for download. It also provides a forna javascript viewing container for the visualization of the cRNAsp12 predicted top-stable structures [32]. Figure 3 shows an example of cRNAsp12 prediction for the CAMSAP1 circRNA with 425-nt in length (its sequence shown in Figure 1). The predicted secondary structures are ranked by their folding stabilities, i.e., the free energies in kcal/mol calculated with the base stacking and loop entropy energies.

2.3. Performance Benchmark

We used the dataset of 25 circRNAs with their sequence lengths ranging from 161 nts to 435 nts to benchmark the performance of the cRNAsp12 model. The detailed SHAPE-Map analysis and SHAPE-directed secondary structure modeling by RNAfold [25,26] reveal that those circRNAs tend to form 16–26 bp imperfect RNA duplexes and act as the inhibitors of double-stranded RNA (dsRNAs)-activated protein kinase (PKR) related to innate immunity [33]. Without integrating the SHAPE data, the cRNAsp12 model predicts their secondary structures at the folding temperature = 37 ℃ .
As listed in Table 1, there are 46 16–26 bp dsRNAs in the SHAPE-directed secondary structures of 25 circRNAs, and cRNAsp12 correctly predicts the majority of them (36 out of 46). Specifically, all the dsRNAs in 19 circRNAs are correctly predicted (see Figure 3 and Figure S1). The dsRNAs in four circRNAs (EPHB4, PVT1, FKBP8, and KIAA0368) are partially predicted, while cRNAsp12 obtains the completely incorrectly predictions of dsRNAs for the CCNB1 and EZH2 circRNAs (see Figure S2). As in the example of the CAMSAP1 circRNA, shown in Figure 3, cRNAsp12 correctly predicts the three 16–26 bp dsRNAs, as indicated by the dashed rectangles.
Moreover, we use the online servers of Mfold and RNAfold with the default parameters, except for the type of RNA sequence (circular), to predict the circRNA secondary structures for the above 25 tested cases. Similar to cRNAsp12, Mfold also correctly predicts the majority of them (32 out of 46). Since the RNAfold server only outputs the minimum free energy (MFE) structure for a given sequence, its prediction accuracy (RNAfold-alone without SHAPE) for the prediction of 16–26 bp dsRNAs is much lower than that of Mfold and cRNAsp12. As shown in Figure S2, most SHAPE-RNAfold predicted structures contain RNA secondary structural motifs with large-size loops. For example, the four-way junction of the SHAPE-RNAfold predicted CCNB1 circRNA has 34 unpaired nucleotides. Without the help of SHAPE data, the predicted structures of RNAfold, Mfold, and cRNAsp12 usually contain only the structural motifs with small-size loops. However, if the 16–26 bp dsRNAs contain stable helices, the helix-based landscape partitioning strategy for alternative structure prediction will more likely capture those dsRNAs.

3. Discussion

RNAs can fold into structures with cross-linked base pairs, such as the pseudoknotted (H-PK), and hairpin–hairpin loop kissing (L-KISS) motifs shown in Figure 4. Because of the coupling effects between helices and loops, the corresponding energy parameters are mutually dependent on the sizes of loops and helices [34,35,36,37,38]. Due to the circular nature of circRNAs, the two above motifs need to be extended with additional loops, as shown in the red lines in Figure 4. The additional loops (L4 for H-PK, and L5 and L6 for L-KISS) are actually coupled with the existing helices and loops. As a result, the previously derived energy parameters from the Vfold model are no longer applicable. Therefore, the current version of the cRNAsp12 model can only treat circular RNA structures without cross-linked base pairs. Once the energy parameters are expanded, the model can be extended for the structure and stability prediction of complex circRNAs.
RNAs are negatively charged molecules. The ionic solution condition, such as ion concentration, size and charge, plays important roles in determining RNA thermal stability and folding kinetics [39,40,41,42]. The Turner parameters for the base stacking energies were experimentally measured with the fixed ionic solution condition (i.e., 1 M NaCl) [43]. However, there are currently no comprehensive energy parameters, similar to the Turner parameters, that have been experimentally measured in other ionic conditions. Modeling with such parameters should generally overestimate the helix stabilities for RNA structures in lower salt conditions. For RNA loop elements, on the other hand, there may be many sequence-dependent non-canonical base pairing interactions besides the loop entropy energies that contribute to the loop stabilities [44,45,46,47,48]. However, the available energy parameters (both experiment-measured and model-derived) are simply loop size-dependent. Effectively accounting for the loop sequence and ion effects on loop stability challenges the further development of models for the better prediction of RNA structures, stabilities and folding kinetics.
In recent years, machine learning (ML), especially deep learning, has made remarkable progresses in a wide range of fields, including RNA secondary structure prediction [49,50,51,52]. Due to the lack of sufficient data for circular RNAs, to our knowledge, currently available ML-based models are designed only for linear RNAs. Moreover, although ML-based methods have enabled us to more accurately predict RNA secondary structures, the estimation of their folding stabilities is also important for applications other than structure prediction. Hybrid methods that combine thermodynamic and ML-based approaches have been developed with the expectation to evaluate thermodynamic stability with high accuracy [53,54]. Therefore, with the further expansion of biological data, developing robust and explainable ML-based approaches with thermodynamic regularization would be an alternative and feasible means of accurately modeling circRNA secondary structures and stabilities.

4. Materials and Methods

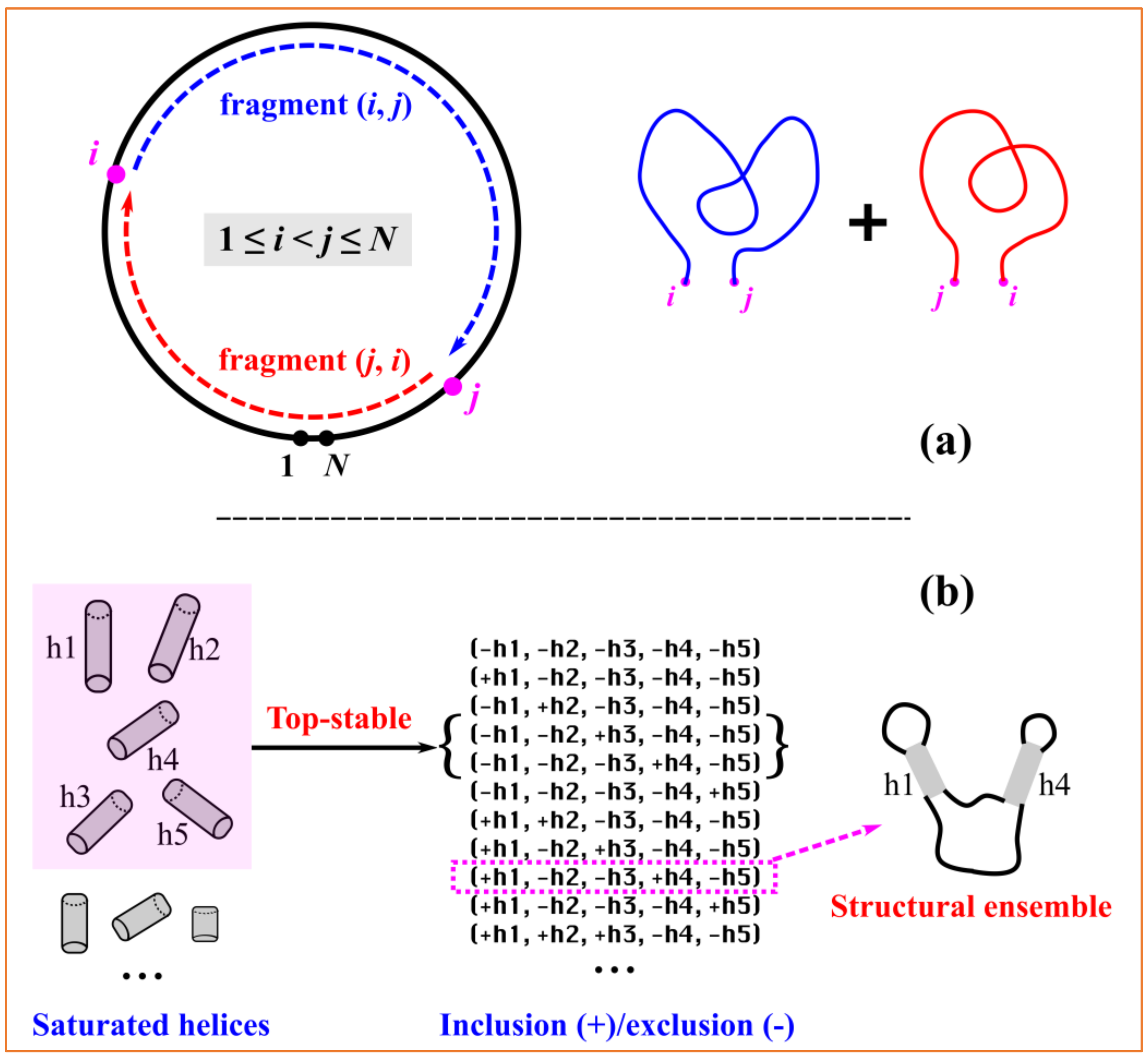
Although the direction of numbering is uniquely defined, any consecutive numbering of the nucleotides beginning at an arbitrary point should be equivalent for circRNAs. By selecting any two (different) nucleotides, a circular sequence can be divided into two linear subsequences. For a given numbering of (1, N), with N as the length of the circRNA sequence, as shown in Figure 5a, the selected ith and jth nucleotides with 1≤ i < j ≤ N divide the entire circular sequence into two linear fragments, i.e., the “internal” fragment (i, j) and the “external” fragment (j, i) spanning over two pseudo-ends. The cRNAsp12 model combines the recursive partition function calculation with the backtracking algorithm to predict secondary structures for each linear fragment. The circRNA secondary structures and folding stabilities are calculated by the additivity assumption characteristic of recursive algorithms.

4.1. Energy Parameters

For the free energy-based RNA structure modeling, the predicted secondary structures, stabilities and folding kinetics could be sensitive to the choice of energy parameters. RNA secondary structures are defined by the base pairing patterns, which can be further divided into helices and loops. Based on the nearest-neighbor model, the total folding stability of an RNA secondary structure can be evaluated through the summation of the folding energies of individual helices and loop elements. For the helical regions, it is quite common to use the Turner parameters [43] to calculate the free energies from base stacks. For the RNA loop elements, such as the hairpin loops, internal/bulge loops, and multi-branched junctions, the cRNAsp12 model uses the Vfold-derived energy parameters to calculate the free energies from loop entropies, which has the advantage of accounting for chain connectivity, excluding the volume between helices and loops and the completeness of conformational ensemble [34,35,36,37,38].

4.2. Helix-Based Landscape Partitioning

For a given circRNA sequence, cRNAsp12 enumerates all the possible saturated helices formed by the canonical base pairs (A–U, G–C, and G–U), which cannot be further extended on either side through the canonical base pairs. As shown in Figure 2A, each helix is denoted by (i, j, k) with (i, j) the starting base pair and k is the number of canonical base pairs. If (i − 1, j + 1) and (i + k, j − k) are both noncanonical, then (i, j, k) is a saturated helix. The stability of each saturated helix is evaluated by the base stacking energies from the Turner parameters. The cRNAsp12 model ranks all the helices according to their free energies and selects top-stable helices to divide the entire folding landscape into discrete folding partitions. By enumerating all the possible helix combinations (inclusion/exclusion of selected top-stable helices) and deleting those with helix overlaps (nucleotides belonging to two or more helices) or crossing (involving the cross-linked base pairs) among included helices, a list of folding partitions featured by the selected helices is obtained. As shown the example in Figure 5b, five top-stable helices are selected and the partition of (+h1, −h2, −h3, +h4, and −h5) contains helices h1 and h4 and excludes helices h2, h3, and h5, representing a structural ensemble containing all the secondary structures with the base pairs from the included helices but without the base pairs from the excluded helices. The total number of partitions is determined by the size of the selected top-stable helix pool. The more the stable helices are selected, the larger the number of partitions, and the smaller the difference between partitions.

4.3. Alternative Structure Determination

Through the fragment-based strategy shown in Figure 5a and the recursive partition function calculation for linear RNAs, the cRNAsp12 model calculates the conditional partition function of each partition for the structural ensemble conditioned by the formation of the i–j base pair:
Q p a r t i t i o n i − j = Q f r a g m e n t   i , j i − j · Q f r a g m e n t   j , i j − i ,
where Q f r a g m e n t   i , j i − j and Q f r a g m e n t   j , i j − i are the conditional partition functions of the fragments (i, j) and (j, i), respectively, calculated over the corresponding structural ensembles with the terminal nucleotides base-paired. By minimizing the free energy G p a r t i t i o n i − j = − k B T l n Q p a r t i t i o n i − j ( k B is the Boltzmann constant and T is the folding temperature) over all the possible base pairs, the model determines the minimal free energy (MFE) structure and folding stability of each partition with the backtracking algorithm for the fragments of (i, j) and (j, i). The detailed algorithms of the recursive partition function calculation and backtracking for linear RNAs can be found in the published papers [55,56,57].
Therefore, the selected top-stable helices define the scaffolds of partitions, while all the less-stable (not selected) helices are sampled recursively during the structure enumeration process to characterize the shape of partition landscapes. Each partition is represented by the corresponding MFE structure. Through the helix-based landscape partitioning and MFE structure backtracking, cRNAsp12 predicts the alternative secondary structures of a given circRNA sequence.

5. Conclusions

Combining the helix-based landscape partitioning strategy, recursive partition function calculation and backtracking algorithms, we developed the cRNAsp12 software and web server to predict circular RNA secondary structures and folding stabilities from the sequence. Using stable helices to effectively divide the whole folding landscape into discrete structural ensembles, the helix-based folding model can better address the conformational heterogeneity in RNAs. Currently, the model can only treat circRNA secondary structures without the cross-linked base pairs. In fact, similar to linear RNAs, circular RNAs may fold into structures with long-range tertiary interactions, especially for long-size circRNAs. In a future work, cRNAsp12 will be continuously upgraded to treat circRNA structures including complex structural elements, such as the extended H-PK and L-KISS motifs.
Furthermore, the RNA environment in the solution is usually complicated, involving multiple surrounding molecules and ions. The interplay between them, especially the ion effects, plays important roles in determining RNA structures, stabilities, and functions. In future work, we will also add the effect of the ions to the enthalpy and entropy parameters for the loops and base stack formations to improve the performance of structure predictions. As an alternative future trend, developing the folding scores leant from the rich-parameterized weight parameters of ML-based models with thermodynamic integration for the modeling of circRNA secondary structures would also be a feasible direction for cRNAsp12.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms24043822/s1.

Author Contributions

Methodology, F.W. and X.X.; software, W.L. and B.L.; validation, W.L., L.X., and B.L.; writing—original draft preparation, F.W.; writing—review and editing, X.X. and Y.T.; supervision, X.X. and Y.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (12074151).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We thank Shan Chang for useful discussions and technical support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Memczak, S.; Jens, M.; Elefsinioti, A.; Torti, F.; Krueger, J.; Rybak, A. Circular RNAs are a large class of animal RNAs with regulatory potency. Nature 2013, 495, 333–338. [Google Scholar] [CrossRef] [PubMed]
  2. Holdt, L.M.; Stahringer, A.; Sass, K.; Pichler, G.; Kulak, N.A.; Wilfert, W. Circular non-coding RNA ANRIL modulates ribosomal RNA maturation and atherosclerosis in humans. Nat. Commun. 2016, 7, 12429. [Google Scholar] [CrossRef] [PubMed]
  3. Chen, L.L. The biogenesis and emerging roles of circular RNAs. Nat. Rev. Mol. Cell Biol. 2016, 17, 205–211. [Google Scholar] [CrossRef] [PubMed]
  4. Qu, S.; Zhong, Y.; Shang, R.; Zhang, X.; Song, W.; Kjems, J.; Li, H. The emerging landscape of circular RNA in life processes. RNA Biol. 2017, 14, 992–999. [Google Scholar] [CrossRef]
  5. Chen, L.-L. The expanding regulatory mechanisms and cellular functions of circular RNAs. Nat. Rev. Mol. Cell Biol. 2020, 21, 475–490. [Google Scholar] [CrossRef]
  6. Liu, C.-X.; Chen, L.-L. Circular RNAs: Characterization, cellular roles, and applications. Cell 2022, 185, 2016–2034. [Google Scholar] [CrossRef]
  7. Guarnerio, J.; Bezzi, M.; Jeong, J.C.; Paffenholz, S.V.; Berry, K.; Naldini, M.M. Oncogenic role of fusion-circRNAs derived from cancer-associated chromosomal translocations. Cell 2016, 166, 1055–1056. [Google Scholar] [CrossRef]
  8. Piwecka, M.; Glazar, P.; Hernandez-Miranda, L.R.; Memczak, S.; Wolf, S.A.; Rybak-Wolf, A. Loss of a mammalian circular RNA locus causes miRNA deregulation and affects brain function. Science 2017, 357, eaam8526. [Google Scholar] [CrossRef]
  9. Dube, U.; Del-Aguila, J.L.; Li, Z.; Budde, J.P.; Jiang, S.; Hsu, S. An atlas of cortical circular RNA expression in Alzheimer disease brains demonstrates clinical and pathological associations. Nat. Neurosci. 2019, 22, 1903–1912. [Google Scholar] [CrossRef]
  10. Liu, C.; Ge, H.M.; Liu, B.H.; Dong, R.; Shan, R.; Chen, X. Targeting pericyte-endothelial cell crosstalk by circular RNA-cPWWP2A inhibition aggravates diabetes-induced microvascular dysfunction. Proc. Natl. Acad. Sci. USA 2019, 116, 7455–7464. [Google Scholar] [CrossRef] [Green Version]
  11. Ward, Z.; Pearson, J.; Schmeier, S.; Cameron, V.; Pilbrow, A. Insights into circular RNAs: Their biogenesis, detection, and emerging role in cardiovascular disease. RNA Biol. 2021, 18, 2055–2072. [Google Scholar] [CrossRef] [PubMed]
  12. Tang, X.; Ren, H.; Guo, M.; Qian, J.; Yang, Y.; Gu, C. Review on circular RNAs and new insights into their roles in cancer. Comput. Struct. Biotechnol. J. 2021, 19, 910–928. [Google Scholar] [CrossRef]
  13. Ward, Z.; Schmeier, S.; Pearson, J.; Cameron, V.A.; Fampton, C.M.; Troughton, R.W.; Doughty, R.N.; Richards, A.M.; Pilbrow, A.P. Identifying candidate circulating RNA markers for coronary artery disease by deep RNA-sequencing in human plasma. Cells 2022, 11, 3191. [Google Scholar] [CrossRef]
  14. Dudekula, D.B.; Panda, A.C.; Grammatikakis, I.; De, S.; Abdelmohsen, K.; Gorospe, M. CircInteractome: A web tool for exploring circular RNAs and their interacting proteins and microRNAs. RNA Biol. 2016, 13, 34–42. [Google Scholar] [CrossRef] [PubMed]
  15. Jia, G.-Y.; Wang, D.-L.; Xue, M.-Z.; Liu, Y.-W.; Pei, Y.-C.; Yang, Y.-Q.; Xu, J.-M.; Liang, Y.-C.; Wang, P. CircRNAFisher: A systematic computational approach for de novo circular RNA identification. Acta Pharmacol. Sin. 2019, 40, 55–63. [Google Scholar] [CrossRef] [PubMed]
  16. Jakobi, T.; Dieterich, C. Computational approaches for circular RNA analysis. Wiley Interdiscip. Rev. RNA 2019, 10, e1528. [Google Scholar] [CrossRef] [PubMed]
  17. Chen, L.; Wang, F.; Bruggeman, E.C.; Li, C.; Yao, B. circMeta: A unified computational framework for genomic feature annotation and differential expression analysis of circular RNAs. Bioinformatics 2020, 36, 539–545. [Google Scholar] [CrossRef]
  18. Guo, S.-K.; Nan, F.; Liu, C.-X.; Yang, L.; Chen, L.-L. Mapping circular RNA structures in living cells by SHAPE-MaP. Methods 2021, 196, 47–55. [Google Scholar] [CrossRef]
  19. Gao, Y.; Shang, S.; Guo, S.; Li, X.; Zhou, H.; Liu, H.; Sun, Y.; Wang, J.; Wang, P.; Zhi, H.; et al. Lnc2Cancer 3.0: An updated resource for experimentally supported lncRNA/circRNA cancer associations and web tools based on RNA-seq and scRNA-seq data. Nucleic Acids Res. 2021, 49, D1251–D1258. [Google Scholar] [CrossRef]
  20. Ma, X.-K.; Xue, W.; Chen, L.-L.; Yang, L. CIRCexplorer pipelines for circRNA annotation and quantification from non-polyadenylated RNA-seq datasets. Methods 2021, 196, 3–10. [Google Scholar] [CrossRef] [PubMed]
  21. Chiang, T.-W.; Mai, T.-L.; Chuang, T.-J. CircMiMi: A stand-alone software for constructing circular RNA-microRNA-mRNA interactions across species. BMC Bioinform. 2022, 23, 164. [Google Scholar] [CrossRef] [PubMed]
  22. Molin, A.D.; Gaffo, E.; Difilippo, V.; Buratin, A.; Parenzan, C.T.; Bresolin, S.; Bortoluzzi, S. CRAFT: A bioinformatics software for custom prediction of circular RNA functions. Brief Bioinform. 2022, 23, bbab601. [Google Scholar] [CrossRef]
  23. Zuker, M. On finding all suboptimal foldings of an RNA molecule. Science 1989, 244, 48–52. [Google Scholar] [CrossRef] [PubMed]
  24. Zuker, M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003, 31, 3406–3415. [Google Scholar] [CrossRef] [PubMed]
  25. Hofacker, I.L.; Stadler, P.F. Memory efficient folding algorithms for circular RNA secondary structures. Bioinformatics 2006, 22, 1172–1176. [Google Scholar] [CrossRef]
  26. Hofacker, I.L. Vienna RNA secondary structure server. Nucleic Acids Res. 2003, 31, 3429–3431. [Google Scholar] [CrossRef]
  27. Zhao, P.; Zhang, W.; Chen, S.-J. Cotranscriptional folding kinetics of ribonucleic acid secondary structures. J. Chem. Phys. 2011, 135, 245101. [Google Scholar] [CrossRef]
  28. Sun, T.T.; Zhao, C.; Chen, S.-J. Predicting cotranscriptional folding kinetics for riboswitch. J. Phys. Chem. B 2018, 122, 7484–7496. [Google Scholar] [CrossRef]
  29. Wang, K.; He, Y.; Shen, Y.; Wang, Y.; Xu, X.; Song, X.; Sun, T. Effect of pausing on the cotranscriptional folding kinetics of RNAs. Int. J. Biol. Macromol. 2022, 221, 1345–1355. [Google Scholar] [CrossRef]
  30. Xu, X.; Jin, L.; Xie, L.; Chen, S.-J. Landscape zooming toward the prediction of RNA cotranscriptional folding. J. Chem. Theory Comput. 2022, 18, 2002–2015. [Google Scholar] [CrossRef]
  31. Wang, F.; Sun, L.-Z.; Sun, T.; Chang, S.; Xu, X. Helix-based RNA landscape partition and alternative secondary structure determination. ACS Omega 2019, 4, 15407–15413. [Google Scholar] [CrossRef]
  32. Kerpedjiev, P.; Hammer, S.; Hofacker, I.L. Forna (force-directed RNA): Simple and effective online RNA secondary structure diagrams. Bioinformatics 2015, 31, 3377–3379. [Google Scholar] [CrossRef]
  33. Liu, C.-X.; Li, X.; Nan, F.; Jiang, S.; Gao, X.; Guo, S.-K.; Xue, W.; Cui, Y.; Dong, K.; Ding, H.; et al. Structure and degradation of circular RNAs regulate PKR activation in innate immunity. Cell 2019, 177, 865–880. [Google Scholar] [CrossRef]
  34. Cao, S.; Chen, S.-J. Predicting RNA folding thermodynamics with a reduced chain representation model. RNA 2005, 11, 1884–1897. [Google Scholar] [CrossRef]
  35. Cao, S.; Chen, S.-J. Predicting RNA pseudoknot folding thermodynamics. Nucleic Acids Res. 2006, 34, 2634–2652. [Google Scholar] [CrossRef]
  36. Cao, S.; Chen, S.-J. Predicting structures and stabilities for H-type pseudoknots with inter-helix loop. RNA 2009, 15, 696–706. [Google Scholar] [CrossRef]
  37. Cao, S.; Chen, S.-J. Structure and stability of RNA/RNA kissing complex: With application to HIV dimerization initiation signal. RNA 2011, 17, 2130–2143. [Google Scholar] [CrossRef]
  38. Cao, S.; Xu, X.; Chen, S.-J. Predicting structure and stability for RNA complexes with intermolecular loop-loop base-pairing. RNA 2014, 20, 835–845. [Google Scholar] [CrossRef]
  39. Chen, S.-J. RNA folding: Conformational statistics, folding kinetics, and ion electrostatics. Annu. Rev. Biophys. 2008, 37, 197–214. [Google Scholar] [CrossRef]
  40. Sun, L.-Z.; Zhang, D.; Chen, S.-J. Theory and modeling of RNA structure and interactions with metal ions and small molecules. Annu. Rev. Biophys. 2017, 46, 227–246. [Google Scholar] [CrossRef] [Green Version]
  41. Lipfert, J.; Doniach, S.; Das, R.; Herschlag, D. Understanding nucleic acid-ion interactions. Annu. Rev. Biochem. 2014, 83, 813–841. [Google Scholar] [CrossRef]
  42. Nguyen, H.T.; Hori, N.; Thirumalai, D. Theory and simulations for RNA folding in mixtures of monovalent and divalent cations. Proc. Natl. Acad. Sci. USA 2019, 116, 21022–21030. [Google Scholar] [CrossRef]
  43. Turner, D.H.; Mathews, D.H. NNDB: The nearest neighbor parameter database for predicting stability of nucleic acid secondary structure. Nucleic Acids Res. 2010, 38, D280–D282. [Google Scholar] [CrossRef]
  44. Sheehy, J.P.; Davis, A.R.; Znosko, B.M. Thermodynamic characterization of naturally occurring RNA tetraloops. RNA 2010, 16, 417–429. [Google Scholar] [CrossRef]
  45. Hausmann, N.Z.; Znosko, B.M. Thermodynamic characterization of RNA 2 × 3 nucleotide internal loops. Biochemistry 2012, 51, 5359–5368. [Google Scholar] [CrossRef]
  46. Yesselman, J.D.; Denny, S.K.; Bisaria, N.; Herschlag, D.; Greenleaf, W.J.; Das, R. Sequence-dependent RNA helix conformational preferences predictably impact tertiary structure formation. Proc. Natl. Acad. Sci. USA 2019, 116, 16847–16855. [Google Scholar] [CrossRef]
  47. Zhao, C.; Zhang, D.; Jiang, Y.; Chen, S.-J. Modeling loop composition and ion concentration effects in RNA hairpin folding stability. Biophys. J. 2020, 119, 1439–1455. [Google Scholar] [CrossRef]
  48. Saon, M.S.; Znosko, B.M. Thermodynamic characterization of naturally occurring RNA pentaloops. RNA 2022, 28, 832–841. [Google Scholar] [CrossRef]
  49. Singh, J.; Hanson, J.; Paliwal, K.; Zhou, Y. RNA secondary structure prediction using an ensemble of two-dimensional deep neural networks and transfer learning. Nat. Commun. 2019, 10, 5407. [Google Scholar] [CrossRef] [PubMed]
  50. Fu, L.; Cao, Y.; Wu, J.; Peng, Q.; Nie, Q.; Xie, X. UFold: Fast and accurate RNA secondary structure prediction with deep learning. Nucleic Acids Res. 2022, 50, e14. [Google Scholar] [CrossRef]
  51. Wang, L.; Liu, Y.; Zhong, X.; Liu, H.; Lu, C.; Li, C.; Zhang, H. DMfold: A novel method to predict RNA secondary structure with pseudoknots based on deep learning and improved base pair maximization principle. Front. Genet. 2019, 10, 143. [Google Scholar] [CrossRef]
  52. Willmott, D.; Murrugarra, D.; Ye, Q. Improving RNA secondary structure prediction via state inference with deep recurrent neural networks. Comput. Math. Biophys. 2020, 8, 36–50. [Google Scholar] [CrossRef]
  53. Akiyama, M.; Sato, K.; Sakakibara, Y. A max-margin training of RNA secondary structure prediction integrated with the thermodynamic model. J. Bioinform. Comput. Biol. 2018, 16, 1840025. [Google Scholar] [CrossRef]
  54. Sato, K.; Akiyama, M.; Sakakibara, Y. RNA secondary structure prediction using deep learning with thermodynamic integration. Nat. Commun. 2021, 12, 941. [Google Scholar] [CrossRef]
  55. Dirks, R.M.; Pierce, N.A. An algorithm for computing nucleic acid base-pairing probabilities including pseudoknots. J. Comput. Chem. 2004, 25, 1295–1304. [Google Scholar] [CrossRef]
  56. Xu, X.; Zhao, P.N.; Chen, S.-J. Vfold: A web server for RNA structure and folding thermodynamics prediction. PLoS ONE 2014, 9, e107504. [Google Scholar] [CrossRef]
  57. Xu, X.; Chen, S.-J. VfoldCPX server: Predicting RNA-RNA complex structure and stability. PLoS ONE 2016, 11, e0163454. [Google Scholar] [CrossRef] [Green Version]
Ijms 24 03822 g001 550
Figure 1. Snapshot of the input of the cRNAsp12 server. Once a calculation is submitted, a notification page containing the assigned job ID, as indicated by the dashed arrow, is displayed.
Figure 1. Snapshot of the input of the cRNAsp12 server. Once a calculation is submitted, a notification page containing the assigned job ID, as indicated by the dashed arrow, is displayed.
Ijms 24 03822 g001
Ijms 24 03822 g002 550
Figure 2. Structural constraints of forcing base pairs (HELIX i j k) in (a) and forcing unpaired bases (LOOP i k) in (b). (c) Example of setting the structural constraints for cRNAsp12 prediction. Here, i and j are the nucleotide numbering within the range of (1, N), with N as the length of the circRNA sequence, and k as the number of base pairs or unpaired bases.
Figure 2. Structural constraints of forcing base pairs (HELIX i j k) in (a) and forcing unpaired bases (LOOP i k) in (b). (c) Example of setting the structural constraints for cRNAsp12 prediction. Here, i and j are the nucleotide numbering within the range of (1, N), with N as the length of the circRNA sequence, and k as the number of base pairs or unpaired bases.
Ijms 24 03822 g002
Ijms 24 03822 g003 550
Figure 3. Snapshot of the output of the cRNAsp12 server. The model correctly predicts the three 16–26 bp dsRNAs, as indicated by the dashed rectangles, for the CAMSAP1 circRNA.
Figure 3. Snapshot of the output of the cRNAsp12 server. The model correctly predicts the three 16–26 bp dsRNAs, as indicated by the dashed rectangles, for the CAMSAP1 circRNA.
Ijms 24 03822 g003
Ijms 24 03822 g004 550
Figure 4. Extension of the H-PK and L-KISS motifs. (a) The H-PK motif of a linear RNA contains two helices and three loops (left). (b) The L-KISS motif of two linear RNAs contains three helices (H2 is the kissing helix) and four loops (left). For circular RNAs (right), the H-PK and L-KISS motifs need to be extended with the additional loops (marked in red).
Figure 4. Extension of the H-PK and L-KISS motifs. (a) The H-PK motif of a linear RNA contains two helices and three loops (left). (b) The L-KISS motif of two linear RNAs contains three helices (H2 is the kissing helix) and four loops (left). For circular RNAs (right), the H-PK and L-KISS motifs need to be extended with the additional loops (marked in red).
Ijms 24 03822 g004
Ijms 24 03822 g005 550
Figure 5. Algorithm of the cRNAsp12 model. (a) Two nucleotides are selected to divide a circular RNA sequence into two linear fragments. Secondary structures and folding stabilities of a circRNA are calculated by the additivity assumption characteristic of recursive algorithms. Here, i and j are the nucleotide numbering within the range of (1, N). (b) By selecting top-stable helices, the entire folding landscape is divided into distinct partitions. Each partition defines a structural ensemble featured by the inclusion/exclusion of helices.
Figure 5. Algorithm of the cRNAsp12 model. (a) Two nucleotides are selected to divide a circular RNA sequence into two linear fragments. Secondary structures and folding stabilities of a circRNA are calculated by the additivity assumption characteristic of recursive algorithms. Here, i and j are the nucleotide numbering within the range of (1, N). (b) By selecting top-stable helices, the entire folding landscape is divided into distinct partitions. Each partition defines a structural ensemble featured by the inclusion/exclusion of helices.
Ijms 24 03822 g005
Table
Table 1. Performance of the cRNAsp12 model.
Table 1. Performance of the cRNAsp12 model.
Host Gene of circRNALength (nt)No. of 16–26 bp dsRNAs
SHAPE-RNAfold 1RNAfold 2Mfold 2cRNAsp12 2
CAMSAP14253133
CCNB13784100
EPHB43622011
EZH22531010
FCHO22682122
FGFR1-11791011
PVT14104122
RELL14342012
SDHAF23342012
TBCD3893333
UIMC13972012
ARID1B2862002
CNN22051011
DHX342181011
FKBP82592221
KIAA03684353222
MBOAT22241111
PIP5K1C2491111
PPP1CB2242122
PROSC2201111
PTK23941011
SLC22A232592222
SNHG41611111
TMEM1813241111
VAPB2581101
Average/Total30246203236
1 From Figure 4 of Ref [33]. 2 dsRNAs are considered correctly predicted ones if more than half of base pairs are correctly predicted.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, F.; Li, W.; Li, B.; Xie, L.; Tong, Y.; Xu, X. cRNAsp12 Web Server for the Prediction of Circular RNA Secondary Structures and Stabilities. Int. J. Mol. Sci. 2023, 24, 3822. https://doi.org/10.3390/ijms24043822

AMA Style

Wang F, Li W, Li B, Xie L, Tong Y, Xu X. cRNAsp12 Web Server for the Prediction of Circular RNA Secondary Structures and Stabilities. International Journal of Molecular Sciences. 2023; 24(4):3822. https://doi.org/10.3390/ijms24043822

Chicago/Turabian Style

Wang, Fengfei, Wei Li, Baiyi Li, Liangxu Xie, Yunguang Tong, and Xiaojun Xu. 2023. "cRNAsp12 Web Server for the Prediction of Circular RNA Secondary Structures and Stabilities" International Journal of Molecular Sciences 24, no. 4: 3822. https://doi.org/10.3390/ijms24043822

APA Style

Wang, F., Li, W., Li, B., Xie, L., Tong, Y., & Xu, X. (2023). cRNAsp12 Web Server for the Prediction of Circular RNA Secondary Structures and Stabilities. International Journal of Molecular Sciences, 24(4), 3822. https://doi.org/10.3390/ijms24043822

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop