Impact of Negative Feedbacks on De Novo Pyrimidines Biosynthesis in Escherichia coli
Abstract
1. Introduction
2. Results and Discussion
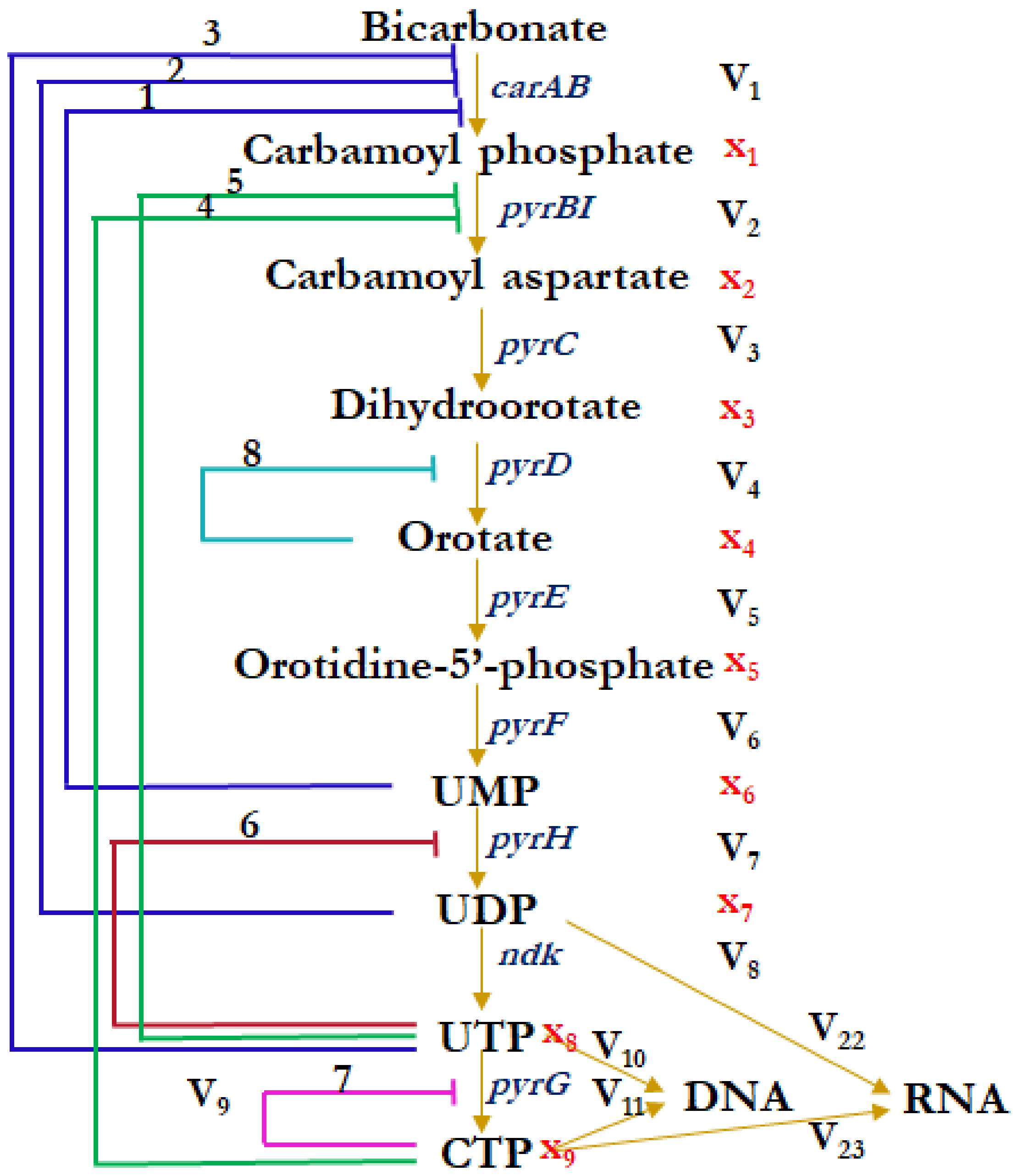
2.1. Integral Mathematical Model of Pyrimidine Biosynthesis
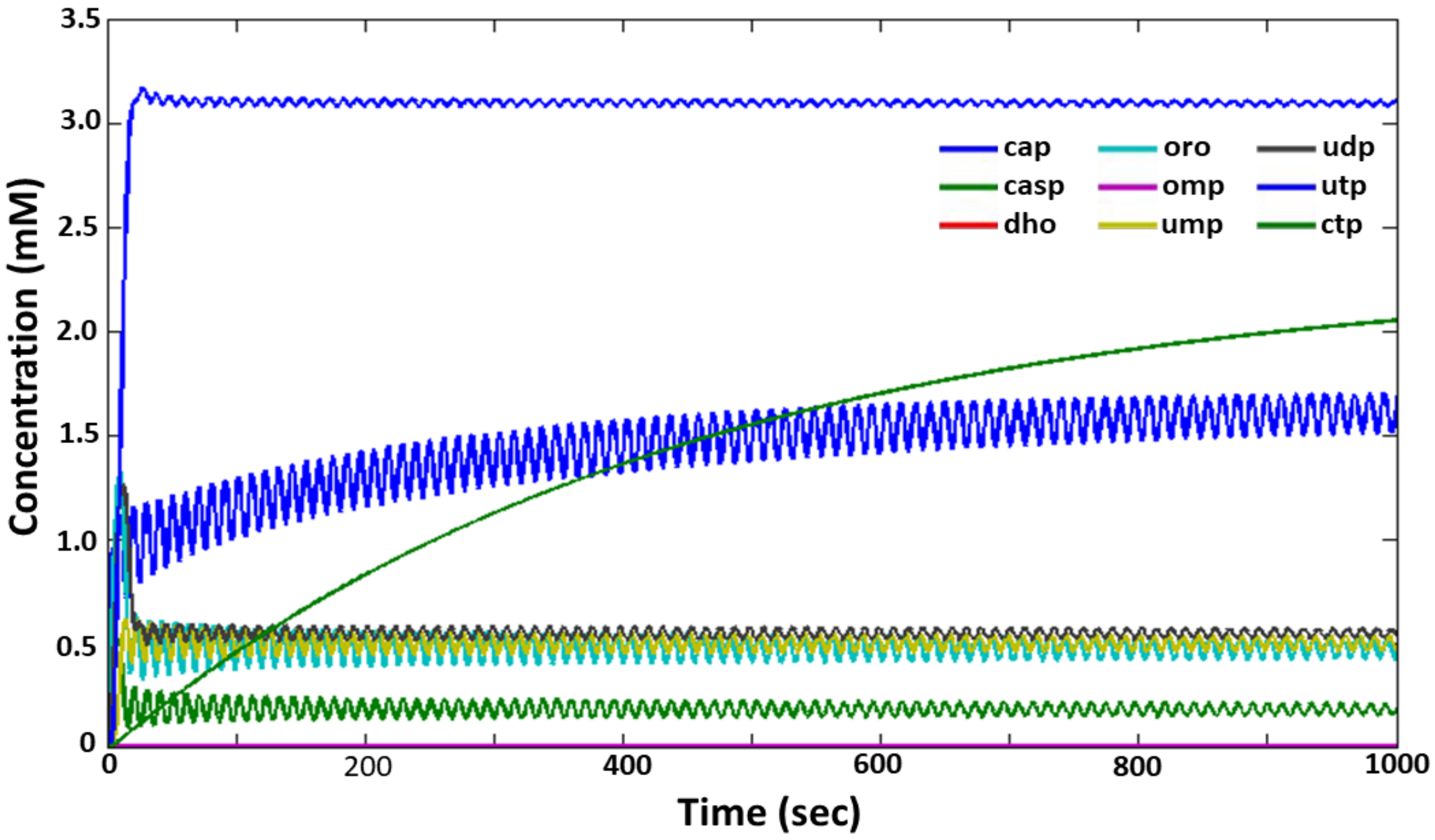
2.2. Adaptation of Model (1) to Experimental Data
2.3. Analysis of the Dynamic Modes of Functioning of the Model (1) De Novo Pyrimidine Nucleotide Synthesis
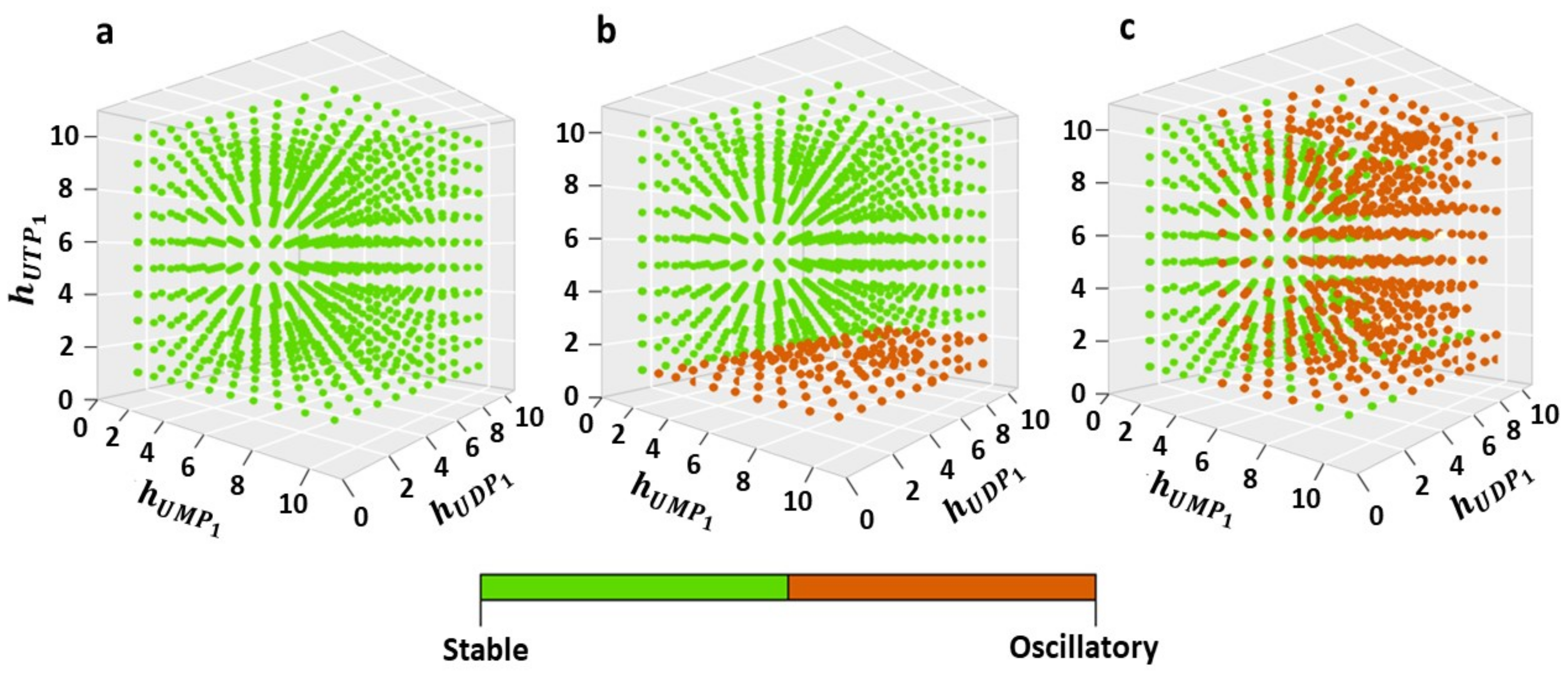
2.4. Effect of the Complexity of Negative Feedbacks on the Functioning Mode of the Model (1)
3. Materials and Methods
3.1. Methods of the Numerical Analysis
3.2. Methods of the Parameter Fitting
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leite, M.C.; Wang, Y. Multistability, oscillations and bifurcations in feedback loops. Math. Biosci. Eng. 2010, 7, 83–97. [Google Scholar] [PubMed]
- Gérard, C.; Goldbeter, A. From simple to complex patterns of oscillatory behavior in a model for the mammalian cell cycle containing multiple oscillatory circuits. Chaos 2010, 20, 045109. [Google Scholar] [CrossRef]
- Kogai, V.V.; Likhoshvai, V.A.; Fadeev, S.I.; Khlebodarova, T.M. Multiple scenarios of transition to chaos in the alternative splicing model. Int. J. Bifurcat. Chaos 2017, 27, e1730006. [Google Scholar] [CrossRef]
- Khlebodarova, T.M.; Kogai, V.V.; Trifonova, E.A.; Likhoshvai, V.A. Dynamic landscape of the local translation at activated synapses. Mol. Psych. 2018, 23, 107–114. [Google Scholar] [CrossRef]
- Tyson, J.J. On the existence of oscillatory solutions in negative feedback cellular control processes. J. Math. Biol. 1974, 1, 311–315. [Google Scholar] [CrossRef]
- Hirata, H.; Yoshiura, S.; Ohtsuka, T.; Bessho, Y.; Harada, T.; Yoshikawa, K.; Kageyama, R. Oscillatory expression of the bHLH factor Hes1 regulated by a negative feedback loop. Science 2002, 298, 840–843. [Google Scholar] [CrossRef]
- Pigolotti, S.; Krishna, S.; Jensen, M.H. Oscillation patterns in negative feedback loops. Proc. Natl. Acad. Sci. USA 2007, 104, 6533–6537. [Google Scholar] [CrossRef]
- Ratushny, A.V.; De Leenheer, P.; Bazhan, S.I.; Bocharov, G.A.; Khlebodarova, T.M.; Likhoshvai, V.A. On the potential for multiscale oscillatory behavior in HIV. In Global Virology II: HIV and NeuroAIDS, 1st ed.; Shapshak, P., Levine, A.J., Foley, B.T., Somboonwit, C., Singer, E., Chiappelli, F., Sinnott, J.T., Eds.; Springer Publishing: New York, NY, USA, 2017; pp. 897–924. [Google Scholar] [CrossRef]
- Likhoshvai, V.A.; Golubyatnikov, V.P.; Khlebodarova, T.M. Limit cycles in models of circular gene networks regulated by negative feedbacks. BMC Bioinform. 2020, 21, 255. [Google Scholar] [CrossRef]
- Khlebodarova, T.M.; Kogai, V.V.; Likhoshvai, V.A. On the dynamical aspects of local translation at the activated synapse. BMC Bioinform. 2020, 21, 258. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Bastos de Figueiredo, J.C.; Diambra, L.; Glass, L.; Malta, C.P. Chaos in two–looped negative feedback systems. Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys. 2002, 65, e051905. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ye, W.; Qian, Y.; Zheng, Z.; Huang, X.; Hu, G. Chaotic motifs in gene regulatory networks. PLoS ONE 2012, 7, e39355. [Google Scholar] [CrossRef] [PubMed]
- Likhoshvai, V.A.; Kogai, V.V.; Fadeev, S.I.; Khlebodarova, T.M. Alternative splicing can lead to chaos. J. Bioinform. Comput. Biol. 2015, 13, 1540003. [Google Scholar] [CrossRef] [PubMed]
- Khlebodarova, T.M.; Kogai, V.V.; Fadeev, S.I.; Likhoshvai, V.A. Chaos and hyperchaos in simple gene network with negative feedback and time delays. J. Bioinform. Comput. Biol. 2017, 15, 1650042. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.K.; Kulasiri, D. On the functional diversity of dynamical behaviour in genetic and metabolic feedback systems. BMC Syst. Biol. 2009, 3, 51. [Google Scholar] [CrossRef] [PubMed]
- Gerhart, J.C.; Pardee, A.B. The enzymology of control by feedback inhibition. J. Biol. Chem. 1962, 237, 891–896. [Google Scholar] [CrossRef]
- Anderson, P.M.; Meister, A. Control of Escherichia coli carbamyl phosphate synthetase by purine and pyrimidine nucleotides. Biochemistry 1966, 5, 3164–3169. [Google Scholar] [CrossRef]
- Wild, J.R.; Loughrey–Chen, S.J.; Corder, T.S. In the presence of CTP, UTP becomes an allosteric inhibitor of aspartate transcarbamoylase. Proc. Natl. Acad. Sci. USA 1989, 86, 46–50. [Google Scholar] [CrossRef]
- Endrizzi, J.A.; Kim, H.; Anderson, P.M.; Baldwin, E.P. Mechanisms of product feedback regulation and drug resistance in cytidine triphosphate synthetases from the structure of a CTP–inhibited complex. Biochemistry 2005, 44, 13491–13499. [Google Scholar] [CrossRef]
- Johansson, E.; Thymark, M.; Bynck, J.H.; Fanø, M.; Larsen, S.; Willemoës, M. Regulation of dCTP deaminase from Escherichia coli by nonallosteric dTTP binding to an inactive form of the enzyme. FEBS J. 2007, 274, 4188–4198. [Google Scholar] [CrossRef]
- Reaves, M.L.; Young, B.D.; Hosios, A.M.; Xu, Y.F.; Rabinowitz, J.D. Pyrimidine homeostasis is accomplished by directed overflow metabolism. Nature 2013, 500, 237–241. [Google Scholar] [CrossRef] [PubMed]
- Huzyk, L.; Clark, D.J. Nucleoside triphosphate pools in synchronous cultures of Escherichia coli. J. Bacteriol. 1971, 108, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Fustin, J.M.; Doi, M.; Yamada, H.; Komatsu, R.; Shimba, S.; Okamura, H. Rhythmic nucleotide synthesis in the liver: Temporal segregation of metabolites. Cell Rep. 2012, 1, 341–349. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Görling, B.; Luy, B.; Du, J.; Yan, J. Integrative analysis of circadian transcriptome and metabolic network reveals the role of de novo purine synthesis in circadian control of cell cycle. PLoS Comput. Biol. 2015, 11, e1004086. [Google Scholar] [CrossRef] [PubMed]
- Goldbeter, A. Organisation Spatio–Temporelle Dans Les Systèmes Enzymatiques Ouverts. Ph.D. Thesis, Universite Libre de Bruxelles, Brussels, Belgium, 1973. [Google Scholar]
- Rodríguez, M.; Good, T.A.; Wales, M.E.; Hua, J.P.; Wild, J.R. Modeling allosteric regulation of de novo pyrimidine biosynthesis in Escherichia coli. J. Theor. Biol. 2005, 234, 299–310. [Google Scholar] [CrossRef]
- Likhoshvai, V.A.; Khlebodarova, T.M.; Ree, M.T.; Kolchanov, N.A. Metabolic engineering in silico. Appl. Biochem. Micribiol. 2010, 46, 671–687. [Google Scholar] [CrossRef]
- Kozlov, K.; Samsonov, A. DEEP—Differential evolution entirely parallel method for gene regulatory networks. J. Supercomput. 2011, 57, 172–178. [Google Scholar] [CrossRef]
- Granqvist, E.; Hartley, M.; Morris, R.J. BaSAR—A tool in R for frequency detection. Biosystems 2012, 110, 60–63. [Google Scholar] [CrossRef]
- Kazantsev, F.; Akberdin, I.; Lashin, S.; Ratushny, A.; Ree, N.; Timonov, V.; Khlebodarova, T.; Likhoshvai, V. MAMMOTh: A new database for curated mathematical models of biomolecular systems. J. Bioinf. Comput. Biol. 2018, 16, 1740010. [Google Scholar] [CrossRef] [PubMed]
- Likhoshvai, V.A.; Matushkin, Y.G.; Vatolin, Y.N.; Bazhan, S.I. A generalized chemical kinetic method for simulating complex biological systems. A computer model of λ phage ontogenesis. Comput. Technol. 2000, 5, 87–99. [Google Scholar]
- Likhoshvai, V.A.; Matushkin, Y.G.; Ratushny, A.V.; Ananko, E.A.; Ignatieva, E.V.; Podkolodnaya, O.A. Generalized chemokinetic method for gene network simulation. Mol. Biol. 2001, 35, 919–925. [Google Scholar] [CrossRef]
- Bennett, B.D.; Kimball, E.H.; Gao, M.; Osterhout, R.; Van Dien, S.J.; Rabinowitz, J.D. Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nat. Chem. Biol. 2009, 5, 593–599. [Google Scholar] [CrossRef]
- Ishii, N.; Nakahigashi, K.; Baba, T.; Robert, M.; Soga, T.; Kanai, A.; Tomita, M. Multiple high–throughput analyses monitor the response of E. coli to perturbations. Science 2007, 316, 593–597. [Google Scholar] [CrossRef] [PubMed]
- Welch, B.L. On the comparison of several mean values: An alternative approach. Biometrika 1951, 38, 330–336. [Google Scholar] [CrossRef]
- Kolpakov, F.; Akberdin, I.; Kiselev, I.; Kolmykov, S.; Kondrakhin, Y.; Kulyashov, V.; Kutumova, E.; Pintus, S.; Ryabova, A.; Sharipov, R.; et al. BioUML—Towards a universal research platform. Nucl. Acids Res. 2022, 50, W124–W131. [Google Scholar] [CrossRef]
- Fadeev, S.I.; Kogai, V.V. Using parameter continuation based on the multiple shooting method for numerical research of nonlinear boundary value problems. Int. J. Pure Appl. Math. 2004, 14, 467–498. [Google Scholar]
- Fadeev, S.I.; Korolev, V.K.; Gainova, I.A.; Medvedev, A.E. The package STEP+ for numerical study of autonomous systems arising when modeling dynamics of genetic–molecular systems. In Proceedings of the Fifth International Conference on Bioinformatics of Genome Regulation and Structure, Novosibirsk, Russia, 16–22 July 2006; Kolchanov, N., Hofestadt, R., Eds.; Russian Academy of Sciences Siberian Branch: Novosibirsk, Russia, 2006; Volume 2, pp. 118–120. [Google Scholar]
- Lu, P.; Vogel, C.; Wang, R.; Yao, X.; Marcotte, E.M. Absolute protein expression profiling estimates the relative contributions of transcriptional and translational regulation. Nat. Biotechnol. 2007, 25, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Li, G.W.; Burkhardt, D.; Gross, C.; Weissman, J.S. Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell 2014, 157, 624–635. [Google Scholar] [CrossRef]
- Liu, L.; Wales, M.E.; Wild, J.R. Temperature effects on the allosteric responses of native and chimeric aspartate transcarbamoylases. J. Mol. Biol. 1998, 282, 891–901. [Google Scholar] [CrossRef] [PubMed]
- Hack, E.S.; Vorobyova, T.; Sakash, J.B.; West, J.M.; Macol, C.P.; Hervé, G.; Williams, M.K.; Kantrowitz, E.R. Characterization of the aspartate transcarbamoylase from Methanococcus jannaschii. J. Biol. Chem. 2000, 275, 15820–15827. [Google Scholar] [CrossRef]
- Foote, J.; Lauritzen, A.M.; Lipscomb, W.N. Substrate specificity of aspartate transcarbamylase. Interaction of the enzyme with analogs of aspartate and succinate. J. Biol. Chem. 1985, 260, 9624–9629. [Google Scholar] [CrossRef] [PubMed]
- Albe, K.R.; Butler, M.H.; Wright, B.E. Cellular concentrations of enzymes and their substrates. J. Theor. Biol. 1990, 143, 163–195. [Google Scholar] [CrossRef]
- Xu, W.; Kantrowitz, E.R. Function of serine–52 and serine–80 in the catalytic mechanism of Escherichia coli aspartate transcarbamoylase. Biochemistry 1991, 30, 2535–2542. [Google Scholar] [CrossRef] [PubMed]
- Pastra–Landis, S.C.; Evans, D.R.; Lipscomb, W.N. The effect of pH on the cooperative behavior of aspartate transcarbamylase from Escherichia coli. J. Biol. Chem. 1978, 253, 4624–4630. [Google Scholar] [CrossRef]
- Wales, M.E.; Madison, L.L.; Glaser, S.S.; Wild, J.R. Divergent allosteric patterns verify the regulatory paradigm for aspartate transcarbamylase. J. Mol. Biol. 1999, 294, 1387–1400. [Google Scholar] [CrossRef] [PubMed]
- Lei, Z.; Wang, N.; Tan, H.; Zheng, J.; Jia, Z. Conformational plasticity of the active site entrance in E. coli aspartate transcarbamoylase and its implication in feedback regulation. Int. J. Mol. Sci. 2020, 21, 320. [Google Scholar] [CrossRef] [PubMed]
- Patel, C.; Vaishnav, A.; Edwards, B.F.P.; Evans, D.R. Characterization and assembly of the Pseudomonas aeruginosa aspartate transcarbamoylase–pseudo dihydroorotase complex. PLoS ONE 2020, 15, e0229494. [Google Scholar] [CrossRef]
- Ahuja, A.; Purcarea, C.; Ebert, R.; Sadecki, S.; Guy, H.I.; Evans, D.R. Aquifex aeolicus dihydroorotase: Association with aspartate transcarbamoylase switches on catalytic activity. J. Biol. Chem. 2004, 279, 53136–53144. [Google Scholar] [CrossRef]
- Truong, L.; Hevener, K.E.; Rice, A.J.; Patel, K.; Johnson, M.E.; Lee, H. High–level expression, purification, and characterization of Staphylococcus aureus dihydroorotase (PyrC) as a cleavable His–SUMO fusion. Protein Expr. Purif. 2013, 88, 98–106. [Google Scholar] [CrossRef]
- Rice, A.J.; Lei, H.; Santarsiero, B.D.; Lee, H.; Johnson, M.E. Ca–asp bound X–ray structure and inhibition of Bacillus anthracis dihydroorotase (DHOase). Bioorg. Med. Chem. 2016, 24, 4536–4543. [Google Scholar] [CrossRef]
- Krungkrai, J.; Cerami, A.; Henderson, G.B. Pyrimidine biosynthesis in parasitic protozoa: Purification of a monofunctional dihydroorotase from Plasmodium berghei and Crithidia fasciculata. Biochemistry 1990, 29, 6270–6275. [Google Scholar] [CrossRef] [PubMed]
- Krungkrai, S.R.; Wutipraditkul, N.; Krungkrai, J. Dihydroorotase of human malarial parasite Plasmodium falciparum differs from host enzyme. Biochem. Biophys. Res. Commun. 2008, 366, 821–826. [Google Scholar] [CrossRef]
- Tiwari, K.; Kumar, R.; Dubey, V.K. Biochemical characterization of dihydroorotase of Leishmania donovani: Understanding pyrimidine metabolism through its inhibition. Biochimie 2016, 131, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Washabaugh, M.W.; Collins, K.D. Dihydroorotase from Escherichia coli. J. Biol. Chem. 1984, 259, 3293–3298. [Google Scholar] [CrossRef]
- Daniel, R.; Kokel, B.; Caminade, E.; Martel, A.; Le Goffic, F. Assay of Escherichia coli dihydroorotase with enantiomeric substrate: Practical preparation of carbamyl L–aspartate and high–performance liquid chromatography analysis of catalysis product. Anal. Biochem. 1996, 239, 130–135. [Google Scholar] [CrossRef] [PubMed]
- Davidi, D.; Noor, E.; Liebermeister, W.; Bar–Even, A.; Flamholz, A.; Tummler, K.; Barenholz, U.; Goldenfeld, M.; Shlomi, T.; Milo, R. Global characterization of in vivo enzyme catalytic rates and their correspondence to in vitro kcat measurements. Proc. Natl. Acad. Sci. USA 2016, 113, 3401–3406. [Google Scholar] [CrossRef] [PubMed]
- Teusink, B.; Passarge, J.; Reijenga, C.A.; Esgalhado, E.; Van der Weijden, C.C.; Schepper, M.; Walsh, M.C.; Bakker, B.M.; Van Dam, K.; Westerhoff, H.V.; et al. Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem. 2000, 267, 5313–5329. [Google Scholar] [CrossRef]
- Schnell, S.; Turner, T.E. Reaction kinetics in intracellular environments with macromolecular crowding: Simulations and rate laws. Prog. Biophys. Mol. Biol. 2004, 85, 235–260. [Google Scholar] [CrossRef]
- Good, N.M.; Moore, R.S.; Suriano, C.J.; Martinez–Gomez, N.C. Contrasting in vitro and in vivo methanol oxidation activities of lanthanide–dependent alcohol dehydrogenases XoxF1 and ExaF from Methylobacterium extorquens AM1. Sci. Rep. 2019, 9, 4248. [Google Scholar] [CrossRef]
- Briozzo, P.; Evrin, C.; Meyer, P.; Assairi, L.; Joly, N.; Barzu, O.; Gilles, A.M. Structure of Escherichia coli UMP kinase differs from that of other nucleoside monophosphate kinases and sheds new light on enzyme regulation. J. Biol. Chem. 2005, 280, 25533–25540. [Google Scholar] [CrossRef]
- Serina, L.; Blondin, C.; Krin, E.; Sismeiro, O.; Danchin, A.; Sakamoto, H.; Gilles, A.M.; Bârzu, O. Escherichia coli UMP–kinase, a member of the aspartokinase family, is a hexamer regulated by guanine nucleotides and UTP. Biochemistry 1995, 34, 5066–5074. [Google Scholar] [CrossRef] [PubMed]
- Vecchiarelli, A.G.; Li, M.; Mizuuchi, M.; Hwang, L.C.; Seol, Y.; Neuman, K.C.; Mizuuchi, K. Membrane–bound MinDE complex acts as a toggle switch that drives Min oscillation coupled to cytoplasmic depletion of MinD. Proc. Natl. Acad. Sci. USA 2016, 113, E1479–E1488. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.L.; Brynildsen, M.P. Discovery and dissection of metabolic oscillations in the microaerobic nitric oxide response network of Escherichia coli. Proc. Natl. Acad. Sci. USA 2016, 113, E1757–E1766. [Google Scholar] [CrossRef]
- Sherratt, D.J. Oscillation helps to get division right. Proc. Natl. Acad. Sci. USA 2016, 113, 2803–2805. [Google Scholar] [CrossRef] [PubMed]
- Gentleman, R.; Carey, V.; Huber, W.; Hahne, F. Genefilter: Methods for filtering genes from high-throughput experiments. R Package Version 2015, 1. [Google Scholar]
- Gentleman, R.C.; Carey, V.J.; Bates, D.M.; Bolstad, B.; Dettling, M.; Dudoit, S.; Ellis, B.; Gautier, L.; Ge, Y.; Gentry, J.; et al. Bioconductor: Open software development for computational biology and bioinformatics. Genome Biol. 2004, 5, R80. [Google Scholar] [CrossRef] [PubMed]
- Ivanisenko, N.V.; Mishchenko, E.L.; Akberdin, I.R.; Demenkov, P.S.; Likhoshvai, V.A.; Kozlov, K.N.; Todorov, D.I.; Gursky, V.V.; Samsonova, M.G.; Samsonov, A.M.; et al. A new stochastic model for subgenomic hepatitis C virus replication considers drug resistant mutants. PLoS ONE 2014, 29, e91502. [Google Scholar] [CrossRef] [PubMed]
- Ivanisenko, N.V.; Mishchenko, E.L.; Akberdin, I.R.; Demenkov, P.S.; Likhoshvai, V.A.; Kozlov, K.N.; Todorov, D.I.; Samsonova, M.G.; Samsonov, A.M.; Kolchanov, N.A.; et al. Replication of the subgenomic hepatitis C virus replicon in the presence of the NS3 protease inhibitors: A stochastic model. Biophysics 2013, 58, 592. [Google Scholar] [CrossRef]
- Kozlov, K.; Gursky, V.; Kulakovskiy, I.; Samsonova, M. Sequence-based model of gap gene regulatory network. In Proceedings of the 9th International Conference on Bioinformatics of Genome Regulation and Structure/Systems Biology, Novosibirsk, Russia, 23–28 June 2014. [Google Scholar]
- Kozlov, K.; Gursky, V.; Kulakovskiy, I.; Samsonova, M. Sequence-based model of gap gene regulatory network. BMC Genom. 2014, 15, S6. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, K.; Gursky, V.V.; Kulakovskiy, I.V.; Dymova, A.; Samsonova, M. Analysis of functional importance of binding sites in the Drosophila gap gene network model. BMC Genom. 2015, 16, S7. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, K.; Surkova, S.; Myasnikova, E.; Reinitz, J.; Samsonova, M. Modeling of gap gene expression in Drosophila Kruppel mutants. PLoS Comput Biol. 2012, 8, e1002635. [Google Scholar] [CrossRef] [PubMed]
- Nuriddinov, M.A.; Kazantsev, F.V.; Rozanov, A.S.; Kozlov, K.N.; Peltek, S.E.; Akberdin, I.R.; Kolchanov, N.A. Mathematical modeling of ethanol and lactic acid biosynthesis by theromphilic Geobacillus bacteria. Russ. J. Genet. Appl. Res. 2013, 17, 686–704. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]


| Parameter | Value of the Parameter | ||
|---|---|---|---|
| Table S4, “Manual” | Table S4, “Best” | Oscillation | |
| hump1 | 1.4 | 4 | 2.1 |
| k2, mM/s | 0.31 | 0.073 | 0.0031 |
| k3, mM/s | 0.351 | 0.486 | 0.00351 |
| k9, mM/s | 0.0000174 | 0.000174 | 0.000174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akberdin, I.R.; Kozlov, K.N.; Kazantsev, F.V.; Fadeev, S.I.; Likhoshvai, V.A.; Khlebodarova, T.M. Impact of Negative Feedbacks on De Novo Pyrimidines Biosynthesis in Escherichia coli. Int. J. Mol. Sci. 2023, 24, 4806. https://doi.org/10.3390/ijms24054806
Akberdin IR, Kozlov KN, Kazantsev FV, Fadeev SI, Likhoshvai VA, Khlebodarova TM. Impact of Negative Feedbacks on De Novo Pyrimidines Biosynthesis in Escherichia coli. International Journal of Molecular Sciences. 2023; 24(5):4806. https://doi.org/10.3390/ijms24054806
Chicago/Turabian StyleAkberdin, Ilya R., Konstantin N. Kozlov, Fedor V. Kazantsev, Stanislav I. Fadeev, Vitaly A. Likhoshvai, and Tamara M. Khlebodarova. 2023. "Impact of Negative Feedbacks on De Novo Pyrimidines Biosynthesis in Escherichia coli" International Journal of Molecular Sciences 24, no. 5: 4806. https://doi.org/10.3390/ijms24054806
APA StyleAkberdin, I. R., Kozlov, K. N., Kazantsev, F. V., Fadeev, S. I., Likhoshvai, V. A., & Khlebodarova, T. M. (2023). Impact of Negative Feedbacks on De Novo Pyrimidines Biosynthesis in Escherichia coli. International Journal of Molecular Sciences, 24(5), 4806. https://doi.org/10.3390/ijms24054806





