Waiting Time Distributions in Hybrid Models of Motor–Bead Assays: A Concept and Tool for Inference
Abstract
:1. Introduction
2. Setup and Theory
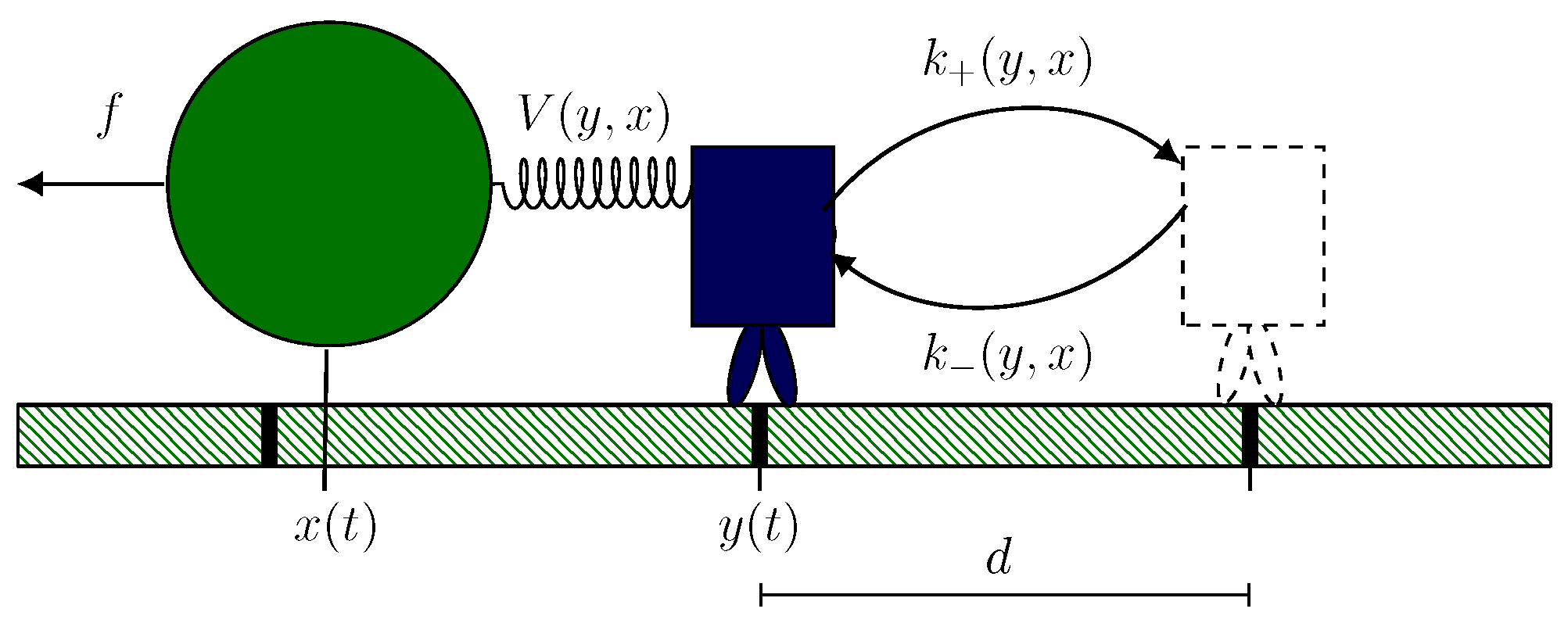
2.1. Hybrid Motor–Bead Model
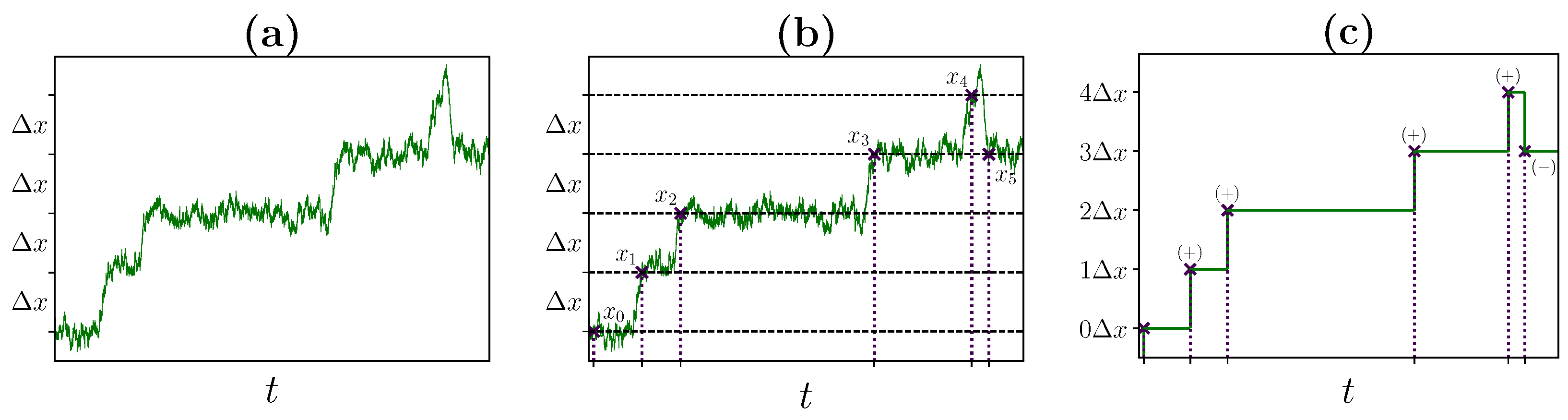
2.2. Identifying Transitions via Milestoning
2.3. Transition Statistics and Conditioned Counting
3. Application to F1-ATPase
3.1. Simulation Method and Model Parameters
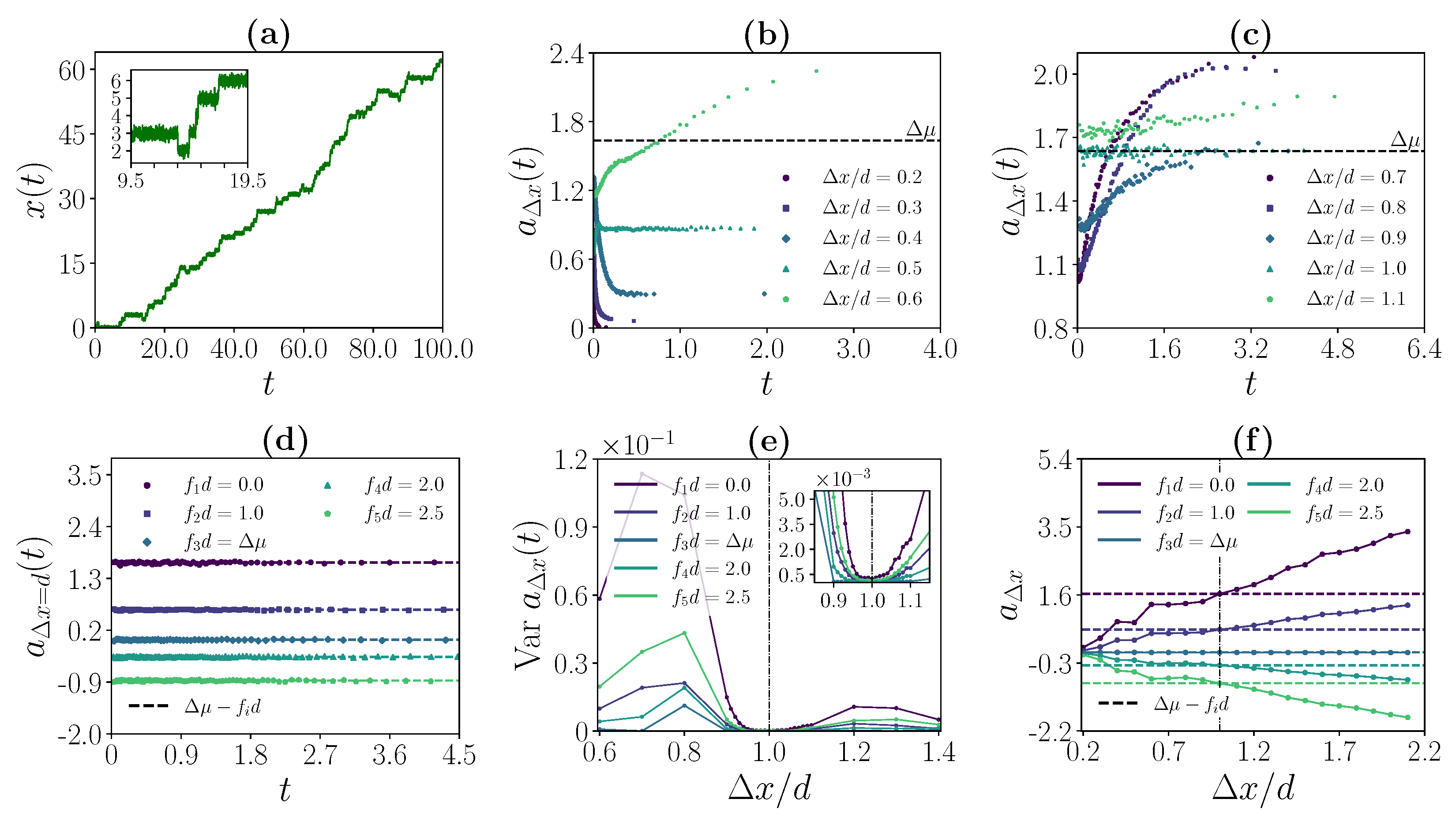
3.2. Strong Coupling Regime
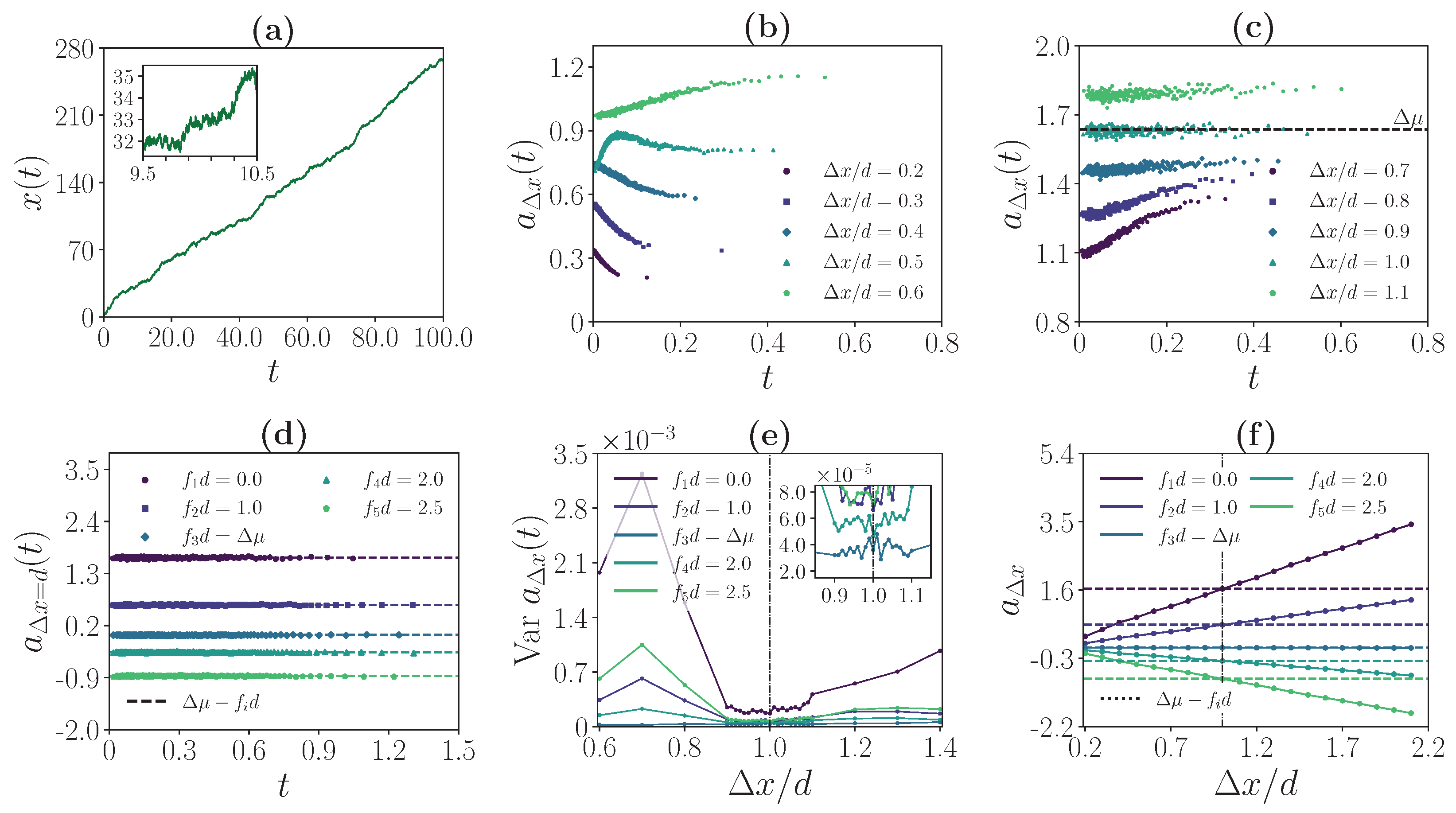
3.3. Weak Coupling Regime
4. Discussion
4.1. Relation to Established Inference Tools
4.2. The Crucial Role of Waiting Time Distributions
4.3. Alternative Observables
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, H. A simple theory of motor protein kinetics and energetics. Biophys. Chem. 1997, 67, 263–267. [Google Scholar] [CrossRef] [PubMed]
- Andrieux, D.; Gaspard, P. Fluctuation theorems and the nonequilibrium thermodynamics of molecular motors. Phys. Rev. E 2006, 74, 011906. [Google Scholar] [CrossRef] [PubMed]
- Gaspard, P.; Gerritsma, E. The stochastic chemomechanics of the -ATPase molecular motor. J. Theor. Biol. 2007, 247, 672–686. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, D. Stochastic mechano-chemical kinetics of molecular motors: A multidisciplinary enterprise from a physicist’s perspective. Phys. Rep. 2013, 529, 1–197. [Google Scholar] [CrossRef]
- Ritort, F. Single-molecule experiments in biological physics: Methods and applications. J. Phys. Condens. Matter 2006, 18, R531. [Google Scholar] [CrossRef]
- Herbert, K.M.; Greenleaf, W.J.; Block, S.M. Single-Molecule Studies of RNA Polymerase: Motoring Along. Annu. Rev. Biochem. 2008, 77, 149–176. [Google Scholar] [CrossRef]
- Veigel, C.; Schmidt, C.F. Moving into the cell: Single-molecule studies of molecular motors in complex environments. Nat. Rev. Mol. Cell Biol. 2011, 12, 163–176. [Google Scholar] [CrossRef]
- Ariga, T.; Tomishige, M.; Mizuno, D. Nonequilibrium Energetics of Molecular Motor Kinesin. Phys. Rev. Lett. 2018, 121, 218101. [Google Scholar] [CrossRef]
- Bustamante, C.; Yan, S. The development of single molecule force spectroscopy: From polymer biophysics to molecular machines. Q. Rev. Biophys. 2022, 55, e9. [Google Scholar] [CrossRef]
- Kolomeisky, A.B.; Fisher, M.E. Molecular Motors: A Theorist’s Perspective. Annu. Rev. Phys. Chem. 2007, 58, 675–695. [Google Scholar] [CrossRef] [PubMed]
- Liepelt, S.; Lipowsky, R. Kinesin’s Network of Chemomechanical Motor Cycles. Phys. Rev. Lett. 2007, 98, 258102. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R.; Liepelt, S. Chemomechanical Coupling of Molecular Motors: Thermodynamics, Network Representations, and Balance Conditions. J. Stat. Phys. 2008, 130, 39–67. [Google Scholar] [CrossRef]
- Astumian, R.D. Thermodynamics and Kinetics of Molecular Motors. Biophys. J. 2010, 98, 2401–2409. [Google Scholar] [CrossRef]
- Kolomeisky, A.B. Motor Proteins and Molecular Motors; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jülicher, F.; Ajdari, A.; Prost, J. Modeling molecular motors. Rev. Mod. Phys. 1997, 69, 1269–1282. [Google Scholar] [CrossRef]
- Reimann, P. Brownian motors: Noisy transport far from equilibrium. Phys. Rep. 2002, 361, 57–265. [Google Scholar] [CrossRef]
- Ait-Haddou, R.; Herzog, W. Brownian ratchet models of molecular motors. Cell Biochem. Biophys. 2003, 38, 191–213. [Google Scholar] [CrossRef]
- Astumian, R.D.; Mukherjee, S.; Warshel, A. The Physics and Physical Chemistry of Molecular Machines. ChemPhysChem 2016, 17, 1719–1741. [Google Scholar] [CrossRef]
- Xing, J.; Liao, J.C.; Oster, G. Making ATP. Proc. Natl. Acad. Sci. USA 2005, 102, 16539–16546. [Google Scholar] [CrossRef]
- Zimmermann, E.; Seifert, U. Efficiencies of a molecular motor: A generic hybrid model applied to the F1-ATPase. New J. Phys. 2012, 14, 103023. [Google Scholar] [CrossRef]
- Zimmermann, E.; Seifert, U. Effective rates from thermodynamically consistent coarse-graining of models for molecular motors with probe particles. Phys. Rev. E 2015, 91, 022709. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D. Exact distribution for work and stochastic efficiency of an isothermal machine. J. Stat. Mech. Theory Exp. 2018, 2018, 073201. [Google Scholar] [CrossRef]
- Blackwell, R.; Jung, D.; Bukenberger, M.; Smith, A.S. The Impact of Rate Formulations on Stochastic Molecular Motor Dynamics. Sci. Rep. 2019, 9, 18373. [Google Scholar] [CrossRef]
- Brown, A.I.; Sivak, D.A. Theory of Nonequilibrium Free Energy Transduction by Molecular Machines. Chem. Rev. 2020, 120, 434–459. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D.; Large, S.J.; Toyabe, S.; Sivak, D.A. Optimal Control of the F1-ATPase Molecular Motor. J. Phys. Chem. Lett. 2022, 13, 11844–11849. [Google Scholar] [CrossRef] [PubMed]
- Leighton, M.P.; Sivak, D.A. Inferring subsystem efficiencies in bipartite molecular machines. arXiv 2022, arXiv:2209.12084. [Google Scholar]
- Wang, H. Several Issues in Modeling Molecular Motors. J. Comput. Theor. Nanosci. 2008, 5, 2311–2345. [Google Scholar] [CrossRef]
- Brown, A.I.; Sivak, D.A. Pulling cargo increases the precision of molecular motor progress. Europhys. Lett. 2019, 126, 40004. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Makarov, D.E. From Nonequilibrium Single-Molecule Trajectories to Underlying Dynamics. J. Phys. Chem. Lett. 2020, 11, 1682–1688. [Google Scholar] [CrossRef]
- Godec, A.; Makarov, D.E. Challenges in Inferring the Directionality of Active Molecular Processes from Single-Molecule Fluorescence Resonance Energy Transfer Trajectories. J. Phys. Chem. Lett. 2023, 14, 49–56. [Google Scholar] [CrossRef]
- Barato, A.C.; Seifert, U. Thermodynamic Uncertainty Relation for Biomolecular Processes. Phys. Rev. Lett. 2015, 114, 158101. [Google Scholar] [CrossRef] [PubMed]
- Gingrich, T.R.; Horowitz, J.M.; Perunov, N.; England, J.L. Dissipation Bounds All Steady-State Current Fluctuations. Phys. Rev. Lett. 2016, 116, 120601. [Google Scholar] [CrossRef] [PubMed]
- Pietzonka, P.; Barato, A.C.; Seifert, U. Universal bound on the efficiency of molecular motors. J. Stat. Mech. Theory Exp. 2016, 2016, 124004. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics: From principles to the cost of precision. Phys. A Stat. Mech. Appl. 2018, 504, 176–191. [Google Scholar] [CrossRef]
- Seifert, U. From Stochastic Thermodynamics to Thermodynamic Inference. Annu. Rev. Condens. Matter Phys. 2019, 10, 171–192. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Gingrich, T.R. Thermodynamic uncertainty relations constrain non-equilibrium fluctuations. Nat. Phys. 2020, 16, 15–20. [Google Scholar] [CrossRef]
- Berezhkovskii, A.; Hummer, G.; Bezrukov, S. Identity of Distributions of Direct Uphill and Downhill Translocation Times for Particles Traversing Membrane Channels. Phys. Rev. Lett. 2006, 97, 020601. [Google Scholar] [CrossRef]
- van der Meer, J.; Ertel, B.; Seifert, U. Thermodynamic Inference in Partially Accessible Markov Networks: A Unifying Perspective from Transition-Based Waiting Time Distributions. Phys. Rev. X 2022, 12, 031025. [Google Scholar] [CrossRef]
- Harunari, P.E.; Dutta, A.; Polettini, M.; Roldán, E. What to Learn from a Few Visible Transitions’ Statistics? Phys. Rev. X 2022, 12, 041026. [Google Scholar] [CrossRef]
- van der Meer, J.; Degünther, J.; Seifert, U. Time-resolved statistics of snippets as general framework for model-free entropy estimators. arXiv 2022, arXiv:2211.17032. [Google Scholar]
- Berezhkovskii, A.M.; Makarov, D.E. On the forward/backward symmetry of transition path time distributions in nonequilibrium systems. J. Chem. Phys. 2019, 151, 065102. [Google Scholar] [CrossRef]
- Gladrow, J.; Ribezzi-Crivellari, M.; Ritort, F.; Keyser, U.F. Experimental evidence of symmetry breaking of transition-path times. Nat. Commun. 2019, 10, 55. [Google Scholar] [CrossRef] [PubMed]
- Berezhkovskii, A.M.; Makarov, D.E. On distributions of barrier crossing times as observed in single-molecule studies of biomolecules. Biophys. Rep. 2021, 1, 100029. [Google Scholar] [CrossRef]
- Toyabe, S.; Okamoto, T.; Watanabe-Nakayama, T.; Taketani, H.; Kudo, S.; Muneyuki, E. Nonequilibrium Energetics of a Single F 1 -ATPase Molecule. Phys. Rev. Lett. 2010, 104, 198103. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M.E.; Kolomeisky, A.B. The force exerted by a molecular motor. Proc. Natl. Acad. Sci. USA 1999, 96, 6597–6602. [Google Scholar] [CrossRef]
- Hayashi, K.; Ueno, H.; Iino, R.; Noji, H. Fluctuation Theorem Applied to F1-ATPase. Phys. Rev. Lett. 2010, 104, 218103. [Google Scholar] [CrossRef]
- Faradjian, A.K.; Elber, R. Computing time scales from reaction coordinates by milestoning. J. Chem. Phys. 2004, 120, 10880–10889. [Google Scholar] [CrossRef]
- Schütte, C.; Noé, F.; Lu, J.; Sarich, M.; Vanden-Eijnden, E. Markov state models based on milestoning. J. Chem. Phys. 2011, 134, 204105. [Google Scholar] [CrossRef]
- Elber, R. Milestoning: An Efficient Approach for Atomically Detailed Simulations of Kinetics in Biophysics. Annu. Rev. Biophys. 2020, 49, 69–85. [Google Scholar] [CrossRef]
- Hartich, D.; Godec, A. Emergent Memory and Kinetic Hysteresis in Strongly Driven Networks. Phys. Rev. X 2021, 11, 041047. [Google Scholar] [CrossRef]
- Rahav, S.; Jarzynski, C. Fluctuation relations and coarse-graining. J. Stat. Mech. Theory Exp. 2007, 2007, P09012. [Google Scholar] [CrossRef]
- Pigolotti, S.; Vulpiani, A. Coarse graining of master equations with fast and slow states. J. Chem. Phys. 2008, 128, 154114. [Google Scholar] [CrossRef]
- Puglisi, A.; Pigolotti, S.; Rondoni, L.; Vulpiani, A. Entropy production and coarse graining in Markov processes. J. Stat. Mech. Theory Exp. 2010, 2010, P05015. [Google Scholar] [CrossRef]
- Knoch, F.; Speck, T. Cycle representatives for the coarse-graining of systems driven into a non-equilibrium steady state. New J. Phys. 2015, 17, 115004. [Google Scholar] [CrossRef]
- Seiferth, D.; Sollich, P.; Klumpp, S. Coarse graining of biochemical systems described by discrete stochastic dynamics. Phys. Rev. E 2020, 102, 062149. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Yasuda, R.; Noji, H.; Yoshida, M.; Kinosita, K.; Itoh, H. Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-ATPase. Nature 2001, 410, 898–904. [Google Scholar] [CrossRef]
- Bilyard, T.; Nakanishi-Matsui, M.; Steel, B.C.; Pilizota, T.; Nord, A.L.; Hosokawa, H.; Futai, M.; Berry, R.M. High-resolution single-molecule characterization of the enzymatic states in Escherichia coli F1-ATPase. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013, 368, 20120023. [Google Scholar] [CrossRef]
- Martin, J.L.; Ishmukhametov, R.; Hornung, T.; Ahmad, Z.; Frasch, W.D. Anatomy of F1-ATPase powered rotation. Proc. Natl. Acad. Sci. USA 2014, 111, 3715–3720. [Google Scholar] [CrossRef]
- Makarov, D.E.; Berezhkovskii, A.; Haran, G.; Pollak, E. The Effect of Time Resolution on Apparent Transition Path Times Observed in Single-Molecule Studies of Biomolecules. J. Phys. Chem. B 2022, 126, 7966–7974. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ertel, B.; van der Meer, J.; Seifert, U. Waiting Time Distributions in Hybrid Models of Motor–Bead Assays: A Concept and Tool for Inference. Int. J. Mol. Sci. 2023, 24, 7610. https://doi.org/10.3390/ijms24087610
Ertel B, van der Meer J, Seifert U. Waiting Time Distributions in Hybrid Models of Motor–Bead Assays: A Concept and Tool for Inference. International Journal of Molecular Sciences. 2023; 24(8):7610. https://doi.org/10.3390/ijms24087610
Chicago/Turabian StyleErtel, Benjamin, Jann van der Meer, and Udo Seifert. 2023. "Waiting Time Distributions in Hybrid Models of Motor–Bead Assays: A Concept and Tool for Inference" International Journal of Molecular Sciences 24, no. 8: 7610. https://doi.org/10.3390/ijms24087610
APA StyleErtel, B., van der Meer, J., & Seifert, U. (2023). Waiting Time Distributions in Hybrid Models of Motor–Bead Assays: A Concept and Tool for Inference. International Journal of Molecular Sciences, 24(8), 7610. https://doi.org/10.3390/ijms24087610






