Phase-Dependent Response to Electrical Stimulation of Cortical Networks during Recurrent Epileptiform Short Discharge Generation In Vitro
Abstract
1. Introduction
2. Results
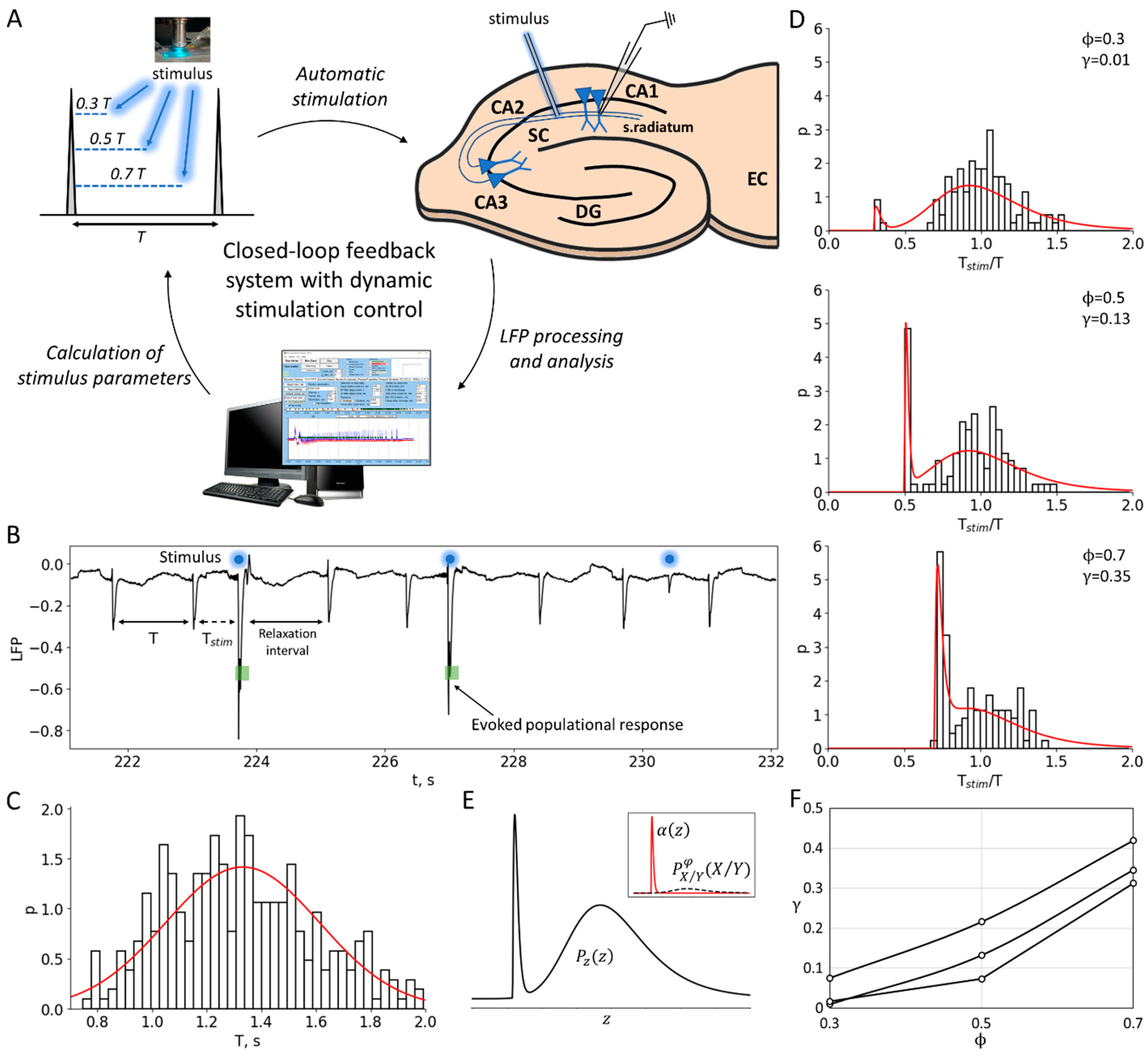
2.1. Experiments: Regime of Short Discharge Generation and Weak Stimulation
2.2. Experiments: Phase-Dependent Sensitivity to Stimulation
2.3. LIF Model: Sample Traces
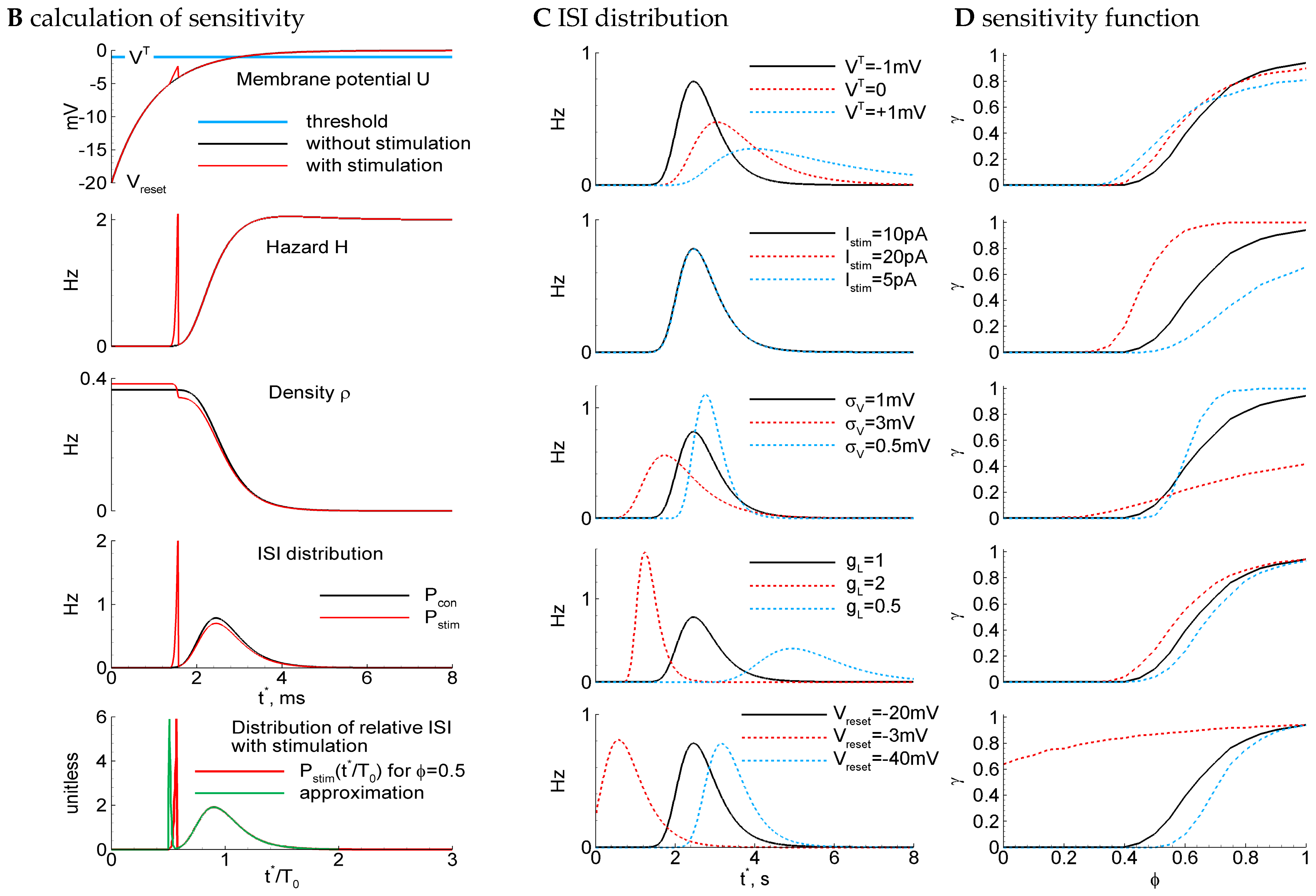
2.4. An Analytical Approximation of the ISI Distribution with the Refractory Density Approach
2.4.1. RD Approach for Arbitrary Time-Dependent Process and Arbitrary Threshold-Type Network Model
2.4.2. RD Approach for Steady States
2.4.3. The RD Approach for a Single Interspike Interval
2.4.4. LIF Model: Analytical Approximation of ISI Distribution
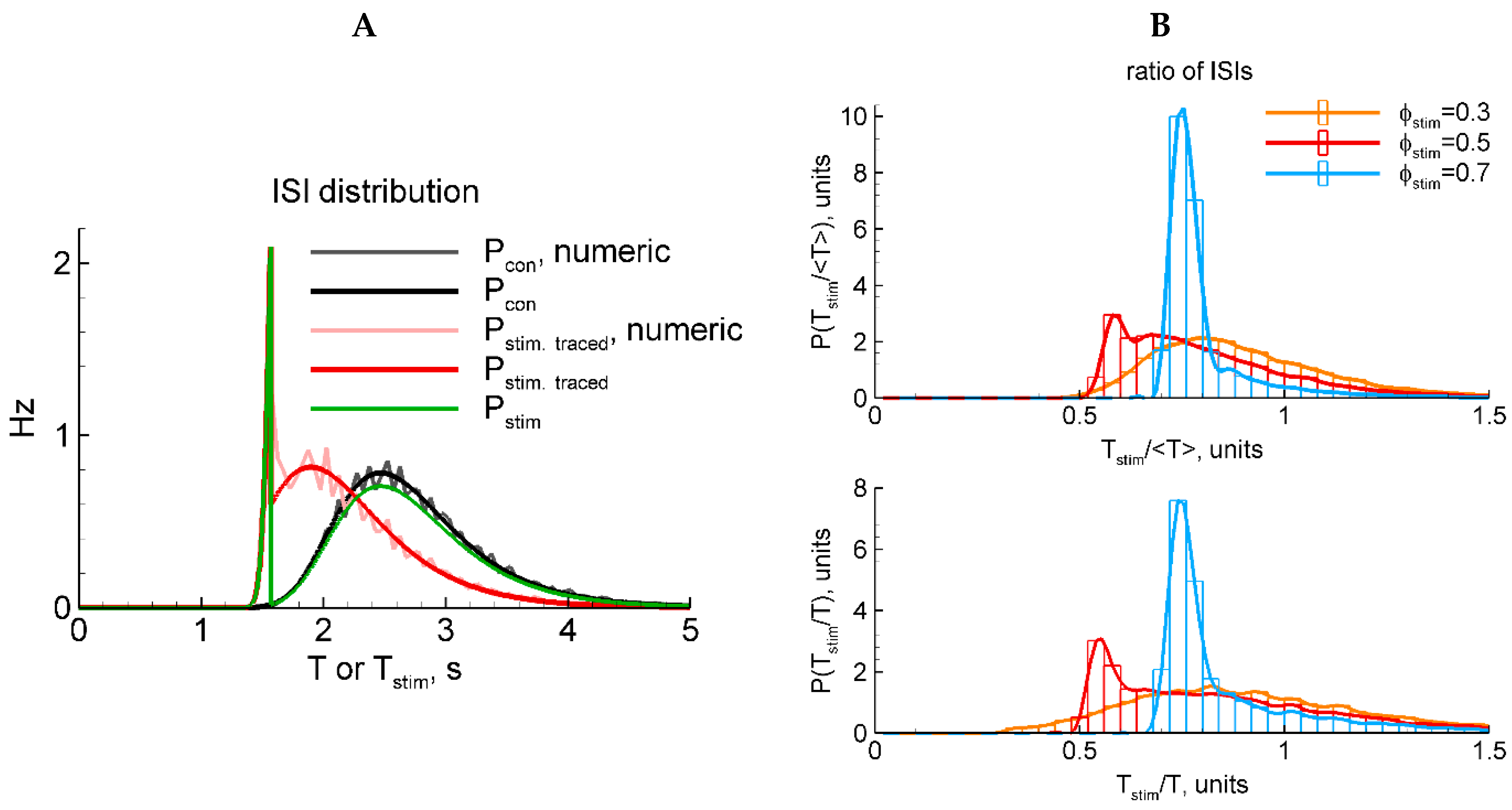
2.4.5. LIF Model: Numerical and Analytical Solutions for Two Types of Stimulation
2.4.6. LIF Model: Phase-Dependent Sensitivity to Stimulation
2.4.7. LIF Model: Dependence of ISI Distribution and Sensitivity Function on Parameters
2.4.8. LIF Model: Normalization of ISI
2.4.9. LIF Model with M-Channels: Class I and Class II
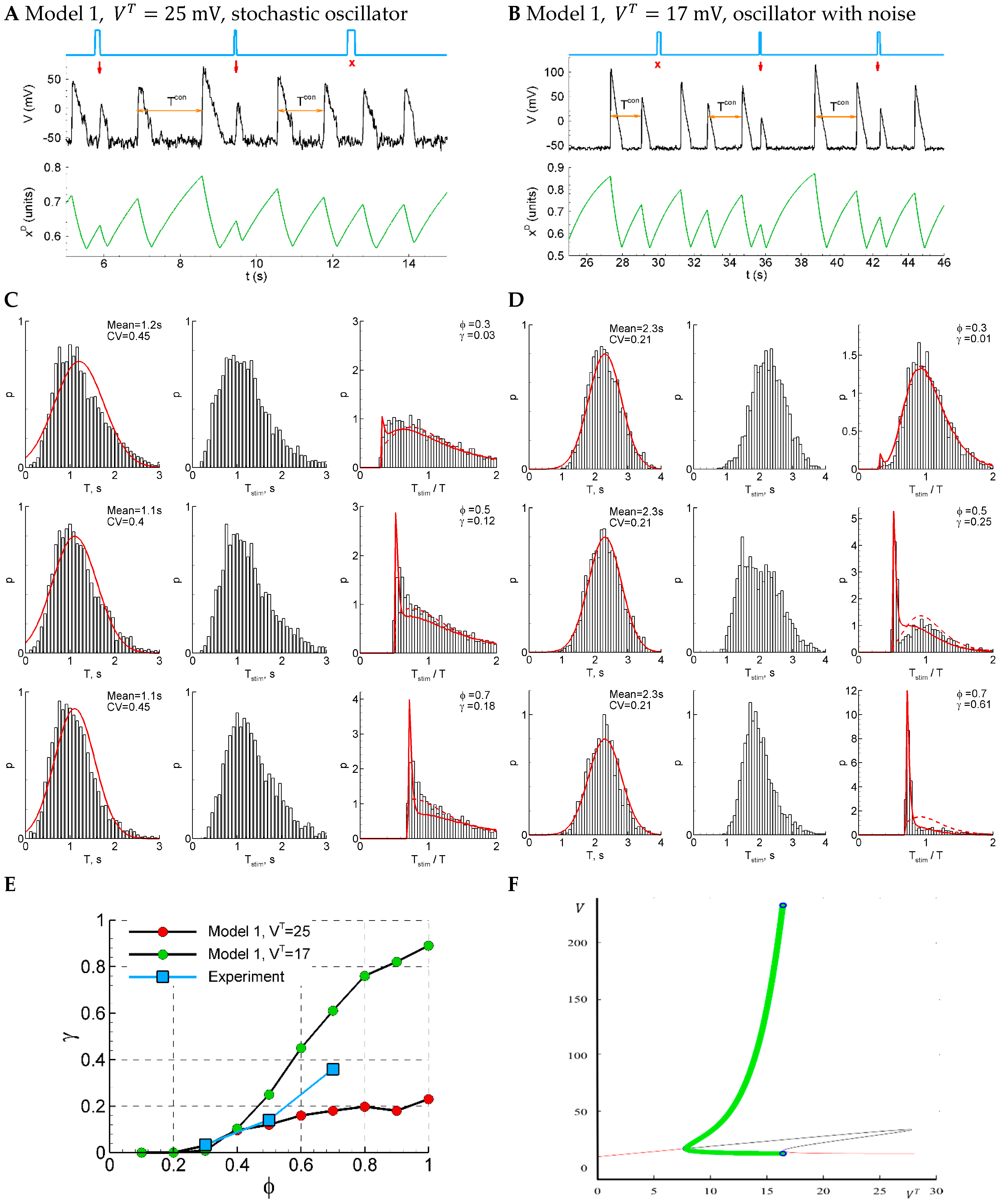
2.4.10. LIF Model: Direct Numerical Simulations
2.4.11. Model 1: Fast Subsystem of Epileptor-2 Model with Synaptic Resource
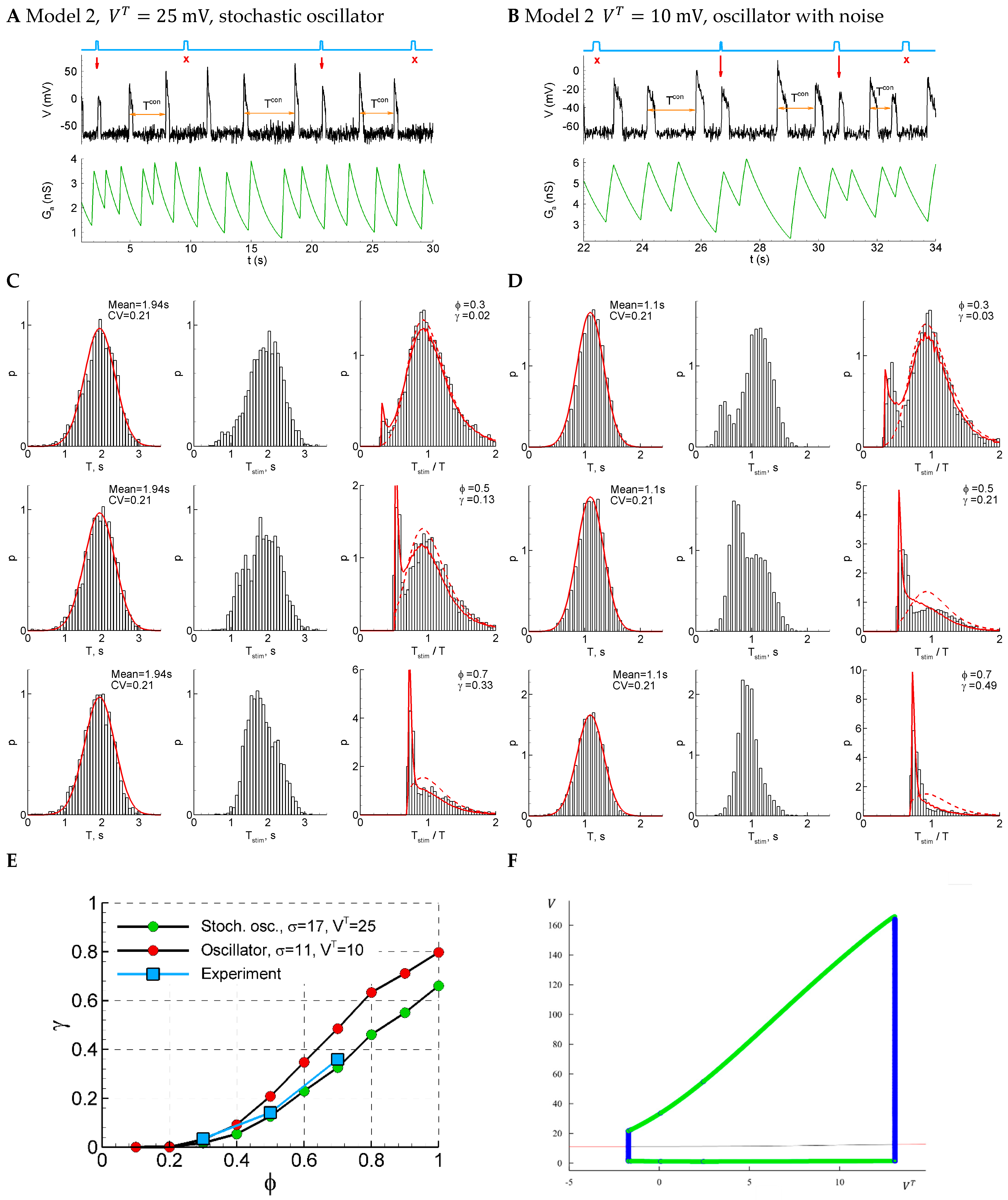
2.4.12. Model 2: Fast Subsystem of Epileptor-2 Model with Shunting
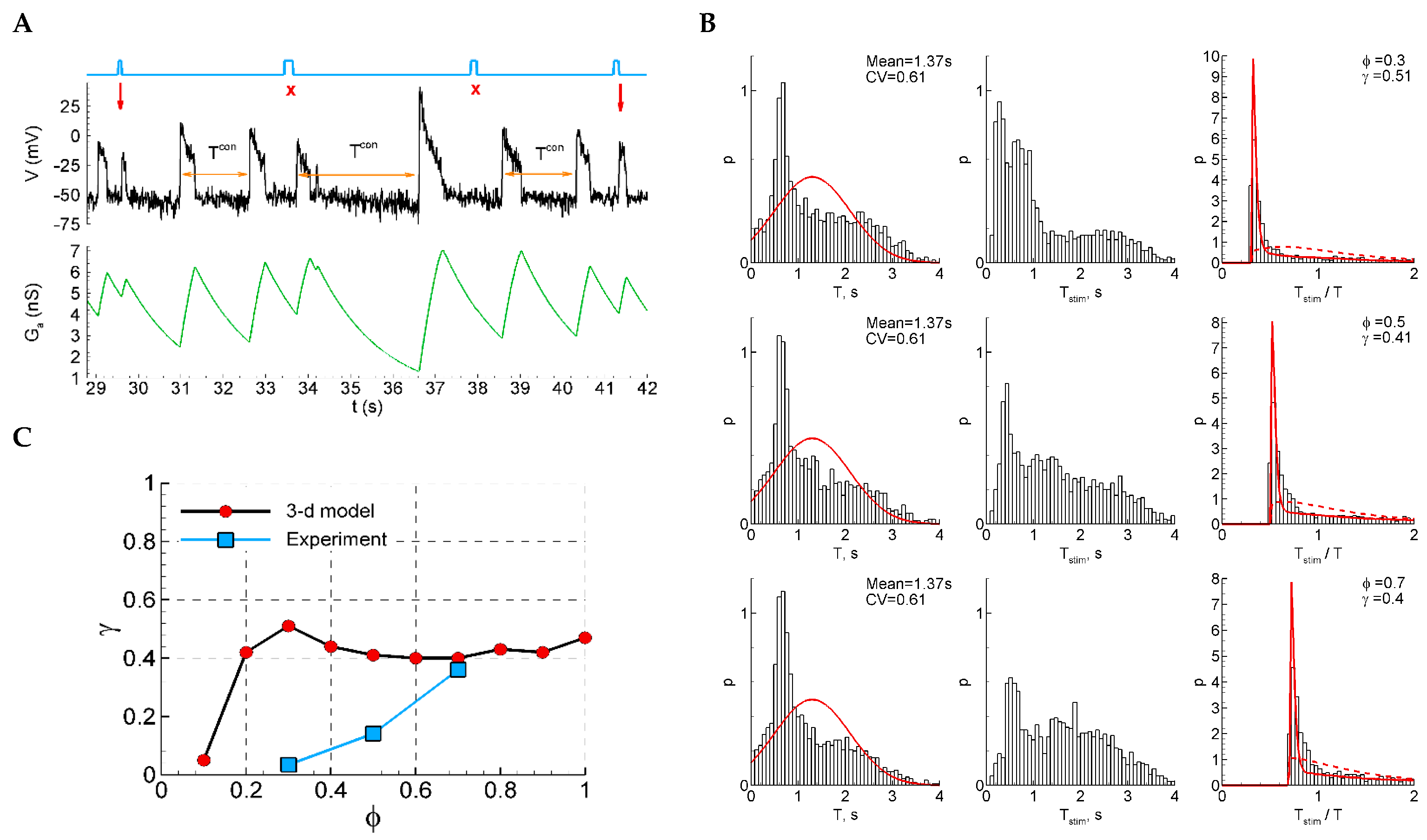
2.4.13. Model 2 with Shunting and After-Spike Depolarization
3. Discussion
4. Methods
4.1. Experimental Techniques
4.1.1. Electrophysiological Recordings
4.1.2. Stimulation Protocols
4.1.3. Calculation of Experimental Phase-Dependent Sensitivity to Stimulation
4.2. Mathematical Methods
4.2.1. Model 1: Fast Subsystem of Epileptor-2 Model with Synaptic Resource
4.2.2. Model 2: Fast Subsystem of Epileptor-2 Model with Shunting
4.2.3. LIF Model
4.2.4. LIF Model with M-Channels
4.2.5. Model 2 with Shunting and After-Spike Depolarization
4.2.6. Optimization Problem for Parameter Fitting
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Winfree, A.T. Patterns of phase compromise in biological cycles. J. Math. Biology 1974, 1, 73–93. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Dynamical Systems in Neuroscience; MIT Press: Cambridge, UK, 2007. [Google Scholar]
- Schultheiss, N.W.; Prinz, A.A.; Butera, R.J. Phase Response Curves in Neuroscience: Theory, Experiment, and Analysis; Springer: Berlin/Heidelberg, Germany, 2012; 518p. [Google Scholar] [CrossRef]
- Burman, R.J.; Selfe, J.S.; Lee, J.H.; van den Berg, M.; Calin, A.; Codadu, N.K.; Wright, R.; Newey, S.E.; Parrish, R.R.; Katz, A.A.; et al. Excitatory GABAergic signalling is associated with benzodiazepine resistance in status epilepticus. Brain 2019, 142, 3482–3501. [Google Scholar] [CrossRef] [PubMed]
- Borisyuk, R.M.; Kazanovich, Y.B. Oscillatory neural network model of attention focus formation and control. Biosystems 2003, 71, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Klinshov, V.V.; Nekorkin, V.I. Synchronization of delay-coupled oscillator networks. Phys. Uspekhi 2013, 56, 1217–1229. [Google Scholar] [CrossRef]
- Petkoski, S.; Palva, J.M.; Jirsa, V.K. Phase-lags in large scale brain synchronization: Methodological considerations and in-silico analysis. PLoS Comput. Biol. 2018, 14, e1006160. [Google Scholar] [CrossRef] [PubMed]
- Chizhov, A.V.; Zefirov, A.V.; Amakhin, D.V.; Smirnova, E.Y.; Zaitsev, A.V. Minimal model of interictal and ictal discharges “Epileptor-2”. PLoS Comput. Biol. 2018, 14, e1006186. [Google Scholar] [CrossRef] [PubMed]
- Caron, D.; Canal-Alonso, Á.; Panuccio, G. Mimicking CA3 Temporal Dynamics Controls Limbic Ictogenesis. Biology 2022, 11, 371. [Google Scholar] [CrossRef]
- Chizhov, A.V.; Graham, L.J. Population model of hippocampal pyramidal neurons linking a refractory density approach to conductance-based neurons. Phys. Rev. E 2007, 75, 011924. [Google Scholar] [CrossRef]
- Tarniceriu, C.O. Age-structure in neuronal models. Ann. Alexandru Ioan Cuza Univ. Math. 2020, 66, 385–396. [Google Scholar]
- Knight, B.W. Dynamics of encoding in a population of neurons. J. Gen. Physiol. 1972, 59, 734. [Google Scholar] [CrossRef]
- Eggert, J.; van Hemmen, J.L. Modeling neuronal assemblies: Theory and implementation. Neural. Comput. 2001, 13, 1923–1974. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M. Noise in spiking neuron models. In Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002; pp. 147–200. [Google Scholar]
- Stiefel, K.M.; Gutkin, B.S.; Sejnowski, T.J. Cholinergic Neuromodulation Changes Phase Response Curve Shape and Type in Cortical Pyramidal Neurons. PLoS ONE 2008, 3, e3947. [Google Scholar] [CrossRef]
- Al-Darabsah, I.; Campbell, S.A. M-current induced Bogdanov–Takens bifurcation and switching of neuron excitability class. J. Math. Neurosc. 2021, 11, 5. [Google Scholar] [CrossRef]
- Soboleva, E.B.; Amakhin, D.V.; Sinyak, D.S.; Zaitsev, A.V. Modulation of seizure-like events by the small conductance and ATP-sensitive potassium ion channels. Biochem. Biophys. Res. Commun. 2022, 623, 74–80. [Google Scholar] [CrossRef]
- Avoli, M.; D’Antuono, M.; Louvel, J.; Köhling, R.; Biagini, G.; Pumain, R.; D’Arcangelo, G.; Tancredi, V. Network and pharmacological mechanisms leading to epileptiform synchronization in the limbic system in vitro. Prog. Neurobiol. 2002, 68, 167–207. [Google Scholar] [CrossRef]
- Scalmani, P.; Paterra, R.; Mantegazza, M.; Avoli, M.; de Curtis, M. Involvement of GABAergic Interneuron Subtypes in 4-Aminopyridine-Induced Seizure-Like Events in Mouse Entorhinal Cortex In Vitro. J. Neurosci. 2023, 43, 1987–2001. [Google Scholar] [CrossRef]
- Trevelyan, A.J.; Graham, R.T.; Parrish, R.R.; Codadu, N.K. Synergistic Positive Feedback Mechanisms Underlying Seizure Initiation. Epilepsy Curr. 2022, 23, 38–43. [Google Scholar] [CrossRef]
- Ostojic, S. Interspike interval distributions of spiking neurons driven byfluctuating inputs. J. Neurophysiol. 2011, 106, 361–373. [Google Scholar] [CrossRef]
- Middleton, J.W.; Chacron, M.J.; Lindner, B.; Longtin, A. Firing statistics of a neuron model driven by long-range correlated noise. Phys. Rev. E 2003, 68, 021920. [Google Scholar] [CrossRef]
- Schwalger, T.; Fisch, K.; Benda, J.; Lindner, B. How Noisy Adaptation of Neurons Shapes Interspike Interval Histograms and Correlations. PLoS Comput. Biol. 2010, 6, e1001026. [Google Scholar] [CrossRef]
- Chizhov, A.V.; Amakhin, D.V.; Zaizev, A.V.; Magazanik, L.G. AMPAR-mediated Interictal Discharges in Neurons of Entorhinal Cortex: Experiment and Model. Dokl. Biol. Sci. 2018, 479, 47–50. [Google Scholar] [CrossRef]
- Amakhin, D.V.; Ergina, J.L.; Chizhov, A.V.; Zaitsev, A.V. Synaptic conductances during interictal discharges in pyramidal neurons of rat entorhinal cortex. Front. Cell. Neurosc. 2016, 10, 233. [Google Scholar] [CrossRef]



| Models | Type | Order of ODEs | Variables | |
|---|---|---|---|---|
| 1 | Fast subsystem of Epileptor-2 with synaptic resource | Stochastic, mean-field based on sigmoid function | 2 | membrane potential
and synaptic resource |
| 2 | Fast subsystem of Epileptor-2 with shunting conductance | Stochastic, mean-field based on sigmoid function | 2 | membrane potential
and shunting conductance |
| 3 | LIF model | Stochastic, threshold | 1 | membrane potential |
| 4 | LIF model with KM-channel | Stochastic, threshold, with HH-like approximation | 2 | membrane potential
and M-channel conductance |
| 5 | Model 2 with after-spike depolarization | Stochastic, mean-field based on sigmoid function | 3 | membrane potential , shunting conductance and after-spike depolarizing current |
| Model/Experiment | Parameters Differed from the Control Set | Mean IS, s | CV | . |
|---|---|---|---|---|
| Experiments | - | 1.49 (1.54, 1.60, 1.34) | 0.20 (0.15, 0.21, 0.23) | 1 |
| LIF | Control | 2.72 | 0.22 | 1 |
| LIF | 3.65 | 0.30 | 1 | |
| LIF | 5.72 | 0.43 | 1 | |
| LIF | 8.76 | 0.57 | 1 | |
| LIF | 2.18 | 0.41 | 1 | |
| LIF | 2.88 | 0.14 | 1 | |
| LIF | 1.36 | 0.22 | 1 | |
| LIF | 5.46 | 0.22 | 1 | |
| LIF | 0.87 | 0.67 | 1 | |
| LIF | 3.41 | 0.18 | 1 | |
| LIF+KM | 2.76 | 0.45 | 1 | |
| LIF+KM | 3.62 | 0.26 | 0.015 | |
| Model 1 with syn. resource, “Stoch. oscillator” | 1.1 | 0.45 | 1 | |
| Model 1 with syn. resource, close to “Oscillator” | 2.3 | 0.21 | 1 | |
| Model 2 with shunting, “Oscillator” | 1.9 | 0.21 | 1 | |
| Model 2 with shunting, “Stoch. oscillator” | 1.1 | 0.21 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chizhov, A.V.; Tiselko, V.S.; Postnikova, T.Y.; Zaitsev, A.V. Phase-Dependent Response to Electrical Stimulation of Cortical Networks during Recurrent Epileptiform Short Discharge Generation In Vitro. Int. J. Mol. Sci. 2024, 25, 8287. https://doi.org/10.3390/ijms25158287
Chizhov AV, Tiselko VS, Postnikova TY, Zaitsev AV. Phase-Dependent Response to Electrical Stimulation of Cortical Networks during Recurrent Epileptiform Short Discharge Generation In Vitro. International Journal of Molecular Sciences. 2024; 25(15):8287. https://doi.org/10.3390/ijms25158287
Chicago/Turabian StyleChizhov, Anton V., Vasilii S. Tiselko, Tatyana Yu. Postnikova, and Aleksey V. Zaitsev. 2024. "Phase-Dependent Response to Electrical Stimulation of Cortical Networks during Recurrent Epileptiform Short Discharge Generation In Vitro" International Journal of Molecular Sciences 25, no. 15: 8287. https://doi.org/10.3390/ijms25158287
APA StyleChizhov, A. V., Tiselko, V. S., Postnikova, T. Y., & Zaitsev, A. V. (2024). Phase-Dependent Response to Electrical Stimulation of Cortical Networks during Recurrent Epileptiform Short Discharge Generation In Vitro. International Journal of Molecular Sciences, 25(15), 8287. https://doi.org/10.3390/ijms25158287






