Analytical and Numerical Investigation of Star Polymers in Confined Geometries
Abstract
:1. Introduction
2. The Method
2.1. The Model and the Polymer–Magnet Analogy
2.2. Thermodynamic Description
3. Results
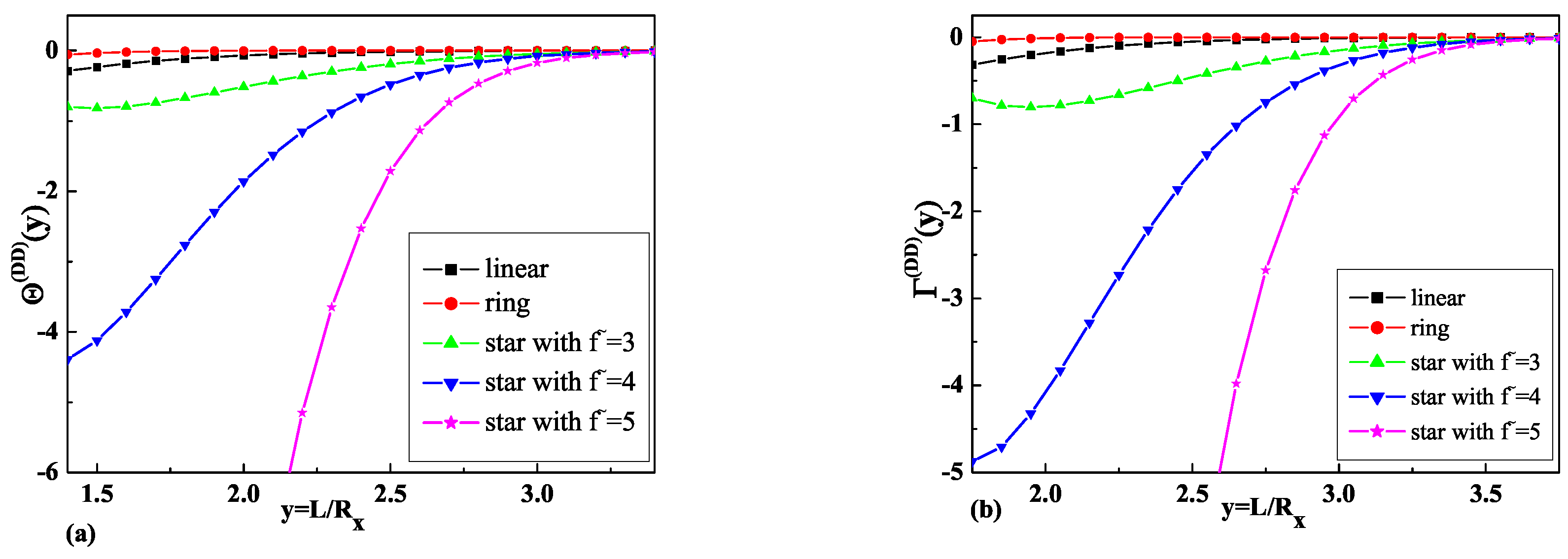
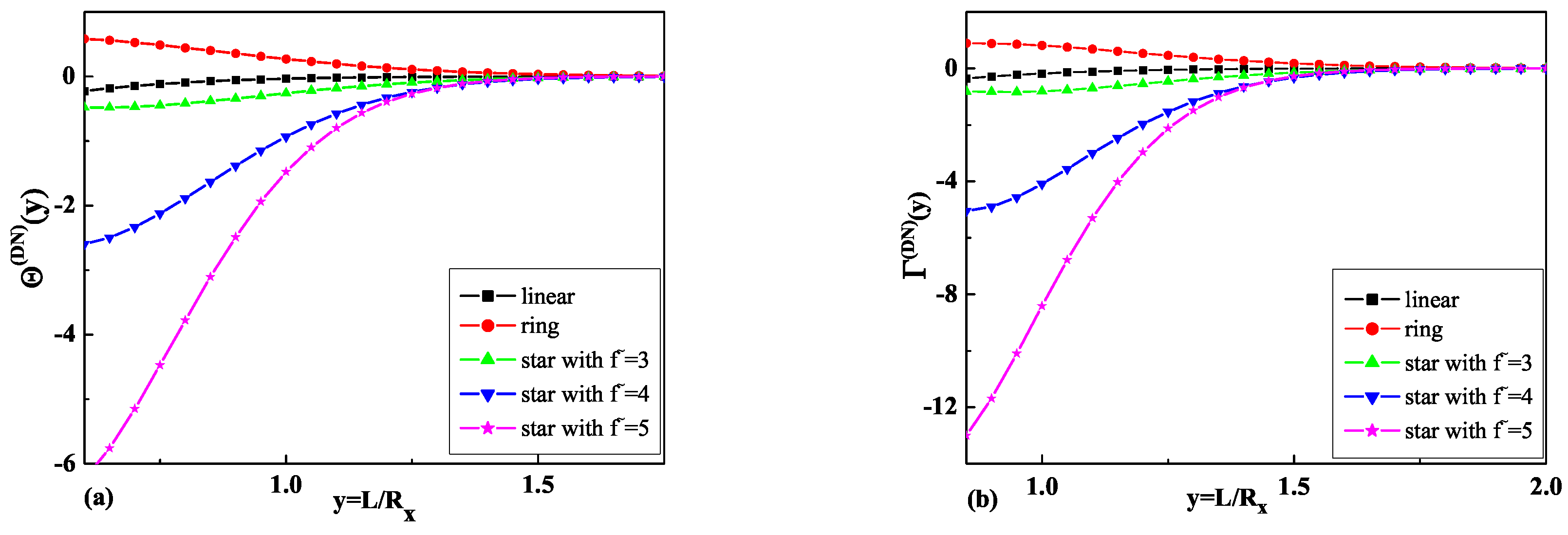
3.1. Results of the Depletion Interaction Potentials and the Depletion Force Calculations for Star Polymers with an Odd Number of Arms
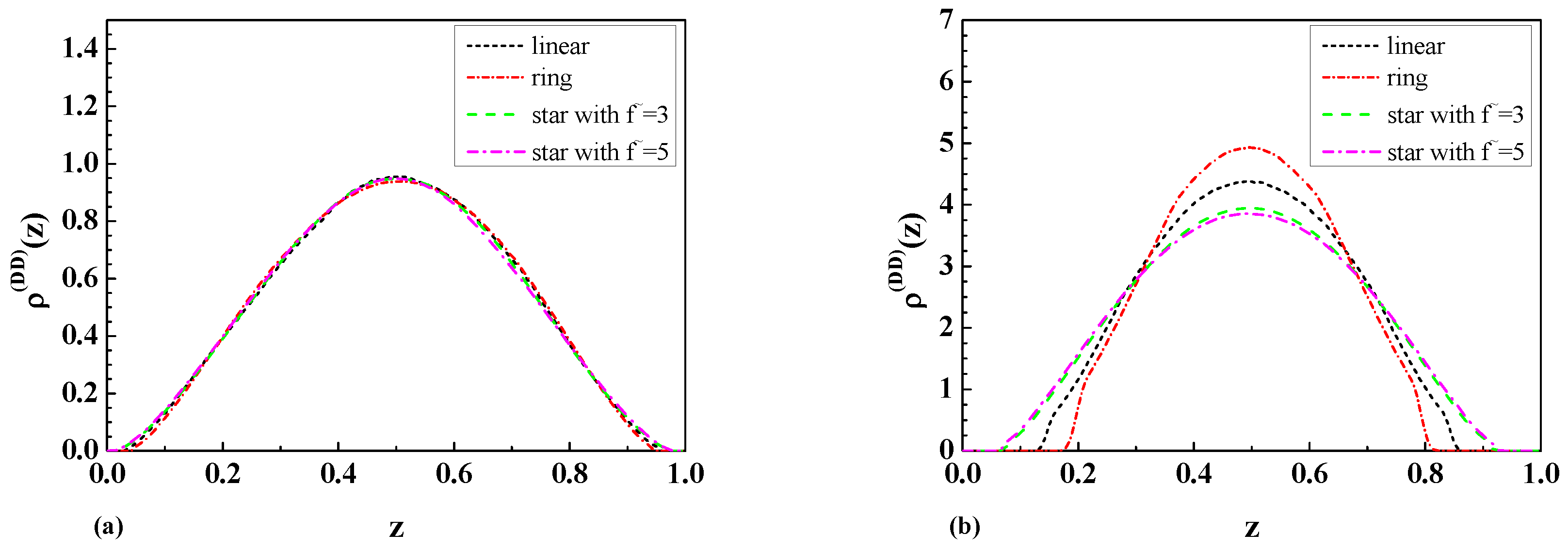
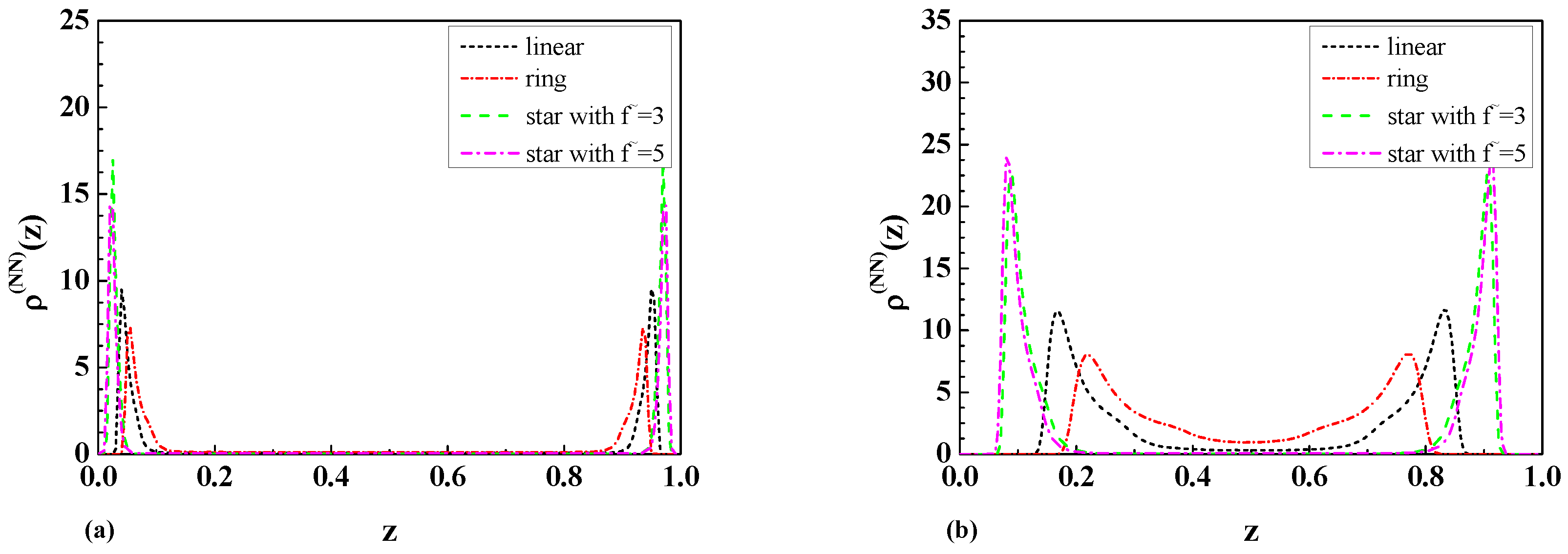
3.2. The Layer Monomer Density for Star-Shaped Polymers
3.3. Results of Molecular Dynamic Simulations of Linear, Ring, and Star-Shaped Polymers in a Slit
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ren, J.M.; McKenzie, T.G.; Fu, Q.; Wong, E.H.H.; Xu, J.; An, Z.; Shanmugam, S.; Davis, T.P.; Boyer, C.; Qiao, G.G. Star polymers. Chem. Rev. 2016, 116, 6743–6836. [Google Scholar] [CrossRef] [PubMed]
- Grest, G.S.; Fetters, L.J.; Huang, J.S.; Richter, D. Star polymers: Experiment, theory, and simulation. Adv. Chem. Phys. 1996, 94, 67. [Google Scholar]
- von Feber, C.; Holovatch, Y. Special Issue “Star Polymer”. Condens. Matter Phys. 2002, 5. [Google Scholar] [CrossRef]
- Duplantier, B. Statistical mechanics of polymer networks of any topology. J. Stat. Phys. 1989, 54, 581. [Google Scholar] [CrossRef]
- Schäfer, L.; von Feber, C.; Lehr, U.; Duplantier, B. Renormalization of polymer networks and stars. Nucl. Phys. B 1992, 374, 473. [Google Scholar] [CrossRef]
- Dadi, S.; Ocsoy, I. Role of pretty nanoflowers as novel versatile analytical tools for sensing in biomedical and bioanalytical applications. Smart Med. 2023, 3, e20230040. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, C.; Li, C.; Wu, W.; Jiang, X. Shape Effects of cylindrical versus spherical unimolecular polymer nanomaterials on in vitro and in vivo behaviors. Research 2019, 13, 2391486. [Google Scholar] [CrossRef]
- Halun, J.; Karbowniczek, P.; Kuterba, P.; Danel, Z. Investigation of ring and star polymers in confined geometries: Theory and simulations. Entropy 2021, 23, 242. [Google Scholar] [CrossRef]
- Napper, D.H. Polymeric Stabilization of Colloidal Dispersions; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Carvalho, B.L.; Tong, P.; Huang, J.S.; Witten, T.A.; Fetters, L.J. Adsorption of end-functionalized polymers on colloidal spheres. Macromolecules 1993, 26, 4632. [Google Scholar] [CrossRef]
- Rudhardt, D.; Bechinger, C.; Leiderer, P. Direct measurement of depletion potentials in mixtures of colloids and nonionic polymers. Phys. Rev. Lett. 1998, 81, 1330. [Google Scholar] [CrossRef]
- Verma, R.; Crocker, J.C.; Lubensky, T.C.; Yodh, A.G. Entropic colloidal interactions in concentrated DNA solutions. Phys. Rev. Lett. 1998, 81, 4004. [Google Scholar] [CrossRef]
- Ohshima, Y.N.; Sakagami, H.; Okumoto, K.; Tokoyoda, A.; Igarashi, T.; Shintaku, K.B.; Toride, S.; Sekino, H.; Kabuto, K.; Nishio, I. Direct measurement of infinitesimal depletion force in a colloid–polymer mixture by laser radiation pressure. Phys. Rev. Lett. 1997, 78, 3963. [Google Scholar] [CrossRef]
- Joanny, J.F.; Leibler, L.; de Gennes, P.G. Effects of polymer solutions on colloid stability. J. Polym. Sci. Polym. Phys. Ed. 1979, 17, 1073. [Google Scholar] [CrossRef]
- Eisenriegler, E. Universal density-force relations for polymers near a repulsive wall. Phys. Rev. E 1997, 55, 3116. [Google Scholar] [CrossRef]
- Milchev, A.; Binder, K. A polymer chain trapped between two parallel repulsive walls: A Monte-Carlo test of scaling behavior. Eur. Phys. J. B 1998, 3, 477, Erratum in Eur. Phys. J. B 2000, 13, 607. [Google Scholar] [CrossRef]
- Hsu, H.P.; Grasberger, P. Polymers confined between two parallel plane walls. J. Chem. Phys. 2004, 120, 2034. [Google Scholar] [CrossRef]
- Usatenko, Z. Monomer density profiles for polymer chains in confined geometries: Massive field theory approach. J. Chem. Phys. 2011, 134, 024119. [Google Scholar] [CrossRef]
- Usatenko, Z. Monomer density profiles of real polymer chains in confined geometries. J. Mol. Liq. 2011, 164, 59. [Google Scholar] [CrossRef]
- Bringer, A.; Eisenriegler, E.; Schlesener, F.; Hanke, A. Polymer depletion interaction between a particle and a wall. Eur. Phys. J. B 1999, 11, 101. [Google Scholar] [CrossRef]
- Hanke, A.; Eisenriegler, E.; Dietrich, S. Polymer depletion effects near mesoscopic particles. Phys. Rev. B 1999, 59, 6853. [Google Scholar] [CrossRef]
- Jun, S.; Mulder, B. Entropy-driven spatial organization of highly confined polymers: Lessons for the bacterial chromosome. Proc. Natl. Acad. Sci. USA 2006, 103, 12388. [Google Scholar] [CrossRef] [PubMed]
- Vargas-Lara, F.; Pazmino Betancourt, B.A.; Douglas, J.F. Communication: A comparison between the solution properties of knotted ring and star polymers. J. Chem. Phys. 2018, 149, 161101. [Google Scholar] [CrossRef]
- Usatenko, Z.; Halun, J.; Kuterba, P. Ring polymers in confined geometries. Condens. Matter Phys. 2016, 19, 43602. [Google Scholar] [CrossRef]
- Usatenko, Z.; Halun, J. Ring polymer chains confined in a slit geometry of two parallel walls. J. Stat. Mech. 2017, 2017, 013303. [Google Scholar] [CrossRef]
- Usatenko, Z.; Kuterba, P.; Chamati, H.; Romeis, D. Linear and ring polymers in confined geometries. Eur. Phys. J. Spec. Top. 2017, 226, 651665. [Google Scholar] [CrossRef]
- Cordeiro, C.E. Confined polymer chains in poor solvent. J. Phys. Chem. Solids 1999, 60, 1645. [Google Scholar] [CrossRef]
- Singh, Y.; Kumar, S.; Giri, D. Surface adsorption and collapse transition of a linear polymer chain in three dimensions. J. Phys. A 1999, 32, L407. [Google Scholar] [CrossRef]
- De Gennes, P.G. Exponents for the excluded volume problem as derived by the Wilson method. Phys. Lett. A 1972, 38, 339. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling theory of polymer adsorption. J. Phys. 1976, 37, 1445–1452. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: New York, NY, USA, 1979. [Google Scholar]
- Barber, M.N.; Guttmann, A.J.; Middlemiss, K.M.; Torrie, G.M.; Whittington, S.G. Some tests of scaling theory for a self-avoiding walk attached to a surface. J. Phys. A. 1978, 11, 1833. [Google Scholar] [CrossRef]
- Eisenriegler, E.; Kremer, K.; Binder, K. Adsorption of polymer chains at surfaces: Scaling and Monte Carlo analyses. J. Chem. Phys. 1982, 77, 6296. [Google Scholar] [CrossRef]
- Diehl, H.W. Phase Transitions and Critical Phenomena; Domb, C., Lebowitz, J.L., Eds.; Academic Press: London, UK, 1986; Volume 10. [Google Scholar]
- Eisenriegler, E. Polymers Near Surfaces; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1993. [Google Scholar]
- Romeis, D.; Usatenko, Z. Polymer chains in confined geometries: Massive field theory approach. Phys. Rev. E 2009, 80, 041802. [Google Scholar] [CrossRef]
- Diehl, H.W.; Shpot, M. Massive field-theory approach to surface critical behavior in three-dimensional systems. Nucl. Phys. B 1998, 528, 595. [Google Scholar] [CrossRef]
- Ohno, K.; Binder, K. Scaling theory of star polymers and general polymer networks in bulk and semi-infinite good solvents. J. Phys. (Paris) 1988, 49, 1329. [Google Scholar] [CrossRef]
- Wallace, D.J.; Zia, R.K.P. Harmonic perturbations of generalized Heisenberg spin systems. J. Phys. C 1975, 8, 839. [Google Scholar] [CrossRef]
- des Cloizeaux, J.; Jannink, G. Polymers in Solution; Clarendon Press: Oxford, UK, 1980. [Google Scholar]
- Schäfer, L. Excluded Volume Effects in Polymer Solutions as Explained by the Renormalization Group; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Derjaguin, B.V. Untersuchungen über die Reibung und Adhäsion, IV. Kolloid-Z. 1934, 69, 155. [Google Scholar] [CrossRef]
- Eisenriegler, E. Field Theory of Polymer-Colloid Interactions; WILEY-VCH: Hoboken, NJ, USA, 2005. [Google Scholar]
- Schlesener, F.; Hanke, A.; Klimpel, R.; Dietrich, S. Polymer depletion interaction between two parallel repulsive walls. Phys. Rev. E 2001, 63, 041803. [Google Scholar] [CrossRef] [PubMed]
- Orlini, E.; Whittington, S. Statistical topology of closed curves: Some applications in polymer physics. Rev. Mod. Phys. 2007, 79, 611. [Google Scholar] [CrossRef]
- Dietrich, S.; Diehl, H.W. Critical behavior of the energy density in semi-infinite systems. Z. Phys. B 1981, 43, 315. [Google Scholar] [CrossRef]
- Cardy, J.L. Universal critical-point amplitudes in parallel-plate geometries. Phys. Rev. Lett. 1990, 65, 1443. [Google Scholar] [CrossRef]
- Diehl, H.W.; Dietrich, S.; Eisenriegler, E. Universality, irrelevant surface operators, and corrections to scaling in systems with free surfaces and defect planes. Phys. Rev. B 1983, 27, 2937. [Google Scholar] [CrossRef]
- Abraham, F.F.; Singh, Y. The structure of a hard sphere fluid in contact with a soft repulsive wall. J. Chem. Phys. 1977, 67, 2384. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]


| L | b.c. | ||
|---|---|---|---|
| ND | 0.007 | 0.007 | |
| DD | 0.082 | 0.076 | |
| ND | 0.008 | 0.010 | |
| DD | 0.341 | 0.326 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danel, Z.; Halun, J.; Karbowniczek, P. Analytical and Numerical Investigation of Star Polymers in Confined Geometries. Int. J. Mol. Sci. 2024, 25, 9561. https://doi.org/10.3390/ijms25179561
Danel Z, Halun J, Karbowniczek P. Analytical and Numerical Investigation of Star Polymers in Confined Geometries. International Journal of Molecular Sciences. 2024; 25(17):9561. https://doi.org/10.3390/ijms25179561
Chicago/Turabian StyleDanel, Zoriana, Joanna Halun, and Pawel Karbowniczek. 2024. "Analytical and Numerical Investigation of Star Polymers in Confined Geometries" International Journal of Molecular Sciences 25, no. 17: 9561. https://doi.org/10.3390/ijms25179561






