Density Functional Theory Calculations: A Useful Tool to Investigate Mechanisms of 1,3-Dipolar Cycloaddition Reactions
Abstract
:1. Introduction
1.1. Computational Methods
1.2. 1,3-Dipolar Cycloaddition
2. Computational Mechanistic Studies of 1,3-Dipoles
2.1. 1,3-Dipoles of Propargyl-Allenyl Type

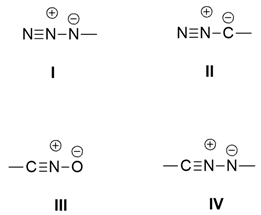
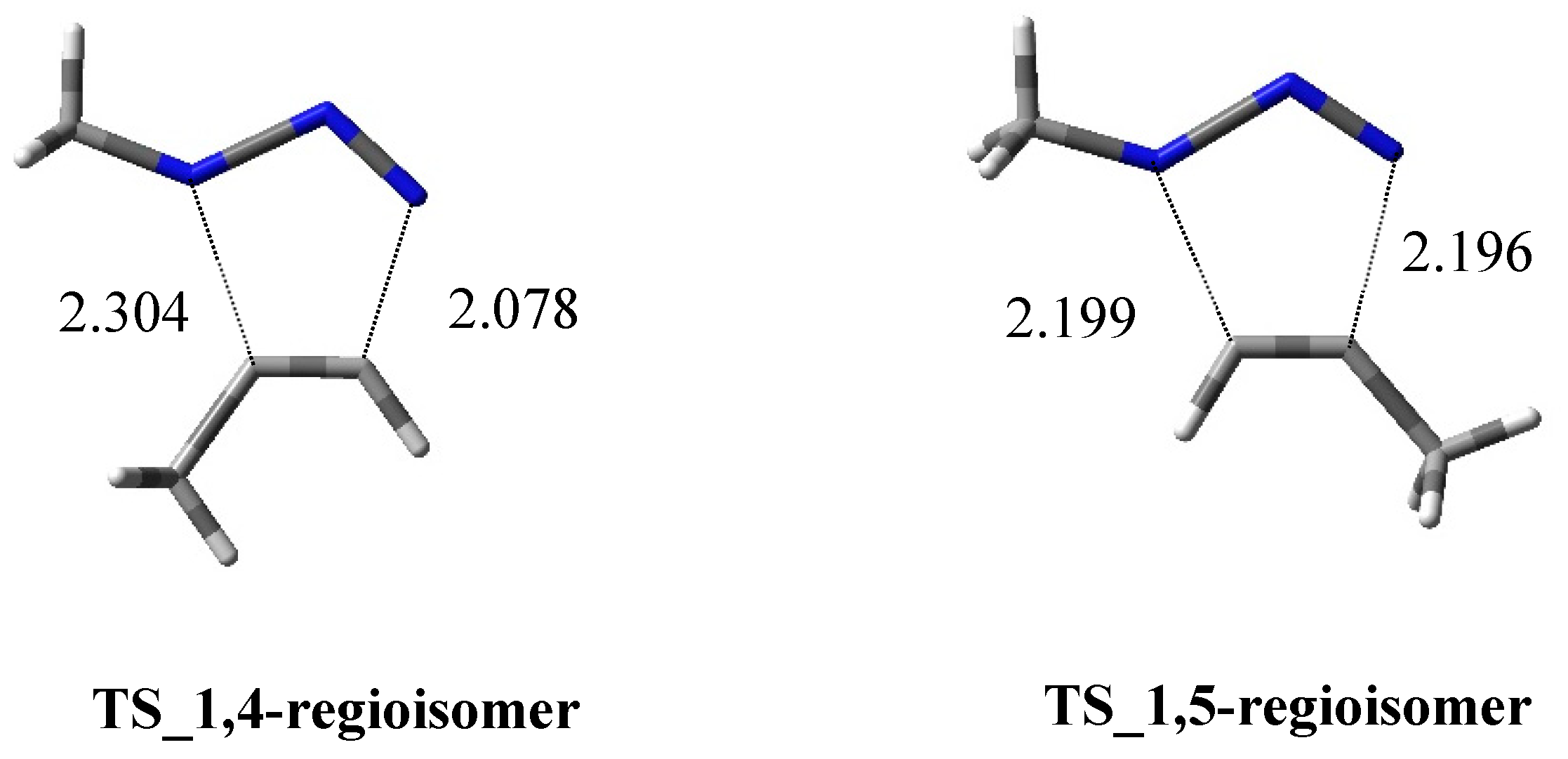
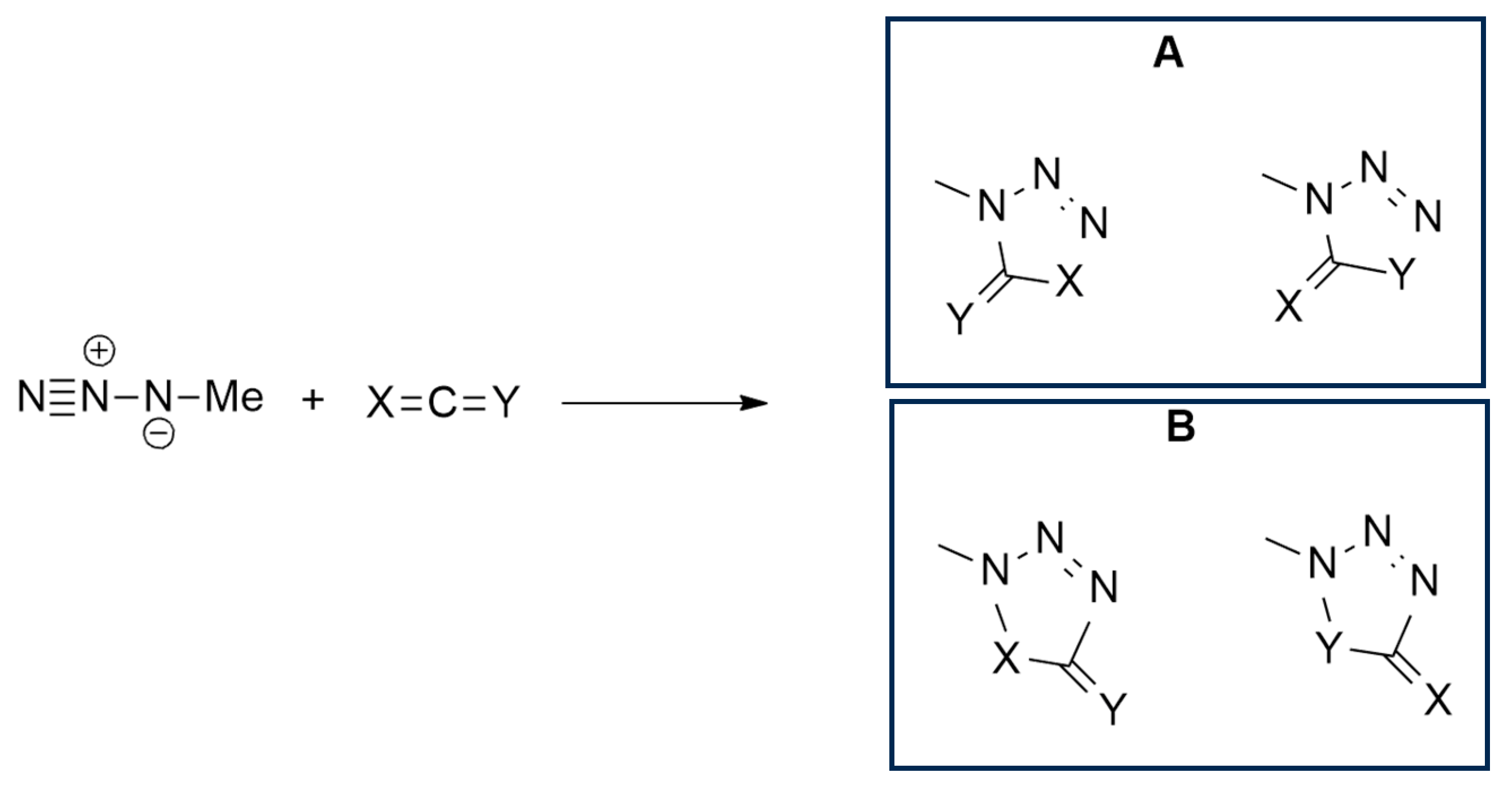
2.1.1. Aza-Ylides
2.1.2. Nitrile Oxides
2.2. 1,3-Dipoles of Allyl Type

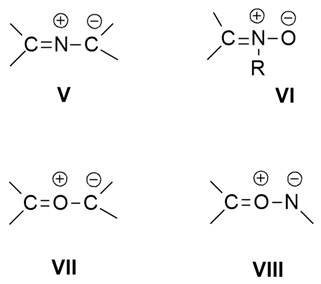
2.2.1. Azomethyne Ylides
2.2.2. Nitrones
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Hohenberg, H.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Sham, L.J.; Kohn, W. One-particle properties of an inhomogeneous interacting electron gas. Phys. Rev. 1966, 145, 561–567. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colic-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M.; Tomasi, J. Geometry optimization of molecular structures in solution by the polarizable continuum model. J. Comput. Chem. 1998, 19, 404–417. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Mode. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Groenhof, G. Introduction to QM/MM simulations. Methods Mol. Biol. 2013, 924, 43–66. [Google Scholar] [PubMed]
- Molteni, G.; Ponti, A. Is DFT Accurate Enough to Calculate Regioselectivity? The case of 1,3-dipolar cycloaddition of azide to alkynes and alkenes. ChemPhysChem 2023, 24, e202300114. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Houk, K.N. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem. 2017, 56, 10070–10086. [Google Scholar] [CrossRef]
- Kanemasa, S. Metal-assisted stereocontrol of 1,3-dipolar cycloaddition reactions. Synlett 2002, 2002, 1371–1387. [Google Scholar] [CrossRef]
- Roca-López, D.; Tejero, T.; Caramella, P.; Merino, P. Cycloadditions: An alternative to forbidden [4π + 4π] processes. the case of nitrone dimerization. Org. Biomol. Chem. 2014, 14, 517–525. [Google Scholar] [CrossRef]
- Yu, Z.-X.; Caramella, P.; Houk, K.N. Dimerizations of Nitrile Oxides to Furoxans Are Stepwise via Dinitrosoalkene Diradicals: A Density Functional Theory Study. J. Am. Chem. Soc. 2003, 125, 15420–15425. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Aurell, M.J.; Jalal, R.; Esseffar, M. A DFT study of the role of Lewis acid catalysts in the mechanism of the 1,3-dipolar cycloaddition of nitrile imines towards electron-deficient acryloyl derivatives. Comp. Theor. Chem. 2012, 986, 6–13. [Google Scholar] [CrossRef]
- Domingo, L.R.; Picher, M.T.; Arroyo, P.; Saez, J.A. 1,3-Dipolar Cycloadditions of Electrophilically Activated Benzonitrile N-Oxides. Polar Cycloaddition versus Oxime Formation. J. Org. Chem. 2006, 71, 9319–9330. [Google Scholar] [CrossRef] [PubMed]
- Ugur, I.; Agopcan, C.S.; Dedeoglu, B.; Aviyente, V.; Hawthorne, M.F.; Liu, P.; Liu, F.; Houk, K.N.; Jimenez-Oses, G.J. 1,3-Dipolar Cycloaddition Reactions of Low-Valent Rhodium and Iridium Complexes with Arylnitrile N-Oxides. Org. Chem. 2017, 82, 5096–5101. [Google Scholar] [CrossRef] [PubMed]
- Schoenebeck, F.; Ess, D.H.; Jones, G.O.; Houk, K.N. Reactivity and Regioselectivity in 1,3-Dipolar Cycloadditions of Azides to Strained Alkynes and Alkenes: A Computational Study. J. Am. Chem. Soc. 2009, 131, 8121–8133. [Google Scholar] [CrossRef]
- Kolb, H.C.; Finn, M.G.; Sharpless, K.B. Click chemistry: Diverse chemical function from a few good reactions. Angew. Chem. 2001, 40, 2004–2021. [Google Scholar] [CrossRef]
- Tornøe, C.W.; Christensen, C.; Meldal, M.J. Peptidotriazoles on solid phase:[1,2,3]-triazoles by regiospecific copper (I)-catalyzed 1,3-dipolar cycloadditions of terminal alkynes to azides. Org. Chem. 2002, 67, 3057–3064. [Google Scholar] [CrossRef]
- Ben El Ayouchia, H.; Bahsis, L.; Anane, H.; Domingo, L.R.; Stiriba, S.-E. Understanding the mechanism and regioselectivity of the copper(I) catalyzed [3 + 2] cycloaddition reaction between azide and alkyne: A systematic DFT study. RSC Adv. 2018, 8, 7670–7678. [Google Scholar] [CrossRef]
- Hamlin, T.A.; Levandowski, B.J.; Narsaria, A.K.; Houk, K.N.; Bickelhaupt, F.M. Structural Distortion of Cycloalkynes Influences Cycloaddition Rates both by Strain and Interaction Energies. Chem. Eur. J. 2019, 25, 6342–6348. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Chen, Y.-J.; Shih, T.-Y.; Chen, Y.H.; Lai, Y.-C.; Chiang, M.Y.; Senadi, G.C.; Chen, H.-Y.; Chen, H.-Y. Mechanistic Study in Click Reactions by Using (N-Heterocyclic carbene)Copper(I) Complexes: Anionic Effects. Organometallics 2019, 38, 223–230. [Google Scholar] [CrossRef]
- Yu, S.; Vermeeren, P.; van Dommelen, K.; Bickelhaupt, F.M.; Hamlin, T.A. Understanding the 1,3-dipolar cycloadditions of allenes. Chem.-Eur. J. 2020, 26, 11529–11539. [Google Scholar] [CrossRef] [PubMed]
- Ben El Ayouchia, H.; Bahsis, L.; Fichtali, I.; Domingo, L.R.; Ríos-Gutiérrez, M.; Julve, M.; Stiriba, S.-E. Deciphering the mechanism of silver catalysis of “Click” chemistry in water by combining experimental and MEDT studies. Catalyst 2020, 10, 956. [Google Scholar] [CrossRef]
- Kim, W.G.; Baek, S.-Y.; Jeong, S.Y.; Nam, D.; Jeon, J.H.; Choe, W.; Baik, M.-H.; Hong, S.Y. Chemo- and regioselective click reactions through nickel-catalyzed azide–alkyne cycloaddition. Org. Biomol. Chem. 2020, 18, 3374–3381. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.-J.; Lin, Y.; Xu, M.; Xia, Y.; Wink, D.J.; Lee, D. C-H Insertion by alkylidene carbenes to form 1,2,3-triazines and anionic [3 + 2] dipolar cycloadditions to form tetrazoles: Crucial roles of stereoelectronic and steric effects. Org. Lett. 2020, 22, 718–723. [Google Scholar] [CrossRef] [PubMed]
- Navarro, Y.; García López, J.; Iglesias, M.J.; López Ortiz, F. Chelation-Assisted Interrupted Copper(I)-Catalyzed Azide–Alkyne–Azide Domino Reactions: Synthesis of Fully Substituted 5-Triazenyl-1,2,3-triazoles. Org. Lett. 2021, 23, 334–339. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Bao, K.; Zhang, P.; Sheng, H.; Yun, Y.; Hu, S.-X.; Astruc, D.; Zhunsight, M. Into the mechanism of the CuAAC reaction by capturing the crucial Au4Cu4–π-alkyne intermediate. J. Am. Chem. Soc. 2021, 143, 1768–1772. [Google Scholar] [CrossRef]
- Zhu, L.; Kinjo, R. An inorganic Huisgen reaction between a 1,2-diboraallene and an azide to access a diboratriazole. Angew. Chem. Int. Ed. 2022, 61, e202207631. [Google Scholar] [CrossRef]
- Singh, G.; George, N.; Singh, R.; Singh, G.; Kaur, J.D.; Kaur, G.; Singh, H.; Singh, J. CuAAC-Derived selective fluorescent probe as a recognition agent for Pb(II) and Hg(II): DFT and docking studies. ACS Omega 2022, 7, 39159–39168. [Google Scholar] [CrossRef]
- Chiavegatti Neto, A.; Soares, K.C.; da Silva Santos, M.; Jardini Aímola, T.; Ferreira, A.G.; Jardim, G.A.M.; Tormena, C.F.; Weber Paixão, M.; Barbosa Ferreira, M.A. Mechanistic investigation of enolate/stabilized vinylogous carbanion-mediated organocatalytic azide (3 + 2) cycloaddition reactions for the synthesis of 1,2,3-triazoles. Org. Biomol. Chem. 2022, 20, 6019–6026. [Google Scholar] [CrossRef]
- Gholivand, K.; Faraghi, M.; Malekshah, R.E.; Jafari, M.; Akbarzadeh, A.R.; Latifi, R.; Fadaei-Tirani, F.; Fallah, N.; Farshadfar, K. New Cu (I) complexes as catalyst for “click” reaction: An experimental and computational study. Appl. Organomet. Chem. 2023, 37, e6924. [Google Scholar] [CrossRef]
- Song, G.; Rong, W.; Liu, Y.; Li, J. Mechanisms and origin of regioselectivity for manganese-catalyzed denitrogenative annulation and click reactions. Org. Chem. Front. 2023, 10, 3642–3653. [Google Scholar] [CrossRef]
- Fukuura, S.; Yumura, T. Roles of carbon nanotube confinement in modulating regioselectivity of 1,3-dipolar cycloadditions. J. Phys. Chem. A 2023, 127, 6962–6973. [Google Scholar] [CrossRef] [PubMed]
- Chiacchio, M.A.; Lanza, G.; Chiacchio, U.; Giofrè, S.V.; Romeo, R.; Iannazzo, D.; Legnani, L. Oxazole-based compounds as anticancer agents. Curr. Med. Chem. 2019, 26, 7337–7371. [Google Scholar] [CrossRef] [PubMed]
- Bucci, R.; Giofré, S.; Clerici, F.; Contini, A.; Pinto, A.; Erba, E.; Soave, R.; Pellegrino, S.; Gelmi, M.L. Tetrahydro-4H-(pyrrolo[3,4-d]isoxazol-3-yl)methanamine: A bicyclic diamino scaffold stabilizing parallel turn conformations. J. Org. Chem. 2018, 83, 11493–11501. [Google Scholar] [CrossRef] [PubMed]
- Uceta, E.; Vizuete, M.; Carrillo, J.R.; Barrejón, M.; Fierro, J.L.J.; Prieto, M.P.; Langa, F. Cycloaddition of nitrile oxides to graphene: A theoretical and experimental approach. Chem. Eur. J. 2019, 25, 14644–14650. [Google Scholar] [CrossRef]
- Barrejón, M.; Gómez-Escalonilla, M.J.; Fierro, J.L.G.; Prieto, P.; Carrillo, J.R.; Rodríguez, A.M.; Abellán, G.M.; López-Escalante, C.; Gabas, M.; López-Navarrete, J.T.; et al. Modulation of the exfoliated graphene work function through cycloaddition of nitrile imines. Phys. Chem. Chem. Phys. 2016, 18, 29582–29590. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Nana, C.N.; Ketcha-Mbadcam, J.; Ndassa, I.M.; Andrés, J.; Oliva, M.; Safont, V.S. Deciphering the curly arrow representation and electron flow for the 1,3-dipolar rearrangement between acetonitrile oxide and (1S,2R,4S)-2-cyano-7-oxabicyclo[2.2.1]hept-5-en-2-yl acetate derivatives. ACS Omega 2020, 5, 22215–22225. [Google Scholar] [CrossRef]
- Goyard, D.; Kónya, B.; Czifrák, K.; Larini, P.; Demontrond, F.; Leroy, J.; Balzarin, S.; Tournier, M.; Tousch, D.; Petit, P.; et al. Glucose-based spiro-oxathiazoles as in vivo anti-hyperglycemic agents through glycogen phosphorylase inhibition. Org. Biomol. Chem. 2020, 18, 931–940. [Google Scholar] [CrossRef]
- Holman, S.D.L.; Wills, A.G.; Fazakerley, N.J.; Poole, D.L.; Coe, D.M.; Berlouis, L.A.; Reid, M. Electrochemical synthesis of isoxazolines: Method and mechanism. Chem. Eur. J. 2022, 28, e202103728. [Google Scholar] [CrossRef]
- Kiss, L.; Escorihuela, J. A computational study of 1,3-dipolar cycloadditions of nitrile oxides with dienes. Tetrahedron 2023, 139, 133435. [Google Scholar] [CrossRef]
- Dubey, S.; Pal, A.; Roy, S.; Sasmal, S.; Tamrakar, A.; Jana, R.; Das, T. Recent advances in the (3 + 2) cycloaddition of azomethine ylide. New J. Chem. 2023, 47, 8997–9034. [Google Scholar] [CrossRef]
- Esteban, F.; Cieślik, W.; Arpa, E.M.; Guerrero-Corella, A.; Díaz-Tendero, S.; Perles, J.; Fernández-Salas, J.A.; Fraile, A.; Alemán, J. Intramolecular Hydrogen Bond Activation: Thiourea-organocatalyzed enantioselective 1,3-dipolar cycloaddition of salicylaldehyde-derived azomethine ylides with nitroalkenes. ACS Catal. 2018, 8, 1884–1890. [Google Scholar] [CrossRef] [PubMed]
- Selva, V.; Selva, E.; Merino, P.; Najera, C.; Sansano, J.M. Sequential metal-free thermal 1,3-dipolar cycloaddition of unactivated azomethine ylides. Org. Lett. 2018, 20, 3522–3526. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Du, Z.; Chen, H.; Yang, Z.; Tan, Q.; Zhang, C.; Zhu, L.; Lan, Y.; Zhang, M. Well-designed phosphine–urea ligand for highly diastereo- and enantioselective 1,3-dipolar cycloaddition of methacrylonitrile: A combined experimental and theoretical study. J. Am. Chem. Soc. 2019, 141, 961–971. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Kalita, S.J.; Zhao, Z.-N.; Yang, X.; Zhao, Y.; Schneider, U.; Shibata, N.; Huang, Y.-Y. Diastereodivergent asymmetric 1,3-dipolar cycloaddition of azomethine ylides and β-fluoroalkyl vinylsulfones: Low copper(II) catalyst loading and theoretical studies. Angew. Chem. Int. Ed. 2019, 58, 16637–16643. [Google Scholar] [CrossRef] [PubMed]
- Filatov, A.S.; Wang, S.; Khoroshilova, O.V.; Lozovskiy, S.V.; Larina, A.G.; Boitsov, V.M.; Stepakov, A.V. Stereo- and regioselective 1,3-dipolar cycloaddition of the stable ninhydrin-derived azomethine ylide to cyclopropenes: Trapping of unstable cyclopropene dipolarophiles. J. Org. Chem. 2019, 84, 7017–7036. [Google Scholar] [CrossRef]
- Caleffi, G.S.; Larrañaga, O.; Ferrándiz-Saperas, M.; Costa, P.R.R.; Nájera, C.; de Cózar, A.; Cossío, F.P.; Sansano, J.M. Switching diastereoselectivity in catalytic enantioselective (3 + 2) cycloadditions of azomethine ylides promoted by metal salts and privileged segphos-derived ligands. J. Org. Chem. 2019, 84, 10593–10605. [Google Scholar] [CrossRef]
- Semivrazhskaya, O.; Romero-Rivera, A.; Aroua, S.; Troyanov, S.I.; Garcia-Borràs, M.; Stevenson, S.; Osuna, S.; Yamakoshi, Y. Structures of Gd3N@C80 Prato bis-ddducts: Crystal structure, thermal isomerization, and computational study. J. Am. Chem. Soc. 2019, 141, 10988–10993. [Google Scholar] [CrossRef]
- Alonso, D.; Hernández-Castillo, D.; Almagro, L.; González-Alemán, R.; Molero, D.; Herranz, M.A.; Medina-Páez, E.; Coro, J.; Martínez-Álvarez, R.; Suárez, M.; et al. Diastereoselective synthesis of steroid–[60]fullerene hybrids and theoretical underpinning. J. Org. Chem. 2020, 85, 2426–2437. [Google Scholar] [CrossRef]
- Rivilla, I.; de Cózar, A.; Schäfer, T.; Hernandez, F.J.; Bittner, A.M.; Eleta-Lopez, A.; Aboudzadeh, A.; Santos, J.I.; Miranda, J.I.; Cossio, F.P. Catalysis of a 1,3-dipolar reaction by distorted DNA incorporating a heterobimetallic platinum(II) and copper(II) complex. Chem. Sci. 2017, 8, 7038–7046. [Google Scholar] [CrossRef]
- Rivilla, I.; Odriozola-Gimeno, M.; Aires, A.; Gimeno, A.; Jiménez-Barbero, J.; Torrent-Sucarrat, M.; Cortajarena, A.L.; Cossío, F.P. Discovering Biomolecules with Huisgenase activity: Designed repeat proteins as biocatalysts for (3 + 2) cycloadditions. J. Am. Chem. Soc. 2020, 142, 762–776. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, K.; Gabriel, P.; Di Carmine, G.; Pedroni, J.; Farizyan, M.; Hamlin, T.A.; Dixon, D.J. General pyrrolidine synthesis via iridium-catalyzed reductive azomethine ylide generation from tertiary amides and lactams. Adv. Syn. Catal. 2021, 11, 7489–7497. [Google Scholar] [CrossRef] [PubMed]
- Vermeeren, P.; Hamlin, T.A.; Fernández, I.; Bickelhaupt, F.M. Origin of rate enhancement and asynchronicity in iminium catalyzed Diels−Alder reactions. Chem. Sci. 2020, 11, 8105–8112. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.; Yang, Y.; Shen, C.; Xue, K.-S.; Wang, Z.-F.; Cong, H.; Tao, H.Y.; Chung, L.W.; Wang, C.-J. β-Substituted alkenyl heteroarenes as dipolarophiles in the Cu(I)-catalyzed asymmetric 1,3-dipolarc cycloaddition of azomethine ylides empowered by a dual activation strategy: Stereoselectivity and mechanistic insight. J. Am. Chem. Soc. 2021, 143, 3519–3535. [Google Scholar] [CrossRef] [PubMed]
- Filatov, A.S.; Pronina, J.A.; Selivanov, S.I.; Shmakov, S.V.; Uspenski, A.A.; Boitsov, V.M.; Stepakov, A.V. 1,11H-Benzo[4,5]imidazo[1,2-a]indol-11-one as a new precursor of azomethine ylides: 1,3-Dipolar cycloaddition reactions with cyclopropenes and maleimides. Int. J. Mol. Sci. 2022, 23, 13202. [Google Scholar] [CrossRef] [PubMed]
- Gugkaeva, Z.T.; Panova, M.V.; Smol’yakov, A.F.; Medvedev, M.G.; Tsaloev, A.T.; Godovikov, I.A.; Maleev, V.I.; Larionov, V.A. Asymmetric metal-templated route to amino acids with 3-spiropyrrolidine oxindole core via a 1,3-dipolar addition of azomethine ylides to a chiral dehydroalanine Ni(II) complex. Adv. Syn. Catal. 2022, 364, 2395–2402. [Google Scholar] [CrossRef]
- Radwan, M.F.; Elboray, E.E.; Dardeer, H.M.; Kobayashi, Y.; Furuta, T.; Hamada, S.; Dohi, T.; Aly, M.F. 1,3-Dipolar cycloaddition of 3-chromonyl-substituted glycine imino esters with arylidenes and in situ diastereodivergent via retrocycloaddition. Chem. Asian J. 2023, 18, e202300215. [Google Scholar] [CrossRef]
- Selva, E.; Castello, L.M.; Mancebo-Aracil, J.; Selva, V.; Najera, C.; Foubelo, F.; Sansano, J.M. Synthesis of pharmacophores containing a prolinate core using a multicomponent 1,3-dipolar cycloaddition of azomethine ylides. Tetrahedron 2017, 73, 6840–6846. [Google Scholar] [CrossRef]
- Chiacchio, M.A.; Legnani, L.; Chiacchio, U. Recent advances on the synthesis of isoxazolidines. In Chapter 7 in Synthetic Approaches to Nonaromatic Nitrogen Heterocycles; Faisca Phillips, A.M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020; Volume 2, pp. 161–177. ISBN 9781119708704. [Google Scholar]
- Chiacchio, U.; Padwa, A.; Romeo, G. Cycloaddition methodology: A useful entry towards biologically active heterocycles. Curr. Org. Chem. 2009, 13, 422–447. [Google Scholar] [CrossRef]
- Romeo, G.; Chiacchio, U.; Corsaro, A.; Merino, P. Chemical synthesis of heterocyclic sugar nucleoside analogues. Chem. Rev. 2010, 110, 3337–3370. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, W.; Lin, Q.; Yang, W.; Li, H.; Wang, L.; Gu, F.; Yang, D. 1,3-Dipolar cycloaddition of nitrones to oxa(aza)bicyclic alkenes. Org. Chem. Front. 2019, 6, 3360–3364. [Google Scholar] [CrossRef]
- Legnani, L.; Iannazzo, D.; Pistone, A.; Celesti, C.; Giofrè, S.; Romeo, R.; Di Pietro, A.; Visalli, G.; Fresta, M.; Bottino, P.; et al. Functionalized polyhedral oligosilsesquioxane (POSS) based composites for bone tissue engineering: Synthesis, computational and biological studies. RSC Adv. 2020, 10, 11325–11334. [Google Scholar] [CrossRef] [PubMed]
- Alves, A.J.S.; Pinho e Melo, T.M.V.D. Synthesis of novel chiral spiroisoxazolidine-β-lactams from 6-alkylidenepenicillanates: A 1,3-dipolar cycloaddition approach. Eur. J. Org. Chem. 2020, 39, 6259–6269. [Google Scholar] [CrossRef]
- Mekheimer, R.A.; Al-Zaydi, K.; Ibrahim, M.A.A.; Al-Shamary, A.; Sadek, K. Regio and stereoselective 1,3-dipolar cycloaddition reactions of C-aryl (or hetaryl)-N-phenylnitrones to monosubstituted ylidene malononitriles and 4-benzylidene-2-phenyloxazol-5(4H)-one. Z. Naturforsch B J. Chem. Sci. 2017, 72, 317e326. [Google Scholar] [CrossRef]
- Pipim, G.B.; Opoku, E.; Tia, R.; Adei, E. Peri-, chemo-, regio-, stereo- and enantio-selectivities of 1,3-dipolar cycloaddition reaction of C, N-disubstituted nitrones with disubstituted 4-methylene-1,3-oxazol-5(4H)- one: A quantum mechanical study. J. Mol. Graph. Model. 2020, 97, 107542. [Google Scholar] [CrossRef]
- Briccolani-Bandini, L.; Pagliai, M.; Cordero, F.M.; Brandi, A.; Cardini, G. Cyclopropylidene effect in the 1, 3-dipolar cycloaddition of nitrones to alkylidene cyclopropanes: A computational rationalization. J. Phys. Chem. A 2021, 125, 3892–3899. [Google Scholar] [CrossRef]
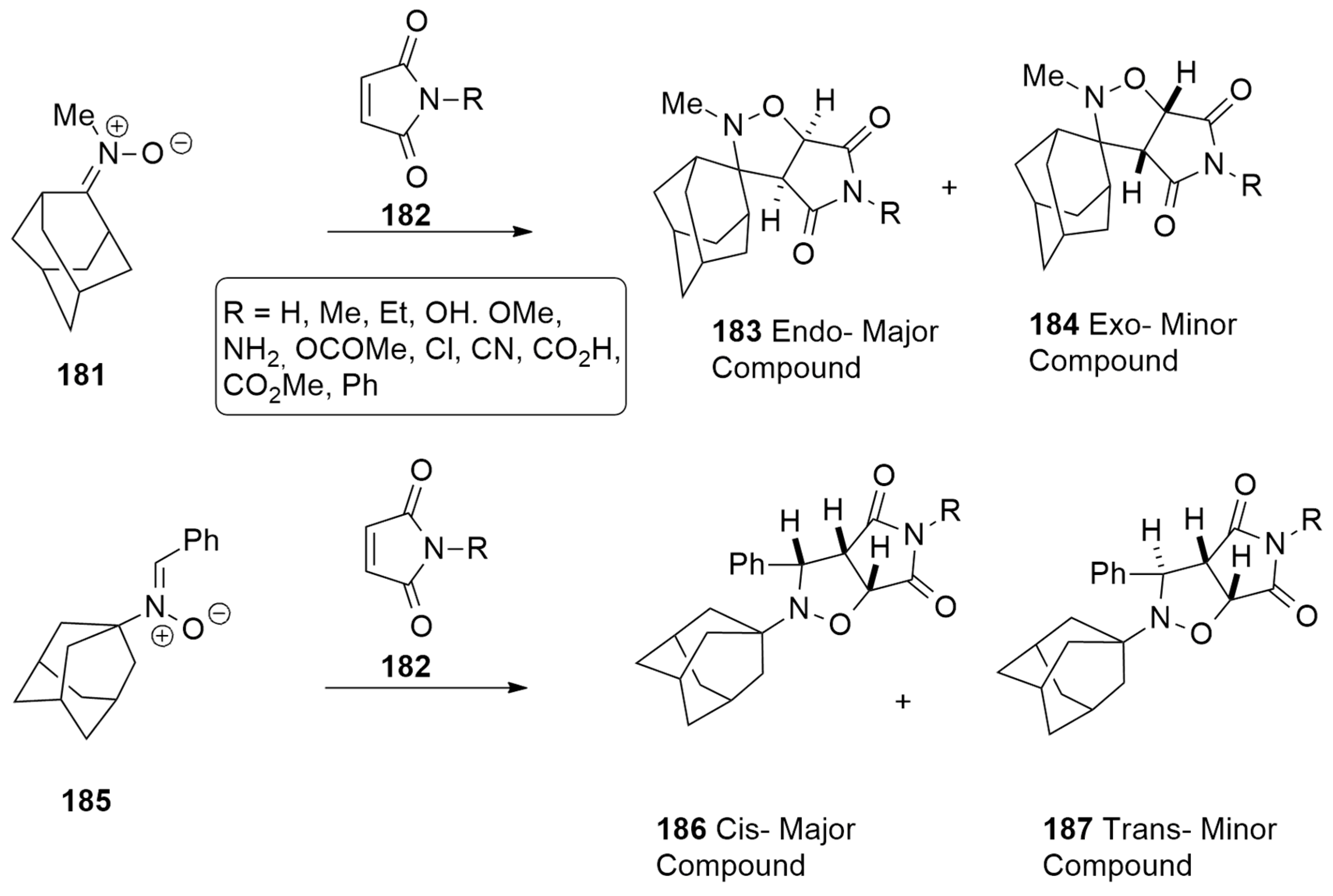
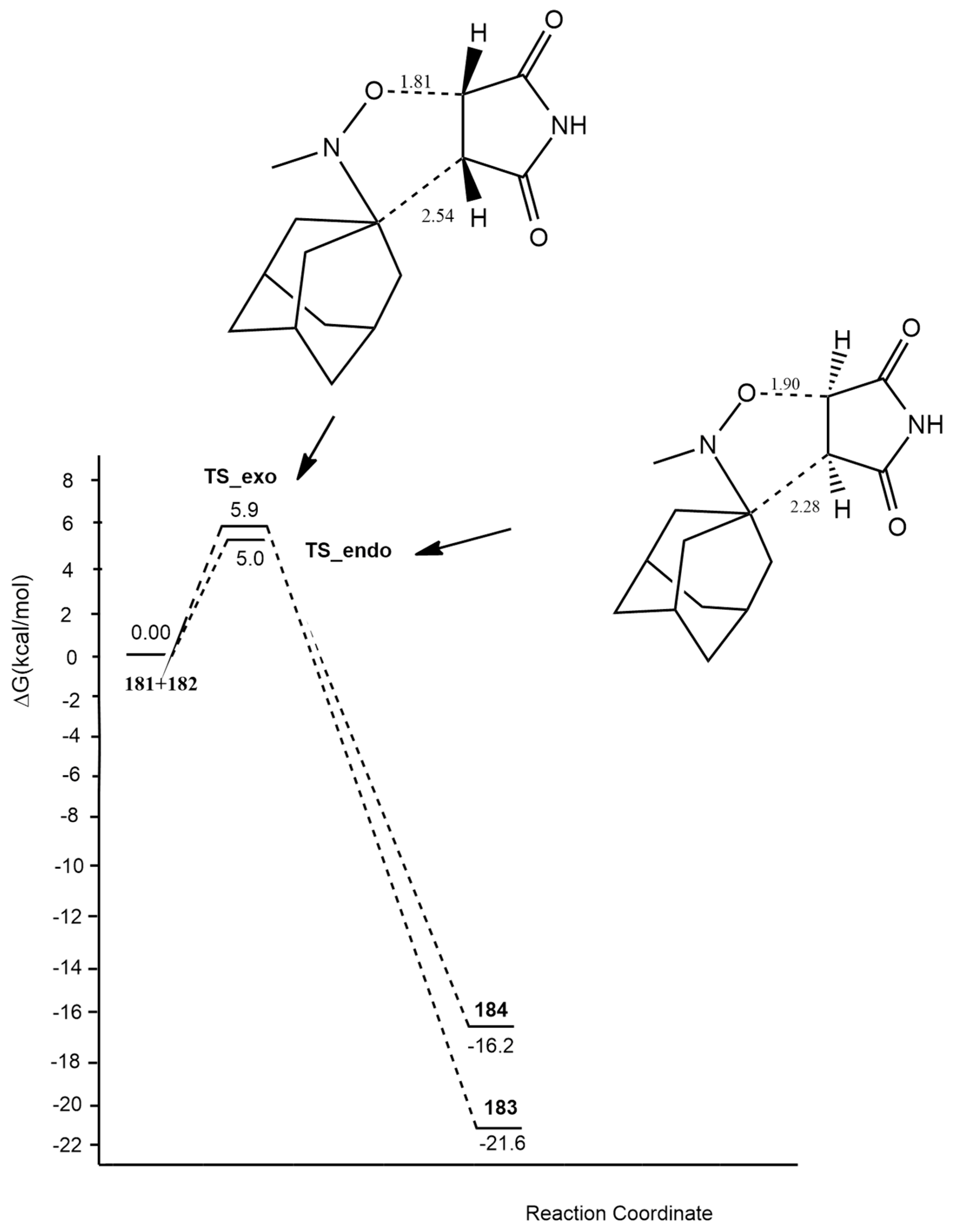
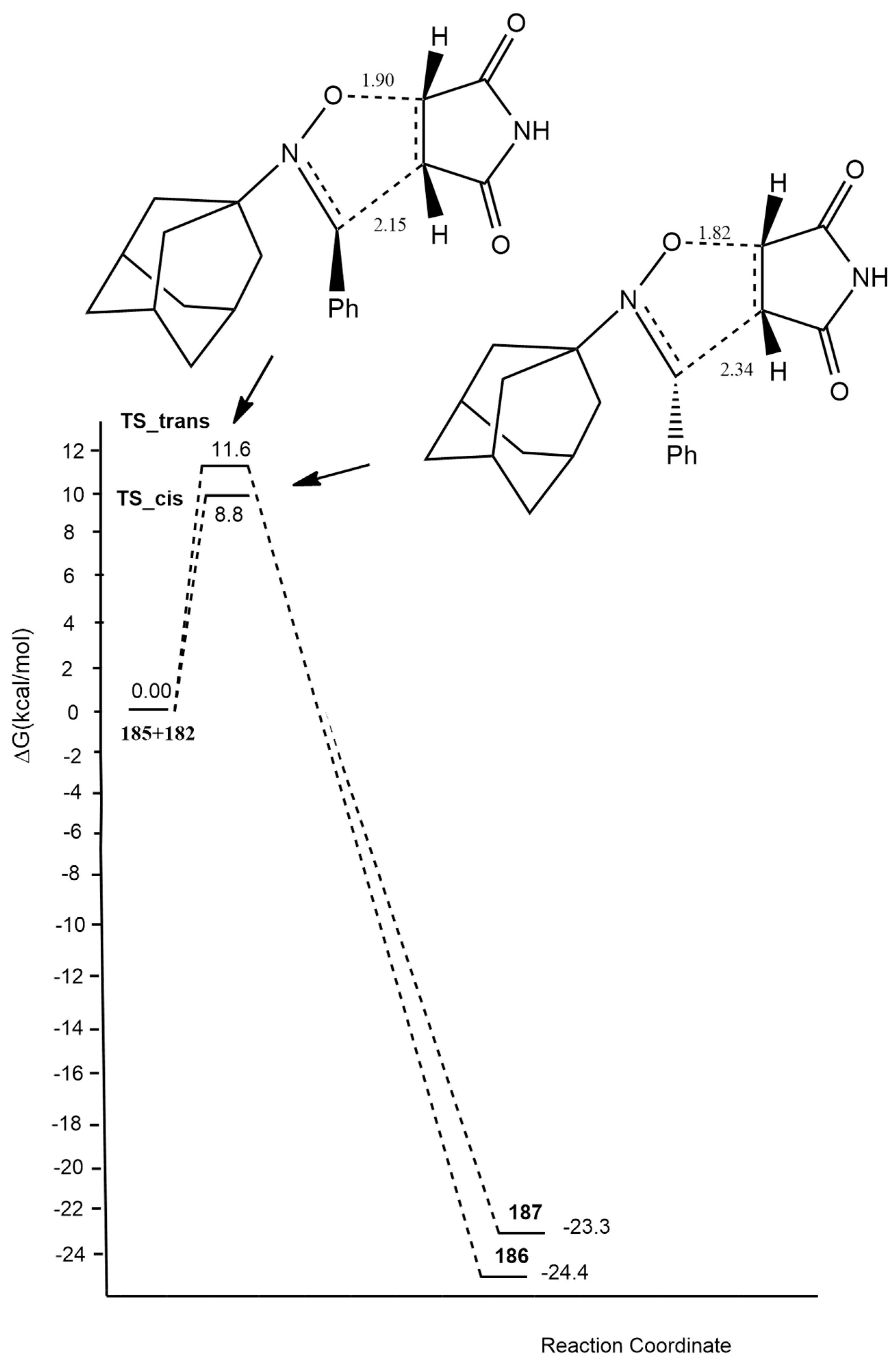
- Molchanov, A.P.; Lukina, V.M.; Efremova, M.M.; Muryleva, A.A.; Slita, A.V.; Zarubaev, V.V. The 1,3-dipolar cycloaddition of adamantine-derived nitrones with maleimides. Synth. Commun. 2020, 50, 1367–1374. [Google Scholar] [CrossRef]
- Umar, A.R.; Tia, R.; Adei, E. The 1,3-dipolar cycloaddition of adamantine-derived nitrones with maleimides: A computational study. Comput. Theor. Chem. 2021, 1195, 113099. [Google Scholar] [CrossRef]

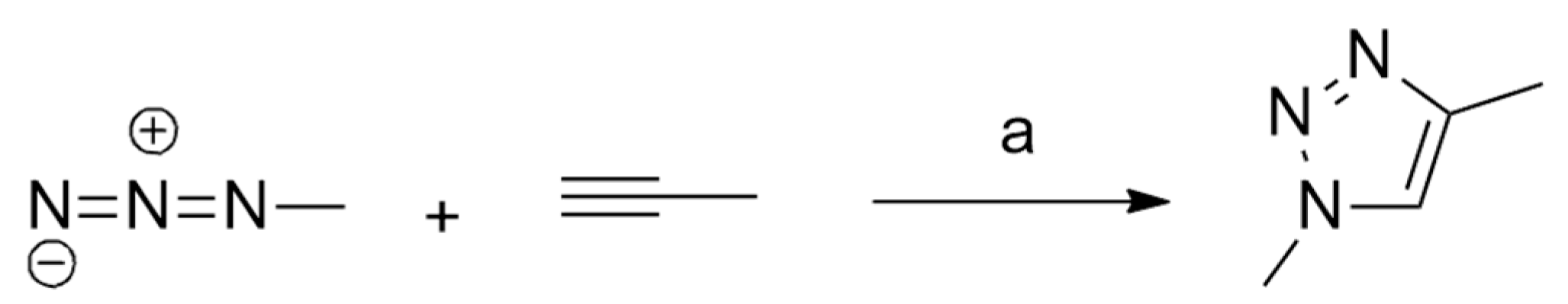

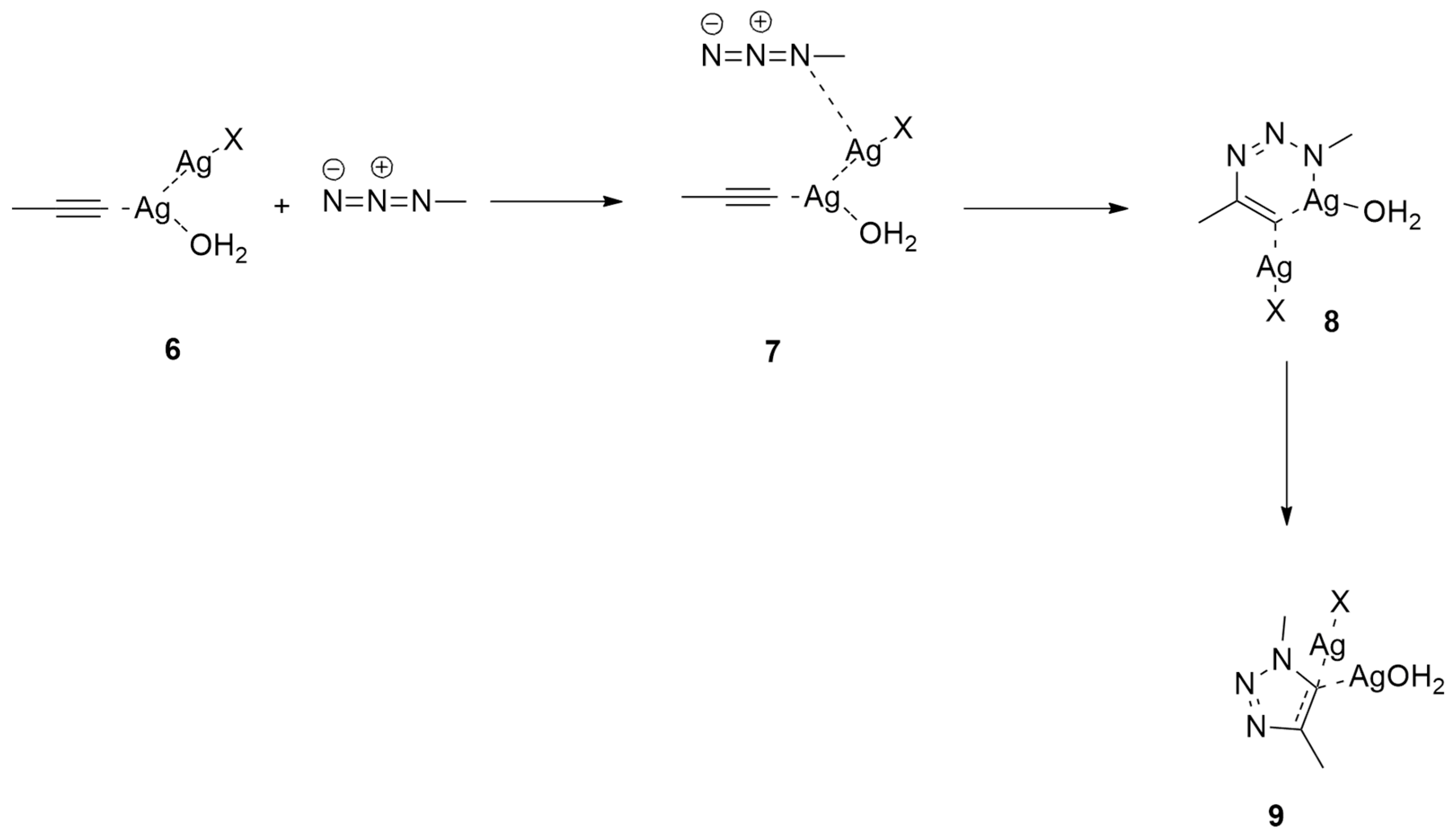

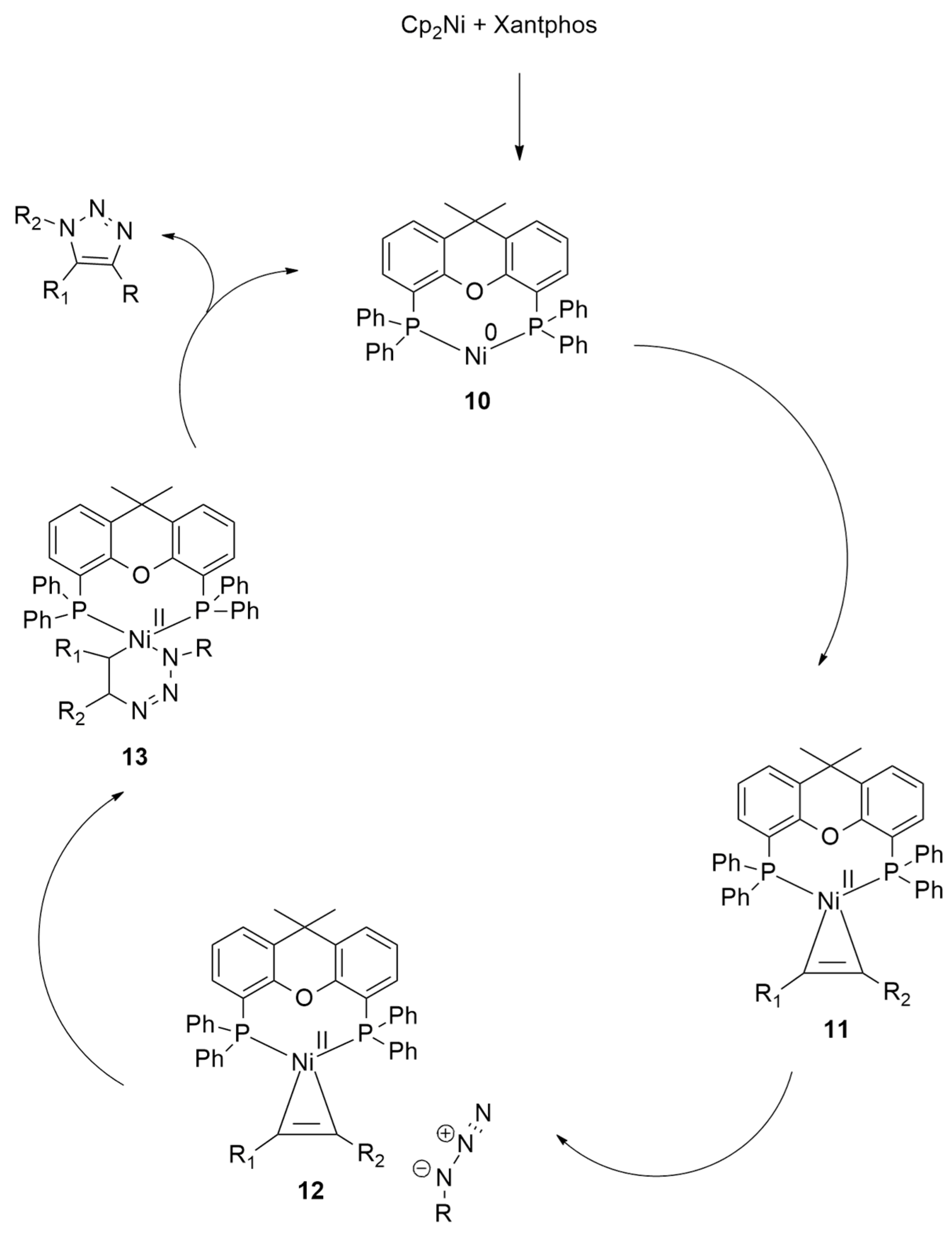
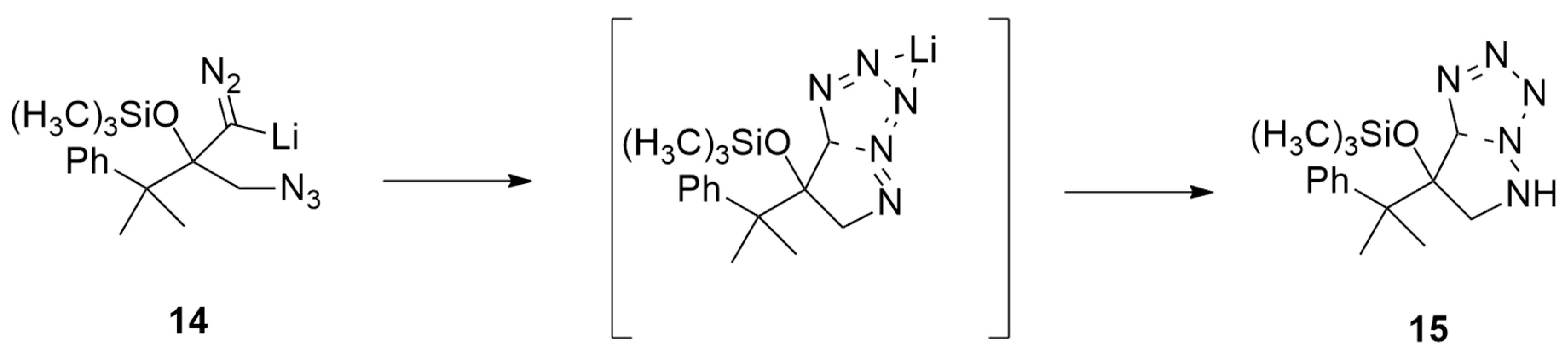
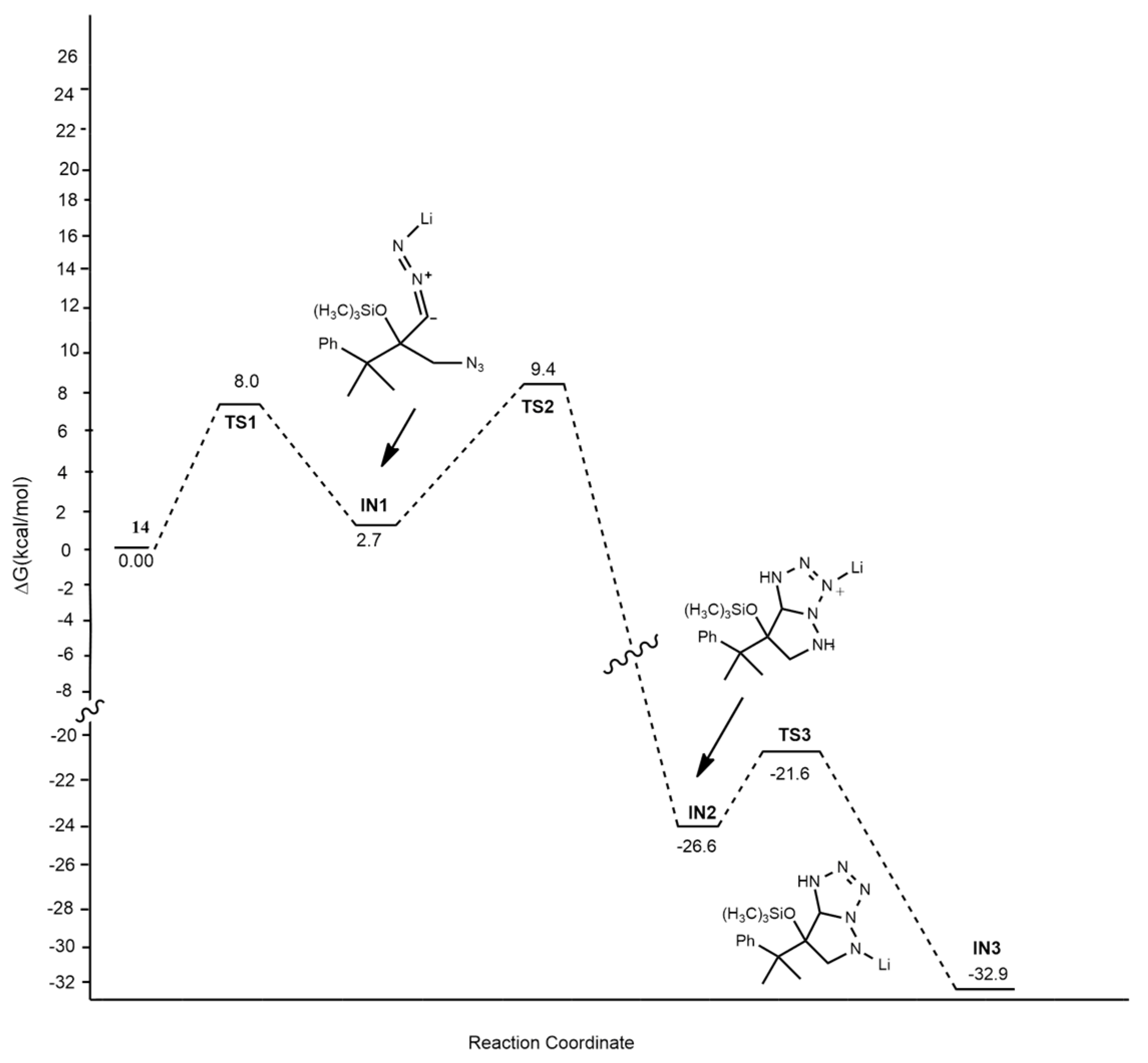
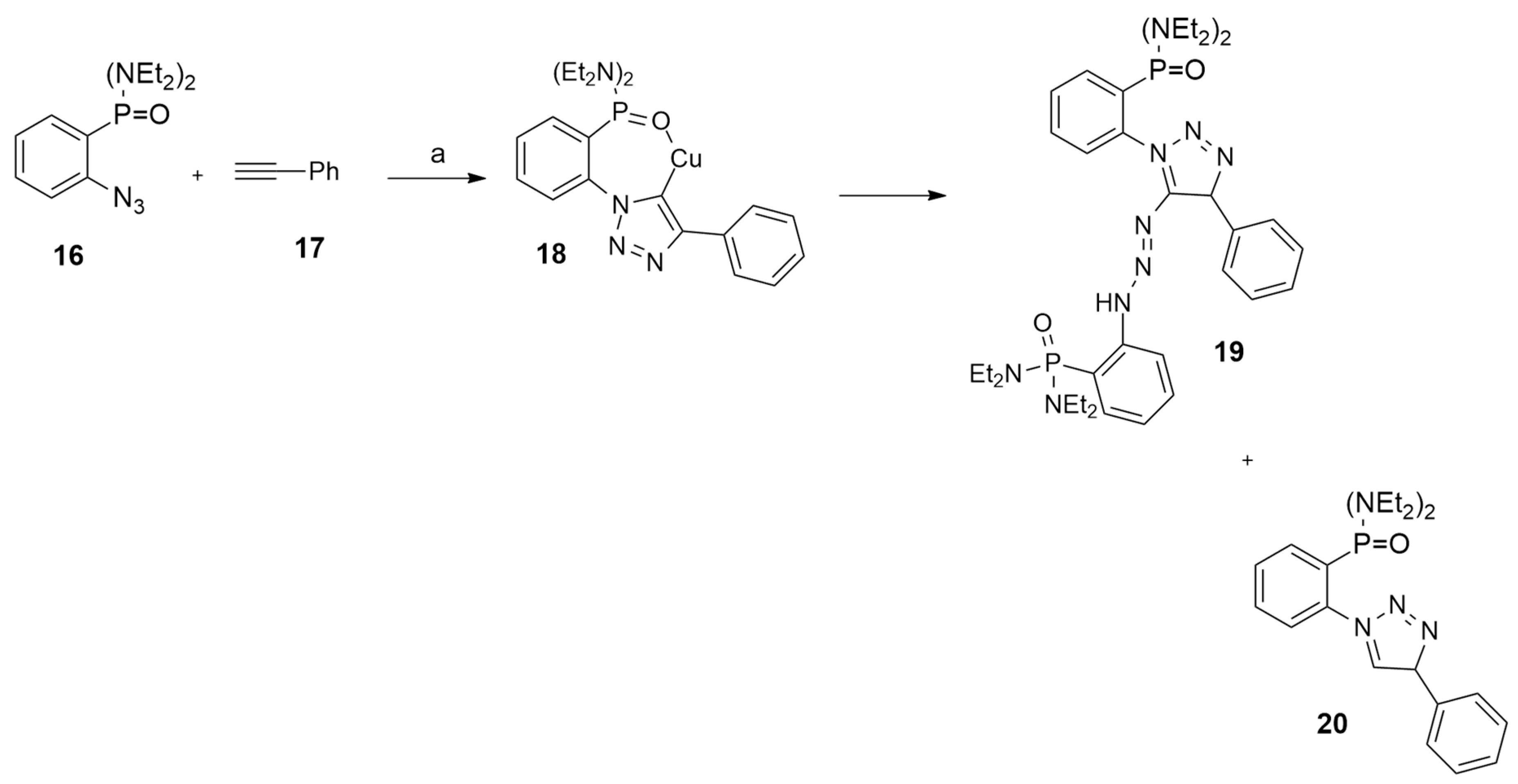
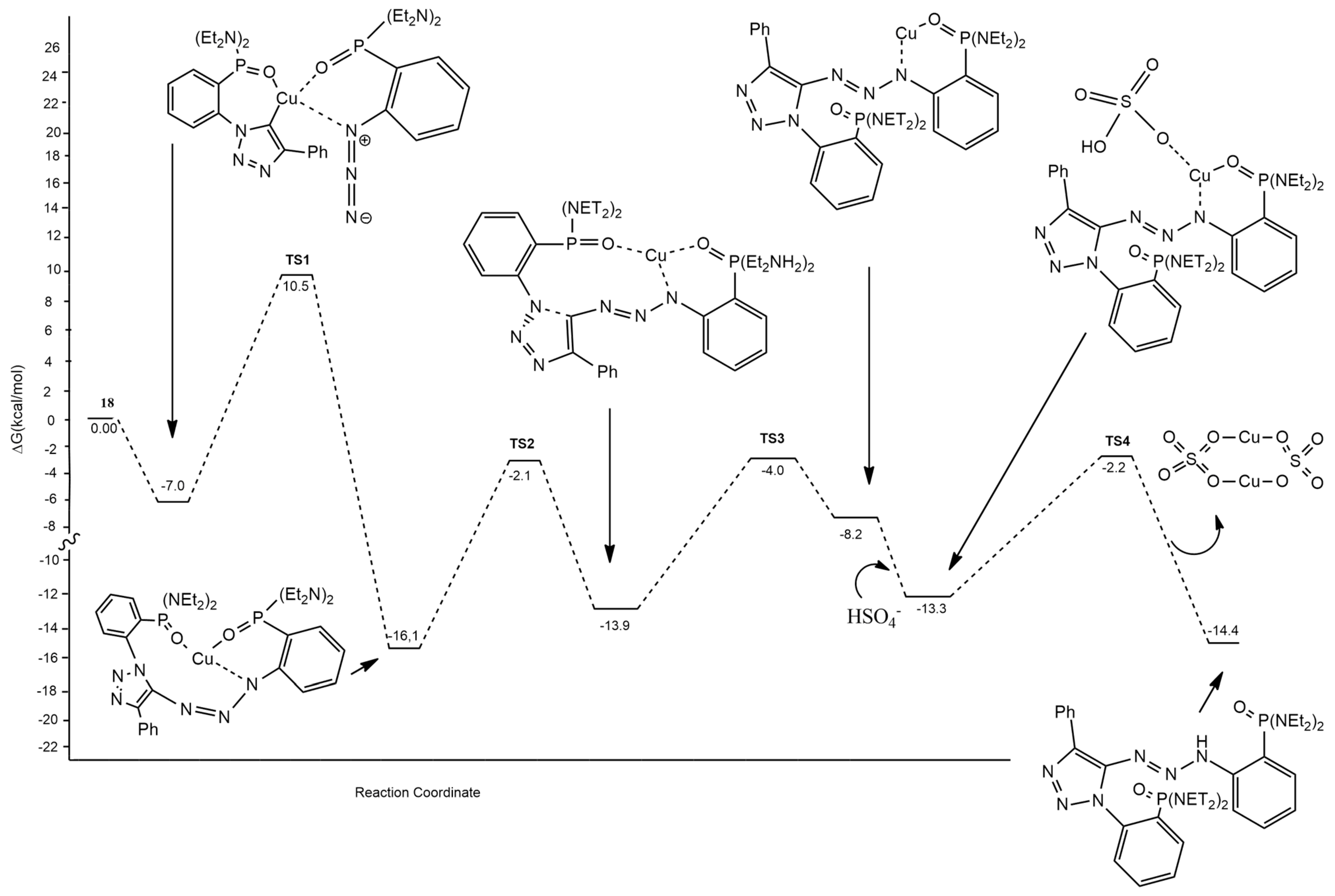
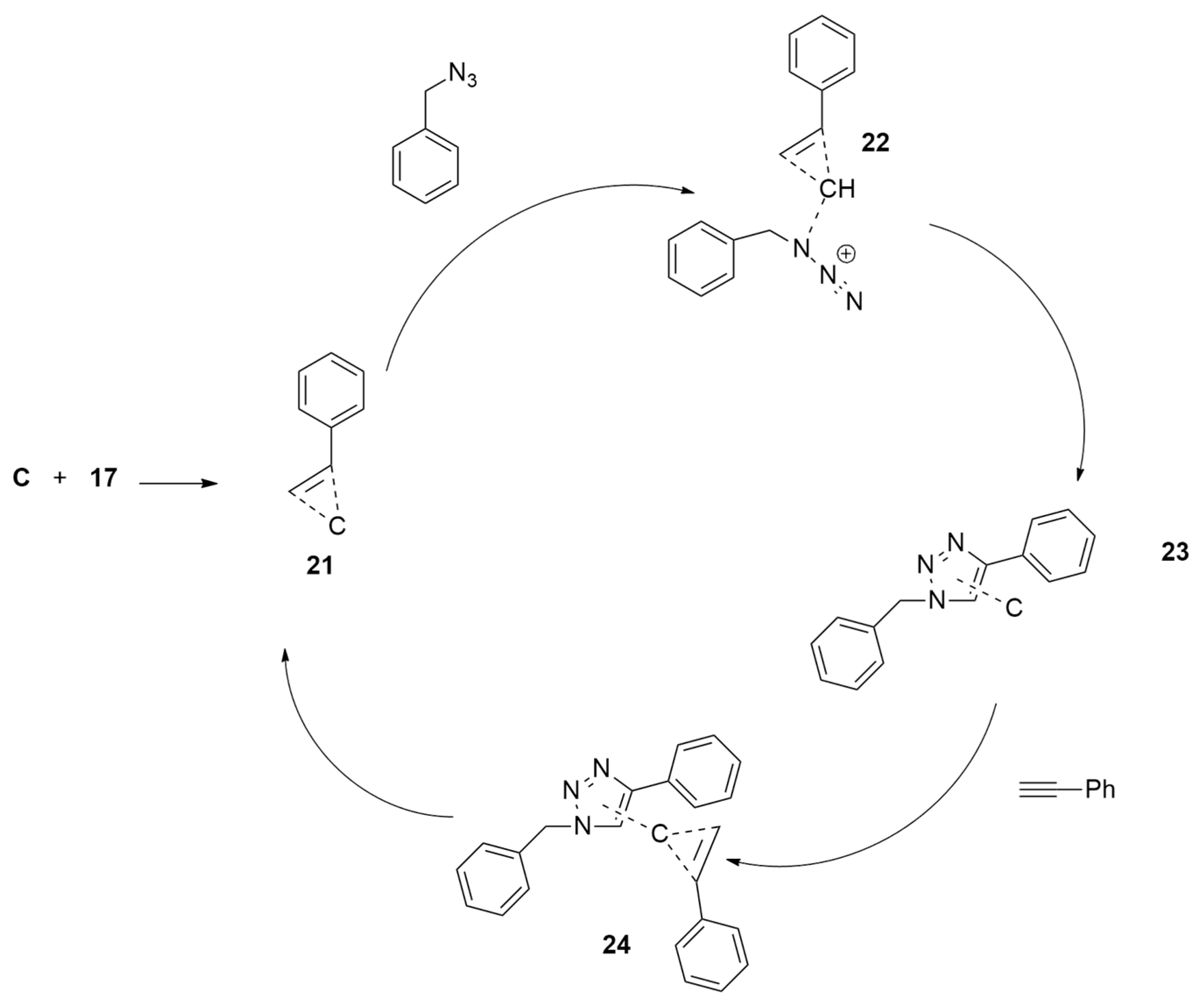


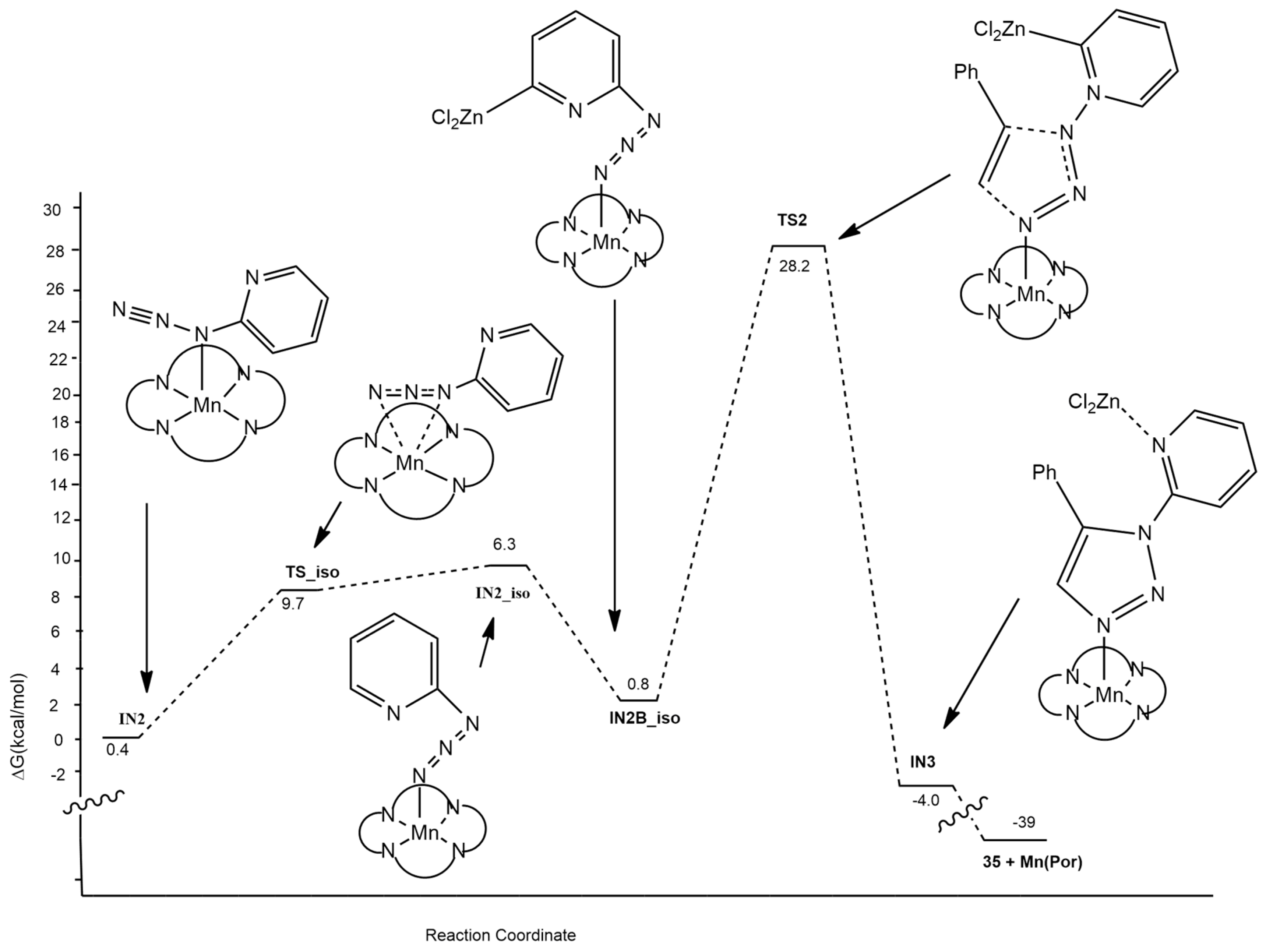

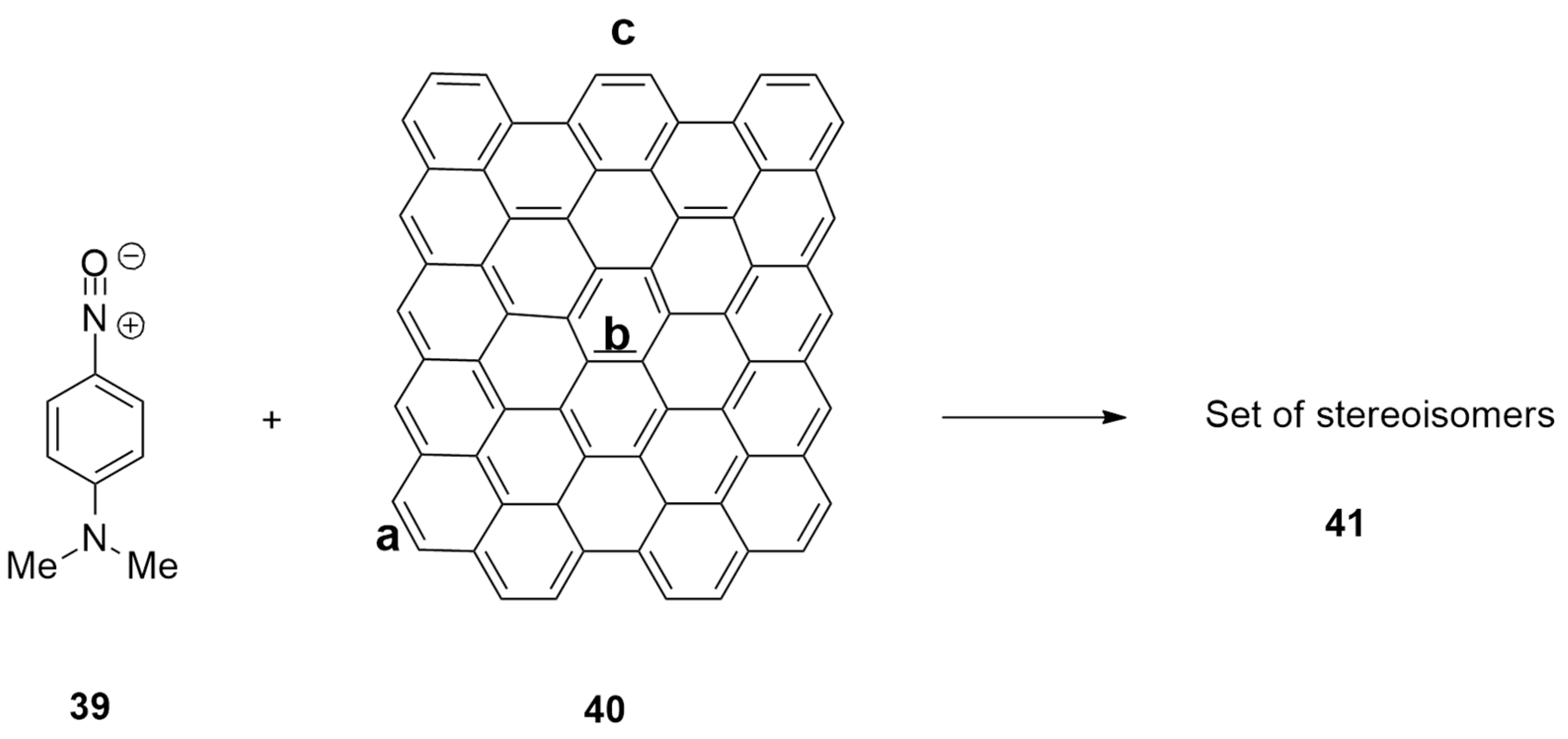
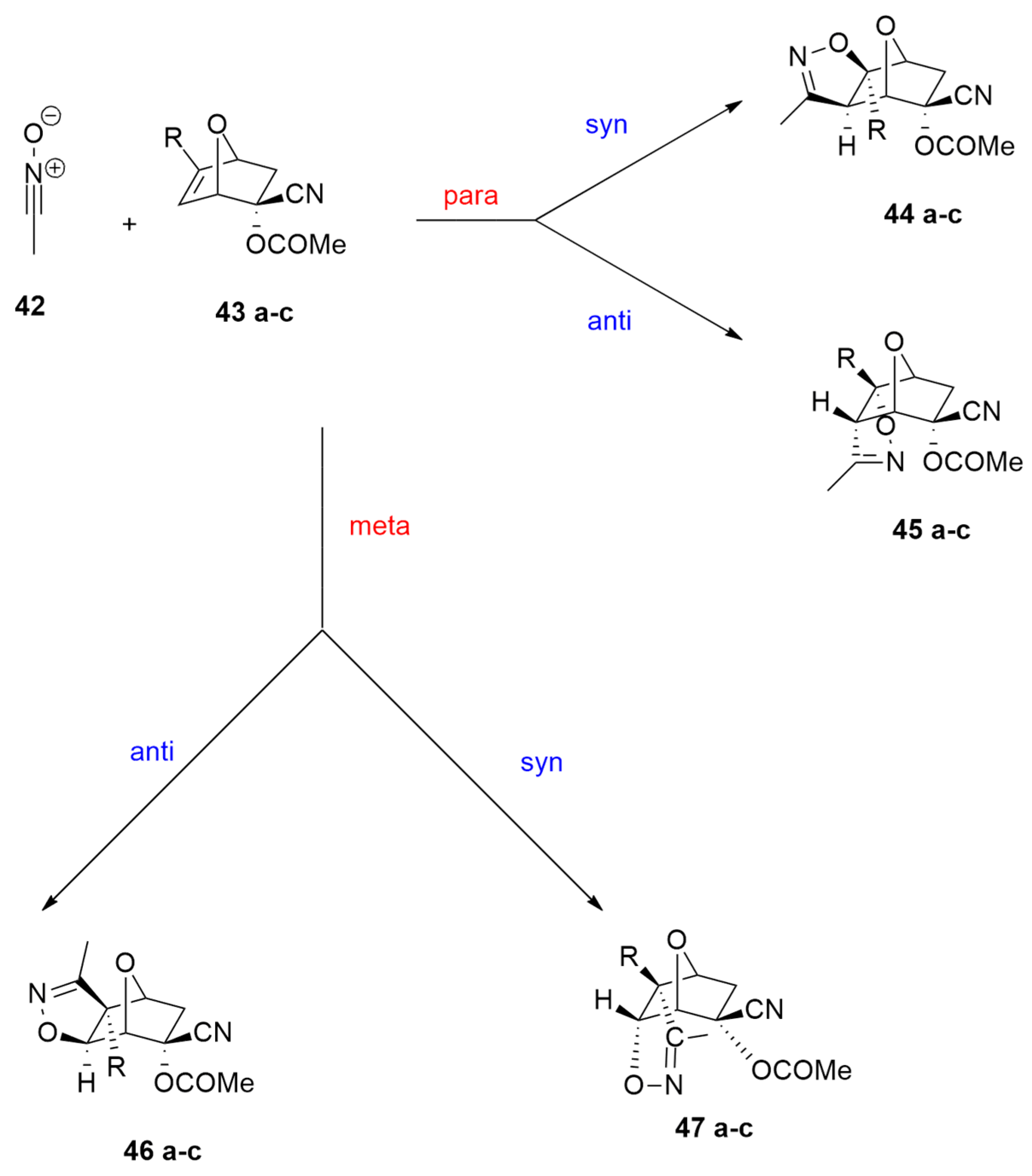



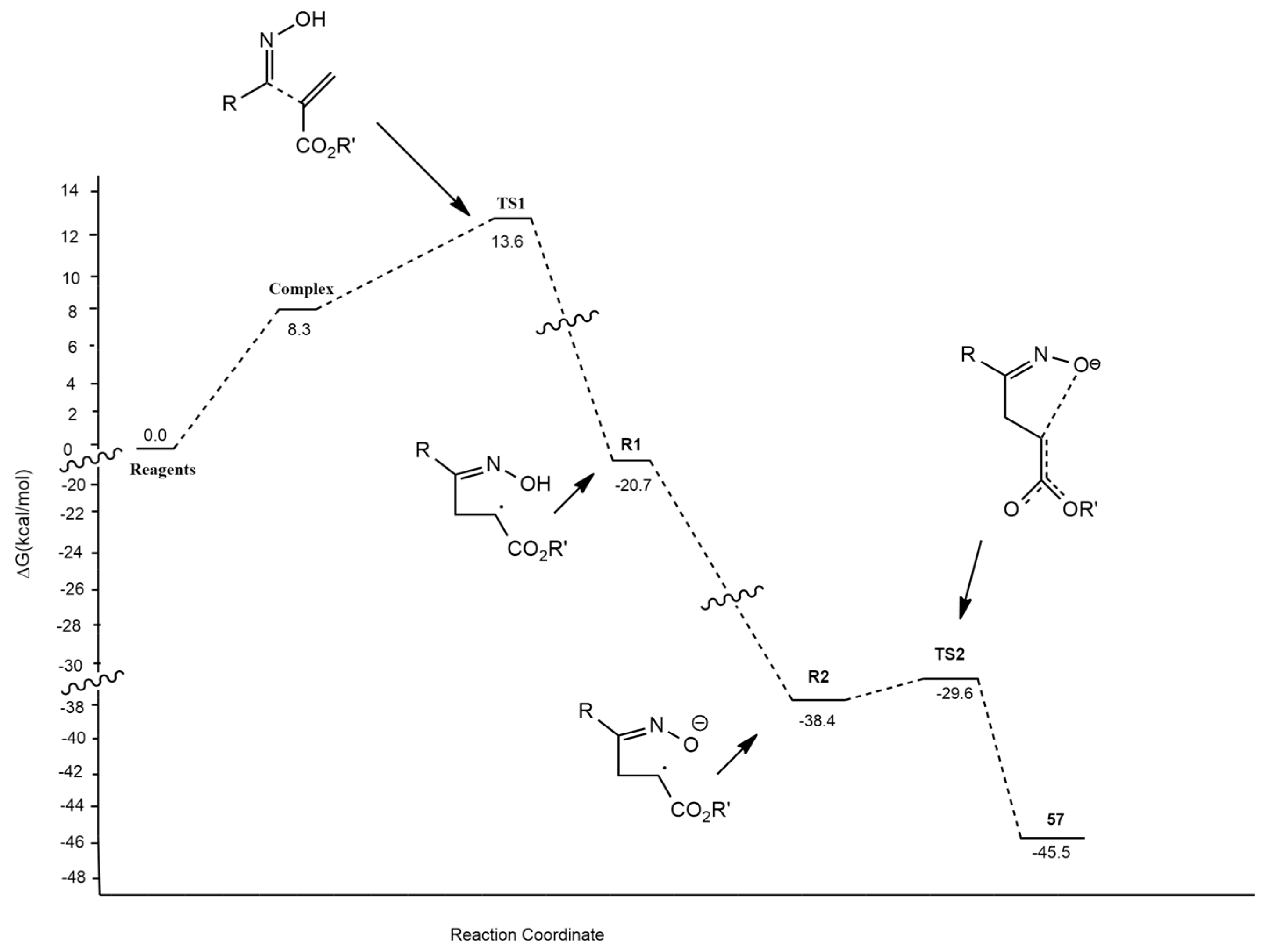



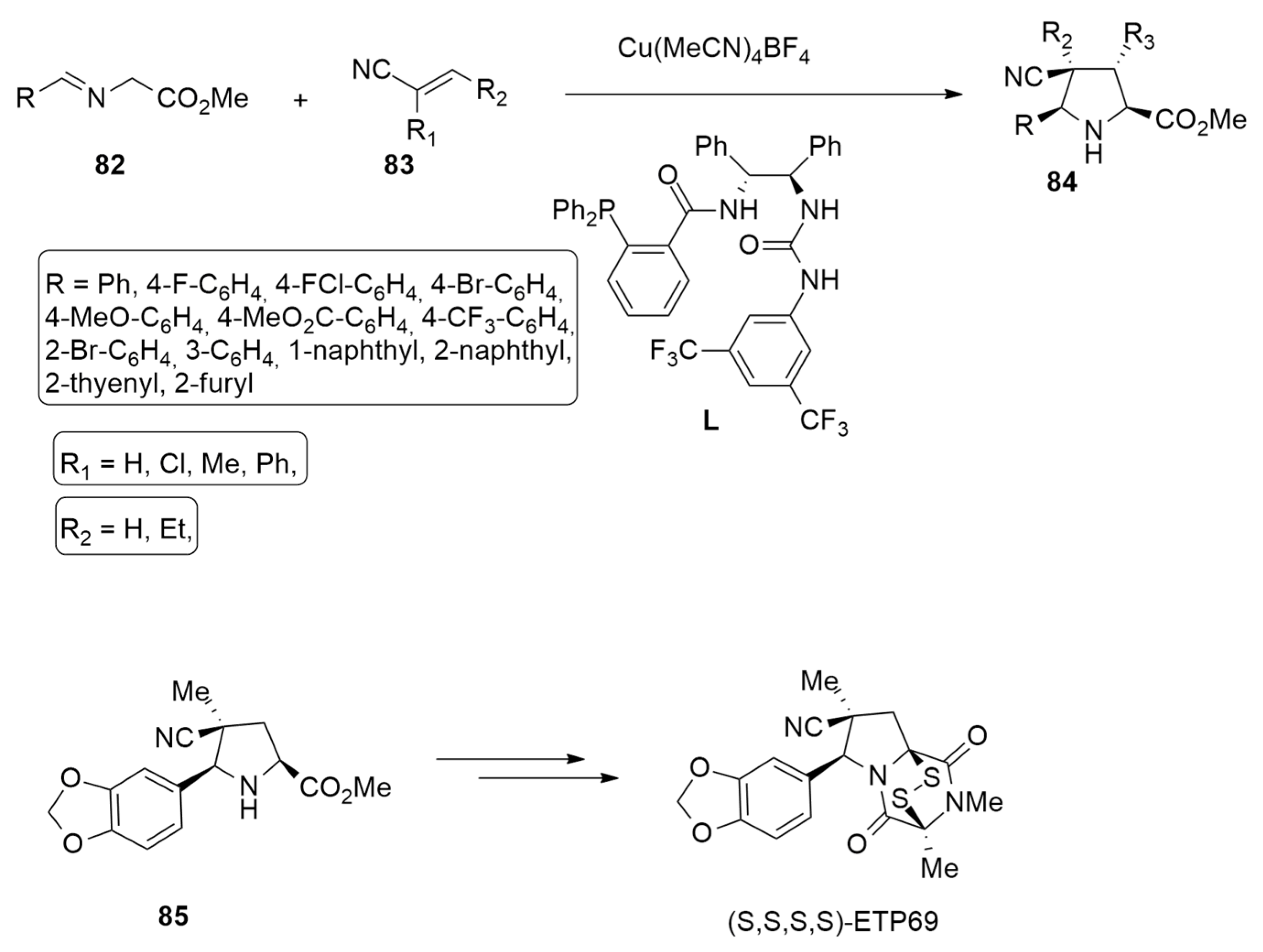
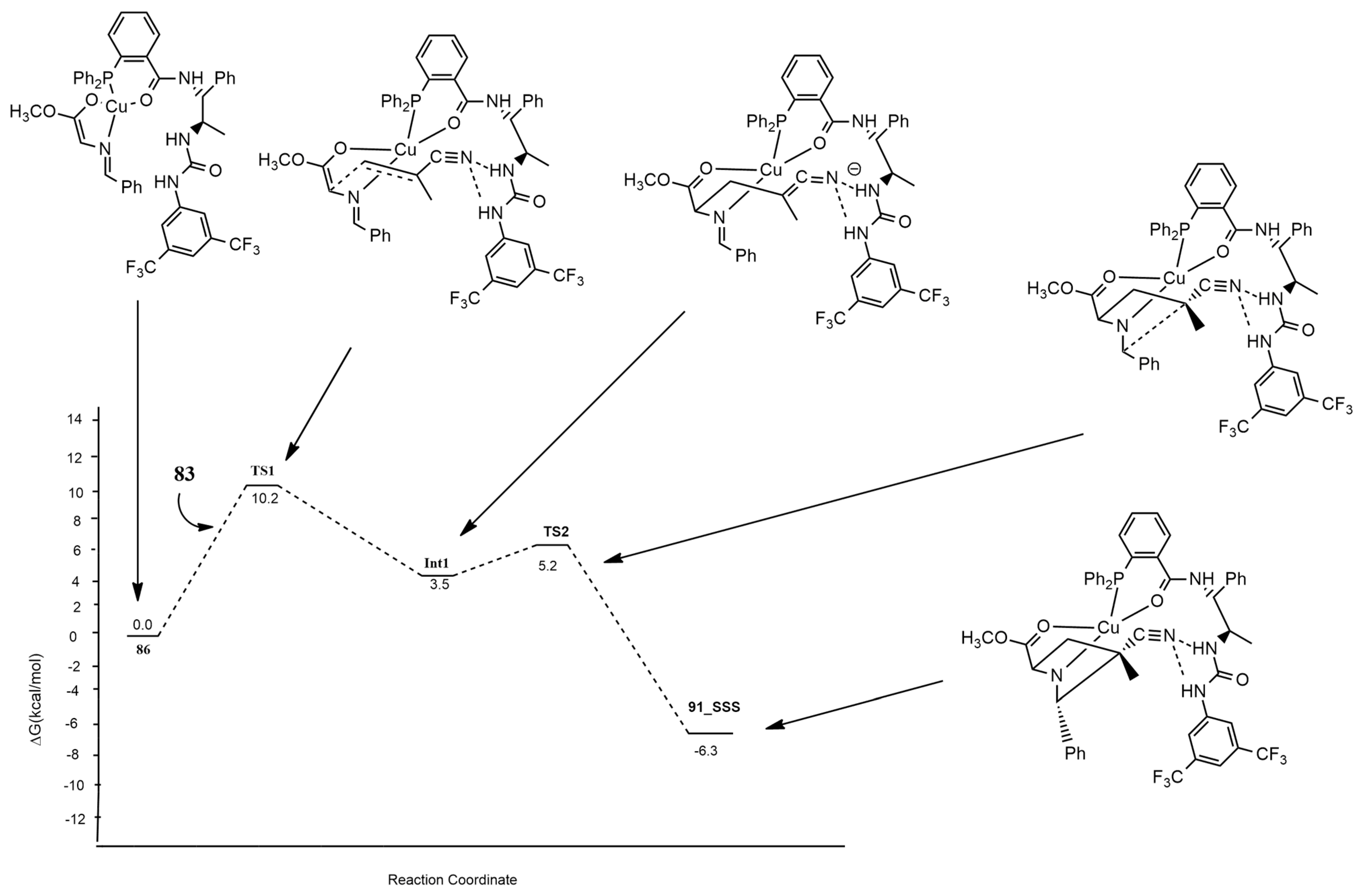
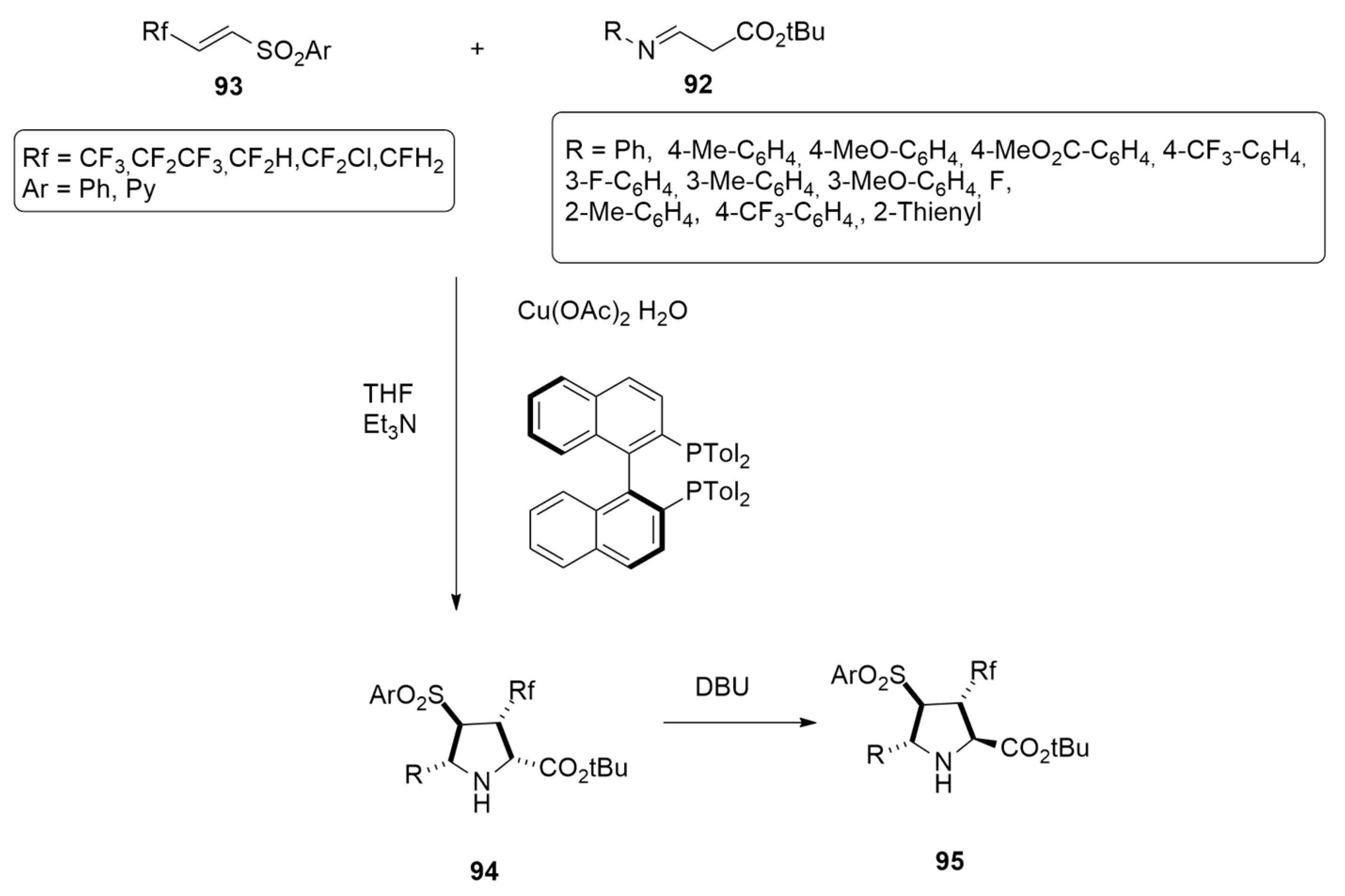

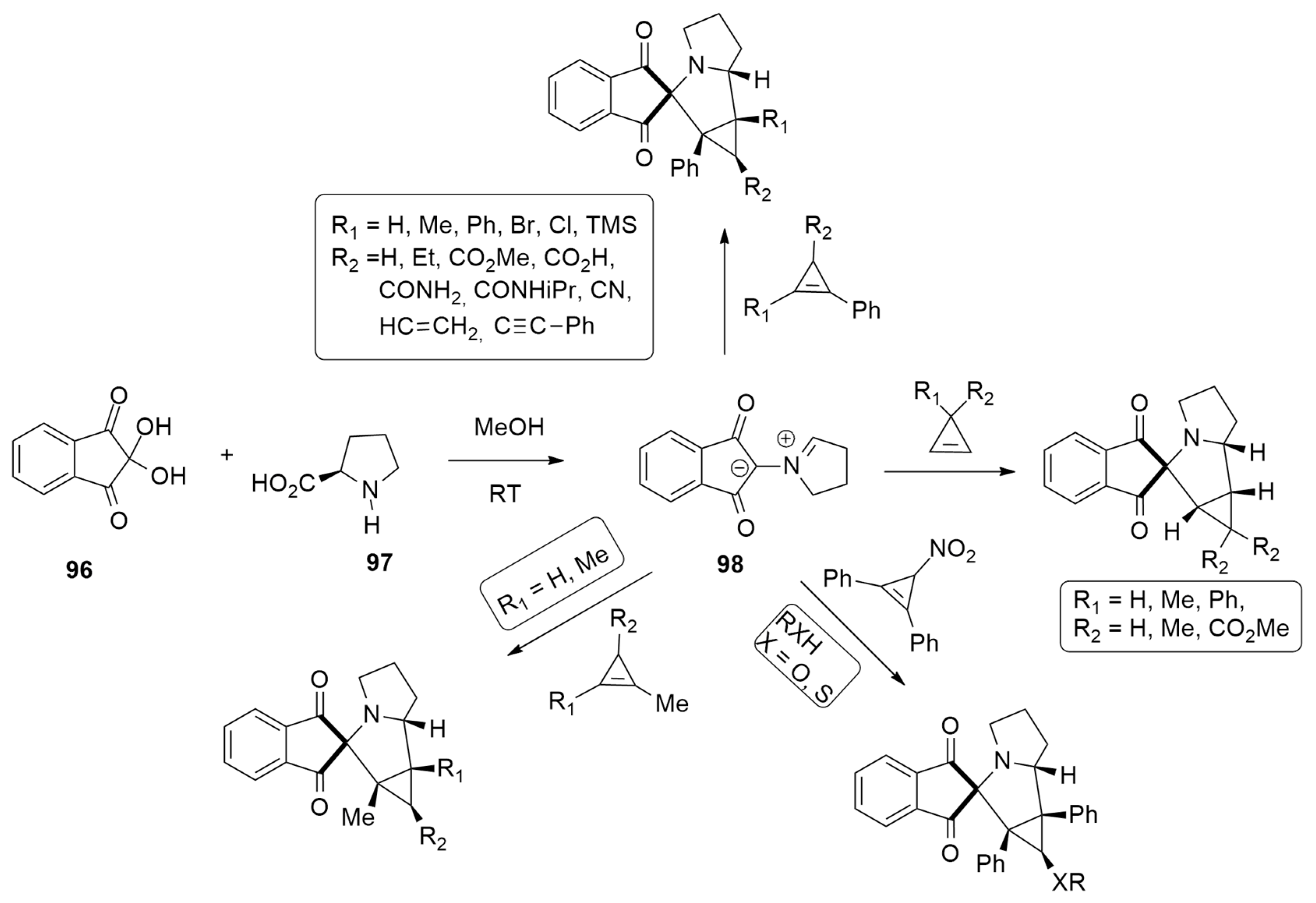
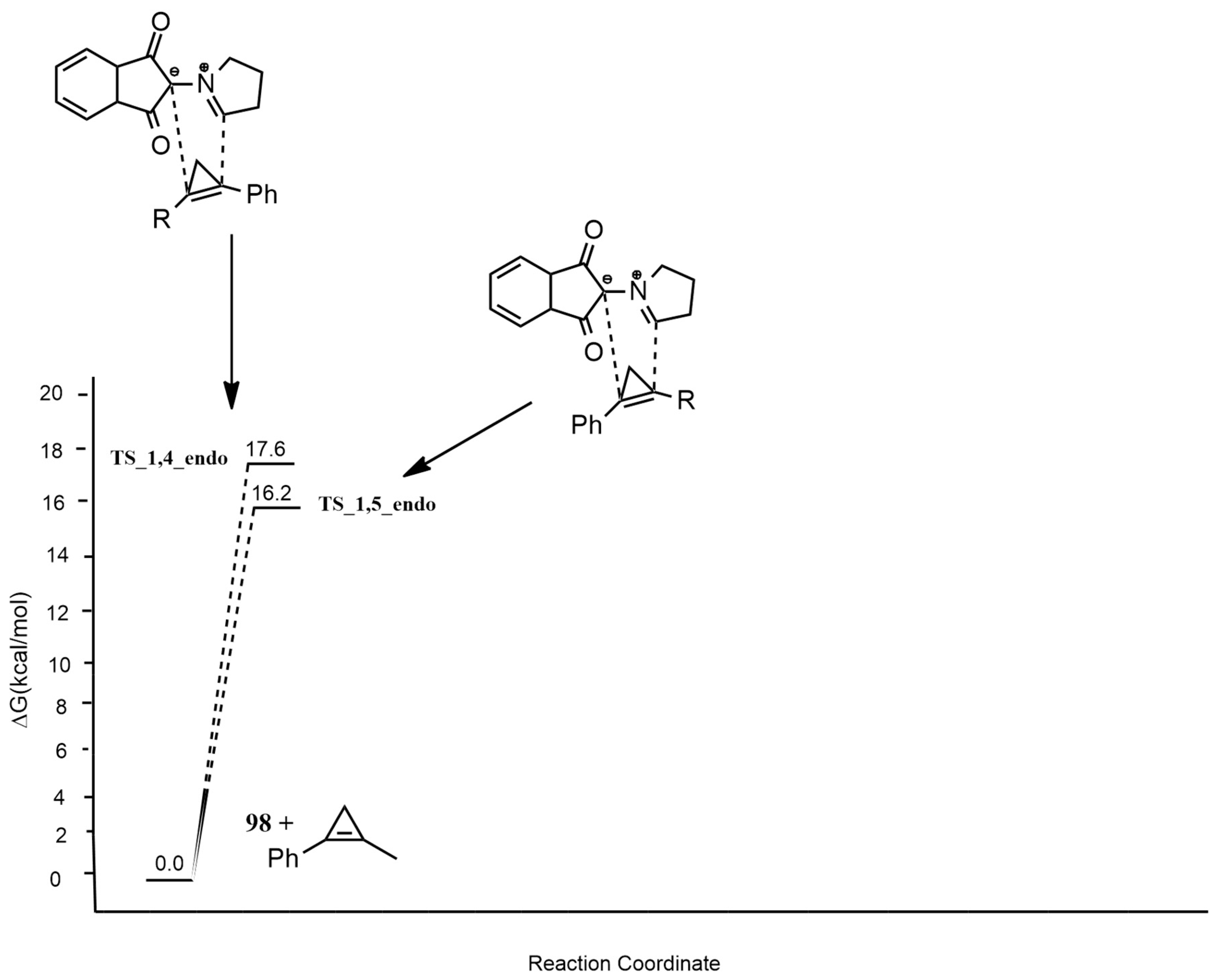

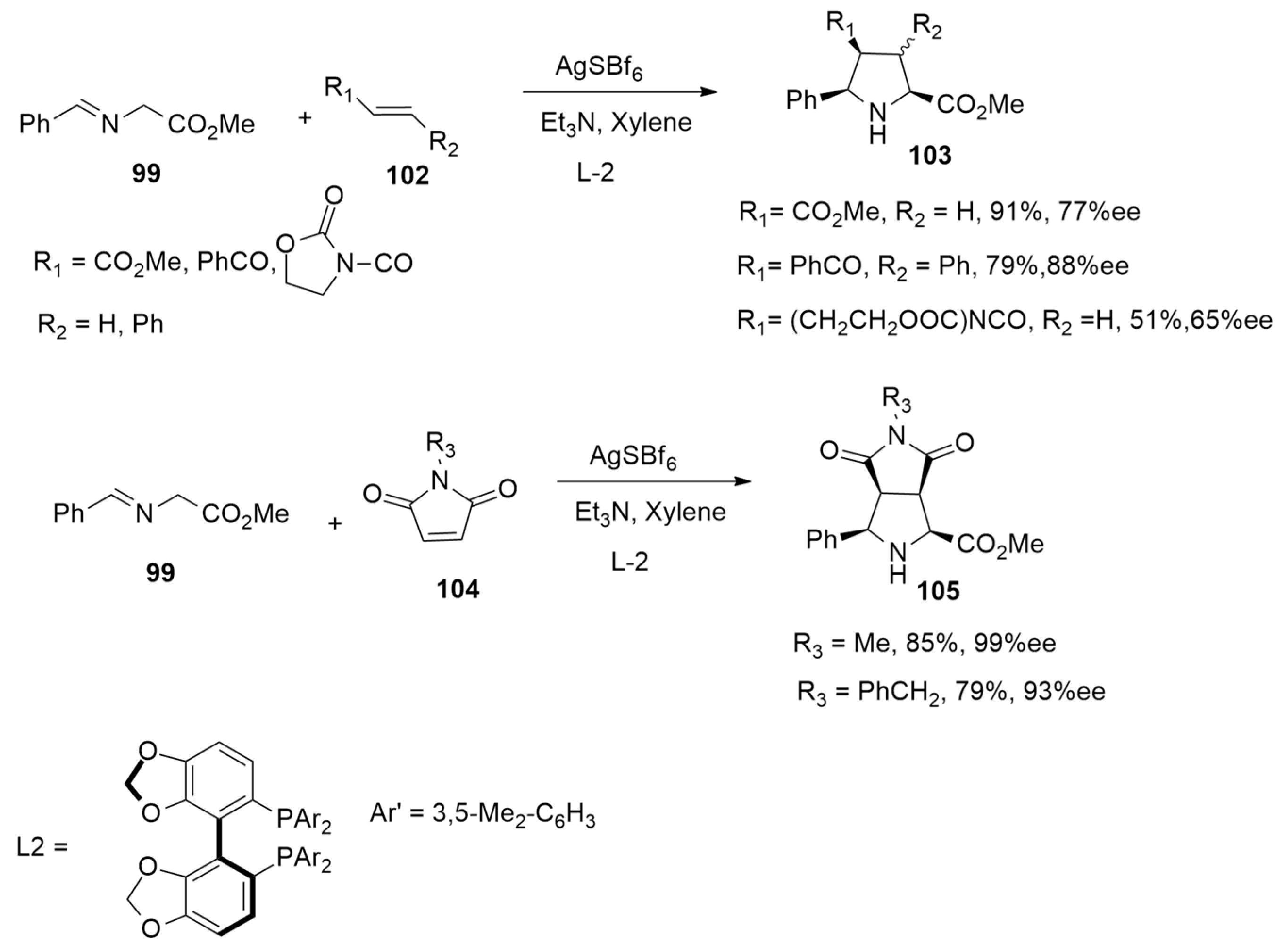
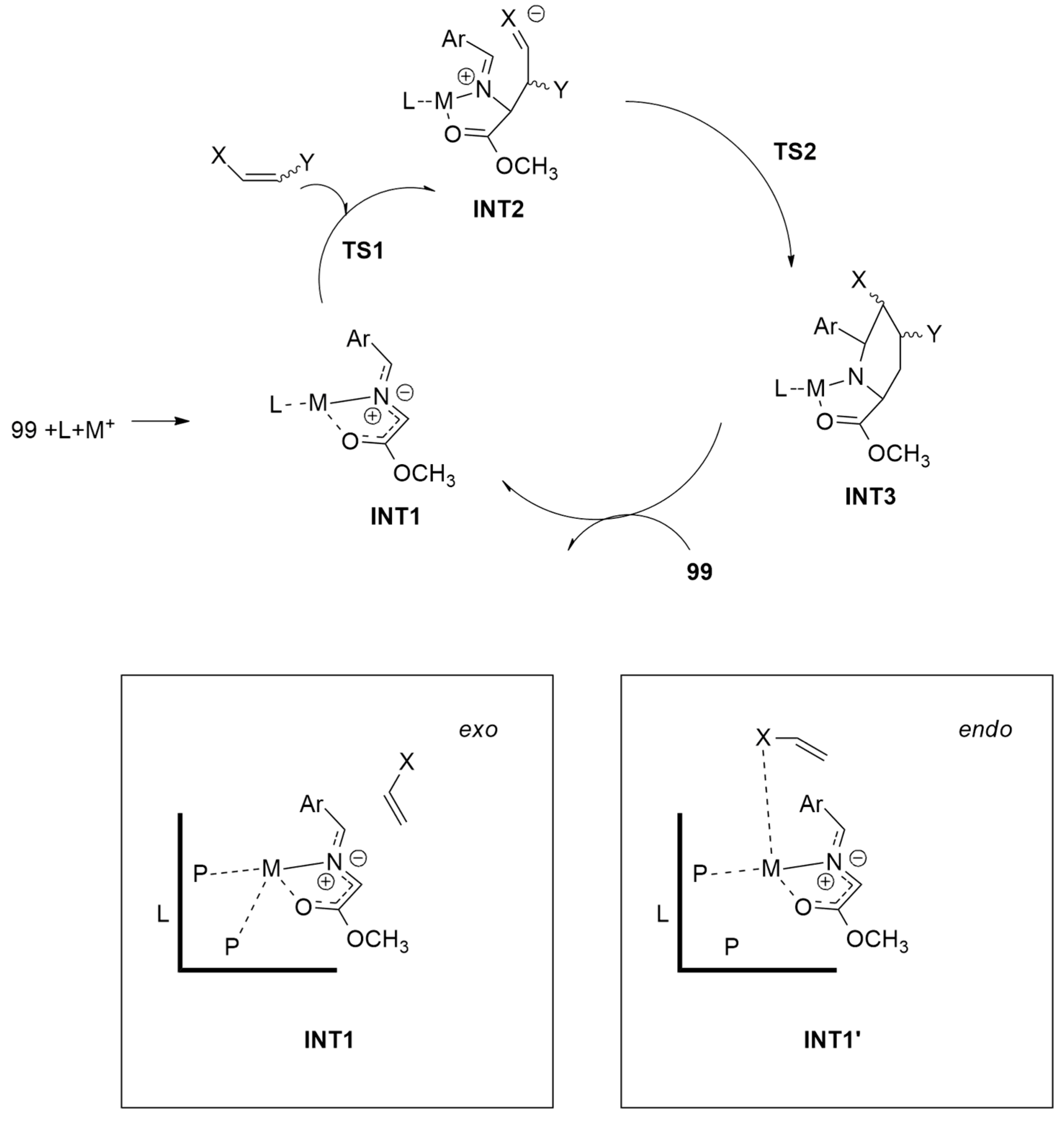


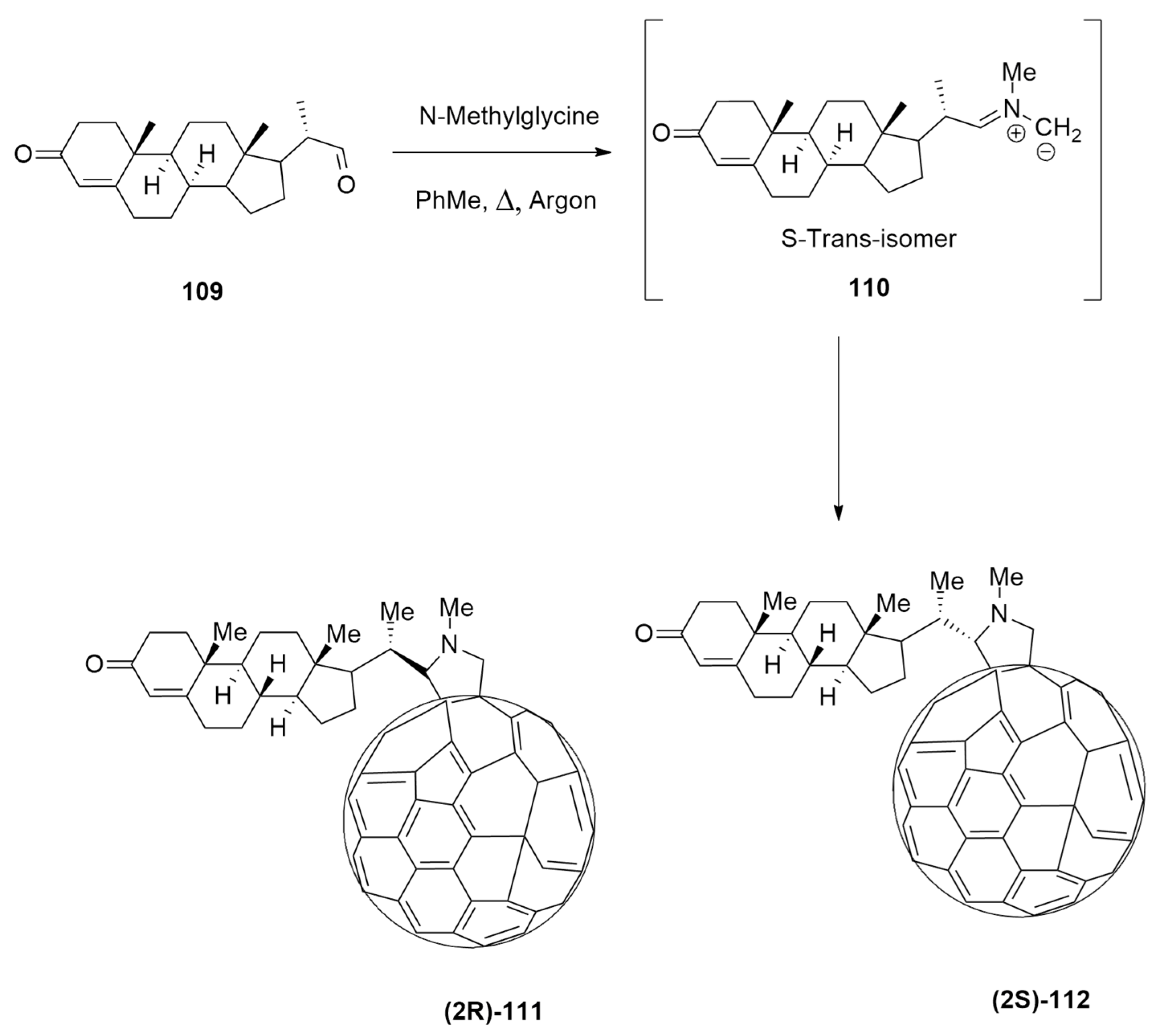
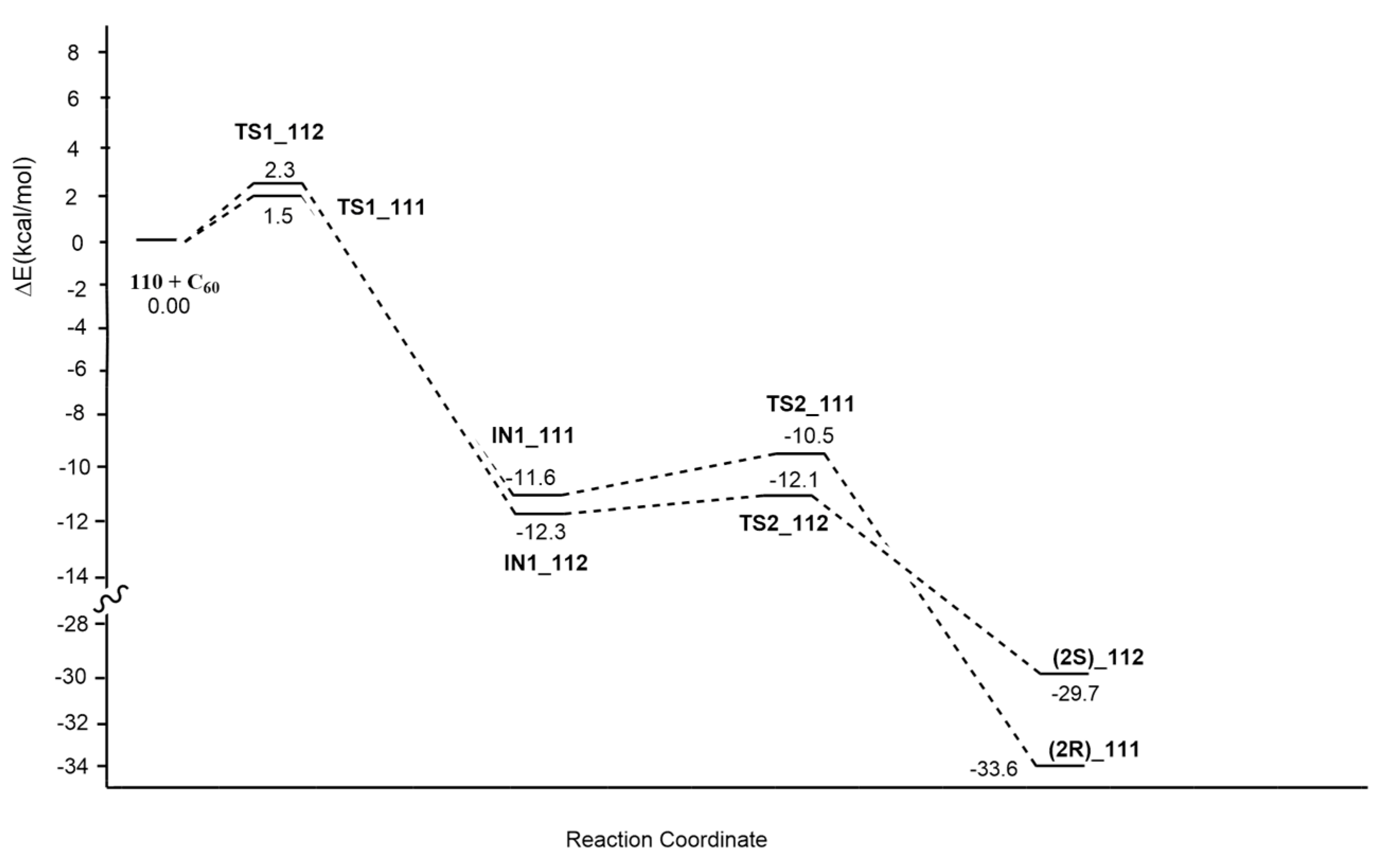
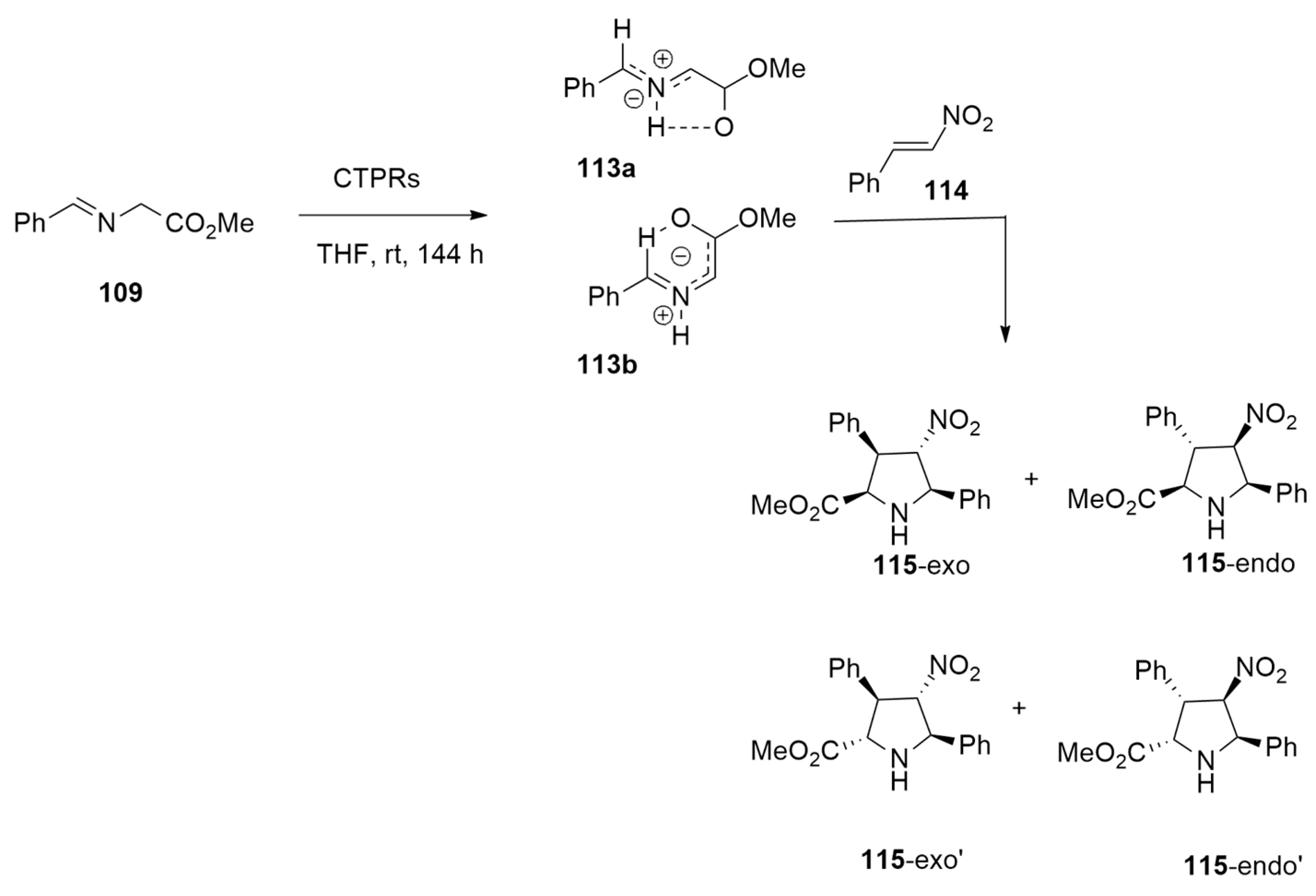

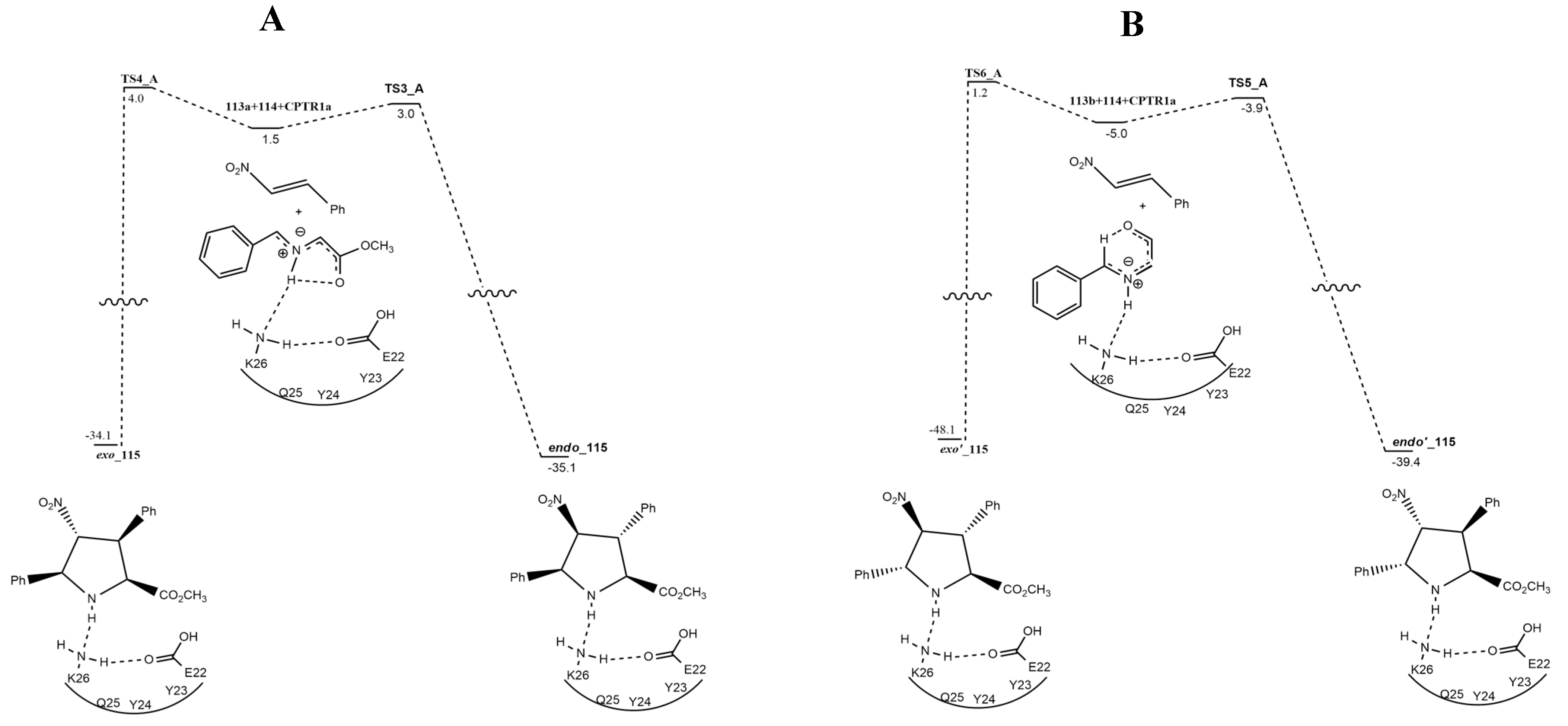
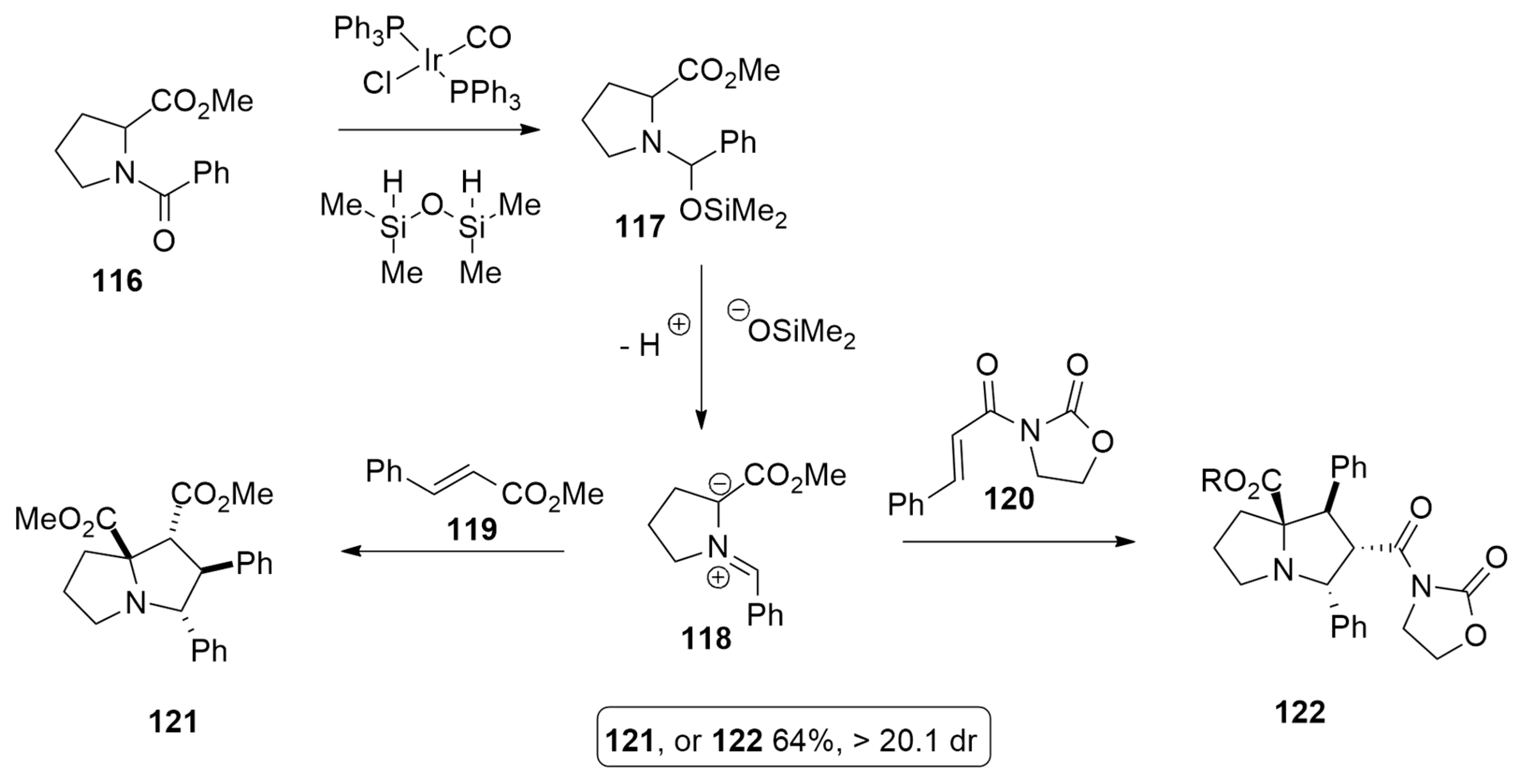


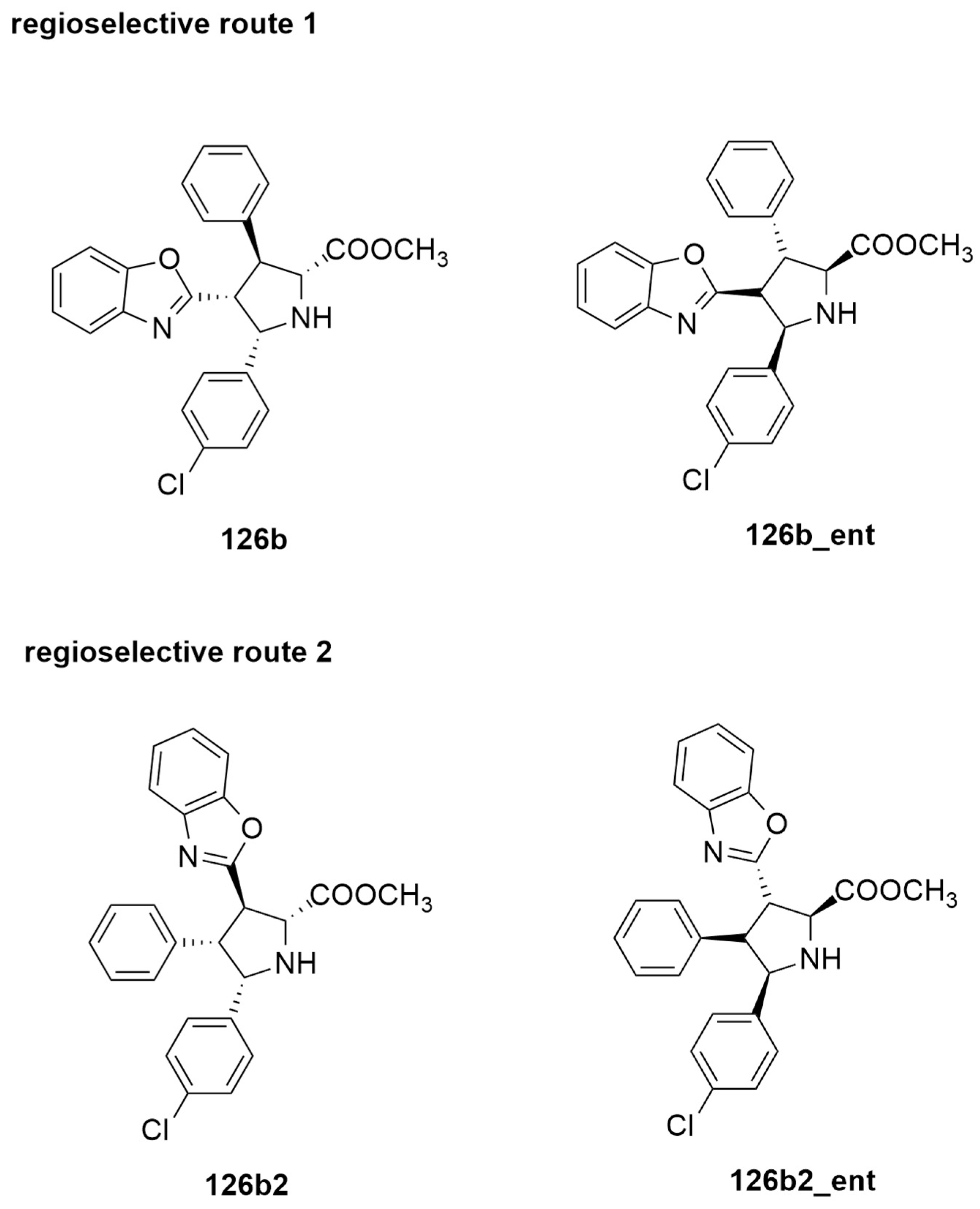

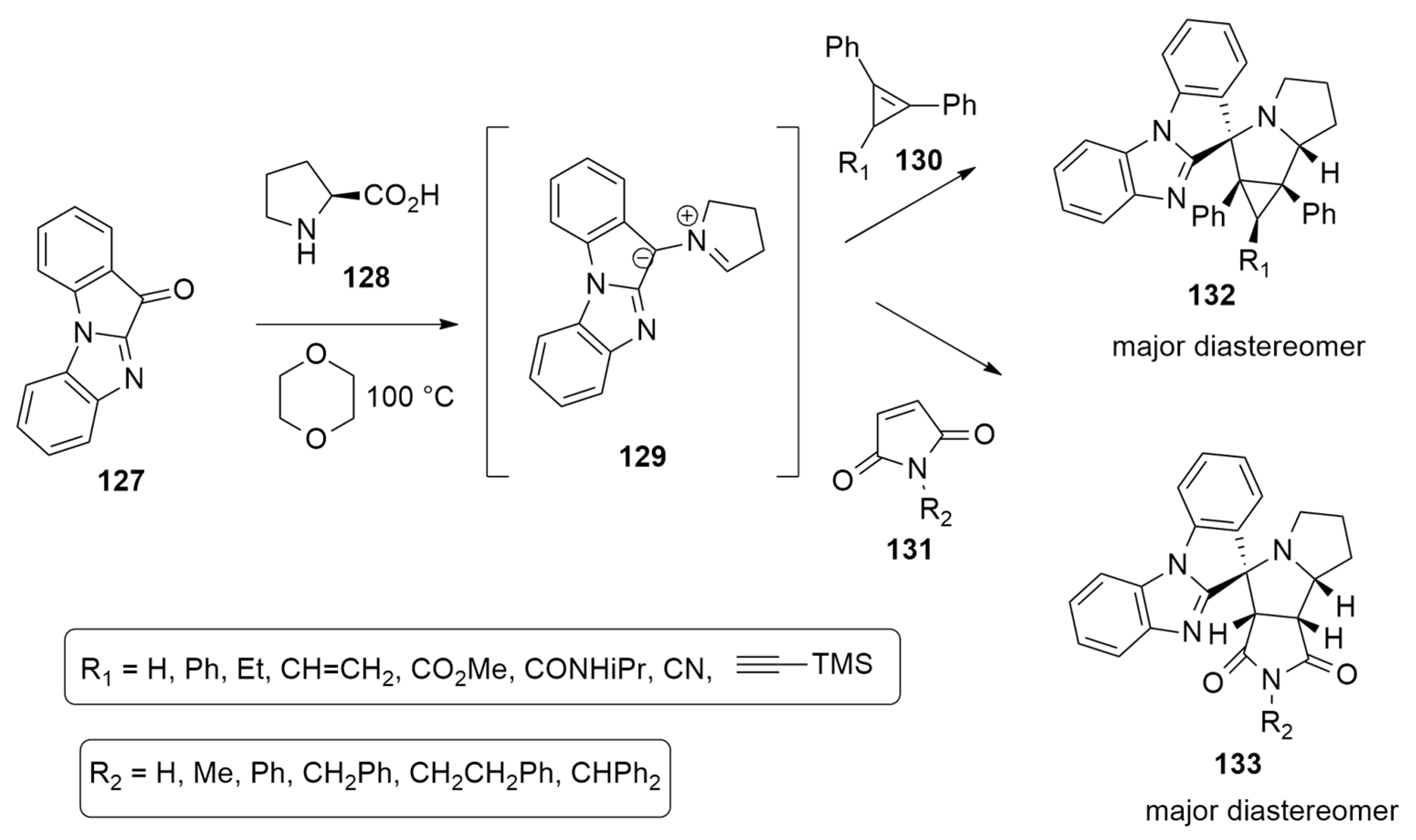
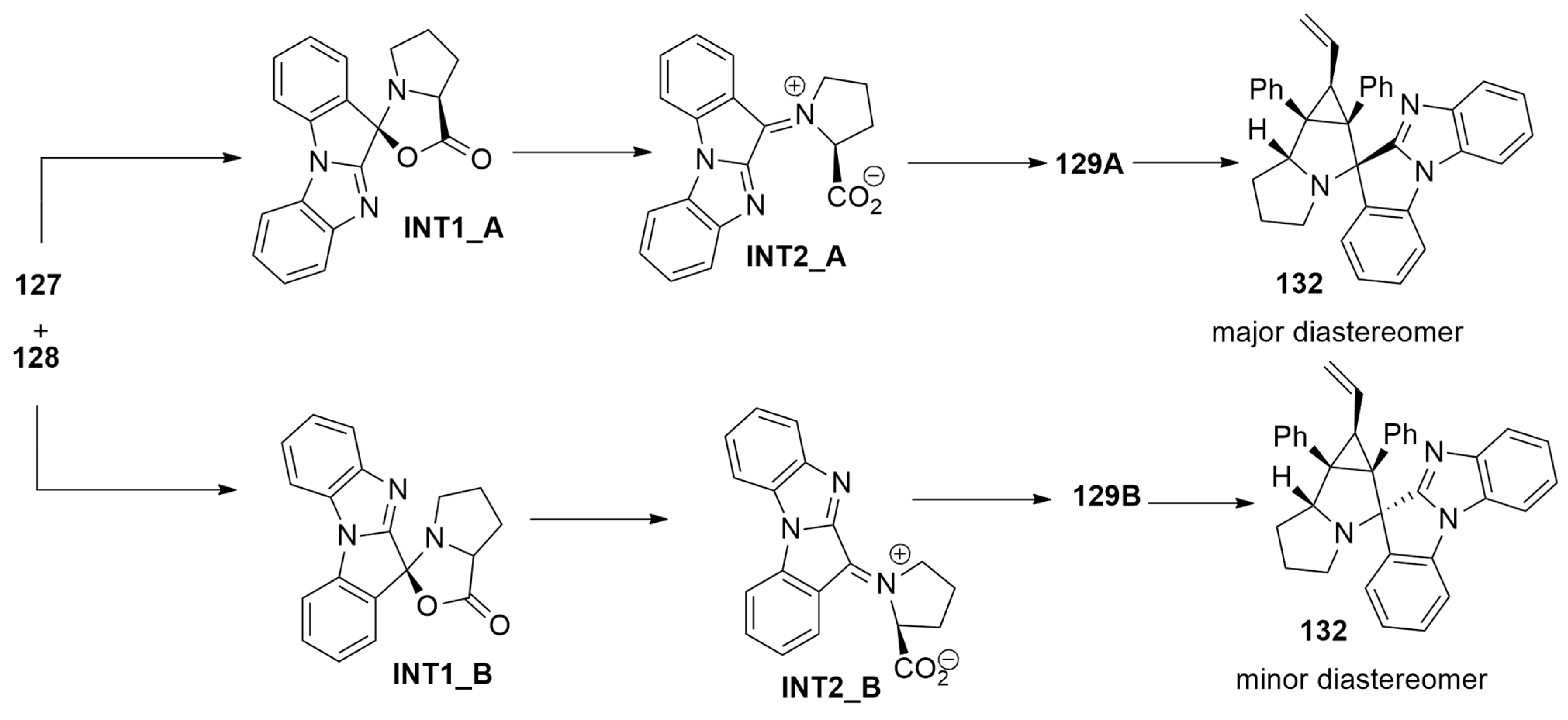
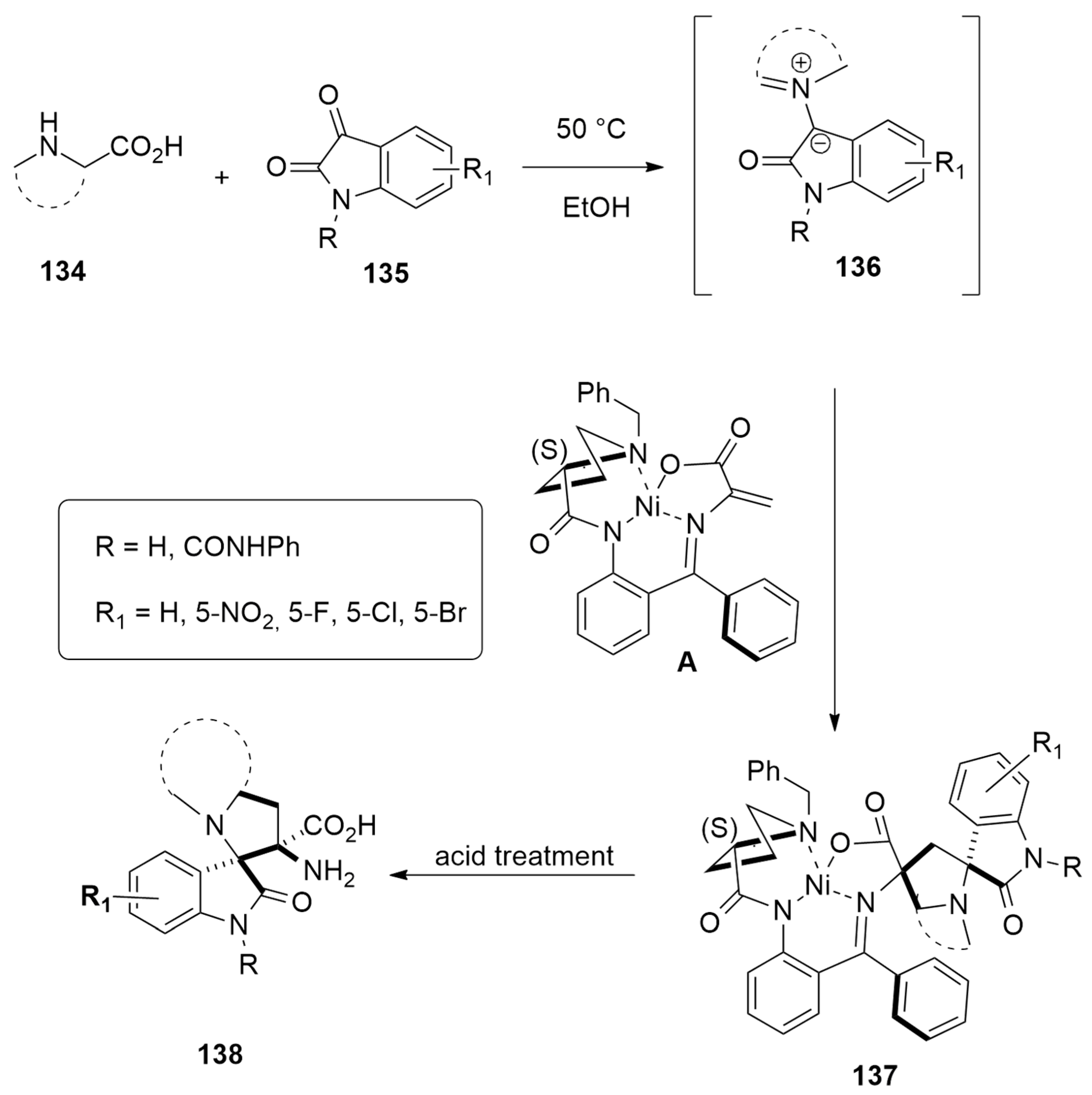


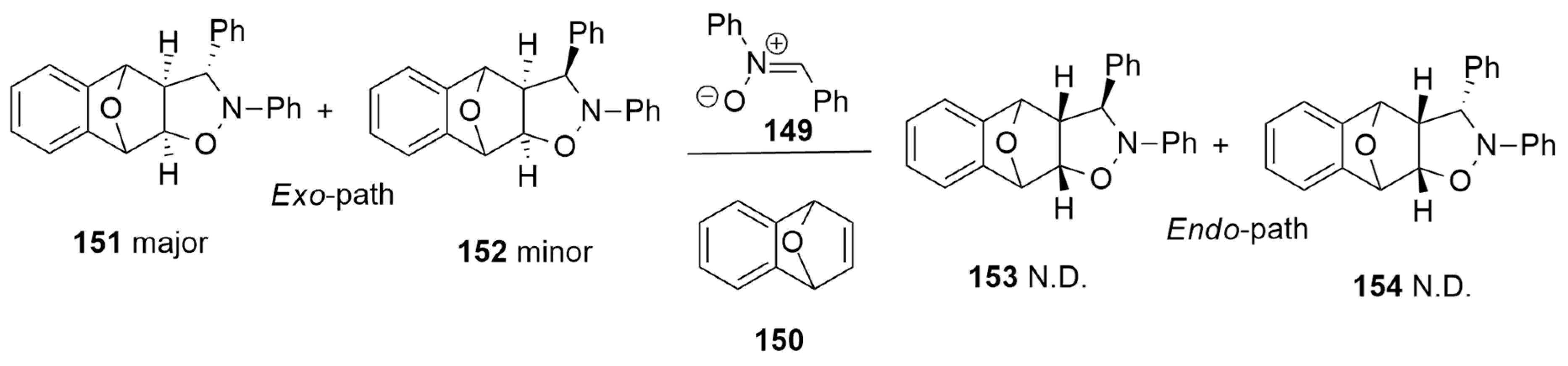
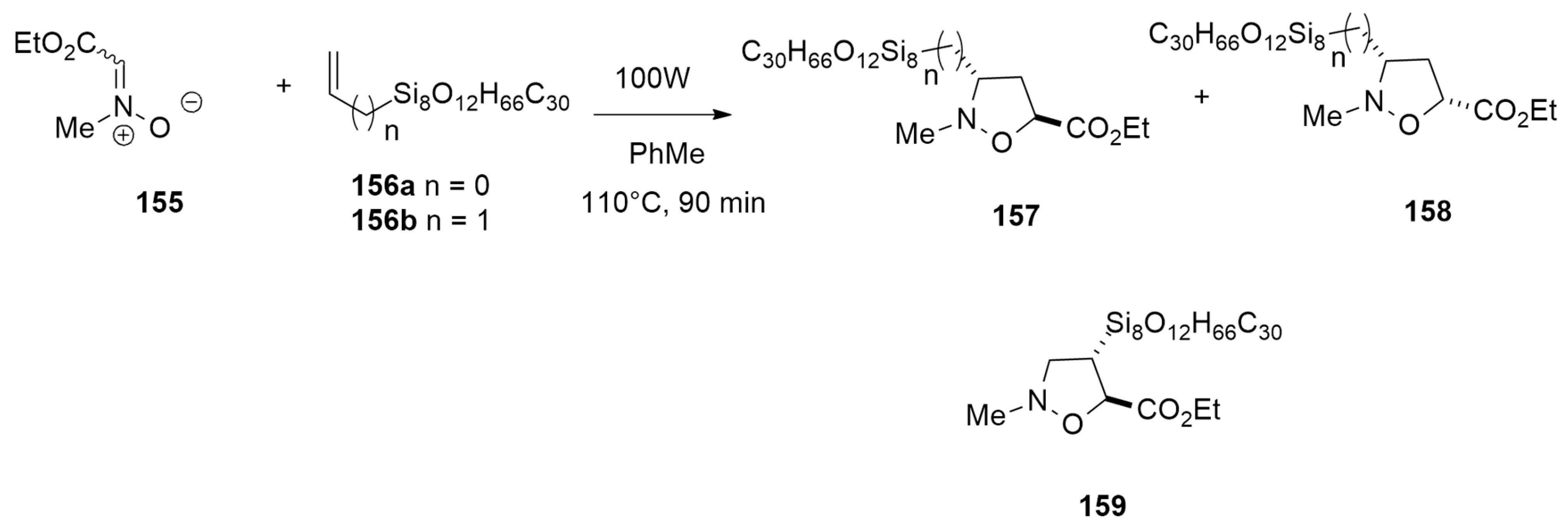
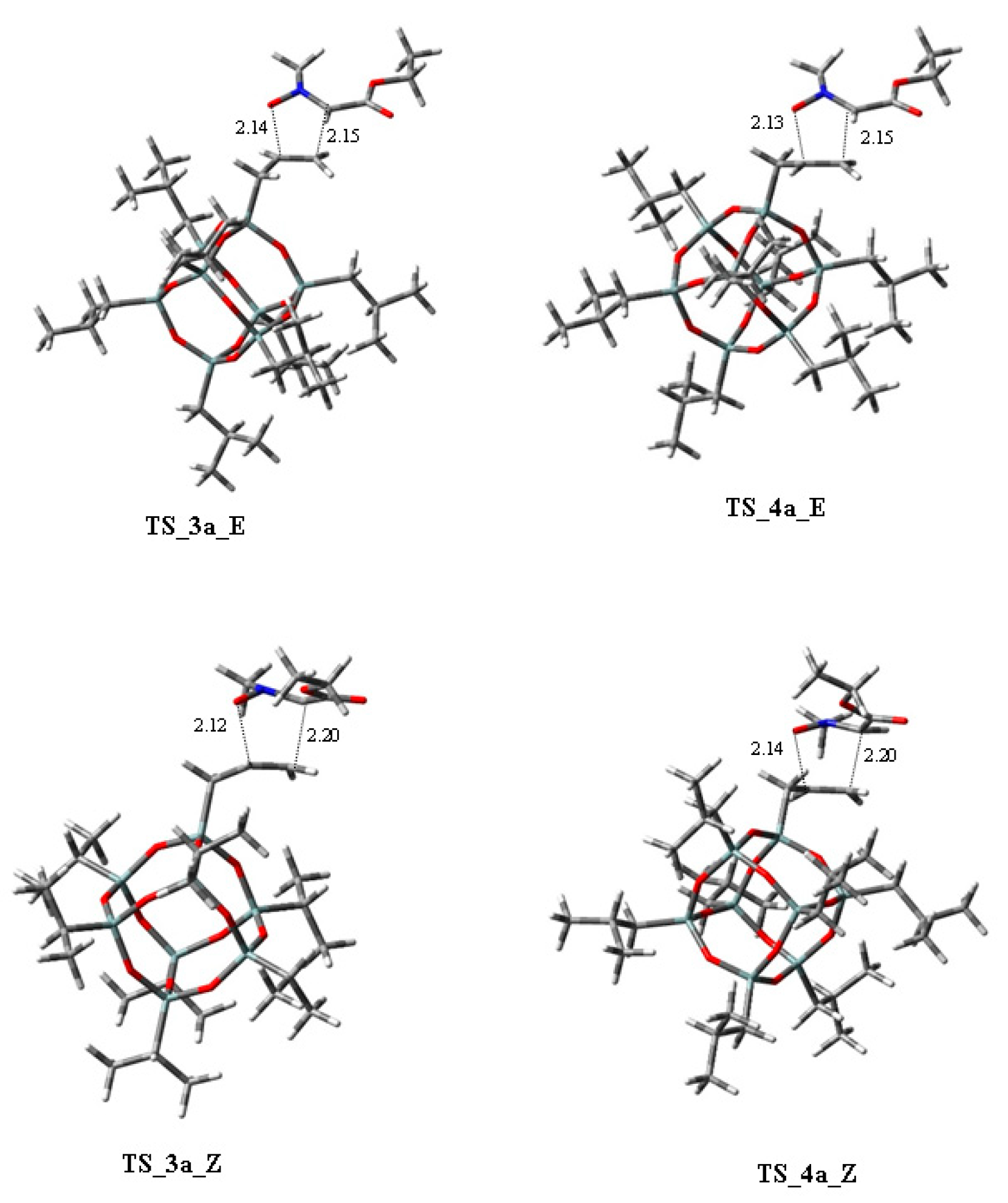
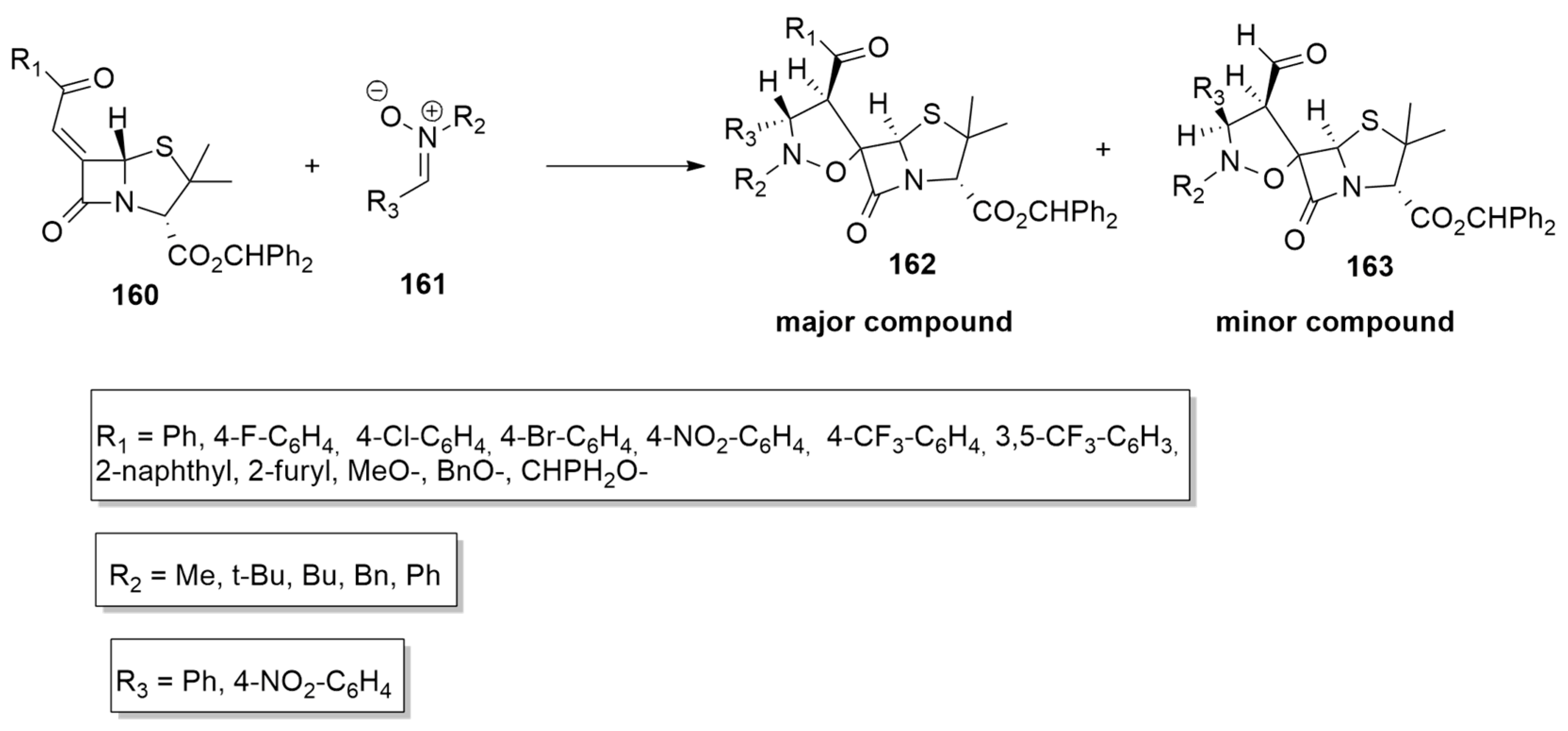

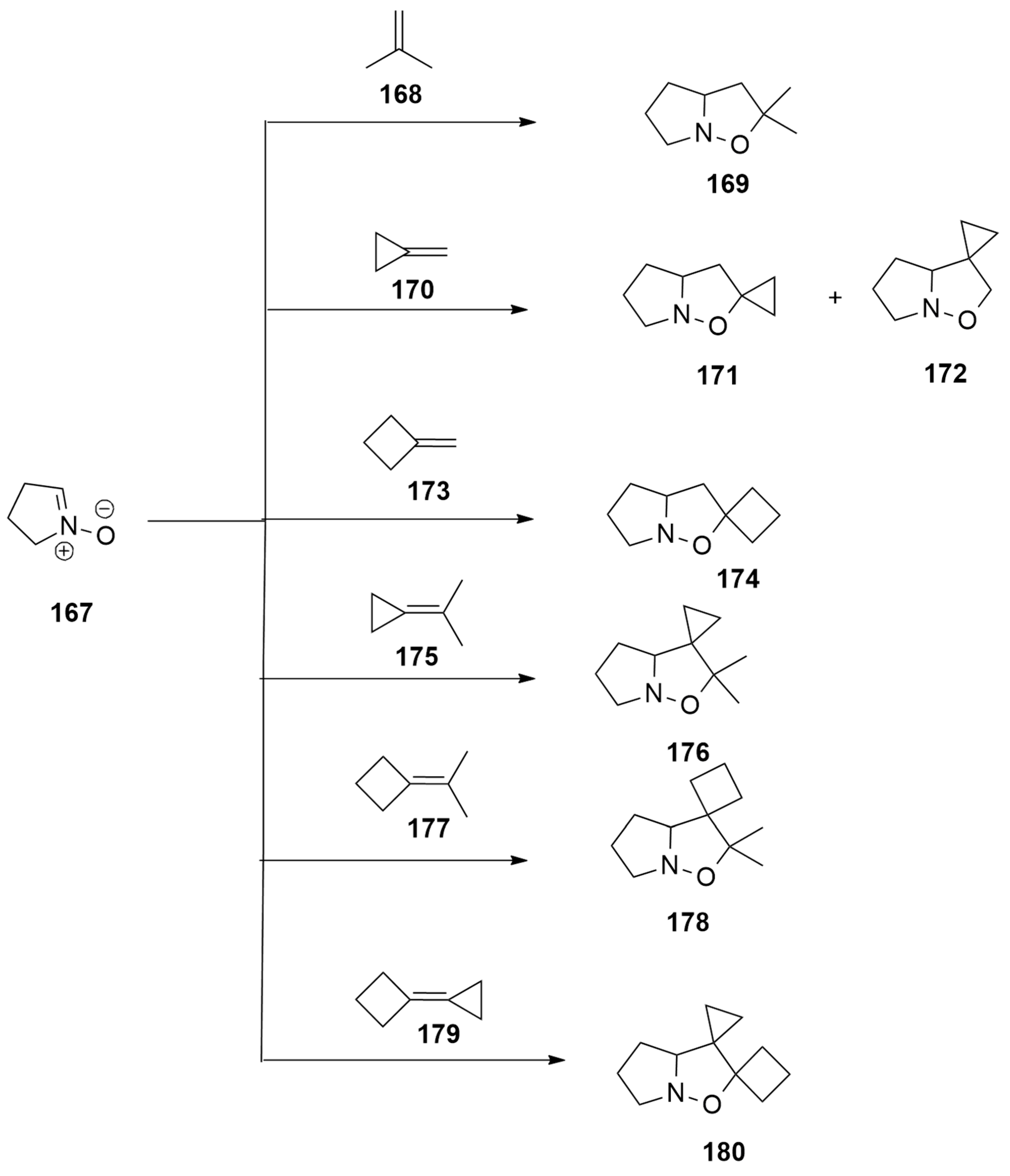
| 1,3-Dipoles of Propargyl-Allenyl Type | |||
|---|---|---|---|
| Aza-Ylides | |||
| Reagents | Reaction Conditions | Catalyst | Level of Calculations |
| methylazide + propine | Δ, catalyst | Cu (I) | B3LYP/6-31G(d) and LANL2DZ for Cu |
| methylazide + 2-butine or cycloalkyne | Δ | / | M062X/6-311++G(d) |
| methyl azide and various allenes | Bu4NF/CsF, CH3CN | / | PB86/TZ2P |
| methyl azide and propyne | r.t., catalyst | Ag(I) | B3LYP/6-31G(d) and LANL2DZ for Ag |
| differently substituted azides + alkynes, cyanoalkynes, thioalkynes, and ynamides | Cp2Ni (10 mol %), Xantphos (10 mol %), Cs2CO3 (1 eqv), DCM, r.t., 24 h | Ni | M06/6-31G(d,p) and cc-pVTZ for Ni |
| lithiated trimethylsilyldiazomethane and α-azido ketones | LTMSD, −78 °C, 1h then r.t. | / | M06/6-31+G |
| arylazide + phenylacetylene | CuSO4·5H2O/5 Na+ L-Asc. 1 eq, DMF (1mL), t = 42 min, 25 °C, air | Cu | M06/6-311+G(d,p) SDD |
| benzylazide+terminal alkynes | 50 °C, catalyst, EtOH | Cu(I), Au4Cu4/CNT | PBE/ECP6MWB and def2-TZVPP for Cu, def2-SVP for other |
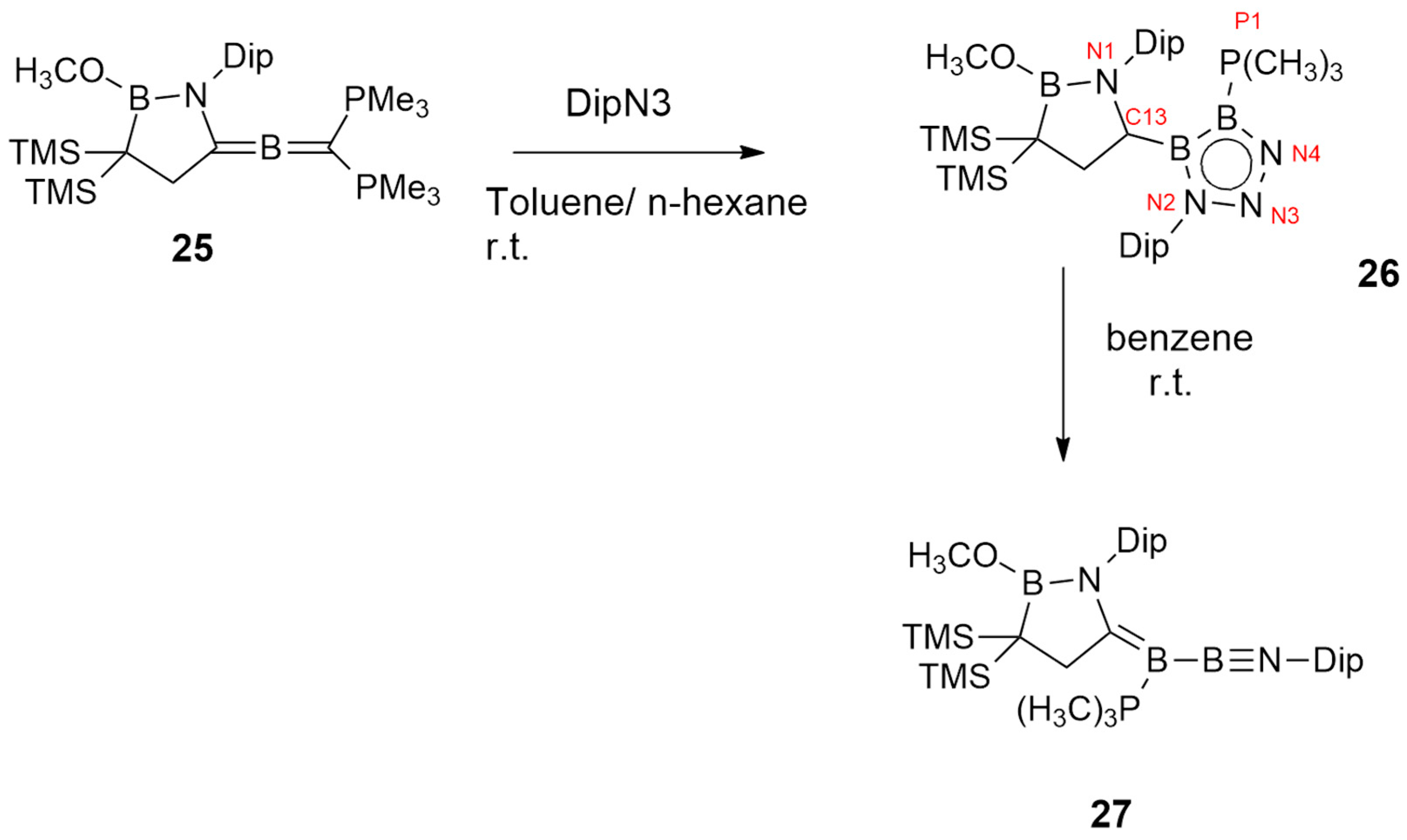
| 1,2-diboraallene+2,6-diisopropylphenyl azide | Toluene/n-hexane/r.t. | / | B3LYP/6-311G(d,p) |
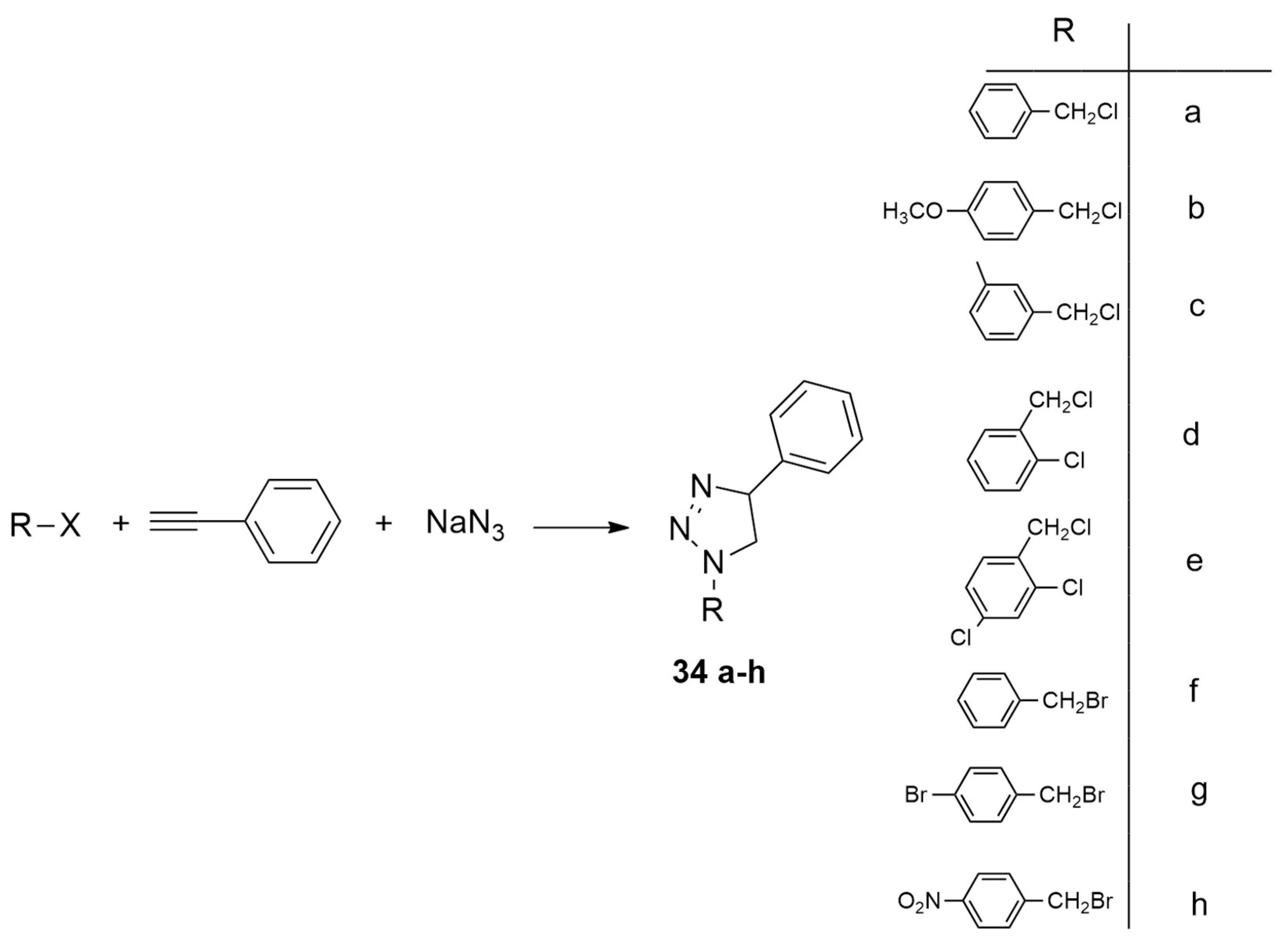
| alkyne+(azidomethyl)benzene | (a) Cs2CO3, DMF, r.t.; (b) THF/TEA (1:1), 55–60 °C, CuBr(PPh3)3, 5.5 h, | Cu(I) | B3LYP/6-311++G(d,p) level and B3LYP/LANL2DZ for metals |
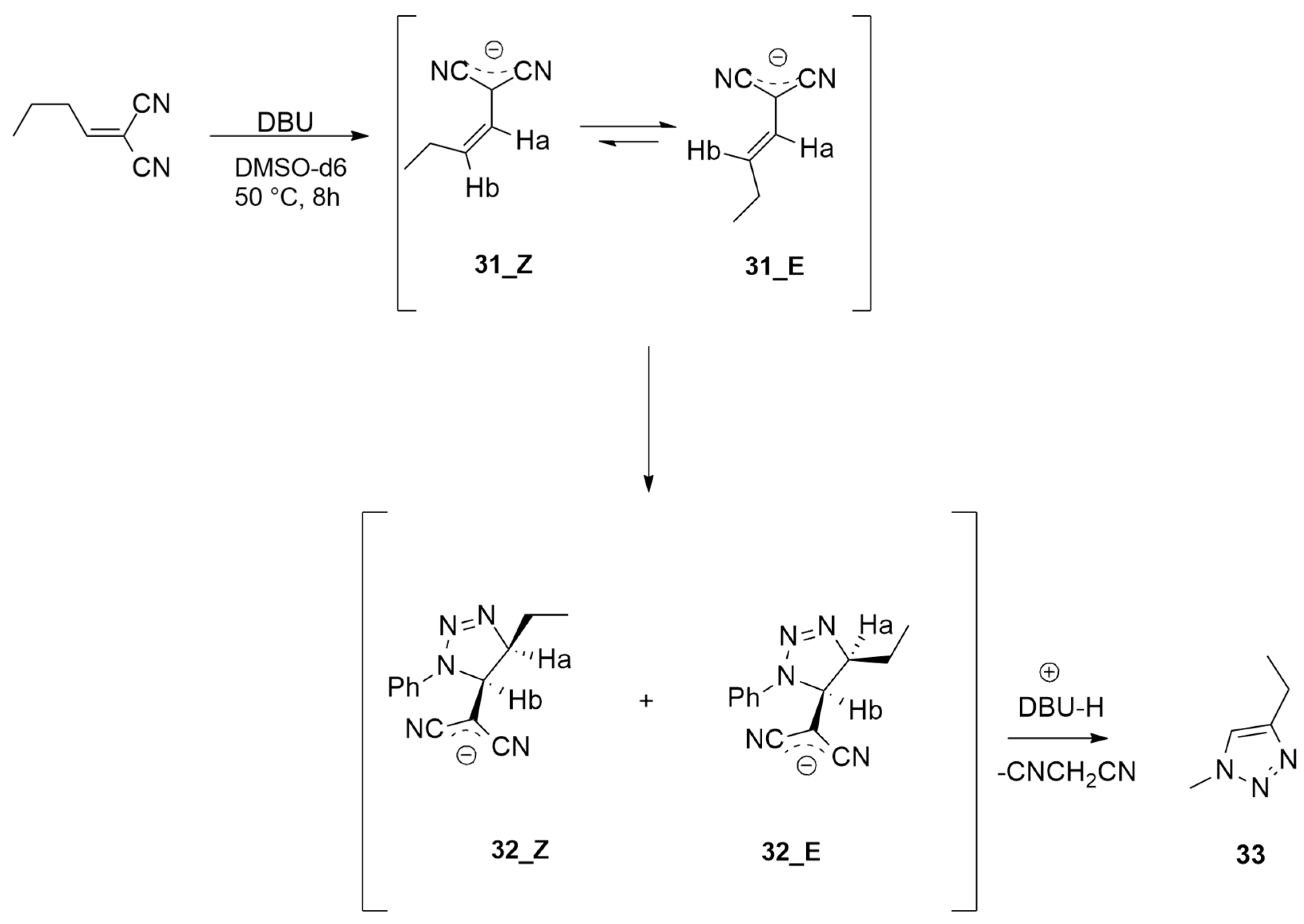
| 2-butylidenemalononitrile + phenylazide | DBU, DMSO-d6 at 50 °C | / | M06-2X/6-31+G(d,p) |
| azide + alkyne | 15 mol % catalyst, 45 °C, 30 min and water | CuC20H20N2)PPh3Cl and Cu(C20H20N2)PPh3Br | LDA/PWC |
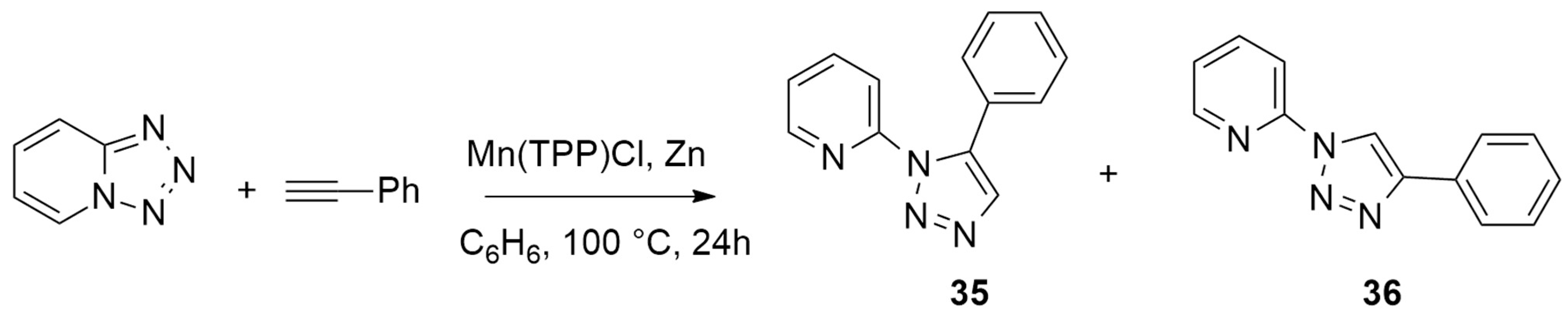
| 1,2,3,4-tetrazole + phenylacetylene | Mn(TPP)Cl, Zn, C6H6, 100 °C, 24 h | manganese-copper/zinc | M06/6-311++G** for all other atoms and LANL2DZ for metals |
| phenylacetylene + phenyl azide | carbon nanotubes | / | QM/MM ONIOM B97D/UFFs |
| Nitrile Oxides | |||
| Reagents | Reaction conditions | Catalyst | Level of calculations |
| N-tert-Butoxycarbonyl [1-Chloro-1-(hydroxyimino)-3-phenylpro-pan-2-yl)]carbamate + N-benzyl-3-pyrroline | Base/r.t. | / | CPCMHCTC/6-11+G(d,p)//HCTH/6-31+G(d) |
| nitrile oxide + graphene sheets | MW | / | (U)M06-2X/6-31+G(d,p) |
| acetonitrile oxide +(1S,2R,4S)-2-cyano-7-oxabicyclo[2.2.1]hept-5-en-2-yl acetate derivatives | r.t. | / | ωB97X-D/6-311G(d) |
| oxime + t-but acrylate | Et4NCl/CH3CN | / | M06-2X/Def2TZVP |
| nitrile oxides + cyclodienes | MeCN, 25 °C or 70 °C | / | M06-2X/6-311+G(d,p) |
| 1,3-Dipoles of Allyl Type | |||
|---|---|---|---|
| Azomethyne Ylides | |||
| Reagents | Reaction Conditions | Catalyst | Level of Calculations |
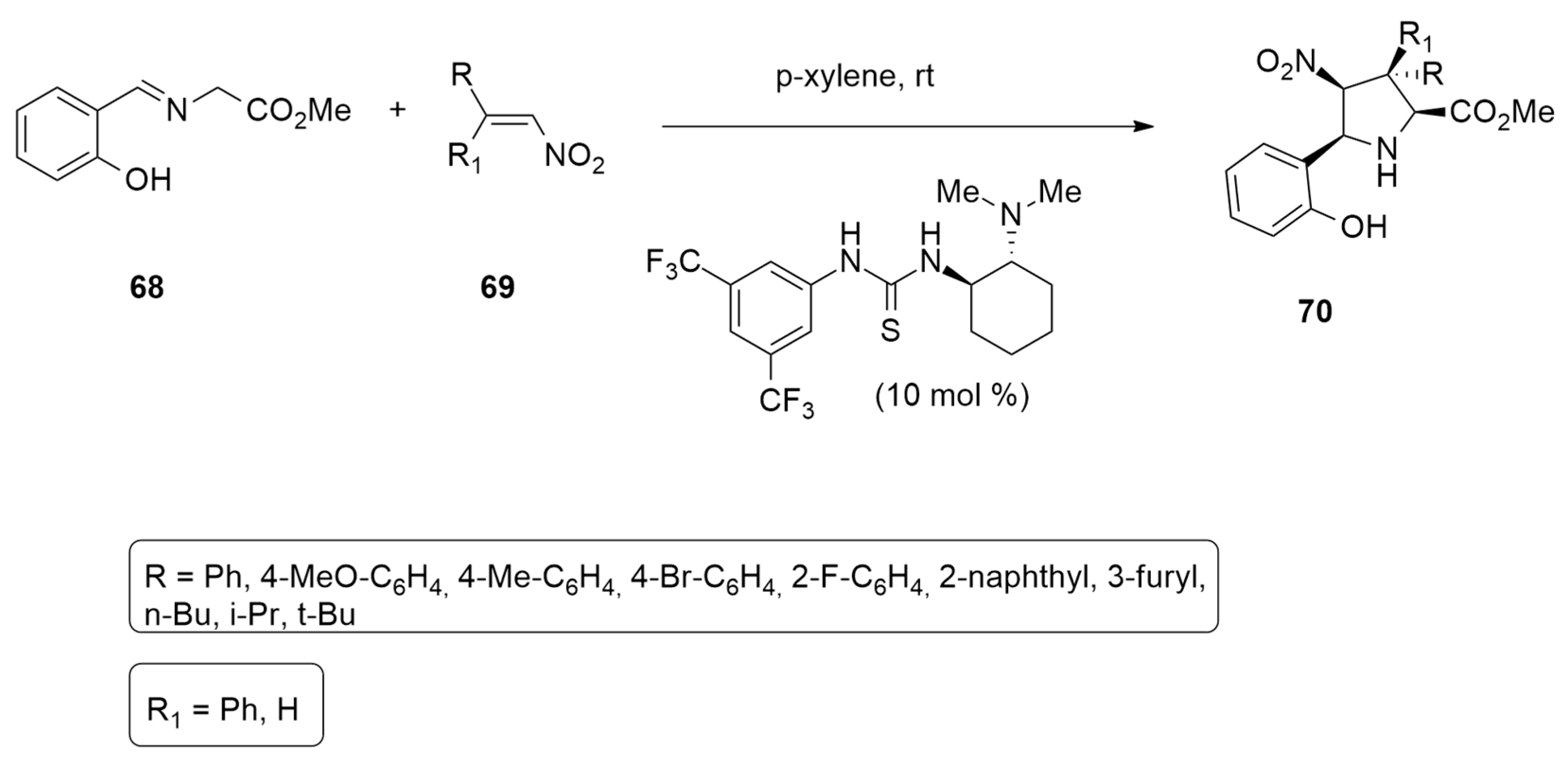
| ortho hydroxy imine + nitro alkanes | p-xylene, r.t., cat | N,N′−bis[3,5−bis(trifluoromethyl)phenyl]−thiourea | M06-2X/6-31g(d,p) |
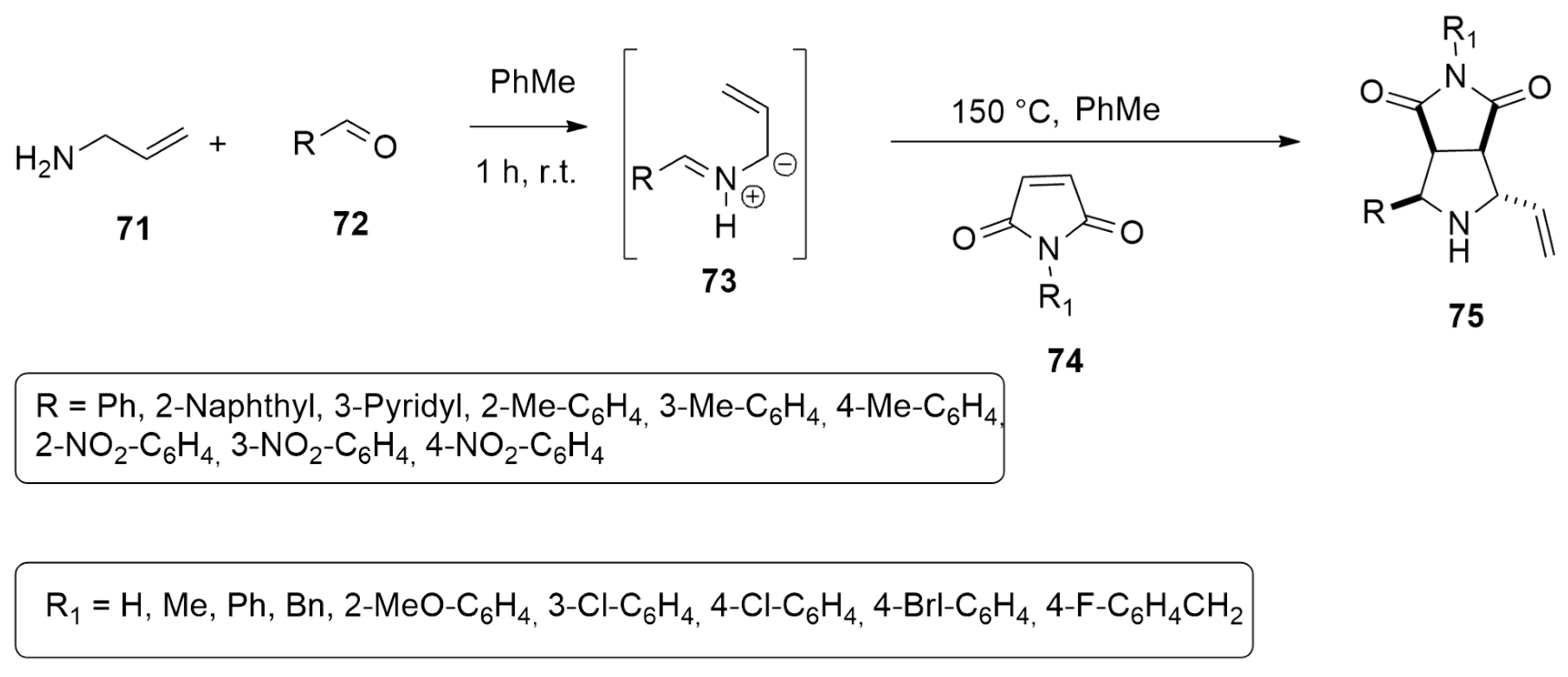
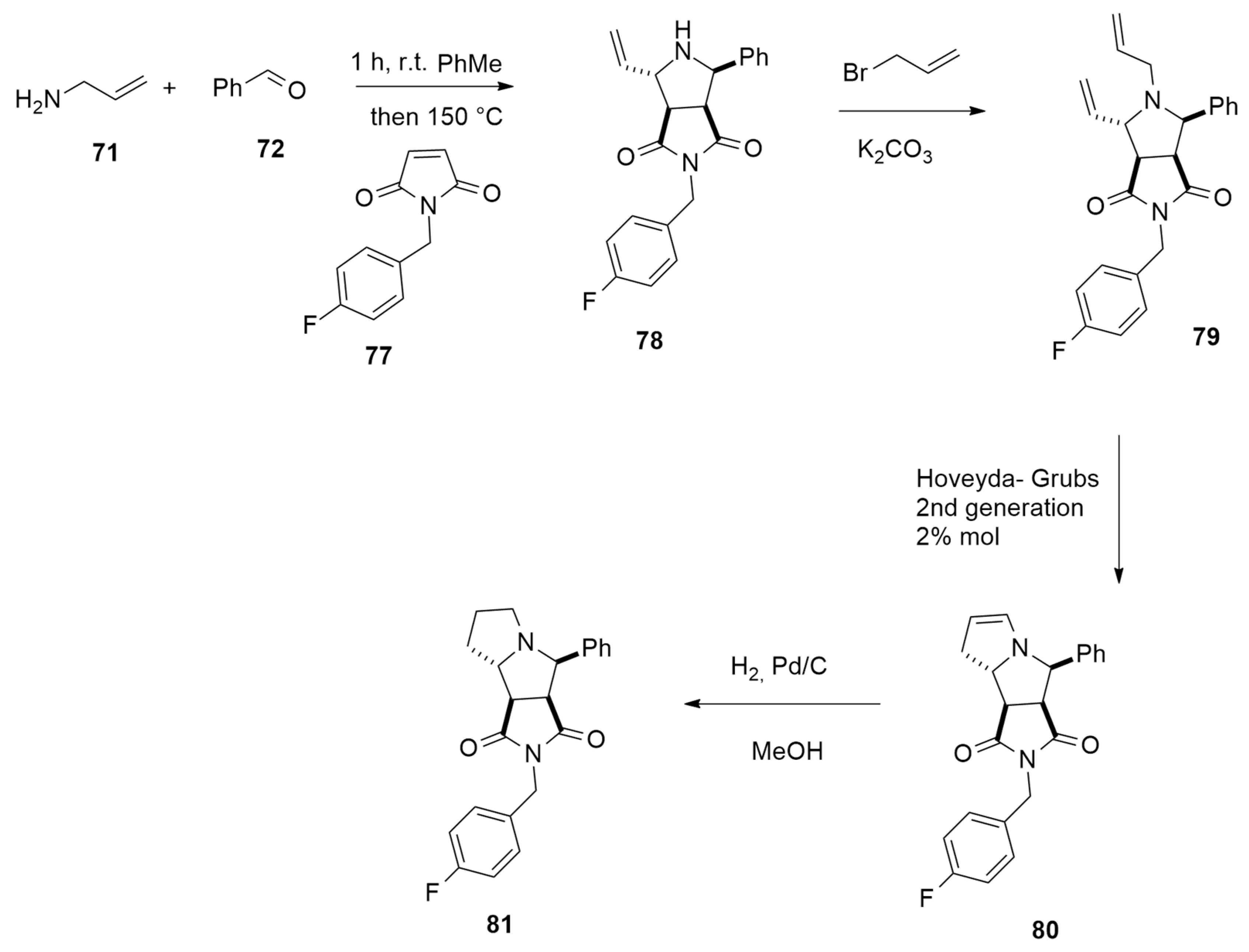
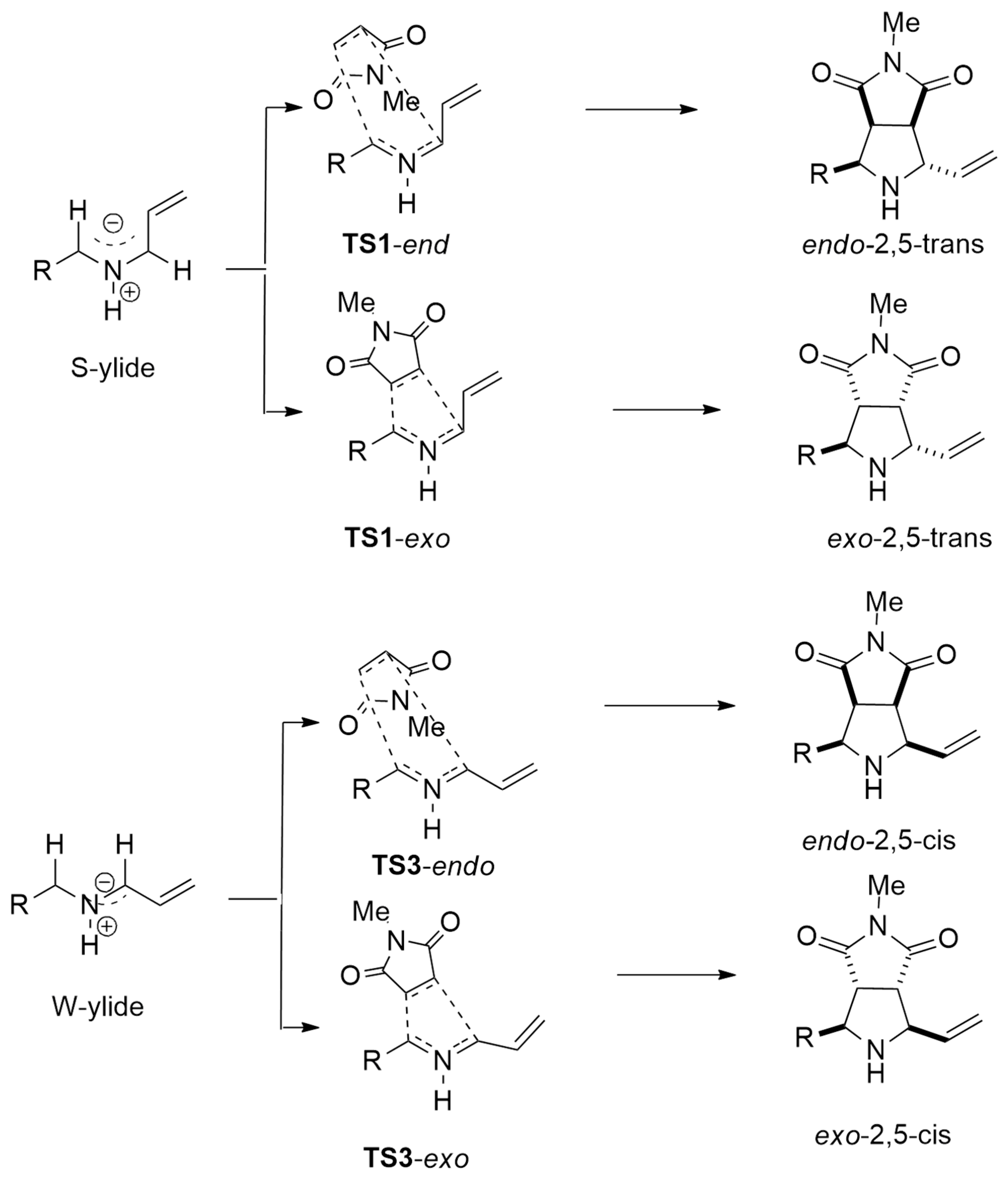
| allyl ammine + aldehydes | PhMe, r.t/ maleimide, 150 °C, PhMe | / | B3LYP/def2SVP |
| azomethine ylide+ acrylonitriles | Cu(CH3CN)4BF4 and chiral phosphine−urea bifunctional ligand | M11/6–311+G(d,p) | |
| glycine imino ester + beta-fluoroalkyl alkenyl arylsulfones | THF, Et3N | BINAP-Cu(II) | M06-L/def2-TZVPP |
| ninhydrin + L-Prolin | MeOH, r.t. | / | M11 / cc-pVDZ |
| imino esters + electron deficient alkenes | Et3N, PhMe | L1-CuOTf·PhMe or L2-AgSbF6 | B3LYP/6-31G(d) |
| N-ethylglycine (50equiv) + paraformaldehyde | o-ClC6H4, 120 °C | Gd3N@Ih-C80 | BP86-D2/TZP |
| azomethine ylide+[60]fullerene | PhMe, Δ, Ar | / | B3LYP/6-31+G(d,p)/C-PCM = toluene//OLYP/6-31G(d):PM6 |
| azomethine ylide +nitrostyrene | CTPRs, THF, r.t. | / | ONIOM M06-2X/6-311+G(2d,2p):dreiding//B3LYP/6-31G-(d,p):dreiding |
| azomethine ylide + methyl cinnamate or N-enoyl oxazolidinone | [Ir], TMDS, PhMe, r.t. | iridium complex | BP86/TZ2P |
| azomethine ylide + alkenyl derivatives | THF, r.t. | Cu(I) | M06-L/6-31G(d), SDD for Cu |
| azomethine ylide + cyclopropenesor maleimide | 1,4-dioxane, 100 °C, N2 | / | M11/cc-pVDZ |
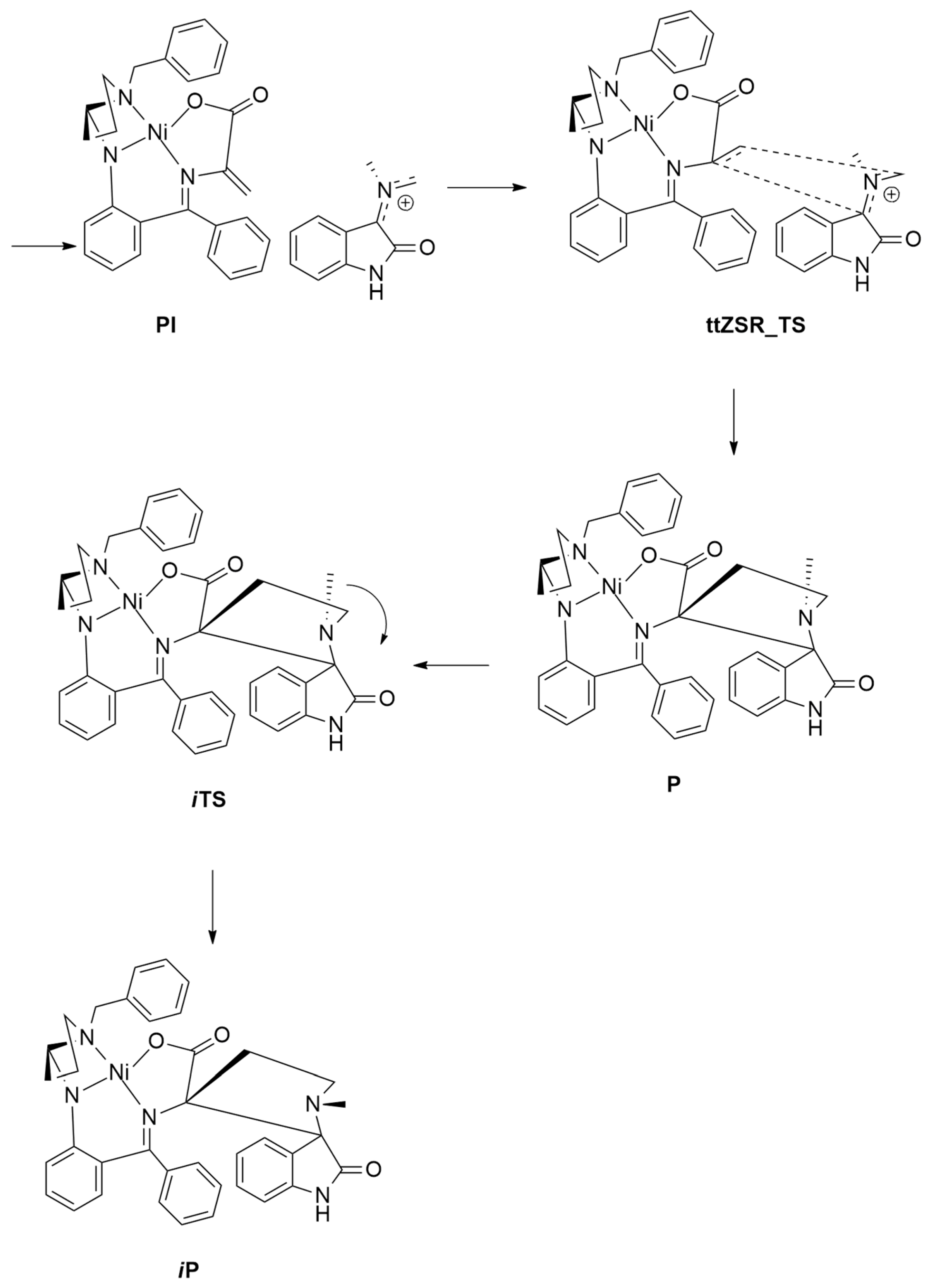
| amino acids + isatins | EtOH, 50 °C | Ni(II) | PBE0-D3BJ/def2SVP |
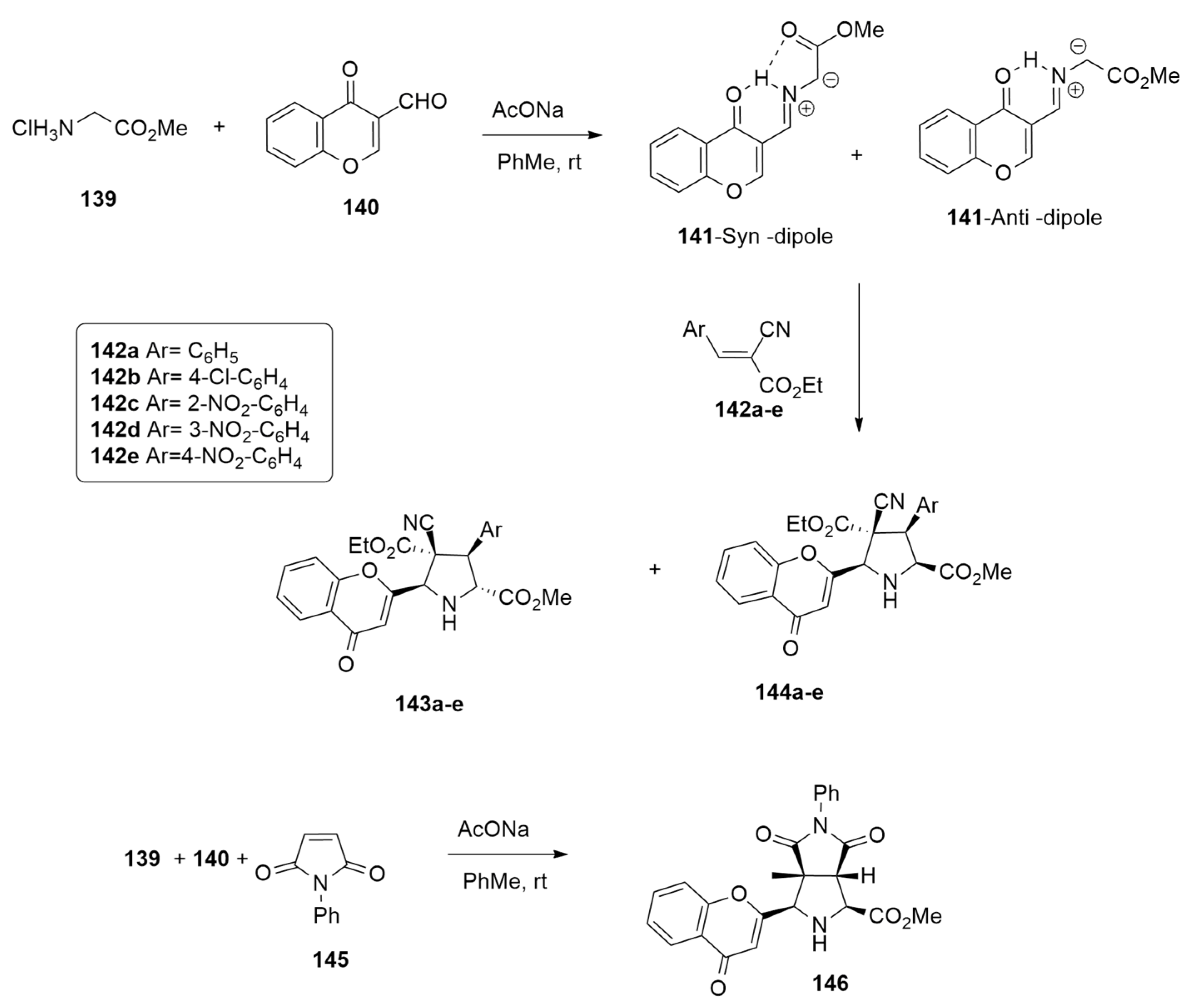
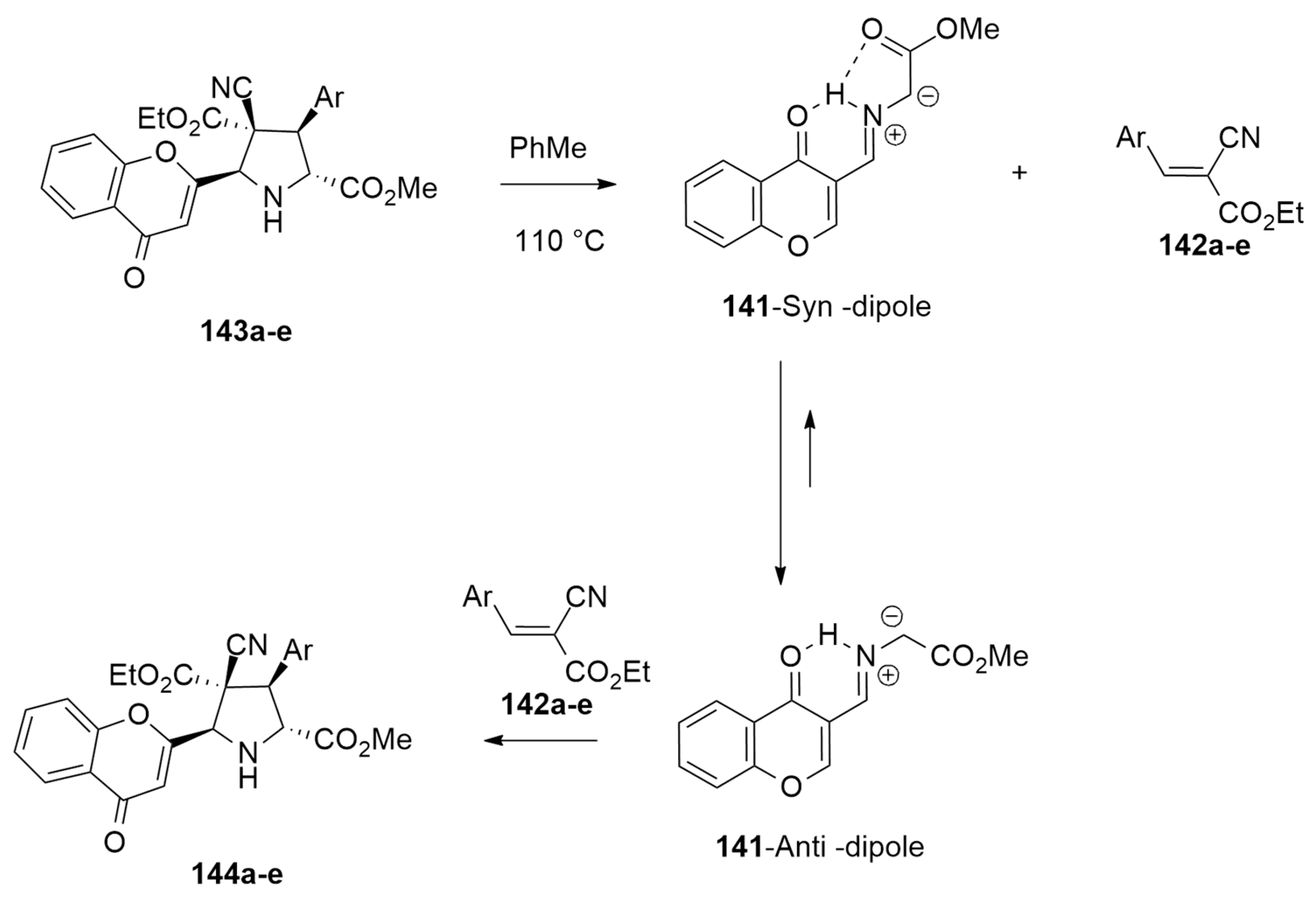
| azomethine ylide + arylidenes or phenylmaleimide | AcONa, PhMe, r.t. or 110 °C | / | wB97xd/6-31G(d,p) |
| glycine imino ester + N-phenylmaleimide | AcONa, TEA, EtOH, reflux | AgOAc | wB97xd/6-31G(d,p)/ Lanl2dz for Ag |
| Nitrones | |||
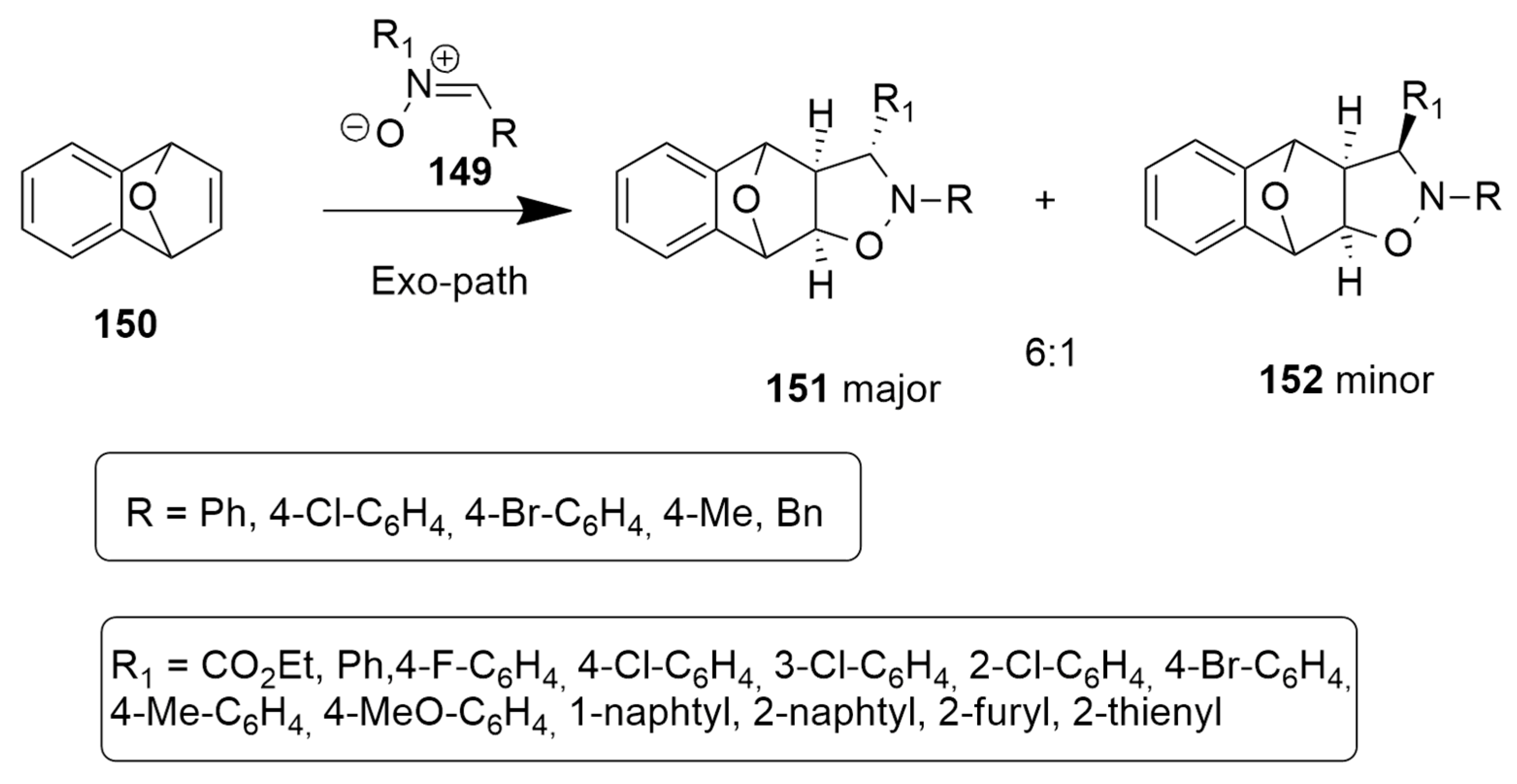
| nitrones + oxa(aza)bicyclic alkenes | PhMe, 60 °C | / | B3LYP/6-311G(d,p) |
| N-methyl-C-ethoxycarbonylnitrone + allyl-heptaisobutyl-POSS | 100W, PhMe, 110 °C | / | B3LYP/6-31G(d) |
| nitrone +6-alkylidenepenicillanates | PhMe, 80 °C | / | B3LYP/6-31G(d) level |
| C,N-disubstituted nitrones + disubstituted 4-methylene-1,3-oxazol-5(4H)-one | PhMe, reflux | / | M062X/6-311G(d,p) |
| adamantine aldo and ketonitrones + maleimides | PhMe, reflux | / | M06-2X/6-311++G(d,p) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiacchio, M.A.; Legnani, L. Density Functional Theory Calculations: A Useful Tool to Investigate Mechanisms of 1,3-Dipolar Cycloaddition Reactions. Int. J. Mol. Sci. 2024, 25, 1298. https://doi.org/10.3390/ijms25021298
Chiacchio MA, Legnani L. Density Functional Theory Calculations: A Useful Tool to Investigate Mechanisms of 1,3-Dipolar Cycloaddition Reactions. International Journal of Molecular Sciences. 2024; 25(2):1298. https://doi.org/10.3390/ijms25021298
Chicago/Turabian StyleChiacchio, Maria Assunta, and Laura Legnani. 2024. "Density Functional Theory Calculations: A Useful Tool to Investigate Mechanisms of 1,3-Dipolar Cycloaddition Reactions" International Journal of Molecular Sciences 25, no. 2: 1298. https://doi.org/10.3390/ijms25021298






