Platelet Biorheology and Mechanobiology in Thrombosis and Hemostasis: Perspectives from Multiscale Computation
Abstract
:1. Introduction
2. Platelet Margination
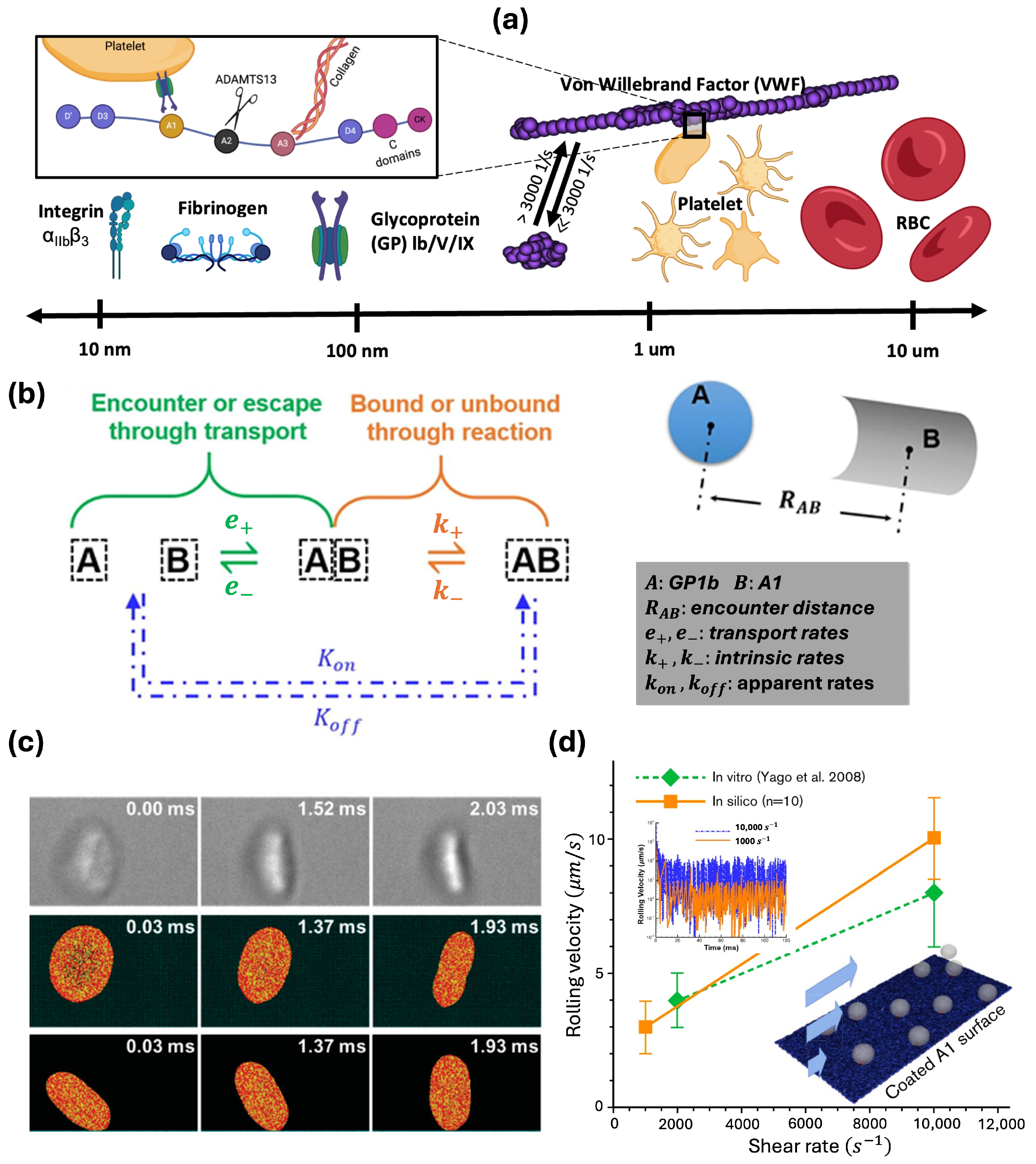
3. Platelet Adhesion
3.1. Recent Progress on Quantifying Shear-Dependent Binding Kinetics
3.2. Recent Progress in Multiscale Modelling of Platelet Adhesion
4. Platelet Activation
4.1. Shear-Induced Platelet Activation through Mechanotransduction
4.2. Resting and Activated Platelet Morphology under Flow Conditions
4.3. Recent Progress of Multiscale Modelling of Shear-Induced Platelet Activation
5. Platelet Aggregation

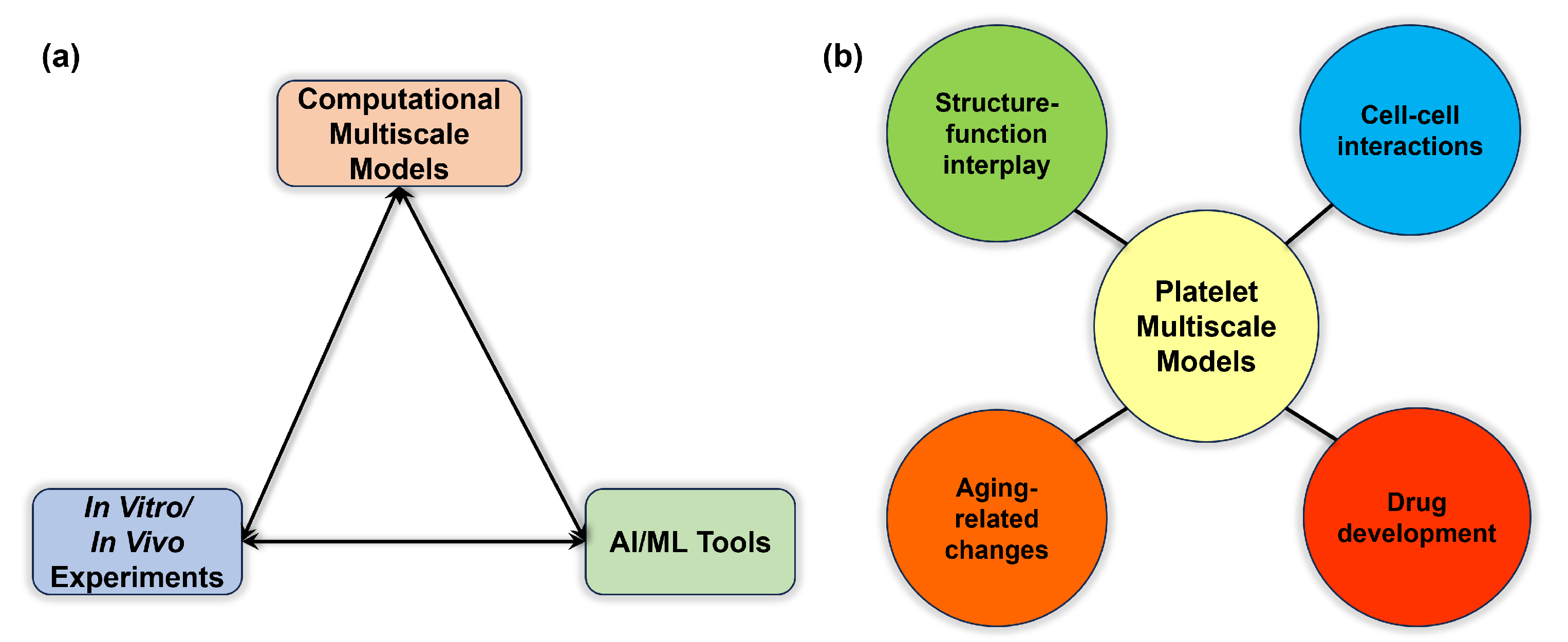
6. Further Discussion and Outlook
6.1. Multiscale Computation as a Tool to Bridge the Gap
6.2. Developing a Multiscale Model: A Note of Caution
6.3. Potential New Directions
7. Summary
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Watson, T.; Shantsila, E.; Lip, G.Y. Mechanisms of thrombogenesis in atrial fibrillation: Virchow’s triad revisited. Lancet 2009, 373, 155–166. [Google Scholar] [CrossRef] [PubMed]
- Casa, L.D.; Deaton, D.H.; Ku, D.N. Role of high shear rate in thrombosis. J. Vasc. Surg. 2015, 61, 1068–1080. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.L.; Bresette, C.; Aidun, C.K.; Ku, D.N. SIPA in 10 milliseconds: VWF tentacles agglomerate and capture platelets under high shear. Blood Adv. 2022, 6, 2453–2465. [Google Scholar] [CrossRef]
- Casa, L.D.; Ku, D.N. Thrombus Formation at High Shear Rates. Annu. Rev. Biomed. Eng. 2017, 19, 415–433. [Google Scholar] [CrossRef]
- Kim, D.; Bresette, C.; Liu, Z.; Ku, D.N. Occlusive thrombosis in arteries. APL Bioeng. 2019, 3, 041502. [Google Scholar] [CrossRef]
- Jackson, S.P. The growing complexity of platelet aggregation. Blood J. Am. Soc. Hematol. 2007, 109, 5087–5095. [Google Scholar] [CrossRef]
- Liu, Z.L.; Ku, D.N.; Aidun, C.K. Mechanobiology of shear-induced platelet aggregation leading to occlusive arterial thrombosis: A multiscale in silico analysis. J. Biomech. 2021, 120, 110349. [Google Scholar] [CrossRef] [PubMed]
- Chow, T.W.; Hellums, J.D.; Moake, J.L.; Kroll, M.H. Shear stress-induced von Willebrand factor binding to platelet glycoprotein Ib initiates calcium influx associated with aggregation. Blood 1992, 80, 113–120. [Google Scholar] [CrossRef]
- Jackson, S.; Nesbitt, W.; Westein, E. Dynamics of platelet thrombus formation. J. Thromb. Haemost. 2009, 7, 17–20. [Google Scholar] [CrossRef]
- Moake, J.L.; Turner, N.A.; Stathopoulos, N.A.; Nolasco, L.H.; Hellums, J.D. Involvement of large plasma von Willebrand factor (vWF) multimers and unusually large vWF forms derived from endothelial cells in shear stress-induced platelet aggregation. J. Clin. Investig. 1986, 78, 1456–1461. [Google Scholar] [CrossRef] [PubMed]
- Ruggeri, Z.M. Platelet Adhesion under Flow. Microcirculation 2009, 16, 58–83. [Google Scholar] [CrossRef]
- Brass, L.; Diamond, S. Transport physics and biorheology in the setting of hemostasis and thrombosis. J. Thromb. Haemost. 2016, 14, 906–917. [Google Scholar] [CrossRef] [PubMed]
- Shiozaki, S.; Takagi, S.; Goto, S. Prediction of molecular interaction between platelet glycoprotein Ibα and von Willebrand factor using molecular dynamics simulations. J. Atheroscler. Thromb. 2016, 23, 455–464. [Google Scholar] [CrossRef]
- Tong, D.; Soley, N.; Kolasangiani, R.; Schwartz, M.A.; Bidone, T.C. Integrin αIIbβ3 intermediates: From molecular dynamics to adhesion assembly. Biophys. J. 2023, 122, 533–543. [Google Scholar] [CrossRef] [PubMed]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Dzwinel, W.; Yuen, D.A.; Boryczko, K. Mesoscopic dynamics of colloids simulated with dissipative particle dynamics and fluid particle model. Mol. Model. Annu. 2002, 8, 33–43. [Google Scholar]
- Dzwinel, W.; Boryczko, K.; Yuen, D.A. A discrete-particle model of blood dynamics in capillary vessels. J. Colloid Interface Sci. 2003, 258, 163–173. [Google Scholar] [CrossRef] [PubMed]
- N’dri, N.A.; Shyy, W.; Tran-Son-Tay, R. Computational modeling of cell adhesion and movement using a continuum-kinetics approach. Biophys. J. 2003, 85, 2273–2286. [Google Scholar] [CrossRef] [PubMed]
- Shyy and, W.; Francois, M.; Udaykumar, H.S.; N’dri and, N.; Tran-Son-Tay, R. Moving boundaries in micro-scale biofluid dynamics. Appl. Mech. Rev. 2001, 54, 405–454. [Google Scholar] [CrossRef]
- Rao, R.R.; Clausen, J.; Roberts, S.A.; Lechman, J.B.; Wagner, J.; Butler, K.; Bolintineanu, D.; Brinker, C.J.; Liu, L. Continuum Modeling of Nanoparticle Transport in the Vasculature; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2017. [Google Scholar]
- Rao, R.R.; Wagner, J.; Butler, K.; Clausen, J.; Martin, R.M.; Liu, L. Continuum Modeling of Nanoparticles Transport In Vivo through Bifurcations; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2018. [Google Scholar]
- Mehrabadi, M.; Ku, D.N.; Aidun, C.K. Effects of shear rate, confinement, and particle parameters on margination in blood flow. Phys. Rev. E 2016, 93, 023109. [Google Scholar] [CrossRef] [PubMed]
- Crowl, L.; Fogelson, A.L. Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions. J. Fluid Mech. 2011, 676, 348–375. [Google Scholar] [CrossRef]
- Aarts, P.A.; van den Broek, S.A.; Prins, G.W.; Kuiken, G.D.; Sixma, J.J.; Heethaar, R.M. Blood platelets are concentrated near the wall and red blood cells, in the center in flowing blood. Arteriosclerosis 1988, 8, 819–824. [Google Scholar] [CrossRef]
- Reasor, D.A.; Mehrabadi, M.; Ku, D.N.; Aidun, C.K. Determination of Critical Parameters in Platelet Margination. Ann. Biomed. Eng. 2013, 41, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shaqfeh, E.S. Shear-induced platelet margination in a microchannel. Phys. Rev. E 2011, 83, 061924. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Clausen, J.R.; Rao, R.R.; Aidun, C.K. A unified analysis of nano-to-microscale particle dispersion in tubular blood flow. Phys. Fluids 2019, 31, 081903. [Google Scholar] [CrossRef]
- Zhao, H.; Shaqfeh, E.S.; Narsimhan, V. Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids 2012, 24, 011902. [Google Scholar] [CrossRef]
- Kumar, A.; Graham, M.D. Margination and segregation in confined flows of blood and other multicomponent suspensions. Soft Matter 2012, 8, 10536–10548. [Google Scholar] [CrossRef]
- Kumar, A.; Graham, M.D. Mechanism of Margination in Confined Flows of Blood and Other Multicomponent Suspensions. Phys. Rev. Lett. 2012, 109, 108102. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, Y.; Clausen, J.R.; Lechman, J.B.; Rao, R.R.; Aidun, C.K. Multiscale method based on coupled lattice-Boltzmann and Langevin-dynamics for direct simulation of nanoscale particle/polymer suspensions in complex flows. Int. J. Numer. Methods Fluids 2019, 91, 228–246. [Google Scholar] [CrossRef]
- Liu, Z.; Clausen, J.R.; Rao, R.R.; Aidun, C.K. Nanoparticle diffusion in sheared cellular blood flow. J. Fluid Mech. 2019, 871, 636–667. [Google Scholar] [CrossRef]
- Ruggeri, Z.M.; Mendolicchio, G.L. Adhesion Mechanisms in Platelet Function. Circ. Res. 2007, 100, 1673–1685. [Google Scholar] [CrossRef]
- Savage, B.; Saldívar, E.; Ruggeri, Z.M. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell 1996, 84, 289–297. [Google Scholar] [CrossRef] [PubMed]
- Savage, B.; Almus-Jacobs, F.; Ruggeri, Z.M. Specific synergy of multiple substrate–receptor interactions in platelet thrombus formation under flow. Cell 1998, 94, 657–666. [Google Scholar] [CrossRef] [PubMed]
- Ruggeri, Z.M.; Orje, J.N.; Habermann, R.; Federici, A.B.; Reininger, A.J. Activation-independent platelet adhesion and aggregation under elevated shear stress. Blood 2006, 108, 1903–1910. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Jiang, Y.; Yang, D.; Scheiflinger, F.; Wong, W.P.; Springer, T.A. Flow-induced elongation of von Willebrand factor precedes tension-dependent activation. Nat. Commun. 2017, 8, 324. [Google Scholar] [CrossRef] [PubMed]
- Wellings, P.J.; Ku, D.N. Mechanisms of Platelet Capture Under Very High Shear. Cardiovasc. Eng. Technol. 2012, 3, 161–170. [Google Scholar] [CrossRef]
- Hantgan, R.R.; Stahle, M.C.; Lord, S.T. Dynamic Regulation of Fibrinogen: Integrin αIIbβ3 Binding. Biochemistry 2010, 49, 9217–9225. [Google Scholar] [CrossRef]
- Yago, T.; Lou, J.; Wu, T.; Yang, J.; Miner, J.J.; Coburn, L.; López, J.A.; Cruz, M.A.; Dong, J.F.; McIntire, L.V. Platelet glycoprotein Ibα forms catch bonds with human WT vWF but not with type 2B von Willebrand disease vWF. J. Clin. Investig. 2008, 118, 3195–3207. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liao, J.; Yuan, Z.; Li, K.; Liu, B.; Ju, L.A.; Zhu, C. Fast force loading disrupts molecular binding stability in human and mouse cell adhesions. Mol. Cell. Biomech. MCB 2019, 16, 211. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ju, L.A.; Zhou, F.; Liao, J.; Xue, L.; Su, Q.P.; Jin, D.; Yuan, Y.; Lu, H.; Jackson, S.P. An integrin αIIbβ3 intermediate affinity state mediates biomechanical platelet aggregation. Nat. Mater. 2019, 18, 760–769. [Google Scholar] [CrossRef] [PubMed]
- Hammer, D.A.; Lauffenburger, D.A. A dynamical model for receptor-mediated cell adhesion to surfaces. Biophys. J. 1987, 52, 475–487. [Google Scholar] [CrossRef]
- Hammer, D.A.; Apte, S.M. Simulation of cell rolling and adhesion on surfaces in shear flow: General results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 1992, 63, 35–57. [Google Scholar] [CrossRef] [PubMed]
- Mody, N.A.; Lomakin, O.; Doggett, T.A.; Diacovo, T.G.; King, M.R. Mechanics of transient platelet adhesion to von Willebrand factor under flow. Biophys. J. 2005, 88, 1432–1443. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Sheriff, J.; Zhang, P.; Deng, Y.; Bluestein, D. A Multiscale Model for Shear-Mediated Platelet Adhesion Dynamics: Correlating In Silico with In Vitro Results. Ann. Biomed. Eng. 2023, 51, 1094–1105. [Google Scholar] [CrossRef] [PubMed]
- Belyaev, A.V.; Kushchenko, Y.K. Biomechanical activation of blood platelets via adhesion to von Willebrand factor studied with mesoscopic simulations. Biomech. Model. Mechanobiol. 2023, 22, 785–808. [Google Scholar] [CrossRef] [PubMed]
- Cosemans, J.M.; Angelillo-Scherrer, A.; Mattheij, N.J.; Heemskerk, J.W. The effects of arterial flow on platelet activation, thrombus growth, and stabilization. Cardiovasc. Res. 2013, 99, 342–352. [Google Scholar] [CrossRef] [PubMed]
- Versteeg, H.H.; Heemskerk, J.W.M.; Levi, M.; Reitsma, P.H. New Fundamentals in Hemostasis. Physiol. Rev. 2013, 93, 327–358. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.A.; Ashworth, K.J.; Di Paola, J.; Ku, D.N. Platelet α-granules are required for occlusive high-shear-rate thrombosis. Blood Adv. 2020, 4, 3258–3267. [Google Scholar] [CrossRef] [PubMed]
- Jennings, L. Mechanisms of platelet activation: Need for new strategies to protect against platelet-mediated atherothrombosis. Thromb. Haemost. 2009, 102, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Kroll, M.H.; Harris, T.S.; Moake, J.L.; Handin, R.I.; Schafer, A.I. von Willebrand factor binding to platelet GpIb initiates signals for platelet activation. J. Clin. Investig. 1991, 88, 1568–1573. [Google Scholar] [CrossRef] [PubMed]
- Meyer, A.L.; Malehsa, D.; Bara, C.; Budde, U.; Slaughter, M.S.; Haverich, A.; Strueber, M. Acquired von Willebrand Syndrome in Patients With an Axial Flow Left Ventricular Assist Device. Circ. Heart Fail. 2010, 3, 675–681. [Google Scholar] [CrossRef] [PubMed]
- Slepian, M.J.; Sheriff, J.; Hutchinson, M.; Tran, P.; Bajaj, N.; Garcia, J.G.; Saavedra, S.S.; Bluestein, D. Shear-mediated platelet activation in the free flow: Perspectives on the emerging spectrum of cell mechanobiological mechanisms mediating cardiovascular implant thrombosis. J. Biomech. 2017, 50, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Hellums, J.; Peterson, D.; Stathopoulos, N.; Moake, J.; Giorgio, T. Studies on the mechanisms of shear-induced platelet activation. In Proceedings of the Cerebral Ischemia and Hemorheology; Springer: Berlin/Heidelberg, Germany, 1987; pp. 80–89. [Google Scholar]
- Kroll, M.H.; Hellums, J.D.; McIntire, L.V.; Schafer, A.I.; Moake, J.L. Platelets and shear stress. Blood 1996, 88, 1525–1541. [Google Scholar] [CrossRef] [PubMed]
- Girdhar, G.; Bluestein, D. Biological effects of dynamic shear stress in cardiovascular pathologies and devices. Expert Rev. Med. Devices 2008, 5, 167–181. [Google Scholar] [PubMed]
- Ingber, D.E.; Wang, N.; Stamenović, D. Tensegrity, cellular biophysics, and the mechanics of living systems. Rep. Prog. Phys. 2014, 77, 046603. [Google Scholar] [PubMed]
- Sheriff, J.; Bluestein, D.; Girdhar, G.; Jesty, J. High-Shear Stress Sensitizes Platelets to Subsequent Low-Shear Conditions. Ann. Biomed. Eng. 2010, 38, 1442–1450. [Google Scholar] [PubMed]
- Sheriff, J.; Tran, P.L.; Hutchinson, M.; DeCook, T.; Slepian, M.J.; Bluestein, D.; Jesty, J. Repetitive Hypershear Activates and Sensitizes Platelets in a Dose-Dependent Manner. Artif. Organs 2016, 40, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Girdhar, G.; Xenos, M.; Alemu, Y.; Chiu, W.C.; Lynch, B.E.; Jesty, J.; Einav, S.; Slepian, M.J.; Bluestein, D. Device thrombogenicity emulation: A novel method for optimizing mechanical circulatory support device thromboresistance. PLoS ONE 2012, 7, e32463. [Google Scholar]
- Sheriff, J.; Soares, J.S.; Xenos, M.; Jesty, J.; Bluestein, D. Evaluation of Shear-Induced Platelet Activation Models Under Constant and Dynamic Shear Stress Loading Conditions Relevant to Devices. Ann. Biomed. Eng. 2013, 41, 1279–1296. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.A.; Wright, J.R.; Mahaut-Smith, M.P. Regulation of Pannexin-1 channel activity. Biochem. Soc. Trans. 2015, 43, 502–507. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.A.; Wright, J.R.; Vial, C.; Evans, R.J.; Mahaut-Smith, M.P. Amplification of human platelet activation by surface pannexin-1 channels. J. Thromb. Haemost. 2014, 12, 987–998. [Google Scholar] [CrossRef] [PubMed]
- Ilkan, Z.; Wright, J.R.; Goodall, A.H.; Gibbins, J.M.; Jones, C.I.; Mahaut-Smith, M.P. Evidence for shear-mediated Ca2+ entry through mechanosensitive cation channels in human platelets and a megakaryocytic cell line. J. Biol. Chem. 2017, 292, 9204–9217. [Google Scholar] [CrossRef] [PubMed]
- Mammadova-Bach, E.; Gudermann, T.; Braun, A. Platelet Mechanotransduction: Regulatory Cross Talk Between Mechanosensitive Receptors and Calcium Channels. ATVB 2023, 43, 1339–1348. [Google Scholar] [CrossRef] [PubMed]
- Zainal Abidin, N.A.; Poon, E.K.W.; Szydzik, C.; Timofeeva, M.; Akbaridoust, F.; Brazilek, R.J.; Tovar Lopez, F.J.; Ma, X.; Lav, C.; Marusic, I.; et al. An extensional strain sensing mechanosome drives adhesion-independent platelet activation at supraphysiological hemodynamic gradients. BMC Biol. 2022, 20, 73. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Wei, Z.; Xin, G.; Li, Y.; Yuan, J.; Ming, Y.; Ji, C.; Sun, Q.; Li, S.; Chen, X. Piezo1 initiates platelet hyperreactivity and accelerates thrombosis in hypertension. J. Thromb. Haemost. 2021, 19, 3113–3125. [Google Scholar] [CrossRef] [PubMed]
- Di-Luoffo, M.; Ben-Meriem, Z.; Lefebvre, P.; Delarue, M.; Guillermet-Guibert, J. PI3K functions as a hub in mechanotransduction. Trends Biochem. Sci. 2021, 46, 878–888. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, T.; Kareem, K.; Tran, D.; Griffith, B.P.; Wu, Z.J. The role of PI3K/Akt signaling pathway in non-physiological shear stress-induced platelet activation. Artif. Organs 2019, 43, 897–908. [Google Scholar] [CrossRef] [PubMed]
- Yap, C.L.; Anderson, K.E.; Hughan, S.C.; Dopheide, S.M.; Salem, H.H.; Jackson, S.P. Essential role for phosphoinositide 3-kinase in shear-dependent signaling between platelet glycoprotein Ib/V/IX and integrin αIIbβ3. Blood J. Am. Soc. Hematol. 2002, 99, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Guidetti, G.F.; Canobbio, I.; Torti, M. PI3K/Akt in platelet integrin signaling and implications in thrombosis. Adv. Biol. Regul. 2015, 59, 36–52. [Google Scholar] [CrossRef]
- Ghigo, A.; Morello, F.; Perino, A.; Hirsch, E. Therapeutic applications of PI3K inhibitors in cardiovascular diseases. Future Med. Chem. 2013, 5, 479–492. [Google Scholar] [CrossRef] [PubMed]
- Jackson, S.P.; Schoenwaelder, S.M.; Goncalves, I.; Nesbitt, W.S.; Yap, C.L.; Wright, C.E.; Kenche, V.; Anderson, K.E.; Dopheide, S.M.; Yuan, Y. PI 3-kinase p110β: A new target for antithrombotic therapy. Nat. Med. 2005, 11, 507–514. [Google Scholar] [CrossRef] [PubMed]
- Laurent, P.A.; Séverin, S.; Hechler, B.; Vanhaesebroeck, B.; Payrastre, B.; Gratacap, M.P. Platelet PI3Kβ and GSK3 regulate thrombus stability at a high shear rate. Blood J. Am. Soc. Hematol. 2015, 125, 881–888. [Google Scholar] [CrossRef] [PubMed]
- Frojmovic, M.M.; Panjwani, R. Geometry of normal mammalian platelets by quantitative microscopic studies. Biophys. J. 1976, 16, 1071–1089. [Google Scholar] [CrossRef] [PubMed]
- Chesnutt, J.K.; Han, H.C. Platelet size and density affect shear-induced thrombus formation in tortuous arterioles. Phys. Biol. 2013, 10, 056003. [Google Scholar] [CrossRef]
- Litvinenko, A.; Moskalensky, A.; Karmadonova, N.; Nekrasov, V.; Strokotov, D.; Konokhova, A.; Yurkin, M.; Pokushalov, E.; Chernyshev, A.; Maltsev, V. Fluorescence-free flow cytometry for measurement of shape index distribution of resting, partially activated, and fully activated platelets. Cytom. Part A 2016, 89, 1010–1016. [Google Scholar] [CrossRef] [PubMed]
- Hartwig, J.H. The platelet: Form and function. In Proceedings of the Seminars in Hematology; Elsevier: Amsterdam, The Netherlands, 2006; Volume 43, pp. S94–S100. [Google Scholar]
- White, J.G. CHAPTER 3—Platelet Structure. In Platelets, 2nd ed.; Michelson, A.D., Ed.; Academic Press: Burlington, MA, USA, 2007; pp. 45–73. [Google Scholar]
- Raucher, D.; Sheetz, M.P. Characteristics of a membrane reservoir buffering membrane tension. Biophys. J. 1999, 77, 1992–2002. [Google Scholar] [CrossRef] [PubMed]
- Moskalensky, A.E.; Litvinenko, A.L. The platelet shape change: Biophysical basis and physiological consequences. Platelets 2019, 30, 543–548. [Google Scholar] [CrossRef] [PubMed]
- White, J.G.; Rao, G. Microtubule coils versus the surface membrane cytoskeleton in maintenance and restoration of platelet discoid shape. Am. J. Pathol. 1998, 152, 597. [Google Scholar]
- Italiano, J.E., Jr.; Bergmeier, W.; Tiwari, S.; Falet, H.; Hartwig, J.H.; Hoffmeister, K.M.; André, P.; Wagner, D.D.; Shivdasani, R.A. Mechanisms and implications of platelet discoid shape. Blood 2003, 101, 4789–4796. [Google Scholar] [CrossRef] [PubMed]
- Hartwig, J.H.; DeSisto, M. The cytoskeleton of the resting human blood platelet: Structure of the membrane skeleton and its attachment to actin filaments. J. Cell Biol. 1991, 112, 407–425. [Google Scholar] [CrossRef] [PubMed]
- Hartwig, J.; Barkalow, K.; Azim, A.; Italiano, J. The Elegant Platelet: Signals Controlling Actin Assembly. Thromb. Haemost. 1999, 82, 392–398. [Google Scholar] [PubMed]
- Ajzenberg, N.; Haghighat Talab, A.T.; Massé, J.M.; Drouin, A.; Jondeau, K.; Kobeiter, H.; Baruch, D.; Cramer, E.M. Platelet shape change and subsequent glycoprotein redistribution in human stenosed arteries. Platelets 2005, 16, 13–18. [Google Scholar] [CrossRef]
- Du Plooy, J.N.; Buys, A.; Duim, W.; Pretorius, E. Comparison of platelet ultrastructure and elastic properties in thrombo-embolic ischemic stroke and smoking using atomic force and scanning electron microscopy. PLoS ONE 2013, 8, e69774. [Google Scholar] [CrossRef] [PubMed]
- Wurzinger, L.J.; Blasberg, P.; Schmid-Schönbein, H. Towards a concept of thrombosis in accelerated flow: Rheology, fluid dynamics, and biochemistry. Biorheology 1985, 22, 437–450. [Google Scholar] [CrossRef]
- Wurzinger, L.J.; Opitz, R.; Wolf, M.; Schmid-Schönbein, H. Ultrastructural investigations on the question of mechanical activation of blood platelets. Blut 1987, 54, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Purvis, N.B., Jr.; Giorgio, T.D. The effects of elongational stress exposure on the activation and aggregation of blood platelets. Biorheology 1991, 28, 355–367. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Mondal, N.K.; Ding, J.; Gao, J.; Griffith, B.P.; Wu, Z.J. Shear-induced platelet receptor shedding by non-physiological high shear stress with short exposure time: Glycoprotein Ibα and glycoprotein VI. Thromb. Res. 2015, 135, 692–698. [Google Scholar] [CrossRef]
- Chen, Z.; Mondal, N.K.; Ding, J.; Koenig, S.C.; Slaughter, M.S.; Griffith, B.P.; Wu, Z.J. Activation and shedding of platelet glycoprotein IIb/IIIa under non-physiological shear stress. Mol. Cell. Biochem. 2015, 409, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Mondal, N.K.; Zheng, S.; Koenig, S.C.; Slaughter, M.S.; Griffith, B.P.; Wu, Z.J. High shear induces platelet dysfunction leading to enhanced thrombotic propensity and diminished hemostatic capacity. Platelets 2019, 30, 112–119. [Google Scholar] [CrossRef]
- Holme, P.A.; Ørvim, U.; Hamers, M.J.A.G.; Solum, N.O.; Brosstad, F.R.; Barstad, R.M.; Sakariassen, K.S. Shear-Induced Platelet Activation and Platelet Microparticle Formation at Blood Flow Conditions as in Arteries With a Severe Stenosis. ATVB 1997, 17, 646–653. [Google Scholar] [CrossRef] [PubMed]
- Mody, N.A.; King, M.R. Three-dimensional simulations of a platelet-shaped spheroid near a wall in shear flow. Phys. Fluids 2005, 17, 113302. [Google Scholar] [CrossRef]
- Mody, N.A.; King, M.R. Platelet adhesive dynamics. Part I: Characterization of platelet hydrodynamic collisions and wall effects. Biophys. J. 2008, 95, 2539–2555. [Google Scholar] [CrossRef] [PubMed]
- Mody, N.A.; King, M.R. Platelet adhesive dynamics. Part II: High shear-induced transient aggregation via GPIbα-vWF-GPIbα bridging. Biophys. J. 2008, 95, 2556–2574. [Google Scholar] [CrossRef] [PubMed]
- Pozrikidis, C. Flipping of an adherent blood platelet over a substrate. J. Fluid Mech. 2006, 568, 161–172. [Google Scholar] [CrossRef]
- Sweet, C.R.; Chatterjee, S.; Xu, Z.; Bisordi, K.; Rosen, E.D.; Alber, M. Modelling platelet–blood flow interaction using the subcellular element Langevin method. J. R. Soc. Interface 2011, 8, 1760–1771. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Z.; Kim, O.; Alber, M. Three-dimensional multi-scale model of deformable platelets adhesion to vessel wall in blood flow. Philos. Trans. R. Soc. A 2014, 372, 20130380. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Gao, C.; Zhang, N.; Slepian, M.J.; Deng, Y.; Bluestein, D. Multiscale Particle-Based Modeling of Flowing Platelets in Blood Plasma Using Dissipative Particle Dynamics and Coarse Grained Molecular Dynamics. Cell. Mol. Bioeng. 2014, 7, 552–574. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhang, L.; Slepian, M.J.; Deng, Y.; Bluestein, D. A multiscale biomechanical model of platelets: Correlating with in-vitro results. J. Biomech. 2017, 50, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Pothapragada, S.; Zhang, P.; Sheriff, J.; Livelli, M.; Slepian, M.J.; Deng, Y.; Bluestein, D. A phenomenological particle-based platelet model for simulating filopodia formation during early activation. Int. J. Numer. Methods Biomed. Eng. 2015, 31, e02702. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Sheriff, J.; Einav, S.; Slepian, M.J.; Deng, Y.; Bluestein, D. A predictive multiscale model for simulating flow-induced platelet activation: Correlating in silico results with in vitro results. J. Biomech. 2021, 117, 110275. [Google Scholar] [CrossRef] [PubMed]
- Zainal Abidin, N.A.; Timofeeva, M.; Szydzik, C.; Akbaridoust, F.; Lav, C.; Marusic, I.; Mitchell, A.; Hamilton, J.R.; Ooi, A.S.H.; Nesbitt, W.S. A microfluidic method to investigate platelet mechanotransduction under extensional strain. Res. Pract. Thromb. Haemost. 2023, 7, 100037. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, M.J.; Westein, E.; Nesbitt, W.S.; Giuliano, S.; Dopheide, S.M.; Jackson, S.P. Identification of a 2-stage platelet aggregation process mediating shear-dependent thrombus formation. Blood 2007, 109, 566–576. [Google Scholar] [CrossRef]
- Ruggeri, Z.M. Mechanisms Initiating Platelet Thrombus Formation. Thromb. Haemost. 1997, 78, 611–616. [Google Scholar] [CrossRef]
- Flamm, M.H.; Colace, T.V.; Chatterjee, M.S.; Jing, H.; Zhou, S.; Jaeger, D.; Brass, L.F.; Sinno, T.; Diamond, S.L. Multiscale prediction of patient-specific platelet function under flow. Blood J. Am. Soc. Hematol. 2012, 120, 190–198. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Zhang, P.; Sheriff, J.; Bluestein, D.; Deng, Y. A Multiscale Model for Recruitment Aggregation of Platelets by Correlating with In Vitro Results. Cell. Mol. Bioeng. 2019, 12, 327–343. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Zhang, P.; Sheriff, J.; Bluestein, D.; Deng, Y. A multiscale model for multiple platelet aggregation in shear flow. Biomech. Model. Mechanobiol. 2021, 20, 1013–1030. [Google Scholar] [CrossRef] [PubMed]
- Fogelson, A.L.; Guy, R.D. Immersed-boundary-type models of intravascular platelet aggregation. Comput. Methods Appl. Mech. Eng. 2008, 197, 2087–2104. [Google Scholar] [CrossRef]
- Mori, D.; Yano, K.; Tsubota, K.i.; Ishikawa, T.; Wada, S.; Yamaguchi, T. Simulation of platelet adhesion and aggregation regulated by fibrinogen and von Willebrand factor. Thromb. Haemost. 2008, 99, 108–115. [Google Scholar] [PubMed]
- Shankar, K.N.; Zhang, Y.; Sinno, T.; Diamond, S.L. A three-dimensional multiscale model for the prediction of thrombus growth under flow with single-platelet resolution. PLoS Comput. Biol. 2022, 18, e1009850. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Kim, D.; Alhawael, G.; Ku, D.N.; Fogelson, A.L. Clot permeability, agonist transport, and platelet binding kinetics in arterial thrombosis. Biophys. J. 2020, 119, 2102–2115. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Fogelson, A.L. A computational investigation of occlusive arterial thrombosis. Biomech. Model. Mechanobiol. 2023, 23, 157–178. [Google Scholar] [CrossRef]
- Alber, M.; Buganza Tepole, A.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; Petzold, L.; et al. Integrating machine learning and multiscale modeling—perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digit. Med. 2019, 2, 115. [Google Scholar] [CrossRef] [PubMed]
- Weisel, J.; Litvinov, R. Red blood cells: The forgotten player in hemostasis and thrombosis. J. Thromb. Haemost. 2019, 17, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Hao, H.; Leeper, N.; Zhu, L.; Committee, E.C. Thrombotic Regulation from the Endothelial Cell Perspectives. Arterioscler. Thromb. Vasc. Biol. 2018, 38, e90–e95. [Google Scholar] [CrossRef] [PubMed]
- Cerletti, C.; Tamburrelli, C.; Izzi, B.; Gianfagna, F.; de Gaetano, G. Platelet-leukocyte interactions in thrombosis. Thromb. Res. 2012, 129, 263–266. [Google Scholar] [CrossRef] [PubMed]
- Stark, K.; Massberg, S. Interplay between inflammation and thrombosis in cardiovascular pathology. Nat. Rev. Cardiol. 2021, 18, 666–682. [Google Scholar] [CrossRef] [PubMed]
- Gross, P.; Chan, N. Thromboembolism in Older Adults. Front. Med. 2021, 7, 470016. [Google Scholar] [CrossRef]
- Clancy, C.; An, G.; Cannon, W.; Liu, Y.; May, E.; Ortoleva, P.; Popel, A.; Sluka, J.; Su, J.; Vicini, P.; et al. Multiscale Modeling in the Clinic: Drug Design and Development. Ann. Biomed. Eng. 2016, 44, 2591–2610. [Google Scholar] [CrossRef] [PubMed]

| Vessel/Condition | Shear Rate (s−1) | Shear Stress (dyne/cm2) |
|---|---|---|
| Normal physiology | ||
| Ascending aorta | 300 | 2–10 |
| Large arteries | 300–800 | 10–30 |
| Coronary artery (LCA/RCA) | 300–1500 | 10–60 |
| Carotid artery | 250 | 10 |
| Arterioles | 500–1600 | 20–60 |
| Capillary | 200–2000 | high a |
| Postcapillary venules | 50–200 | 1–2 |
| Veins | 20–2000 | 0.8–8 |
| Disease conditions | ||
| Coronary stenosis (LAD) | 5000–100,000 b | - |
| Carotid stenosis | - | 40–360 |
| Aortic coarctation g | - | 140–>1000 c |
| Atrioventricular fistula g | - | 100–1000 d |
| Deep vein thrombosis g | 0–200 e | |
| Prosthetic devices | ||
| Mechanical heart valves g | - | up to 6000 |
| Left ventricular assist devices g | 5000–>100,000 f | 0–>1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuna, R.; Yi, W.; Crespo Cruz, E.; Romero, J.; Ren, Y.; Guan, J.; Li, Y.; Deng, Y.; Bluestein, D.; Liu, Z.L.; et al. Platelet Biorheology and Mechanobiology in Thrombosis and Hemostasis: Perspectives from Multiscale Computation. Int. J. Mol. Sci. 2024, 25, 4800. https://doi.org/10.3390/ijms25094800
Tuna R, Yi W, Crespo Cruz E, Romero J, Ren Y, Guan J, Li Y, Deng Y, Bluestein D, Liu ZL, et al. Platelet Biorheology and Mechanobiology in Thrombosis and Hemostasis: Perspectives from Multiscale Computation. International Journal of Molecular Sciences. 2024; 25(9):4800. https://doi.org/10.3390/ijms25094800
Chicago/Turabian StyleTuna, Rukiye, Wenjuan Yi, Esmeralda Crespo Cruz, JP Romero, Yi Ren, Jingjiao Guan, Yan Li, Yuefan Deng, Danny Bluestein, Zixiang Leonardo Liu, and et al. 2024. "Platelet Biorheology and Mechanobiology in Thrombosis and Hemostasis: Perspectives from Multiscale Computation" International Journal of Molecular Sciences 25, no. 9: 4800. https://doi.org/10.3390/ijms25094800
APA StyleTuna, R., Yi, W., Crespo Cruz, E., Romero, J., Ren, Y., Guan, J., Li, Y., Deng, Y., Bluestein, D., Liu, Z. L., & Sheriff, J. (2024). Platelet Biorheology and Mechanobiology in Thrombosis and Hemostasis: Perspectives from Multiscale Computation. International Journal of Molecular Sciences, 25(9), 4800. https://doi.org/10.3390/ijms25094800










