Short- and Long-Term Evolution of Microbial Cultures: A Thermodynamic Perspective
Abstract
1. Introduction
2. Short-Term Evolution of a Microbial Culture
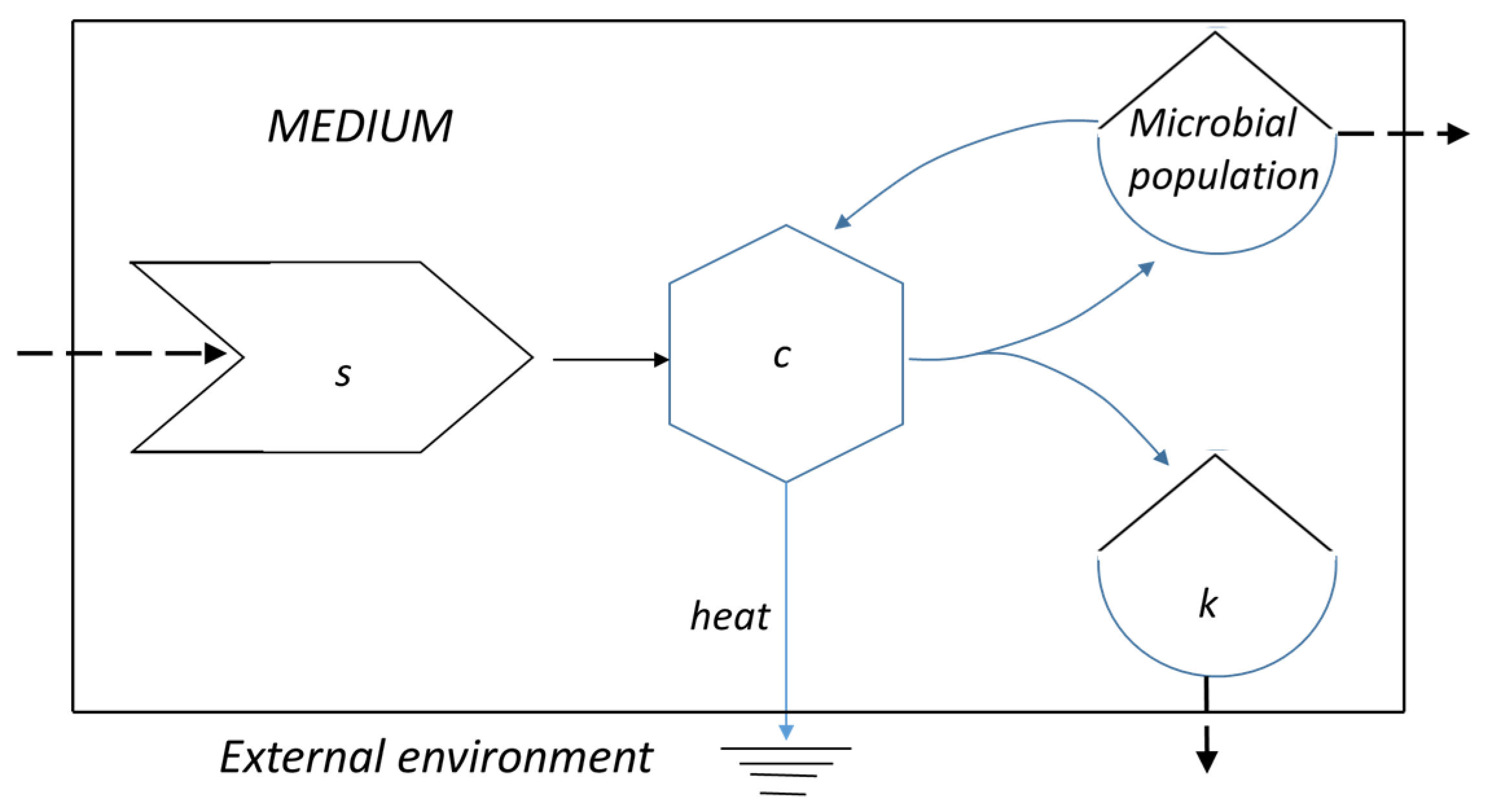
2.1. A Classic Thermodynamic Balance
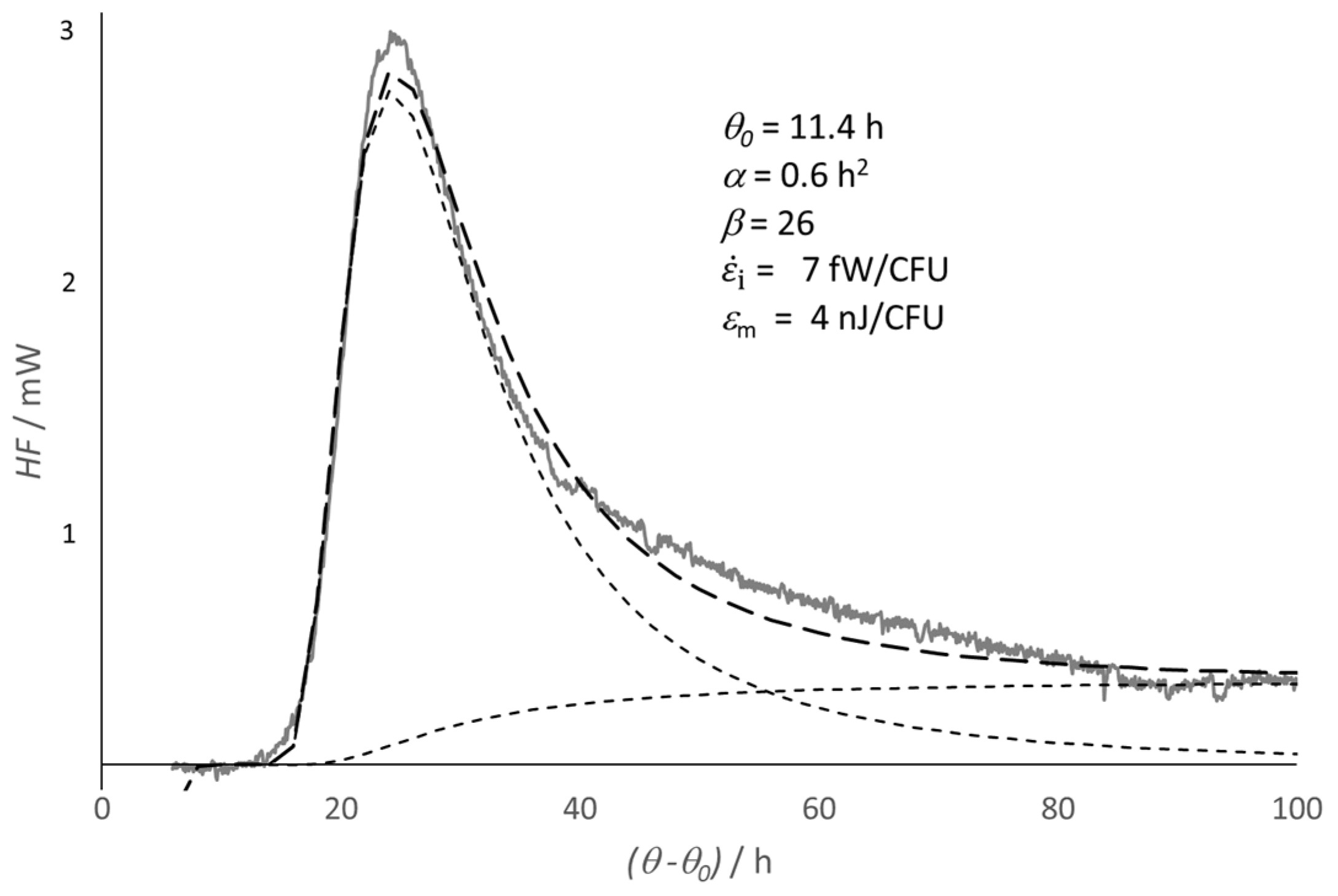
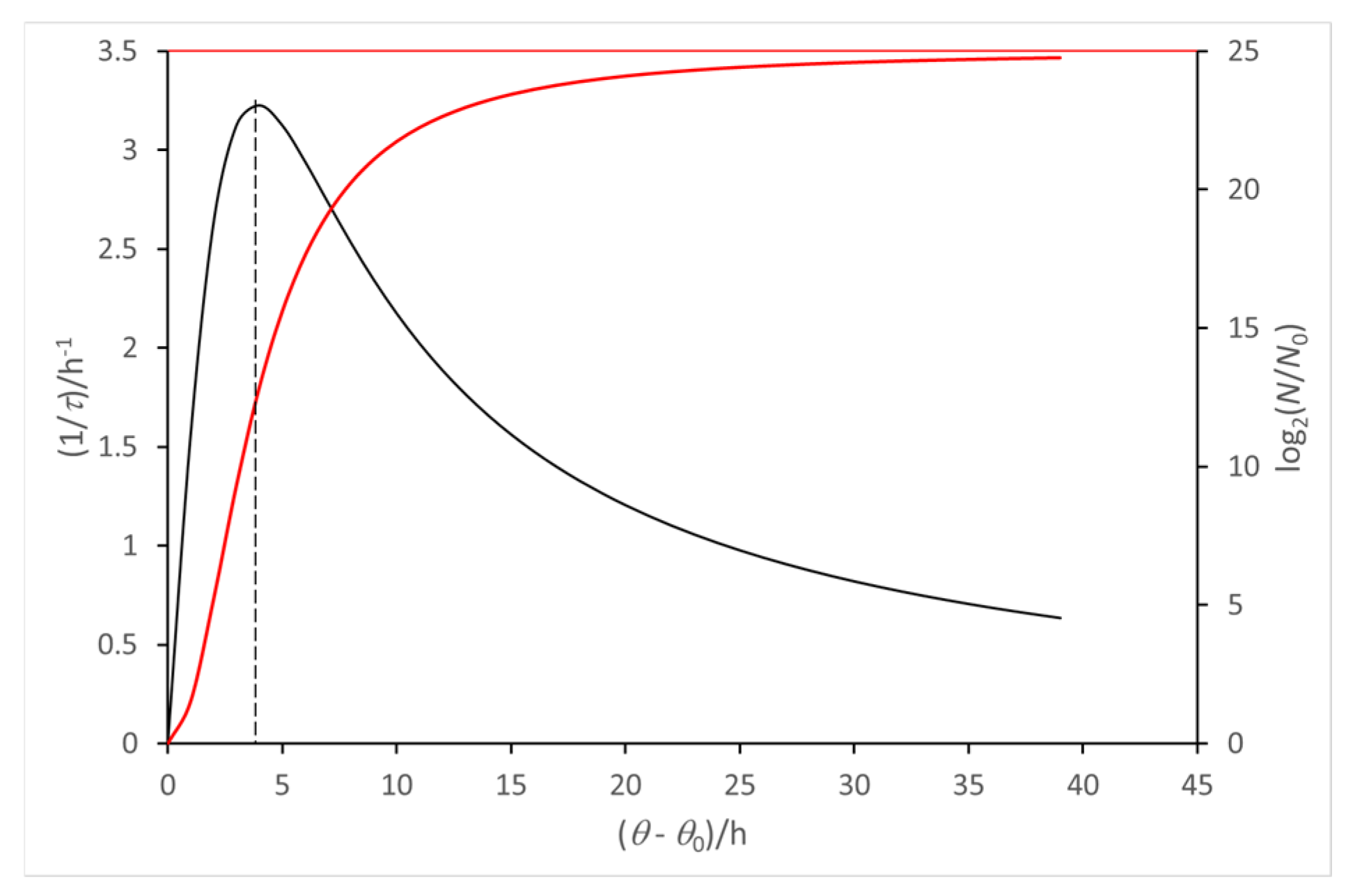
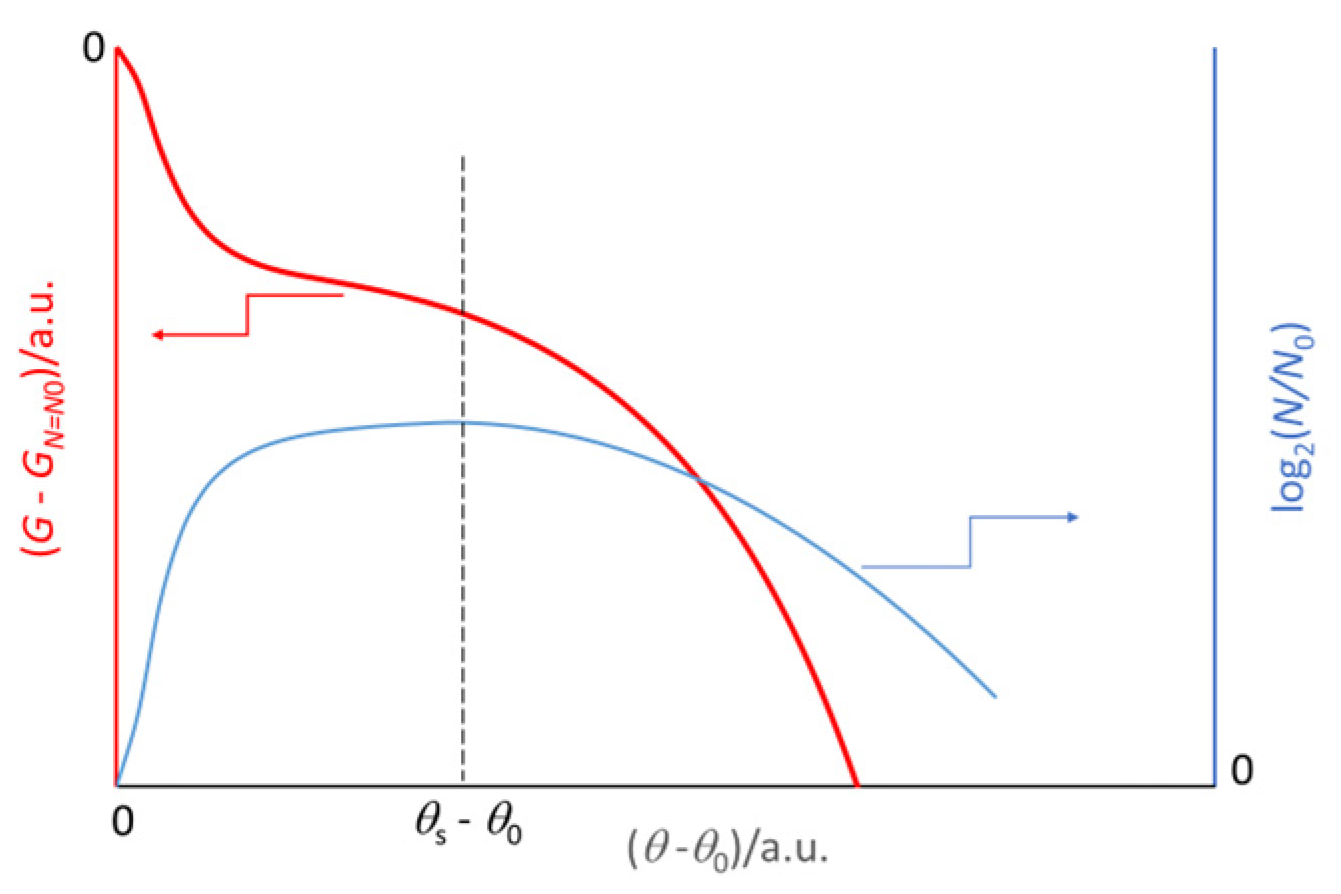
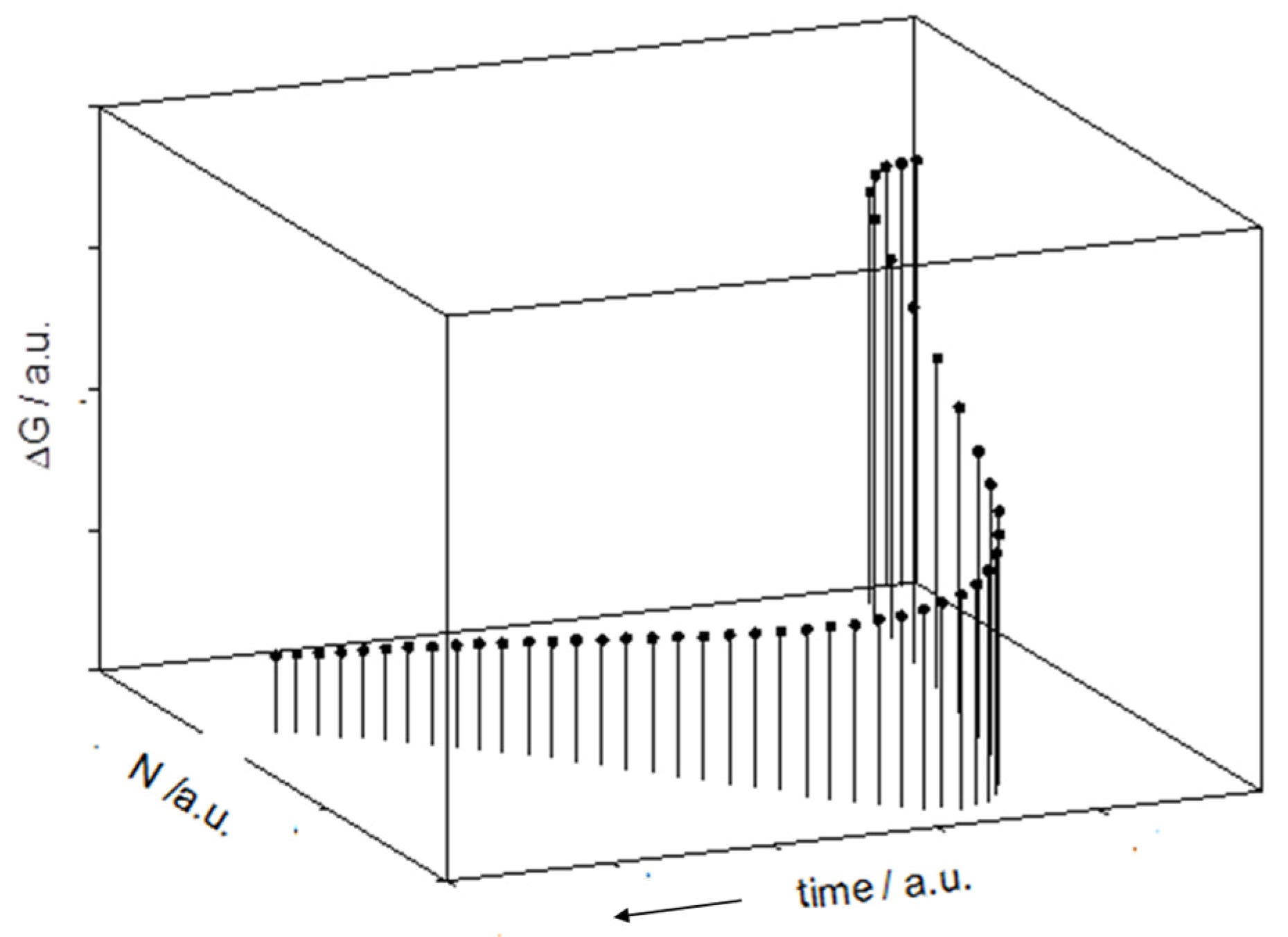
2.2. The Gibbs Free Energy Trend in a Virtual Batch Culture
2.3. The Osmotic Balance
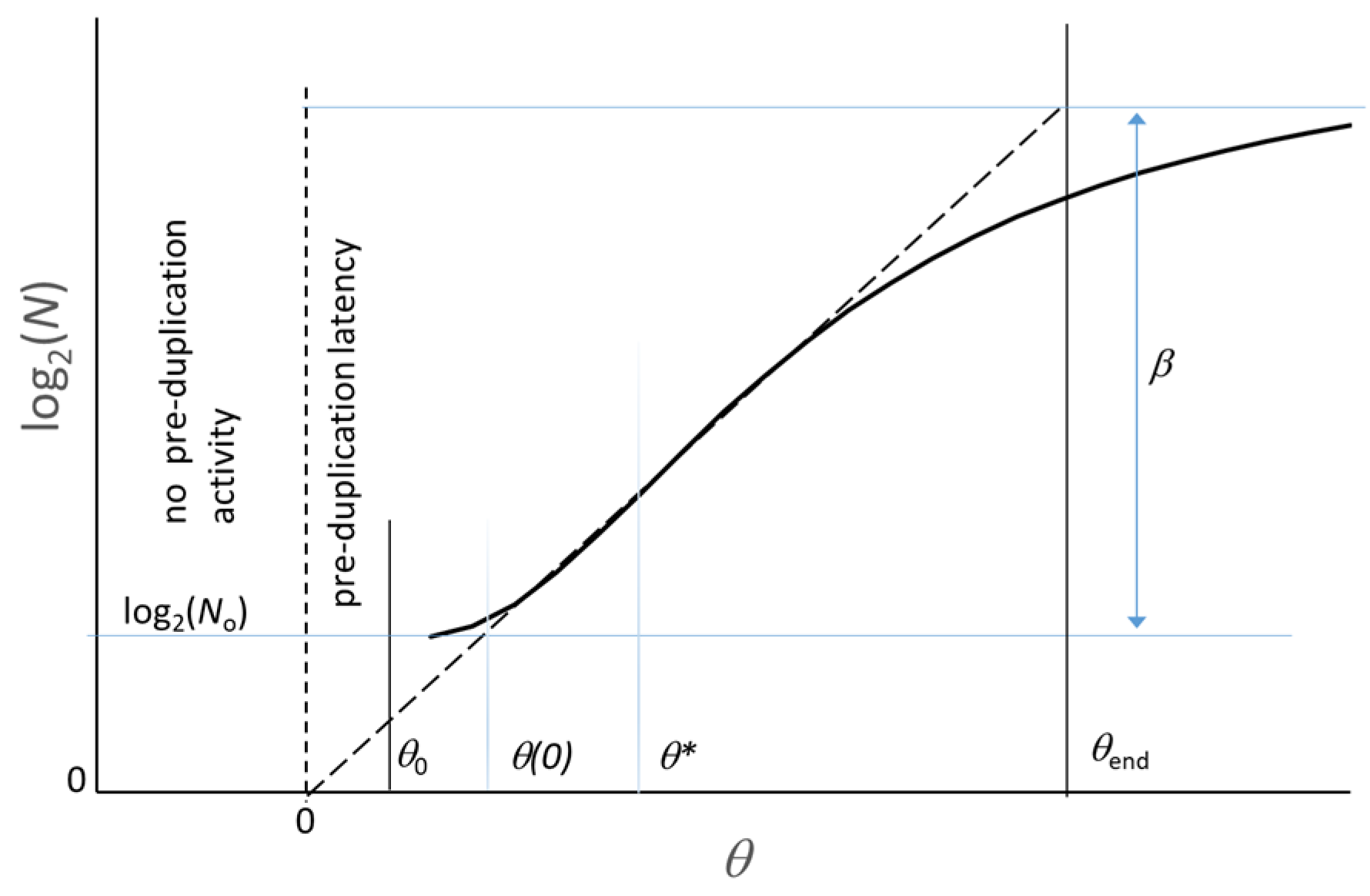
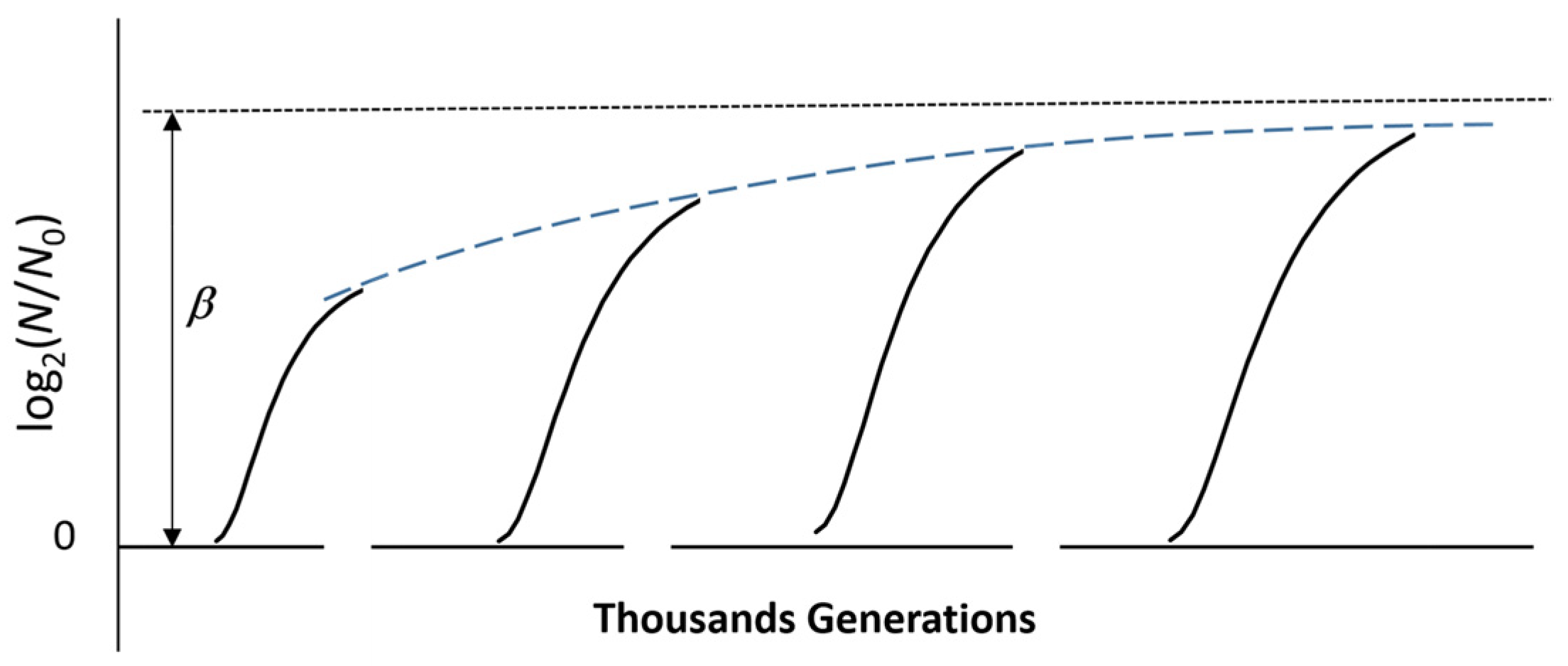
3. Long-Term Evolution of a Microbial Culture
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Battley, E.H. The development of direct and indirect methods for the study of the thermodynamics of microbial growth. Thermochim. Acta 1998, 309, 17–37. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Non-Equilibrium Systems: From Dissipative Structures to Order Through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Liu, J.-S.; Vojinovic, V.; Patiño, R.; Maskow, T.; von Stockar, U. A comparison of various Gibbs energy dissipation correlations for predicting microbial growth yields. Thermochim. Acta 2007, 458, 38–46. [Google Scholar] [CrossRef]
- Mäkelä, T.; Annila, A. Natural patterns of energy dispersal. Phys. Life Rev. 2010, 7, 477–498. [Google Scholar] [CrossRef] [PubMed]
- Skene, K.R. Systems theory, thermodynamics and life: Integrated thinking across ecology, organization and biological evolution. BioSystems 2024, 236, 105123. [Google Scholar] [CrossRef]
- Schaechter, M. From Growth Physiology to Systems Biology. Int. Microbiol. 2006, 9, 157–161. [Google Scholar]
- Neidhardt, F.C. Bacterial Growth: Constant Obsession with dN/dt. J. Bacteriol. 1999, 181, 7405–7408. [Google Scholar] [CrossRef]
- Swinnen, I.A.M.; Bernaerts, K.; Dens, E.J.J.; Geeraerd, A.H.; Van Impe, J.F. Predictive modelling of the microbial lag phase: A review. Int. J. Food Microbiol. 2004, 94, 137–159. [Google Scholar] [CrossRef]
- Kutalik, Z.; Razaz, M.; Baranyi, J. Connection between Stochastic and Deterministic Modelling of Microbial Growth. J. Theor. Biol. 2005, 232, 285–299. [Google Scholar] [CrossRef]
- Peleg, M.; Corradini, M.G.; Normand, M.D. The logistic (Verhulst) model for sigmoid microbial growth curves revisited. Food Res. Int. 2007, 40, 808–818. [Google Scholar] [CrossRef]
- Atolia, E.; Cesar, S.; Arjes, H.A.; Rajendram, M.; Shi, H.; Knapp, B.D.; Khare, S.; Aranda-Díaz, A.; Lenski, R.; EHuan, K.C. Environmental and physiological factors affecting high-throughput measurements of bacterial growth. mBio 2020, 11, e01378-20. [Google Scholar] [CrossRef]
- Bertrand, R.L. Lag phase is a dynamic, organized, adaptive, and evolvable period that prepares bacteria for cell division. J. Bacteriol. 2019, 201, e00697-18. [Google Scholar] [CrossRef] [PubMed]
- Ahmer, B.M.M. Cell-to-cell signalling in Escherichia coli and Salmonella enterica. Mol. Microbiol. 2004, 52, 933–945. [Google Scholar] [CrossRef] [PubMed]
- Leiphart, R.J.; Chen, D.; Peredo, A.P.; Loneker, A.E.; Janmey, P.A. Mechanosensing at Cellular Interfaces. Langmuir 2019, 35, 7509–7519. [Google Scholar] [CrossRef] [PubMed]
- Egli, T. Microbial Growth and Physiology: A Call for Better Craftsmanship. Front. Microbiol. 2015, 6, 287. [Google Scholar] [CrossRef]
- Hellingwerf, K.J.; Lolkema, J.S.; Otto, R.; Neijssel, O.M.; Stouthamer, A.H.; Harder, W.; van Dam, K.; Westerhoff, H.V. Energetics of microbial growth: An analysis of the relationship between growth and its mechanistic basis by mosaic non-equilibrium thermodynamics. FEMS Microbiol. Lett. 1982, 15, 7–17. [Google Scholar] [CrossRef]
- Westerhoff, H.V.; Lolkema, J.S.; Otto, R.; Hellingwerf, K.J. Thermodynamics of growth; non-equilibrium thermodynamics of bacterial growth; the phenomenological and the mosaic approach. Biochim. Biophys. Acta 1982, 683, 181–220. [Google Scholar] [CrossRef]
- Singh, A.; Parvin, P.; Saha, B.; Das, D. Non-equilibrium self-assembly for living matter-like properties. Nat. Rev. Chem. 2024, 8, 723–740. [Google Scholar] [CrossRef]
- Schiraldi, A. The “Growth Curve”: An Autocorrelation Effect. Appl. Microbiol. 2024, 4, 1257–1267. [Google Scholar] [CrossRef]
- Schiraldi, A. The growth curve of microbial cultures: A model for a visionary reappraisal. Appl. Microbiol. 2023, 3, 288–296. [Google Scholar] [CrossRef]
- Schiraldi, A. Microbial Growth and Decay: A Commented Review of the Model. Adv. Microbiol. 2024, 14, 1–10. [Google Scholar] [CrossRef]
- Schiraldi, A. The growth of microbial cultures complies with the laws of thermodynamics. Biophys. Chem. 2024, 307, 107177. [Google Scholar] [CrossRef] [PubMed]
- Odum, H.T. Self organization and maximum power. In Maximum Power; Hall, C.A.S., Ed.; University Press of Colorado: Niwot, CO, USA, 1995; Chapter 28; pp. 311–330. [Google Scholar]
- Liu, J.-S.; Marison, I.W.; von Stockar, U. Microbial Growth by a Net Heat Up-take: A Calorimetric and Thermodynamic Study on Acetotrophic Methanogenesis by Methanosarcina barkeri. Biotechnol. Bioeng. 2001, 75, 170–180. [Google Scholar] [CrossRef] [PubMed]
- von Stockar, U.; Maskow, T.; Liu, J.; Marison, I.W.; Patiño, R. Thermodynamics of microbial growth and metabolism: An analysis of the current situation. J. Biotechnol. 2006, 2, 517–533. [Google Scholar] [CrossRef]
- Liu, J.S.; Marison, I.W.; von Stockar, U. Anaerobic calorimetry of the growth of Lactobacillus helveticus using a highly sensitive BioRC1. J. Therm. Anal. Calorim. 1999, 56, 1191–1195. [Google Scholar] [CrossRef]
- Fessas, D.; Schiraldi, A. Isothermal calorimetry and microbial growth: Beyond modeling. J. Therm. Anal. Calorim. 2017, 130, 567–572. [Google Scholar] [CrossRef]
- England, J.L. Dissipative adaptation in driven self-assembly. Nat. Nanotechnol. 2015, 10, 919–923. [Google Scholar] [CrossRef]
- Chirife, J.; Buera, M. Water activity, water glass dynamics and the control of microbiological growth in foods. Crit. Rev. Food Sci. Nutr. 1996, 36, 465–513. [Google Scholar] [CrossRef]
- Davies, P.C.W.; Rieper, E.; Tuszynski, J.A. Self-organization and entropy reduction in a living cell. BioSystems 2013, 111, 1–10. [Google Scholar] [CrossRef]
- Schiraldi, A. Structural Relaxation and Thermodynamics of Viscous Aqueous Systems: A Simplified Reappraisal. J. Solut. Chem. 2023, 52, 367–384. [Google Scholar] [CrossRef]
- Mellefont, L.A.; McMeekin, T.A.; Ross, T. Viable count estimates of lag time responses for Salmonella typhimurium M48 subjected to abrupt osmotic shifts. Int. J. Food Microbiol. 2005, 105, 399–410. [Google Scholar] [CrossRef]
- Passot, S.; Cenard, S.; Douania, I.; Tréléa, I.C.; Fonseca, F. Critical water activity and amorphous state for optimal preservation of lyophilised lactic acid bacteria. Food Chem. 2012, 132, 1699–1705. [Google Scholar] [CrossRef]
- Bartlett, J. Alternate mutation modalities in models of population dynamics. Acad. Biol. 2024, 2, 1–11. [Google Scholar] [CrossRef]
- Lenski, R.E. What is adaptation by natural selection? Perspectives of an experimental microbiologist. PLoS Genet. 2017, 13, e1006668. [Google Scholar] [CrossRef]
- Michael, J.; Wiser, M.J.; Ribeck, N.; Lenski, R.E. Long-Term Dynamics of Adaptation in Asexual Populations. Science 2013, 342, 1364–1367. [Google Scholar]
- Baverstock, K. The gene: An appraisal. Prog. Biophys. Mol. Biol. 2021, 167, 12–17. [Google Scholar] [CrossRef]
- Annila, A. All in Action. Entropy 2010, 12, 2333–2358. [Google Scholar] [CrossRef]
- Annila, A.; Baverstock, K. Genes without prominence: A reappraisal of the foundations of biology. J. R. Soc. Interface 2014, 11, 20131017. [Google Scholar] [CrossRef]
- Wiser, M.J.; Lenski, R.E. A Comparison of Methods to Measure Fitness in Escherichia coli. PLoS ONE 2015, 10, e0126210. [Google Scholar] [CrossRef]
- Wang, P.; Robert, L.; Pelletier, J.; Dang, W.L.; Taddei, F.; Wright, A.; Jun, S. Robust Growth of Escherichia coli. Curr. Biol. 2010, 20, 1099–1103. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schiraldi, A. Short- and Long-Term Evolution of Microbial Cultures: A Thermodynamic Perspective. Int. J. Mol. Sci. 2025, 26, 4187. https://doi.org/10.3390/ijms26094187
Schiraldi A. Short- and Long-Term Evolution of Microbial Cultures: A Thermodynamic Perspective. International Journal of Molecular Sciences. 2025; 26(9):4187. https://doi.org/10.3390/ijms26094187
Chicago/Turabian StyleSchiraldi, Alberto. 2025. "Short- and Long-Term Evolution of Microbial Cultures: A Thermodynamic Perspective" International Journal of Molecular Sciences 26, no. 9: 4187. https://doi.org/10.3390/ijms26094187
APA StyleSchiraldi, A. (2025). Short- and Long-Term Evolution of Microbial Cultures: A Thermodynamic Perspective. International Journal of Molecular Sciences, 26(9), 4187. https://doi.org/10.3390/ijms26094187






