Structure of Stacked Dimers of N-Methylated Watson–Crick Adenine–Thymine Base Pairs

Abstract

The structure of two isomeric stacked dimers of Watson-Crick 9-methyladenine-1-methylthymine pairs was fully optimized using an approximate density functional theory (DFT) method augmented with an empirical dispersion interaction. The results of the calculations reveal that head-to-tail (AT-TA) and head-to-head (AT-AT) dimers possess a significantly different geometry. The structure of both complexes is stabilized by vertical C-H…O and C-H…N hydrogen bonds with the participation of the hydrogen atoms of the methyl groups. The energy of hydrogen bonding and stacking interactions was additionally calculated using the MP2/6-31G*(0.25) method. Differences in the mutual arrangement of the base pairs in two isomeric dimers lead to significant changes of intra and interstrand stacking interaction energies.

Introduction

Hydrogen bonded and stacked nucleic acid bases — adenine (A), thymine(T), guanine (G) and cytosine (C) — play a pivotal role in the structure and function of DNA [1]. They influence the formation of the secondary structure of biopolymers, the interaction with drugs and proteins, the conformational dynamics and polymorphism of DNA, etc. [2,3].

Bases in a DNA molecule are involved mainly in two types of interactions. The first one includes the formation of the Watson-Crick base pairs due to hydrogen bonding between adenine and thymine (AT pair) and guanine and cytosine (GC pair). These dimers are mainly stabilized by electrostatic interactions. The second type of interactions is represented by stacking between neighboring bases along the vertical axis of a double-stranded biopolymer. The stacking interactions mainly originate from dispersion interactions between two parallel bases. Overall H-bonded pairs of nucleic acid bases are more favored on the potential energy surface than stacked pairs, but both interactions are of equal importance in nucleic acids.

The structure and energetics of hydrogen bonded and stacked dimers of nucleic acid bases were extensively investigated using different quantum-chemical and force field methods (for the most recent and comprehensive reviews see ref. 4-6). The different nature of stabilization forces in these two types of dimers cause different approaches to their theoretical investigation. The electrostatic origin of the hydrogen bonds allows to study H-bonded complexes of bases with a wide range of quantum chemical and force field methods [4,5,6,7], and , therefore, these calculations were easily extended from base pairs to trimers, tetramers, etc. [8], studying effects of cooperativity of interactions, different ways of hydrogen bonding, non-planarity of base pairs, etc.

The significant contribution of dispersion forces into stacking interactions is a considerable challenge for computational methods, since a correct description of dispersion requires an adequate inclusion of electron correlation and an application of extended basis sets [4,5,6,9].

The computationally least expensive ab initio method covering electron correlation is second order Moller-Plesset perturbation theory (MP2), which can be applied to molecular systems of the size of DNA base pairs. However, for a quantitative accurate description higher level treatment of correlation in combination with large basis sets is required, which limits these calculations to system sizes containing few atoms. Fortunately, the effects of higher level treatment of correlation and increasing basis sets have opposite effect on the stabilization energies. Exploiting this error compensation, a cheaper computational model utilizing MP2 and the 6-31G(0.25) basis set has been proposed for the study of base pair stacking. [10], providing an accurate and reliable description of dispersion interactions. However, MP2 calculations are considerably more time and resource consuming as compared to HF and DFT methods. This limits the applicability of this method for systems larger than dimers of bases.

Empirical force field methods are widely used for the simulation of the structure and dynamics of large fragments of DNA and it has been demonstrated recently, that several force fields describe hydrogen bonding and stacking interactions between bases very accurately [7]. However, force fields do not cover the polarization of DNA bases due to interaction with each other. They also failed to reproduce some structural effects like pyramidalization of the amino group, conformational flexibility of the pyrimidine rings in DNA bases, etc [11,12].

In computational studies, the geometry of stacked dimers is usually generated in two ways: i) geometrical parameters of individual bases are optimized by ab initio methods and they are fixed to be rigid in a stacked dimer, while the mutual orientation of the bases is derived either from crystallographic data or from a set of single point calculations; ii) the geometry of the stacked dimer is optimized by force field methods. However, a recent full optimization of cytosine, uracil and thymine stacked dimers at the MP2 level of theory [13] revealed a significant deformation of the geometry of DNA bases. Such effects can not be reproduced by force field methods. However, the application of MP2 calculations for the investigation of the geometry of stacked dimers and especially of larger stacked complexes is limited because of their high computation costs.

Recently, a new quantum chemical method for the calculation of large molecules has been developed on the basis of an approximation to density functional theory [14,15]. This method can be described as a general extension of tight-binding methods to charge self-consistency. All parameters of this model are calculated from DFT, and the method is, therefore, called a self-consistent charge, density functional tight binding method (SCC-DFTB). Application of this method to various organic molecules [14,16], polypeptides, H-bonded complexes [17,18] and DNA bases [19] revealed good agreement in energetics, geometrical parameters and vibrational properties between SCC-DFTB and experimental data and results of DFT and post-Hartree-Fock methods. Recently [20], this method was complemented with an empirical dispersion energy correction (SCC-DFTB-D method) in order to reproduce the interaction energy of stacked nucleobases. The results of the calculations demonstrated very good agreement between SCC-DFTB-D and MP2 data for the energy of hydrogen bonding and stacking interactions for a wide range of nucleic acid base pairs. Another important advantage of this method is its very high computational efficiency. Therefore, the SCC-DFTB method seems to be a reasonable alternative to force field methods for calculations of large parts of DNA, for example, stacked complexes of nucleic acid bases containing more than two molecules.

Application of SCC-DFTB-D allows to analyze the optimal arrangement of base pairs in DNA as function only interactions between bases. Based on these results one can evaluate influence of backbone on orientation of base pairs in DNA. Another question is related to the deformation of bases and base pairs in stacked dimers due to the vertical interaction between stacked bases.

In the present paper we report results of quantum-chemical optimization of geometry of stacked dimers of Watson–Crick 9-methyladenine-1-methylthymine base pairs using SCC-DFTB-D methods. Two isomeric dimers are considered with head-to-head (AT-AT) and head-to-tail (AT-TA) orientation of base pairs with respect to each other. The interaction energy between nucleobases is also calculated at the MP2/6-31G*(0.25) level of theory using SCC-DFTB-D optimized geometry.

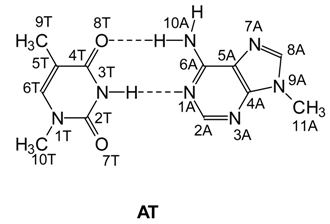
Method of Calculations

The geometry of stacked dimers was optimized by the SCC-DFTB-D method [14,15,16,17,18] without any constrains. The character of the local minima on the potential energy surface was analyzed by calculations of vibrational frequencies within the harmonic approximation using a numerical Hessian. No imaginary frequencies were found.

The energy of interaction between bases and base pairs was calculated as the difference between the energies of the dimer and individual moieties (for example, energy of interaction between two thymine molecules has been calculated as difference in energy between T1…T2 dimer and sum of energy of two thymine moieties). Additional calculations of the interaction energies were performed at the MP2 level of theory using the non-standard 6-31G*(0.25) basis set. In this case, d polarization functions with the exponent α=0.8 used in the standard 6-31G* basis set were replaced by more diffuse ones (α=0.25). All interaction energies calculated by the MP2/6-31G*(0.25) method were corrected for the basis set superposition error (BSSE) using a standard counterpoise method [21].

According to Ref. [22], a set of parameters was used in order to describe the orientation of one base pair with respect to another. Three of them are angles (twist, roll and tilt) which characterize the mutual rotation of base pairs. They describe the rotation of base pairs along the z (twist), y (roll) and x (tilt) axes. In other words, the twist angle describes the rotation of a base pair around the helical axis. The roll and tilt angles correspond to the inclination of long and short axes of base pairs. Three additional parameters describe the translation of a base pair along the same axes: rise (D_z) along the z axis, slide (D_y) along the y axis and shift (D_x) along the x axis.

The orientation of individual bases within each base pair can be described in terms of propeller twist and buckle parameters. They characterize the rotation of bases around the N3T-N1A line and the inclination of mean planes of bases with respect to each other.

Results and Discussion

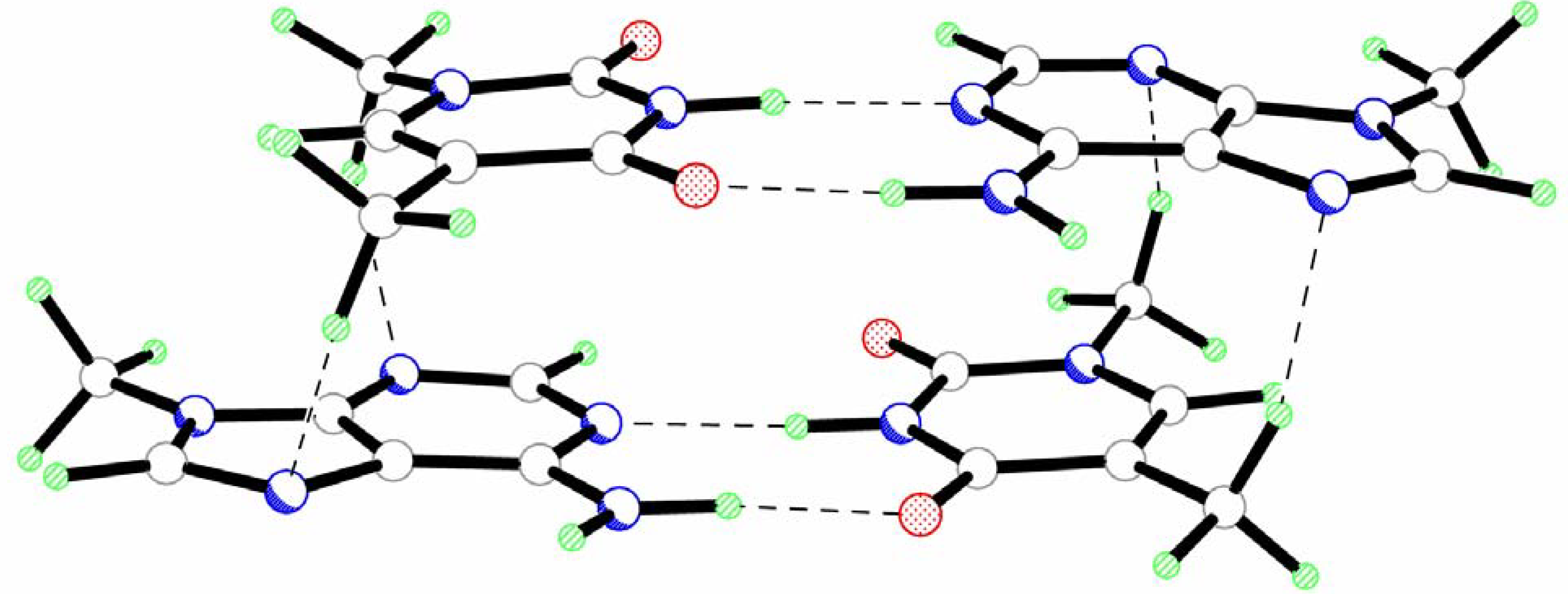
The calculated geometry of the head-to-head isomer of a stacked dimer of the AT pairs (AT-AT) is presented in Fig.1. The results of the calculations demonstrate that the values of roll and tilt angles are rather small (Table 1). This indicates that two base pairs keep an almost parallel orientation of their mean planes. However, their long axes (y axes) form an angle of about 15^o. This value is considerably smaller than the standard helix twist angle (32-45^o [1]). Nevertheless, one can assume that the rotation of two base pairs with respect to each other is an intrinsic property of stacked base pairs.

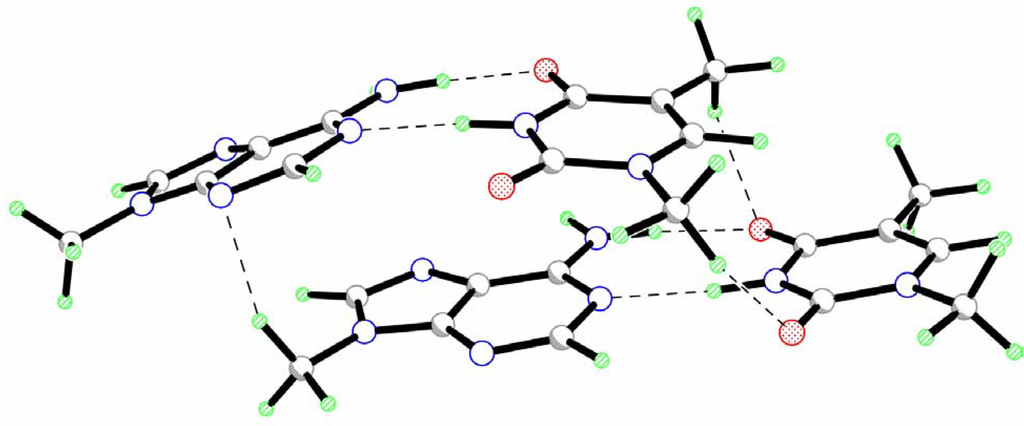
Figure 1. Geometry of the head-to-head isomer of a stacked dimer of the AT pairs (AT-AT).

Figure 1. Geometry of the head-to-head isomer of a stacked dimer of the AT pairs (AT-AT).

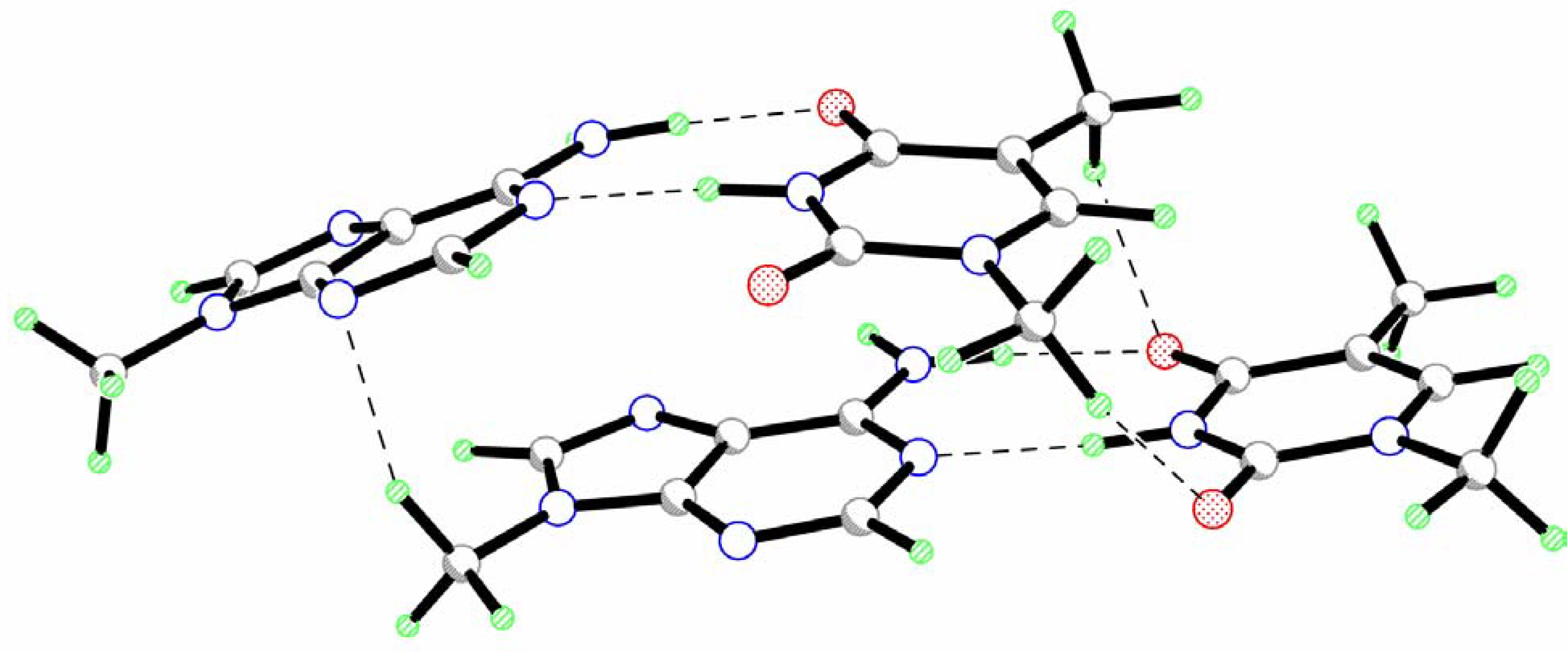
Two base pairs are significantly displaced with respect to each other toward the y axis (Table 1). Only a small shift is observed for the x axis. The analysis of intermolecular interactions within the AT-AT complex reveals the existence of several vertical hydrogen bonds formed by the hydrogen atoms of the methyl groups (Fig.1, Table 2). The presence of these H-bonds is, probably, responsible for the significant slide of one base pair along the y-axis. Such displacement creates favorable conditions for these interactions. The formation of vertical hydrogen bonds can also influence the twist angle between base pairs.

The value of the rise parameter (D_z) is unexpectedly small as compared to the standard magnitude of 3.4 Å [1]. However, as can be seen from Fig. 1 the AT-AT complex is significantly asymmetric. One base pair is only slightly perturbed as compared to the isolated AT pair (see propeller twist and buckle angles in Table 1). The second base pair is considerably buckled (Table 1). Such an arrangement of bases is, probably, caused by the sliding of this base pair with respect to the first one. As results, the peripheral parts of the bases are bounded to the first base pair by vertical hydrogen bonds while the O7T, O8T, N3T, N1A and N10A atoms of the buckled base pair are placed over negatively charged nitrogen atoms of adenine moiety of the first pair. Electrostatic repulsion between these atoms requires larger interatomic distances. This leads to the buckling of this base pair. Because of the buckled character of the second base pair the origin of the local coordinate system lies considerably lower than the mean plane of the base pair. This causes a significant decrease of the rise parameter. Therefore, the decrease of the rise parameter may be used as indicator of the buckle deformation of this base pair. In particular, such small values of the D_z were found for A-DNA [1].

Table 1. Geometrical parameters characterizing the arrangement of base pairs with respect to each other (interpair) and bases within each base pair (intrapair) in a stacked dimer and isolated AT base pair.

Parameter	AT-AT	AT-TA
Interpair
Twist, deg.	-14.9	16.1
Roll, deg.	-4.5	-11.5
Tilt, deg.	3.4	-4.6
Rise (Dz), Å	2.56	2.93
Slide (Dy), Å	-3.61	-1.55
Shift (Dx), Å	0.26	0.25
Intrapair
Propeller twist A1-T1, deg.	-6.7	8.1
Propeller twist A2-T2, deg.	5.1	8.1
Buckle A1-T1, deg.	4.8	3.5
Buckle A2-T2, deg.	24.5	3.5
Isolated pair
Propeller twist, deg.	4.8
Buckle, deg.	0.1
ΣNH2 (A)	360.0

Table 1. Geometrical parameters characterizing the arrangement of base pairs with respect to each other (interpair) and bases within each base pair (intrapair) in a stacked dimer and isolated AT base pair.

Parameter	AT-AT	AT-TA
Interpair
Twist, deg.	-14.9	16.1
Roll, deg.	-4.5	-11.5
Tilt, deg.	3.4	-4.6
Rise (Dz), Å	2.56	2.93
Slide (Dy), Å	-3.61	-1.55
Shift (Dx), Å	0.26	0.25
Intrapair
Propeller twist A1-T1, deg.	-6.7	8.1
Propeller twist A2-T2, deg.	5.1	8.1
Buckle A1-T1, deg.	4.8	3.5
Buckle A2-T2, deg.	24.5	3.5
Isolated pair
Propeller twist, deg.	4.8
Buckle, deg.	0.1
ΣNH2 (A)	360.0

Table 2. Geometrical parameters of the hydrogen bonds in stacked dimers and in isolated AT base pair.

D-H…A	H…A, Å	D-H…A, deg.
Isolated AT
O8T…H-N10A	1.861	179.4
N3T-H…N1A1	1.929	178.7
AT-AT
N10A1-H…O8T1	1.879	175.0
N3T1-H…N1A1	1.920	174.6
N10A2-H…O8T2	1.854	176.1
N3T1-H…N1A1	1.931	174.0
C9T1-H…O8T2	2.320	140.4
C10T1-H…O7T2	2.089	156.3
C11A2-H…N3A1	2.163	153.3
AT-TA
N10A1-H…O8T1	1.843	176.0
N3T1-H…N1A1	1.980	176.3
N10A2-H...O8T2	1.843	176.0
N3T1-H…N1A1	1.980	176.3
C9T1-H...N7A2	2.146	149.6
C10T1-HT1...N3A2	2.170	137.6
C9T2-H...N7A1	2.145	149.6
C10T2-H...N3A1	2.169	137.6

Table 2. Geometrical parameters of the hydrogen bonds in stacked dimers and in isolated AT base pair.

D-H…A	H…A, Å	D-H…A, deg.
Isolated AT
O8T…H-N10A	1.861	179.4
N3T-H…N1A1	1.929	178.7
AT-AT
N10A1-H…O8T1	1.879	175.0
N3T1-H…N1A1	1.920	174.6
N10A2-H…O8T2	1.854	176.1
N3T1-H…N1A1	1.931	174.0
C9T1-H…O8T2	2.320	140.4
C10T1-H…O7T2	2.089	156.3
C11A2-H…N3A1	2.163	153.3
AT-TA
N10A1-H…O8T1	1.843	176.0
N3T1-H…N1A1	1.980	176.3
N10A2-H...O8T2	1.843	176.0
N3T1-H…N1A1	1.980	176.3
C9T1-H...N7A2	2.146	149.6
C10T1-HT1...N3A2	2.170	137.6
C9T2-H...N7A1	2.145	149.6
C10T2-H...N3A1	2.169	137.6

A comparison of the geometry of an isolated AT pair and AT-AT dimer only reveals two considerable changes in the geometrical parameters. Intermolecular interaction results in the elongation of the N10A1-H…O8T1 hydrogen bond (Δl=0.028 Å). This is caused, probably, by the formation of a vertical C-H..O hydrogen bond with the participation of the O8T1 atom (Fig.1, Table 2) resulting in the weakening of the N-H…O bond. Electrostatic interactions between the amino group of adenine moiety of the buckled AT pair and the negatively charged nitrogen atoms of adenine of the other pair result in the pyramidalization of the amino group (the sum of the bond angles at the nitrogen atom is 355.4^o). The hydrogen atoms of this substituent are displaced toward the other adenine moiety.

The results of the calculations reveal that the head-to-tail stacked dimer of AT pairs (AT-TA) has a significantly more symmetric structure (Fig.2, Table 1 and Table 2). Such geometry of the AT-TA dimer is determined by the formation of two pairs of equivalent C-H…O hydrogen bonds with the participation of the hydrogen atoms of the methyl groups (Fig. 2, Table 2). Nevertheless, the analysis of interpair geometrical parameters reveals considerable twist and roll rotation of one base pair with respect to the other (Table 1). The values of these angles are even greater than for the AT-AT complex.

The formation of intermolecular C-H…O hydrogen bonds results in a significantly smaller sliding of base pairs along the y axis in AT-TA as compared to AT-AT (Table 1). The shift parameter along the x axis remains the same in both complexes.

The base pairs in the AT-TA dimer have the same geometrical parameters. The bases are slightly propeller twisted and buckled for the same angles in both pairs (Table 1). An essentially more planar geometry of the AT pairs leads to a considerable increase of the vertical separation of the base pairs. However, the value of the D_z parameter (2.93 Å) is also significantly smaller as compared to the standard value (3.4 Å). This is partly caused by the formation of vertical intermolecular hydrogen bonds in the AT-TA complex. However, SCC-DFTB-D in general tends to yield slightly smaller vertical seperatoins than MP2, as has been found for stacked base pairs Ref 20.

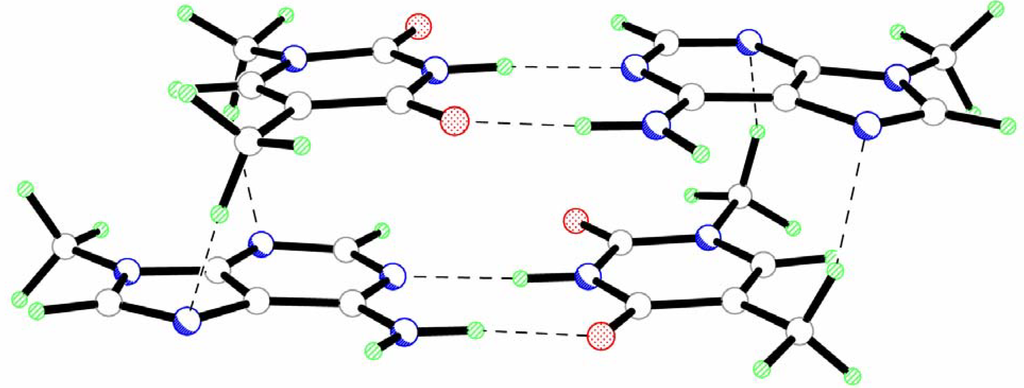
Figure 2. Geometry of the head-to-tail isomer of a stacked dimer of the AT pairs (AT-TA).

Figure 2. Geometry of the head-to-tail isomer of a stacked dimer of the AT pairs (AT-TA).

The results of the calculations demonstrate a considerable deformation of the N-H…O and N-H…N hydrogen bonds in Watson-Crick pairs of bases. A shortening of the N-H…O bond (Δl=0.018 Å) and an elongation of the N-H…N bond (Δl=0.051 Å) are observed. Contrary to the AT-AT complex, both amino groups in the AT-TA dimer adopt an almost planar configuration.

The interaction energies for both dimers were calculated at the MP2/6-31G*(0.25) level of theory using geometry optimized by the SCC-DFTB-D method (Table 3). The results of the calculations demonstrate that the energy of interaction between the hydrogen bonded bases depends on the nature of complex and geometry of the base pair within the dimer. In the case of the AT-AT complex, the energy of hydrogen bonding in the planar AT pair is slightly greater as compared to the buckled base pair (Table 3). The energy of interaction between bases in AT pairs of the AT-TA dimer is the same for both base pairs and its value is intermediate between relevant interaction energies in AT-AT. It should be noted that the values of the interaction energy in hydrogen bonded AT pairs of both dimers is about 1-3 kcal/mol higher as compared to values obtained for Watson-Crick pairs of unsubstituted [6] and methylated [23,24] adenine and thymine.

The energy of interaction between two stacked AT pairs depends on their mutual orientation in agreement with previous data [25,26]. This value is higher in the AT-AT dimer as compared to AT-TA.

The stacking interaction between bases in both dimers can be divided into intrastrand and interstrand interactions according to the location of the interacting bases [26,27]. In general, the energy of intrastrand stacking is significantly larger than the interstrand one [26,27]. Such a situation is observed for the AT-TA dimer (Table 3). The total energy for intrastrand stacking interactions (-11.64 kcal/mol) indicates a strong attraction between bases. In contrast, interstrand stacking interactions are repulsive. However, it should be noted that the energy of such interactions (+0.48 kcal/mol) is rather small (Table 3).

Opposite results are obtained for the AT-AT dimer. A significant sliding of the base pairs with respect to each other along the y axis results in a considerable increase of interstrand stacking interactions. Their total value (-5.59 kcal/mol) becomes comparable with the energy of intrastrand stacking (-7.29 kcal/mol). The main contribution to this significant increase of the interstrand stacking interaction energy is provided by the A1…T2 pair of bases (Fig. 1). It should also be noted that no repulsive interactions between bases are found in the AT-AT dimer (Table 3). The significant increase of the energy of interstrand stacking interactions is, probably, responsible for the larger value of total stacking interactions between AT pairs in the AT-AT dimer as compared to the AT-TA one.

The comparison of the total and the sum of pairwise interaction energies between bases in complexes under study (Σ(total) and Σ(pairwise) in Table 3, respectively) indicates some non-additivity in these values due to the existence of many-body corrections. The analysis of two types of interactions in dimers under consideration reveals that non-additivity is due to the stacking interactions (Table 3) in agreement with previous data [27]. Many-body corrections are rather small for both dimers, but they have opposite signs (+0.1 kcal/mol for AT-AT and -0.16 for AT-TA, respectively).

Table 3. Energy (kcal/mol) of intermolecular interactions between different moieties of stacked dimers and relative energies of dimers (ΔE_rel).

	AT-AT		AT-TA
Interacting moieties, X…Y	EDFTB	EMP2	EDFTB	EMP2
AT1…AT2	-19.92	-12.79	-23.75	-11.33
A1…T1	-12.28	-14.04	-12.32	-13.82
A2…T2	-12.22	-13.65	-12.32	-13.82
A1…A2	-7.48	-4.83	+0.03	+0.17
T1…T2	-5.21	-2.46	+0.74	+0.31
A1…T2	-7.20	-5.44	-12.15	-5.82
A2…T1	-0.17	-0.15	-12.14	-5.82
A1A2…T1T2	-31.72	-33.19	-24.09	-39.44
Σ(total)a	-44.42	-40.47	-48.38	-38.96
Σ(pairwise)b	-44.56	-40.57	-48.16	-38.80
Σ(stack)c	-20.06	-12.88	-23.52	-11.16
ΔErel	3.01	0.82	0	0

^a The energy of total interactions between bases is calculated as the difference between the total energy of the system and the sum of the individual energies of each base. ^b Sum of energies of interactions between all possible pairs of bases. ^c Sum of stacking interaction energies between all pairs of bases.

Table 3. Energy (kcal/mol) of intermolecular interactions between different moieties of stacked dimers and relative energies of dimers (ΔE_rel).

	AT-AT		AT-TA
Interacting moieties, X…Y	EDFTB	EMP2	EDFTB	EMP2
AT1…AT2	-19.92	-12.79	-23.75	-11.33
A1…T1	-12.28	-14.04	-12.32	-13.82
A2…T2	-12.22	-13.65	-12.32	-13.82
A1…A2	-7.48	-4.83	+0.03	+0.17
T1…T2	-5.21	-2.46	+0.74	+0.31
A1…T2	-7.20	-5.44	-12.15	-5.82
A2…T1	-0.17	-0.15	-12.14	-5.82
A1A2…T1T2	-31.72	-33.19	-24.09	-39.44
Σ(total)a	-44.42	-40.47	-48.38	-38.96
Σ(pairwise)b	-44.56	-40.57	-48.16	-38.80
Σ(stack)c	-20.06	-12.88	-23.52	-11.16
ΔErel	3.01	0.82	0	0

^a The energy of total interactions between bases is calculated as the difference between the total energy of the system and the sum of the individual energies of each base. ^b Sum of energies of interactions between all possible pairs of bases. ^c Sum of stacking interaction energies between all pairs of bases.

Comparing the interaction energies of SCC-DFTB-D and MP2 (Table 3), the largest differences occur for the stacking contributions. These differences can be explained by the use of SCC-DFTB-D geometries to calculate the MP2 energies. As has been shown recently, the stacking interaction energies of base pairs agree very well between the two methods, if the geometries are optimized for the respective method. SCC-DFTB-D underestimates the stacking distances of base pairs by about 0.1-0.2 Å [20]. MP2 stacking energies evaluated for SCC-DFTB-D geometries will, therefore, be significantly lower (in absolute values) than for MP2 geometries. If the geometries of the AT-TA and AT-AT conformers would be optimized at the MP2 level of theory, which is computationally prohibitive at the moment, the MP2 interaction energies would agree better with the SCC-DFTB-D ones than in the present case, where the rise parameter is probably underestimated by the SCC-DFTB-D method.

However, despite the deviation in the absolute values of the interaction energies, both methods describe the same trends for the interaction of the bases. In particular both methods indicate that the AT-AT dimer is less stable than the AT-TA one (Table 3).

Conclusion

The results of our calculations reveal that two isomeric stacked dimers of Watson-Crick 9-methyladenine-1-methylthymine pairs possess significantly different geometries. The head-to-tail dimer (AT-TA) adopts nearly a symmetric structure while the one of the AT pair in the head-to-head complex (AT-AT) is significantly buckled and displaced along the long axis of the base pair. The structure of both dimers is stabilized by vertical C-H…O and C-H…N hydrogen bonds with the participation of the hydrogen atoms of the methyl groups.

Based on these data we can assume that arrangement of stacked AT dimers in DNA molecules is significantly influenced by backbone in the case of head-to-head orientation. This should lead to an appearance of some steric strain in the relevant part of macromolecule.

Unlike previous calculations for stacked dimers of pyrimidine nucleobases [10] the six-membered ring in thymine moieties has a planar conformation in both dimers. This may be caused by replacement of the hydrogen atom at the N1T by methyl group as it was suggested earlier [10]. However, it was demonstrated [27] that formation of the hydrogen bonds in base pairs results in decrease of conformational flexibility of pyrimidine rings. Therefore, we can suggest that hydrogen bonding and stacking interactions favor a planar geometry of thymine moiety.

The displacement of one AT base pair with respect to the other in the AT-AT dimer results in a significant increase of the interstrand stacking energy as compared to AT-TA. Non-additivity of stacking interactions is observed for both complexes, but many-body corrections are rather small (less than 0.2 kcal/mol). The AT-AT dimer has a higher energy as compared to AT-TA despite of the greater value of the stacking interaction energy between the two base pairs.