Step Response Characteristics of Polymer/Ceramic Pressure-Sensitive Paint
Abstract
:1. Introduction

2. Analytical Model and Numerical Implementation

3. Experimental Framework


4. Results and Discussion
4.1. Experimental Results and Determination of Model Parameters
| Sample | Thickness | Roughness | Sensitivity | |
|---|---|---|---|---|
| Typical | 44.12 μm | 3.16 μm | 7.30 µs | 0.65 |
| Rough | 104.2 μm | 23.85 μm | 6.75 µs | 0.64 |




| Sample | Parameter | Step Response Study | Frequency Response Study [5] |
|---|---|---|---|
| Typical roughness with PtTFPP | Lifetime (µs) | 7.30 | 7.04 |
| D1 (m2/s) | 5 × 10–8 | 9.78 × 10−8 | |
| Hiding Factor (1/m) | 1.67 × 106 | 1.67 × 106 | |
| Larger roughness with PtTFPP | Lifetime (µs) | 6.75 | 6.75 |
| D1 (m2/s) | 2.5 × 10–6 | 7.51 × 10−6 | |
| Hiding Factor (1/m) | 3.13 × 105 | 3.13 × 105 | |
| Typical roughness with RuDPP | Lifetime (µs) | 2.00 | N/A |
| D1 (m2/s) | 5 × 10–8 | N/A | |
| Hiding Factor (1/m) | 2.90 × 106 | N/A |
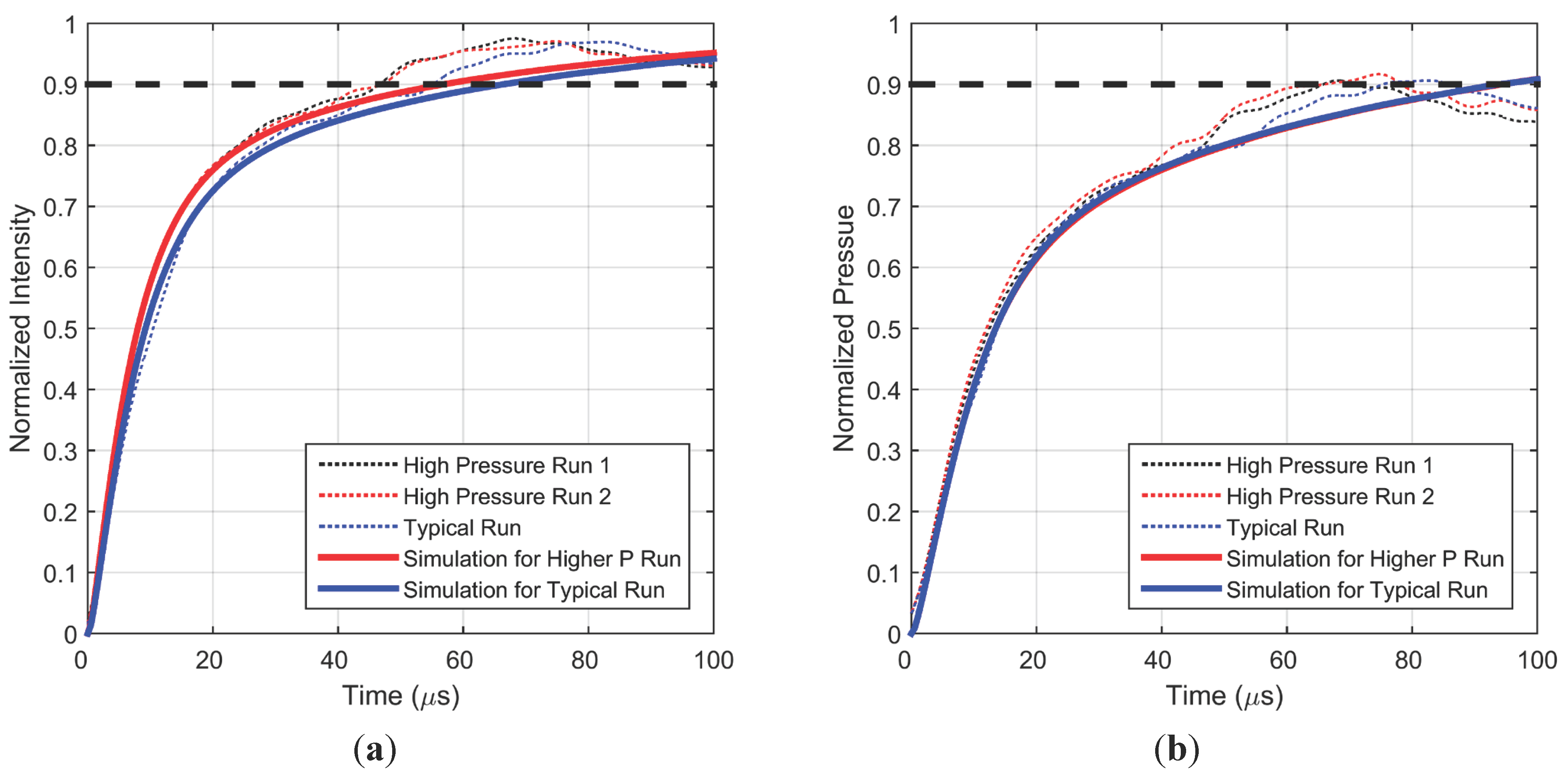
4.2. Numerical Simulations
4.2.1. Estimate of Response Time


4.2.2. Origin of Differences in Intensity and Pressure Response

4.2.3. Effects of Parameters




5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, T.; Sullivan, J.P. Pressure and Temperature Sensitive Paints; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bell, J.H.; Schairer, E.T.; Hand, L.A.; Mehta, R.D. Surface pressure measurements using luminescent coatings. Annu. Rev. Fluid Mech. 2001. [Google Scholar] [CrossRef]
- Gregory, J.W.; Asai, K.; Kameda, M.; Liu, T.; Sullivan, J.P. A review of pressure-sensitive paint for high-speed and unsteady aerodynamics. J. Aerosp. Eng. 2007, 222, 249–290. [Google Scholar] [CrossRef]
- Gregory, J.W.; Sakaue, H.; Liu, T.; Sullivan, J.P. Fast pressure-sensitive paint for flow and acoustic diagnostics. Annu. Rev. Fluid Mech. 2014, 46, 303–330. [Google Scholar] [CrossRef]
- Pandey, A.; Gregory, J.W. Frequency response characteristics of polymer/ceramic pressure-sensitive paint. AIAA J. 2015. [Google Scholar] [CrossRef]
- Sugimoto, T.; Kitashima, S.; Numata, D.; Nagai, H.; Asai, K. Characterization of frequency response of pressure-sensitive paints. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012.
- Kitashima, S.; Numata, D.; Asai, K. Characterization of pressure-sensitive paint containing ceramic particles. In Proceedings of the 16th International Symposium on Flow Visualization, Okinawa, Japan, 24–27 June 2014.
- Kameda, M.; Seki, H.; Makoshi, T.; Amao, Y.; Nakakita, K. A fast-response pressure sensor based on a dye-adsorbed silica nanoparticle film. Sens. Actuators B Chem. 2012, 171, 343–349. [Google Scholar] [CrossRef]
- McMullen, R.M.; Huynh, D.P.; Gregory, J.W.; Crafton, J. Dynamic calibrations for fast response porous polymer/ceramic pressure-sensitive paint. In Proceedings of the AIAA Ground Testing Conference, San Diego, CA, USA, 24–26 June 2013.
- Kameda, M. Effect of luminescence lifetime on the frequency response of fast-response pressure-sensitive paints. Trans. Jpn. Soc. Mech. Eng. Ser. B 2012, 78, 1942–1950. [Google Scholar] [CrossRef]
- Baron, A.E.; Danielson, J.D.S.; Gouterman, M.; Wan, J.R.; Callis, J.B.; McLachlan, B. Submillisecond response times of oxygen‐quenched luminescent coatings. Rev. Sci. Instrum. 1993, 64, 3394–3402. [Google Scholar] [CrossRef]
- Carroll, B.E.; Abbitt, J.D.; Likas, E.W.; Morris, M.J. Step response of pressure-sensitive paints. AIAA J. 1996, 34, 521–526. [Google Scholar] [CrossRef]
- Asai, K.; Nakakita, K.; Kameda, M.; Teduka, K. Recent topics in fast-responding pressure-sensitive paint technology at National Aerospace Laboratory. In Proceedings of the Instrumentation in Aerospace Simulation Facilities, 19th International Congress on ICIASF 2001, Cleveland, OH, USA, 27–30 August 2001.
- Sakaue, H.; Sullivan, J.P. Time response of anodized aluminum pressure-sensitive paint. AIAA J. 2001, 39, 1944–1949. [Google Scholar] [CrossRef]
- Kameda, M.; Tezuka, N.; Hangai, T.; Asai, K.; Nakakita, K.; Amao, Y. Adsorptive pressure-sensitive coatings on porous anodized aluminium. Meas. Sci. Technol. 2004, 15. [Google Scholar] [CrossRef]
- Sakaue, H.; Morita, K.; Iijima, Y.; Sakamura, Y. Response time scales of anodized-aluminum pressure-sensitive paints. Sens. Actuators A Phys. 2013, 199, 74–79. [Google Scholar] [CrossRef]
- Egami, Y.; Ueyama, J.; Furukawa, S.; Kameya, T.; Matsuda, Y.; Yamaguchi, H.; Niimi, T. Development of fast response bi-luminophore pressure-sensitive paint by means of an inkjet printing technique. Meas. Sci. Technol. 2015, 26. [Google Scholar] [CrossRef]
- Sakaue, H.; Gregory, J.W.; Sullivan, J.P.; Raghu, S. Porous pressure-sensitive paint for characterizing unsteady flowfields. AIAA J. 2002, 40, 1094–1098. [Google Scholar] [CrossRef]
- Scroggin, A.M.; Slamovich, E.B.; Crafton, J.W.; Lachendo, N.; Sullivan, J.P. Porous polymer/ceramic composites for luminescent-based temperature and pressure measurement. Mater. Res. Soc. Proc. 1999, 560, 347–352. [Google Scholar] [CrossRef]
- Gregory, J.W. Porous pressure-sensitive paint for measurement of unsteady pressures in turbomachinery. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004.
- Gregory, J.W.; Sullivan, J.P. Effect of quenching kinetics on unsteady response of pressure-sensitive paint. AIAA J. 2006, 44, 634–645. [Google Scholar] [CrossRef]
- Pandey, A.; Gregory, J.W. Estimating Response Time of Polymer/Ceramic Pressure Sensitive Paint. In Proceedings of the 10th Pacific Symposium on Flow Visualization and Image Processing, Naples, Italy, 15–18 June 2015.
- Crank, J. The Mathematics of Diffusion; Oxford University Press: London, UK, 1956. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, A.; Gregory, J.W. Step Response Characteristics of Polymer/Ceramic Pressure-Sensitive Paint. Sensors 2015, 15, 22304-22324. https://doi.org/10.3390/s150922304
Pandey A, Gregory JW. Step Response Characteristics of Polymer/Ceramic Pressure-Sensitive Paint. Sensors. 2015; 15(9):22304-22324. https://doi.org/10.3390/s150922304
Chicago/Turabian StylePandey, Anshuman, and James W. Gregory. 2015. "Step Response Characteristics of Polymer/Ceramic Pressure-Sensitive Paint" Sensors 15, no. 9: 22304-22324. https://doi.org/10.3390/s150922304
APA StylePandey, A., & Gregory, J. W. (2015). Step Response Characteristics of Polymer/Ceramic Pressure-Sensitive Paint. Sensors, 15(9), 22304-22324. https://doi.org/10.3390/s150922304






