Biosensing by WGM Microspherical Resonators
Abstract
:1. Introduction
2. WGM Resonators
2.1. Different Types of WGM Resonators
2.2. Coupling Systems
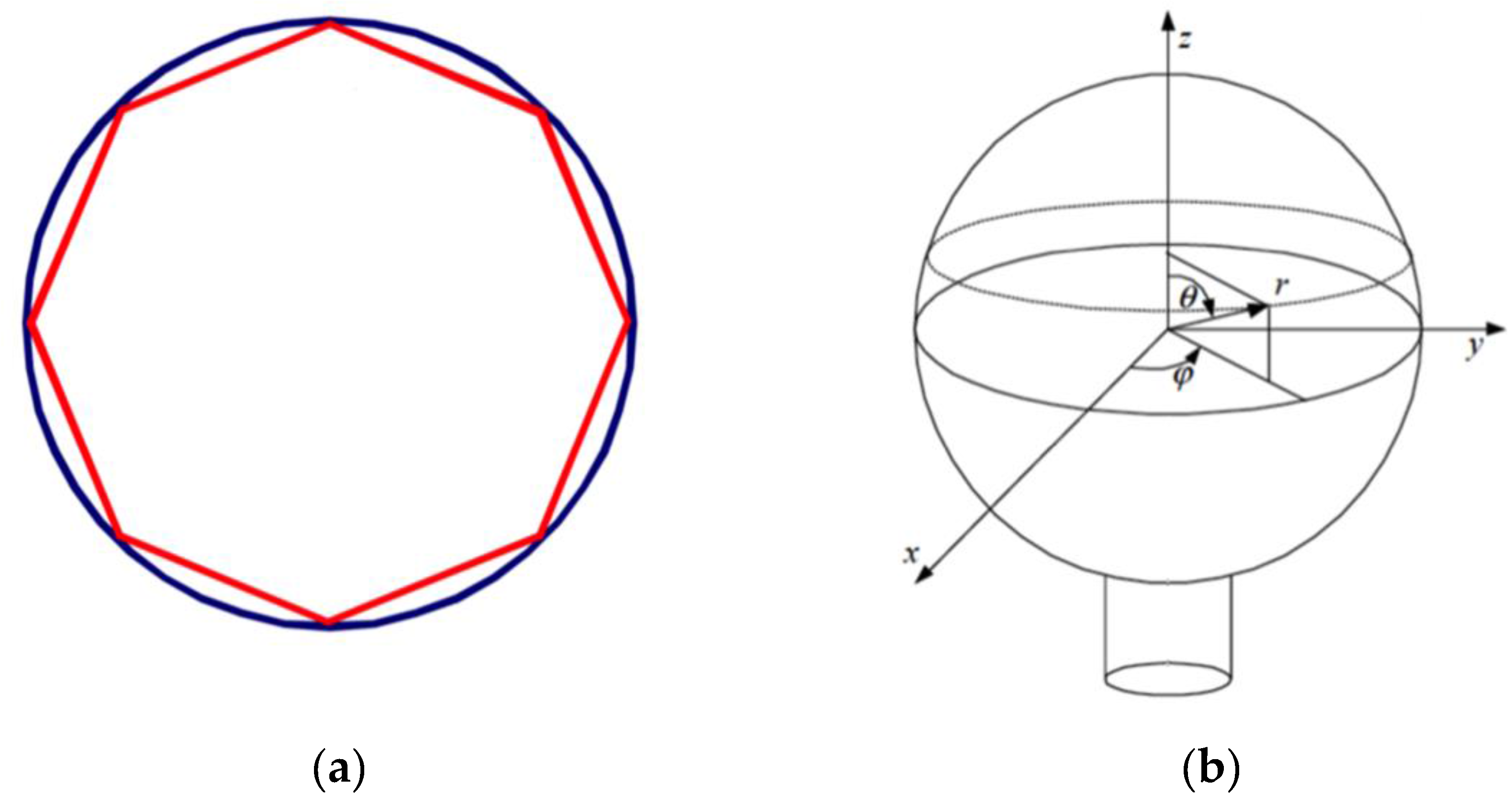
3. Microspherical Resonators
3.1. Polymer Microspheres
3.2. Glass Microspheres
3.2.1. Melting of Glass Microspheres
3.2.2. Sol-Gel Glass Microspheres
3.2.3. Crystalline Microspheres
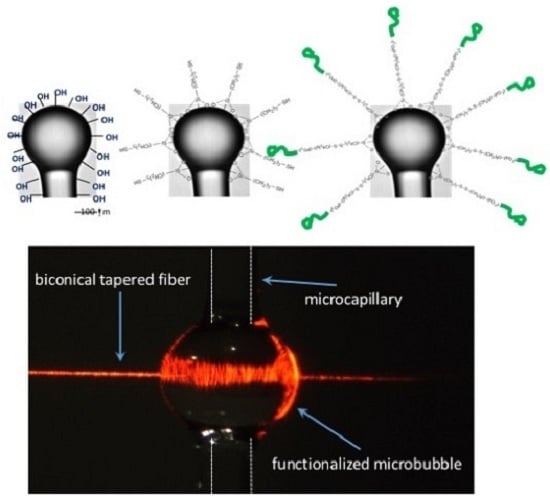
3.3. Microbubbles
4. Surface Functionalization
4.1. Selection of the Biorecognition Element
4.2. Covalent Functionalization Techniques
5. Biosensing by WGM-MSR: State of the Art
6. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
Abbreviations
| APD | Avalanche photo diode |
| ARC | Asymmetric resonant cavity |
| GFP | Green fluorescent protein |
| LCORR | Liquid core optical ring resonator |
| MBR | Micro-bubble resonator |
| MDPI | Multidisciplinary Digital Publishing Institute |
| OMR | Optical microring resonator |
| PBS | Phosphate-buffered saline |
| PDMS | Polydimethylsiloxane |
| PMMA | Poly(methyl methacrylate) |
| RIU | Refractive index unit |
| r.m.s. | Root mean square |
| TEM | Transmission electronic microscope |
| WGM | Whispering gallery mode |
| WGMR | Whispering gallery mode resonator |
| YIG | Yttrium iron garnet |
References
- Chang, R.K.; Campillo, A.J. Optical Processes in Microcavities; World Scientific: Singapore, 1996. [Google Scholar]
- Vahala, K. Optical Microcavities; World Scientific: Singapore, 2004. [Google Scholar]
- Kavokin, A.; Baumberg, J.; Malpuech, G.; Lauss, F.P. Microcavities; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Rayleigh, L. The problem of whispering gallery. Sci. Pap. 1912, 5, 617–620. [Google Scholar]
- Richtmyer, R.D. Dielectric resonators. J. Appl. Phys. 1939, 10, 391–398. [Google Scholar] [CrossRef]
- Wu, J.H.; Ang, L.K.; Liu, A.Q.; Teo, H.G.; Lu, C. Tunable high-Q photonic-bandgap Fabry–Perot resonator. J. Opt. Soc. Am. B 2005, 22, 1770–1777. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Heebner, J.; Grover, R.; Ibrahim, T. Optical Microresonators; Springer: Berlin, Germany, 2007. [Google Scholar]
- Matsko, A. Practical Applications of Microresonators in Optics and Photonics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Boriskina, S.V.; Benson, T.M.; Sewell, P.; Nosich, A.I. Tuning of Elliptic Whispering-Gallery-Mode Microdisk Waveguide Filters. J. Lightwave Technol. 2003, 21, 1987–1995. [Google Scholar] [CrossRef]
- Mohageg, M.; Savchenkov, A.; Maleki, L. High-Q optical whispering gallery modes in elliptical LiNbO3 resonant cavities. Opt. Express 2007, 15, 4869–4875. [Google Scholar] [CrossRef] [PubMed]
- Nockel, J.U.; Stone, A.D. Ray and wave chaos in asymmetric resonant optical cavities. Nature 1997, 385, 45–47. [Google Scholar] [CrossRef]
- Podolskiy, V.A.; Narimanov, E.E. Chaos-assisted tunneling in dielectric microcavities. Opt. Lett. 2005, 30, 474–476. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.L.; ShuShu, F.J.; Sun, F.W.; Gong, Z.J.; Han, Z.F.; Guo, G.C. Theory of free space coupling to high-Q whispering gallery modes. Opt. Express 2013, 21, 9982–9995. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.F.; Jiang, X.F.; Cui, Y.L.; Shao, L.; Xiao, Y.F. Dynamical tunneling-assisted coupling of high-Q deformed microcavities using a free-space beam. Phys. Rev. 2013, 88, 023810. [Google Scholar] [CrossRef]
- Ballard, Z.; Baaske, M.D.; Vollmer, F. Stand-Off Biodetection with Free-Space Coupled Asymmetric Microsphere Cavities. Sensors 2015, 15, 8968–8980. [Google Scholar] [CrossRef] [PubMed]
- Arnold, S.; Ramjit, R.; Keng, D.; Kolchenko, V.; Teraoka, I. MicroParticle photophysics illuminates viral bio-sensing. Faraday Discuss. 2008, 137, 65. [Google Scholar] [CrossRef] [PubMed]
- Righini, G.; Dumeige, Y.; Feron, P.; Ferrari, M.; Nunzi Conti, G.; Soria, S.; Ristiić, D. Whispering gallery mode microresonators: Fundamentals and applications. Riv. Nuovo Cimento 2011, 34, 435. [Google Scholar]
- Soria, S.; Berneschi, S.; Brenci, M.; Cosi, F.; Conti, G.N.; Pelli, S.; Righini, G.C. Optical Microspherical Resonators for Biomedical Sensing. Sensors 2011, 11, 785–805. [Google Scholar] [CrossRef] [PubMed]
- Chiasera, A.; Dumeige, Y.; Féron, P.; Ferrari, M.; Jestin, Y.; Conti, G.N.; Pelli, S.; Soria, S.; Righini, G. Spherical whispering-gallery-mode microresonators. Laser Photonics Rev. 2010, 4, 457–482. [Google Scholar] [CrossRef]
- Foreman, M.R.; Swaim, J.D.; Vollmer, F. Whispering Gallery Mode Sensors. Adv. Opt. Photonics 2015, 7, 168–240. [Google Scholar] [CrossRef] [PubMed]
- Gorodetsky, M.; Savchenkov, A.; Ilchenko, V. Ultimate Q of optical microsphere resonators. Opt. Lett. 1996, 21, 453–455. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, A.; Wang, S.; Clarke, J.; Ja, S.J.; Goad, D.; Wald, L.; Flood, E.M.; Knobbe, E.; Hryniewicz, J.; Chu, S.; et al. A universal biosensing platform based on optical micro-ring resonators. Biosens. Bioelectron. 2008, 23, 939–944. [Google Scholar] [CrossRef] [PubMed]
- Krioukov, E.; Klunder, D.; Driessen, A.; Greve, J.; Otto, C. Sensor based on an integrated optical microcavity. Opt. Lett 2002, 27, 512–514. [Google Scholar] [CrossRef] [PubMed]
- Vos, K.D.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef] [PubMed]
- Chao, C.Y.; Fung, W.; Guo, L. Polymer microring resonators for biochemical sensing applications. J. Sel. Top. Quantum Electron. 2006, 12, 134–142. [Google Scholar] [CrossRef]
- Girault, P.; Lorraina, N.; Lemaitre, J.; Poffo, L.; Guendouz, M.; Hardy, I.; Gadonna, M.; Gutierrez, A.; Bodiou, L.; Charrier, J. Racetrack micro-resonators based on ridge waveguides made of porous silica. Opt. Mater. 2015, 50, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Guider, R.; Gandolfi, D.; Chalyan, T.; Pasquardini, L.; Samusenko, A.; Pucker, G.; Pederzolli, C.; Pavesi, L. Design and Optimization of SiON Ring Resonator-Based Biosensors for Aflatoxin M1 Detection. Sensors 2015, 15, 17300–17312. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.; Mai, M.; Grossmann, T.; Wienhold, T.; Hauser, M.; Mappes, T.; Kalt, H. High-Q polymer resonators with spatial controlled phot-funcionalization for biosensing applications. Appl. Phys. Lett. 2013, 102, 121108. [Google Scholar] [CrossRef]
- Gandolfi, D.; Ramiro-Manzano, F.; Aparicio Rebollo, F.; Ghulinyan, M.; Pucker, G.; Pavesi, L. Role of edge inclination in an optical microdisk resonator for label-free sensing. Sensors 2015, 15, 4796–4809. [Google Scholar] [CrossRef] [PubMed]
- Tien, M.C.; Bauters, J.F.; Heck, M.J.R.; Spencer, D.T.; Blumenthal, D.J.; Bowers, J.E. Ultra-high quality factor planar Si3N4 ring resonators on Si substrates. Opt. Express 2011, 19, 13551–13556. [Google Scholar] [CrossRef] [PubMed]
- Soltani, M.; Yegnanarayanan, S.; Adibi, A. Toward ultimate miniaturization of high Q silicon traveling-wave microresonators. Opt. Express 2010, 18, 19541–19557. [Google Scholar] [CrossRef] [PubMed]
- Maximov, M.V.; Kryzhanovskaya, N.V.; Nadtochiy, A.M.; Moiseev, E.I.; Shostak, I.I.; Bogdanov, A.A.; Sadrieva, Z.F.; Zhukov, A.E.; Lipovskii, A.A.; Karpov, D.V.; et al. Ultrasmall microdisk and microring lasers based on InAs/InGaAs/GaAs quantum dots. Nanoscale Res. Lett. 2014, 9, 657. [Google Scholar] [CrossRef] [PubMed]
- Kryzhanovskaya, N.V.; Zhukov, A.E.; Maximov, M.V.; Moiseev, E.I.; Shostak, I.I.; Kudashova, Y.V.; Kulagina, M.M.; Lipovskii, A.A.; Korpijärvi, V.M.; Karjalainen, H.; et al. Ultrasmall microdisk and microring lasers. In Proceedings of the OSA Conference on Lasers and Electro-Optics, Munich, Germany, 21–25 June 2015.
- Armani, D.K.; Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Ultra-high-Q toroid microcavity on a chip. Nature 2003, 421, 925–928. [Google Scholar] [CrossRef] [PubMed]
- Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Demonstration of ultra-high-Q small mode volume toroid microcavities on a chip. Appl. Phys. Lett. 2004, 85, 6113–6115. [Google Scholar] [CrossRef]
- Choi, H.S.; Armani, A.M. Thermal nonlinear effects in hybrid optical microresonators. Appl. Phys. Lett. 2010, 97, 223306. [Google Scholar] [CrossRef]
- Spillane, S.M.; Kippenberg, T.J.; Vahala, K.J.; Goh, K.W.; Wilcut, E.; Kimble, H.J. Ultrahigh-Q toroidal microresonators for cavity quantum electrodynamics. Phys. Rev. A 2005, 71, 013817. [Google Scholar] [CrossRef]
- White, I.M.; Oveys, H.; Fan, X.; Smith, T.L.; Zhang, J. Integrated multiplexed biosensors based on liquid core optical ring resonators and antiresonant reflecting optical waveguides. Appl. Phys. Lett. 2006, 49, 191106. [Google Scholar] [CrossRef]
- Zamora, V.; Diez, A.; Andres, M.V.; Gimeno, B. Cylindrical optical microcavities: Basic properties and sensor applications. Photonics. Nanostruct.—Fundam. Appl. 2010. [Google Scholar] [CrossRef]
- Sumetsky, M.; Dulashko, Y.; Windeler, R.S. Optical microbubble resonator. Opt. Lett. 2010, 35, 898–900. [Google Scholar] [CrossRef] [PubMed]
- Nunzi Conti, G.; Barucci, A.; Berneschi, S.; Brenci, M.; Cosi, F.; Farnesi, D.; Pelli, S.; Righini, G.; Soria, S. Coupling approaches and new geometries in whispering-gallery-mode resonators. Proc. SPIE 2012, 8236, 82360V. [Google Scholar]
- Panitchob, Y.; Murugan, G.S.; Zervas, M.N.; Horak, P.; Berneschi, S.; Pelli, S.; Conti, G.N.; Wilkinson, J.S. Whispering gallery mode spectra of channel waveguide coupled microspheres. Opt. Express 2008, 16, 11066. [Google Scholar] [CrossRef] [PubMed]
- Laine, J.P.; Little, B.E.; Lim, D.R.; Tapalian, H.C.; Kimerling, L.C.; Haus, H.A. Microsphere Resonator Mode Characterization by Pedestal Anti-Resonant Reflecting Waveguide Coupler. IEEE Photonics Technol. Lett. 2000, 12, 1004–1006. [Google Scholar] [CrossRef]
- Lin, Y.; Ilchenko, V.; Nadeau, J.; Maleki, L. Biochemical detection with optical whispering-gallery resonators. Proc. SPIE 2007, 6452, 64520U. [Google Scholar]
- Farnesi, D.; Chiavaioli, F.; Righini, G.; Soria, S.; Trono, C.; Jorge, P.; Conti, G.N. Long period grating-based fiber coupler to whispering gallery mode resonators. Opt. Lett. 2014, 39, 6525–6528. [Google Scholar] [CrossRef] [PubMed]
- Farnesi, D.; Chiavaioli, F.; Righini, G.; Soria, S.; Trono, C.; Baldini, F.; Conti, G.N. Quasi distributed and wavelegnth selective addressing of optical microresonators based on long period fiber gratings. Opt. Express 2015, 23, 21175–21180. [Google Scholar] [CrossRef] [PubMed]
- Mie, G. Beitung zur optik trüber melien, speziell kolloïdaler metallosungen. Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Observation of Resonances in the Radiation Pressure on Dielectric Spheres. Phys. Rev. Lett. 1977, 38, 1351–1354. [Google Scholar] [CrossRef]
- Benner, R.E.; Barber, P.W.; Owen, J.F.; Chang, R.K. Observation of structure resonances in the fluorescence spectra from microspheres. Phys. Rev. Lett. 1980, 44, 475–478. [Google Scholar] [CrossRef]
- Tzeng, H.; Long, M.; Chang, R.; Barber, P.W. Laser-induced shape distortions of flowing droplets deduced from morphology-dependent resonances in fluorescence spectra. Opt. Lett. 1985, 10, 209–211. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Pitwon, R.; Feng, J. Polymer Photonics and Its Applications—Special Issue. Opt. Commun. 2016, 362, 1–114. [Google Scholar] [CrossRef]
- Meziane, F.; Raimbault, V.; Hallil, H.; Joly, S.; Conédéra, V.; Lachaud, J.; Béchou, L.; Rebière, D.; Dejous, C. Study of a polymer optical microring resonator for hexavalent chromium sensing. Sens. Actuators B Chem. 2015, 209, 1049–1056. [Google Scholar] [CrossRef]
- Aldea, A.; Albu, A.M.; Rau, I. New polymeric materials for photonic applications: Preliminary investigations. Opt. Mater. 2016, 56, 90–93. [Google Scholar] [CrossRef]
- Leong, W.; Wang, D.A. Cell-laden Polymeric Microspheres for Biomedical Applications. Trends Biotechnol. 2015, 33, 653–666. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, H. Functional polymer microspheres. Prog. Polym. Sci. 2000, 25, 1171–1210. [Google Scholar] [CrossRef]
- Ioppolo, T.; Kozhevnikov, M.; Stepaniuk, V.; Otugen, M.; Sheverev, V. Micro-optical force sensor concept based on whispering gallery mode resonators. Appl Opt. 2008, 47, 3009–3014. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.H.; He, L.; Xiao, Y.F.; Gaddam, V.R.; Ozdemir, S.K.; Han, Z.F.; Guo, G.C.; Yang, L. Fabrication of high-Q polydimethylsiloxane optical microspheres for thermal sensing. Appl. Phys. Lett. 2009, 94, 231119. [Google Scholar] [CrossRef]
- Ozin, G.A.; Arsenault, A.C.; Cademartiri, L. Nanochemistry: A Chemical Approach to Nanomaterials; Royal Society of Chemistry: Cambridge, UK, 2009. [Google Scholar]
- Li, H.; Lei, L.; Zeng, Q.; Shi, J.; Luo, C.; Ji, H.; Ouyang, Q.; Chen, Y. Laser emission from dye doped microspheres produced on a chip. Sens. Actuators B Chem. 2010, 145, 570–574. [Google Scholar] [CrossRef]
- Song, J.S.; Tronc, F.; Winnik, M.A. Monodisperse, controlled micron-size dye-labeled polystyrene particles by two-stage dispersion polymerization. Polymer 2006, 47, 817–825. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Hao, S.; Qiang, L.; Zhang, Y. Whispering gallery modes of dye-doped polymer microspheres in microtube. Opt. Commun. 2015, 354, 66–70. [Google Scholar] [CrossRef]
- Vanga, S.K.; Nalla, V.; Bettiol, A.A. Polymer microlasers with a suspended cavity design. Opt. Mater. 2015, 42, 144–147. [Google Scholar] [CrossRef]
- Fantini, D.; Zanetti, M.; Costa, L. Polystyrene microspheres and nanospheres produced by electrospray. Macromol. Rapid Commun. 2006, 27, 2038–2042. [Google Scholar] [CrossRef]
- Berkland, C.; Kim, K.; Pack, D.W. Fabrication of PLG microspheres with precisely controlled and monodisperse size distributions. J. Controll. Release 2001, 73, 59–74. [Google Scholar] [CrossRef]
- Vernooy, D.W.; Ilchenko, V.S.; Mabuchi, H.; Streed, E.W.; Kimble, H.J. High-Q measurements of fused-silica microspheres in the near infrared. Opt. Lett. 1998, 23, 247–249. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Song, F.; Jiang, S.; Peyghambarian, N.; Kuwata-Gonokami, M.; Xu, L. Fiber-taper-coupled L-band Er3+-doped tellurite glass microsphere laser. Appl. Phys. Lett. 2003, 82, 1497. [Google Scholar] [CrossRef]
- Miura, K.; Tanaka, K.; Hirao, K. Laser oscillation on both the 4F3/2-4 I11/2 et 4F3/2-4 I13/2 transitions on Nd3+ ions using a fluoride glass microsphere. J. Non Cryst. Solids 1997, 213–214, 276. [Google Scholar] [CrossRef]
- Lissillour, F.; Ameur, K.A.; Dubreuil, N.; Stephan, G.M.; Poulain, M. Whispering-gallery-mode Nd-ZBLAN microlasers at 1.05 μm. Proc. SPIE 1998, 3416, 150. [Google Scholar]
- Conti, G.N.; Chiasera, A.; Ghisa, L.; Berneschi, S.; Brenci, M.; Dumeige, Y.; Pelli, S.; Sebastiani, S.; Féron, P.; Ferrari, M.; et al. Spectroscopic and lasing properties of Er3+-doped glass microspheres. J. Non Cryst. Solids 2006, 352, 2360. [Google Scholar] [CrossRef]
- Ward, J.M.; Wu, Y.; Khalfi, K.; Chormaic, S.N. Short vertical tube furnace for the fabrication of doped glass microsphere lasers. Rev. Sci. Instrum. 2010, 81, 073106. [Google Scholar] [CrossRef] [PubMed]
- Bica, I. Formation of glass microspheres with rotating electrical arc. Mater. Sci. Eng. B 2000, 77, 210–212. [Google Scholar] [CrossRef]
- Wilson, K.A.; Finch, C.A.; Anderson, P.; Vollmer, F.; Hickman, J.J. Whispering Gallery Mode Biosensor Quantification of Fibronectin Adsorption Kinetics onto Alkylsilane Monolayers and Interpretation of Resultant Cellular Response. Biomaterials 2012, 33, 225–236. [Google Scholar] [CrossRef] [PubMed]
- Collot, L.; Lefèvre-Seguin, V.; Brune, B.; Raimond, J.; Haroche, S. Very high Q WGM resonances observed on fused silica microspheres. Europhys. Lett. 1992, 23, 327. [Google Scholar] [CrossRef]
- Hoi, P.V.; Ha, C.T.T.; Hung, H.Q. Long-band emission of microsphere lasers based on erbium-doped sol-gel silica-alumina glasses. Appl. Phys. Lett. 2005, 87, 161110. [Google Scholar]
- Brenci, M.; Calzolai, R.; Cosi, F.; Nunzi Conti, G.; Pelli, S.; Righini, G. Microspherical resonators for biophotonic sensors. Proc. SPIE 2006, 6158, 61580S. [Google Scholar]
- Ferreira, M.S.; Santos, J.L.; Frazao, O. Silica microspheres array strain sensor. Opt. Lett. 2014, 39, 5937–5940. [Google Scholar] [CrossRef] [PubMed]
- Fan, K.C.; Hsu, H.Y.; Hung, P.Y.; Wang, W. Experimental study of fabricating a microball tip on an optical fibre. J. Opt. A: Pure Appl. Opt. 2006, 8, 782. [Google Scholar] [CrossRef]
- Yu, H.; Huang, Q.; Zhao, J. Fabrication of an Optical Fiber Micro-Sphere with a Diameter of Several Tens of Micrometers. Materials 2014, 7, 4878–4895. [Google Scholar] [CrossRef]
- Stober, W.; Fink, A.; Bohn, E. Controlled growth of monodisperse silica spheres in the micron size range. J. Colloidal Interface Sci. 1968, 26, 62. [Google Scholar] [CrossRef]
- De Dood, M.J.A.; Berkhout, B.; van Kats, C.M.; Polman, A.; van Blaaderen, A. Acid-Based Synthesis of Monodisperse Rare-Earth-Doped Colloidal SiO2 Spheres. Chem. Mater. 2002, 14, 2849–2853. [Google Scholar] [CrossRef]
- Righini, G.C.; Armellini, C.; Chiasera, A.; Jestin, Y.; Ferrari, M.; Chiappini, A.; Montagna, M.; Duverger, C.A.; Féron, P.; Berneschi, S.; et al. Er3+-activated sol-gel silica derived spherical microresonators. Glass Technol. Eur. J. Glass Sci. & Technol. Part A 2007, 48, 200–203. [Google Scholar]
- Beltaos, A.M.; Meldrum, A. Whispering gallery modes in silicon-nanocrystal-coated silica microspheres. J. Lumin. 2007, 126, 607–613. [Google Scholar] [CrossRef]
- Shibata, S.; Ashida, S.; Segawa, H.; Yano, T. Coated microsphere as spherical cavity Raman laser. J. Sol-Gel Sci. Technol. 2006, 40, 379–384. [Google Scholar] [CrossRef]
- Hightower, R.L.; Richardson, C.B. Resonant Mie Scattering from a layered sphere. Appl Opt. 1988, 27, 4850–4855. [Google Scholar] [CrossRef] [PubMed]
- Teraoka, I.; Arnold, S. Enhancing the sensitivity of a whispering-gallery mode microsphere sensor by a high-refractive-index surface layer. J. Opt. Soc. Am. B 2006, 23, 1434–1441. [Google Scholar] [CrossRef]
- Ristic, D.; Chiappini, A.; Mazzola, M.; Farnesi, D.; Nunzi-Conti, G.; Righini, G.; Feron, P.; Cibiel, G.; Ferrari, M.; Ivanda, M. Whispering gallery mode profiles in a coated microsphere. Eur. Phys. J. Spec. Top. 2014, 223, 1959–1969. [Google Scholar] [CrossRef]
- Tapalian, H.; Laine, J.P.; Lane, P. Thermo-optical switches using coated microsphere resonators. IEEE Photonics Technol. Lett. 2002, 14, 1118–1120. [Google Scholar] [CrossRef]
- Lin, N.; Jiang, L.; Wang, S.; Xiao, H.; Lu, Y.; Tsai, H. Thermostable refractive index sensors based on whispering gallery modes in a microsphere coated with poly(methyl methacrylate). Appl. Opt. 2011, 50, 992–998. [Google Scholar] [CrossRef] [PubMed]
- Schiro, P.G.; Kwok, A.S. Cavity-enhanced emission from a dye-coated microsphere. Opt. Express 2004, 12, 2857–2863. [Google Scholar] [CrossRef] [PubMed]
- Dantham, V.R.; Bisht, P.B. High-Q whispering gallery modes of doped and coated single microspheres and their effect on radiative rate. J. Opt. Soc. Am. B 2009, 26, 290–300. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Liu, L.; Hao, W.; Hou, B.; Lu, Y. Light emission from a dye-coated glass microsphere. J. Lumin. 2007, 122, 949–950. [Google Scholar] [CrossRef]
- Righini, G.; Berneschi, S.; Conti, G.N.; Pelli, S.; Moser, E.; Retoux, R.; Féron, P.; Gonçalves, R.; Speranza, G.; Jestin, Y.; et al. Er3+-doped silica-hafnia films for optical waveguides and spherical resonators. J. Non-Cryst. Solids 2009, 355, 1853–1860. [Google Scholar] [CrossRef]
- Righini, G.C.; Cosi, F.; Conti, G.N.; Pelli, S.; Soria, S.; Moser, E.; Jestin, Y.; Ferrari, M.; Féron, P.; Chiasera, A.; Chiappini, A.; Armellini, C. Photonic properties and applications of glass micro- and nanospheres. Phys. Status Solidi A 2009, 206, 898–903. [Google Scholar] [CrossRef]
- Han, M.; Wang, A. Temperature compensation of optical microresonators using a surface layer with negative thermo-optic coefficient. Opt. Lett. 2007, 32, 1800. [Google Scholar] [CrossRef] [PubMed]
- Lin, N.; Jiang, L.; Wang, S.; Yuan, L.; Xiao, H.; Lu, Y.; Tsai, H. Ultrasensitive chemical sensors based on whispering gallery modes in a microsphere coated with zeolite. Appl. Opt. 2010, 49, 6463–6471. [Google Scholar] [CrossRef] [PubMed]
- Shopova, S.I.; Farca, G.; Rosenberger, A.T.; Wickramanayake, W.M.S.; Kotov, N.A. Microsphere whispering-gallery-mode laser using HgTe quantum dots. Appl. Phys. Lett. 2004, 85, 6101–6103. [Google Scholar] [CrossRef]
- Ristić, D.; Holý, V.; Ivanda, M.; Marciuš, M.; Buljan, M.; Gamulin, O.; Furić, K.; Ristić, M.; Musić, S.; Mazzola, M.; et al. Surface characterization of thin silicon-rich oxide films. J. Mol. Struct. 2011, 993, 214–218. [Google Scholar] [CrossRef]
- Yang, L.; Vahala, K. Gain functionalization of silica microresonators. Opt. Lett. 2003, 28, 592–594. [Google Scholar] [CrossRef] [PubMed]
- Ristić, D.; Berneschi, S.; Camerini, M.; Farnesi, D.; Pelli, S.; Trono, C.; Chiappini, A.; Chiasera, A.; Ferrari, M.; Lukowiak, A.; et al. Photoluminescence and lasing in whispering gallery mode glass microspherical resonators. J. Lumin. 2016, 170, 755–760. [Google Scholar] [CrossRef]
- Yu, L.; Fernicola, V. Spherical-sapphire-based whispering gallery mode resonator thermometer. Rev. Sci. Instrum. 2012, 83, 094903. [Google Scholar] [CrossRef] [PubMed]
- Creedon, D.L.; Reshitnyk, Y.; Farr, W.; Martinis, J.M.; Duty, T.L.; Tobar, M.E. High Q-factor sapphire whispering gallery mode microwave resonator at single photon energies and millikelvin temperatures. Appl. Phys. Lett. 2001, 98, 222903. [Google Scholar] [CrossRef]
- Goryachev, M.; Farr, W.G.; Creedon, D.L.; Fan, Y.; Kostylev, M.; Tobar, M.E. High-Cooperativity Cavity QED with Magnons at Microwave Frequencies. Phys. Rev. Appl. 2014, 2, 054002. [Google Scholar] [CrossRef]
- Damiao, V.B.; Fotheringham, E.; Shkunov, V.; Czaia, L.; Anderson, D.Z. Photorefractive BaTiO3 spheres and spherical disk. Opt. Lett. 2001, 26, 611–613. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Pyatenko, A.; Kawaguchi, K.; Li, X.; Swiatkowska-Warkocka, Z.; Koshizaki, N. Selective Pulsed Heating for the Synthesis of Semiconductor and Metal Submicrometer Spheres. Angew. Chem. Int. Ed. 2010, 49, 6361–6364. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, S.; Inaba, K.; Iida, T.; Ishihara, H.; Ichikawa, S.; Ashida, M. Fabrication of single-crystalline microspheres with high sphericity from anisotropic materials. Sci. Rep. 2014, 4, 5186. [Google Scholar] [CrossRef] [PubMed]
- Berneschi, S.; Farnesi, D.; Cosi, F.; Conti, G.N.; Pelli, S.; Righini, G.C.; Soria, S. High Q silica microbubble resonators fabricated by arc discharge. Opt. Lett. 2011, 36, 3521–3523. [Google Scholar] [CrossRef] [PubMed]
- Berneschi, S.; Barucci, A.; Brenci, M.; Cosi, F.; Farnesi, D.; Conti, G.N.; Pelli, S.; Soria, S.; Righini, G.C. Optical Microbubble Resonator: A Novel Structure for Sensing Applications. In Proceedings of the First National Conference on Sensor, Rome, Italy, 15–17 February 2012; pp. 359–362.
- Cosci, A.; Quercioli, F.; Farnesi, D.; Berneschi, S.; Giannetti, A.; Cosi, F.; Barucci, A.; Conti, G.N.; Righini, G.; Pelli, S. Confocal reflectance microscopy for determination of microbubble resonator thickness. Opt. Express 2015, 23, 16693–16701. [Google Scholar] [CrossRef] [PubMed]
- Soria, S.; Baldini, F.; Berneschi, S.; Cosi, F.; Giannetti, A.; Nunzi Conti, G.; Pelli, S.; Righini, G. High-Q polymer-coated microspheres for immunosensing applications. Opt. Express 2009, 17, 14694. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Braun, D.; Libchaber, A.; Khoshsima, M.; Teraoka, I.; Arnold, S. Protein Detection by Optical Shift of a Resonant Microcavity. Appl. Phys. Lett. 2002, 80, 4057. [Google Scholar] [CrossRef]
- Nadeau, J.L.; Ilchenko, V.S.; Kossakovski, D.; Bearman, G.H.; Maleki, L. High-Q whispering-gallery mode sensor in liquids. Proc. SPIE 2002, 4629, 172. [Google Scholar]
- Zhu, H.; Suter, J.D.; White, I.M.; Fan, X. Aptamer Based Microsphere Biosensor for Thrombin Detection. Sensors 2006, 6, 785–795. [Google Scholar] [CrossRef]
- Vollmer, F.; Arnold, S.; Braun, D.; Teraoka, I.; Libchaber, A. Multiplexed DNA Quantification by Spectroscopic Shift of Two Microsphere Cavities. Biophys. J. 2003, 85, 1974. [Google Scholar] [CrossRef]
- Nuhiji, E.; Mulvanely, P. Detection of unlabeled oligonucleotide targets using whispering gallery modes in single, fluorescent microspheres. Small 2007, 3, 1408. [Google Scholar] [CrossRef] [PubMed]
- Hanumegowda, N.M.; Stica, C.J.; Patel, B.C.; White, I.M.; Fan, X. Refractometric sensors based on microsphere resonators. Appl. Phys. Lett. 2005, 87, 201107. [Google Scholar] [CrossRef]
- Berneschi, S.; Baldini, F.; Barucci, A.; Cosci, A.; Cosi, F.; Farnesi, D.; Conti, G.N.; Righini, G.C.; Soria, S.; Tombelli, S.; Trono, C.; Pelli, S.; Giannetti, A. Localized biomolecules immobilization in optical microbubble resonators. Proc. SPIE 2016, 9727, 972719. [Google Scholar]
- Pastells, C.; Marco, P.; Merino, D.; Loza-Alvarez, P.; Quercioli, F.; Pasquardini, L.; Lunelli, L.; Pederzolli, C.; Daldoso, N.; Farnesi, D.; et al. Two photon versus one photon fluorescence excitation in whispering gallery mode microresonators. J. Lumin. 2016, 170, 860–865. [Google Scholar] [CrossRef]
- Pasquardini, L.; Berneschi, S.; Barucci, A.; Cosi, F.; Dallpiccola, R.; Lunelli, L.; Nunzi Conti, G.; Pederzolli, C.; Soria, S. Whispering Gallery Modes Aptasensors for detection of blood proteins. J. Biophotonics 2013, 6, 785–795. [Google Scholar] [CrossRef] [PubMed]
- Carlborg, C.F.; Gylfason, K.B.; Kazmierczak, A.; Dortu, F.; nuls Polo, M.J.B.; Catala, A.M.; Kresbach, G.M.; Sohlstrom, H.; Moh, T.; Vivien, L.; et al. A packaged optical slot-waveguide ring resonator sensor array for multiplex label-free assays in labs-on-chips. Lab Chip 2010, 10, 281–290. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Dale, P.S.; Caldwell, C.; Fan, X. Rapid and label-free detection of breast cancer biomarker CA15-3 in clinical human serum samples with optofluidic ring resonator sensors. Anal. Chem. 2009, 81, 9858–9865. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.; Gleeson, M.; Spaugh, B.; Tybor, F.; Gunn, W.; Hochberg, M.; Baehr-Jones, T.; Bailey, R.; Gunn, L. Label-free biosensor arrays based on silicon ring resonators and high-speed optical scanning instrumentation. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 654–661. [Google Scholar] [CrossRef]
- Balakirev, M.Y.; Porte, S.; Vernaz-Gris, M.; Berger, M.; Arié, J.P.; Fouqué, B.; Chatelain, F. Photochemical patterning of biological molecules inside a glass capillary. Anal. Chem. 2005, 77, 5474–5479. [Google Scholar] [CrossRef] [PubMed]
- Bog, U.; Brinkmann, F.; Kalt, H.; Koos, C.; Mappes, T.; Hirtz, M.; Fuchs, H.; Koeber, S. Large Scale parallel surface functionalization of goblet-type whsipering gallery mode microcavity arrays for biosensing applications. Small 2014, 10, 3863–3868. [Google Scholar] [CrossRef] [PubMed]
- Soteropulos, C.E.; Zurick, K.M.; Bernards, M.T.; Hunt, H.K. Tailoring the Protein Adsorption Properties of Whispering Gallery Mode Optical Biosensors. Langmuir 2012, 28, 15743–15750. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Cao, Z. Ultralow-Fouling, Functionalizable, and Hydrolyzable Zwitterionic Materials and Their Derivatives for Biological Applications. Adv. Mater. 2010, 22, 920–922. [Google Scholar] [CrossRef] [PubMed]
- Washburn, A.; Luchansky, M.S.; Bowman, A.L.; Bailey, R. Label-free quantitation of a cancer biomarker in complex media using silicon photonic microring resonators. Anal. Chem. 2009, 81, 9499–9506. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.Y.; White, I.; Suter, J.; Fan, X.D. Phage-based label-free biomolecule detection in an opto-fluidic ring resonator. Biosens. Bioelectron. 2008, 24, 461–466. [Google Scholar] [CrossRef] [PubMed]
- Arnold, S.; Keng, D.; Shopova, S.I.; Holler, S.; Zurawsky, W.; Vollmer, F. Whispering gallery mode carousel—A photonic mechanism for enhanced nanoparticle detection in biosensing. Opt. Express 2009, 17, 6230–6238. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Y.; Boyd, K.; Ji, H.; Francois, A.; Munch, H.E.H.J.; Monro, T.M. Tellurite microspheres for nanoparticle sensing and novel light sources. Opt. Express 2014, 22, 11995–12006. [Google Scholar] [CrossRef] [PubMed]
- Gorodetsky, M.L.; Grudinin, I.S. Fundamental thermal fluctuations in microspheres. J. Opt. Soc. Am. B 2004, 21, 697–705. [Google Scholar] [CrossRef]
- Arnold, S.; Shopova, S.; Holler, S. Whispering gallery mode bio-sensor for label-free detection of single molecules: thermo-optic vs. reactive mechanism. Opt. Express 2010, 18, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Boriskina, S.; Dal Negro, L. Self-referenced photonic molecule bio(chemical)sensor. Opt. Lett. 2010, 35, 2496–2498. [Google Scholar] [CrossRef] [PubMed]
- Ozdemir, S.K.; Zhu, J.; Yang, X.; Peng, B.; Yilmaz, H.; He, L.; Monifi, F.; Huan, S.H.; Long, G.L.; Yang, L. Highly sensitive detection of nanoparticles with a self-referenced and self-heterodyned whispering-gallery Raman microlaser. Proc. Natl. Acad. Sci. USA 2014, 111, E3836–E3844. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Ozdemir, S.K.; Zhu, J.; Kim, W.; Yang, L. Detecting single viruses and nanoparticles using whispering gallery microlasers. Nat. Nanotechnol. 2011, 6, 428–432. [Google Scholar] [CrossRef] [PubMed]
- Ye, M.Y.; Shen, M.X.; Lin, X.M. Ringing phenomenon based whispering-gallery-mode sensing. Sci. Rep. 2016, 6, 19597. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Zou, C.; Cui, J.; Yang, Y.; Han, Z.; Guo, G. Ringing phenomenon in silica microspheres. Chin. Opt. Lett. 2009, 7, 299–301. [Google Scholar]
- Trebaol, S.; Dumeige, Y.; Feron, P. Ringing phenomenon in coupled cavities: Application to modal coupling in whispering-gallery mode resonators. Phys. Rev. A 2010, 81, 043828. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, K.; Jin, X. Packaged microsphere-taper coupling system with a high Q factor. Appl. Opt. 2015, 54, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Hanumegowda, N.M.; White, I.M.; Fan, X. Aqueous mercuric ion detection with microsphere optical ring resonator sensors. Sens. Actuators B Chem. 2006, 120, 207–212. [Google Scholar] [CrossRef]
- Westcott, S.; Zhang, J.; Shelton, R.; Bruce, N.; Gupta, S.; Keen, S.; Tillman, J.; Wald, L.; Strecker, B.; Rosenberger, A.; et al. Broadband optical absorbance spectroscopy using a whispering gallery mode microsphere resonator. Rev. Sci. Instrum. 2008, 79, 033106. [Google Scholar] [CrossRef] [PubMed]
- Wildgen, S.M.; Dunn, R.C. Whispering Gallery Mode Resonators for Rapid Label-Free Biosensing in Small Volume Droplets. Biosensors 2015, 5, 118–130. [Google Scholar] [CrossRef] [PubMed]
- Francois, A.; Zhi, Y.; Meldrum, A. Whispering Gallery Mode Devices for Sensing and Biosensing. In Photonic Materials for Sensing, Biosensing and Display Devices; Springer: Berlin, Germany, 2016; pp. 237–288. [Google Scholar]
- Vollmer, F.; Arnold, S.; Keng, D. Single virus detection from the reactive shift of a whispering-gallery mode. Proc. Natl. Acad. Sci. USA 2008, 105, 20701. [Google Scholar] [CrossRef] [PubMed]
- Armani, A.M.; Kulkarni, R.P.; Fraser, S.E.; Flagan, R.C.; Vahala, K.J. Label-Free, Single-Molecule Detection with Optical Microcavities. Science 2007, 317, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Baaske, M.D.; Foreman, M.R.; Vollmer, F. Single-molecule nucleic acid interactions monitored on a label-free microcavity biosensor platform. Nat. Nanotechnol. 2014, 9, 933–939. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Goldberg, A.F.; Stoltz, B.M. Label-free detection of single nanoparticles and biological molecules using microtoroid optical resonators. Light Sci. Appl. 2016, 5, e16001. [Google Scholar] [CrossRef]
- Fan, X.; White, I.M.; Zhu, H.; Suter, J.; Oveys, H. Overview of novel integrated optical ring resonator bio/chemical sensors. Proc. SPIE 2007, 6452, 64520M4. [Google Scholar]
- Li, H.; Guo, Y.; Sun, Y.; Reddy, K.; Fan, X. Analysis of single nanoparticle detection by using 3-dimensionally confined optofluidic ring resonators. Opt. Express 2010, 18, 25081–25088. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ward, J.; Chormaic, S.N. Quasi-droplet microbubbles for high resolution sensing applications. Opt. Express 2014, 22, 6881–6898. [Google Scholar] [CrossRef] [PubMed]
- Charlebois, M.; Paquet, A.; Verret, L.S.; Boissinot, K.; Boissinot, M.; Bergeron, M.G.; Allen, C.N. Toward Automatic Label-Free Whispering Gallery Modes Biodetection with a Quantum Dot-Coated Microsphere Population. Nanoscale Res. Lett. 2010, 5, 524–532. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.E.; O’Brien, E.C.; Grayek, E.N.; Hermansen, J.K.; Hunt, H.K. The Detection of Helicobacter hepaticus Using Whispering-Gallery Mode Microcavity Optical Sensors. Biosensors 2015, 5, 562–576. [Google Scholar] [CrossRef] [PubMed]












© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Righini, G.C.; Soria, S. Biosensing by WGM Microspherical Resonators. Sensors 2016, 16, 905. https://doi.org/10.3390/s16060905
Righini GC, Soria S. Biosensing by WGM Microspherical Resonators. Sensors. 2016; 16(6):905. https://doi.org/10.3390/s16060905
Chicago/Turabian StyleRighini, Giancarlo C., and Silvia Soria. 2016. "Biosensing by WGM Microspherical Resonators" Sensors 16, no. 6: 905. https://doi.org/10.3390/s16060905
APA StyleRighini, G. C., & Soria, S. (2016). Biosensing by WGM Microspherical Resonators. Sensors, 16(6), 905. https://doi.org/10.3390/s16060905