The Vector Matching Method in Geomagnetic Aiding Navigation
Abstract
:1. Introduction
2. The Error Model of Geomagnetic Vector Matching System
2.1. Geomagnetic Field Vector Measurement Error
2.2. Error Model of INS
3. Geomagnetic Matching Algorithm
3.1. The Principle of ICCP Algorithm
3.2. VICCP Algorithm
4. Simulation
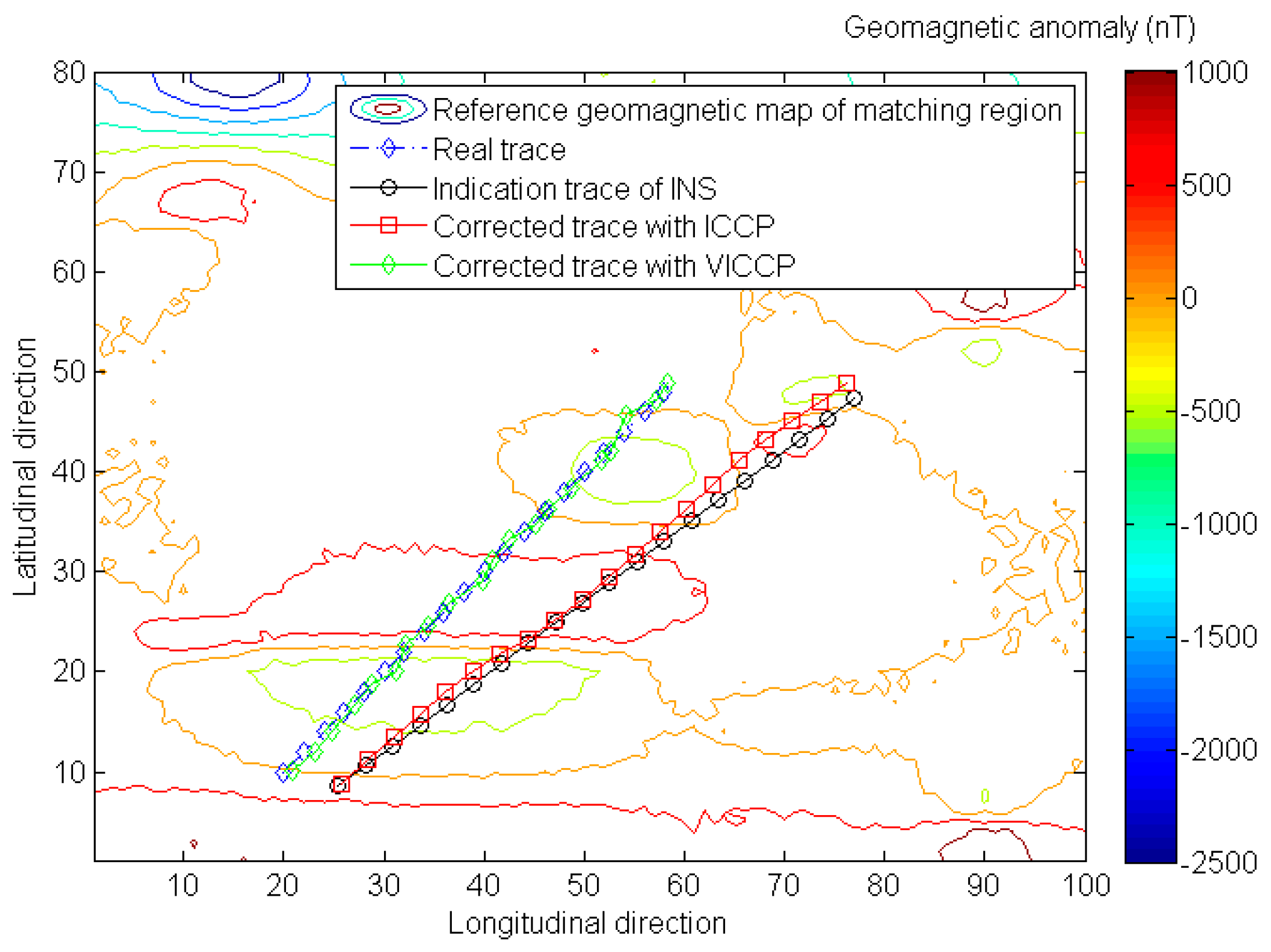
4.1. The Comparison of ICCP and VICCP
4.2. The Validity of Affine Transformation Based VICCP
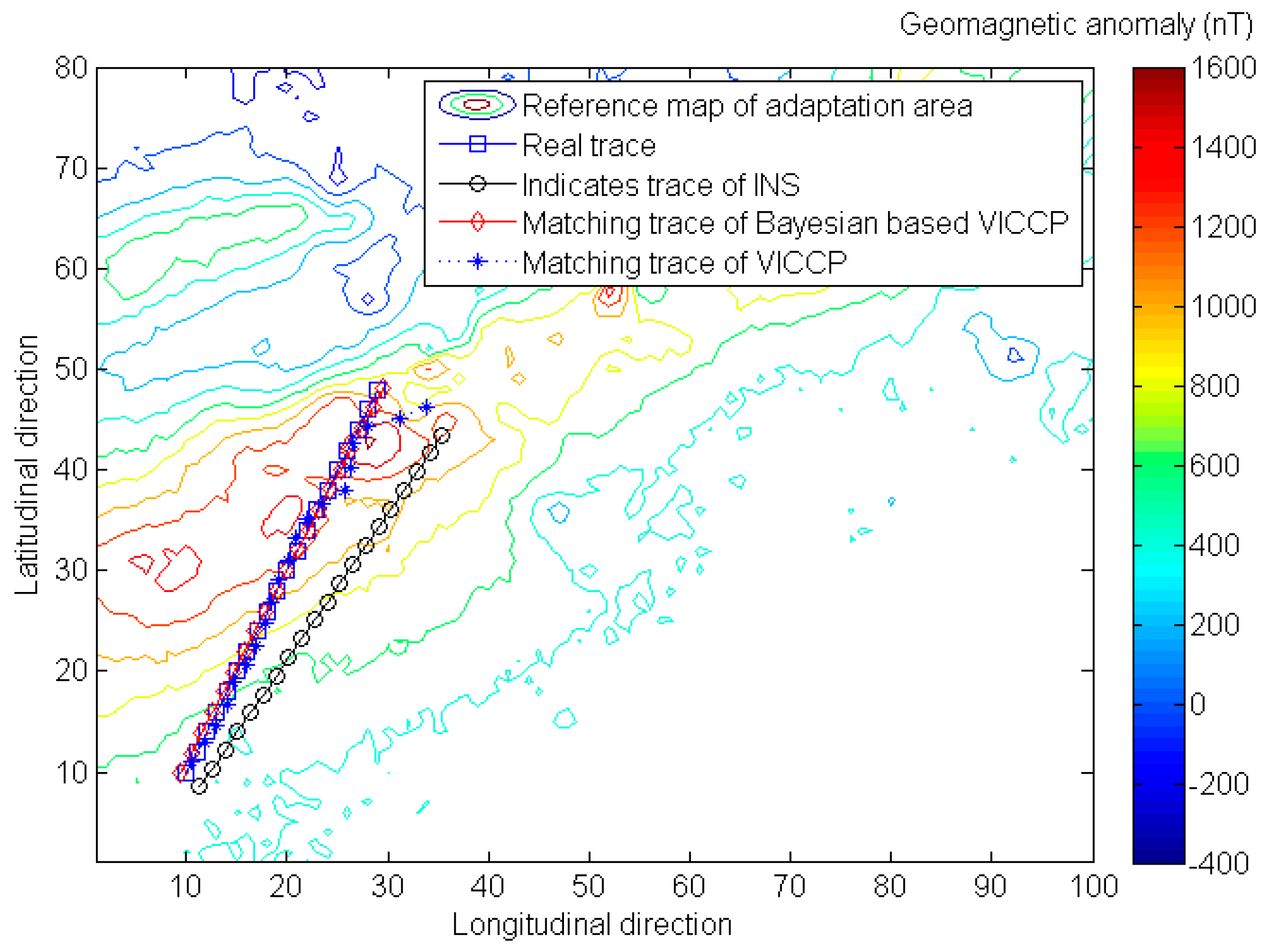
4.3. The Comparison of VICCP and Bayesian Based VICCP
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Tyren, C. Magnetic anomalies as a reference for ground-speed and map matching navigation. J. Navig. 1982, 35, 242–254. [Google Scholar] [CrossRef]
- Tyren, C. Magnetic terrain navigation. In Proceedings of the 5th International Symposium on Unmanned Untethered Submersible Technology, Durham, NH, USA, June 1987; pp. 245–256.
- Peng, W.; Wu, Y.; Hu, X.; Ruan, Q.; Yuan, H. Geomagnetic aided navigation suitability evaluation based on principal component analysis. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering (ICICEE), Xi’an, China, 23–25 August 2012; pp. 324–329.
- Yang, G.; Li, S.; Jiang, Z. Data fusing algorithm in geomagnetic aided INS. J. Chin. Inertial Technol. 2007, 15, 47–50. [Google Scholar]
- Mu, H.; Wu, M.; Hu, X.; Ma, H. Geomagnetic surface navigation using adaptive EKF. In Proceedings of the 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007.
- Ejaz, M.; Iqbal, J.; Ahsan, N.; Nawaz, A. Robust geomagnetic aided inertial navigation of underwater vehicles using the ICP algorithm. In Proceedings of the Asia-Pacific Conference on Computational Intelligence and Industrial Applications, Wuhan, China, 28–29 November 2009; pp. 257–262.
- Zhao, J.; Wang, S.; Wang, A. Study on underwater navigation system based on geomagnetic match technique. In Proceedings of the 9th International Conference on Electronic Measurement & Instruments (ICEMI ‘09), Beijing, China, 16–19 August 2009; pp. 16–19.
- Ren, Z.; Chen, L.; Zhang, H.; Wu, M. Research on geomagnetic-matching localization algorithm for unmanned underwater vehicles. In Proceedings of the International Conference on Information and Automation (ICIA 2008), Changsha, China, 20–23 June 2008; pp. 20–23.
- Wei, L.; Zhi, W.; Wu, M.; Hu, X. Geomagnetic matching technology based on Iterative Contour Matching algorithm. In Proceedings of the 10th International Conference on Electronic Measurement & Instruments (ICEMI), Chengdu, China, 16–18 August 2016; pp. 342–345.
- Zhou, J.; Liu, Y.; Ge, Z. Geomagnetic matching algorithm based on the probabilistic neural network. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2011, 225, 120–126. [Google Scholar] [CrossRef]
- Kauffman, K.; Raquet, J. Navigation via H-field signature map correlation and INS integration. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1390–1395.
- Včelák, J.; Ripka, P.; Zikmund, A. Precise magnetic sensors for navigation and prospection. J. Supercond. Novel Magn. 2015, 28, 1077–1080. [Google Scholar] [CrossRef]
- Ripka, P. Magnetic sensors for navigation and security applications. In Proceedings of the 2006 IEEE Instrumentation and Measurement Technology Conference Proceedings, Sorrento, Italy, 24–27 April 2006.
- Renaudin, V.; Afzal, M.H.; Lachapelle, G. Complete triaxis mag-netometer calibration in the magnetic domain. J. Sens. 2010, 2010, 967245. [Google Scholar] [CrossRef]
- Unsal, D.; Demirbas, K. Estimation of deterministic and stochastic IMU error parameters. In Proceedings of the 2012 IEEE/ION Position Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012.
- Titterton, D.; Weston, J. Strapdown Inertial Navigation Technology; Peter Peregrinus Ltd.: London, UK, 1997. [Google Scholar]
- Kamgar-Parsi, B.; Kamgar-Parsi, B. Vehicle localization of gravity maps. Proc. SPIE 1999, 3693, 182–191. [Google Scholar]
- Dorst, L. First order error propagation of the procrustes method for 3D attitude estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 221–229. [Google Scholar] [CrossRef] [PubMed]





| Parameter | Parameter Values |
|---|---|
| Matching points | 20 |
| Reference map noise | ~(0, 25) nT |
| Matching region size | 8 km × 10 km |
| Center location of matching region | (108.98° E, 34.91° N) |
| Average altitude | ~20 km |
| Gird size of matching region | 100 × 80 |
| Measurement Gaussian noise | ~10 nT/axis |
| Matching tolerance | 200% of uncorrected trace’s mean error |
| Symbol | Quantity | Unit |
|---|---|---|
| Platform misalignment angles | 30 | ″ |
| Initial velocity error | 0.1 | m/s |
| Initial position error | 10 | m |
| Gyro constant bias | 0.01 | °/h |
| Gyro random walk | 0.001 | °/h |
| Accelerometor constant bias | 100 | μg |
| Accelerometor random walk | 10 | μg |
| Scale factor error | 10 | ppm |
| Askew installation error | 10 | ″ |
| Statistical Quantity | Indication Trace of INS | VICCP with Rigid Transformation | VICCP with Affine Transformation |
|---|---|---|---|
| Mean (m) | 679.05 | 267.66 | 127.4 |
| Var (m) | 530.49 | 265.65 | 483.8 |
| Matching probability (percentage) | - | 93% | 98% |
| Statistical Quantity | Indication Trace of INS | VICCP with Rigid Transformation | VICCP with Affine Transformation |
|---|---|---|---|
| Mean (m) | 1225.14 | 600.20 | 153.16 |
| Var (m) | 1726.78 | 1142.51 | 50.07 |
| Matching probability (percentage) | - | 90% | 98% |
| Matching Method | Mean (m) | Var (m) | Matching Probability (percentage) | |
|---|---|---|---|---|
| ICCP | X | 235.37 | 240.28 | 88% |
| Y | 531.31 | 662.51 | 64% | |
| Z | 185.42 | 201.27 | 92% | |
| VICCP | 124.72 | 51.05 | 97% | |
| Bayesian-based VICCP | 88.36 | 34.96 | 99% | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Zhang, J.; Zhu, W.; Xi, X. The Vector Matching Method in Geomagnetic Aiding Navigation. Sensors 2016, 16, 1120. https://doi.org/10.3390/s16071120
Song Z, Zhang J, Zhu W, Xi X. The Vector Matching Method in Geomagnetic Aiding Navigation. Sensors. 2016; 16(7):1120. https://doi.org/10.3390/s16071120
Chicago/Turabian StyleSong, Zhongguo, Jinsheng Zhang, Wenqi Zhu, and Xiaoli Xi. 2016. "The Vector Matching Method in Geomagnetic Aiding Navigation" Sensors 16, no. 7: 1120. https://doi.org/10.3390/s16071120
APA StyleSong, Z., Zhang, J., Zhu, W., & Xi, X. (2016). The Vector Matching Method in Geomagnetic Aiding Navigation. Sensors, 16(7), 1120. https://doi.org/10.3390/s16071120





