Improving the Accuracy and Training Speed of Motor Imagery Brain–Computer Interfaces Using Wavelet-Based Combined Feature Vectors and Gaussian Mixture Model-Supervectors
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Data
2.1.1. BCI Competition II, Dataset III
2.1.2. BCI Competition III, Dataset IIIb
2.1.3. BCI Competition IV, Dataset 2b
2.2. Combined Feature Vectors Based on Wavelets and PCA
2.2.1. Feature Extraction by CWT
2.2.2. Feature Extraction by DWT
- (1)
- Mean of the absolute values of the wavelet coefficients in each sub-band
- (2)
- Average power of the wavelet coefficients in each sub-band
- (3)
- Standard deviation of the wavelet coefficients in each sub-band
- (4)
- Ratio of the absolute mean values of adjacent sub-bands
- (5)
- Energy of the wavelet coefficients in each sub-band
- (6)
- Entropy of the wavelet coefficients in each sub-band
- (7)
- Skewness of the wavelet coefficients in each sub-band
- (8)
- Kurtosis of the wavelet coefficients in each sub-band
2.2.3. Combined Feature Vectors by PCA
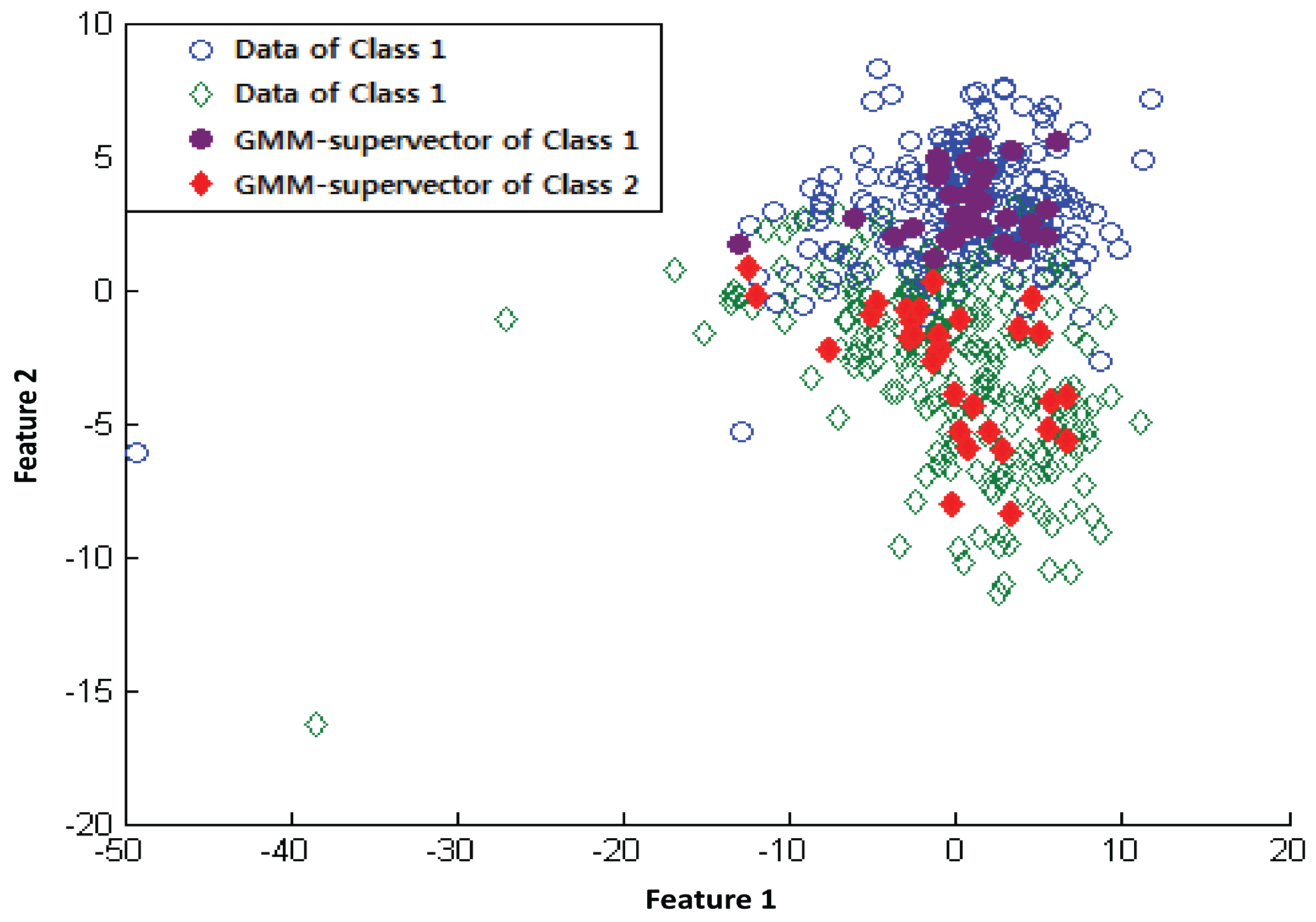
2.3. GMM-Supervectors
2.4. Support Vector Machine (SVM)
3. Experimental Results
3.1. Performance of the Combined Features Vector
3.2. Performance of a Fast and Robust SVM Training Method
3.3. Comparison with State-of-the-Art Algorithms
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BCI | Brain–Computer Interface |
| CV | Cross-Validation |
| CWT | Continuous Wavelet Transform |
| CSP | Common spatial pattern |
| DWT | Discrete Wavelet Transform |
| EEG | Electroencephalography |
| EM | Expectation–Maximization |
| ERD | Event-Related Desynchronization |
| ERS | Event-Related Synchronization |
| FFT | Fast Fourier Transform |
| GMM | Gaussian Mixture Model |
| GMM-UBM | Gaussian Mixture Model Universal Background Model |
| LDA | Linear Discriminant Analysis |
| PCA | Principal Component Analysis |
| STFT | Short-Time Fourier Transform |
| SVMs | Support Vector Machines |
| WT | Wavelet Transform |
References
- Hsu, W. EEG-Based Motor Imagery Classification using Neuro-Fuzzy Prediction and Wavelet Fractal Features. J. Neurosci. Methods 2010, 189, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W. Embedded Prediction in Feature Extraction: Application to Single-Trial EEG Discrimination. Clin EEG Neurosci. 2013, 44, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Kalcher, J.; Flotzinger, D.; Neuper, C.; Gölly, S.; Pfurtscheller, G. Graz Brain-Computer Interface II: Towards Communication between Humans and Computers Based on Online Classification of Three Different EEG Patterns. Med. Biol. Eng. Comput. 1996, 34, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Wolpaw, J.R.; McFarland, D.J. Multichannel EEG-Based Brain-Computer Communication. Electroencephalogr. Clin. Neurophysiol. 1994, 90, 444–449. [Google Scholar] [CrossRef]
- Song, X.; Perera, V.; Yoon, S. A Study of EEG Features for Multisubject Brain-Computer Interface Classification. In Proceedings of the IEEE Signal Processing in Medicine and Biology Symposium (SPMB 2014), Philadelphia, PA, USA, 13 December 2014; p. 1. [Google Scholar]
- Santhanam, G.; Ryu, S.I.; Byron, M.Y.; Afshar, A.; Shenoy, K.V. A High-Performance brain–computer Interface. Nature 2006, 442, 195–198. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.E.; Blain-Moraes, S.; Huggins, J.E. Performance Assessment in Brain-Computer Interface-Based Augmentative and Alternative Communication. Biomed. Eng. Online 2013, 12, 43. [Google Scholar] [CrossRef] [PubMed]
- Nicolas-Alonso, L.F.; Gomez-Gil, J. Brain Computer Interfaces, a Review. Sensors 2012, 12, 1211–1279. [Google Scholar] [CrossRef] [PubMed]
- Coyle, D.; Prasad, G.; McGinnity, T.M. A Time-Series Prediction Approach for Feature Extraction in a Brain-Computer Interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 461–467. [Google Scholar] [CrossRef] [PubMed]
- Besserve, M.; Martinerie, J.; Garnero, L. Improving Quantification of Functional Networks with Eeg Inverse Problem: Evidence from a Decoding Point of View. Neuroimage 2011, 55, 1536–1547. [Google Scholar] [CrossRef] [PubMed]
- Kayikcioglu, T.; Aydemir, O. A Polynomial Fitting and k-NN Based Approach for Improving Classification of Motor Imagery BCI Data. Pattern Recog. Lett. 2010, 31, 1207–1215. [Google Scholar] [CrossRef]
- Ang, K.K.; Guan, C. EEG-Based Strategies to Detect Motor Imagery for Control and Rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 392–401. [Google Scholar] [CrossRef] [PubMed]
- Martin-Smith, P.; Ortega, J.; Asensio-Cubero, J.; Gan, J.Q.; Ortiz, A. A Supervised Filter Method for Multi-Objective Feature Selection in EEG Classification Based on Multi-Resolution Analysis for BCI. Neurocomputing 2017, 250, 45–56. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Optimizing Spatial Patterns with Sparse Filter Bands for Motor Imagery Based brain computer Interface. J. Neurosci. Methods 2015, 255, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Park, C.; Took, C.C.; Mandic, D.P. Augmented Complex Common Spatial Patterns for Classification of Noncircular EEG from Motor Imagery Tasks. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Sankar, A.S.; Nair, S.S.; Dharan, V.S.; Sankaran, P. Wavelet Sub Band Entropy Based Feature Extraction Method for BCI. Procedia Comput. Sci. 2015, 46, 1476–1482. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Meyer, D.; Leisch, F.; Hornik, K. The Support Vector Machine Under Test. Neurocomputing 2003, 55, 169–186. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Zhong, X.; Zhang, Y. Analysis and Classification of Speech Imagery EEG for BCI. Biomed. Signal Process. Control 2013, 8, 901–908. [Google Scholar] [CrossRef]
- Dokare, I.; Kant, N. Performance Analysis of SVM, KNN and BPNN Classifiers for Motor Imagery. Int. J. Eng. Trends Technol. 2014, 10, 19–23. [Google Scholar] [CrossRef]
- Xu, Q.; Zhou, H.; Wang, Y.; Huang, J. Fuzzy Support Vector Machine for Classification of EEG Signals Using Wavelet-Based Features. Med. Eng. Phys. 2009, 31, 858–865. [Google Scholar] [CrossRef] [PubMed]
- Eslahi, S.V.; Dabanloo, N.J. Fuzzy Support Vector Machine Analysis in EEG Classification. Int. Res. J. Appl. Basic Sci. 2013, 5, 161–165. [Google Scholar]
- Perseh, B.; Sharafat, A.R. An Efficient P300-Based BCI using Wavelet Features and IBPSO-Based Channel Selection. J. Med. Signals Sens. 2012, 2, 128–143. [Google Scholar] [PubMed]
- Dornhege, G.; Blankertz, B.; Curio, G.; Muller, K. Boosting Bit Rates in Noninvasive EEG Single-Trial Classifications by Feature Combination and Multiclass Paradigms. IEEE Trans. Biomed. Eng. 2004, 51, 993–1002. [Google Scholar] [CrossRef] [PubMed]
- Pavlidis, G. Using Other Statistical Features. In Mixed Raster Content: Segmentation, Compression, Transmission; Springer: Singapore, 2016; p. 324. [Google Scholar]
- Li, Y.; Lin, C.; Huang, J.; Zhang, W. A New Method to Construct Reduced Vector Sets for Simplifying Support Vector Machines. In Proceedings of the IEEE International Conference on Engineering of Intelligent Systems (ICEIS 2006), Islamabad, Pakistan, 14–15 January 2006; pp. 1–5. [Google Scholar]
- Wu, Y.; Liu, Y. Robust Truncated Hinge Loss Support Vector Machines. J. Am. Stat. Assoc. 2007, 102, 974–983. [Google Scholar] [CrossRef]
- Almasi, O.N.; Rouhani, M. Fast and De-Noise Support Vector Machine Training Method Based on Fuzzy Clustering Method for Large Real World Datasets. Turk. J. Elec. Eng. Comp. Sci. 2016, 24, 219–233. [Google Scholar] [CrossRef]
- Fu, Z.; Robles-Kelly, A.; Zhou, J. Mixing Linear SVMs for Nonlinear Classification. IEEE Trans. Neural Networks 2010, 21, 1963–1975. [Google Scholar] [PubMed]
- Angiulli, F.; Astorino, A. Scaling Up Support Vector Machines using Nearest Neighbor Condensation. IEEE Trans. Neural Netw. 2010, 21, 351–357. [Google Scholar] [CrossRef] [PubMed]
- Fung, G.M.; Mangasarian, O.L. Multicategory Proximal Support Vector Machine Classifiers. Mach. Learning 2005, 59, 77–97. [Google Scholar] [CrossRef]
- Lee, Y.; Huang, S. Reduced Support Vector Machines: A Statistical Theory. IEEE Trans. Neural Networks 2007, 18, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Shalev-Shwartz, S.; Singer, Y.; Srebro, N.; Cotter, A. Pegasos: Primal estimated sub-gradient solver for SVM. Math. Program. 2011, 127, 3–30. [Google Scholar] [CrossRef]
- Jing, C.; Hou, J. SVM and PCA Based Fault Classification Approaches for Complicated Industrial Process. Neurocomputing 2015, 167, 636–642. [Google Scholar] [CrossRef]
- Blankertz, B.; Muller, K.; Curio, G.; Vaughan, T.M.; Schalk, G.; Wolpaw, J.R.; Schlogl, A.; Neuper, C.; Pfurtscheller, G.; Hinterberger, T. The BCI Competition 2003: Progress and Perspectives in Detection and Discrimination of EEG Single Trials. IEEE Trans. Biomed. Eng. 2004, 51, 1044–1051. [Google Scholar] [CrossRef] [PubMed]
- Blankertz, B.; Muller, K.; Krusienski, D.J.; Schalk, G.; Wolpaw, J.R.; Schlogl, A.; Pfurtscheller, G.; Millan, J.R.; Schroder, M.; Birbaumer, N. The BCI Competition III: Validating Alternative Approaches to Actual BCI Problems. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Tangermann, M.; Müller, K.; Aertsen, A.; Birbaumer, N.; Braun, C.; Brunner, C.; Leeb, R.; Mehring, C.; Miller, K.J.; Mueller-Putz, G. Review of the BCI Competition IV. Front. Neurosci. 2012, 6, 55. [Google Scholar] [CrossRef] [PubMed]
- Yaacoub, C.; Mhanna, G.; Rihana, S. A Genetic-Based Feature Selection Approach in the Identification of Left/Right Hand Motor Imagery for a Brain-Computer Interface. Brain Sci. 2017, 7, 12. [Google Scholar] [CrossRef] [PubMed]
- Pfurtscheller, G.; Da Silva, F.L. Event-Related EEG/MEG Synchronization and Desynchronization: Basic Principles. Clin. Neurophysiol. 1999, 110, 1842–1857. [Google Scholar] [CrossRef]
- Yamawaki, N.; Wilke, C.; Liu, Z.; He, B. An Enhanced Time-Frequency-Spatial Approach for Motor Imagery Classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 205–254. [Google Scholar] [CrossRef] [PubMed]
- Ahn, M.; Cho, H.; Ahn, S.; Jun, S.C. High Theta and Low Alpha Powers may be Indicative of BCI-Illiteracy in Motor Imagery. PLoS ONE 2013, 8, e80886. [Google Scholar] [CrossRef] [PubMed]
- Yong, X.; Ward, R.K.; Birch, G.E. Generalized Morphological Component Analysis for EEG Source Separation and Artifact Removal. In Proceedings of the 4th International IEEE/EMBS Conference on Neural Engineering, Antalya, Turkey, 29 April 2009–2 May 2009; pp. 343–346. [Google Scholar]
- Chinarro, D. Wavelet Transform Techniques. In System Engineering Applied to Fuenmayor Karst Aquifer (San Julián De Banzo, Huesca) and Collins Glacier (King George Island, Antarctica); Springer: Berlin, Germany, 2014; pp. 26–27. [Google Scholar]
- Valens, C. A really Friendly Guide to Wavelets. Available online: http://www.cs.unm.edu/~williams/cs530/arfgtw.pdf (accessed on 22 August 2017).
- Chen, S.; Zhu, H.Y. Wavelet Transform for Processing Power Quality Disturbances. EURASIP J. Adv. Signal Process. 2007, 1, 047695. [Google Scholar] [CrossRef]
- Addison, P.S.; Walker, J.; Guido, R.C. Time–Frequency Analysis of Biosignals. IEEE Eng. Med. Biol. Mag. 2009, 28, 14–29. [Google Scholar] [CrossRef] [PubMed]
- Najmi, A.; Sadowsky, J. The Continuous Wavelet Transform and Variable Resolution Time-Frequency Analysis. Johns Hopkins APL Tech. Dig. 1997, 18, 134–140. [Google Scholar]
- Herman, P.; Prasad, G.; McGinnity, T.M.; Coyle, D. Comparative Analysis of Spectral Approaches to Feature Extraction for EEG-Based Motor Imagery Classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 16, 317–326. [Google Scholar] [CrossRef] [PubMed]
- Lemm, S.; Schafer, C.; Curio, G. BCI Competition 2003-Data Set III: Probabilistic Modeling of sensorimotor/spl mu/rhythms for Classification of Imaginary Hand Movements. IEEE Trans. Biomed. Eng 2004, 51, 1077–1080. [Google Scholar] [CrossRef] [PubMed]
- Brodu, N.; Lotte, F.; Lécuyer, A. Exploring Two Novel Features for EEG-Based Brain-Computer Interfaces: Multifractal Cumulants and Predictive Complexity. Neurocomputing 2012, 79, 87–94. [Google Scholar] [CrossRef]
- Brodu, N.; Lotte, F.; Lécuyer, A. Comparative Study of Band-Power Extraction Techniques for Motor Imagery Classification. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence, Cognitive Algorithms, Mind, and Brain (CCMB 2011), Paris, France, 11–15 April 2011; pp. 1–6. [Google Scholar]
- Subasi, A. EEG Signal Classification using Wavelet Feature Extraction and a Mixture of Expert Model. Expert Syst. Appl. 2007, 32, 1084–1093. [Google Scholar] [CrossRef]
- Subasi, A. Application of Adaptive Neuro-Fuzzy Inference System for Epileptic Seizure Detection Using Wavelet Feature Extraction. Comput. Biol. Med. 2007, 37, 227–244. [Google Scholar] [CrossRef] [PubMed]
- Murugappan, M.; Rizon, M.; Nagarajan, R.; Yaacob, S.; Zunaidi, I.; Hazry, D. EEG Feature Extraction for Classifying Emotions Using FCM and FKM. Int. J. Comput. Commun. 2007, 1, 21–25. [Google Scholar]
- Hashemi, A.; Arabalibiek, H.; Agin, K. Classification of Wheeze Sounds Using Wavelets and Neural Networks. In Proceedings of the 2011 International Conference on Biomedical Engineering and Technology, Kuala Lumpur, Malaysia, 17–19 June 2011; pp. 127–131. [Google Scholar]
- Yu, Y.; McKelvey, T.; Kung, S. A Classification Scheme for High-Dimensional-Small-Smaple-Size Data Using Soda and Ridege-SVM with Microwave Measurement Applications. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 3542–3546. [Google Scholar]
- Li, H.; Chutatape, O. Automated Feature Extraction in Color Retinal Images by a Model Based Approach. IEEE Trans. Biomed. Eng 2004, 51, 246–254. [Google Scholar] [CrossRef] [PubMed]
- Sinha, R.K.; Aggarwal, Y.; Das, B.N. Backpropagation Artificial Neural Network Classifier to Detect Changes in Heart Sound due to Mitral Valve Regurgitation. J. Med. Syst. 2007, 31, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Naeem, M.; Brunner, C.; Pfurtscheller, G. Dimensionality Reduction and Channel Selection of Motor Imagery Electroencephalographic Data. Comput. Intell. Neurosci. 2009, 2009, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, Z.; Liu, C.; Zhang, X.; Zhang, H. Training Data Reduction to Speed Up SVM Training. Appl. Intell. 2014, 41, 405–420. [Google Scholar] [CrossRef]
- Campbell, W.M.; Sturim, D.E.; Reynolds, D.A. Support Vector Machines using GMM Supervectors for Speaker Verification. IEEE Signal Process. Lett. 2006, 13, 308–311. [Google Scholar] [CrossRef]
- Reynolds, D. Gaussian Mixture Models. In Encyclopedia of Biometrics; Springer: Boston, MA, USA, 2009; pp. 827–832. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–38. [Google Scholar]
- Hsu, C.; Chang, C.; Lin, C. A Practical Guide to Support Vector Classification. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 6 October 2017).
- Zhou, S.; Gan, J.Q.; Sepulveda, F. Classifying Mental Tasks Based on Features of Higher-Order Statistics from EEG Signals in brain-computer Interface. Inf. Sci. 2008, 178, 1629–1640. [Google Scholar] [CrossRef]
- Rozado, D.; Duenser, A.; Howell, B. Improving the performance of an EEG-based motor imagery brain computer interface using task evoked changes in pupil diameter. PLoS ONE 2015, 10, e0121262. [Google Scholar] [CrossRef] [PubMed]





| Subject | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Training Data Points | 140 | 540 | 540 | 400 | 400 | 400 | 420 | 420 | 400 | 400 | 440 | 400 |
| Number of Test Data Points | 140 | 540 | 540 | 320 | 280 | 320 | 320 | 320 | 320 | 320 | 320 | 320 |
| Subject | DWT | CWT | Combined Feature Vectors | |||
|---|---|---|---|---|---|---|
| without PCA | with PCA | |||||
| Accuracy | Number of Features | Accuracy | Number of Features | |||
| 1 | 92.9 | 94.1 | 96.4 | 96 | 97.5 | 33 |
| 2 | 73.3 | 81.4 | 83.1 | 96 | 83.1 | 40 |
| 3 | 62.5 | 80.7 | 80.5 | 96 | 83.3 | 39 |
| 4 | 75.2 | 77.7 | 79.1 | 96 | 76.7 | 35 |
| 5 | 52.6 | 60.1 | 60.0 | 96 | 61.4 | 34 |
| 6 | 55.4 | 55.6 | 51.8 | 96 | 56.2 | 32 |
| 7 | 95.5 | 96.2 | 96.2 | 96 | 96.1 | 30 |
| 8 | 88.3 | 87.4 | 94.0 | 96 | 94.1 | 32 |
| 9 | 79.2 | 87.8 | 90.2 | 96 | 88.1 | 34 |
| 10 | 74.8 | 72.6 | 81.4 | 96 | 80.7 | 36 |
| 11 | 90.6 | 87.7 | 89.3 | 96 | 90.0 | 32 |
| 12 | 78.7 | 83.3 | 84.2 | 96 | 84.8 | 34 |
| Mean | 76.6 | 80.4 | 82.2 | 96 | 82.7 | 34.3 |
| p-value | p < 0.05 | p < 0.05 | p = 0.20 | - | - | - |
| Ranking | Methods | Subject 1 | |
|---|---|---|---|
| Maximal MI (bit) | Accuracy (%) | ||
| 1 | ALL-SVM | 0.84 | 97.50 |
| 2 | 30%-SVM | 0.67 | 93.79 |
| 3 | FSVM in [21] | 0.66 | 87.86 |
| 4 | SVM in [21] | 0.65 | 89.83 |
| 5 | NN in [65] | 0.64 | 90.00 |
| 6 | LDA in [65] | 0.63 | 89.29 |
| 7 | 1st winner | 0.61 | 89.29 |
| 8 | SVM in [65] | 0.58 | 90.00 |
| 9 | 2nd winner | 0.46 | 84.29 |
| Ranking | Methods | Maximal MI(bit) | ||
|---|---|---|---|---|
| Subject 2 | Subject 3 | Mean | ||
| 1 | 1st winner | 0.4382 | 0.3489 | 0.3936 |
| 2 | ALL-SVM | 0.3447 | 0.3562 | 0.3505 |
| 3 | 30%-SVM | 0.3105 | 0.3216 | 0.3161 |
| 4 | 2nd winner | 0.4174 | 0.1719 | 0.2947 |
| 5 | FSVM in [21] | 0.0718 | 0.0863 | 0.0791 |
| 6 | SVM in [21] | 0.0718 | 0.0809 | 0.0764 |
| Ranking | Methods | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ALL-SVM | 0.54 | 0.24 | 0.12 | 0.92 | 0.88 | 0.76 | 0.61 | 0.80 | 0.70 | 0.62 |
| 2 | 1st winner | 0.40 | 0.21 | 0.22 | 0.95 | 0.86 | 0.61 | 0.56 | 0.85 | 0.74 | 0.60 |
| 3 | 30%-SVM | 0.51 | 0.17 | 0.12 | 0.92 | 0.83 | 0.76 | 0.55 | 0.79 | 0.67 | 0.59 |
| 3 | 2nd winner | 0.42 | 0.21 | 0.14 | 0.94 | 0.71 | 0.62 | 0.61 | 0.84 | 0.78 | 0.59 |
| 5 | 3rd winner | 0.19 | 0.12 | 0.12 | 0.77 | 0.57 | 0.49 | 0.37 | 0.85 | 0.61 | 0.45 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Park, S.-H.; Lee, S.-G. Improving the Accuracy and Training Speed of Motor Imagery Brain–Computer Interfaces Using Wavelet-Based Combined Feature Vectors and Gaussian Mixture Model-Supervectors. Sensors 2017, 17, 2282. https://doi.org/10.3390/s17102282
Lee D, Park S-H, Lee S-G. Improving the Accuracy and Training Speed of Motor Imagery Brain–Computer Interfaces Using Wavelet-Based Combined Feature Vectors and Gaussian Mixture Model-Supervectors. Sensors. 2017; 17(10):2282. https://doi.org/10.3390/s17102282
Chicago/Turabian StyleLee, David, Sang-Hoon Park, and Sang-Goog Lee. 2017. "Improving the Accuracy and Training Speed of Motor Imagery Brain–Computer Interfaces Using Wavelet-Based Combined Feature Vectors and Gaussian Mixture Model-Supervectors" Sensors 17, no. 10: 2282. https://doi.org/10.3390/s17102282
APA StyleLee, D., Park, S.-H., & Lee, S.-G. (2017). Improving the Accuracy and Training Speed of Motor Imagery Brain–Computer Interfaces Using Wavelet-Based Combined Feature Vectors and Gaussian Mixture Model-Supervectors. Sensors, 17(10), 2282. https://doi.org/10.3390/s17102282





