Flexible Sensors for Pressure Therapy: Effect of Substrate Curvature and Stiffness on Sensor Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sensors Used for Evaluation
2.2. Experimental Setup
2.3. Data Acquisition System
2.4. Test Procedure
3. Results
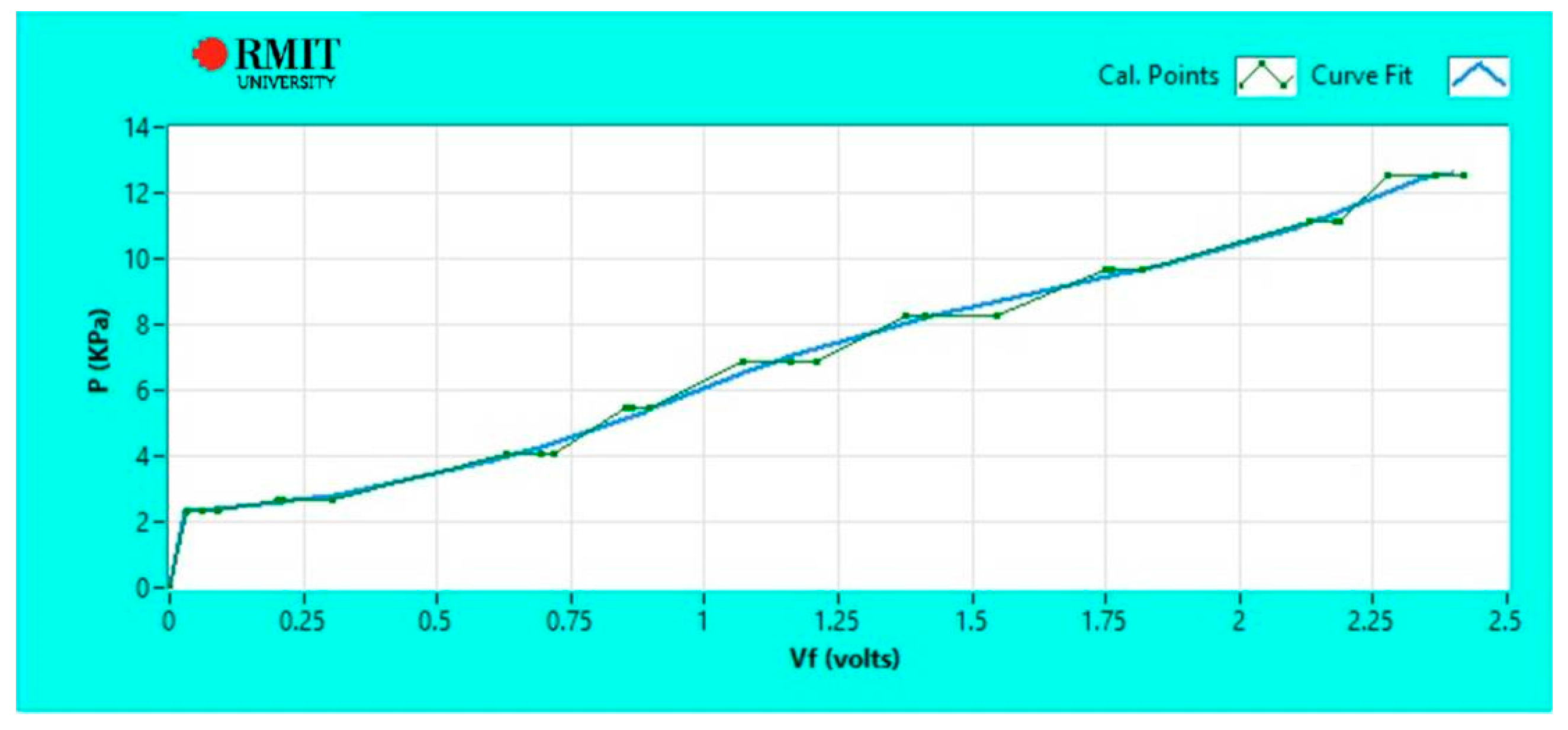
3.1. Static Evaluation
3.2. Dynamic Evaluation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pantelopoulos, A.; Bourbakis, N.G. A survey on wearable sensor-based systems for health monitoring and prognosis. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2010, 40, 1–12. [Google Scholar] [CrossRef]
- Chaudhry, B.; Wang, J.; Wu, S.; Maglione, M.; Mojica, W.; Roth, E.; Morton, S.C.; Shekelle, P.G. Systematic review: Impact of health information technology on quality, efficiency, and costs of medical care. Ann. Intern. Med. 2006, 144, 742–752. [Google Scholar] [CrossRef] [PubMed]
- Banaee, H.; Ahmed, M.; Loutfi, A. Data mining for wearable sensors in health monitoring systems: A review of recent trends and challenges. Sensors 2013, 13, 17472–17500. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, S.C. Wearable sensors for human activity monitoring: A review. IEEE Sens. J. 2015, 15, 1321–1330. [Google Scholar] [CrossRef]
- Zang, Y.; Zhang, F.; Di, C.-a.; Zhu, D. Advances of flexible pressure sensors toward artificial intelligence and health care applications. Mater. Horiz. 2015, 2, 140–156. [Google Scholar] [CrossRef]
- Rodgers, M.M.; Pai, V.M.; Conroy, R.S. Recent advances in wearable sensors for health monitoring. IEEE Sens. J. 2015, 15, 3119–3126. [Google Scholar] [CrossRef]
- Parmar, S.; Bafekrpour, E.; Fuss, F.K.; Troynikov, O. Design and characterization of flexible pressure sensors for integration in smart medical textiles. In Proceedings of the 9th Textile Bioengineering and Informatics Symposium (TBIS 2016), Melbourne, Australia, 12–15 July 2016; pp. 1019–1027. [Google Scholar]
- Chen, L.Y.; Tee, B.C.-K.; Chortos, A.L.; Schwartz, G.; Tse, V.; Lipomi, D.J.; Wong, H.-S.P.; McConnell, M.V.; Bao, Z. Continuous wireless pressure monitoring and mapping with ultra-small passive sensors for health monitoring and critical care. Nat. Commun. 2014, 5, 5028. [Google Scholar] [CrossRef] [PubMed]
- Parmar, S.; Bafekrpour, E.; Fuss, F.K.; Troynikov, O. Evaluation of pressure sensors based on piezoresistive films for integration in smart medical textiles. In Proceedings of the 9th Textile Bioengineering and Informatics Symposium (TBIS 2016), Melbourne, Australia, 12–15 July 2016; pp. 951–958. [Google Scholar]
- Baranoski, S.; Ayello, E.A.; Mclntosh, A.; Galvan, L.; Scarborough, P. Wound treatment options. In Wound Care Essentials: Practice Principles, 2nd ed.; Baranoski, S., Ayello, E.A., Eds.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2008; pp. 136–171. [Google Scholar]
- Van Geest, A.; Franken, C.; Neumann, H. Medical elastic compression stockings in the treatment of venous insufficiency. In Textiles and the Ski; Elsner, P., Hatch, K., Wigger, W., Eds.; Karger Publishers: Basel, Switzerland, 2003; Volume 31, pp. 98–107. [Google Scholar]
- Price, C.; Parker, D.; Nester, C. Validity and repeatability of three in-shoe pressure measurement systems. Gait Posture 2016, 46, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Figueiredo, J.; Ferreira, C.; Costa, L.; Sepúlveda, J.; Reis, L.P.; Moreno, J.C.; Santos, C.P. In Instrumented insole system for ambulatory and robotic walking assistance: First advances. In Proceedings of the IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Coimbra, Portugal, 26–28 April 2017; pp. 116–121. [Google Scholar]
- Al Khaburi, J.A.J. Pressure Mapping of Medical Compression Bandages Used for Venous Leg Ulcer Treatment. Ph.D. Thesis, University of Leeds, Leeds, UK, 2010. [Google Scholar]
- Baldoli, I.; Mazzocchi, T.; Paoletti, C.; Ricotti, L.; Salvo, P.; Dini, V.; Laschi, C.; Francesco, F.D.; Menciassi, A. Pressure mapping with textile sensors for compression therapy monitoring. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2016, 230, 795–808. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, M.; Blaber, A.P.; Menon, C. In Towards the evaluation of force-sensing resistors for in situ measurement of interface pressure during leg compression therapy. In Proceedings of the IEEE Healthcare Innovation Point-Of-Care Technologies Conference (HI-POCT), Cancun, Mexico, 9–11 November 2016; pp. 25–28. [Google Scholar]
- Lebosse, C.; Renaud, P.; Bayle, B.; Mathelin, M.D. Modeling and evaluation of low-cost force sensors. IEEE Trans. Robot. 2011, 27, 815–822. [Google Scholar] [CrossRef]
- Dabling, J.G.; Filatov, A.; Wheeler, J.W. In Static and cyclic performance evaluation of sensors for human interface pressure measurement. In Proceedings of the IEEE Annual International Conference of the Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August 2012–1 September 2012; pp. 162–165. [Google Scholar]
- Giovanelli, D.; Farella, E. Force sensing resistor and evaluation of technology for wearable body pressure sensing. J. Sens. 2016, 2016, 9391850. [Google Scholar] [CrossRef]
- Khaburi, J.A.; Dehghani-Sanij, A.A.; Nelson, E.A.; Hutchinson, J. In Measurement of interface pressure applied by medical compression bandages. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 289–294. [Google Scholar]
- Mehmood, N.; Hariz, A.; Templeton, S.; Voelcker, N. An improved flexible telemetry system to autonomously monitor sub-bandage pressure and wound moisture. Sensors 2014, 14, 21770–21790. [Google Scholar] [CrossRef] [PubMed]
- Ferguson-Pell, M.; Hagisawa, S.; Bain, D. Evaluation of a sensor for low interface pressure applications. Méd. Eng. Phys. 2000, 22, 657–663. [Google Scholar] [CrossRef]
- Komi, E.R.; Roberts, J.R.; Rothberg, S. Evaluation of thin, flexible sensors for time-resolved grip force measurement. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 1687–1699. [Google Scholar] [CrossRef]
- Likitlersuang, J.; Leineweber, M.J.; Andrysek, J. Evaluating and improving the performance of thin film force sensors within body and device interfaces. Méd. Eng. Phys. 2017, 48, 206–211. [Google Scholar] [CrossRef] [PubMed]
- Parmar, S.; Khodasevych, I.; Troynikov, O. Evaluation of flexible force sensors for pressure monitoring in treatment of chronic venous disorders. Sensors 2017, 17, 1923. [Google Scholar] [CrossRef] [PubMed]
- Peratech Holdco Limited. Peratech QTC® SP200 Series Datasheet Single Point Sensors. Available online: https://www.peratech.com/assets/uploads/datasheets/Peratech-QTC-DataSheet-SP200-Series-Nov15.pdf (accessed on 17 July 2017).
- Sensitronics Inc. Half Inch ThruMode FSR. Available online: http://www.sensitronics.com/products-half-inch-thru-mode-fsr.php (accessed on 17 July 2017).
- Troynikov, O.; Ashayeri, E. 3D body scanning method for close-fitting garments in sport and medical applications. In Proceedings of the 47th Annual Conference of Human Factors and Ergonomics Society of Australia (HFESA), Crows Nest, Australia, 7–9 November 2011; pp. 11–16. [Google Scholar]











| Sensor | Manufacturer | Sensing Area | Claimed Operating Range |
|---|---|---|---|
| QTCTM SP 200-10 | Peratech Ltd. | 10.0 mm | 0.1–20 N [26] |
| Half Inch ThruMode FSR | Sensitronics® Inc. | 12.7 mm | 0.3–30 psi [27] |
| Sensor | Surface Type | Accuracy, % | ||
|---|---|---|---|---|
| 30.5 mmHg | 51.4 mmHg | 72.7 mmHg | ||
| Peratech | Flat rigid | 90.0 | 91.7 | 98.7 |
| Flat soft | 98.0 | 97.2 | 96.5 | |
| 7 cm curved soft | 94.1 | 92.1 | 91.5 | |
| 11 cm curved soft | 95.8 | 95.4 | 91.9 | |
| 13 cm curved soft | 83.7 | 98.2 | 95.6 | |
| Sensitronics | Flat rigid | 86.8 | 96.4 | 80.6 |
| Flat soft | - | 94.6 | 75.5 | |
| 7 cm curved soft | 89.7 | 89.8 | 90.0 | |
| 11 cm curved soft | 91.2 | 92.8 | 92.4 | |
| 13 cm curved soft | 84.2 | 87.1 | 85.0 | |
| Sensor | Surface Type | Accuracy, % | ||
|---|---|---|---|---|
| 30.5 mmHg | 51.4 mmHg | 72.7 mmHg | ||
| Peratech | Flat rigid | 90.8 ± 5.5 | 91.9 ± 3.5 | 96.0 ± 1.7 |
| Flat soft | 97.9 ± 1.2 | 95.1 ± 3.0 | 97.1 ± 1.1 | |
| 7 cm curved soft | 95.6 ± 2.9 | 96.6 ± 2.7 | 97.5 ± 1.6 | |
| 11 cm curved soft | 97.0 ± 2.4 | 95.3 ± 2.3 | 97.8 ± 1.4 | |
| 13 cm curved soft | 94.3 ± 1.7 | 95.9 ± 2.3 | 96.1 ± 1.8 | |
| Sensitronics | Flat rigid | 84.2 ± 11.2 | 84.7 ± 6.2 | 85.3 ± 2.0 |
| Flat soft | 90.6 ± 6.1 | 94.2 ± 3.1 | 90.1 ± 2.7 | |
| 7 cm curved soft | 90.9 ± 3.2 | 92.4 ± 3.4 | 94.3 ± 2.6 | |
| 11 cm curved soft | 95.1 ± 2.8 | 94.6 ± 1.2 | 97.9 ± 1.7 | |
| 13 cm curved soft | 90.5 ± 7.2 | 91.8 ± 4.9 | 93.0 ± 2.2 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodasevych, I.; Parmar, S.; Troynikov, O. Flexible Sensors for Pressure Therapy: Effect of Substrate Curvature and Stiffness on Sensor Performance. Sensors 2017, 17, 2399. https://doi.org/10.3390/s17102399
Khodasevych I, Parmar S, Troynikov O. Flexible Sensors for Pressure Therapy: Effect of Substrate Curvature and Stiffness on Sensor Performance. Sensors. 2017; 17(10):2399. https://doi.org/10.3390/s17102399
Chicago/Turabian StyleKhodasevych, Iryna, Suresh Parmar, and Olga Troynikov. 2017. "Flexible Sensors for Pressure Therapy: Effect of Substrate Curvature and Stiffness on Sensor Performance" Sensors 17, no. 10: 2399. https://doi.org/10.3390/s17102399
APA StyleKhodasevych, I., Parmar, S., & Troynikov, O. (2017). Flexible Sensors for Pressure Therapy: Effect of Substrate Curvature and Stiffness on Sensor Performance. Sensors, 17(10), 2399. https://doi.org/10.3390/s17102399





