Penalized Maximum Likelihood Angular Super-Resolution Method for Scanning Radar Forward-Looking Imaging
Abstract
:1. Introduction
2. Signal Model for Forward-Looking Scanning Radar
3. Methodology
3.1. Likelihood
3.2. Joint Square-Laplacian Penalty
3.3. Solution for the Optimal Problem
4. Numerical Results
4.1. Simulation Experiment
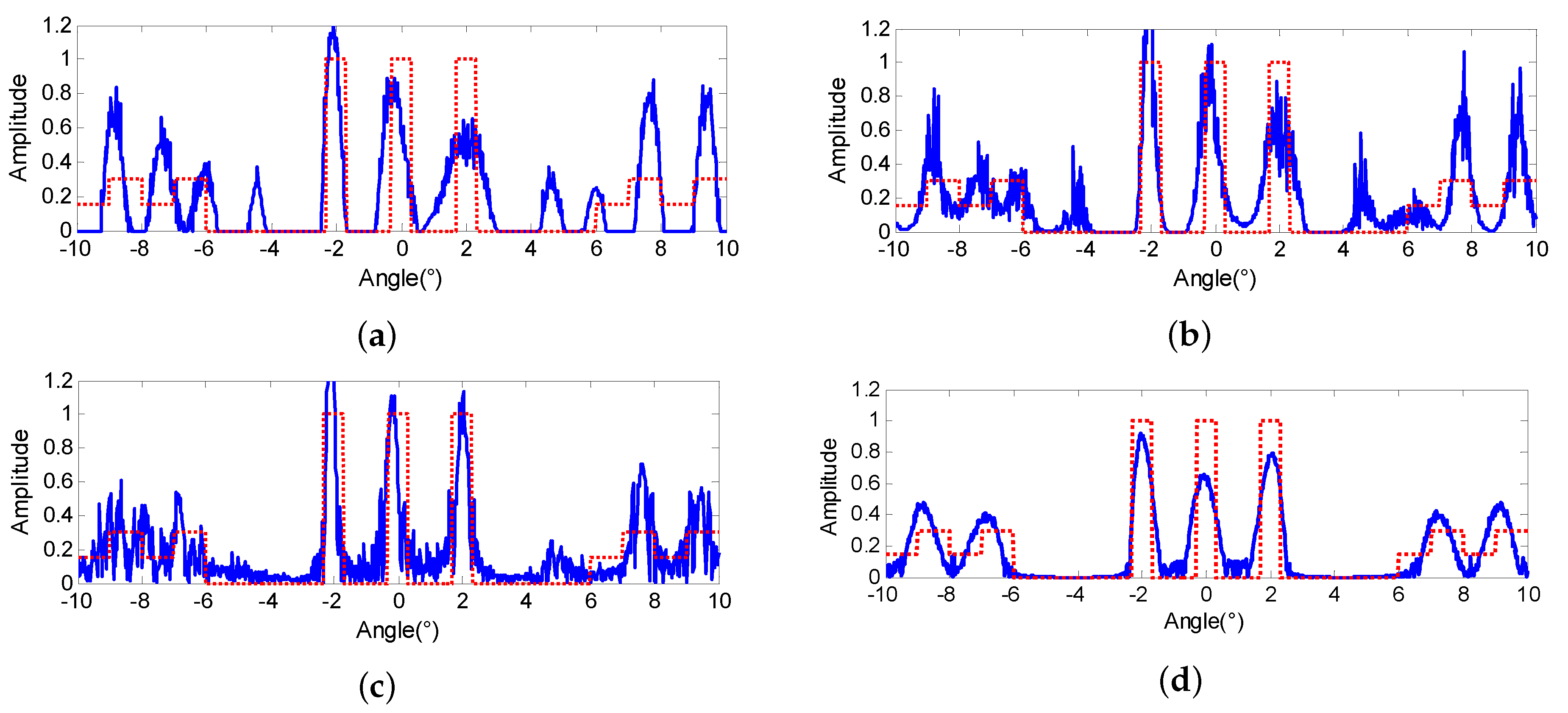
4.1.1. Effectiveness Verification for Noise Resistance
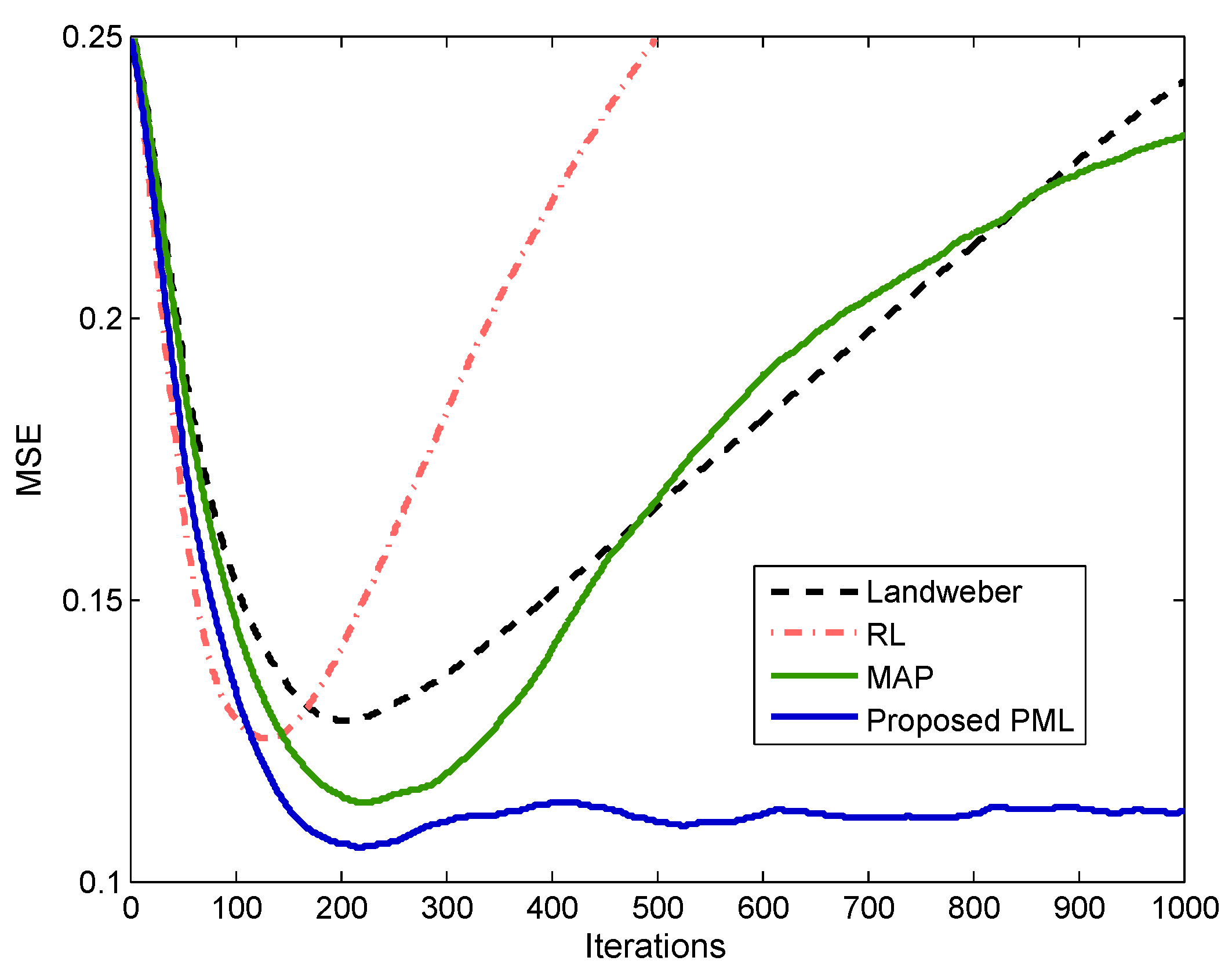
4.1.2. Effectiveness Verification for Iterative Robustness
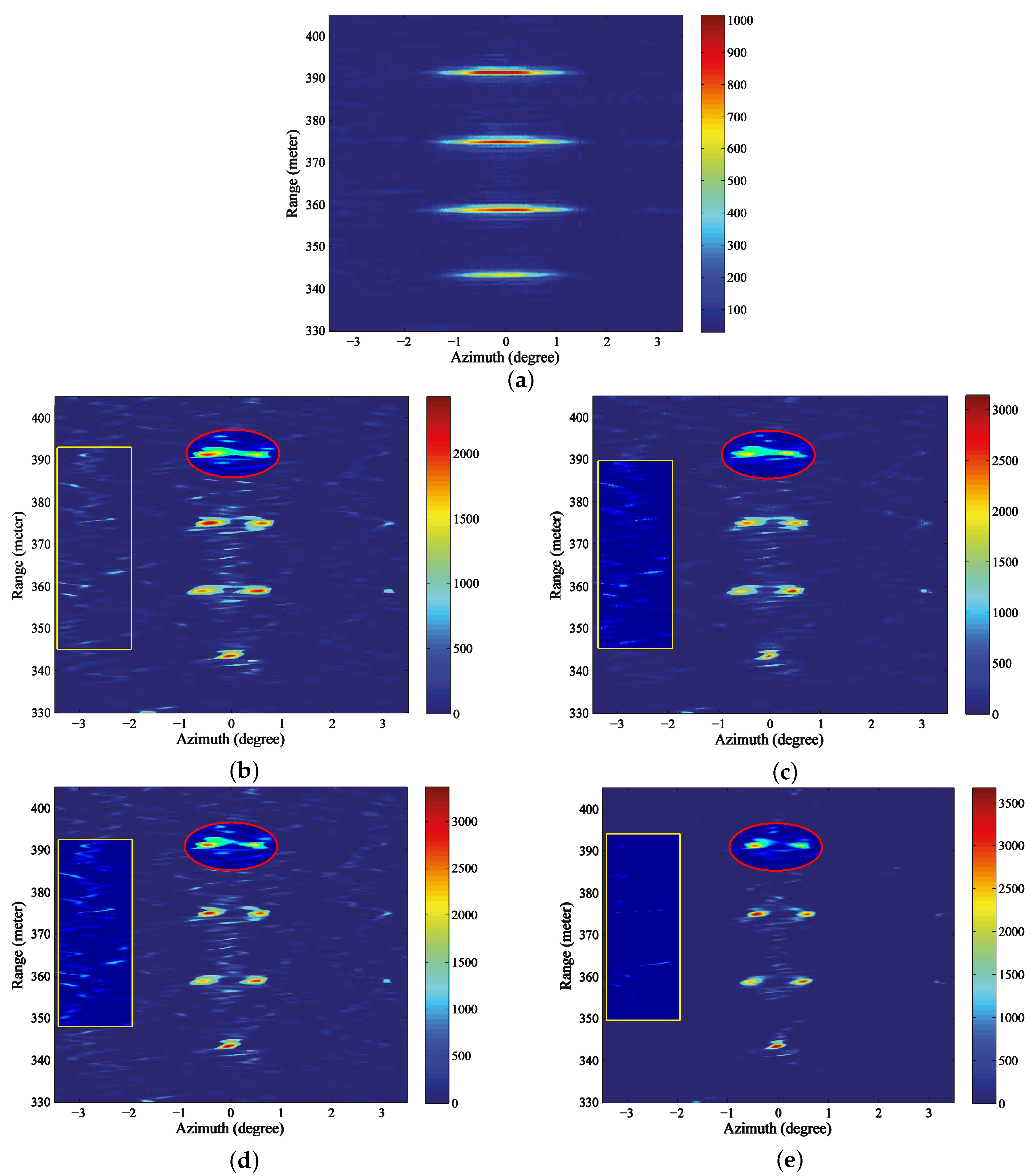
4.2. Real Data Processing
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Walterscheid, I.; Espeter, T.; Klare, J.; Brenner, A.R.; Ender, J. Potential and limitations of forward-looking bistatic SAR. In Proceedings of the 2010 IEEE Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 216–219. [Google Scholar]
- Wang, Y.; Sun, Y.; Li, J.; Stoica, P. Adaptive imaging for forward-looking ground penetrating radar. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 922–936. [Google Scholar] [CrossRef]
- Walterscheid, I.; Espeter, T.; Klare, J.; Brenner, A. In Bistatic spaceborne-airborne forward-looking SAR. In Proceedings of the 2010 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Loehner, A. Improved azimuthal resolution of forward looking SAR by sophisticated antenna illumination function design. IEE Proc. Radar Sonar Navig. 1998, 145, 128–134. [Google Scholar] [CrossRef]
- Dai, S.; Wiesbeck, W. In High resolution imaging for forward looking SAR with multiple receiving antennas. In Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 24–28 July 2000; pp. 2254–2256. [Google Scholar]
- Wu, J.; Yang, J.; Huang, Y.; Yang, H.; Wang, H. In Bistatic forward-looking SAR: Theory and challenges. In Proceedings of the 2009 IEEE National Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–4. [Google Scholar]
- Wu, J.; Li, Z.; Huang, Y.; Yang, J.; Yang, H.; Liu, Q. Focusing Bistatic Forward-Looking SAR With Stationary Transmitter Based on Keystone Transform and Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2014, 11, 148–152. [Google Scholar] [CrossRef]
- Li, W.; Yang, Y.; Huang, Y.; Kong, L.; Wu, J. An improved radon-transform-based scheme of doppler centroid estimation for bistatic forward-looking SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 379–383. [Google Scholar] [CrossRef]
- Li, W.; Yang, J.; Huang, Y.; Wu, J. A geometry-based Doppler centroid estimator for bistatic forward-looking SAR. IEEE Geosci. Remote Sens. Lett. 2012, 9, 388–392. [Google Scholar] [CrossRef]
- Richards, M.A. Iterative noncoherent angular superresolution radar. In Proceedings of the 1988 IEEE National Radar Conference, Ann Arbor, MI, USA, 20–21 April 1988; pp. 100–105. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Li, W.; Huang, Y.; Yang, J. Super-Resolution Surface Mapping for Scanning Radar: Inverse Filtering Based on the Fast Iterative Adaptive Approach. IEEE Trans. Geosci. Remote Sens. 2017, 56, 127–144. [Google Scholar] [CrossRef]
- Zhang, Y.; Jakobsson, A.; Yang, J. Range-Recursive IAA for Scanning Radar Angular Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1675–1679. [Google Scholar] [CrossRef]
- Zha, Y.; Huang, Y.; Yang, J. Augmented lagrangian method for angular super-resolution imaging in forward-looking scanning radar. J. Appl. Remote Sens. 2015, 9, 096055. [Google Scholar] [CrossRef]
- Richards, M.; Morris, C.; Hayes, M. Iterative enhancement of noncoherent radar data. In Proceedings of the 1986 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Tokyo, Japan, 7–11 April 1986; pp. 100–105. [Google Scholar]
- Senmoto, S.; Childers, D. Signal resolution via digital inverse filtering. IEEE Trans. Aerosp. Electron. Syst. 1972, 5, 633–640. [Google Scholar] [CrossRef]
- Sadjadi, F. Radar beam sharpening using an optimum FIR filter. Circuits Syst. Signal Process. 2000, 19, 121–129. [Google Scholar]
- Hansen, P.C. Truncated singular value decomposition solutions to discrete ill-posed problems with ill-determined numerical rank. SIAM J. Sci. Stat. Comput. 1990, 11, 503–518. [Google Scholar] [CrossRef]
- Lenti, F.; Nunziata, F.; Migliaccio, M.; Rodriguez, G. Two-dimensional TSVD to enhance the spatial resolution of radiometer data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2450–2458. [Google Scholar] [CrossRef]
- Huang, Y.; Zha, Y.; Wang, Y.; Yang, J. Forward Looking Radar Imaging by Truncated Singular Value Decomposition and Its Application for Adverse Weather Aircraft Landing. Sensors 2015, 15, 14397–14414. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Setsompop, K.; Ye, H.; Cauley, S.F.; Wald, L.L. Maximum likelihood reconstruction for magnetic resonance fingerprinting. IEEE Trans. Med. Imaging 2016, 35, 1812–1823. [Google Scholar] [CrossRef] [PubMed]
- Shepp, L.A.; Vardi, Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1982, 1, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Piana, M.; Bertero, M. Projected Landweber method and preconditioning. Inverse Probl. 2015, 13, 441–463. [Google Scholar] [CrossRef]
- Jiang, M.; Zhou, T.; Cheng, J.; Cong, W.; Wang, G. Image reconstruction for bioluminescence tomography from partial measurement. Opt. Express 2007, 15, 11095–11116. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, Z.; Luo, Q.; Zeng, S. Richardson-Lucy deconvolution for two-photon fluorescence images via nonlinear diffusion equation pre-filtering. Int. Soc. Opt. Photonics 2007, 6436, 1–6. [Google Scholar]
- Dey, N.; Blanc-Feraud, L.; Zimmer, C.; Roux, P.; Kam, Z.; Olivo-Marin, J.C.; Zerubia, J. Richardson–Lucy algorithm with total variation regularization for 3D confocal microscope deconvolution. Microsc. Res. Tech. 2006, 69, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Zha, Y.; Huang, Y.; Sun, Z.; Wang, Y.; Yang, J. Bayesian deconvolution for angular super-resolution in forward-looking scanning radar. Sensors 2015, 15, 6924–6946. [Google Scholar] [CrossRef] [PubMed]
- Guan, J.; Yang, J.; Huang, Y.; Li, W. Maximum a posteriori-based angular superresolution for scanning radar imaging. Opt. Express 2014, 50, 2389–2398. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. A Sparse Bayesian Approach for Forward-Looking Superresolution Radar Imaging. Sensors 2017, 17, 1353. [Google Scholar] [CrossRef] [PubMed]
- DellAcqua, F.; Scifo, P.; Rizzo, G.; Catani, M.; Simmons, A.; Scotti, G.; Fazio, F. A modified damped Richardson–Lucy algorithm to reduce isotropic background effects in spherical deconvolution. Neuroimage 2010, 49, 1446–1458. [Google Scholar] [CrossRef] [PubMed]
- Lenti, F.; Nunziata, F.; Estatico, C.; Migliaccio, M. Spatial resolution enhancement of Earth observation products using an acceleration technique for iterative methods. IEEE Geosci. Remote Sens. Lett. 2015, 12, 269–273. [Google Scholar] [CrossRef]
- Chen, X.; Phoon, K. Some numerical experiences on convergence criteria for iterative finite element solvers. Comput. Geotech. 2009, 36, 1272–1284. [Google Scholar] [CrossRef]
- Li, W.; Yang, J.; Huang, Y. Keystone transform-based space-variant range migration correction for airborne forward-looking scanning radar. Electron. Lett. 2012, 48, 121–122. [Google Scholar] [CrossRef]
- Spiegel, M.R. Schaum’s Outline of Theory and Problems of Advanced Mathematics for Engineers and Sicentists; McGraw-Hill Education: New York, NY, USA, 2009; pp. 286–290. [Google Scholar]
- Yi, H.; Chen, D.; Li, W.; Zhu, S.; Wang, X.; Liang, J.; Tian, J. Reconstruction algorithms based on l1-norm and l2-norm for two imaging models of fluorescence molecular tomography: A comparative study. J. Biomed. Opt. 2013, 18, 56013. [Google Scholar] [CrossRef] [PubMed]
- Potter, L.C.; Ertin, E.; Parker, J.T.; Cetin, M. Sparsity and compressed sensing in radar imaging. Proc. IEEE 2010, 98, 1006–1020. [Google Scholar] [CrossRef]
- Bao, Q.; Lin, Y.; Hong, W.; Shen, W.; Zhao, Y.; Peng, X. Holographic SAR Tomography Image Reconstruction by Combination of Adaptive Imaging and Sparse Bayesian Inference. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1248–1252. [Google Scholar] [CrossRef]
- Lei, Y.; Lifan, Z.; Song, Z.; Guoan, B. Sparsity-Driven SAR Imaging for Highly Maneuvering Ground Target by the Combination of Time-Frequency Analysis and Parametric Bayesian Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1443–1455. [Google Scholar]
- Wang, B.; Zhang, S.; Wang, W. Bayesian inverse synthetic aperture radar imaging by exploiting sparse probing frequencies. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1698–1701. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Tan, K.; Li, W.; Huang, Y.; Yang, J. Angular resolution enhancement of real-beam scanning radar base on accelerated iterative shinkage/thresholding algorithm. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 929–932. [Google Scholar]











| Initial Step: Take , compute the first two iterative results and through the basic iteration formula Equation (36) |
| and the first two iterative vectors and |
| Repeat |
| Compute the extrapolation step size |
| Calculate the prediction point |
| Compute the next iterative result with the obtained predicted point through the basic iteration formula Equation (36) |
| Calculate the prediction point |
| Compute the next iterative result with the obtained predicted point through the basic iteration formula Equation (36), |
| Update the iterative vector |
| Until (convergence) |
| Output the iterative result |
| Parameters | Values |
|---|---|
| Pulse repetition frequency (PRF) | 4000 Hz |
| Antenna scanning velocity | |
| Main-lobe beam width | |
| Antenna scanning area |
| Parameters | Values |
|---|---|
| Carrier frequency | 30.75 GHz |
| Platform velocity | 30 m/s |
| Pitch angle | |
| Band width | 200 MHz |
| Pulse repetition frequency (PRF) | 4000 Hz |
| Pulse duration | 1 s |
| Antenna scanning velocity | |
| Main-lobe beam width |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, K.; Li, W.; Zhang, Q.; Huang, Y.; Wu, J.; Yang, J. Penalized Maximum Likelihood Angular Super-Resolution Method for Scanning Radar Forward-Looking Imaging. Sensors 2018, 18, 912. https://doi.org/10.3390/s18030912
Tan K, Li W, Zhang Q, Huang Y, Wu J, Yang J. Penalized Maximum Likelihood Angular Super-Resolution Method for Scanning Radar Forward-Looking Imaging. Sensors. 2018; 18(3):912. https://doi.org/10.3390/s18030912
Chicago/Turabian StyleTan, Ke, Wenchao Li, Qian Zhang, Yulin Huang, Junjie Wu, and Jianyu Yang. 2018. "Penalized Maximum Likelihood Angular Super-Resolution Method for Scanning Radar Forward-Looking Imaging" Sensors 18, no. 3: 912. https://doi.org/10.3390/s18030912
APA StyleTan, K., Li, W., Zhang, Q., Huang, Y., Wu, J., & Yang, J. (2018). Penalized Maximum Likelihood Angular Super-Resolution Method for Scanning Radar Forward-Looking Imaging. Sensors, 18(3), 912. https://doi.org/10.3390/s18030912







