A Hybrid Bionic Image Sensor Achieving FOV Extension and Foveated Imaging
Abstract
:1. Introduction
2. Methods
2.1. FOV Extension
2.2. Super-Resolution
2.3. Foveated Imaging
3. Simulations and Analysis
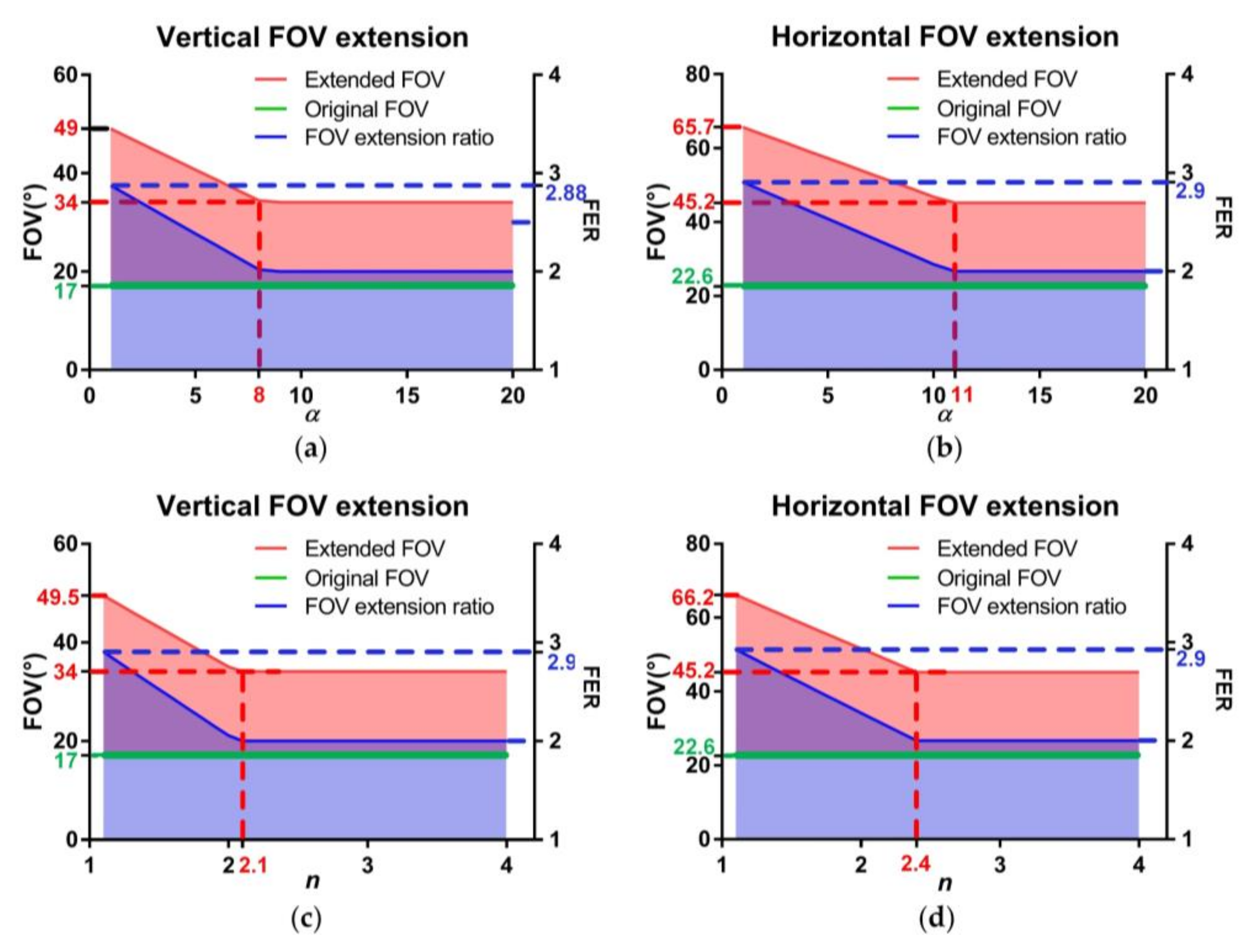
3.1. FOV Extension
3.2. Imaging with Sub-Pixel Shifts for Super-Resolution
3.3. Foveated Imaging
4. Experiments and Results
4.1. Prototype Parameters
4.2. Experimental Results
5. Discussion
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Song, Y.M.; Xie, Y.; Malyarchuk, V.; Xiao, J.; Jung, I.; Choi, K.J.; Liu, Z.; Park, H.; Lu, C.; Kim, R.H. Digital cameras with designs inspired by the arthropod eye. Nature 2013, 497, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Jiang, T.; Zhang, G.; Schoenemann, B.; Neri, F.; Zhu, M.; Bu, C.; Han, J.; Kuhnert, K.-D. Artificial compound eye: A survey of the state-of-the-art. Artif. Intell. Rev. 2017, 48, 573–603. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y.; Liu, C.; Wang, T.; Zhang, H.; Liao, W.; Xu, Z.; Yu, W. SCECam: A spherical compound eye camera for fast location and recognition of objects at a large field of view. Opt. Express 2017, 25, 32333–32345. [Google Scholar] [CrossRef]
- Yi, Q.; Hong, H. Continuously zoom imaging probe for the multi-resolution foveated laparoscope. Biomed. Opt. Express 2016, 7, 1175–1182. [Google Scholar]
- Cao, J.; Hao, Q.; Xia, W.; Peng, Y.; Cheng, Y.; Mu, J.; Wang, P. Design and realization of retina-like three-dimensional imaging based on a moems mirror. Opt. Lasers Eng. 2016, 82, 1–13. [Google Scholar] [CrossRef]
- Borst, A.; Plett, J. Optical devices: Seeing the world through an insect’s eyes. Nature 2013, 497, 47–48. [Google Scholar] [CrossRef] [PubMed]
- Prabhakara, R.S.; Wright, C.H.G.; Barrett, S.F. Motion detection: A biomimetic vision sensor versus a ccd camera sensor. IEEE Sens. J. 2012, 12, 298–307. [Google Scholar] [CrossRef]
- Srinivasan, M.V.; Bernard, G.D. Effect of motion on visual-acuity of compound eye-theoretical-analysis. Vis. Res. 1975, 15, 515–525. [Google Scholar] [CrossRef]
- Zhang, S.W.; Lehrer, M.; Srinivasan, M.V. Eye-specific learning of routes and “signposts” by walking honeybees. J. Comp. Physiol. A Sens. Neural Behav. Physiol. 1998, 182, 747–754. [Google Scholar] [CrossRef]
- Duparré, J.W.; Wippermann, F.C. Micro-optical artificial compound eyes. Bioinspir. Biomim. 2006, 1, R1. [Google Scholar] [CrossRef] [PubMed]
- Druart, G.; Guérineau, N.; Haïdar, R.; Lambert, E.; Tauvy, M.; Thétas, S.; Rommeluère, S.; Primot, J.; Deschamps, J. Multicam: A Miniature Cryogenic Camera for Infrared Detection; SPIE Photonics Europe: Bellingham, DC, USA, 2008. [Google Scholar]
- Carles, G.; Downing, J.; Harvey, A.R. Super-resolution imaging using a camera array. Opt. Lett. 2014, 39, 1889–1892. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.B.; Jang, H.; Park, S.; Song, Y.M.; Lee, H.N. COMPU-EYE: A high resolution computational compound eye. Opt. Express 2016, 24, 2013–2026. [Google Scholar] [CrossRef] [PubMed]
- Brady, D.J.; Gehm, M.E.; Stack, R.A.; Marks, D.L.; Kittle, D.S.; Golish, D.R.; Vera, E.M.; Feller, S.D. Multiscale gigapixel photography. Nature 2012, 486, 386. [Google Scholar] [CrossRef]
- Carles, G.; Chen, S.; Bustin, N.; Downing, J.; Mccall, D.; Wood, A.; Harvey, A.R. Multi-aperture foveated imaging. Opt. Lett. 2016, 41, 1869–1872. [Google Scholar] [CrossRef] [PubMed]
- Floreano, D.; Pericet-Camara, R.; Viollet, S.; Ruffier, F.; Brückner, A.; Leitel, R.; Buss, W.; Menouni, M.; Expert, F.; Juston, R.; et al. Miniature curved artificial compound eyes. Proc. Natl. Acad. Sci. USA 2013, 110, 9267–9272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Viollet, S.; Godiot, S.; Leitel, R.; Buss, W.; Breugnon, P.; Menouni, M.; Juston, R.; Expert, F.; Colonnier, F.; L’Eplattenier, G.; et al. Hardware architecture and cutting-edge assembly process of a tiny curved compound eye. Sensors 2014, 14, 21702–21721. [Google Scholar] [CrossRef] [PubMed]
- Jeong, K.H.; Kim, J.; Lee, L.P. Biologically inspired artificial compound eyes. Science 2006, 312, 557. [Google Scholar] [CrossRef] [PubMed]
- Ko, H.C.; Stoykovich, M.P.; Song, J.; Malyarchuk, V.; Choi, W.M.; Yu, C.J.; Iii, J.B.G.; Xiao, J.; Wang, S.; Huang, Y. A hemispherical electronic eye camera based on compressible silicon optoelectronics. Nature 2008, 454, 748–753. [Google Scholar] [CrossRef] [PubMed]
- Sargent, R.; Bartley, C.; Dille, P.; Keller, J.; Nourbakhsh, I.; Legrand, R. Timelapse Gigapan: Capturing, Sharing, and Exploring Timelapse Gigapixel Imagery. In Proceedings of the Fine International Conference on Gigapixel Imaging for Science, Pittsburgh, PA, USA, 11–13 November 2010. [Google Scholar]
- Hua, H.; Liu, S. Dual-sensor foveated imaging system. Appl. Opt. 2008, 47, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Rasolzadeh, B.; Björkman, M.; Huebner, K.; Kragic, D. An active vision system for detecting, fixating and manipulating objects in the real world. Int. J. Robot. Res. 2010, 29, 133–154. [Google Scholar] [CrossRef]
- Ude, A.; Gaskett, C.; Cheng, G. Foveated Vision Systems with Two Cameras per Eye. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 15–19 May 2006; pp. 3457–3462. [Google Scholar]
- González, M.; Sánchezpedraza, A.; Marfil, R.; Rodríguez, J.; Bandera, A. Data-driven multiresolution camera using the foveal adaptive pyramid. Sensors 2016, 16, 2003. [Google Scholar] [CrossRef] [PubMed]
- Belay, G.Y.; Ottevaere, H.; Meuret, Y.; Vervaeke, M.; Erps, J.V.; Thienpont, H. Demonstration of a multichannel, multiresolution imaging system. Appl. Opt. 2013, 52, 6081–6089. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Zeng, H.; Zhao, Y. Insect-human hybrid eye (IHHE): An adaptive optofluidic lens combining the structural characteristics of insect and human eyes. Lab Chip 2014, 14, 3594–3602. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Wang, X.; Zhang, J.; Yuan, Y.; Chen, X. Design of microcamera for field curvature and distortion correction in monocentric multiscale foveated imaging system. Opt. Commun. 2017, 389, 189–196. [Google Scholar] [CrossRef]
- Cheng, Y.; Cao, J.; Hao, Q.; Zhang, F.H.; Wang, S.P.; Xia, W.Z.; Meng, L.T.; Zhang, Y.K.; Yu, H.Y. Compound eye and retina-like combination sensor with a large field of view based on a space-variant curved micro lens array. Appl. Opt. 2017, 56, 3502–3509. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.J. Closed form analytical inverse solutions for risley-prism-based beam steering systems in different configurations. Appl. Opt. 2011, 50, 4302–4309. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.G. Analytic solution of free space optical beam steering using risley prisms. J. Lightw. Technol. 2008, 26, 3576–3583. [Google Scholar] [CrossRef]
- Land, M.F.; Nilsson, D.E. Animal Eyes, 2nd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Entrance Pupil. Available online: https://en.wikipedia.org/wiki/Entrance_pupil (accessed on 20 March 2018).
- Lavigne, V.; Ricard, B. Fast Risley Prisms Camera Steering System: Calibration and Image Distortions Correction through the Use of a Three-Dimensional Refraction Model. Opt. Eng. 2007, 46, 043201. [Google Scholar]
- Li, A.; Liu, X.; Sun, W. Forward and inverse solutions for three-element risley prism beam scanners. Opt. Express 2017, 25, 7677–7688. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Cao, J.; Meng, L.; Wang, Z.; Zhang, K.; Ning, Y.; Hao, Q. Reducing defocus aberration of a compound and human hybrid eye using liquid lens. Appl. Opt. 2018, 57, 1679–1688. [Google Scholar] [CrossRef] [PubMed]
- Arena, P.; Bucolo, M.; Fortuna, L.; Occhipinti, L. Cellular neural networks for real-time DNA microarray analysis. IEEE Eng. Med. Biol. Mag. 2002, 21, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Arena, P.; Basile, A.; Bucolo, M.; Fortuna, L. An object oriented segmentation on analog cnn chip. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 837–846. [Google Scholar] [CrossRef]









| Parameter Type | Abbreviation | Values |
|---|---|---|
| Pixel pitch | p | 3.75 μm |
| Rows × columns of pixel array | M × N | 960 × 1280 |
| Focal length | f’ | 12 mm |
| F-number | F | 1.4 |
| Wedge angle | α | 4° |
| Object distance | v | 50 mm |
| Refractive index | n | 1.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Q.; Wang, Z.; Cao, J.; Zhang, F. A Hybrid Bionic Image Sensor Achieving FOV Extension and Foveated Imaging. Sensors 2018, 18, 1042. https://doi.org/10.3390/s18041042
Hao Q, Wang Z, Cao J, Zhang F. A Hybrid Bionic Image Sensor Achieving FOV Extension and Foveated Imaging. Sensors. 2018; 18(4):1042. https://doi.org/10.3390/s18041042
Chicago/Turabian StyleHao, Qun, Zihan Wang, Jie Cao, and Fanghua Zhang. 2018. "A Hybrid Bionic Image Sensor Achieving FOV Extension and Foveated Imaging" Sensors 18, no. 4: 1042. https://doi.org/10.3390/s18041042
APA StyleHao, Q., Wang, Z., Cao, J., & Zhang, F. (2018). A Hybrid Bionic Image Sensor Achieving FOV Extension and Foveated Imaging. Sensors, 18(4), 1042. https://doi.org/10.3390/s18041042






