1. Introduction
Large-scale rotating machines, such as steam turbines, wind turbines, and rolling mills, are ubiquitous in industries. With the development of technologies, the technical level and complexity of these systems are increased. Failure of these systems will lead to unexpected downtime, which will result in high operation and maintenance cost. Fault diagnosis, which aims to detect, isolate, and identify the fault before failure happens is, therefore, critical to ensure the safety and reliable operation of these systems.
Vibration signals are widely used for diagnosis of rotating machinery. There are many reported analysis methods, including wavelet transform, empirical mode decomposition (EMD) [
1], Wigner-Ville distribution [
2], Hilbert–Huang transform [
3], order tracking [
4], decision tree [
5], rough sets theory [
6], and principal component analysis (PCA) [
7], etc. Among these methods, wavelet transform is a time-frequency domain analysis tool that provides better local characteristics of the signal. Due to this, it is often used in de-noising, feature extraction, and fault detection [
8,
9]. Wavelet transform was also integrated with other advanced algorithms, such as auto-associative neural networks [
9], support vector machines [
10], genetic algorithms [
11], and support vector regression [
12], among others, to enhance noise reduction, enable feature extraction, and facilitate multiple fault detection and classification.
With these successes, however, existing wavelet transform-based methods have some limitations. One is that they form the features extracted from wavelet transform coefficients in a one-dimensional vector, which is insufficient to describe the two-dimensional time-frequency domain wavelet transform and will result in information loss. The other is that feature selection and extraction significantly depends on expert knowledge, which is inflexible and difficult to obtain a generic solution.
To overcome these limitations, this paper proposes a novel fault diagnosis approach by integrating the continuous wavelet transform scalogram (CWTS) [
13] with a convolutional neural network (CNN). In the proposed approach, wavelet transform decomposes vibration signals in different scales. The wavelet coefficients form the CWTS, which contain the complete time-frequency domain information of the vibration signals. Since the CNN has excellent multi-variable processing capabilities, it can take the full two-dimensional wavelet coefficients as input for fault diagnosis to achieve better performance.
Convolutional Neural Network is an emerging deep learning algorithm with reported successes in recognition of image [
14], face [
15], handwriting [
16], action [
17], materials [
18], and speech processing [
19]. For instance, in image recognition, the CNN takes original image as inputs and, therefore, avoids complex pre-processing. This is because the CNN has a special structure of local weight sharing. There are also some examples of CNN applications in disease diagnosis [
20,
21,
22]. All of these applications show the advantages of CNNs in image and multivariate time series analysis, which indicates that CNNs have potential in diagnosis and prognosis [
23]. However, through the inspection of these advantages, the applications of CNNs in fault diagnosis of mechanical equipment are very limited. A WDCNN (Deep Convolutional Neural Networks with Wide First-layer Kernels) method for fault diagnosis of a bearing is proposed in [
24], but the influence of varying rotating speed on signals is not considered. This paper aims to introduce a new application of CNN in fault diagnosis. The contributions of the proposed approach are that:
For the first time, it integrates the CWTS and the CNN for fault diagnosis of rotating machinery. In this integration, the CNN has the multidimensional processing capability that can directly use two-dimensional CWTS as the input. This configuration takes full advantage of the CWTS and the CNN in a single deep learning framework;
The full two-dimensional wavelet coefficients are used in fault diagnosis without dimensionality reduction. The CWTS contains the complete time-frequency domain information of the vibration signals and avoids information loss of the original signal. Additionally, the wavelet transform also helps to remove noise from the raw signals at the same time;
A data preprocessing step is introduced to avoid the different distributions of the CWTS caused by different sample frequencies and different rotating speeds;
Parallel CNNs are used for fault classification in the experiment. Several CNNs are trained and each of them scores for a type of fault. Then the fault mode is obtained by comparing the scores of the CNNs.
The data pre-processing and the CNN algorithm are not data- and system-dependent. Thus indicates that the proposed solution is a universal, generic, and scalable one that can be applied to other diagnostic applications. Experiments on two different testbeds are presented to demonstrate the effectiveness and versatility of the proposed approach.
The paper is organized as follows:
Section 2 elaborates the integration of the CNN and CWTS for fault diagnosis, with a detailed procedure of the proposed method; Experimental verification of the method is described in
Section 3;
Section 4 presents the experiments of the trained CNN on a similar experimental testbed, but with different configuration to verify the universality of the method; and, finally, concluding remarks are given in
Section 5.
2. Proposed Method
As discussed above, the CWTS has been used in the fault diagnosis of rotating machinery. However, the existing methods only use the CWTS to extract features manually, which not only requires extensive knowledge of the system, but also results in information loss. Therefore, a CNN is introduced to process the CWTS with its great capabilities in image recognition. The integration of the CWTS with a CNN brings some immediate challenges, as follows:
The structure of the CNN and the format of the input image need to be defined. The structure of the CNN will influence the training time of the CNN. The format of the input images and the number of convolution layers have an influence on whether appropriate feature maps can be obtained.
The data format needs to be unified. Vibration data collected in different sample frequencies, with different rotating speeds, or from different equipment, will result in different distributions of the CWTS. This may cause difficulty in CNN recognition if the data format is not unified.
The proposed approach aims to address these challenges in fault diagnosis of rotating machinery.
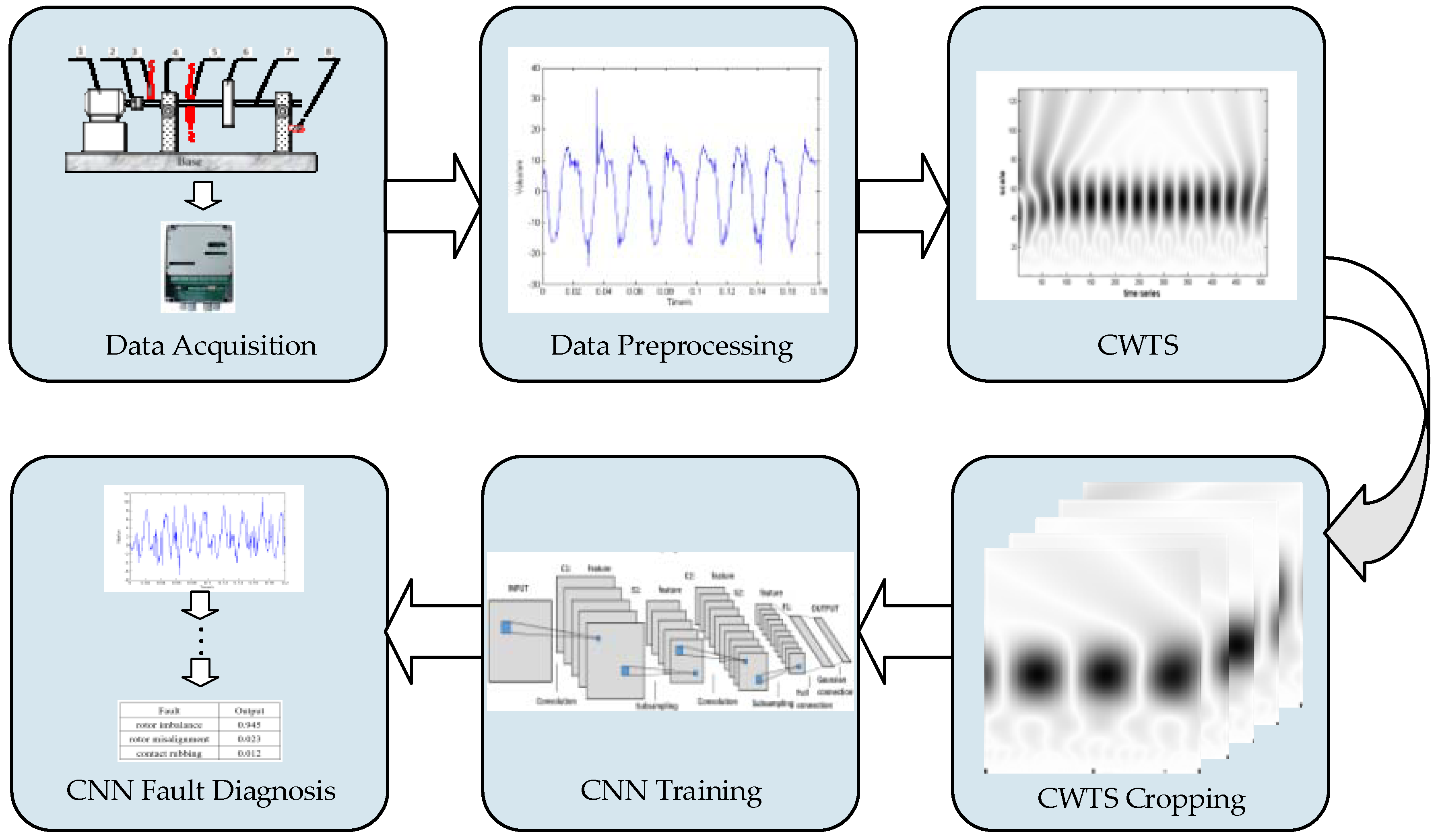
Figure 1 illustrates the procedure of the proposed method, which consists of data acquisition (different types of fault data), data pre-processing (including data formatting), CWTS construction (decompose the vibration signal using the multi-scale continuous wavelet transform to obtain the CWTS), CWTS cropping (using part of the CWTS as the CNN input), CNN training, and real-time system diagnosis. Details of the each step of the proposed method are described below.
2.1. Data Acquisition
A rotating machinery can be operated with a variety of rotating speeds and loads. To perform fault diagnosis under various operating conditions, the vibration signals from the machine in a full speed range and a full load range need to be obtained for training. However, if the sample frequencies of the signals are not the same multiple of the rotating frequency, the different rotating speed will cause a substantial difference in CWTS. To eliminate this influence, vibration signal is collected (as a training instance) with the rotating speed information so that it will be taken into consideration when this instance is processed. Note that the rotating speed in a training instance is considered as constant as it is collected when the machinery is in a stable operating condition.
2.2. Data Preprocessing
First, the DC component of the vibration signal is removed as it does not contribute to fault diagnosis. The DC part is removed by simply subtracting the mean value of the signal. Note that if the vibration signal is from displacement sensors, the DC part will only denote the distance between the sensor and the rotating rotor. The DC part will also cause mistakes in the wavelet transform.
Second, the variation of rotating speed leads to changes in the CWTS. Since the rotating speed changes in operation when the operating mode changes, load changes, and during startup and shutdown, the CWTS will yield significantly different results if signals at different rotating speeds are not preprocessed. To eliminate the influence of rotating speed on CWTS, signal resampling with a virtual resampling frequency (VSF) is introduced. For the vibration signal in a training instance, as its rotating speed is known, the VSF is set as a frequency that is q multiples of the rotating speed. Note that q remains the same for all training instances. With this resampled vibration signal, every rotation of the rotor has the same number of sampling points. Then the wavelet coefficients corresponding to the same harmonic of the rotating frequency in different samples will locate at the same scale of CWTS.
Suppose a vibration signal is collected at a sampling frequency f(Hz) with m sampling data points. The rotating speed is n (rpm), corresponding to a machine rotating frequency . Define fd as the virtual re-sampling frequency that is the required multiple number of times of the machine rotating frequency, i.e., , where q is the required multiple number. To unify the sampling frequency as fd, the data is processed using the following method.
With re-sampling frequency
fd, the
k-th re-sampled data point should be
. If
f is a multiple of
fd, then we only need to select
as the new
. Otherwise, using a quartic polynomial interpolation function Φ with the original samples around
, the new
(
k = 1, 2, 3 …,) can be obtained by using Equation (1):
After preprocessing, all data have the same length at the sampling frequencies that are the same multiples of the rotating frequency.
2.3. CWTS
The wavelet transform decomposes a signal in the time-frequency domain by using a family of wavelet functions. Different from Fourier transform, whose basis function is the sinusoidal function, wavelet transform uses the wavelet basis function, which is of finite bandwidth both in the time domain and the frequency domain. By scaling and translating the wavelet basis function, the signal can be decomposed with different resolutions at different time and frequency scales. The scaling and translation of a basic wavelet function can be mathematically described as:
where Ψ
a,b(
t) is a continuous wavelet whose shape and displacement are determined by
a, the scale parameter, and
b, the translation parameter, respectively.
The continuous wavelet transform inherits and develops the localization idea of the short time Fourier transform (STFT). Different from STFT, scale and translation parameters a and b enable the adjustment of the resolution in time and frequency axes and, therefore, provide different frequency resolution and time resolution. The continuous wavelet transform is an ideal tool for signal time-frequency analysis and processing.
The continue wavelet transform of a signal
x(
t) is defined as the convolution of the signal
x(
t) with the wavelet function Ψ
a,b(
t). In this method, continuous wavelet transform is implemented to decompose the data from scale 1 to
l, where
l is usually equal to, or larger than, 2
q:
where
Ca (
a = 1, 2, 3, …,
l) is the wavelet coefficients of
x(
t) at the
a-th scale and
is the complex conjugate of the wavelet function at scale
a and translation
b.
Continuous wavelet transform generates coefficients on different parts of the signal under different scaling factors. Using these wavelet coefficients, the signal in the time-frequency domain can be directly expressed by a two-dimensional image. The graph of the wavelet coefficients constructs the continuous wavelet transform scalogram (CWTS).
Putting all wavelet coefficients in a matrix
P = [
C1,
C2, …,
Cl], it can be transformed to a gray matrix
Pnew by:
where
pmin and
pmax are the minimal and maximal elements of
, respectively. The value of element in
Pnew represents a gray value in the range from 0 to 255. Therefore,
Pnew is the continuous wavelet transform scalogram of the original signal.
Figure 2 shows the time domain waveform and CWTS of a normal signal. As a comparison,
Figure 3 shows the time domain waveform and CWTS of a fault signal with rotor imbalance. The signals both have 512 data points and are sampled at a frequency of 64
fm and decomposed by the Morlet wavelet from a 1 to 128 scale. The horizontal axis represents the position along the direction of time signals, and the vertical axis represents the scale. The color of each point represents the magnitude of the wavelet coefficients.
As shown in
Figure 2 and
Figure 3, the CWTS of the fault signal is different from that of the normal signal. This result indicates the possibility to carry out fault diagnosis using CWTS. However, it is difficult to explicitly build a relationship between the CWTS and fault conditions. Although statistical feature [
25] and one-dimensional vector were developed to recognize the difference, they are not sensitive to small changes in CWTS. For example, the wavelet grey moment (WGM) of the CWTS in
Figure 2 and
Figure 3 are 20.24 and 20.51, respectively. The difference between their WGM is trivial and is not reliable for diagnosis. In other words, it is difficult to detect rotor imbalance fault through WGM of CWTS obtained from the signals. To address this issue, CNN is proposed for fault diagnosis based on CWTS of vibration signals by taking full advantage of its capabilities in multidimensional signal processing and image recognition.
When choosing the wavelet type, we refer to the wavelet selection in other papers of machinery fault diagnosis. Zhang et al. [
13] use eight types of wavelet to calculate the first-order WGM. WGM distributing lines of fault signals corresponding to eight wavelets are presented. It shows that three wavelets, Dmeyer, Meyer, and Morlet, have better distinguishability for machinery faults. Yan and Gao [
26] use an energy-to-Shannon entropy measure to choose an appropriate wavelet for a vibration signal. The test signal extracted by the Morlet wavelet has the higher energy-to-Shannon entropy ratio than the other wavelet types listed in the paper. It shows that the Morlet wavelet is the most appropriate wavelet for analyzing the signal. According to the analysis in these papers, the Morlet wavelet was chosen as the wavelet used in this paper. If other wavelet functions commonly used in vibration signal analysis are selected, this method may also have a good result.
2.4. CWTS Cropping
CWTS obtained from continuous wavelet transform usually has a large number of pixels. Recognition of large images often requires a more complex CNN structure and more computation, which lead to longer training and computing time. On the other hand, large images will diminish the effects of small local features and reduce the sensitivity and accuracy of fault diagnosis. To accommodate this, CWTS cropping is introduced, which is conducted with the following three principles:
The cropping result must contain at least the continuous wavelet transform coefficients of one complete rotating period.
The length of one side of the square result must be greater than 2q.
If the coordinate of the pixel at scale axis ia is greater than the coordinate at the time axis ib or the coordinate to the last point of the sample m − ib (ia > ib or ia > m − ib), then the pixel cannot be used as the output.
The first principle is to ensure that the result contains the complete information of one period. The second principle is to obtain the wavelet transform of low scales from 1 to 2q, which often have the characteristics of the fault. Oil whirl, for instance, has fault characteristics in scales from q to 2q of CWTS. The third principle is introduced to avoid the following scenario: when the center of wavelet transform window is located in the first or last several points of the sample, there will not be enough points to perform the wavelet transform when the scale parameter is larger.
Meanwhile, as the fundamental rotating frequency fm is the major and common constituent of the vibration data, it corresponds to a considerable fraction of area in CWTS. If the signal is not synchronized, the difference in CWTS caused by fundamental rotating frequency fm will be significant and affect the accuracy of diagnosis.
Following these three principles and the needs of signal synchronism, a CWTS cropping scheme is proposed. First,
P0, the phase of fundamental rotating frequency
fm, is calculated by Fourier transform for every samples. Next, the first point after 2
q, which has a zero phase of one multiple of the rotating frequency, is chosen as the start coordinate of cropping in the time axis. Thus, the start coordinate
ic can be calculated by:
Finally, the output can be obtained by extracting 1 to 2q in the scale axis and ic to ic + 2q − 1 in the time axis from the original scalogram.
Figure 4 illustrates the CWTS cropping process of the signal in
Figure 2.
P0 of the signal is 250.6,
q is 64, and the time series number corresponding to
P0 . Thus, 1 to 128 in the scale axis and 147 to 274 in the time axis index that is cropped as the output.
Using the above method, the influence of different starting phase of the one1 multiple of the rotating frequency can be eliminated. In addition, it helps to improve the speed of convergence compared to the cropping method without considering the one multiple of rotating frequency. After this step, we obtain a number of square preprocessed CWTSs as the training input of the CNN.
2.5. CNN Training
A convolutional neural network (CNN) is a kind of neural network that uses a convolution operation to replace the general multiplication in a neural network. It has excellent performance in dealing with data with a grid structure. Convolution operations improve the machine learning system through three important concepts: sparse interaction, parameter sharing, and equivariant representation [
27]. Sparse interaction is achieved by making the size of convolution kernels much smaller than the size of the input. It reduces the computational complexity of algorithm and improves its statistical efficiency. Parameter sharing refers to using the same parameters in multiple functions of a model. The parameters of each convolution kernel are the same when dealing with different positions of the input. Equivariant representation roots in the properties of convolution operation, which is equivariant to any translation functions. This means that the features can be acquired no matter where they are located in the input [
28].
CNN has many different structures. The basic structure of CNN used in this paper,
Figure 5, consists of two types of layers, feature extraction layer (also known as convolution layer) and feature mapping layer (or pooling layer) [
14]. Each computing layer of the CNN, such as C1, S1, C2, and S2 in
Figure 5, is composed of a number of feature maps. Each feature map is mapped to a plane, and the convolution operations share the same convolutional kernel at different locations of the feature map. The feature mapping structure uses the sigmoid function as the activation function.
The convolution layer consists of a number of feature maps. Each neuron of the convolution layer receives a limited range of the input feature maps and performs the convolution operation on the input. For each input feature map,
K output maps will be obtained if the convolution layer has
K convolution kernels. Suppose the input
X is the matrix of
M ×
N, the output of the convolution layer can be computed as:
where
is the value at coordinate (
i, j) of the convolution layer’s output of the
k-th feature map by the
kth convolution kernel,
i = 1, 2, …,
M −
s + 1,
j = 1, 2, …,
N −
s + 1,
Wk ∈
Rs is a weight vector representing the
k-th filter,
is the kernel size,
bk is the bias of the
k-th feature kernel, and
θ(
x) is the activation function, which is set as the sigmoid function in this paper.
Each convolution layer is followed by a pooling layer to conduct aggregate statistics on characteristics at different location of the feature map. This will reduce the dimension of convolution features of a convolution layer by pooling. Two types of pooling, average pooling and maximum pooling, are widely used. The average pooling is employed in this research, which is computed as:
where
is the value at coordinate (
i, j) of the pooling layer’s output,
s is the pooling size,
is the value at corresponding place of the convolution layer’s output.
A classifier is then trained for fault diagnosis. In this paper, a fully-connected neural network is used as a classifier. The input of the neural network is a one-dimensional vector constructed by all the values in feature maps. The fully-connected neural network calculates the dot product between the input vector and the weight vector, plus a bias. The outcome is sent to the sigmoid function in the output layer for diagnosis.
To fully determine the CNN structure, some parameters need to be determined. Such parameters include the number of convolution layer, the number of convolution kernels in each layer, the size of kernels, the pooling size of each layer, the learning rate of the neural network, and the format of the training output.
Number of convolution layers and number of convolution kernels: The number of convolution layers depends on the size of the input CWTS image. More global characteristics of the image requires a higher number of layers and convolution kernels. However, the convergence speed will decrease with the increase of convolution layers or convolution kernels.
Size of kernels and pooling size: To reduce the training time and increase the convergence speed, a small kernel size and pooling size is often used. It also requires that the input and output images of each layer must have integer pixels.
Learning rate of the neural network: A high learning rate may lead to divergence of training. On the contrary, a low learning rate will lead to slow convergence. In general, the learning rate needs to be determined in training by trial-and-error to ensure both the stability and learning speed of training.
The input and output format of the fully-connected neural network: The input of the neural network is a one-dimensional vector formed by all the values in the feature maps. An n × 1 zero vector is created with n being the number of fault modes. If the k-th fault mode is detected, the k-th value of the output vector is set as 1 while all other values are 0.
With all initial parameters, the CNN is trained for fault diagnosis with a supervised learning algorithm. The basic idea of training is to adjust the weights and bias of the CNN by minimizing the residual. First, the residual of the fully-connected layer is calculated by a squared error loss function. Then error back propagation is carried out from the last layer to the first layer using the chain rule. The pooling layer uses the upsample to propagate errors back. For an average pooling layer, errors will be equally distributed in the pooling area. The convolution layer uses deconvolution for error back propagation. Deconvolution is performed by performing convolution with the reversed convolution kernel. After obtaining the errors of each layer, a gradient descent method is applied to update the kernels, weights, and bias of the convolution layer and the fully-connected layer in the direction of steepest descent.
Figure 6 (left) shows a 128 × 128 CWTS of a rotor misalignment fault signal. By using the CNN with a structure given in
Figure 5, the original CWTS generates twelve 29 × 29 feature maps as shown in
Figure 6 (right). This shows that the feature maps concentrating on different parts of CWTS are obtained by the CNN. Then the fully-connected neural network can classify the fault accurately.
2.6. CNN Fault Diagnosis
To perform fault diagnosis using the trained CNN, the raw vibration data are transformed to the same format of the training data. The transformed data are decomposed with the continuous wavelet transform to obtain the CWTSs. The CWTSs are then cropped to construct the input of the CNN. The CNN output is the result of fault detection, which indicates the detected fault mode.
4. Universality of CNN Fault Diagnosis
The objective of this research is to propose an accurate, robust, and universal solution for rotating machinery fault diagnosis. While the accuracy and robustness are demonstrated in
Section 3, more research is needed to show the proposed method is universal, which indicates that the trained CNN from one equipment can be extended to the diagnosis of other equipment with similar structure or similar function. Universality is critical for most intelligent fault diagnosis algorithms as one with a high level of universality will greatly reduce the design and maintenance costs. To verify the universality of the proposed CNN fault diagnosis method, the trained CNN is applied to fault diagnosis of a gas turbine rotor testbed as shown in
Figure 12. This testbed has a similar structure with the rotor testbed, but with a longer and thicker shaft and bearings of different sizes.
The vibration data is collected and processed in the same manner as that for the rotor testbed, as discussed in
Section 3. The displacement sensing data of two faults, i.e., rotor imbalance and rotor misalignment, are used in this case study.
Table 8 shows the diagnosis results with the same CNNs trained in
Section 3 based on rotor testbed data. It is clear from
Table 8 that the diagnosis results of all faults are greater than 70%, which demonstrates that the proposed approach is a universal and generic solution for diagnosis of other rotating machines. Note that this offers fast deployment of fault diagnosis with existing trained CNNs. With more data from the new equipment, the CNNs can be trained and updated to further improve the performance.