Electrolyte Magnetohydrondyamics Flow Sensing in an Open Annular Channel—A Vision System for Validation of the Mathematical Model
Abstract
:1. Introduction
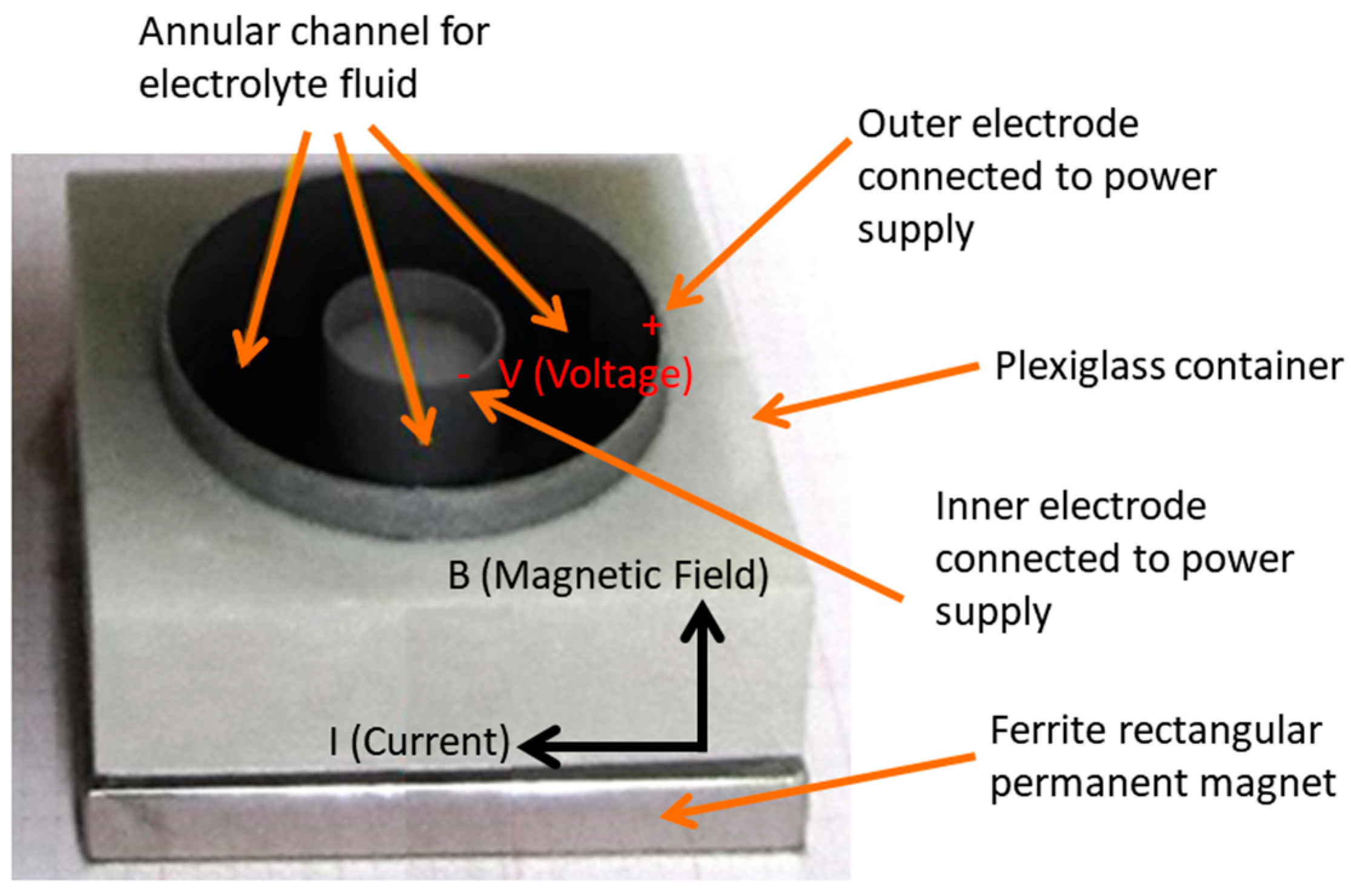
2. MHD Microfluidic System Overall
3. Theoretical Validation of Mathematical Model
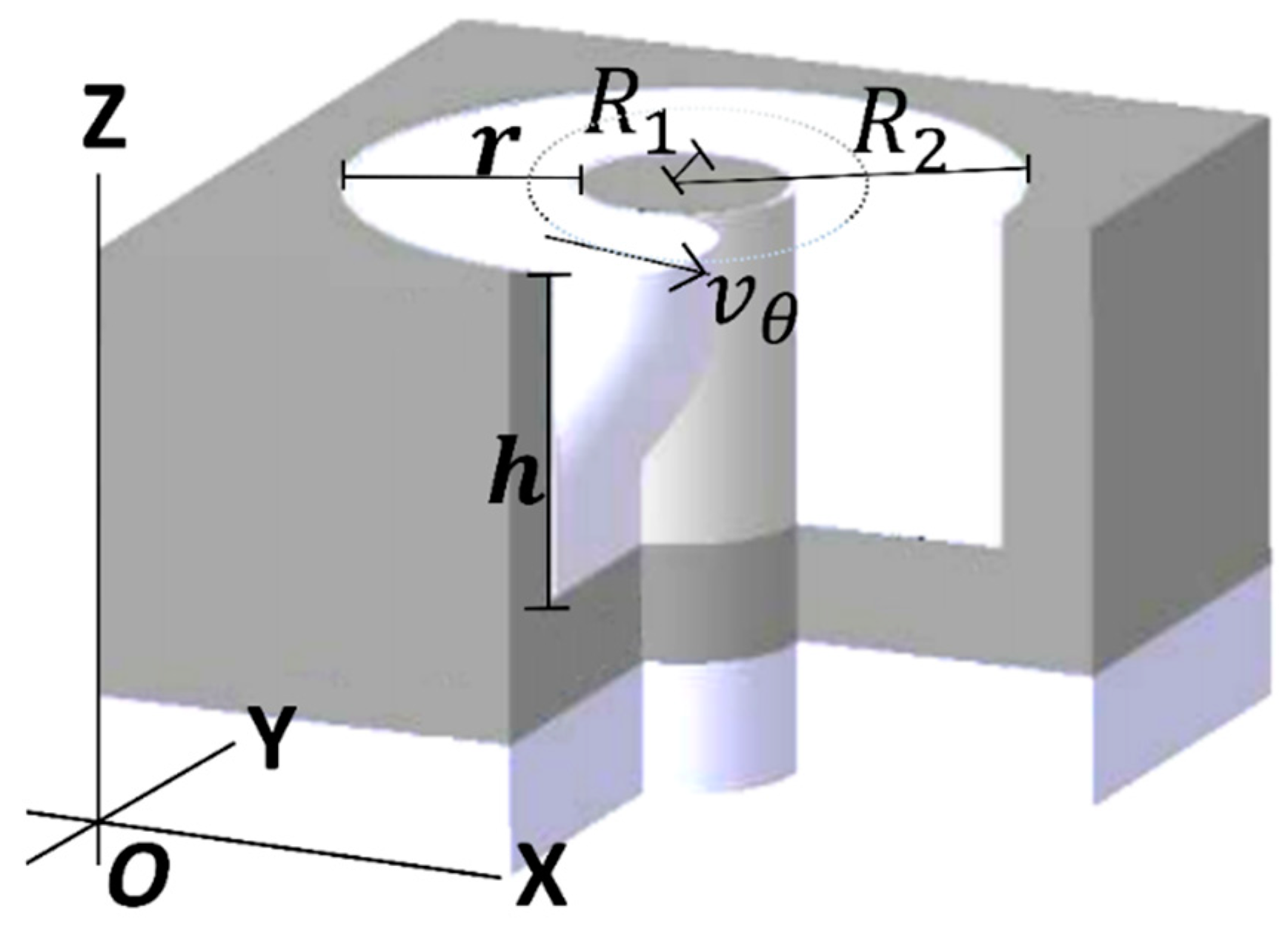
3.1. Mathematical Formulation of the Problem and Governing Equations
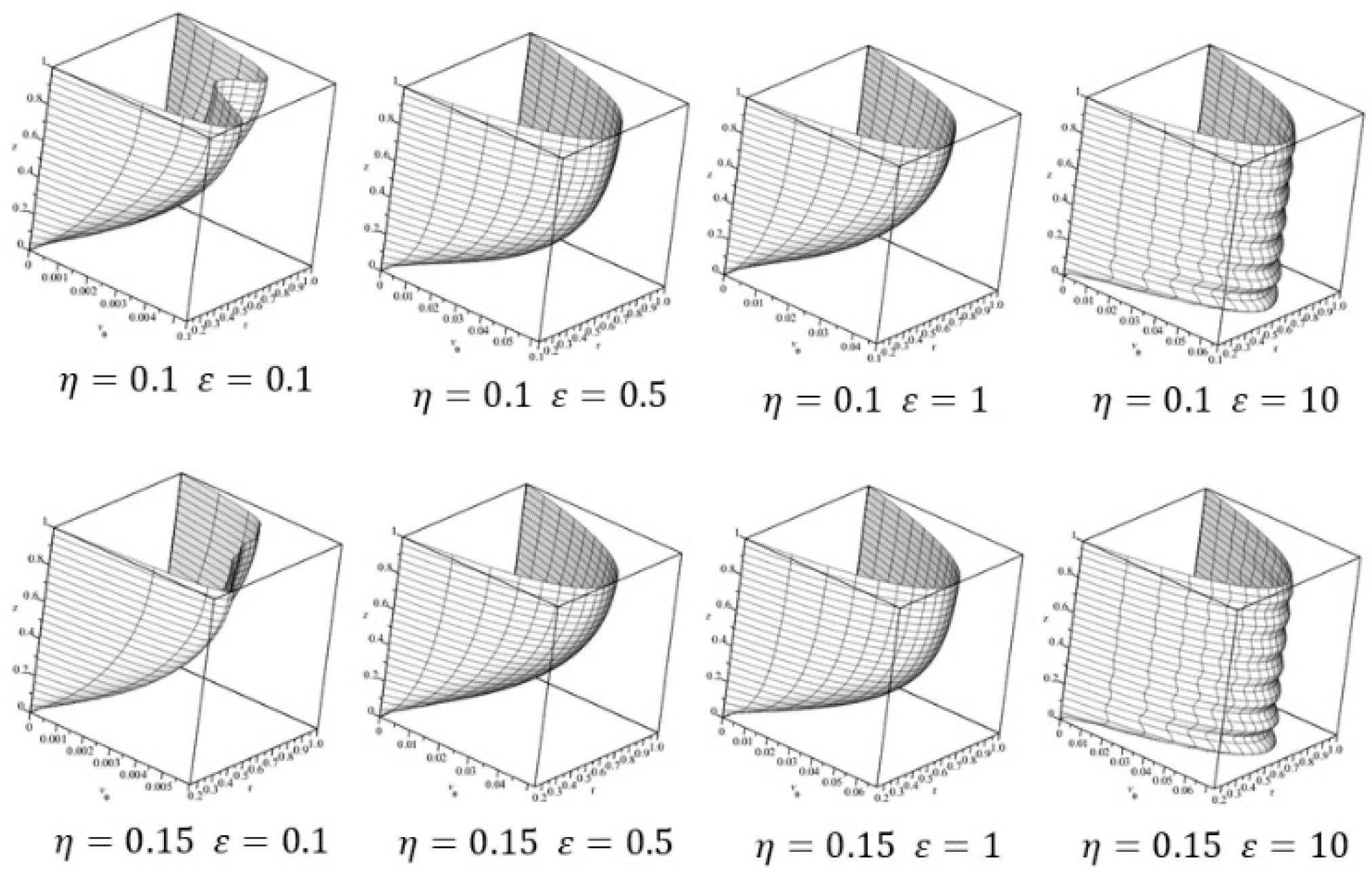
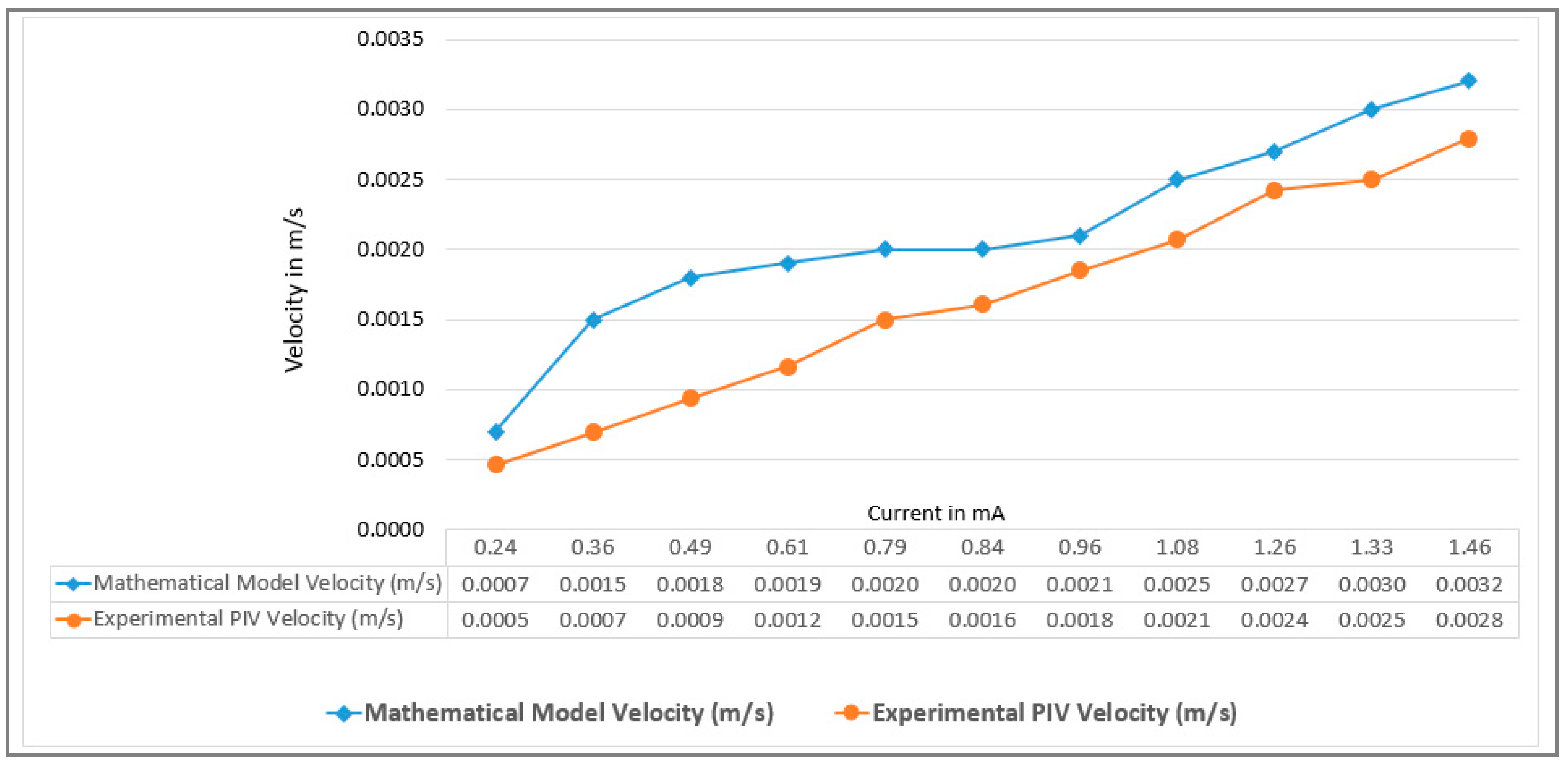
3.2. Computing Results of the Mathematical Model
3.3. Comparison of the Proposed Mathematical Model with Other Models Found in Previous Research Literature
4. Experimental Validation of the Mathematical Model
4.1. Vision System
4.2. Methodology
4.3. Set up for Mathematical Model Validation
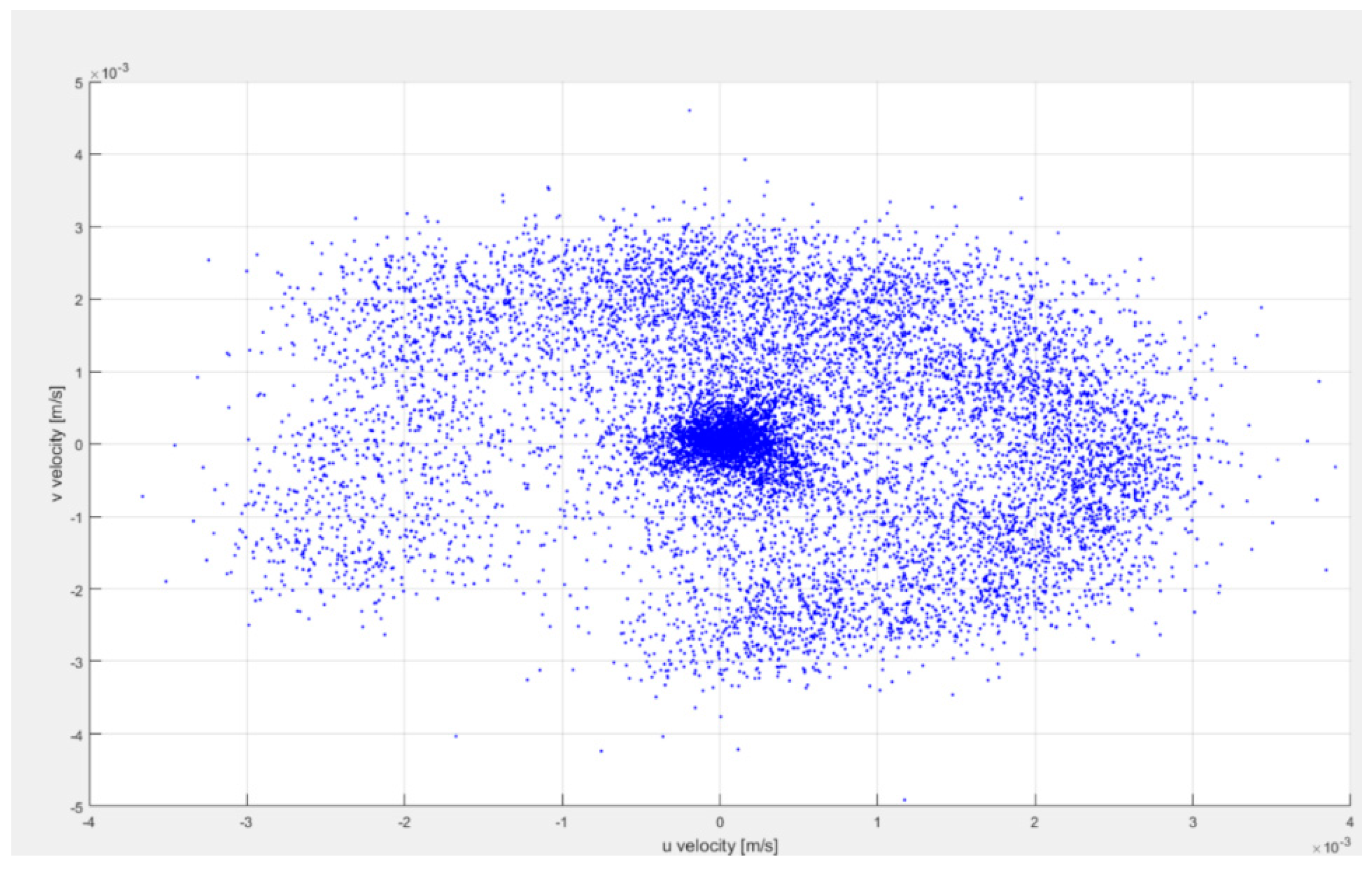
4.4. PIVLAB Toolbox for PIV
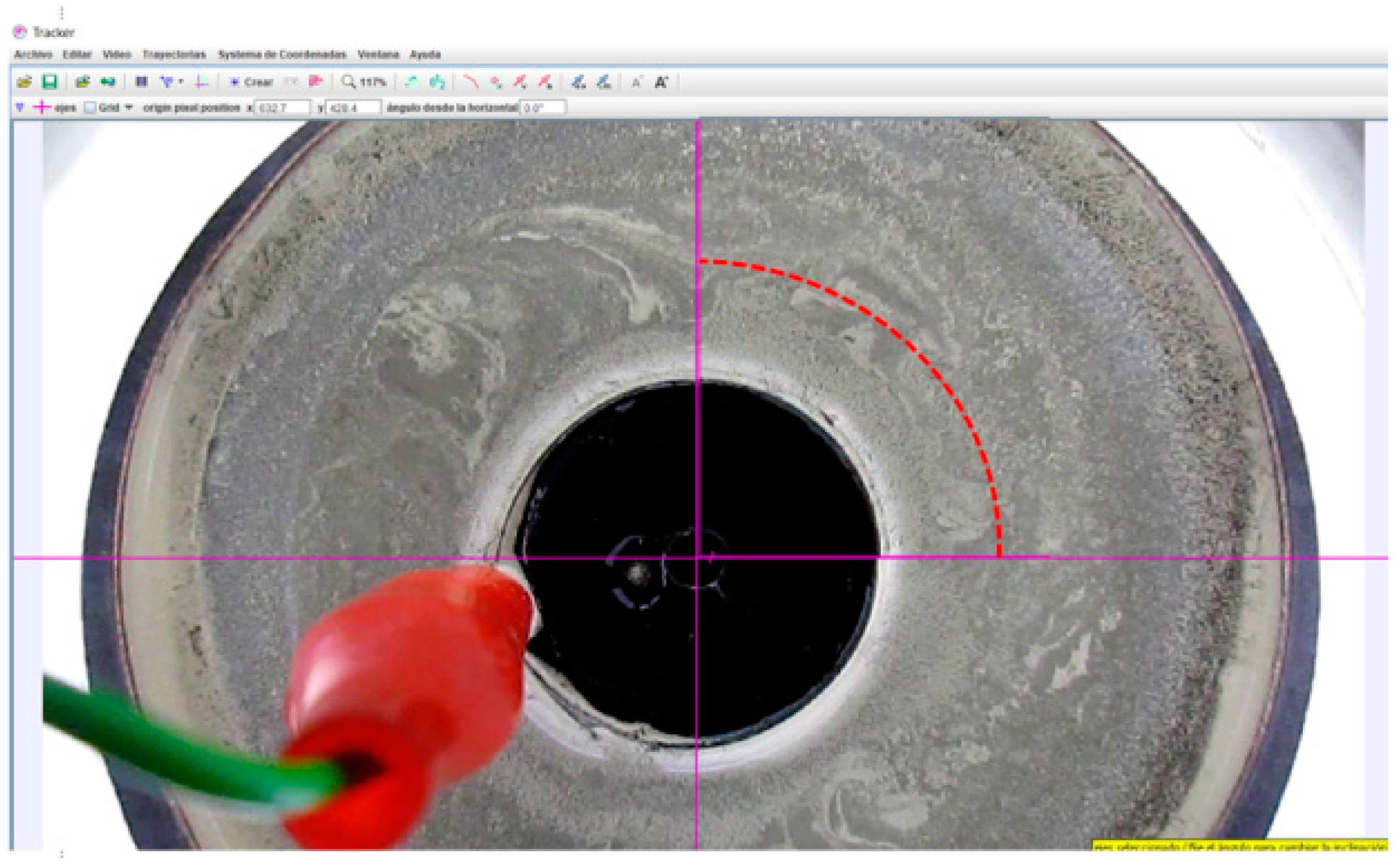
4.5. Tracker for PTV
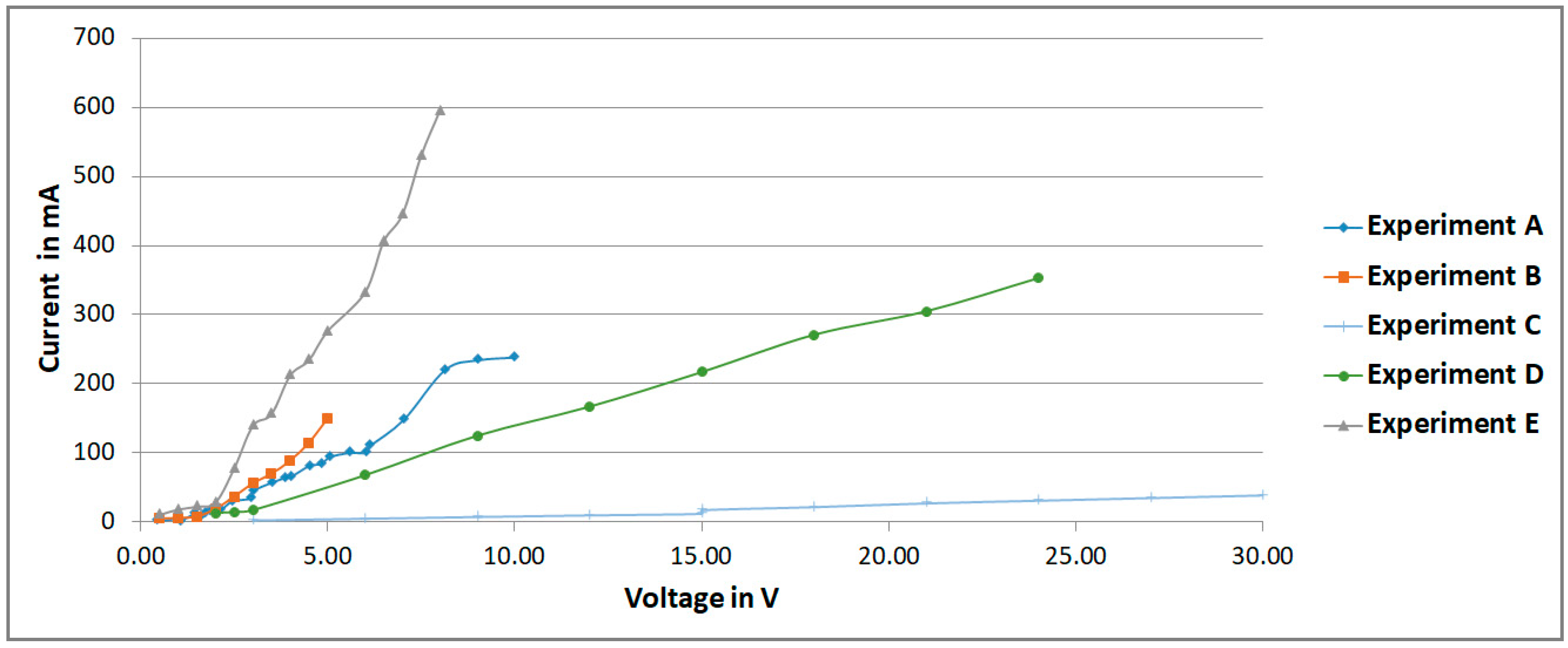
4.6. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- AL-Habahbeh, O.M.; Al-Saqqa, M.; Safi, M.; Abo Khater, T. Review of magnetohydrodynamic pump applications. Alex. Eng. J. 2016, 55, 1347–1358. [Google Scholar] [CrossRef]
- Yuan, F.; Isaac, K.M. A study of MHD-based chaotic advection to enhance mixing in microfluidics using transient three dimensional CFD simulations. Sens. Actuators B Chem. 2017, 238, 226–238. [Google Scholar]
- Mitra, S.K.; Chakraborty, S. (Eds.) Microfluidics and Nanofluidics Handbook: Chemistry, Physics, and Life Science Principles; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Yuan, F.; Isaac, K.M. A study of MHD-induced mixing in microfluidics using CFD simulations. Micro Nanosyst. 2014, 6, 178–192. [Google Scholar] [CrossRef]
- Jang, J.; LEE, S.S. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sens. Actuators A Phys. 2000, 80, 84–89. [Google Scholar]
- Rashidi, S.; Esfahani, J.A.; Maskaniyan, M. Applications of magnetohydrodynamics in biological systems—A review on the numerical studies. J. Magn. Magn. Mater. 2017, 439, 358–372. [Google Scholar] [CrossRef]
- Lemoff, A.V.; LEE, A.P. An AC magnetohydrodynamic micropump. Sens. Actuators B Chem. 2000, 63, 178–185. [Google Scholar]
- Bau, H.H.; Zhu, J.; Qian, S.; Zhiang, Y. A magneto-hydrodynamically controlled fluidic network. Sens. Actuators B Chem. 2003, 88, 205–216. [Google Scholar]
- Zhao, G.; Jian, Y.; Chang, L.; Buren, M. Magnetohydrodynamic flow of generalized Maxwell fluids in a rectangular micropump under an AC electric field. J. Magn. Magn. Mater. 2015, 387, 111–117. [Google Scholar] [CrossRef]
- Flores-Fuentes, W.; Delgado-Valenzuela, M.; Bravo-Zanoguera, M.E.; Rivas-Lopez, M.; Sergiyenko, O.; Lindner, L. Mechanical Systems and Microfluidics: The Application of a Vision System in the Testing of Fluids Behavior. In Mechanical Systems: Research, Applications And Technology, 1st ed.; Kadry, S., Ed.; Nova Publisher: Hauppauge, NJ, USA, 2017; p. 305. [Google Scholar]
- Qian, S.; Bau, H.H. Magneto-hydrodynamics based microfluidics. Mech. Res. Commun. 2009, 36, 10–21. [Google Scholar] [CrossRef] [PubMed]
- Das, C.; Wang, G.; Payne, F. Some practical applications of magnetohydrodynamic pumping. Sens. Actuators A Phys. 2013, 201, 43–48. [Google Scholar]
- West, J.; Karamata, B.; Lillis, B.; Gleeson, J.P.; Alderman, J.; Collins, J.K.; Lane, W.; Mathewson, A.; Berney, H. Application of magnetohydrodynamic actuation to continuous flow chemistry. Lab Chip 2002, 2, 224–230. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Paraschivoiu, M.; Nigam, K.D.P. Single-phase fluid flow and mixing in microchannels. Chem. Eng. Sci. 2011, 66, 1329–1373. [Google Scholar] [CrossRef]
- Ortiz-Pérez, A.S.; García-Ángel, V.; Acuña-Ramírez, A.; Vargas-Osuna, L.E.; Pérez-Barrera, J.; Cuevas, S. Magnetohydrodynamic flow with slippage in an annular duct for microfluidic applications. Microfluid. Nanofluid. 2017, 21, 138. [Google Scholar] [CrossRef]
- Digilov, R.M. Making a fluid rotate: Circular flow of a weakly conducting fluid induced by a Lorentz body force. Am. J. Phys. 2007, 75, 361–367. [Google Scholar] [CrossRef]
- West, J.; Gleeson, J.P.; Alderman, J.; Collins, J.K.; Berney, H. Structuring laminar flows using annular magnetohydrodynamic actuation. Sens. Actuators B Chem. 2003, 96, 190–199. [Google Scholar] [CrossRef]
- Software “Maplesoft”, Version 8.61. A Division of Waterloo Maple Inc.: Waterloo, ON, Canada, 2018. Available online: https://www.maplesoft.com/products/maple/Mapleplayer/ (accessed on 1 January 2018).
- Qin, M.; Bau, H.H. Magnetohydrodynamic flow of a binary electrolyte in a concentric annulus. Phys. Fluids 2012, 24, 037101. [Google Scholar] [CrossRef]
- Pérez-Barrera, J.; Ortiz, A.; Cuevas, S. Analysis of an annular MHD stirrer for microfluidic applications. In En Recent Advances in Fluid Dynamics with Environmental Applications; Springer: Cham, Germany, 2016; pp. 275–288. [Google Scholar]
- Przybyło, J.; Kańtoch, E.; Jabłoński, M.; Augustyniak, P. Distant measurement of plethysmographic signal in various lighting conditions using configurable frame-rate camera. Metrol. Meas. Syst. 2016, 23, 579–592. [Google Scholar] [CrossRef]
- Khoo, S.W.; Karuppanan, S.; Tan, C.-S. A review of surface deformation and strain measurement using two-dimensional digital image correlation. Metrol. Meas. Syst. 2016, 23, 461–480. [Google Scholar] [CrossRef]
- Mickiewicz, W. Systematic error of acoustic particle image velocimetry and its correction. Metrol. Meas. Syst. 2014, 21, 447–460. [Google Scholar] [CrossRef]
- Kavitha, C.; Ashok, S.D. A New Approach to Spindle Radial Error Evaluation Using a Machine Vision System. Metrol. Meas. Syst. 2017, 24, 201–219. [Google Scholar] [CrossRef]
- Flores-Fuentes, W.; Valenzuela-Delgado, M.; Sebastian Ortiz-Perez, A.; Bravo-Zanoguera, M. Machine vision system to measuring the velocity field in a fluid by Particle Image Velocimetry: Special Case of Magnetohydrodynamics. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1621–1625. [Google Scholar]
- Thielicke, W.; Stamhuis, E. PIVlab—Towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef]
- Brown, D. Tracker Video Analysis and Modeling Tool 2017. Available online: https://physlets.org/tracker/ (accessed on 15 January 2018).
- Weston, M.C.; Fritsch, I. Manipulating fluid flow on a chip through controlled-current redox magnetohydrodynamics. Sens. Actuators B Chem. 2012, 173, 935–944. [Google Scholar] [CrossRef]







| Experiment Number | Geometrical Characteristics | Flow Solution Parameters | Induced Fields | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Distilled Water | Sodium Bicarbonate | S-HGS Particles | dc Voltage | |||||||
| A | 18.76 mm | 31.44 mm | 7 mm | 0.6 | 0.22 | 100 mL | 0.84 g | None | 0.1624 T | |
| B | 18.76 mm | 31.44 mm | 7 mm | 0.6 | 0.22 | 100 mL | 8.4 g | None | 0.1624 T | |
| C | 18.76 mm | 31.44 mm | 7 mm | 0.6 | 0.22 | 100 mL | None | 0.1 g | 0.1624 T | |
| D | 18.76 mm | 31.44 mm | 7 mm | 0.6 | 0.22 | 100 mL | 0.84 g | 0.1 g | 0.1624 T | |
| E | 18.76 mm | 31.44 mm | 7 mm | 0.6 | 0.22 | 100 mL | 8.4 g | 0.1 g | 0.1624 T | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valenzuela-Delgado, M.; Flores-Fuentes, W.; Rivas-López, M.; Sergiyenko, O.; Lindner, L.; Hernández-Balbuena, D.; Rodríguez-Quiñonez, J.C. Electrolyte Magnetohydrondyamics Flow Sensing in an Open Annular Channel—A Vision System for Validation of the Mathematical Model. Sensors 2018, 18, 1683. https://doi.org/10.3390/s18061683
Valenzuela-Delgado M, Flores-Fuentes W, Rivas-López M, Sergiyenko O, Lindner L, Hernández-Balbuena D, Rodríguez-Quiñonez JC. Electrolyte Magnetohydrondyamics Flow Sensing in an Open Annular Channel—A Vision System for Validation of the Mathematical Model. Sensors. 2018; 18(6):1683. https://doi.org/10.3390/s18061683
Chicago/Turabian StyleValenzuela-Delgado, Mónica, Wendy Flores-Fuentes, Moisés Rivas-López, Oleg Sergiyenko, Lars Lindner, Daniel Hernández-Balbuena, and Julio C. Rodríguez-Quiñonez. 2018. "Electrolyte Magnetohydrondyamics Flow Sensing in an Open Annular Channel—A Vision System for Validation of the Mathematical Model" Sensors 18, no. 6: 1683. https://doi.org/10.3390/s18061683
APA StyleValenzuela-Delgado, M., Flores-Fuentes, W., Rivas-López, M., Sergiyenko, O., Lindner, L., Hernández-Balbuena, D., & Rodríguez-Quiñonez, J. C. (2018). Electrolyte Magnetohydrondyamics Flow Sensing in an Open Annular Channel—A Vision System for Validation of the Mathematical Model. Sensors, 18(6), 1683. https://doi.org/10.3390/s18061683








