Development of a Fault Monitoring Technique for Wind Turbines Using a Hidden Markov Model
Abstract
:1. Introduction
2. Wind Turbine and Its Condition Monitoring System
2.1. Operation of Wind Turbine
2.2. Condition Minitoring System of Wind Trubine
3. Vibration Signals and Their Alarm Thresholds
3.1. Relation between Wind Speed, Rotating Speed of Main Shaft, and Generated Power
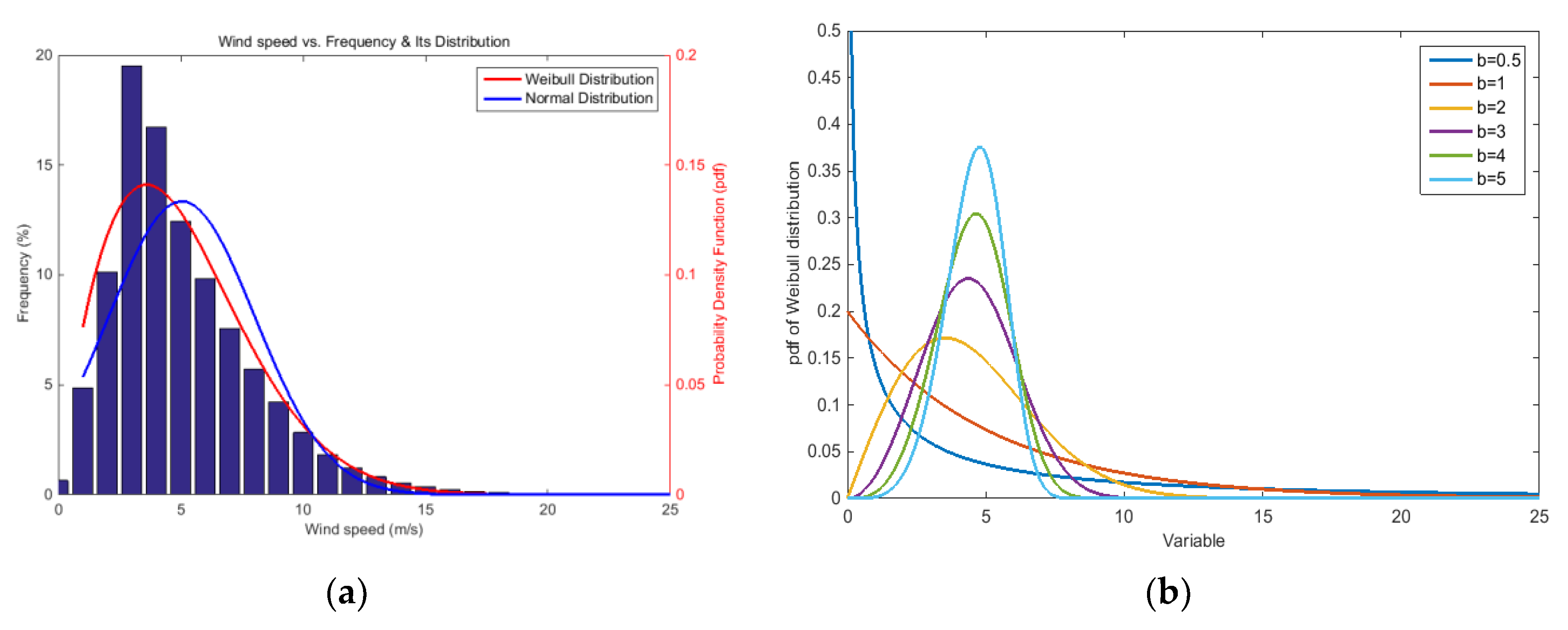
3.1.1. Distribution of Wind Speed
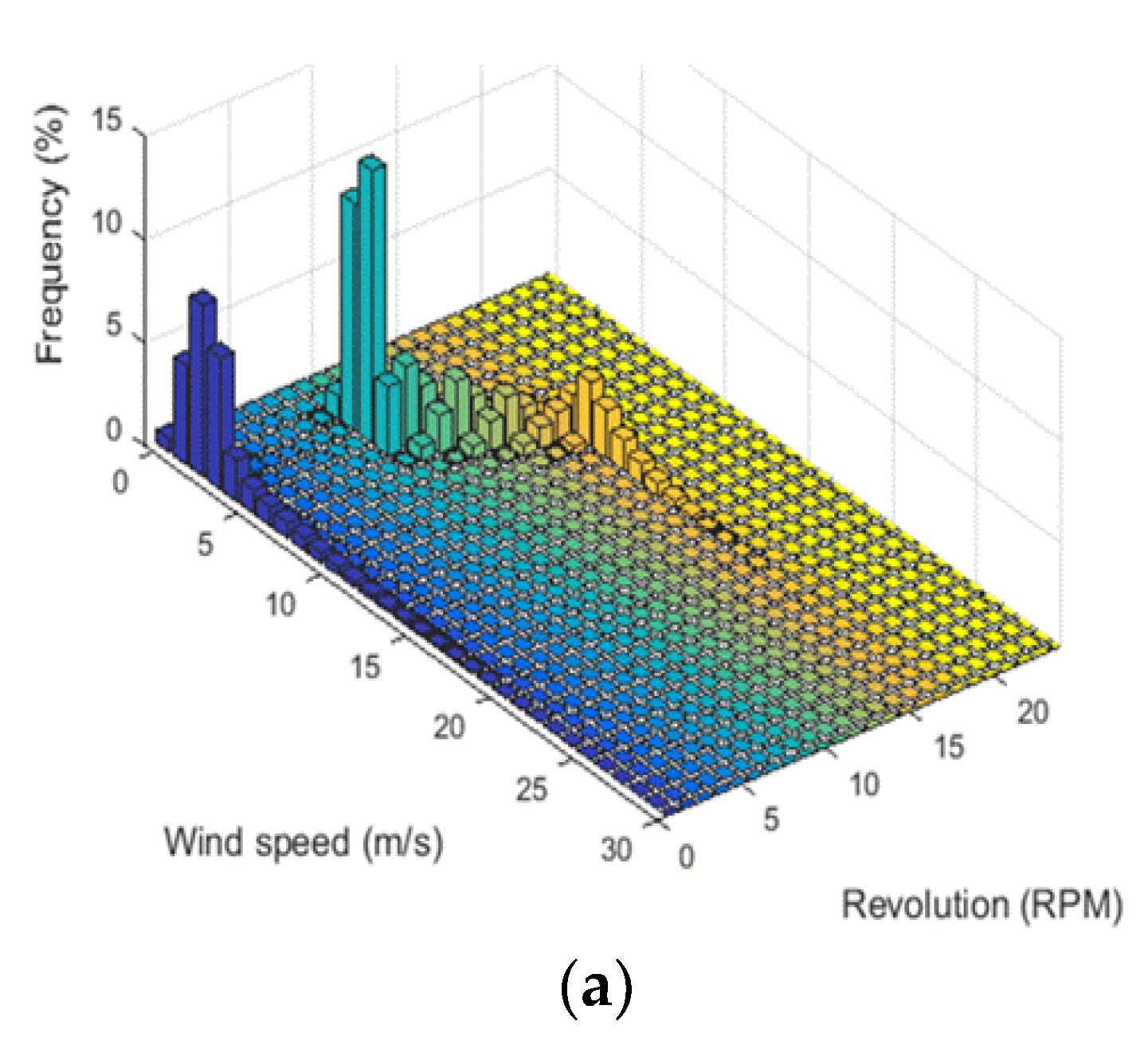
3.1.2. Wind Speed vs. Rotating Speed of Main Shaft
3.1.3. Rotating Speed of Main Shaft vs. Generated Power
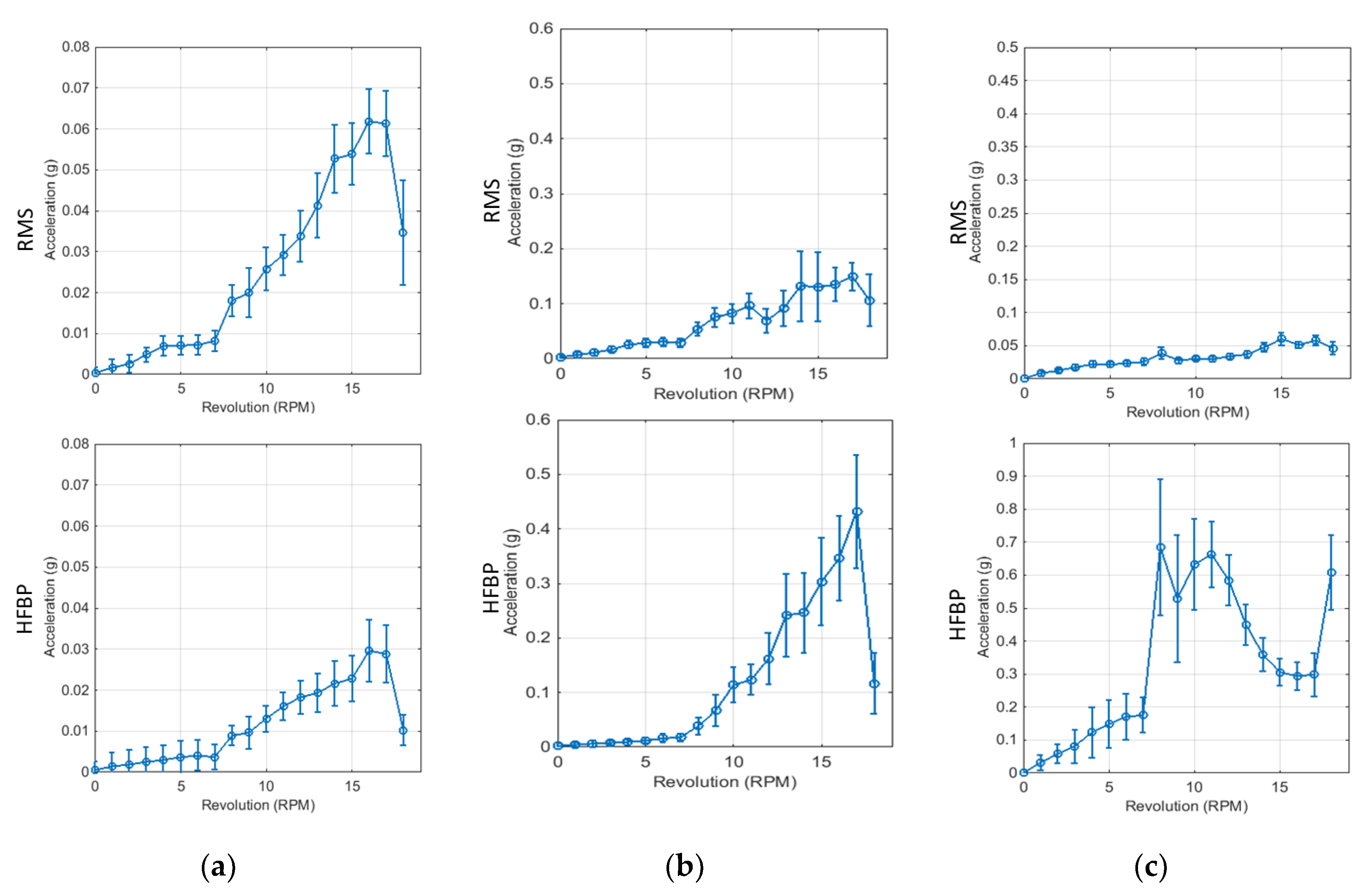
3.2. Trend Analysis of Vibration Signals
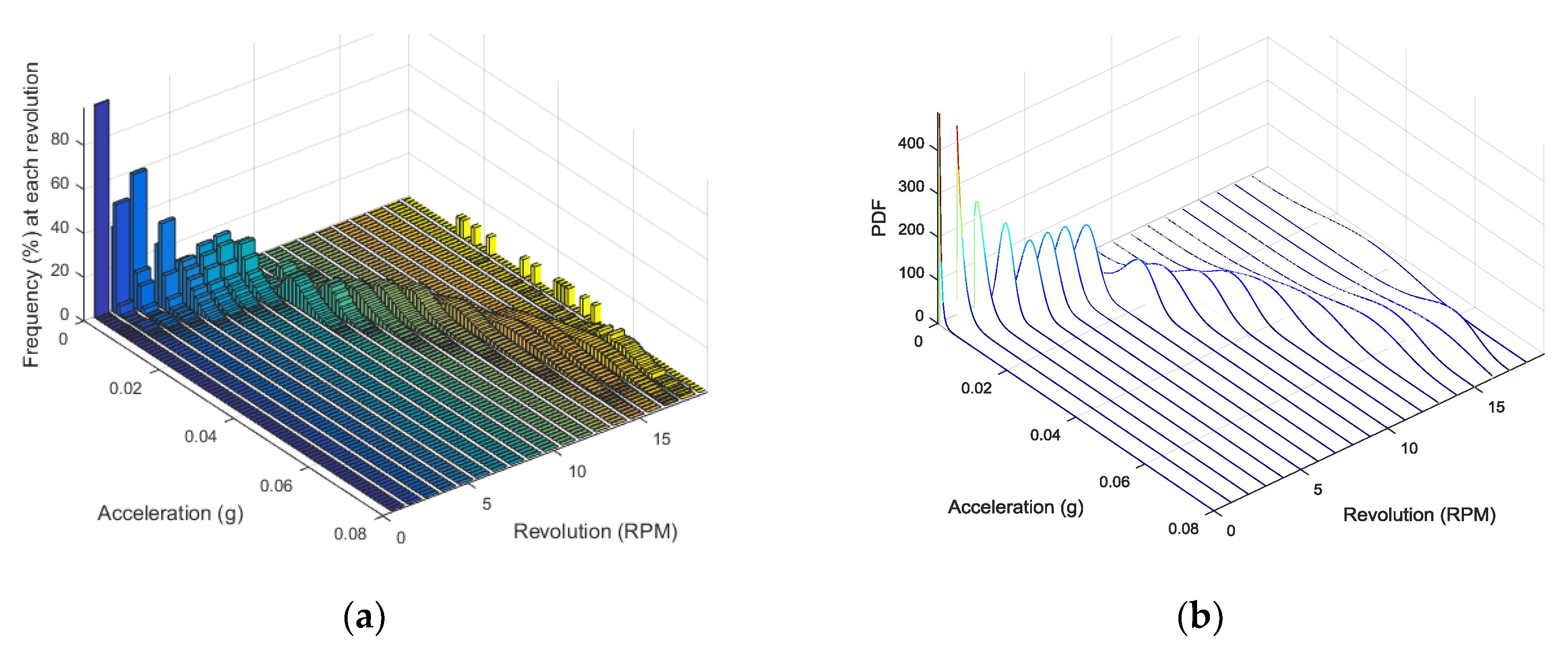
Distribution of Vibration Signals
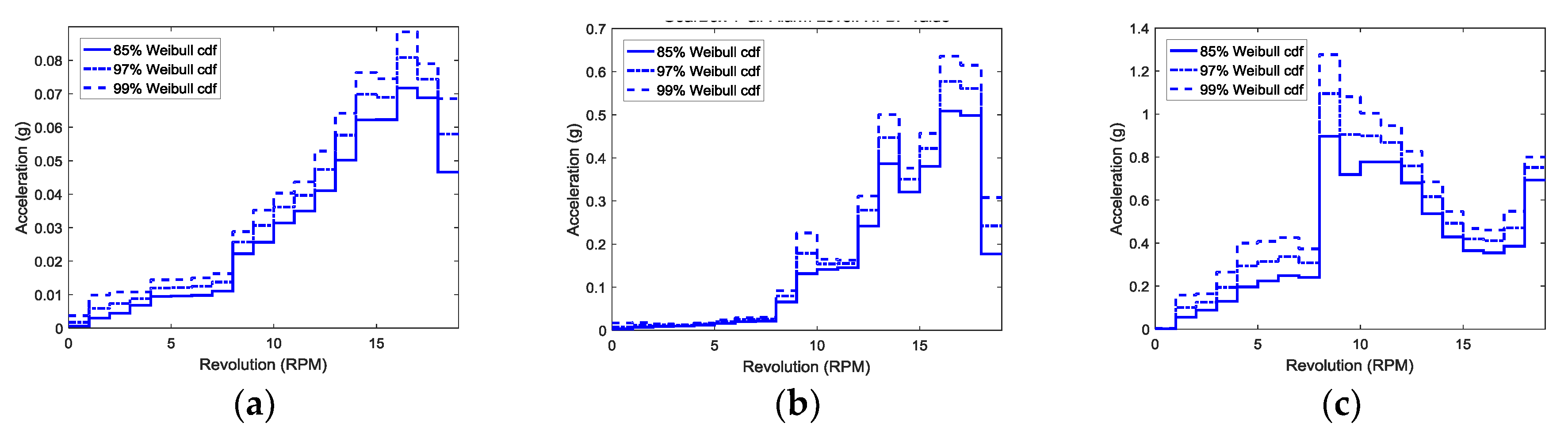
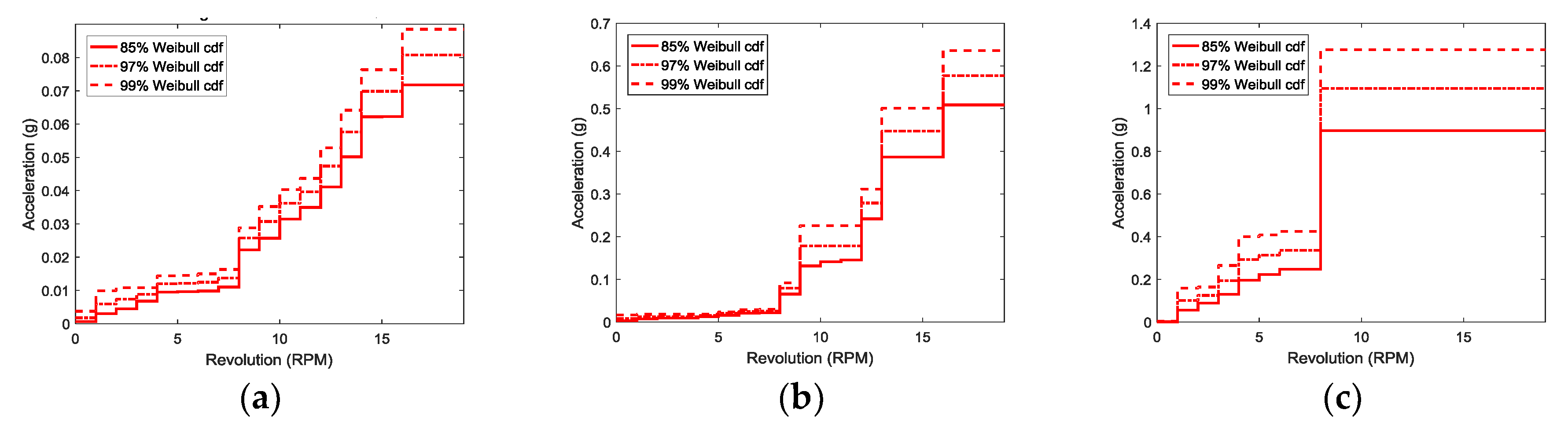
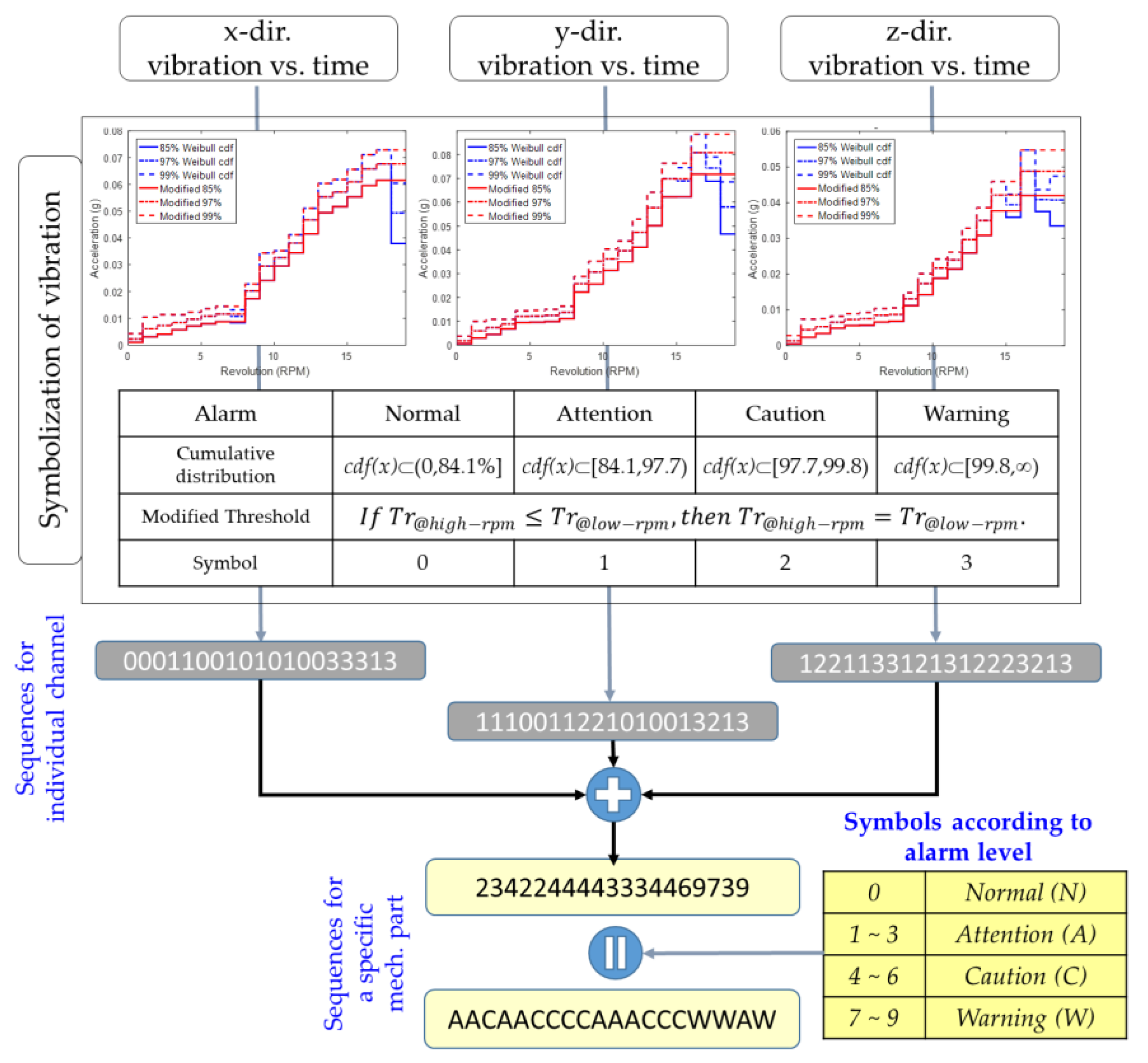
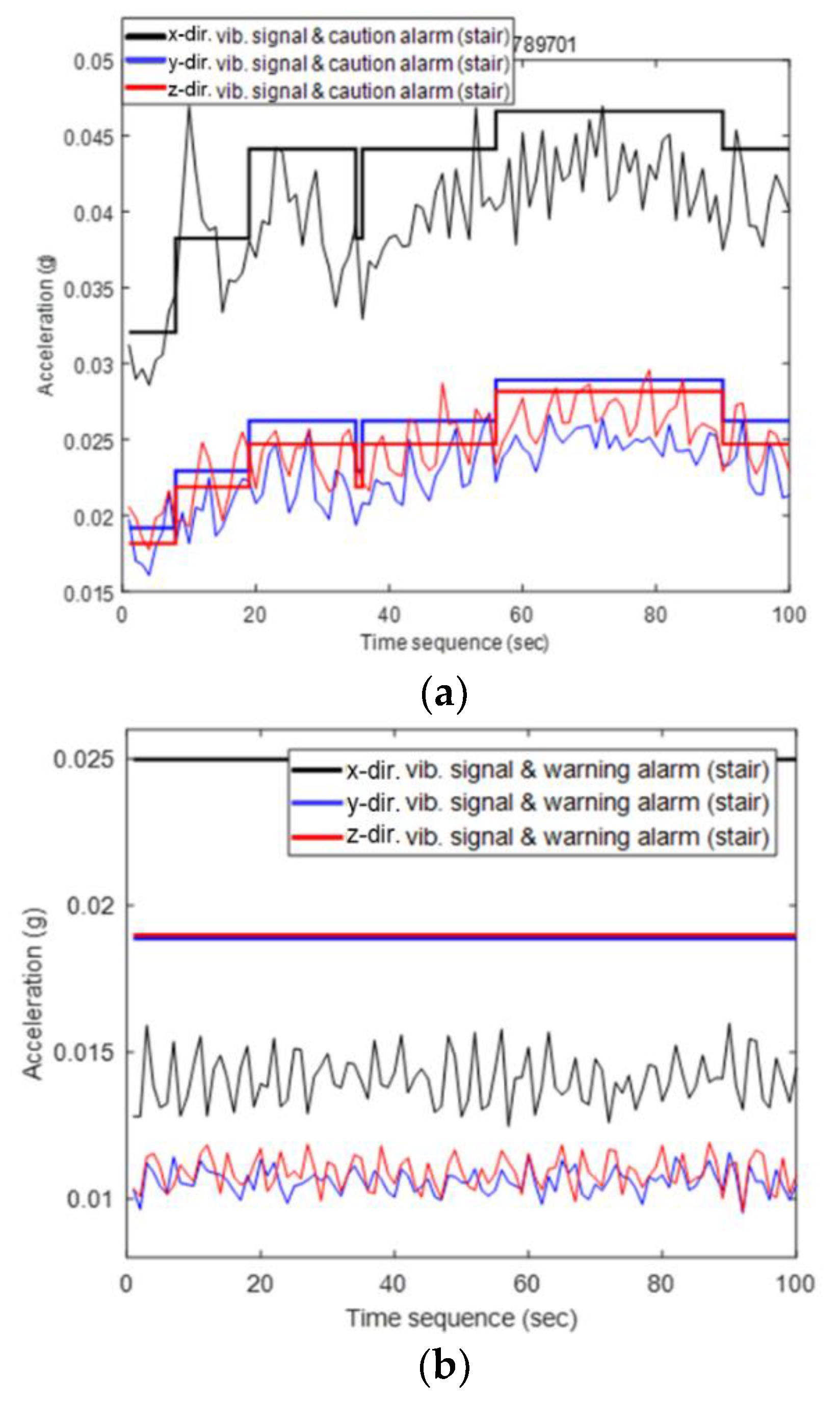
3.3. Threshold Setting based on Alarm Level
4. Fault Monitoring Using Hidden Markov Model
4.1. Fault Detection Algorithm
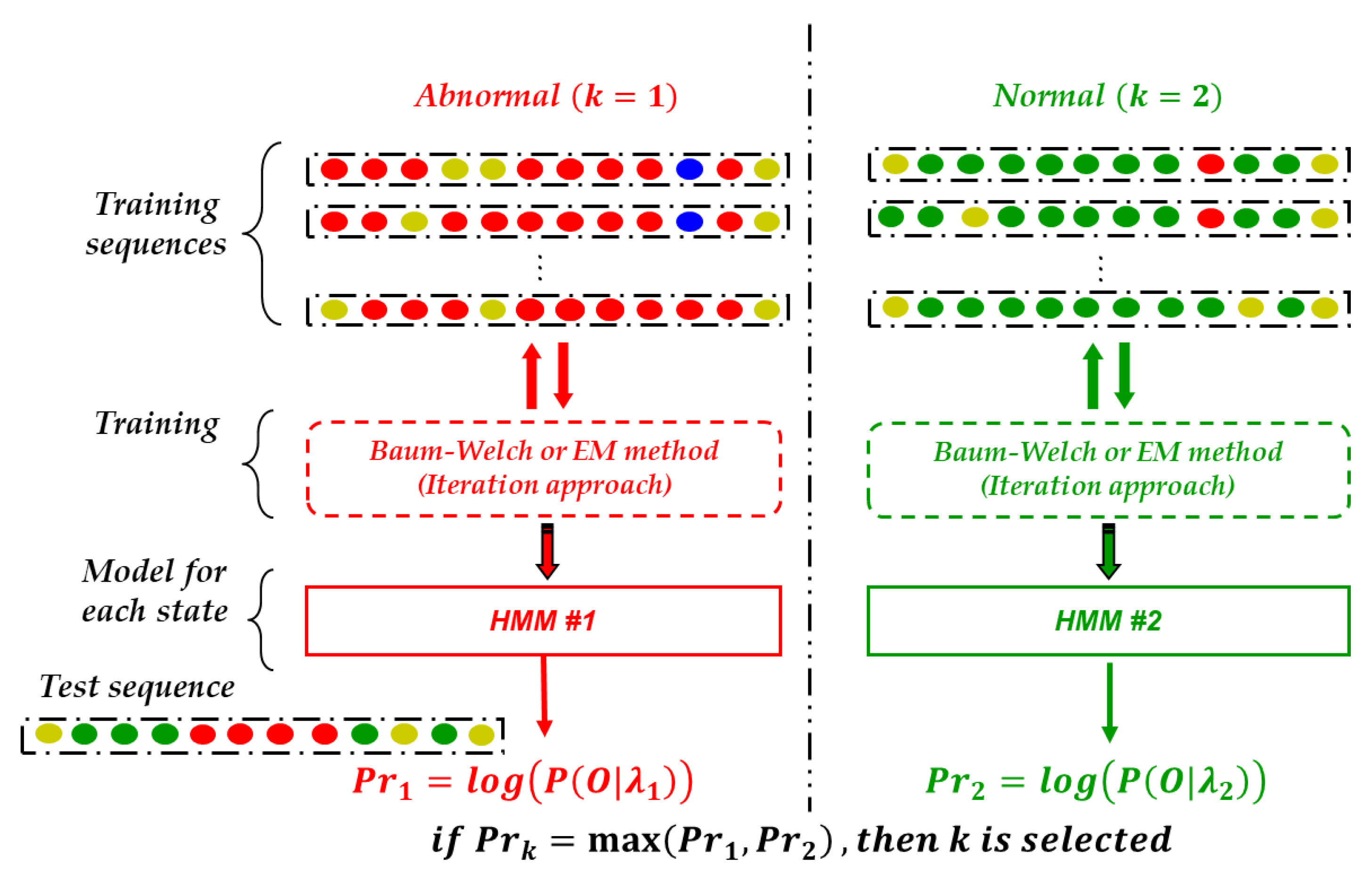
4.1.1. Hidden Markov Model (HMM)
4.1.2. Design of HMMs for Fault Detection
Structure and Input data
Process for Detecting Faults
4.2. Performance of the Proposed Algorithm
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gulati, R. Maintenance and Reliability: Best Practices; Industrial Press, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Vachon, W. Long-term O&M costs of wind turbines based on failure rates and repair costs. In Proceedings of the American Wind Energy Association Annual Conference (WINDPOWER), Portland, OR, USA, 2–5 June 2002. [Google Scholar]
- Jardine, A.; Lin, D.; Banjevic, D. A Review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Ahmad, R.; Kamaruddin, S. An overview of time-based and condition-based maintenance in industrial application. Comput. Ind. Eng. 2012, 63, 135–149. [Google Scholar] [CrossRef]
- Electric Power Research Institute (EPRI). Improving Maintenance Effectiveness: An Evaluation of Plant Preventive and Predictive Maintenance Activities; EPRI TR-107042; EPRI: Palo Alto, CA, USA, 1998. [Google Scholar]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind turbine condition monitoring: Technical and commercial challenges. Wind Energy 2014, 17, 673–693. [Google Scholar] [CrossRef] [Green Version]
- Akitoshi, T.; Takashi, H.; Hiroshi, I. Application of Condition Monitoring System for Wind Turbines. Available online: https://scholar.google.ch/scholar?hl=en&as_sdt=0%2C5&q=Application+of+Condition+/Monitoring+System+for+Wind+Turbines&btnG= (accessed on 7 May 2017).
- Marquez, F.P.G.; Tobias, A.M.; Perez, J.M.P.; Papaelias, M. Condition monitoring of wind turbine: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Ferguson, D.; Catterson, Y.M.; Booth, C.; Cruden, A. Designing wind turbine condition monitoring systems suitable for harsh environment. In Proceedings of the Renewable Power Generation Conference, Beijing, China, 9–11 September 2009. [Google Scholar]
- Hameed, Z.; Hong, Y.S.; Choa, Y.M.; Ahn, S.H.; Song, C.K. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Lee, C.-W.; Han, Y.-S.; Lee, Y.-S. Use of directional spectra for detection of engine cylinder power fault. Shock Vib. 1997, 4, 391–401. [Google Scholar] [CrossRef]
- Villa, L.F.; Renones, A.; Peran J., R.; Miguel L., J. Augular resampling for vibration analysis in wind turbines under non-linear speed fluctutation. Mech. Syst. Signal Process. 2011, 25, 2157–2168. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 76, 796–808. [Google Scholar]
- Korbicz, J.; Koscielny, J.M.; Kowalczuk, Z.; Cholewa, W. Fault Diagnosis: Models, Artificial Intelligence, Application; Springer: Berlin, Germany, 2004. [Google Scholar]
- Rabiner, L.R. A Tutorial on Hidden Markov Models and Selected Application in Speech Recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Moon, S.J.; Kim, B.K. Control and Condition Monitoring System. In Understanding of Advanced Wind Turbines; A-Jin: Seoul, Korea, 2010; pp. 302–324. [Google Scholar]
- Shin, S.-H.; Kim, S.R.; Seo, Y.-H. Distribution of vibration signals according to operating conditions of wind turbine. J. Acoust. Soc. Korea 2016, 35, 192–201. [Google Scholar] [CrossRef]
- International Electrotechnical Commission (IEC). Communications for Monitoring and Control of Wind Power Plants—Logical Node Classes and Data Classes for Condition Monitoring; IEC 61400-25-6; IEC: Geneva, Switzerland, 2016. [Google Scholar]
- International Electrotechnical Commission (IEC). Communications for Monitoring and Control of Wind Power Plants—Overall Description of Principles and Models; IEC 61400-25-1; IEC: Geneva, Switzerland, 2017. [Google Scholar]
- Weibull Distribution. Available online: https://en.wikipedia.org/wiki/Weibull_distribution (accessed on 28 May 2017).
- Kim, S.R.; Kim, B.K.; Kim, J.S.; Kim, H.S.; Lee, S.H. Application of statistical technique for condition monitoring variables of wind turbines. In Proceedings of the 2012 Autumn Meeting of the KSNVE, Wonju, Korea, 24–26 October 2012. [Google Scholar]
- Cappe, O.; Moulines, E.; Ryden, T. Inference in Hidden Markov Models; Springer: New York, NY, USA, 2005. [Google Scholar]
- Ying, J.; Kirubaraja, T.; Pattipati, K.R. A Hidden Markov Model-Based Algorithm for Fault Diagnosis with Partial and Imperfect Tests. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2000, 30, 463–473. [Google Scholar] [CrossRef]
- Lei, J.; Lin, Z.; He, Z.; Kong, D. A method based on multi-sensor data fusion for fault detection of planetary gearbox. Sensors 2012, 12, 2005–2017. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Santos, P.; Maudes, J.; Bustillo, A. Identifying maximum imbalance in datasets for fault diagnosis of gearboxes. J. Intell. Manuf. 2018, 29, 333–351. [Google Scholar] [CrossRef]
- Bustillo, A.; Rodriguez, A.B. Online breakage detection of multitooth tools using classifier ensembles for imbalanced data. Int. J. Syst. Sci. 2014, 45, 2590–2602. [Google Scholar] [CrossRef]




| Mechanical Part | Acceleration Directions | |||
|---|---|---|---|---|
| X (Horizontal) | Y (Vertical) | Z (Axial) | ||
| Main shaft bearing | RMS | RMS | RMS | |
| - | HFBP | HFBP | ||
| Gearbox | Low-speed part | - | RMS | RMS |
| - | HFBP | HFBP | ||
| High-speed part | - | RMS | RMS | |
| - | HFBP | HFBP | ||
| Generator | Input part | - | RMS | RMS |
| - | HFBP | HFBP | ||
| Output part | - | RMS | RMS | |
| - | HFBP | HFBP | ||
| Alarm Level | Threshold, Tr | Alarm Range of Vibration, x |
|---|---|---|
| Normal | - | cdf(x) < 84.1% |
| Attention | cdf(Tr) = 84.1% | 84.1% ≤ cdf(x) < 97.7% |
| Caution | cdf(Tr) = 97.7% | 97.7% ≤ cdf(x) < 99.8% |
| Warning | cdf(Tr) = 99.8% | 99.8% ≤ cdf(x) |
| Mechanical Part | For Abnormal | For Normal |
|---|---|---|
| Bearing of main shaft | 2250 | 4500 |
| Gearbox | 910 | 4500 |
| Generator | 2250 | 4500 |
| Mechanical Part | HMM | Transient Probability Distribution (2 × 2) | Observation Symbol Probability Distribution (2 × 4) | ||||
|---|---|---|---|---|---|---|---|
| Bearing of main shaft | For abnormal | 0.945171 | 0.054829 | 0.678136 | 0.303485 | 0.018101 | 0.000278 |
| 0.00676 | 0.99324 | 4.11×10−8 | 0.029147 | 0.361074 | 0.609779 | ||
| For normal | 0.987934 | 0.012066 | 0.933989 | 0.065805 | 0.000203 | 2.27×10−6 | |
| 0.023135 | 0.976865 | 0.210395 | 0.697227 | 0.09153 | 0.000848 | ||
| Gearbox | For abnormal | 0.933872 | 0.066128 | 0.129456 | 0.851896 | 0.012909 | 0.005739 |
| 0.02293 | 0.97707 | 6.66×10−6 | 0.003044 | 0.727025 | 0.269925 | ||
| For normal | 0.954631 | 0.045369 | 0.960139 | 0.039777 | 7.67×10−5 | 7.92×10−6 | |
| 0.050568 | 0.949432 | 0.03402 | 0.931385 | 0.034524 | 7.11×10−5 | ||
| Generator | For abnormal | 0.926132 | 0.073868 | 0.264596 | 0.258718 | 0.457806 | 0.018881 |
| 0.020584 | 0.979416 | 1.60×10−41 | 0.000315 | 0.142944 | 0.856741 | ||
| For normal | 0.990231 | 0.009769 | 0.993997 | 0.005972 | 1.48×10−5 | 1.57×10−5 | |
| 0.044451 | 0.955549 | 0.094724 | 0.809085 | 0.095486 | 0.000705 | ||
| Mechanical Part | For Abnormal | For Normal | Total # of Test Sequences |
|---|---|---|---|
| Bearing of main shaft | 1628 | 5843 | 7471 |
| Gearbox | 364 | 6406 | 6770 |
| Generator | 294 | 6622 | 6916 |
| Mechanical Part | Accuracy | TPrate (Recall) | FPrate | Precision | F-Measure |
|---|---|---|---|---|---|
| Bearing of main shaft | 0.961 | 0.848 | 0.000 | 1.000 | 0.918 |
| Gearbox | 0.986 | 0.791 | 0.000 | 1.000 | 0.884 |
| Generator | 0.968 | 0.573 | 0.000 | 1.000 | 0.729 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, S.-H.; Kim, S.; Seo, Y.-H. Development of a Fault Monitoring Technique for Wind Turbines Using a Hidden Markov Model. Sensors 2018, 18, 1790. https://doi.org/10.3390/s18061790
Shin S-H, Kim S, Seo Y-H. Development of a Fault Monitoring Technique for Wind Turbines Using a Hidden Markov Model. Sensors. 2018; 18(6):1790. https://doi.org/10.3390/s18061790
Chicago/Turabian StyleShin, Sung-Hwan, SangRyul Kim, and Yun-Ho Seo. 2018. "Development of a Fault Monitoring Technique for Wind Turbines Using a Hidden Markov Model" Sensors 18, no. 6: 1790. https://doi.org/10.3390/s18061790
APA StyleShin, S.-H., Kim, S., & Seo, Y.-H. (2018). Development of a Fault Monitoring Technique for Wind Turbines Using a Hidden Markov Model. Sensors, 18(6), 1790. https://doi.org/10.3390/s18061790




