Self-Calibration Algorithm for a Pressure Sensor with a Real-Time Approach Based on an Artificial Neural Network
Abstract
:1. Introduction
2. Methods
2.1. Measurement System Consideration and Calibration
2.2. Artificial Neural Network Architectures and Parameters
3. Results
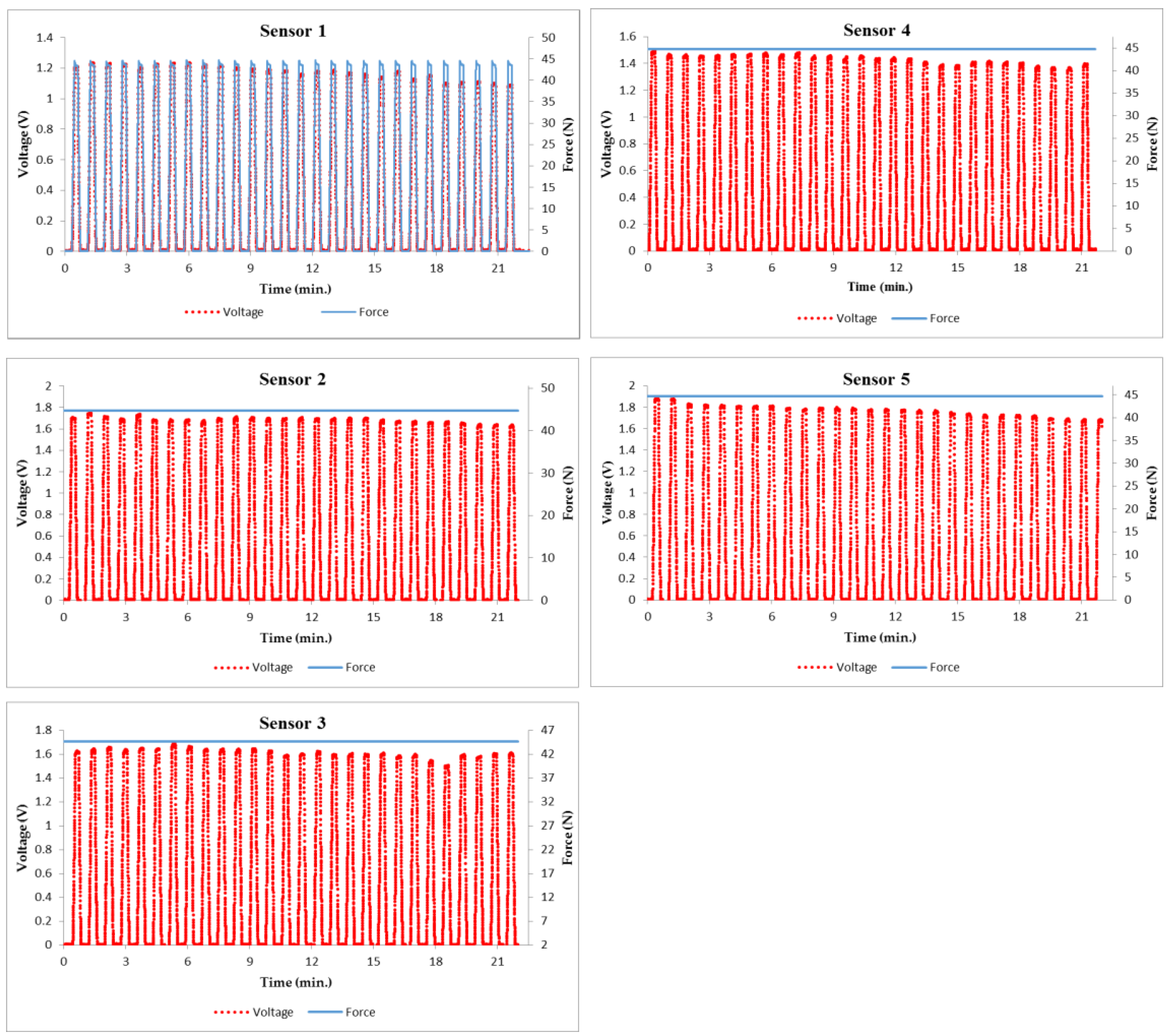
3.1. Calibration Pressure Sensor
3.2. Training and Evaluation
3.3. Performance of the LMBP-ANN Model
4. Neural Network Testing and Evaluation with Untrained Data Sets
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, W.-C. Polymer micromachined flexible tactile sensor for three-axial loads detection. Trans. Electr. Electron. Mater. 2010, 11, 130–133. [Google Scholar] [CrossRef]
- Rodriguez, A.; Mason, M.T.; Srinivasa, S.S. Manipulation capabilities with simple hands. In Experimental Robotics; Springer: Berlin, Germany, 2014; pp. 285–299. [Google Scholar]
- Lee, H.-K.; Chung, J.; Chang, S.-I.; Yoon, E. Normal and shear force measurement using a flexible polymer tactile sensor with embedded multiple capacitors. J. Microelectromech. Syst. 2008, 17, 934–942. [Google Scholar]
- Mizelmoe, L.C. Gripper for Objects. U.S. Patent 8,210,587, 3 July 2012. [Google Scholar]
- Lippiello, V.; Ruggiero, F.; Siciliano, B.; Villani, L. Visual grasp planning for unknown objects using a multifingered robotic hand. IEEE/ASME Trans. Mechatron. 2013, 18, 1050–1059. [Google Scholar] [CrossRef]
- Sale, P.; Lombardi, V.; Franceschini, M. Hand robotics rehabilitation: Feasibility and preliminary results of a robotic treatment in patients with hemiparesis. Stroke Res. Treat. 2012, 2012, 820931. [Google Scholar] [CrossRef] [PubMed]
- Ho, N.S.K.; Tong, K.Y.; Hu, X.L.; Fung, K.L.; Wei, X.J.; Rong, W.; Susanto, E.A. An EMG-driven exoskeleton hand robotic training device on chronic stroke subjects: Task training system for stroke rehabilitation. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–5. [Google Scholar]
- Chang, P.-H.; Lee, S.-H.; Gu, G.M.; Lee, S.-H.; Jin, S.-H.; Yeo, S.S.; Seo, J.P.; Jang, S.H. The cortical activation pattern by a rehabilitation robotic hand: A functional NIRS study. Front. Hum. Neurosci. 2014, 8, 49. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, B.K.; Liu, X.; Sun, Y. Autonomous robotic pick-and-place of microobjects. IEEE Trans. Robot. 2010, 26, 200–207. [Google Scholar] [CrossRef]
- Rivera, J.; Carrillo, M.; Chacón, M.; Herrera, G.; Bojorquez, G. Self-calibration and optimal response in intelligent sensors design based on artificial neural networks. Sensors 2007, 7, 1509–1529. [Google Scholar] [CrossRef]
- Rivera, J.; Herrera, G.; Chacón, M.; Acosta, P.; Carrillo, M. Improved progressive polynomial algorithm for self-adjustment and optimal response in intelligent sensors. Sensors 2008, 8, 7410–7427. [Google Scholar] [CrossRef] [PubMed]
- Khachab, N.I.; Ismail, M. Linearization techniques for nth-order sensor models in MOS VLSI technology. IEEE Trans. Circuits Syst. 1991, 38, 1439–1450. [Google Scholar] [CrossRef]
- Trofimenkoff, F.; Smallwood, R. JFET circuit linearizes transducer output. IEEE Trans. Instrum. Meas. 1973, 22, 191–193. [Google Scholar] [CrossRef]
- Trofimenkoff, F.; Smallwood, R.E. Analog-multiplier circuit linearizes transducer output. IEEE Trans. Instrum. Meas. 1974, 23, 195–197. [Google Scholar] [CrossRef]
- Mahana, P.N.; Trofimenkoff, F. Transducer output signal processing using an eight-bit microcomputer. IEEE Trans. Instrum. Meas. 1986, 1001, 182–186. [Google Scholar] [CrossRef]
- Iglesias, G.E.; Iglesias, E.A. Linearization of transducer signals using an analog-to-digital converter. IEEE Trans. Instrum. Meas. 1988, 37, 53–57. [Google Scholar] [CrossRef]
- Patranabis, D.; Ghosh, D. A novel software-based transducer linearizer. IEEE Trans. Instrum. Meas. 1989, 38, 1122–1126. [Google Scholar] [CrossRef]
- Farias, G.; Fabregas, E.; Peralta, E.; Vargas, H.; Hermosilla, G.; Garcia, G.; Dormido, S. A Neural Network Approach for Building an Obstacle Detection Model by Fusion of Proximity Sensors Data. Sensors 2018, 18, 683. [Google Scholar] [CrossRef] [PubMed]
- Rivas, J.R.; Lou, F.; Harrison, H.; Key, N. Measurement and Calibration of Centrifugal Compressor Pressure Scanning Instrumentation. 2015. Available online: https://docs.lib.purdue.edu/surf/2015/presentations/40/ (accessed on 2 August 2018).
- Rivera-Mejía, J.; Arzabala-Contreras, E.; León-Rubio, Á.G. Approach to the validation function of intelligent sensors based on error’s predictors. In Proceedings of the 2010 IEEE Instrumentation & Measurement Technology Conference, Austin, TX, USA, 3–6 May 2010; pp. 1121–1125. [Google Scholar]
- Rivera-Mejía, J.; Carrillo-Romero, M.; Herrera-Ruíz, G. Quantitative evaluation of self compensation algorithms applied in intelligent sensors. In Proceedings of the 2010 IEEE Instrumentation & Measurement Technology Conference, Austin, TX, USA, 3–6 May 2010; pp. 1116–1120. [Google Scholar]
- Rivera-Mejía, J.; Villafuerte-Arroyo, J.E.; Vega-Pineda, J. Evaluation of the Progressive Polynomial Compensation Algorithm for dynamic or Real-Time applications. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; pp. 861–865. [Google Scholar]
- Rivera-Mejía, J.; Villafuerte-Arroyo, J.E.; Vega-Pineda, J.; Sandoval-Rodríguez, R. Comparison of Compensation Algorithms for Smart Sensors With Approach to Real-Time or Dynamic Applications. IEEE Sens. J. 2015, 15, 7071–7080. [Google Scholar] [CrossRef]
- Lyahou, K.F.; van der Horn, G.; Huijsing, J.H. A noniterative polynomial 2-D calibration method implemented in a microcontroller. IEEE Trans. Instrum. Meas. 1997, 46, 752–757. [Google Scholar] [CrossRef] [Green Version]
- Pereira, J.D.; Postolache, O.; Girao, P.S. Adaptive self-calibration algorithm for smart sensors linearization. In Proceedings of the 2005 IEEE Instrumentationand Measurement Technology Conference, Ottawa, ON, Canada, 16–19 May 2005; pp. 648–652. [Google Scholar]
- Abu-Khalaf, N.; Iversen, J.J.L. Calibration of a sensor array (an electronic tongue) for identification and quantification of odorants from livestock buildings. Sensors 2007, 7, 103–128. [Google Scholar] [CrossRef]
- Lebosse, C.; Renaud, P.; Bayle, B.; de Mathelin, M. Modeling and evaluation of low-cost force sensors. IEEE Trans. Robot. 2011, 27, 815–822. [Google Scholar] [CrossRef]
- Xing, J.; Chen, J. Design of a Thermoacoustic sensor for low intensity ultrasound measurements based on an artificial neural network. Sensors 2015, 15, 14788–14808. [Google Scholar] [CrossRef] [PubMed]
- Al-Salaymeh, A. Optimization of hot-wire thermal flow sensor based on a neural net model. Appl. Therm. Eng. 2006, 26, 948–955. [Google Scholar]
- Ciminski, A.S. Neural network based adaptable control method for linearization of high power amplifiers. AEU-Int. J. Electron. Commun. 2005, 59, 239–243. [Google Scholar] [CrossRef]
- Lo, D.-C.; Wei, C.-C.; Tsai, E.-P. Parameter automatic calibration approach for neural-network-based cyclonic precipitation forecast models. Water 2015, 7, 3963–3977. [Google Scholar] [CrossRef]
- Suleiman, A.R.; Nehdi, M.L. Modeling Self-Healing of Concrete Using Hybrid Genetic Algorithm–Artificial Neural Network. Materials 2017, 10, 135. [Google Scholar] [CrossRef] [PubMed]
- Adeli, H. Neural networks in civil engineering: 1989–2000. Comput.-Aided Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Almassri, A.M.; Hasan, W.W.; Ahmad, S.A.; Ishak, A.J.; Ghazali, A.; Talib, D.N.; Wada, C. Pressure sensor: State of the art, design, and application for robotic hand. J. Sens. 2015, 2015, 846487. [Google Scholar] [CrossRef]
- Almassri, A.M.; Wan Hasan, W.Z.; Ahmad, S.A.; Ishak, A.J. A sensitivity study of piezoresistive pressure sensor for robotic hand. in Micro and Nanoelectronics (RSM). In Proceedings of the RSM 2013 IEEE Regional Symposium on Micro and Nanoelectronics, Langkawi, Malaysia, 25–27 September 2013; pp. 394–397. [Google Scholar] [CrossRef]
- Almassri, A.M.; Abuitbel, M.B.; Wan Hasan, W.Z.; Ahmad, S.A.; Sabry, A.H. Real-time control for robotic hand application based on pressure sensor measurement. In Proceedings of the 2014 IEEE International Symposium on Robotics and Manufacturing Automation (ROMA), Kuala Lumpur, Malaysia, 15–16 December 2014; pp. 80–85. [Google Scholar] [CrossRef]
- Almassri, A.M.; Wada, C.; Wan Hasan, W.Z.; Ahmad, S.A. Auto-Grasping Algorithm of Robot Gripper Based on Pressure Sensor Measurement. Pertanika J. Sci. Technol. 2017, 25, 113–121. [Google Scholar]
- Almassri, A.M.; Wan Hasan, W.Z.; Ahmad, S.A.; Ishak, A.J.; Wada, C. Optimisation of grasping object based on pressure sensor measurement for robotic hand gripper. In Proceedings of the 2015 9th International Conference on Sensing Technology (ICST), Auckland, New Zealand, 8–10 December 2015; pp. 795–798. [Google Scholar] [CrossRef]
- Büscher, G.H.; Kõiva, R.; Schürmann, C.; Haschke, R.; Ritter, H.J. Flexible and stretchable fabric-based tactile sensor. Robot. Auton. Syst. 2015, 63, 244–252. [Google Scholar] [CrossRef]
- Sarıdemir, M. Predicting the compressive strength of mortars containing metakaolin by artificial neural networks and fuzzy logic. Adv. Eng. Softw. 2009, 40, 920–927. [Google Scholar] [CrossRef]
- Maruyama, M.; Girosi, F.; Poggio, T. A connection between GRBF and MLP. In AI Memos; DTIC Document; MIT AI Lab: Cambridge, MA, USA, 1991. [Google Scholar]
- Hu, Y.H.; Hwang, J.-N. Handbook of Neural Network Signal Processing; CRC press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Depari, A.; Flammini, A.; Marioli, D.; Taroni, A. Application of an ANFIS algorithm to sensor data processing. IEEE Trans. Instrum. Meas. 2007, 56, 75–79. [Google Scholar] [CrossRef]
- Depari, A.; Ferrari, P.; Ferrari, V.; Flammini, A.; Ghisla, A.; Marioli, D.; Taroni, A. Digital signal processing for biaxial position measurement with a pyroelectric sensor array. IEEE Trans. Instrum. Meas. 2006, 55, 501–506. [Google Scholar] [CrossRef]
- Hang, T.M.; Howard, D.B.; Mark, B. Neural Net Work Design; PWS Publishing Company: Beijing, China, 2002. [Google Scholar]









| Training Parameters | Values |
|---|---|
| Neural network model used | Feed forward |
| Input nodes | 2 |
| Hidden layer | 1 |
| Hidden layer neurons | 10 |
| Output layer neurons | 1 |
| Output nodes | 1 |
| Training network algorithm | LMBP |
| Training percentage | 70 |
| Testing percentage | 15 |
| Validation percentage | 15 |
| Transfer function hidden layer | Tan-sigmoid |
| Transfer function output layer | Pure line |
| Data division | Random |
| No. of epochs | 1000 |
| Validation checks (iterations) | 6 |
| Performance | Mean squared error (MSE) |
| Input | Target | Note | |
|---|---|---|---|
| X1 (Voltage) | X2 (Pulses/Time) | T (Pressure) | Input (2 × 132,243) Target (1 × 132,243) |
| 0.006557 | 1 | 0.181619 | Start pulse no. 1 |
| 0.002981 | 1 | 0.1831097 | |
| 0.006472 | 1 | 0.1821192 | |
 |  |  | Continue until the end of pulse no. 1 |
| 0.005791 | 1 | 0.093957 | |
| 0.007238 | 1 | 0.096928 | |
| 0.005024 | 1 | 0.094349 | |
| 0.006046 | 2 | 0.085543 | Start pulse no. 2 |
| 0.006472 | 2 | 0.072284 | |
| 0.005876 | 2 | 0.058114 | |
 |  |  | Continue until the middle of last pulse (no. 28) |
| 1.080495 | 28 | 44.222411 | |
| 1.081602 | 28 | 44.216517 | |
| 1.085690 | 28 | 44.209515 | |
 |  |  | |
| 0.005791 | 28 | 0.083052 | This is the last row of 2 inputs and 1 output |
| 0.011241 | 28 | 0.070892 | |
| 0.006472 | 28 | 0.057947 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almassri, A.M.M.; Wan Hasan, W.Z.; Ahmad, S.A.; Shafie, S.; Wada, C.; Horio, K. Self-Calibration Algorithm for a Pressure Sensor with a Real-Time Approach Based on an Artificial Neural Network. Sensors 2018, 18, 2561. https://doi.org/10.3390/s18082561
Almassri AMM, Wan Hasan WZ, Ahmad SA, Shafie S, Wada C, Horio K. Self-Calibration Algorithm for a Pressure Sensor with a Real-Time Approach Based on an Artificial Neural Network. Sensors. 2018; 18(8):2561. https://doi.org/10.3390/s18082561
Chicago/Turabian StyleAlmassri, Ahmed M. M., Wan Zuha Wan Hasan, Siti Anom Ahmad, Suhaidi Shafie, Chikamune Wada, and Keiichi Horio. 2018. "Self-Calibration Algorithm for a Pressure Sensor with a Real-Time Approach Based on an Artificial Neural Network" Sensors 18, no. 8: 2561. https://doi.org/10.3390/s18082561
APA StyleAlmassri, A. M. M., Wan Hasan, W. Z., Ahmad, S. A., Shafie, S., Wada, C., & Horio, K. (2018). Self-Calibration Algorithm for a Pressure Sensor with a Real-Time Approach Based on an Artificial Neural Network. Sensors, 18(8), 2561. https://doi.org/10.3390/s18082561








