A Nonlinear Circuit Analysis Technique for Time-Variant Inductor Systems
Abstract
:1. Introduction
2. Background
3. Analysis Approach
3.1. Proposed Method
3.2. Comparison with Numerical Methods
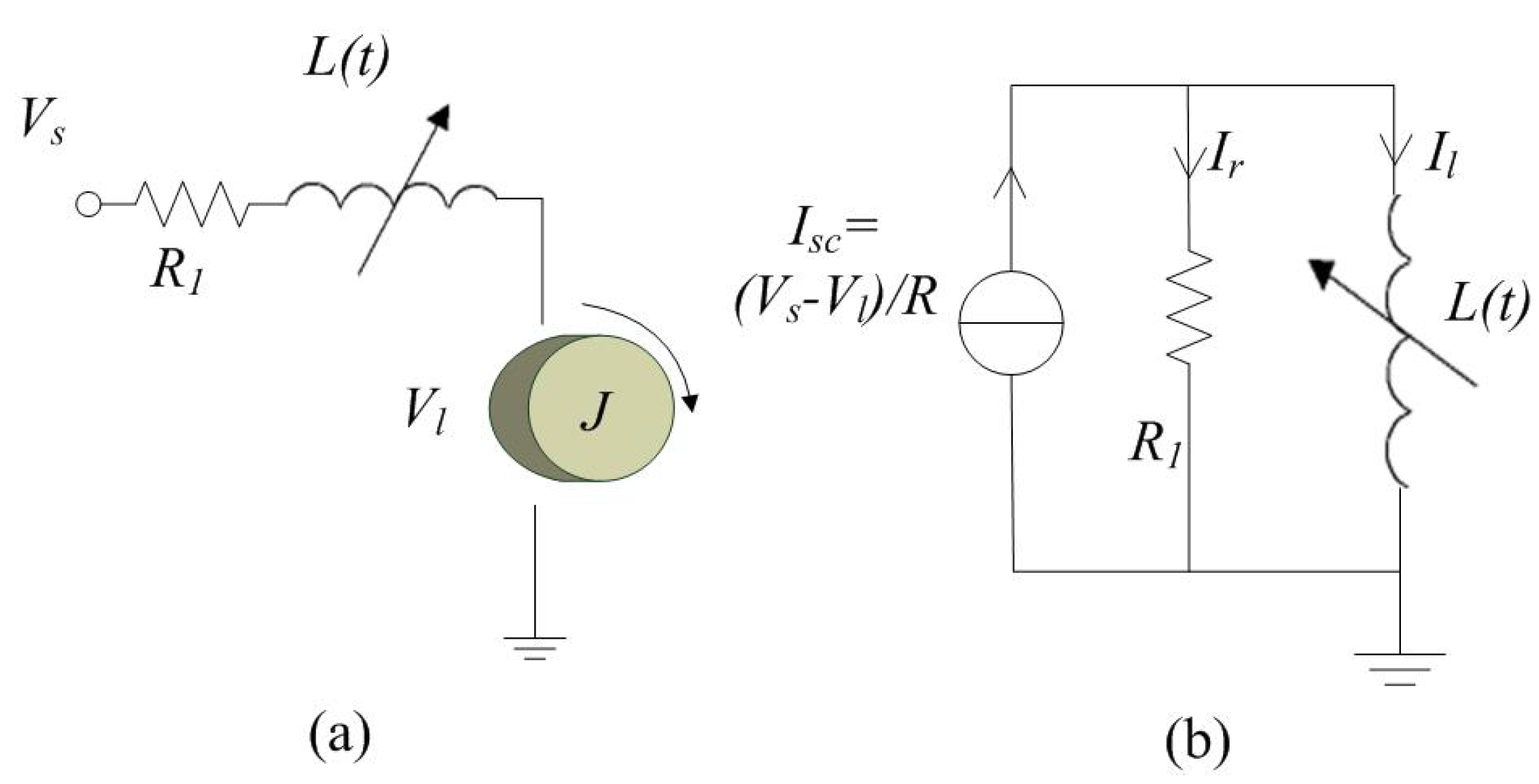
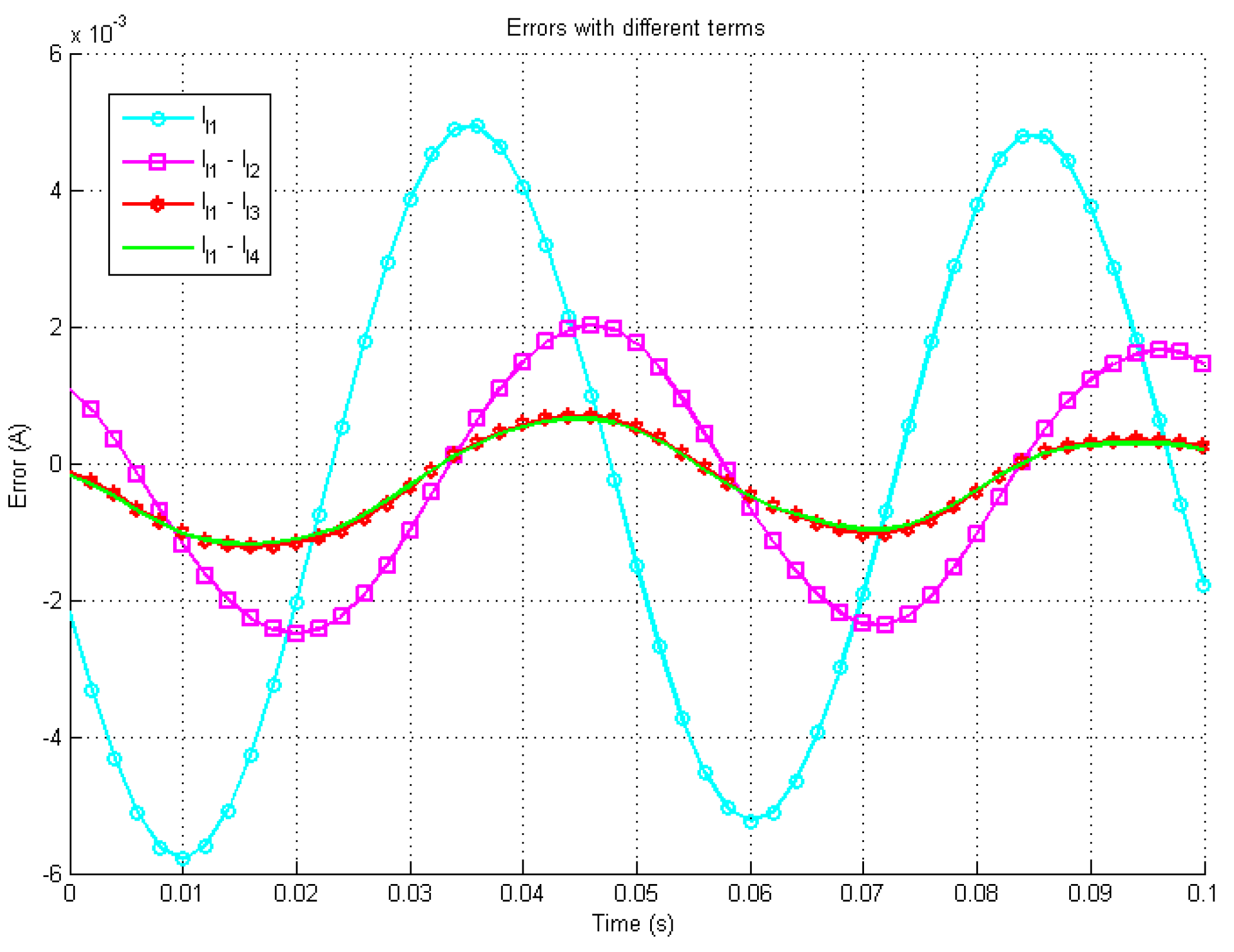
4. Case Study
4.1. System Modeling and Analysis
4.2. Computational Complexity Analysis
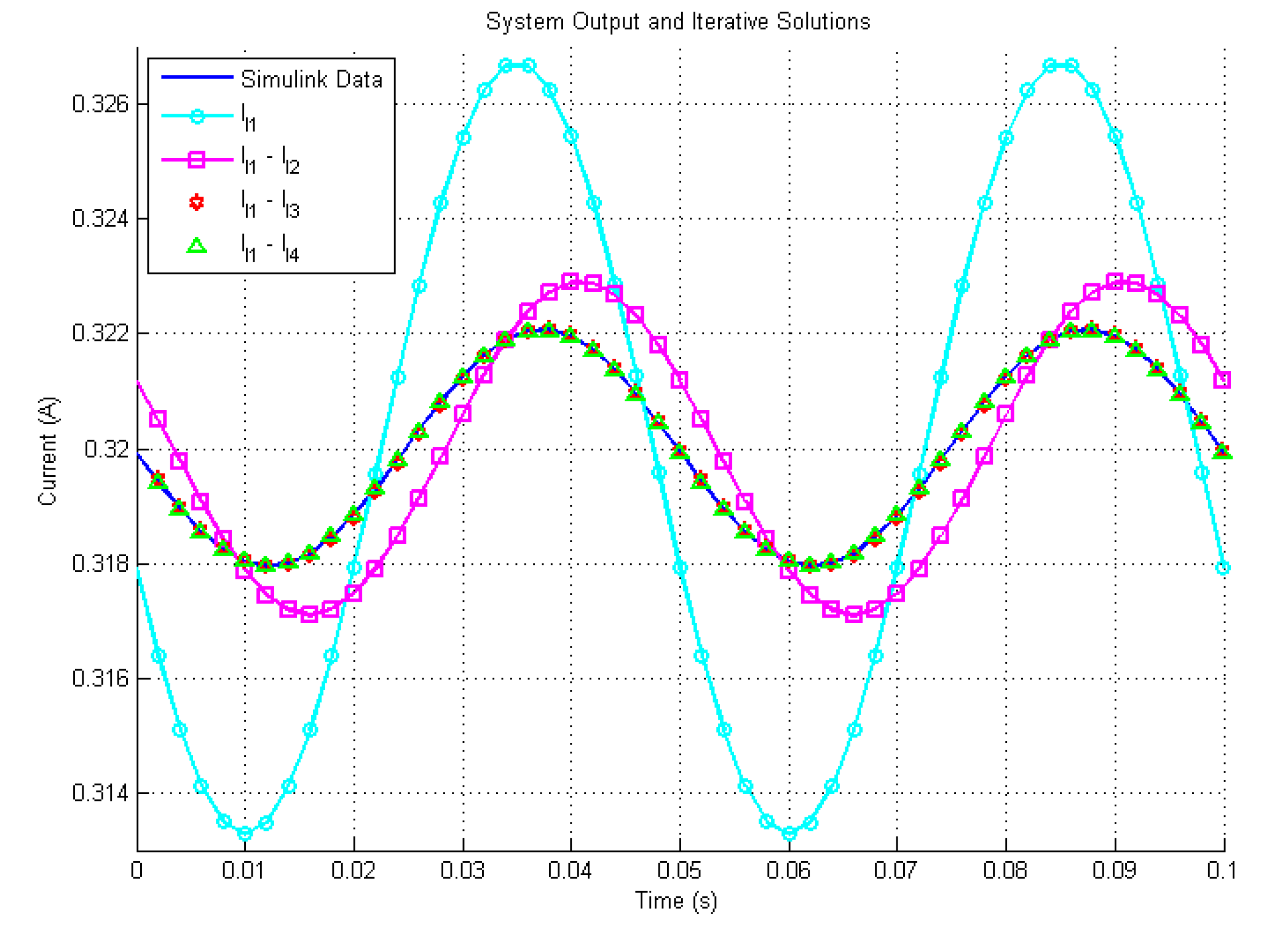
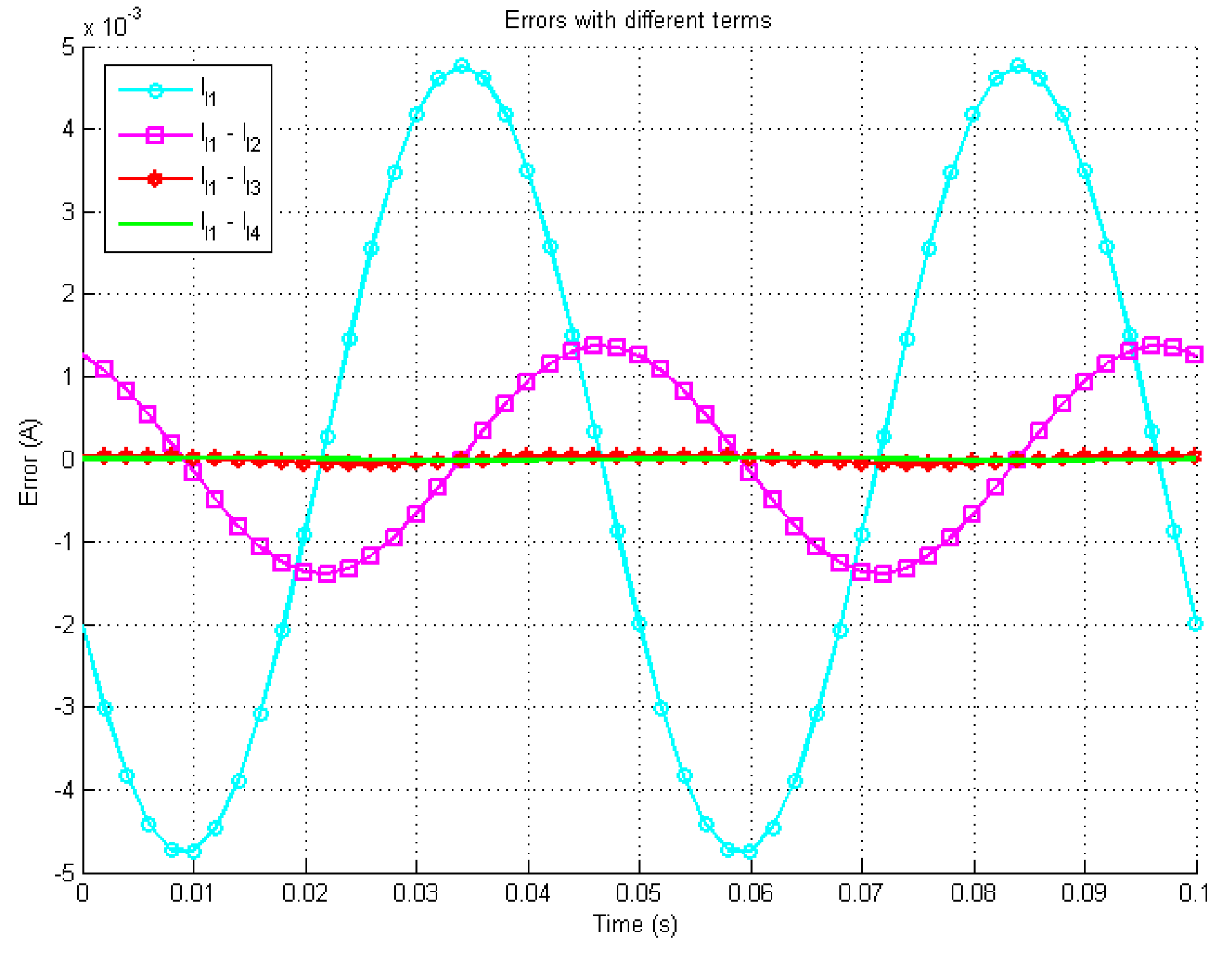
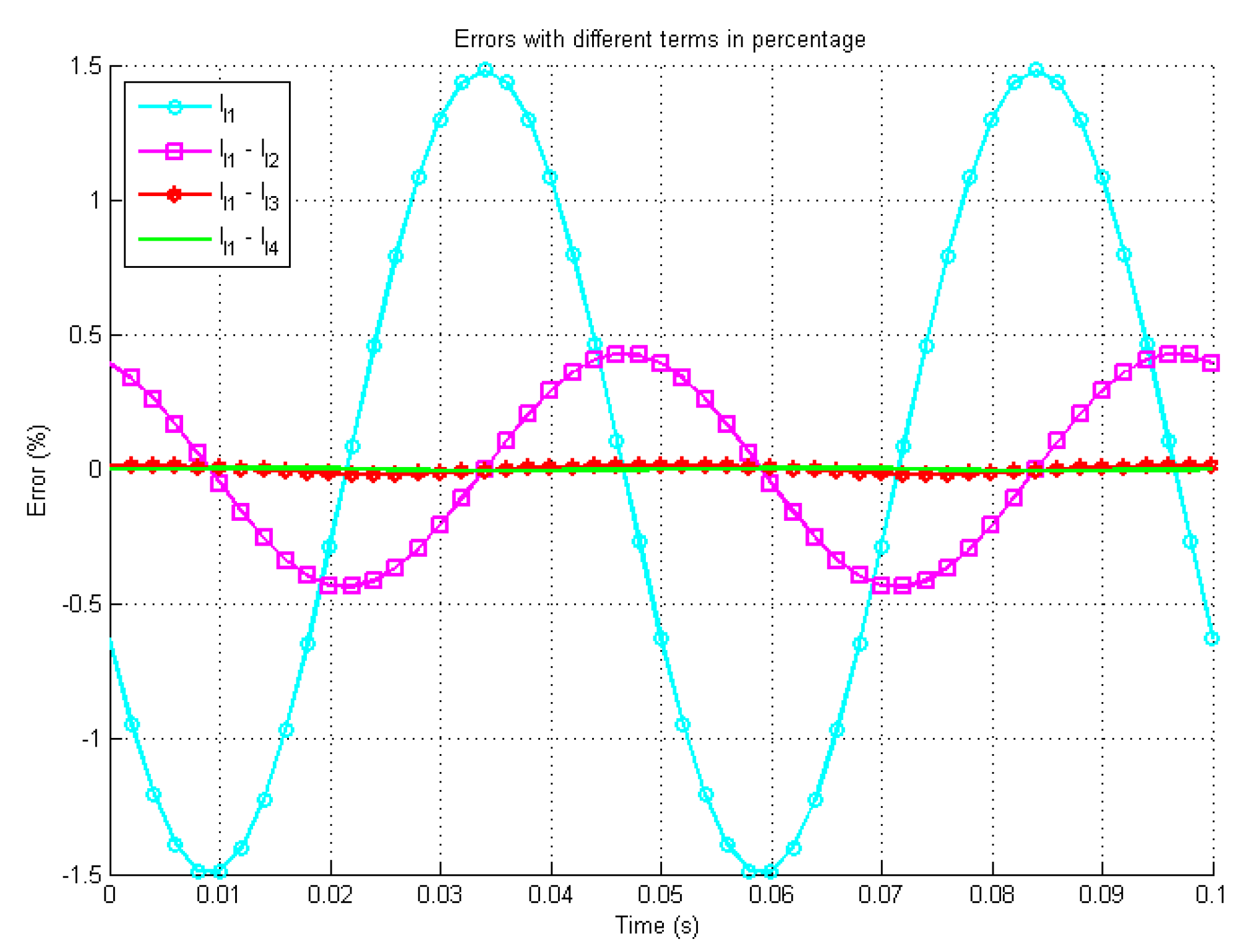
4.3. Simulation Study
4.4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lai, C.; Iyer, L.; Mukherjee, K.; Kar, N. Analysis of Electromagnetic Torque and Effective Winding Inductance in a Surface-Mounted PMSM during Integrated Battery Charging Operation. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Beraki, M.W.; Trovão, J.P.F.; Perdigão, M.S.; Dubois, M.R. Variable Inductor Based Bidirectional DC–DC Converter for Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 8764–8772. [Google Scholar] [CrossRef]
- Hung, J.Y.; Albritton, N.G.; Xia, F. Nonlinear control of a magnetic bearing system. Mechatronics 2003, 13, 621–637. [Google Scholar] [CrossRef]
- Wu, S.T.; Mo, S.C.; Wu, B.S. An LVDT-based self-actuating displacement transducer. Sens. Actuators Phys. 2008, 141, 558–564. [Google Scholar] [CrossRef]
- Bedair, S.; Pulskamp, J.; Meyer, C.; Polcawich, R.; Kierzewski, I. Modeling, fabrication and testing of MEMS tunable inductors varied with piezoelectric actuators. J. Micromech. Microeng. 2014, 24, 095017. [Google Scholar] [CrossRef]
- Xiong, Y.; Wei, J.; Feng, R. Adaptive robust control of a high-response dual proportional solenoid valve with flow force compensation. Proc. Inst. Mech. Eng. Part J. Syst. Control. Eng. 2014, 229, 3–26. [Google Scholar] [CrossRef]
- Saeed, S.; García, J.; Georgious, R. Modeling of variable magnetic elements including hysteresis and Eddy current losses. In Proceedings of the IEEE Applied Power Electronics Conference & Exposition, San Antonio, TX, USA, 4–8 March 2018. [Google Scholar]
- Aarniovuori, L.; Laurila, L.I.; Niemela, M.; Pyrhonen, J.J. Measurements and simulations of DTC voltage source converter and induction motor losses. IEEE Trans. Ind. Electron. 2012, 59, 2277–2287. [Google Scholar] [CrossRef]
- Morimoto, S.; Tong, Y.; Takeda, Y.; Hirasa, T. Loss minimization control of permanent magnet synchronous motor drives. IEEE Trans. Ind. Electron. 1994, 41, 511–517. [Google Scholar] [CrossRef]
- Jiancheng, F.; Xiquan, L.; Han, B.; Wang, K. Analysis of Circulating Current Loss for High-Speed Permanent Magnet Motor. IEEE Trans. Magn. 2015, 51, 1–13. [Google Scholar] [CrossRef]
- Gabriel, F. High-Frequency Effects in Modeling AC Permanent-Magnet Machines. IEEE Trans. Ind. Electron. 2015, 62, 62–69. [Google Scholar] [CrossRef]
- Bruce, I.P.; Petty, C.; Song, A.W. Simultaneous and inherent correction of B0 and eddy-current induced distortions in high-resolution diffusion MRI using reversed polarity gradients and multiplexed sensitivity encoding (RPG-MUSE). NeuroImage 2018, 183, 985–993. [Google Scholar] [CrossRef] [PubMed]
- Reese, T.G.; Heid, O.; Weisskoff, R.; Wedeen, V. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2003, 49, 177–182. [Google Scholar] [CrossRef]
- Mohammed, A.M.; Galea, M.; Cox, T.; Gerada, C. Consideration on Eddy Current Reduction Techniques for Solid Materials Used in Unconventional Magnetic Circuits. IEEE Trans. Ind. Electron. 2019, 66, 4870–4879. [Google Scholar] [CrossRef]
- Yin, W.; Peyton, A. Thickness measurement of non-magnetic plates using multi-frequency eddy current sensors. NDT Int. 2007, 40, 43–48. [Google Scholar] [CrossRef]
- Pinedasanchez, M.; Puchepanadero, R.; Martinezroman, J.; Sapenabano, A.; Rieraguasp, M.; Perezcruz, J. Partial Inductance Model of Induction Machines for Fault Diagnosis. Sensors 2018, 18, 2340. [Google Scholar] [CrossRef]
- García-Martín, J.; Gómez-Gil, J.; Vázquez-Sánchez, E. Non-destructive techniques based on eddy current testing. Sensors 2011, 11, 2525–2565. [Google Scholar] [CrossRef]
- Bae, J.N.; Kim, Y.E.; Son, Y.W.; Moon, H.S.; Yoo, C.H.; Lee, J. Self-Excited Induction Generator as an Auxiliary Brake for Heavy Vehicles and Its Analog Controller. IEEE Trans. Ind. Electron. 2015, 62, 3091–3100. [Google Scholar] [CrossRef]
- Berger, D.; Lanza, G. Development and Application of Eddy Current Sensor Arrays for Process Integrated Inspection of Carbon Fibre Preforms. Sensors 2018, 18, 4. [Google Scholar] [CrossRef]
- Chiu, H.C.; Pao, H.K.; Hsieh, R.H.; Chiu, Y.J.; Jang, J.H. Numerical Analysis on the Eddy Current Losses in a Dry-type 3000 KVA Transformer. Energy Procedia 2019, 156, 332–336. [Google Scholar] [CrossRef]
- Mercorelli, P. An adaptive and optimized switching observer for sensorless control of an electromagnetic valve actuator in camless internal combustion engines. Asian J. Control. 2014, 16, 959–973. [Google Scholar] [CrossRef]
- Mercorelli, P.; Lehmann, K.; Liu, S. Robust Flatness Based Control of an Electromagnetic Linear Actuator Using Adaptive PID Controller. In Proceedings of the 42nd IEEE International Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; Volume 4, pp. 3790–3795. [Google Scholar]
- Anwar, S. Predictive yaw stability control of a brake-by-wire equipped vehicle via eddy current braking. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 2308–2313. [Google Scholar]
- Roewer, F.; Kleine, U.; Salzwedel, K.E.; Mednikov, F.; Pfaffinger, C.; Sellen, M. A programmable inductive position sensor interface circuit. Integr. VLSI J. 2004, 38, 227–243. [Google Scholar] [CrossRef]
- Miller, T.; McGilp, M.; Staton, D.; Bremner, J. Calculation of inductance in permanent-magnet DC motors. IEEE Proc. Electr. Power Appl. 1999, 146, 129–137. [Google Scholar] [CrossRef]
- Shishan, W.; Zeyuan, L.; Zhiquan, D. Solution of inductance for bearingless switched reluctance motor by using enhanced incremental energy method. In Proceedings of the Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, DRPT 2008, Nanjing, China, 6–9 April 2008; pp. 2850–2855. [Google Scholar] [CrossRef]
- Adnan, A.; Ishak, D. Finite element modeling and analysis of external rotor brushless DC motor for electric bicycle. In Proceedings of the 2009 IEEE Student Conference on Research and Development (SCOReD), Serdang, Malaysia, 16–18 November 2009; pp. 376–379. [Google Scholar] [CrossRef]
- Li, Y. Monotone iterative method for numerical solution of nonlinear ODEs in MOSFET RF circuit simulation. Math. Comput. Model. 2010, 51, 320–328. [Google Scholar] [CrossRef]
- Dean, R.N.; Wilson, C.G. Nonlinear circuit analysis for time-variant microelectromechanical system capacitor systems. Micro Nano Lett. 2013, 8, 515–518. [Google Scholar] [CrossRef]
- Jabbour, N.; Mademlis, C. Online Parameters Estimation and Autotuning of a Discrete-Time Model Predictive Speed Controller for Induction Motor Drives. IEEE Trans. Power Electron. 2019, 34, 1548–1559. [Google Scholar] [CrossRef]
- Vaughan, N.; Gamble, J. The modeling and simulation of a proportional solenoid valve. Trans. Am. Soc. Mech. Eng. J. Dyn. Syst. Meas. Control 1996, 118, 120–125. [Google Scholar] [CrossRef]
- Tian, H.; Zhao, Y. Coil Inductance Model Based Solenoid on–off Valve Spool Displacement Sensing via Laser Calibration. Sensors 2018, 18, 4492. [Google Scholar] [CrossRef]
- Arpaia, P.; Petrone, C.; Walckiers, L. Experimental validation of solenoid magnetic centre measurement by vibrating wire system. In Proceedings of the XX IMEKO World Congress Metrology for Green Growth, Busan, Korea, 9–14 September 2012; pp. 9–14. [Google Scholar]
- Choi, K.M.; Jung, H.J.; Lee, H.J.; Cho, S.W. Feasibility study of an MR damper-based smart passive control system employing an electromagnetic induction device. Smart Mater. Struct. 2007, 16, 2323. [Google Scholar] [CrossRef]
- Garrido, M.; Källström, P.; Kumm, M.; Gustafsson, O. CORDIC II: A new improved CORDIC algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 186–190. [Google Scholar] [CrossRef]
- Pérez Fernández, J.; Alcázar Vargas, M.; Velasco García, J.M.; Cabrera Carrillo, J.A.; Castillo Aguilar, J.J. Low-Cost FPGA-Based Electronic Control Unit for Vehicle Control Systems. Sensors 2019, 19, 1834. [Google Scholar] [CrossRef]
- Mao, H.; Yao, S.; Tang, T.; Li, B.; Yao, J.; Wang, Y. Towards real-time object detection on embedded systems. IEEE Trans. Emerg. Top. Comput. 2018, 6, 417–431. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, C.; Song, D.; Dean, R. A Nonlinear Circuit Analysis Technique for Time-Variant Inductor Systems. Sensors 2019, 19, 2321. https://doi.org/10.3390/s19102321
Wang X, Li C, Song D, Dean R. A Nonlinear Circuit Analysis Technique for Time-Variant Inductor Systems. Sensors. 2019; 19(10):2321. https://doi.org/10.3390/s19102321
Chicago/Turabian StyleWang, Xinning, Chong Li, Dalei Song, and Robert Dean. 2019. "A Nonlinear Circuit Analysis Technique for Time-Variant Inductor Systems" Sensors 19, no. 10: 2321. https://doi.org/10.3390/s19102321
APA StyleWang, X., Li, C., Song, D., & Dean, R. (2019). A Nonlinear Circuit Analysis Technique for Time-Variant Inductor Systems. Sensors, 19(10), 2321. https://doi.org/10.3390/s19102321



