Slice Management for Quality of Service Differentiation in Wireless Network Slicing
Abstract
:1. Introduction
- We propose a joint QoS differentiation method for wireless network slices, which adjusts the interference among slices as well as manages priority queues of slices to differentiate their QoS according to their priorities.
- We propose an interference model between wireless network slices, where an edge-to-edge interference is estimated by the interference power and time portions of slices and the interference among slices is obtained by summing up the edge-to-edge interference.
- We propose inter-slice interfere-aware routing and admission control algorithms for in-band wireless networks, which enable multiple slices to be operated in a single-channel network while minimizing the interference among them.
2. Related Work
2.1. Wireless Network Slicing
2.1.1. 5G Radio Access Network Slicing
2.1.2. Multi-Hop Wireless Network Slicing
2.2. Interfere-Aware Routing
3. Prioritized Slice Management
3.1. System Model
3.2. Prioritized Multiple Routing
3.3. Proposed Algorithms
| Algorithm 1k-hop greedy routing. |
| Function greedy-routing (s, , k); Input: A target slice (s), a set of flows (), number of interference hops (k) Output: A routing matrix of slice s, which is a zero-matrix if the routing fails
|
4. Performance Evaluation
4.1. Simulation Environment
4.2. Simulation Scenarios and Results
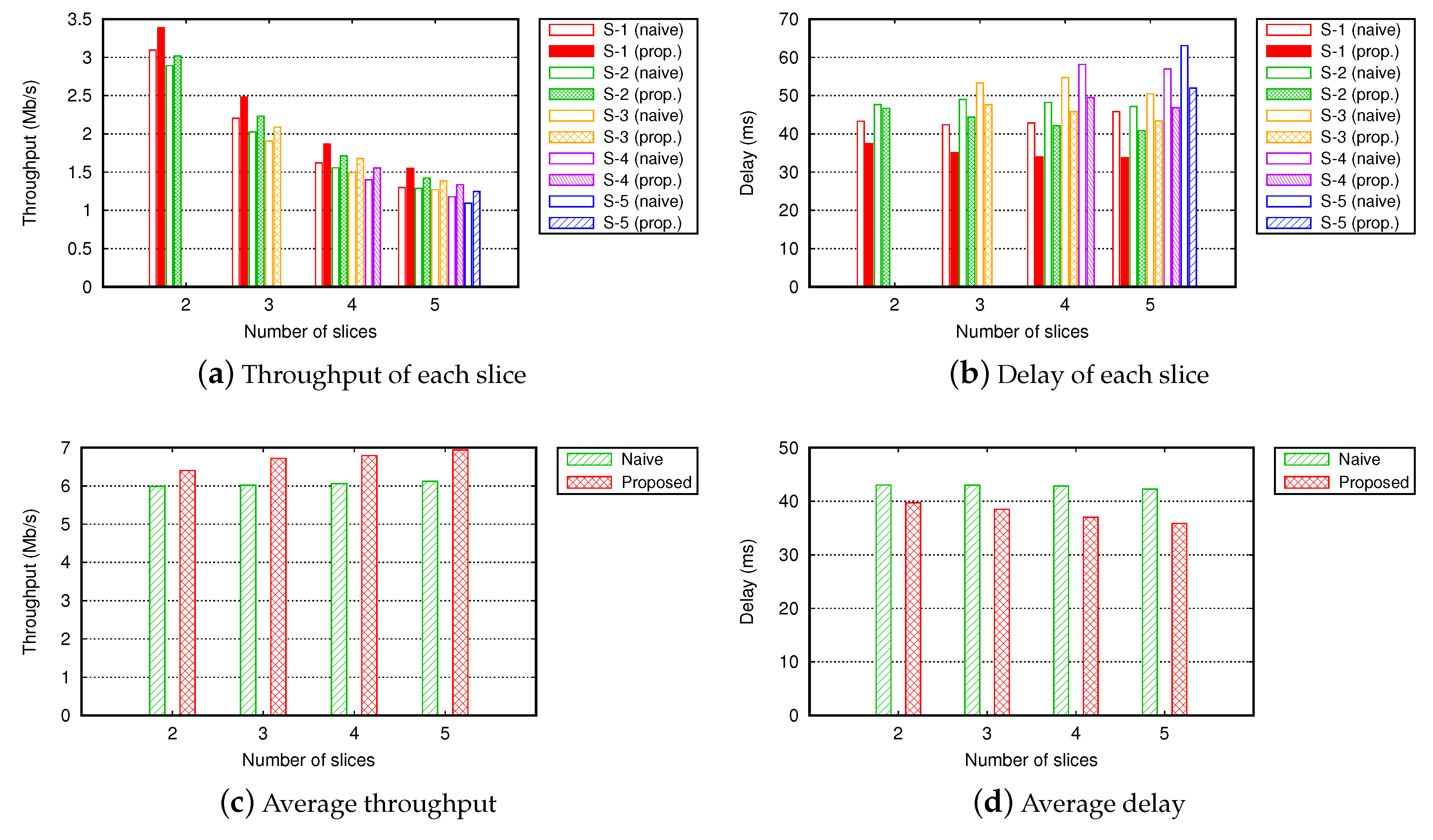
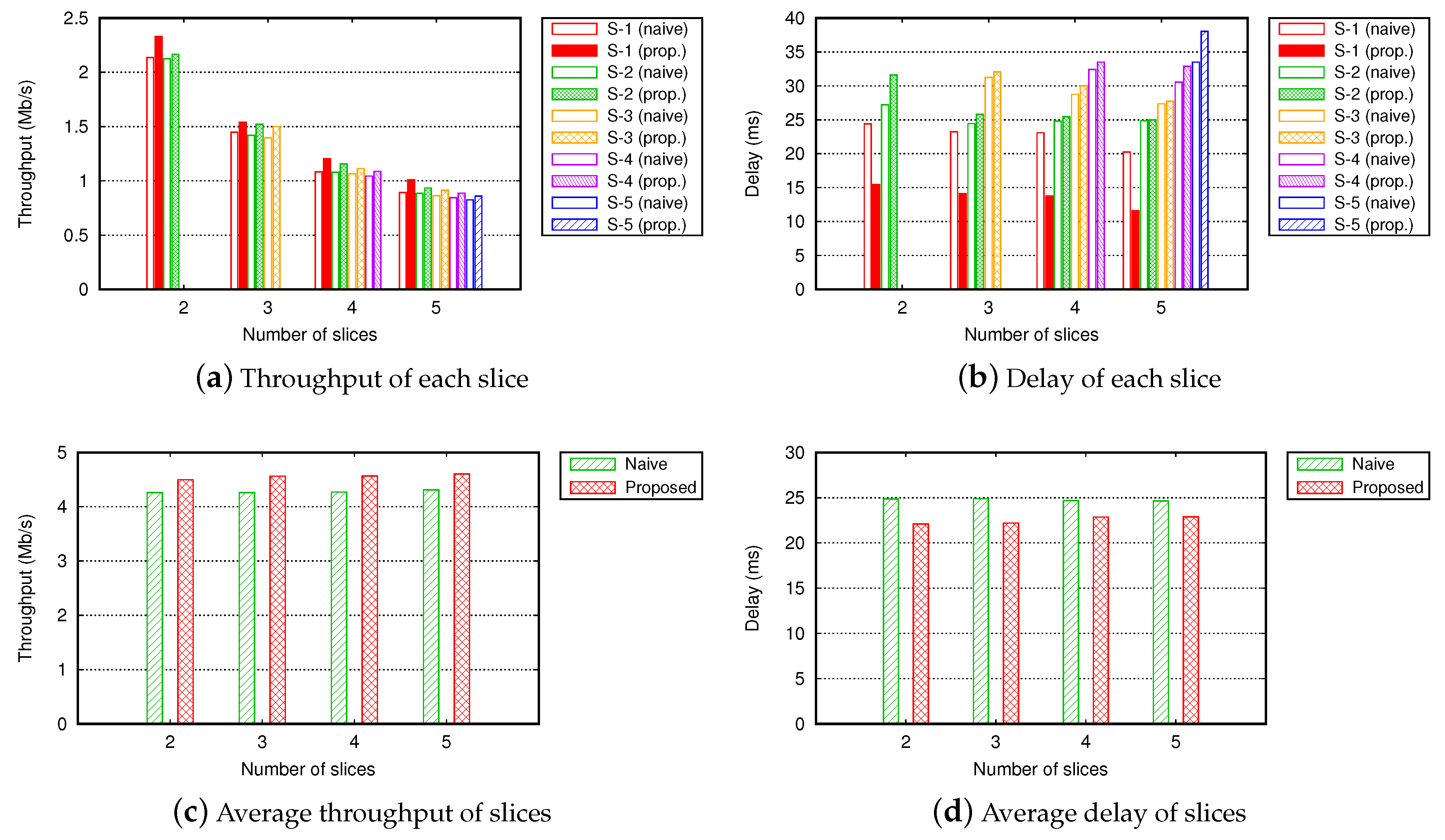
4.2.1. Scenario 1: Small-Sized Grid Topology with 16 Nodes
4.2.2. Scenario 2: Large-Sized Grid Topology with 100 Nodes
4.2.3. Scenario 3: Large-Sized Random Topology with 200 Nodes
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- NGMN 5G White Paper. Available online: http://www.ngmn.org/fileadmin/ngmn/content/images/news/ngmn_news/NGMN_5G_White_Paper_V1_0.pdf (accessed on 18 June 2019).
- View on 5G Architecture. Available online: http://5g-ppp.eu/wp-content/uploads/2014/02/5G-PPP-5G-Architecture-WP-July-2016.pdf (accessed on 18 June 2019).
- Duan, Q.; Ansari, N.; Toy, M. Software-defined network virtualization: An architectural framework for integrating SDN and NFV for service provisioning in future networks. IEEE Netw. 2016, 30, 10–16. [Google Scholar] [CrossRef]
- Lee, Y.L.; Loo, J.; Chuah, T.C.; Wang, L.C. Dynamic network slicing for multitenant heterogeneous cloud radio access networks. IEEE Trans. Wirel. Commun. 2018, 17, 2146–2161. [Google Scholar] [CrossRef]
- Bega, D.; Gramaglia, M.; Banchs, A.; Sciancalepore, V.; Samdanis, K.; Costa-Perez, X. Optimising 5G infrastructure markets: The business of network slicing. In Proceedings of the IEEE INFOCOM, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Han, B.; DeDomenico, A.; Dandachi, G.; Drosou, A.; Tzovaras, D.; Querio, R.; Moggio, F.; Bulakci, O.; Schotten, H.D. Admission and Congestion Control for 5G Network Slicing. In Proceedings of the IEEE Conference on Standards for Communications and Networking (CSCN), Paris, France, 29–31 October 2018; pp. 1–6. [Google Scholar]
- Wang, B.; Sun, Y.; Cao, Q.; Li, S.; Sun, Z. Bandwidth Slicing for Socially-Aware D2D Caching in SDN-Enabled Networks. IEEE Access 2018, 6, 50910–50926. [Google Scholar] [CrossRef]
- Richart, M.; Baliosian, J.; Serrat, J.; Gorricho, J.L. Resource slicing in virtual wireless networks: A survey. IEEE Trans. Netw. Serv. Manag. 2016, 13, 462–476. [Google Scholar] [CrossRef]
- Ksentini, A.; Nikaein, N. Toward enforcing network slicing on RAN: Flexibility and resources abstraction. IEEE Commun. Mag. 2017, 55, 102–108. [Google Scholar] [CrossRef]
- Jiang, M.; Condoluci, M.; Mahmoodi, T. Network slicing management & prioritization in 5G mobile systems. In Proceedings of the European Wireless 2016, Oulu, Finland, 18–20 May 2016; pp. 1–6. [Google Scholar]
- Sallent, O.; Perez-Romero, J.; Ferrus, R.; Agusti, R. On radio access network slicing from a radio resource management perspective. IEEE Wirel. Commun. 2017, 24, 166–174. [Google Scholar] [CrossRef]
- Ye, Q.; Zhuang, W.; Zhang, S.; Jin, A.L.; Shen, X.; Li, X. Dynamic radio resource slicing for a two-tier heterogeneous wireless network. IEEE Trans. Veh. Technol. 2018, 67, 9896–9910. [Google Scholar] [CrossRef]
- Lin, S.C. End-to-End Network Slicing for 5G&B Wireless Software-Defined Systems. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Lv, P.; Wang, X.; Xu, M. Virtual access network embedding in wireless mesh networks. Ad Hoc Netw. 2012, 10, 1362–1378. [Google Scholar] [CrossRef]
- Lv, P.; Cai, Z.; Xu, J.; Xu, M. Multicast service-oriented virtual network embedding in wireless mesh networks. IEEE Commun. Lett. 2012, 16, 375–377. [Google Scholar] [CrossRef]
- Shrestha, S.L.; Lee, J.; Chong, S. Virtualization and slicing of wireless mesh network. In Proceedings of the International Conference on Future Internet Technologies, Seoul, Korea, 18–20 June 2008. [Google Scholar]
- De Figueiredo, F.A.; Jiao, X.; Liu, W.; Moerman, I. Radio hardware virtualization for software-defined wireless networks. Wirel. Pers. Commun. 2018, 100, 113–126. [Google Scholar] [CrossRef]
- De Couto, D.S.; Aguayo, D.; Chambers, B.A.; Morris, R. Performance of multihop wireless networks: Shortest path is not enough. ACM SIGCOMM Comput. Commun. Rev. 2003, 33, 83–88. [Google Scholar] [CrossRef]
- Draves, R.; Padhye, J.; Zill, B. Routing in multi-radio, multi-hop wireless mesh networks. In Proceedings of the ACM Proceedings of the International Conference on Mobile Computing and Networking (MobiCom), Philadelphia, PA, USA, 26 September–1 October 2004; pp. 114–128. [Google Scholar]
- Waharte, S.; Ishibashi, B.; Boutaba, R.; Meddour, D. Interference-aware routing metric for improved load balancing in wireless mesh networks. In Proceedings of the IEEE International Conference on Communications (ICC), Beijing, China, 19–23 May 2008; pp. 2979–2983. [Google Scholar]
- Bezzina, A.; Ayari, M.; Langar, R.; Kamoun, F. An interference-aware routing metric for multi-radio multi-channel wireless mesh networks. In Proceedings of the IEEE International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Hakodate, Japan, 23–25 July 2012; pp. 284–291. [Google Scholar]
- Subramanian, A.P.; Buddhikot, M.M.; Miller, S. Interference aware routing in multi-radio wireless mesh networks. In Proceedings of the IEEE Workshop on Wireless Mesh Networks (WiMesh), Reston, VA, USA, 25–28 September 2006; pp. 55–63. [Google Scholar]
- Kortebi, R.M.; Gourhant, Y.; Agoulmine, N. On the use of SINR for interference-aware routing in wireless multi-hop networks. In Proceedings of the ACM Proceedings of the Symposium on Modeling, Analysis, and Simulation of Wireless and Mobile Systems, Chania, Crete Island, Greece, 22–26 October 2007; pp. 395–399. [Google Scholar]
- Yang, Y.; Wang, J.; Kravets, R. Designing routing metrics for mesh networks. In Proceedings of the IEEE Workshop on Wireless Mesh Networks (WiMesh), Santa Clara, CA, USA, 26 September 2005; pp. 1–9. [Google Scholar]
- Ueda, T.; Tanaka, S.; Roy, S.; Saha, D.; Bandyopadhyay, S. A priority-based QoS routing for multimedia traffic in ad hoc wireless networks with directional antenna using a zone-reservation protocol. IEICE Trans. Commun. 2004, 87, 1085–1094. [Google Scholar]
- Nikseresht, I.; Yousefi, H.; Movaghar, A.; Khansari, M. Interference-aware multipath routing for video delivery in wireless multimedia sensor networks. In Proceedings of the IEEE International Conference on Distributed Computing Systems Workshops (ICDCSW), Macau, China, 18–21 June 2012; pp. 216–221. [Google Scholar]
- Zhao, L.; Al-Dubai, A.; Li, X.; Chen, G.; Min, G. A new efficient cross-layer relay node selection model for wireless community mesh networks. Comput. Electr. Eng. 2017, 61, 361–372. [Google Scholar] [CrossRef]
- Pióro, M.; Medhi, D. Routing, Flow, and Capacity Design in Communication and Computer Networks; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Burer, S.; Letchford, A.N. Non-convex mixed-integer nonlinear programming: A survey. Surv. Oper. Res. Manag. Sci. 2012, 17, 97–106. [Google Scholar] [CrossRef] [Green Version]
- Hariharan, S.; Shroff, N.B. On sample-path optimal dynamic scheduling for sum-queue minimization in trees under the K-hop interference model. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 999–1007. [Google Scholar]
- Martins, E.Q.; Pascoal, M.M. A new implementation of Yen’s ranking loopless paths algorithm. Q. J. Belg. Fr. Ital. Oper. Rese. Soc. 2003, 1, 121–133. [Google Scholar]
- NO Ad-Hoc Routing Agent (NOAH). Available online: http://icapeople.epfl.ch/widmer/uwb/ns-2/noah (accessed on 7 June 2019).
- Lu, Y.; Fu, B.; Xi, X.; Zhang, Z.; Wu, H. An SDN-Based Flow Control Mechanism for Guaranteeing QoS and Maximizing Throughput. Wirel. Pers. Commun. 2017, 97, 417–442. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Carrier sensing threshold | 3.65262 W |
| Transmission power | 0.281838 W |
| Frequency band | 2.4 GHz |
| Loss factor | 1 |
| Minimum contention window | 15 |
| Maximum contention window | 1023 |
| Slot time | 9 s |
| Short interframe space | 16 s |
| Preamble length | 144 bits |
| Length of PLCP header | 48 bits |
| Data rate of PLCP | 6 Mb/s |
| Basic rate | 6 Mb/s |
| Data rate | 9 Mb/s |
| RTS/CTS threshold | 1 byte |
| Limit of short retry | 7 |
| Limit of maximum short retry | 7 |
| Limit of long retry | 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, N.; Kim, Y.; Park, J.; Kwon, D.-H.; Lim, H. Slice Management for Quality of Service Differentiation in Wireless Network Slicing. Sensors 2019, 19, 2745. https://doi.org/10.3390/s19122745
An N, Kim Y, Park J, Kwon D-H, Lim H. Slice Management for Quality of Service Differentiation in Wireless Network Slicing. Sensors. 2019; 19(12):2745. https://doi.org/10.3390/s19122745
Chicago/Turabian StyleAn, Namwon, Yonggang Kim, Juman Park, Dae-Hoon Kwon, and Hyuk Lim. 2019. "Slice Management for Quality of Service Differentiation in Wireless Network Slicing" Sensors 19, no. 12: 2745. https://doi.org/10.3390/s19122745
APA StyleAn, N., Kim, Y., Park, J., Kwon, D.-H., & Lim, H. (2019). Slice Management for Quality of Service Differentiation in Wireless Network Slicing. Sensors, 19(12), 2745. https://doi.org/10.3390/s19122745






