Magnetic Communication Using High-Sensitivity Magnetic Field Detectors
Abstract
:1. Introduction
2. Characteristics of Magnetic Field Detectors
- SQUIDs are ultra-sensitive magnetic field sensors [11]. The sensors can measure magnetic flux densities on the order of fT (for example brain activity tracking by magnetoencephalography). To maintain superconductivity, SQUIDs need to operate within a few degrees of absolute zero. This is ensured by cooling the devices with liquid helium, which is certainly not possible in mobile applications.
- The optical pumping resonance method exhibits very high sensitivity at low frequencies, but the sensor is large and is only able to detect the scalar (i.e., total) value of a magnetic field. The major problem regarding communication purposes is that the sensitivity of these magnetometers decreases rapidly for frequencies above 10 Hz [12]. This prevents communication at reasonable data rates.
- Hall effect sensors are among the most popular magnetic field sensors. The sensors are very cheap and are mainly used as proximity indicators. They cannot be used for navigation purposes due to their low sensitivity [9]. Most properties of Hall effect sensors are suitable for magnetic communication systems. However, the high detection threshold results in very short communication ranges.
- Fluxgate sensors can detect magnetic fields on the order of pT. Due to the small size and battery power supply, fluxgate magnetometers are qualified for mobile applications. The achievable data rate is limited by the upper frequency of a fluxgate sensor, which is about 10 kHz [12].
- Another well-known type of detector is magneto-resistive sensors. GMR and AMR sensors are implemented today in almost every smartphone, e.g. for compass functionality. Both sensor types require ultra-low power consumption and are cheap. The main advantage is the high bandwidth of up to 1 MHz and beyond. Due to the lower detection limit of AMR sensors, this method is favorable for communication systems.
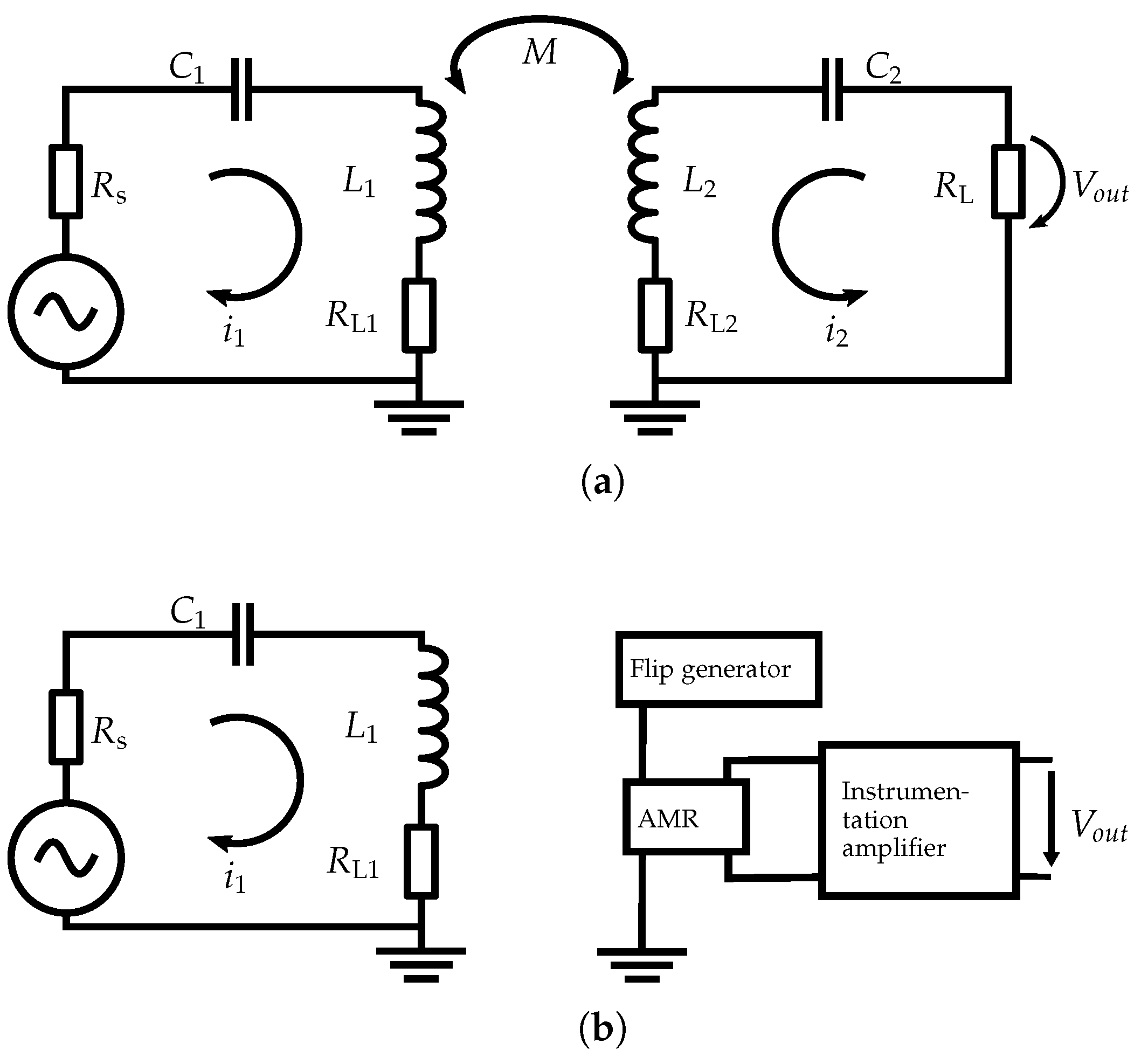
2.1. Receiver Coil (Induction)
2.2. AMR Detector
3. Sensitivity Analysis
3.1. Near-Field Far-Field Boundary
3.2. Communication Range for Lossless Transmission Mediums
3.2.1. Derivation of the Coil-to-Coil Transmission Range
3.2.2. Derivation of the Coil-to-AMR Transmission Range
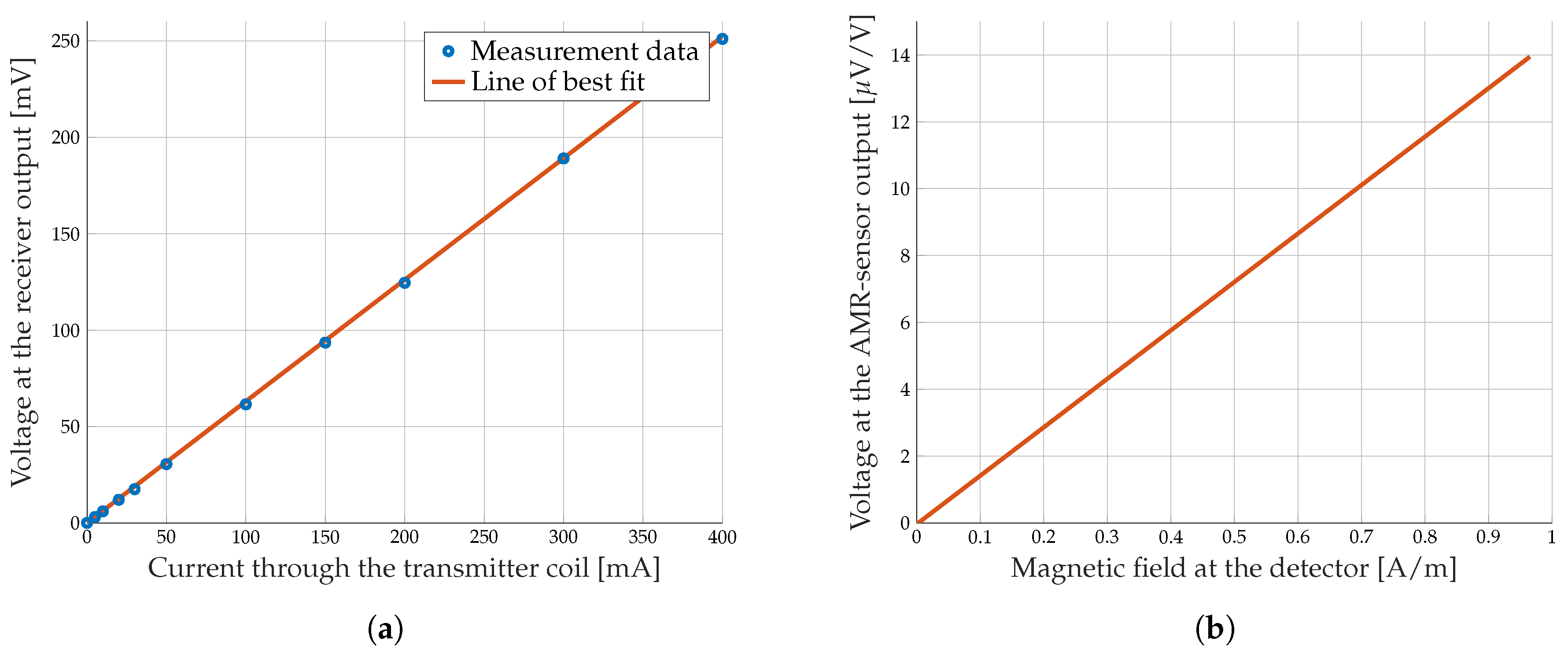
3.2.3. Characterization of the Detection Threshold for the Prototype Implementation
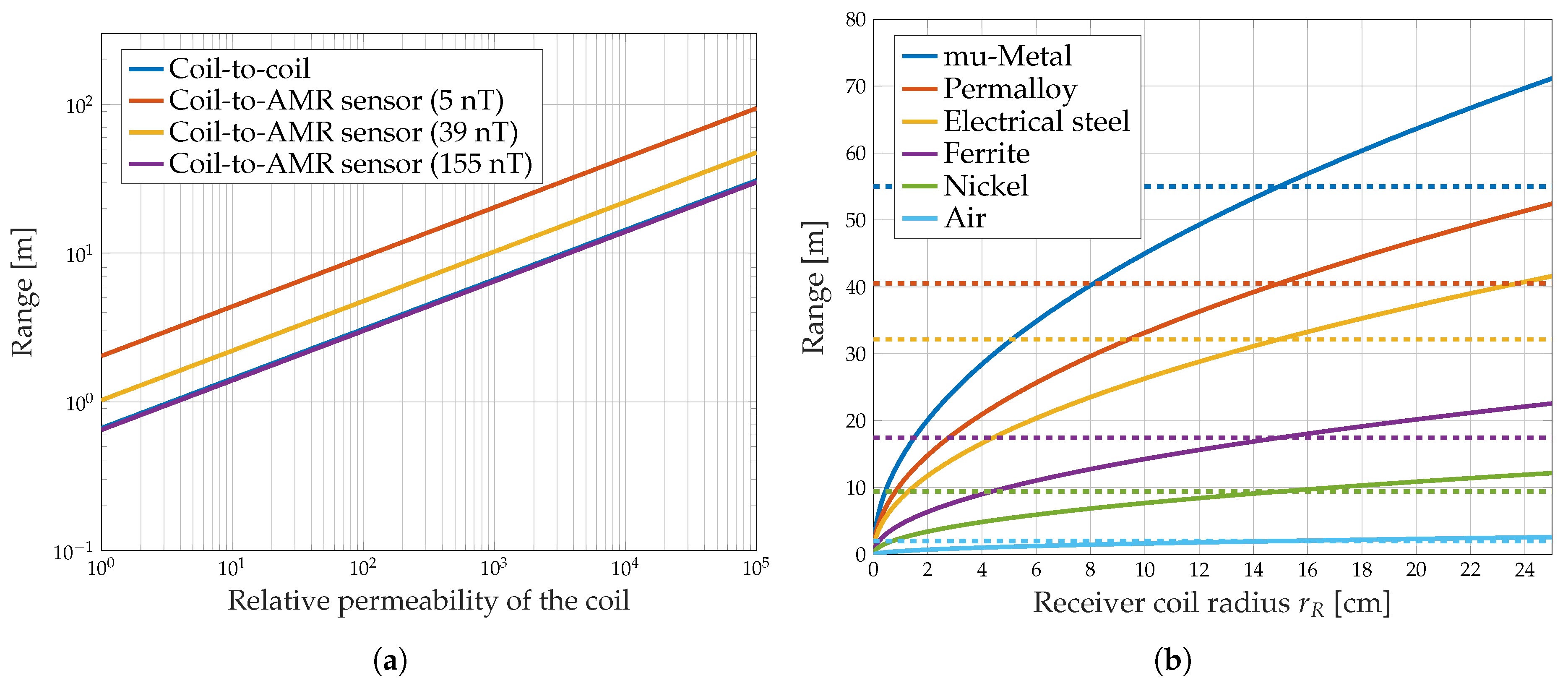
3.2.4. Transmission Range for Different Coil Radii
3.2.5. Transmission Range for Different Core Materials
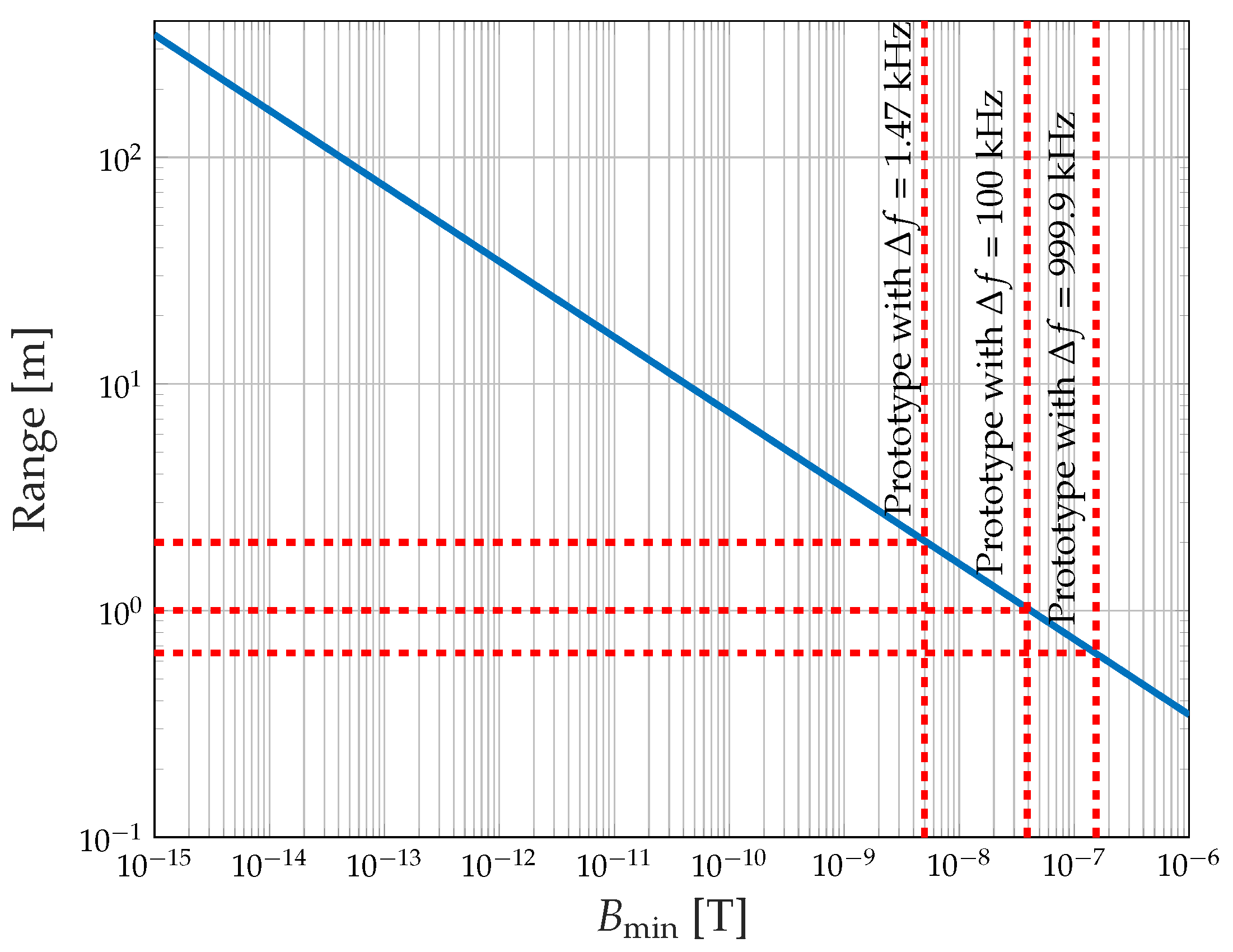
3.2.6. Coil-to-Detector Transmission Range for Different Detection Thresholds
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akyildiz, I.F.; Vuran, M.C. Wireless Sensor Networks; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Domingo, M.C. Magnetic Induction for Underwater Wireless Communication Networks. IEEE Trans. Antennas Propag. 2012, 60, 2929–2939. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Wang, P.; Sun, Z. Realizing underwater communication through magnetic induction. IEEE Commun. Mag. 2015, 53, 42–48. [Google Scholar] [CrossRef]
- Sun, Z.; Akyildiz, I.F. Magnetic Induction Communications for Wireless Underground Sensor Networks. IEEE Trans. Antennas Propag. 2010, 58, 2426–2435. [Google Scholar] [CrossRef]
- Kisseleff, S. Advances in Magnetic Induction Based Underground Communication Systems. Ph.D. Thesis, Friedrich-Alexander-University, Nuremberg, Germany, 2017. [Google Scholar]
- Masihpour, M.; Agbinya, J.I. Cooperative relay in Near Field Magnetic Induction: A new technology for embedded medical communication systems. In Proceedings of the 2010 Fifth International Conference on Broadband and Biomedical Communications, Malaga, Spain, 15–17 December 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Agbinya, J.I. Principles of Inductive Near Field Communications for Internet of Things; River Publishers: Aalborg, Denmark, 2011. [Google Scholar]
- Carrella, S.; Kuncup, I.; Lutz, K.; König, A. 3D-Localization of Low-Power Wireless Sensor Nodes Based on AMR-Sensors in Industrial and AmI Applications. In Proceedings of the Sensoren und Messsysteme, Nürnberg, Germany, 18–19 May 2010. [Google Scholar]
- Včelák, J.; Ripka, P.; Zikmund, A. Precise magnetic sensors for navigation and prospection. J. Supercond. Nov. Magn. 2015, 28, 1077–1080. [Google Scholar] [CrossRef]
- Reinecke, S.F.; Hampel, U. Instrumented flow-following sensor particles with magnetic position detection and buoyancy control. J. Sens. Sens. Syst. 2016, 5, 213–220. [Google Scholar] [CrossRef] [Green Version]
- Ripka, P.; Janosek, M. Advances in Magnetic Field Sensors. IEEE Sens. J. 2010, 10, 1108–1116. [Google Scholar] [CrossRef] [Green Version]
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Thomson, W. On the Electro-Dynamic Qualities of Metals:–Effects of Magnetization on the Electric Conductivity of Nickel and of Iron. Proc. R. Soc. Lond. 1856, 8, 546–550. [Google Scholar]
- Sensitec. AFF755B MagnetoResistive Field Sensor. 2017. Available online: https://www.sensitec.com/fileadmin/sensitec/Service_and_Support/Downloads/Data_Sheets/AFF700_800/SENSITEC_AFF755B_DSE_05.pdf (accessed on 25 June 2019).
- Nording, F.; Bischel, W.; Ludwig, F.; Schilling, M. Offsetunterdrücktes AMR-Magnetometer mit 100 kHz Frequenzbandbreite. tm-Tech. Mess. 2017, 84, 102–105. [Google Scholar] [CrossRef]
- Masihpour, M. Cooperative Communication in Near Field Magnetic Induction Communication Systems. Ph.D. Thesis, University of Technology, Sydney, Australia, 2012. [Google Scholar]
- Coey, J.M. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Devices, A. AD8428 Instrumentation Amplifier. 2012. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD8428.PDF (accessed on 25 June 2019).
- Tumanski, S. Handbook of Magnetic Measurements; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- McLyman, C.W.T. Transformer and Inductor Design Handbook; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]



| SQUID | Optical Pumping | Hall | Fluxgate | GMR/TMR | AMR | Induction | |
|---|---|---|---|---|---|---|---|
| Detection limit | fT | pT | T | pT | nT | nT | fT-T |
| Power supply | Line | Line | Battery | Battery | Battery | Battery | Battery |
| Size | Medium | Medium | Ultra small | Small | Small | Ultra small | Ultra small-large |
| Measured value | Vectorial | Scalar | Vectorial | Vectorial | Vectorial | Vectorial | Vectorial |
| Sensor noise | Ultra-low | Ultra-low | High | Low | High | Medium | Low |
| Bandwidth | Small | Small | Medium | Medium | Medium | Large | Small |
| Saturation by Earth’s magnetic field | Yes | Yes | No | No | No | No | No |
| Operating temperature | Ultra-low | Normal | Normal | Normal | Normal | Normal | Normal |
| Cost | High | High | Low | Medium | Low | Low | Low |
| Suitability for mobile applications | No | No | Yes | Yes | Yes | Yes | Only small coils |
| Meaning | Parameter | Value |
|---|---|---|
| Relative permeability of the core | 1 | |
| Quality factor transmitter | 68 | |
| Quality factor receiver | 35 | |
| Efficiency transmitter | 2.4% | |
| Efficiency receiver | 50% | |
| Bandwidth transmitter | 1.47 kHz | |
| Coil radius | , | 16 mm |
| Number of turns | N | 20 |
| Inductance | L | 14.35 H |
| Resonant frequency | 100 kHz | |
| Series resistance of power supply | 3.2 m | |
| Load resistance | 129 m | |
| Series resistance of coil | , | 129 m @ 100 kHz |
| Transmitting power | 43.3 dBm | |
| Receiver sensitivity | −42 dBm |
| Material | |||
|---|---|---|---|
| Air | H/m | ≈1 | no saturation |
| Nickel | H/m | ≈100 | 0.3–0.5 T |
| Ferrite | > H/m | >640 | 0.3–0.5 T |
| Electrical steel | H/m | ≈4000 | 1.5–1.8 T |
| Permalloy | H/m | ≈8000 | 0.66–0.82 T |
| mu-Metal | ≈ H/m | ≈20,000 | 0.65–0.82 T |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hott, M.; Hoeher, P.A.; Reinecke, S.F. Magnetic Communication Using High-Sensitivity Magnetic Field Detectors. Sensors 2019, 19, 3415. https://doi.org/10.3390/s19153415
Hott M, Hoeher PA, Reinecke SF. Magnetic Communication Using High-Sensitivity Magnetic Field Detectors. Sensors. 2019; 19(15):3415. https://doi.org/10.3390/s19153415
Chicago/Turabian StyleHott, Maurice, Peter A. Hoeher, and Sebastian F. Reinecke. 2019. "Magnetic Communication Using High-Sensitivity Magnetic Field Detectors" Sensors 19, no. 15: 3415. https://doi.org/10.3390/s19153415
APA StyleHott, M., Hoeher, P. A., & Reinecke, S. F. (2019). Magnetic Communication Using High-Sensitivity Magnetic Field Detectors. Sensors, 19(15), 3415. https://doi.org/10.3390/s19153415






