Ground Moving Target 2-D Velocity Estimation and Refocusing for Multichannel Maneuvering SAR with Fixed Acceleration
Abstract
:1. Introduction
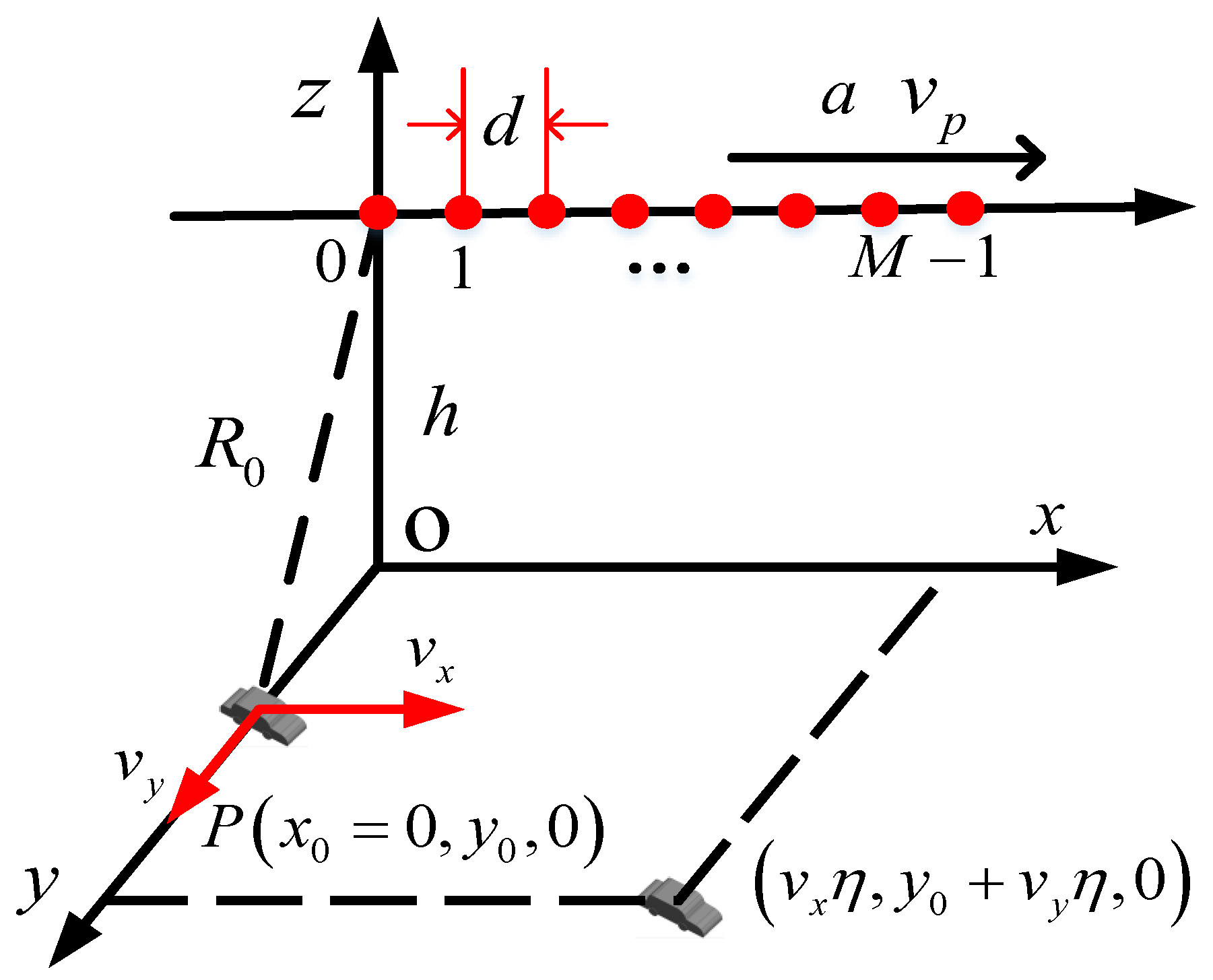
2. Signal Model of a Moving Target in Multichannel Maneuvering SAR
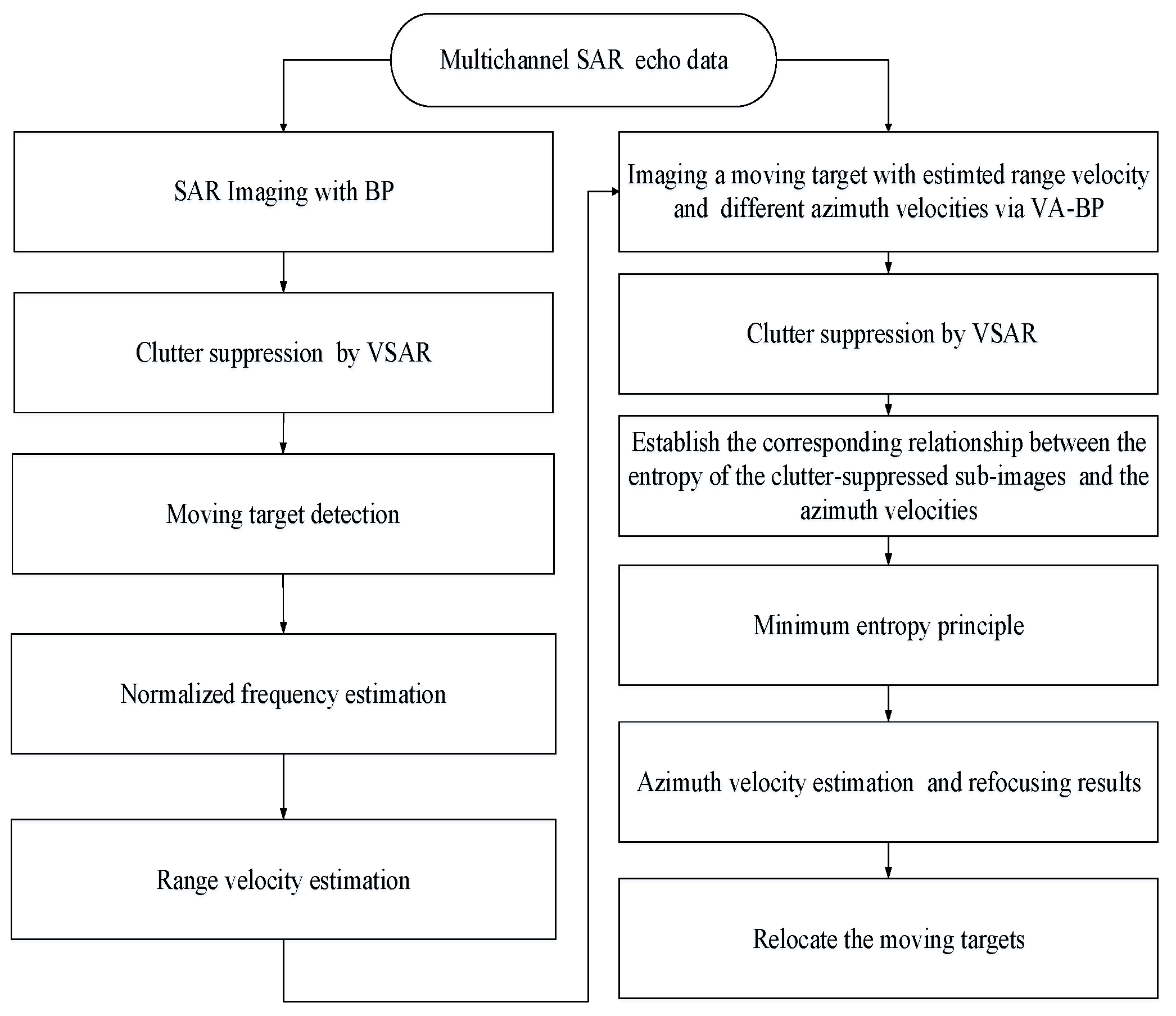
3. Proposed GMTI Method for Multichannel Maneuvering SAR
3.1. Moving Target Detection and Range Velocity Estimation
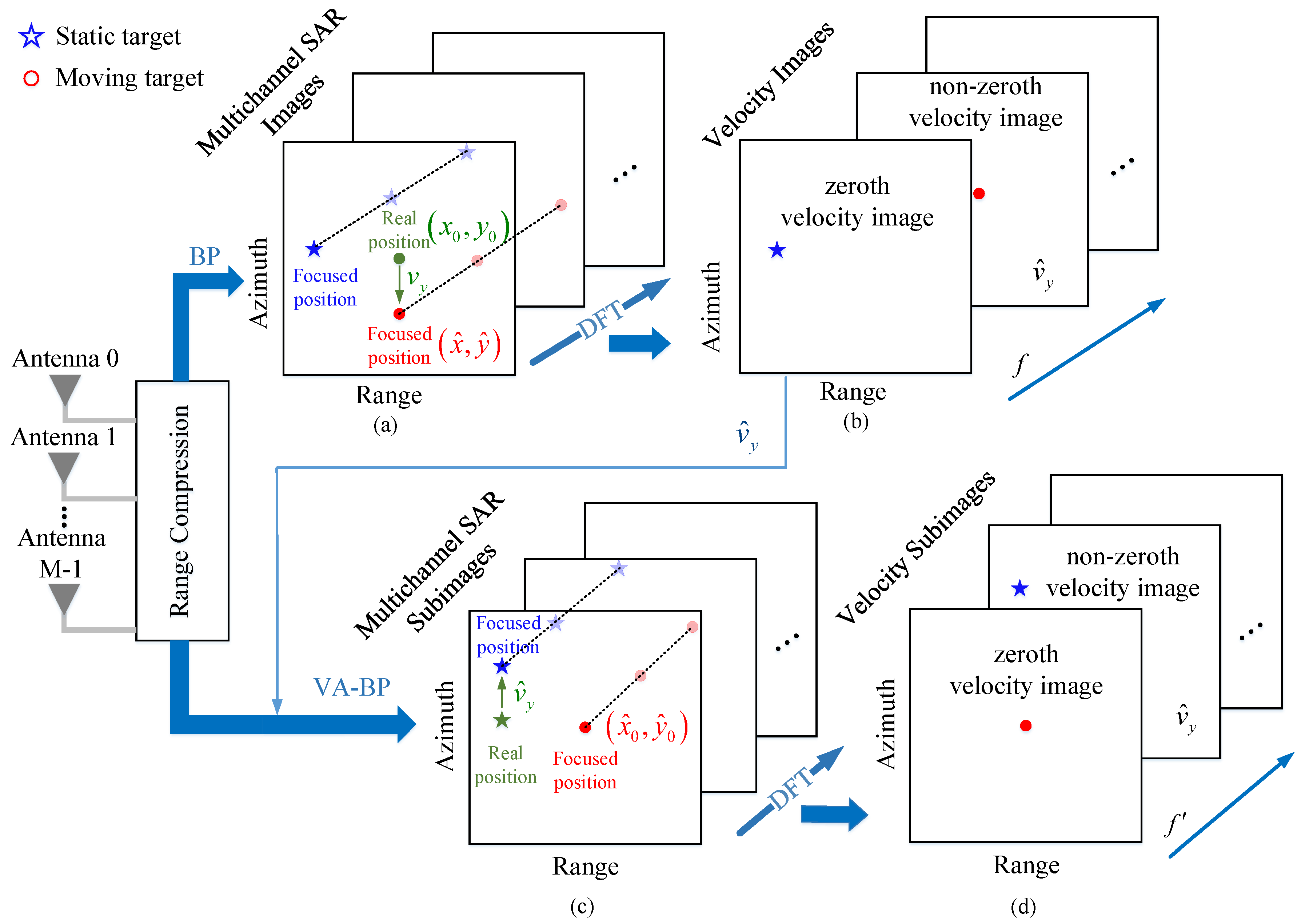
3.1.1. Moving Target Imaging with the BP Algorithm
- Case 1: the target with its 2D velocity :
- Case 2: the target with its 2D velocity :
3.1.2. Locate a Moving Target in the Image Domain
3.1.3. Normalized Frequency of a Moving Target
3.1.4. Moving Target Detection and Range Velocity Estimation
- Step 1: For every pixel of M SAR images, the M-point DFT along the antenna array direction can be taken to transform M SAR images into velocity images.
- Step 2: The stationary clutter can be suppressed by replacing the zeroth velocity image by zero.
- Step 3: The M-point inverse DFT along the antenna array direction can be taken to transform velocity images back to SAR images.
3.2. Moving Target Azimuth Velocity Estimation, Refocusing, and Relocation
3.2.1. Imaging a Moving Target with the VA-BP Algorithm
- Case 1: the target with its 2D velocity :
- Case 2: the target with its 2D velocity :
3.2.2. Location and Peak Response Analysis of a Moving Target via the VA-BP Algorithm
3.2.3. Normalized Frequency Analysis of a Moving Target via the VA-BP Algorithm
3.2.4. Moving Target Azimuth Velocity Estimation, Refocusing, and Relocation
- Step 1: The BP algorithm with the correlation function of the stationary target is used to obtain M SAR images. Here, M is the number of receiving channels.
- Step 2: Perform M-point DFT along the antenna array direction to get the M velocity images.
- Step 3: Take out the zeroth velocity image, i.e., the DC velocity image.
- Step 1: The VA-BP algorithm with the correlation function of the moving target is used to obtain M SAR images.
- Step 2: Perform M-point DFT along the antenna array direction to get M velocity images. Here, the moving target is in the zeroth velocity image, and the azimuth displacement and defocusing of the moving target is corrected.
- Step 3: Take out the zeroth velocity image, i.e., the velocity image of the moving target with both azimuth displacement and defocusing corrected.
4. Numerical Experiments and Performance Analysis
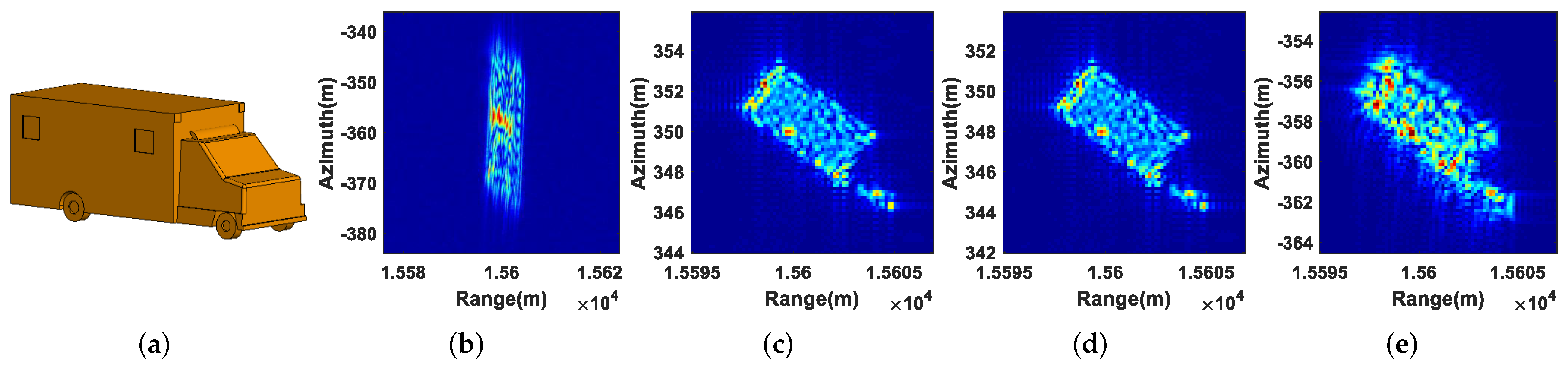
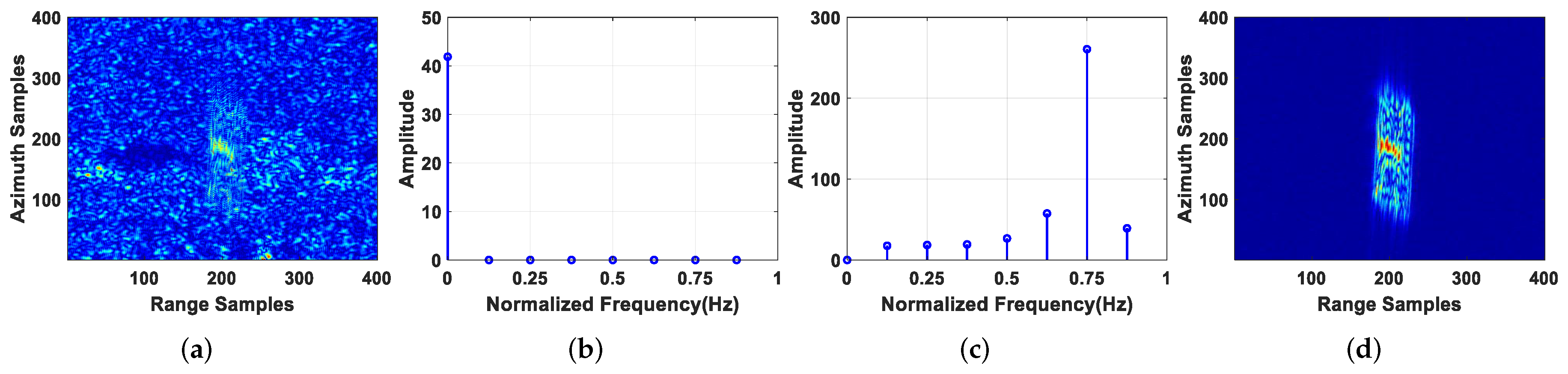
4.1. Moving Target Detection, 2D Velocity Estimation, and Refocusing
4.2. Clutter Suppression Performance Analysis
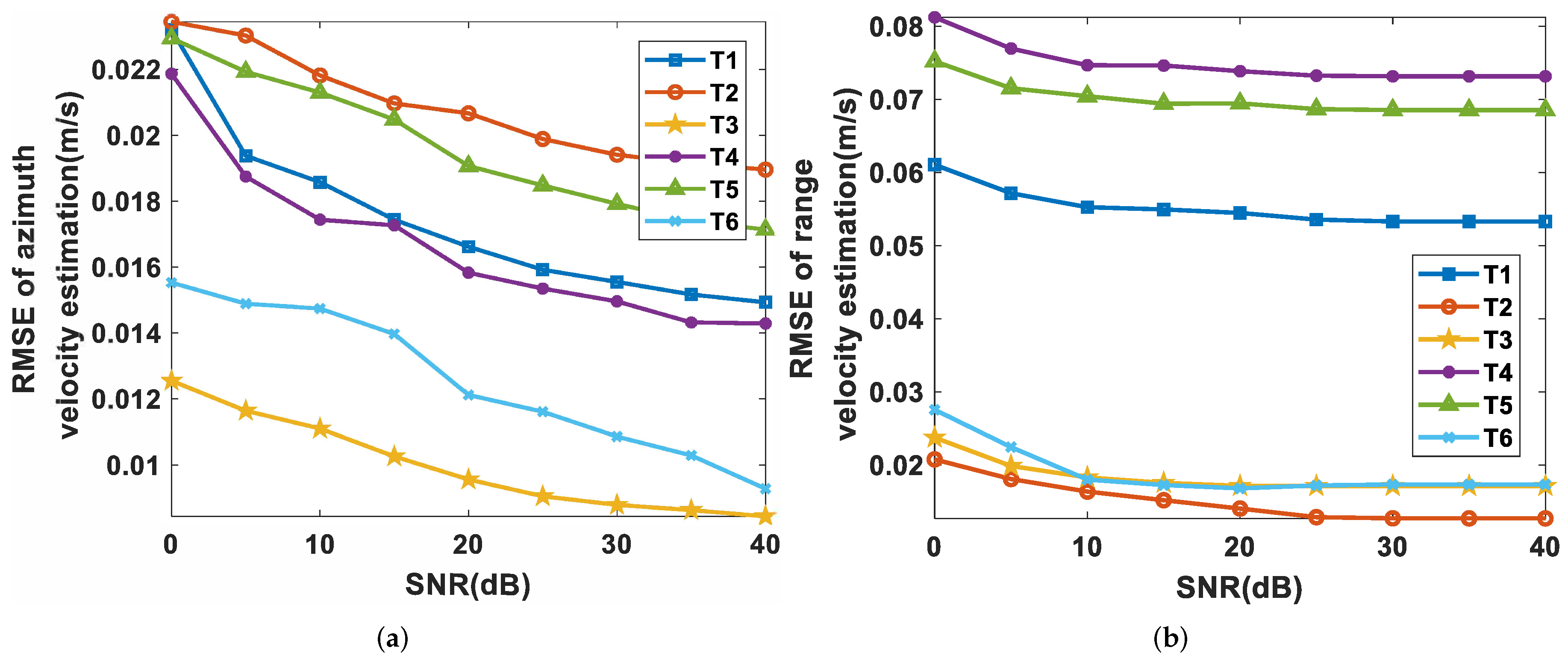
4.3. 2D Velocity Estimation Accuracy Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Equation (12)
- Case 1: the target with its 2D velocity :If , i.e., is a point static target, the phase function can be approximated by its first-order Taylor expansion as [39]:The result of the BP integral is:
- Case 2: the target with its 2D velocity :If , i.e., is a point moving target, the integral in (A1) is an integral of the LFM signal whose time-bandwidth product (TBP) usually satisfies the stationary phase principle (SPP) approximation [40]. Then, the response could be calculated based on the SPP as:where is a complex signal that is represented as:
References
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation [with CDROM](Artech House Remote Sensing Library); Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Wang, Y.; Cao, Y.; Peng, Z.; Su, H. Clutter suppression and moving target imaging approach for multichannel hypersonic vehicle borne radar. Digit. Signal Process. 2017, 68, 81–92. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I.; Sjögren, T.K. Moving Target Focusing in SAR Image With Known Normalized Relative Speed. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 854–861. [Google Scholar] [CrossRef]
- Suwa, K.; Yamamoto, K.; Tsuchida, M.; Nakamura, S.; Wakayama, T.; Hara, T. Image-Based Target Detection and Radial Velocity Estimation Methods for Multichannel SAR-GMTI. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1325–1338. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, Y.; Zhang, S.; Zhao, H. An efficient NLCS algorithm for maneuvering forward-looking linear array SAR with constant acceleration. Signal Process. 2018, 144, 155–162. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, S.; Zhang, S.; Zhao, H. A chirp scaling algorithm for forward-looking linear-array SAR with constant acceleration. IEEE Geosci. Remote Sens. Lett. 2018, 15, 88–91. [Google Scholar] [CrossRef]
- Deng, B.; Li, X.; Wang, H.; Qin, Y.; Wang, J. Fast Raw-Signal Simulation of Extended Scenes for Missile-Borne SAR With Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2011, 8, 44–48. [Google Scholar] [CrossRef]
- Shen, W.; Lin, Y.; Yu, L.; Xue, F.; Hong, W. Single Channel Circular SAR Moving Target Detection Based on Logarithm Background Subtraction Algorithm. Remote Sens. 2018, 10, 742. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, X.; Diao, W.; Zhang, Y.; Yan, M.; Lan, L. Ground Moving Target Indication Based on Optical Flow in Single-Channel SAR. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1051–1055. [Google Scholar] [CrossRef]
- Zhu, S.; Liao, G.; Tao, H.; Yang, Z. Estimating Ambiguity-Free Motion Parameters of Ground Moving Targets From Dual-Channel SAR Sensors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3328–3349. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, F. Multi-channel Interferometric SAR/GMTI method for solving the radial velocity ambiguity of moving target. In Proceedings of the Fifth Symposium on Novel Optoelectronic Detection Technology and Application, Xi’an, China, 24–26 October 2018. [Google Scholar]
- Wang, Z.; Xu, J.; Huang, Z.; Zhang, X.; Xia, X.G.; Long, T.; Bao, Q. Road-Aided Ground Slowly Moving Target 2D Motion Estimation for Single-Channel Synthetic Aperture Radar. Sensors 2016, 16, 383. [Google Scholar] [CrossRef]
- Rosenberg, L.; Gray, D.A. Constrained Fast-Time STAP for Interference Suppression in Multichannel SAR. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1792–1805. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I. A Generalization of DPCA Processing for Multichannel SAR/GMTI Radars. IEEE Trans. Geosci. Remote Sens. 2013, 51, 560–572. [Google Scholar] [CrossRef]
- Xu, J.; Huang, Z.; Yan, L.; Zhou, X.; Zhang, F.; Long, T. SAR ground moving target indication based on relative residue of DPCA processing. Sensors 2016, 16, 1676. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Huang, Y.; Liao, G.; Xu, J. Moving Target Detection via Efficient ATI-GoDec Approach for Multichannel SAR System. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1320–1324. [Google Scholar] [CrossRef]
- Li, G.; Xu, J.; Peng, Y.; Xia, X. Location and Imaging of Moving Targets using Nonuniform Linear Antenna Array SAR. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1214–1220. [Google Scholar] [CrossRef]
- Huadong, S.; Lizhi, Z.; Xuesong, J. Parameter Estimations Based on DPCA-FrFT Algorithm for Three-channel SAR-GMTI System. In Proceedings of the 2011 Fourth International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 28–29 March 2011; Volume 2, pp. 640–644. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, J.; Liu, X.; Wang, K.; Gao, Y. An automatic SAR-GMTI algorithm based on DPCA. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 592–595. [Google Scholar] [CrossRef]
- Romeiser, R.; Runge, H. Theoretical Evaluation of Several Possible Along-Track InSAR Modes of TerraSAR-X for Ocean Current Measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 21–35. [Google Scholar] [CrossRef]
- Budillon, A.; Schirinzi, G. Performance Evaluation of a GLRT Moving Target Detector for TerraSAR-X Along-Track Interferometric Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3350–3360. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J. GMTI based on a combination of DPCA and ATI. In Proceedings of the 2015 IET International Radar Conference, Hangzhou, China, 14–16 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Friedlander, B.; Porat, B. VSAR: A high resolution radar system for detection of moving targets. IEE Proc. Radar, Sonar Navig. 1997, 144, 205–218. [Google Scholar] [CrossRef]
- Rosenberg, L.; Sletten, M. Analysis of maritime X-band velocity SAR imagery. In Proceedings of the 2015 IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; pp. 121–126. [Google Scholar]
- Rosenberg, L.; Sletten, M.; Toporkov, J. Focussing moving objects using the VSAR algorithm. In Novel Radar Techniques and Applications Volume 1: Real Aperture Array Radar, Imaging Radar, and Passive and Multistatic Radar; Radar, Sonar and Navigation, Institution of Engineering and Technology: Beijing, China, 2017; pp. 489–516. [Google Scholar] [CrossRef]
- Sletten, M.A.; Rosenberg, L.; Menk, S.; Toporkov, J.V.; Jansen, R.W. Maritime Signature Correction With the NRL Multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6783–6790. [Google Scholar] [CrossRef]
- Jansen, R.W.; Raj, R.G.; Rosenberg, L.; Sletten, M.A. Practical Multichannel SAR Imaging in the Maritime Environment. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4025–4036. [Google Scholar] [CrossRef]
- Sletten, M.A. Demonstration of SAR Distortion Correction Using a Ground-Based Multichannel SAR Test Bed. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3181–3190. [Google Scholar] [CrossRef]
- Sletten, M.; Hwang, P.; Toporkov, J.; Menk, S.; Rosenberg, L.; Jansen, R. Analysis and correction of maritime SAR signatures with the NRL MSAR. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2489–2492. [Google Scholar] [CrossRef]
- Rosenberg, L.; Jansen, R.; Sletten, M. Correction of azimuthal motion in velocity SAR imagery. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 52–57. [Google Scholar] [CrossRef]
- Huang, Z.; Ding, Z.; Xu, J.; Zeng, T.; Liu, L.; Wang, Z.; Feng, C. Azimuth Location Deambiguity for SAR Ground Moving Targets via Coprime Adjacent Arrays. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 551–561. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, J.; Liu, L.; Long, T.; Wang, Z. SAR ground moving targets relocation via co-prime arrays. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 792–796. [Google Scholar] [CrossRef]
- Yi, L.; Wang, H.; Long, Z.; Zheng, B. An approach to forward looking FMCW radar imaging based on two-dimensional Chirp-Z transform. Sci. China Inf. Sci. 2010, 53, 1653–1665. [Google Scholar]
- Chen, Y.; Deng, B.; Wang, B.; Qin, Y.; Ding, J. Vibration target detection and vibration parameters estimation based on the DPCA technique in dual-channel SAR. Sci. China Inf. Sci. 2012, 55, 2281–2291. [Google Scholar] [CrossRef]
- Jing, K.; Xu, J.; Yao, D.; Huang, Z.; Long, T. SAR Ground Moving Target Indication via Cross-Track Interferometry for a Forward-Looking Array. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 966–982. [Google Scholar] [CrossRef]
- Friedlander, B.; Porat, B. VSAR: A high resolution radar system for ocean imaging. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 755–776. [Google Scholar] [CrossRef]
- Liu, M.; Li, C.; Shi, X. A back-projection fast autofocus algorithm based on minimum entropy for SAR imaging. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Korea, 26–30 September 2011; pp. 1–4. [Google Scholar]
- Dong, Q.; Xing, M.; Xia, X.; Zhang, S.; Sun, G. Moving Target Refocusing Algorithm in 2D Wavenumber Domain After BP Integral. IEEE Geosci. Remote Sens. Lett. 2018, 15, 127–131. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, X.; Shi, J.; Wei, S. A novel synthetic bandwidth method based on BP imaging for stepped-frequency SAR. Remote Sens. Lett. 2016, 7, 741–750. [Google Scholar] [CrossRef]
- Xu, J.; Zuo, Y.; Xia, B.; Xia, X.; Peng, Y.; Wang, Y. Ground Moving Target Signal Analysis in Complex Image Domain for Multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 538–552. [Google Scholar] [CrossRef]







| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Wavelength | 0.03 m | Range bandwidth | 500 MHz | Pulse repetition frequency | 1300 |
| Platform altitude | 3 km | Platform velocity | 150 m/s | Platform acceleration | 1 |
| Aperture time | about 5 s | Number of antennas | 8 | Antenna spacing | 0.5 m |
| Resolution cell | 0.3 m × 0.3 m | Near range | 15 km | Clutter-to-noise-ratio | 20 dB |
| Position | Value | Velocity | True Value | Estimated Value | Absolute Error | ||
|---|---|---|---|---|---|---|---|
| Point Moving Targets | T1 | x (m) | 200 | () | 3.5 | 3.52 | 0.02 |
| y (m) | 14,500 | () | 1.3 | 1.24 | 0.06 | ||
| T2 | x (m) | 280 | () | 3 | 2.98 | 0.02 | |
| y (m) | 14700 | () | 2.3 | 2.28 | 0.02 | ||
| T3 | x (m) | 50 | () | 2.5 | 2.51 | 0.01 | |
| y (m) | 15,000 | () | 3.5 | 3.48 | 0.02 | ||
| Extended Moving Targets | T4 | x (m) | 150 | () | 2 | 2.02 | 0.02 |
| y (m) | 15,200 | () | 4.6 | 4.52 | 0.08 | ||
| T5 | x (m) | 250 | () | −4 | −3.98 | 0.02 | |
| y (m) | 15,400 | () | 5.7 | 5.63 | 0.07 | ||
| T6 | x (m) | 350 | () | −5 | −4.99 | 0.01 | |
| y (m) | 15,600 | () | 6.8 | 6.78 | 0.02 |
| Proposed Refocusing Method | PGA Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Real 2D Velocity | Estimated 2D Velocity | |||||||||
| PSLRL (dB) | PSLRR (dB) | IRW Broad. | PSLRL (dB) | PSLRR (dB) | IRW Broad. | PSLRL (dB) | PSLRR (dB) | IRW Broad. | ||
| T1 | Azimuth | −13.35 | −13.19 | 0% | −13.31 | −13.26 | 0% | −12.7 | −12.9 | 62% |
| Range | −13.24 | −13.2 | 0% | −13.27 | −13.23 | 0% | −13.6 | −13.6 | 0.3% | |
| T2 | Azimuth | −13.29 | −13.28 | 0% | −12.1 | −12.3 | 1% | −14.83 | −14.04 | 81.9% |
| Range | −13.29 | −13.31 | 0% | −13.34 | −13.29 | 0.2% | −13.91 | −13.87 | 0.3% | |
| T3 | Azimuth | −13.34 | −13.22 | 0% | −13.31 | −13.22 | 0.2% | −13.75 | −13.14 | 123% |
| Range | −13.38 | −13.32 | 0% | −13.29 | −13.35 | 0% | −14.31 | −14.36 | 0.3% | |
| BP-VSAR | SCRin (dB) | SCRout (dB) | SCRIm (dB) | VA-BP-VSAR | SCRin (dB) | SCRout (dB) | SCRIm (dB) | |
|---|---|---|---|---|---|---|---|---|
| Point Moving Targets | T1 | −5 | 22 | 27 | T1 | −1 | 21 | 22 |
| T2 | −5 | 21 | 26 | T2 | −2 | 26 | 28 | |
| T3 | −5 | 21 | 26 | T3 | −2 | 25 | 27 | |
| Extended Moving Targets | T4 | −5 | 22 | 27 | T4 | −1 | 27 | 28 |
| T5 | −5 | 21 | 26 | T5 | −4 | 22 | 26 | |
| T6 | −5 | 19 | 24 | T6 | −3 | 21 | 24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Zhang, X.; Shi, J.; Wei, S.; Tian, B. Ground Moving Target 2-D Velocity Estimation and Refocusing for Multichannel Maneuvering SAR with Fixed Acceleration. Sensors 2019, 19, 3695. https://doi.org/10.3390/s19173695
Tang X, Zhang X, Shi J, Wei S, Tian B. Ground Moving Target 2-D Velocity Estimation and Refocusing for Multichannel Maneuvering SAR with Fixed Acceleration. Sensors. 2019; 19(17):3695. https://doi.org/10.3390/s19173695
Chicago/Turabian StyleTang, Xinxin, Xiaoling Zhang, Jun Shi, Shunjun Wei, and Bokun Tian. 2019. "Ground Moving Target 2-D Velocity Estimation and Refocusing for Multichannel Maneuvering SAR with Fixed Acceleration" Sensors 19, no. 17: 3695. https://doi.org/10.3390/s19173695






