Height Variation Depending on the Source of Antenna Phase Centre Corrections: LEIAR25.R3 Case Study
Abstract
:1. Introduction
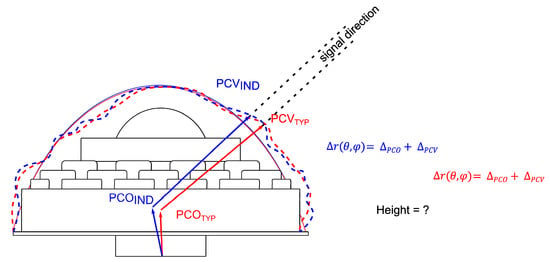
2. Methodology
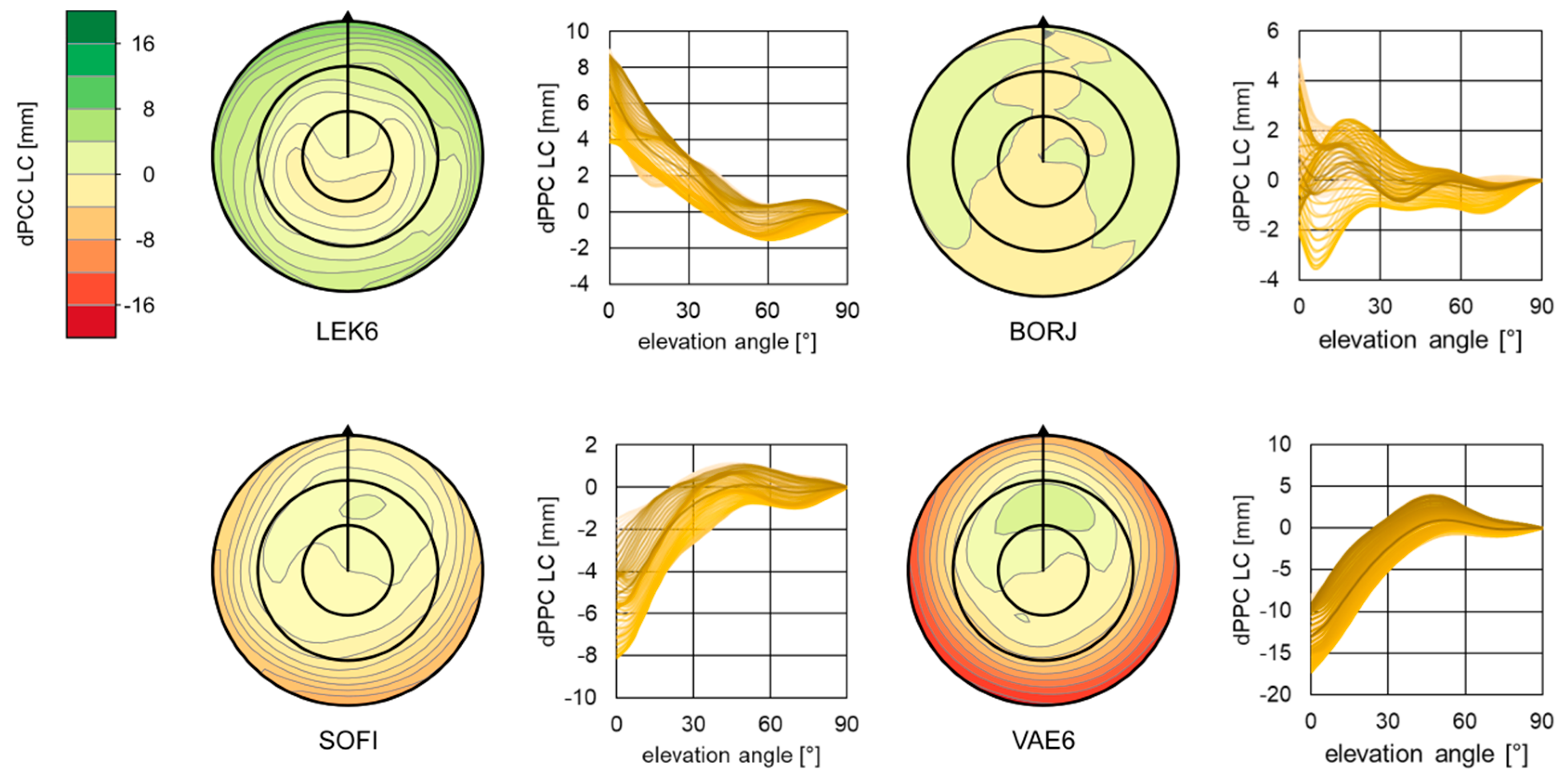
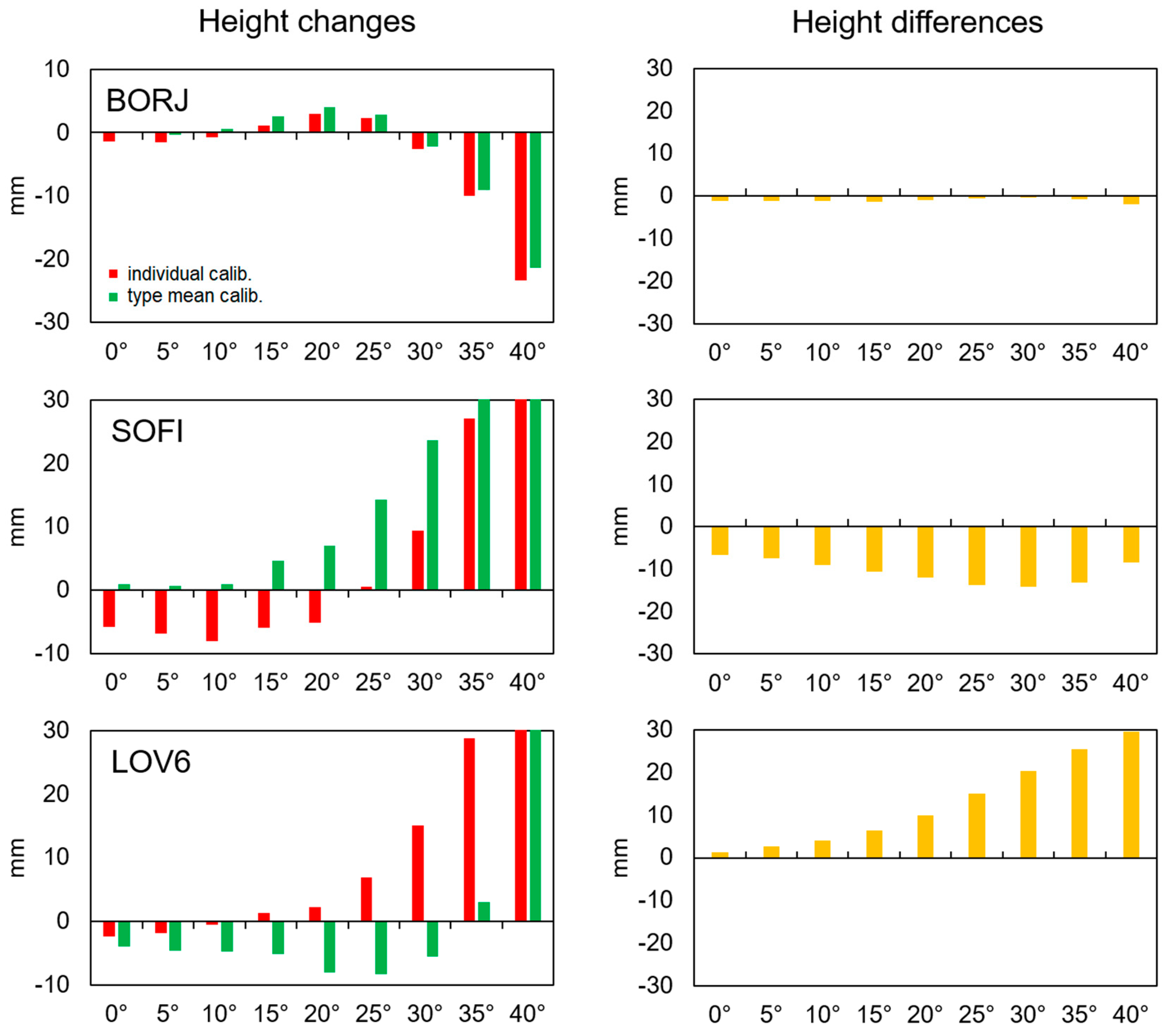
- The first one, where the differences are very small and can be considered as insignificant (e.g., stations BORJ, NOR7).
- The second one, where differences are positive (e.g., LEK6) or negative (e.g., OST6, VAE6) at low elevations and are gradually closer to 0 (e.g., OST6, VAE6).
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Station | L1 | L2 | LC | Station | L1 | L2 | LC |
|---|---|---|---|---|---|---|---|
| ALAC | 0.88 | 0.67 | 1.66 | OST6 | 1.06 | 0.68 | 2.92 |
| ALBA | 0.39 | 0.65 | 1.70 | OVE6 | 0.90 | 0.38 | 2.32 |
| ARJ6 | 0.97 | 0.50 | 2.48 | SKE8 | 0.49 | 0.89 | 1.66 |
| BORJ | 0.58 | 0.52 | 1.03 | SOFI | 0.83 | 0.24 | 2.36 |
| DRES | 0.61 | 1.36 | 1.42 | SVE6 | 0.26 | 0.82 | 1.45 |
| HAS6 | 0.63 | 0.73 | 1.42 | VAE6 | 1.57 | 0.93 | 4.86 |
| JON6 | 0.77 | 0.71 | 2.00 | VALE | 1.21 | 0.94 | 3.19 |
| KAD6 | 0.72 | 0.39 | 2.20 | VIL6 | 0.49 | 0.98 | 1.37 |
| LEK6 | 1.16 | 0.45 | 2.46 | VIS6 | 0.57 | 0.39 | 1.43 |
| LOV6 | 0.71 | 0.37 | 2.14 | WARN | 0.54 | 0.53 | 1.40 |
| NOR7 | 0.51 | 0.54 | 1.15 | WTZR | 0.74 | 0.90 | 1.47 |
| OSK6 | 0.76 | 0.72 | 1.30 |
| Station | 0–10° | 15–25° | 30–40° | 45–55° | 60–70° | 75–85° |
|---|---|---|---|---|---|---|
| ALAC | 1.83 | 1.94 | 1.65 | 1.16 | 0.69 | 0.28 |
| ALBA | 2.47 | 1.59 | 0.92 | 0.48 | 0.54 | 0.47 |
| ARJ6 | 2.80 | 2.33 | 1.93 | 1.91 | 1.60 | 0.89 |
| BORJ | 1.72 | 1.14 | 0.72 | 0.46 | 0.44 | 0.23 |
| DRES | 1.35 | 0.71 | 0.55 | 0.53 | 0.28 | 0.25 |
| HAS6 | 0.80 | 0.59 | 0.33 | 0.68 | 0.97 | 0.70 |
| HOE2 | 1.44 | 0.58 | 0.39 | 0.51 | 0.61 | 0.36 |
| JON6 | 1.00 | 0.75 | 0.57 | 0.79 | 0.59 | 0.14 |
| KAD6 | 1.22 | 0.79 | 0.89 | 1.03 | 1.00 | 0.67 |
| LEK6 | 1.37 | 1.04 | 0.82 | 0.73 | 0.70 | 0.43 |
| LOV6 | 1.77 | 1.54 | 1.34 | 1.09 | 1.06 | 0.56 |
| NOR7 | 1.67 | 1.02 | 0.64 | 0.71 | 0.72 | 0.44 |
| OSK6 | 1.35 | 1.15 | 1.28 | 1.10 | 1.03 | 0.68 |
| OST6 | 2.61 | 2.05 | 1.64 | 1.42 | 1.42 | 0.80 |
| OVE6 | 2.12 | 1.78 | 1.49 | 1.24 | 0.69 | 0.36 |
| SKE8 | 2.49 | 2.22 | 1.46 | 1.10 | 0.85 | 0.49 |
| SOFI | 1.88 | 1.35 | 0.98 | 0.64 | 0.59 | 0.36 |
| SVE6 | 1.75 | 1.42 | 1.26 | 1.10 | 0.86 | 0.49 |
| VAE6 | 2.97 | 2.76 | 2.15 | 1.59 | 0.90 | 0.45 |
| VALE | 2.44 | 2.66 | 2.57 | 2.13 | 1.34 | 0.53 |
| VIL6 | 1.70 | 1.35 | 0.94 | 0.94 | 0.86 | 0.35 |
| VIS6 | 1.91 | 1.36 | 0.74 | 0.66 | 0.62 | 0.40 |
| WARN | 1.69 | 1.38 | 1.51 | 1.20 | 0.80 | 0.38 |
| WTZR | 1.78 | 1.37 | 1.02 | 0.70 | 0.36 | 0.07 |
| Mean | 1.84 | 1.45 | 1.16 | 1.00 | 0.81 | 0.45 |
Appendix B
| Station | 0° | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° |
|---|---|---|---|---|---|---|---|---|---|
| ALAC | 5.2 | 4.9 | 5.6 | 6.6 | 8.2 | 10.2 | 13.9 | 19.4 | 29.6 |
| ALBA | 5.5 | 5.4 | 6.0 | 6.8 | 8.5 | 10.7 | 13.4 | 16.8 | 23.7 |
| ARJ6 | 8.0 | 8.7 | 9.8 | 11.0 | 13.0 | 17.9 | 24.3 | 31.4 | 45.7 |
| BORJ | 4.4 | 4.2 | 4.5 | 5.5 | 7.1 | 9.0 | 10.9 | 15.4 | 21.7 |
| DRES | 4.7 | 4.1 | 4.0 | 4.7 | 5.7 | 7.5 | 9.8 | 12.3 | 16.3 |
| HAS6 | 5.2 | 5.3 | 5.5 | 6.0 | 6.5 | 7.4 | 9.4 | 12.5 | 16.5 |
| HOE2 | 3.9 | 3.6 | 3.9 | 4.4 | 4.8 | 5.1 | 6.8 | 9.2 | 16.0 |
| JON6 | 5.1 | 5.2 | 5.7 | 6.4 | 7.3 | 8.1 | 9.8 | 13.3 | 21.6 |
| KAD6 | 6.0 | 6.1 | 6.3 | 6.8 | 7.7 | 9.2 | 10.8 | 13.9 | 20.1 |
| LEK6 | 5.1 | 5.1 | 5.3 | 5.6 | 6.1 | 6.9 | 8.3 | 10.6 | 16.9 |
| LOV6 | 5.7 | 5.7 | 5.7 | 5.8 | 6.3 | 7.3 | 8.8 | 11.8 | 14.9 |
| NOR7 | 5.0 | 4.8 | 4.8 | 4.9 | 5.2 | 5.6 | 7.1 | 9.9 | 13.7 |
| OSK6 | 5.2 | 5.1 | 5.2 | 5.4 | 5.8 | 6.4 | 7.7 | 10.0 | 14.8 |
| OST6 | 6.1 | 5.7 | 5.7 | 6.2 | 6.8 | 8.2 | 10.1 | 13.0 | 20.9 |
| OVE6 | 6.8 | 6.9 | 7.1 | 7.6 | 8.6 | 10.4 | 14.3 | 23.5 | 31.9 |
| SKE8 | 5.7 | 5.7 | 5.7 | 5.8 | 5.9 | 6.2 | 7.6 | 10.8 | 17.9 |
| SOFI | 6.5 | 6.6 | 6.8 | 7.6 | 8.2 | 9.7 | 10.7 | 13.1 | 21.7 |
| SVE6 | 6.4 | 6.5 | 7.4 | 9.2 | 11.3 | 15.0 | 20.0 | 24.9 | 31.9 |
| VAE6 | 5.9 | 5.7 | 5.7 | 5.8 | 6.1 | 6.8 | 7.9 | 10.4 | 16.2 |
| VALE | 5.2 | 5.3 | 5.7 | 6.1 | 6.5 | 7.1 | 8.7 | 11.8 | 17.5 |
| VIL6 | 4.9 | 4.6 | 5.1 | 6.1 | 7.7 | 9.5 | 13.0 | 16.1 | 22.5 |
| VIS6 | 9.9 | 10.8 | 11.9 | 13.9 | 16.7 | 22.0 | 31.5 | 47.8 | 73.7 |
| WARN | 5.5 | 5.4 | 5.5 | 5.6 | 5.6 | 5.9 | 7.4 | 10.2 | 15.1 |
| WTZR | 4.8 | 4.2 | 4.1 | 4.6 | 5.2 | 5.8 | 7.6 | 9.9 | 14.1 |
| Station | 0° | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° |
|---|---|---|---|---|---|---|---|---|---|
| ALAC | 5.3 | 4.8 | 5.4 | 6.5 | 8.2 | 10.2 | 13.8 | 19.2 | 29.0 |
| ALBA | 5.3 | 5.3 | 5.8 | 6.8 | 8.4 | 10.7 | 13.4 | 16.7 | 23.3 |
| ARJ6 | 8.1 | 8.7 | 9.8 | 11.1 | 13.1 | 17.9 | 24.3 | 31.5 | 45.9 |
| BORJ | 4.4 | 4.1 | 4.5 | 5.4 | 7.0 | 9.0 | 11.1 | 15.6 | 21.3 |
| DRES | 4.7 | 4.1 | 4.1 | 4.6 | 5.7 | 7.5 | 9.8 | 12.2 | 15.8 |
| HAS6 | 5.4 | 5.3 | 5.5 | 6.0 | 6.6 | 7.5 | 9.5 | 12.7 | 16.5 |
| HOE2 | 4.0 | 3.5 | 3.9 | 4.4 | 4.7 | 5.1 | 6.6 | 9.2 | 15.9 |
| JON6 | 5.3 | 5.3 | 5.7 | 6.5 | 7.4 | 8.1 | 9.7 | 13.3 | 21.9 |
| KAD6 | 6.1 | 6.1 | 6.2 | 6.8 | 7.8 | 9.3 | 10.9 | 13.6 | 20.1 |
| LEK6 | 5.1 | 5.2 | 5.4 | 5.7 | 6.2 | 6.9 | 8.4 | 10.5 | 16.7 |
| LOV6 | 5.8 | 5.6 | 5.7 | 5.8 | 6.4 | 7.2 | 8.9 | 11.8 | 14.4 |
| NOR7 | 5.1 | 4.9 | 4.7 | 5.0 | 5.3 | 5.7 | 7.1 | 10.2 | 13.7 |
| OSK6 | 5.4 | 5.2 | 5.1 | 5.4 | 5.9 | 6.4 | 7.8 | 10.1 | 14.4 |
| OST6 | 6.2 | 5.7 | 5.7 | 6.1 | 6.8 | 8.2 | 10.2 | 13.1 | 20.5 |
| OVE6 | 6.9 | 7.0 | 7.1 | 7.8 | 8.9 | 10.6 | 14.5 | 23.6 | 32.3 |
| SKE8 | 5.7 | 5.7 | 5.7 | 5.8 | 6.0 | 6.3 | 7.6 | 10.8 | 17.8 |
| SOFI | 6.7 | 6.6 | 6.8 | 7.7 | 8.3 | 9.7 | 10.7 | 13.1 | 21.7 |
| SVE6 | 6.3 | 6.5 | 7.5 | 9.1 | 11.3 | 15.1 | 19.9 | 25.0 | 31.8 |
| VAE6 | 5.9 | 5.7 | 5.6 | 5.8 | 6.2 | 6.8 | 7.9 | 10.3 | 16.2 |
| VALE | 5.4 | 5.4 | 5.7 | 6.1 | 6.5 | 7.1 | 8.7 | 11.7 | 17.3 |
| VIL6 | 4.8 | 4.6 | 5.1 | 6.1 | 7.8 | 9.7 | 13.2 | 16.1 | 22.2 |
| VIS6 | 9.9 | 10.7 | 11.9 | 13.8 | 16.7 | 22.1 | 31.9 | 48.1 | 73.3 |
| WARN | 5.6 | 5.5 | 5.5 | 5.6 | 5.7 | 6.0 | 7.4 | 10.2 | 14.9 |
| WTZR | 4.9 | 4.2 | 4.0 | 4.6 | 5.2 | 5.8 | 7.6 | 9.9 | 14.1 |
Appendix C
| Station | 0° | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° | RMS |
|---|---|---|---|---|---|---|---|---|---|---|
| ALAC | 2.1 | 2.1 | 1.8 | 1.6 | 1.8 | 2.2 | 1.7 | −1.1 | −7.0 | 2.8 |
| ALBA | 0.2 | 0.0 | −0.5 | −1.7 | −2.6 | −3.1 | −3.4 | −2.4 | 0.7 | 1.5 |
| ARJ6 | 1.3 | 1.4 | 1.3 | 1.2 | 0.4 | −1.8 | −6.2 | −12.6 | −19.2 | 7.0 |
| BORJ | −1.2 | −1.2 | −1.3 | −1.4 | −1.0 | −0.6 | −0.5 | −0.9 | −2.0 | 0.4 |
| DRES | 1.7 | 1.8 | 1.9 | 2.2 | 2.6 | 3.3 | 4.1 | 4.2 | 2.2 | 0.9 |
| HAS6 | −2.8 | −3.4 | −5.0 | −6.5 | −8.0 | −9.9 | −12.8 | −16.5 | −21.1 | 5.9 |
| HOE2 | 0.3 | 0.5 | 0.5 | 0.0 | −0.3 | −0.6 | -0.9 | −1.2 | −2.6 | 0.9 |
| JON6 | 5.7 | 7.0 | 8.7 | 10.7 | 12.9 | 15.5 | 17.8 | 18.4 | 15.6 | 4.4 |
| KAD6 | 2.2 | 2.9 | 3.2 | 3.6 | 4.6 | 5.6 | 6.6 | 6.5 | 5.5 | 1.5 |
| LEK6 | 3.7 | 4.5 | 4.8 | 6.1 | 8.7 | 13.2 | 19.5 | 26.3 | 31.9 | 9.8 |
| LOV6 | 1.5 | 2.8 | 4.2 | 6.5 | 10.2 | 15.2 | 20.5 | 25.7 | 30.9 | 10.0 |
| NOR7 | −0.4 | −1.6 | −4.0 | −6.1 | −7.5 | −8.3 | −8.0 | −6.9 | −6.0 | 2.7 |
| OSK6 | −1.4 | −2.1 | −3.8 | −4.7 | −4.8 | −3.8 | −2.9 | −2.0 | −0.5 | 1.4 |
| OST6 | −11.3 | −13.0 | −15.2 | −17.6 | −19.9 | −22.0 | −23.6 | −23.5 | −20.8 | 4.3 |
| OVE6 | 1.2 | 1.6 | 1.5 | 2.1 | 4.8 | 9.8 | 16.7 | 25.5 | 34.2 | 11.4 |
| SKE8 | 1.4 | 1.9 | 2.5 | 3.5 | 5.5 | 8.2 | 11.2 | 13.0 | 10.5 | 4.2 |
| SOFI | −6.7 | −7.5 | −9.0 | −10.6 | −12.1 | −13.8 | −14.2 | −13.2 | −8.5 | 2.7 |
| SVE6 | 2.7 | 3.0 | 3.2 | 3.1 | 3.0 | 2.0 | −1.0 | -5.8 | −11.8 | 5.0 |
| VAE6 | −10.3 | −13.2 | −17.6 | −21.6 | −26.0 | −30.8 | −36.0 | −40.3 | −43.7 | 11.2 |
| VALE | −5.2 | −6.0 | −7.2 | −9.0 | −10.5 | −12.3 | −13.9 | −15.8 | −17.0 | 4.0 |
| VIL6 | −1.5 | −1.7 | −2.2 | −2.5 | −1.9 | −1.0 | −0.6 | −1.8 | −5.5 | 1.3 |
| VIS6 | −0.9 | −1.9 | −3.7 | −5.7 | −7.1 | −7.0 | −5.4 | −2.3 | 1.0 | 2.7 |
| WARN | −0.6 | −0.8 | −1.4 | −1.6 | −0.9 | 0.9 | 1.9 | 2.3 | 1.2 | 1.4 |
| WTZR | 2.7 | 3.3 | 3.8 | 5.1 | 7.5 | 10.5 | 13.3 | 15.6 | 16.7 | 5.2 |
References
- Chen, H.; Jiang, W.; Li, J. Multi-GNSS Relative Positioning with Fixed Inter-System Ambiguity. Remote Sens. 2019, 11, 454. [Google Scholar] [CrossRef]
- Duong, V.; Harima, K.; Choy, S.; Laurichesse, D.; Rizos, C. An optimal linear combination model to accelerate PPP convergence using multi-frequency multi-GNSS measurements. GPS Solut. 2019, 23, 49. [Google Scholar] [CrossRef]
- Kiliszek, D.; Szolucha, M.; Kroszczynski, K. Accuracy of Precise Point Positioning (PPP) with the use of different International GNSS Service (IGS) products and stochastic modelling. Geod. Cartogr. 2018, 67, 207–238. [Google Scholar] [CrossRef]
- Prochniewicz, D.; Szpunar, R.; Walo, J. A new study of describing the reliability of GNSS Network RTK positioning with the use of quality indicators. Meas. Sci. Technol. 2017, 28, 015012. [Google Scholar] [CrossRef]
- Li, B. Review of triple-frequency GNSS: Ambiguity resolution, benefits and challenges. J. Glob. Position. Syst. 2018, 16. [Google Scholar] [CrossRef]
- Araszkiewicz, A.; Figurski, M.; Jarosiński, M. Erroneous GNSS strain rate patterns and their application to investigate the tectonic credibility of GNSS velocities. Acta Geophys. 2016, 64, 1412–1419. [Google Scholar] [CrossRef]
- Baldysz, Z.; Nykiel, G.; Figurski, M.; Araszkiewicz, A. Assessment of the Impact of GNSS Processing Strategies on the Long-Term Parameters of 20 Years IWV Time Series. Remote Sens. 2018, 10, 496. [Google Scholar] [CrossRef]
- Carlà, T.; Tofani, V.; Lombardi, L.; Raspini, F.; Bianchini, S.; Bertolo, D.; Thuegaz, P.; Casagli, N. Combination of GNSS, satellite InSAR, and GBInSAR remote sensing monitoring to improve the understanding of a large landslide in high alpine environment. Geomorphology 2019, 335, 62–75. [Google Scholar] [CrossRef]
- Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Improving GNSS zenith wet delay interpolation by utilizing tropospheric gradients: Experiments with a dense station network in Central Europe in the warm season. Remote Sens. 2019, 11, 674. [Google Scholar] [CrossRef]
- Zajdel, R.; Sośnica, K.; Dach, R.; Bury, G.; Prange, L.; Jäggi, A. Network effects and handling of the geocenter motion in multi-GNSS processing. JGR Solid Earth 2019. [CrossRef]
- Simonetto, E.; Durand, S.; Burdack, J.; Polidori, L.; Morel, L.; Nicolas-Duroy, J. Combination of INSAR and GNSS measurements for ground displacement monitoring. Procedia Technol. 2014, 16, 192–198. [Google Scholar] [CrossRef]
- Vittuari, L.; Tini, M.A.; Sarti, P.; Serantoni, E.; Borghi, A.; Negusini, M.; Guillaume, S. A comparative study of the applied methods for estimating deflection of the vertical in terrestrial geodetic measurements. Sensors 2016, 16, 565. [Google Scholar] [CrossRef] [PubMed]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, L.; Noll, C.; Macleod, K.; Schmid, R.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. (Eds.) GNSS-Global Navigation Satellite System. GPS, GLONASS, Galileo and More; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Schmid, R.; Rothacher, M.; Thaller, D.; Steigenberger, P. Absolute phase center corrections of satellite and receiver antennas. GPS Solut. 2005, 9, 283–293. [Google Scholar] [CrossRef]
- Mader, G. A comparison of absolute and relative GPS antenna calibrations. GPS Solut. 2001, 4, 37–40. [Google Scholar] [CrossRef]
- Wübbena, G.; Schmitz, M.; Warneke, A. Geo++ Absolute GNSS Antenna Calibration. In Proceedings of the IGS AC Workshop, GFZ Potsdam, Germany, 15–17 April 2019. [Google Scholar]
- Kersten, T.; Schön, S. Receiver Antenna Phase Center Models and Their Impact on Geodetic Parameters. In International Symposium on Earth and Environmental Sciences for Future Generations; Freymueller, J.T., Sánchez, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 147. [Google Scholar]
- Hu, Z.; Zhao, Q.; Chen, G.; Wang, G.; Dai, Z.; Li, T. First Results of Field Absolute Calibration of the GPS Receiver Antenna at Wuhan University. Sensors 2015, 15, 28717–28731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeimetz, P.; Kuhlmann, H. Systematic effects in absolute chamber calibration of GPS antennas. Geomatica 2006, 60, 267–275. [Google Scholar]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef]
- Bruyninx, C.; Habrich, H.; Söhne, W.; Kenyeres, A.; Stangl, G.; Völksen, C. Enhancement of the EUREF permanent network services and products. In Geodesy for Planet Earth; Springer: Berlin/Heidelberg, Germany, 2012; Volume 136, pp. 27–35. [Google Scholar]
- EPN Coordination Group and the EPN Central Bureau; Guidelines for the EPN Analysis Centres; Last Update: 12 July 2018. Available online: http://epncb.oma.be/_documentation/guidelines/guidelines_analysis_centres.pdf (accessed on 3 July 2019).
- Bilich, A.; Schmitz, M.; Görres, B.; Zeimetz, P.; Mader, G.; Wübbena, G. Three-method absolute antenna calibration comparison. In IGS Workshop 2012; University of Warmia and Mazury: Olsztyn, Poland, 2012; pp. 631–653. [Google Scholar]
- Baire, Q.; Bruyninx, C.; Legrand, J.; Pottiaux, E.; Aerts, W.; Defraigne, P.; Bergeot, N.; Chevalier, J.M. Influence of different GPS receiver antenna calibration models on geodetic positioning. GPS Solut. 2014, 18, 529–539. [Google Scholar] [CrossRef]
- Araszkiewicz, A.; Völksen, C. The impact of the antenna phase center models on the coordinates in the EUREF Permanent Network. GPS Solut. 2017, 21, 747–757. [Google Scholar] [CrossRef]
- Ejigu, Y.G.; Hunegnaw, A.; Abraha, K.E.; Teferle, F.N. Impact of GPS antenna phase center models on zenith wet delay and tropospheric gradients. GPS Solut. 2019, 23. [Google Scholar] [CrossRef]
- Pacione, R.; Araszkiewicz, A.; Brockmann, E.; Dousa, J. EPN-Repro2: A reference GNSS tropospheric data set over Europe. Atmos. Meas. Tech. 2017, 10, 1689–1705. [Google Scholar] [CrossRef] [Green Version]
- Kallio, U.; Koivula, H.; Lahtinen, S.; Nikkonen, V.; Poutanen, M. Validating and comparing GNSS antenna calibrations. J. Geod. 2018. [CrossRef]
- Antenna Information for LEIAR25.R3 LEIT. Available online: https://trimbletools.com/Antenna_Info/IGS08/LEIAR25.R3______LEIT.html (accessed on 25 July 2018).
- King, R.W.; Herring, T.A.; McCluscy, S.C. (Eds.) Documentation for the GAMIT GPS Analysis Software 10.6; Technology Report; Massachusetts Institute of Technology: Cambridge, MA, USA, 2015. [Google Scholar]
- Schön, S.; Kersten, T. On adequate comparison of antenna phase center variations. In Proceedings of the American Geophysical Union, Annual Fall Meeting, San Francisco, CA, USA, 9–13 December 2013. [Google Scholar]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A new framework for the IGS products. AGU Fall Meeting Abstracts. 2016. Available online: https://ui.adsabs.harvard.edu/abs/2016AGUFM.G41A0998R (accessed on 3 July 2019).

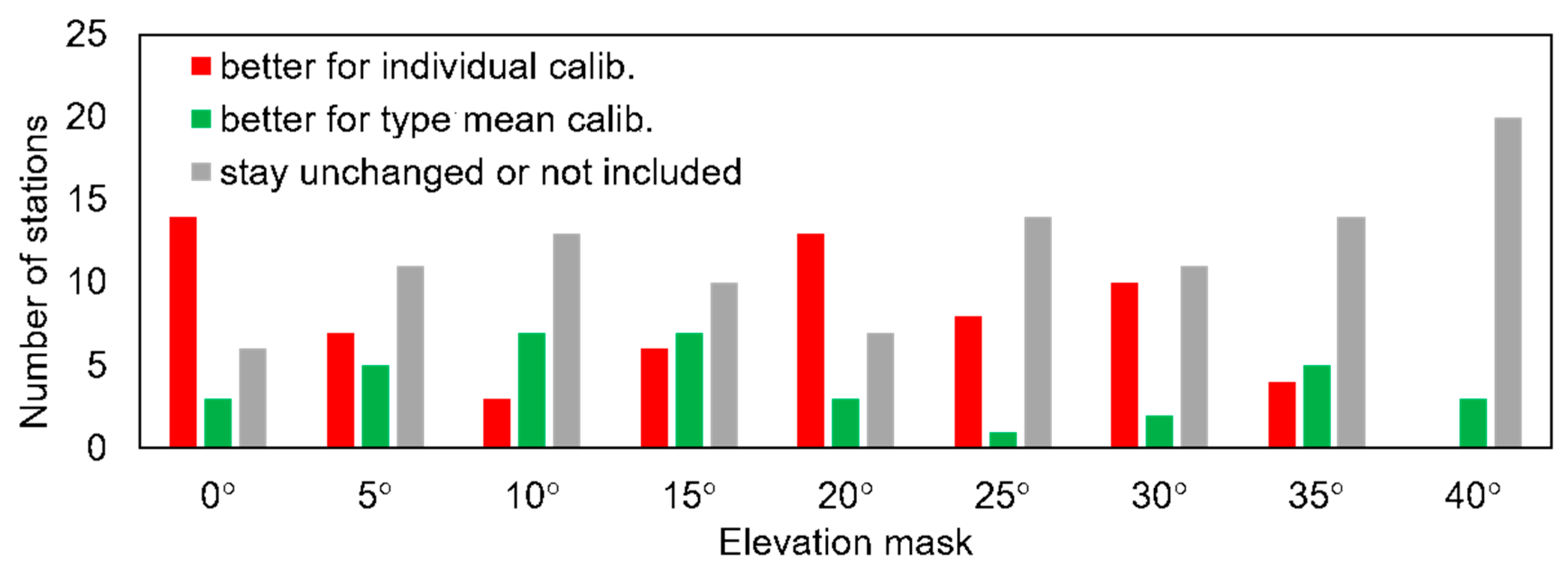



| Name | Source of PCC | Elevation Mask | Name | Source of PCC | Elevation Mask |
|---|---|---|---|---|---|
| sol_t_00 | igs_08.atx | 0° | sol_i_00 | epnc.atx | 0° |
| sol_t_05 | 5° | sol_i_05 | 5° | ||
| sol_t_10 | 10° | sol_i_10 | 10° | ||
| sol_t_15 | 15° | sol_i_15 | 15° | ||
| sol_t_20 | 20° | sol_i_20 | 20° | ||
| sol_t_25 | 25° | sol_i_25 | 25° | ||
| sol_t_30 | 30° | sol_i_30 | 30° | ||
| sol_t_35 | 35° | sol_i_35 | 35° | ||
| sol_t_40 | 40° | sol_i_40 | 40° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araszkiewicz, A.; Kiliszek, D.; Podkowa, A. Height Variation Depending on the Source of Antenna Phase Centre Corrections: LEIAR25.R3 Case Study. Sensors 2019, 19, 4010. https://doi.org/10.3390/s19184010
Araszkiewicz A, Kiliszek D, Podkowa A. Height Variation Depending on the Source of Antenna Phase Centre Corrections: LEIAR25.R3 Case Study. Sensors. 2019; 19(18):4010. https://doi.org/10.3390/s19184010
Chicago/Turabian StyleAraszkiewicz, Andrzej, Damian Kiliszek, and Anna Podkowa. 2019. "Height Variation Depending on the Source of Antenna Phase Centre Corrections: LEIAR25.R3 Case Study" Sensors 19, no. 18: 4010. https://doi.org/10.3390/s19184010
APA StyleAraszkiewicz, A., Kiliszek, D., & Podkowa, A. (2019). Height Variation Depending on the Source of Antenna Phase Centre Corrections: LEIAR25.R3 Case Study. Sensors, 19(18), 4010. https://doi.org/10.3390/s19184010