MEMS Hydrophone Signal Denoising and Baseline Drift Removal Algorithm Based on Parameter-Optimized Variational Mode Decomposition and Correlation Coefficient
Abstract
:1. Introduction
2. Theoretical Basis
2.1. Variational Mode Decomposition (VMD)
- Step 1:
- Initialize the parameters, set , , and to 0;
- Step 2:
- Update the values of , , and according to Formulas (4)–(6);
- Step 3:
- Determine whether the termination condition (7) is satisfied, and repeat step 2 until Formula (7) is satisfied.
2.2. Whale-Optimization Algorithm (WOA)
2.3. Power Spectrum Entropy (PSE)
- Step 1:
- Calculation formula of the power spectrum of signal :where is the signal length and is the Fourier transform of ;
- Step 2:
- Obtain the probability density function of the spectrum of all frequency components by normalization:where is the spectral energy of frequency component ; is the corresponding probability density; is the number of frequency components in the fast Fourier transform of the total probability density;
- Step 3:
- The PSE value is defined as:
2.4. Correlation Coefficient (CC)
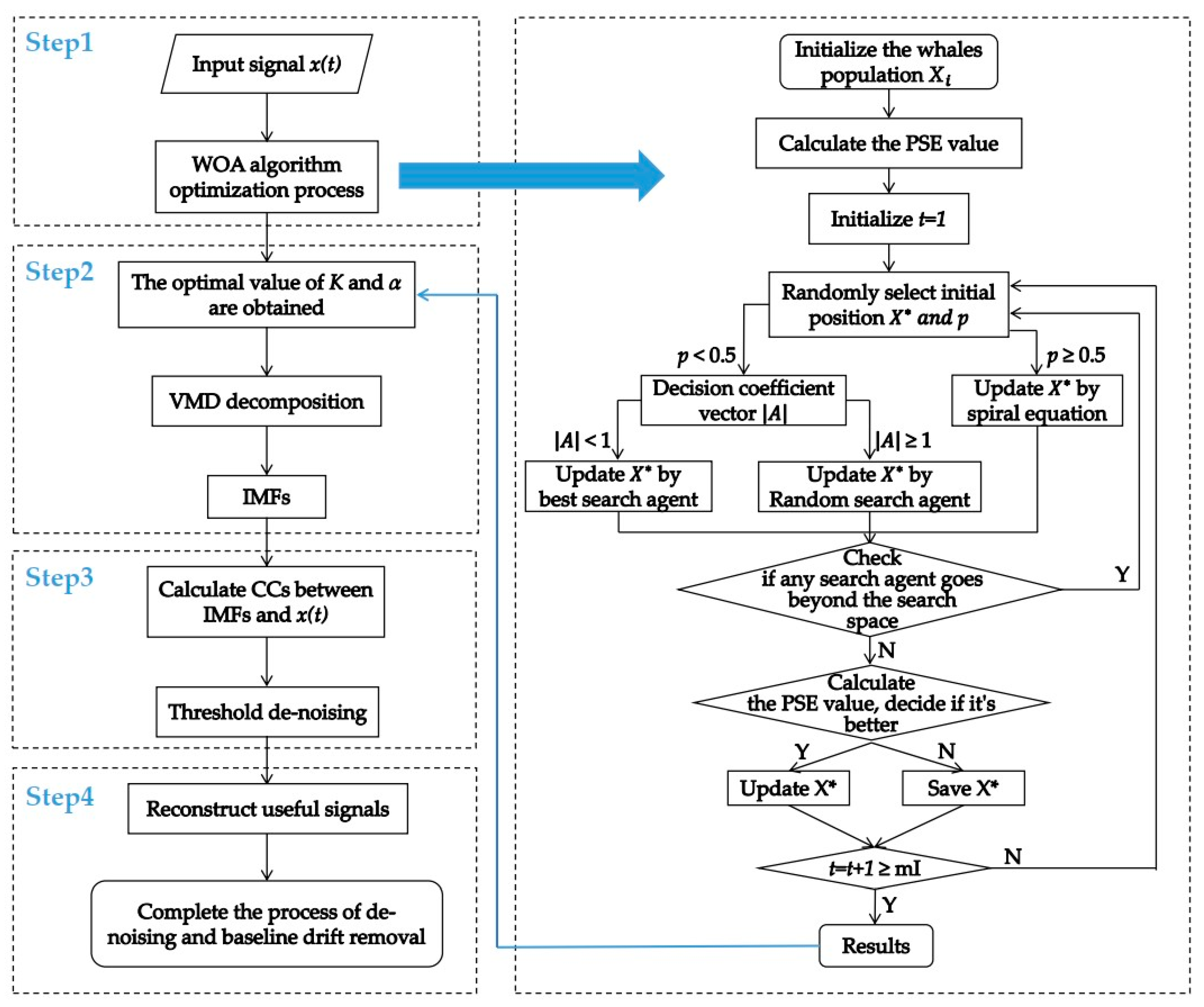
3. The Method Proposed in This Paper (WOA–VMD–CC)
4. Simulation
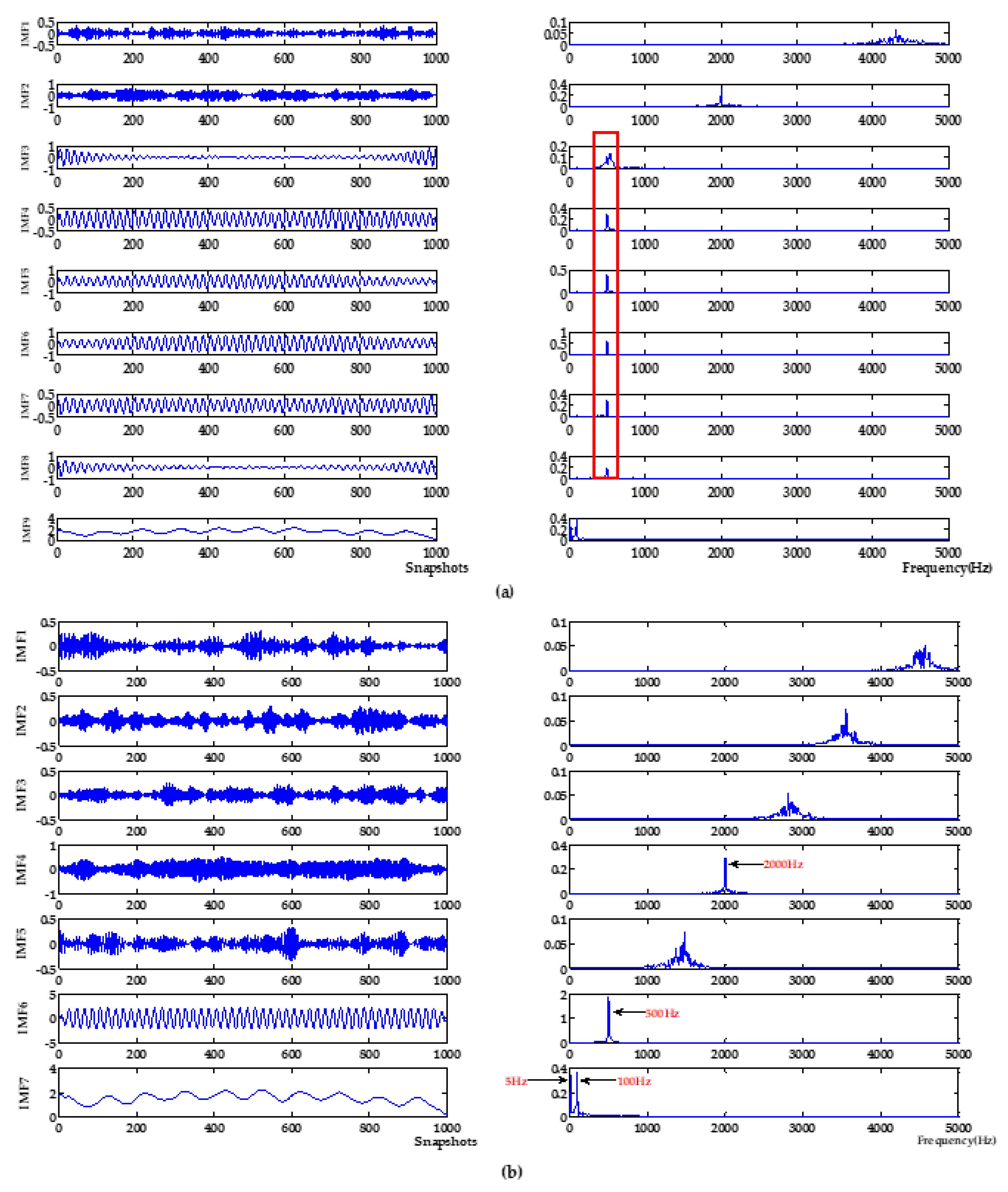
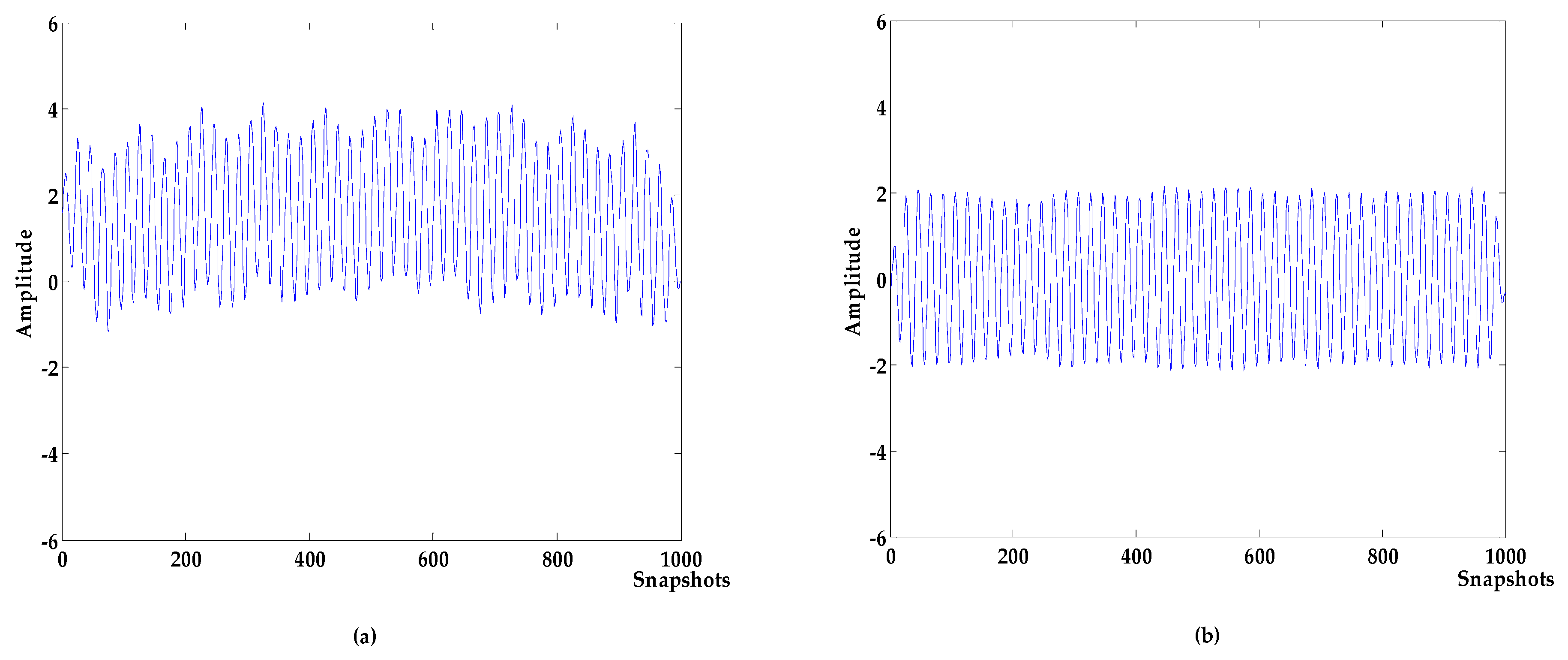
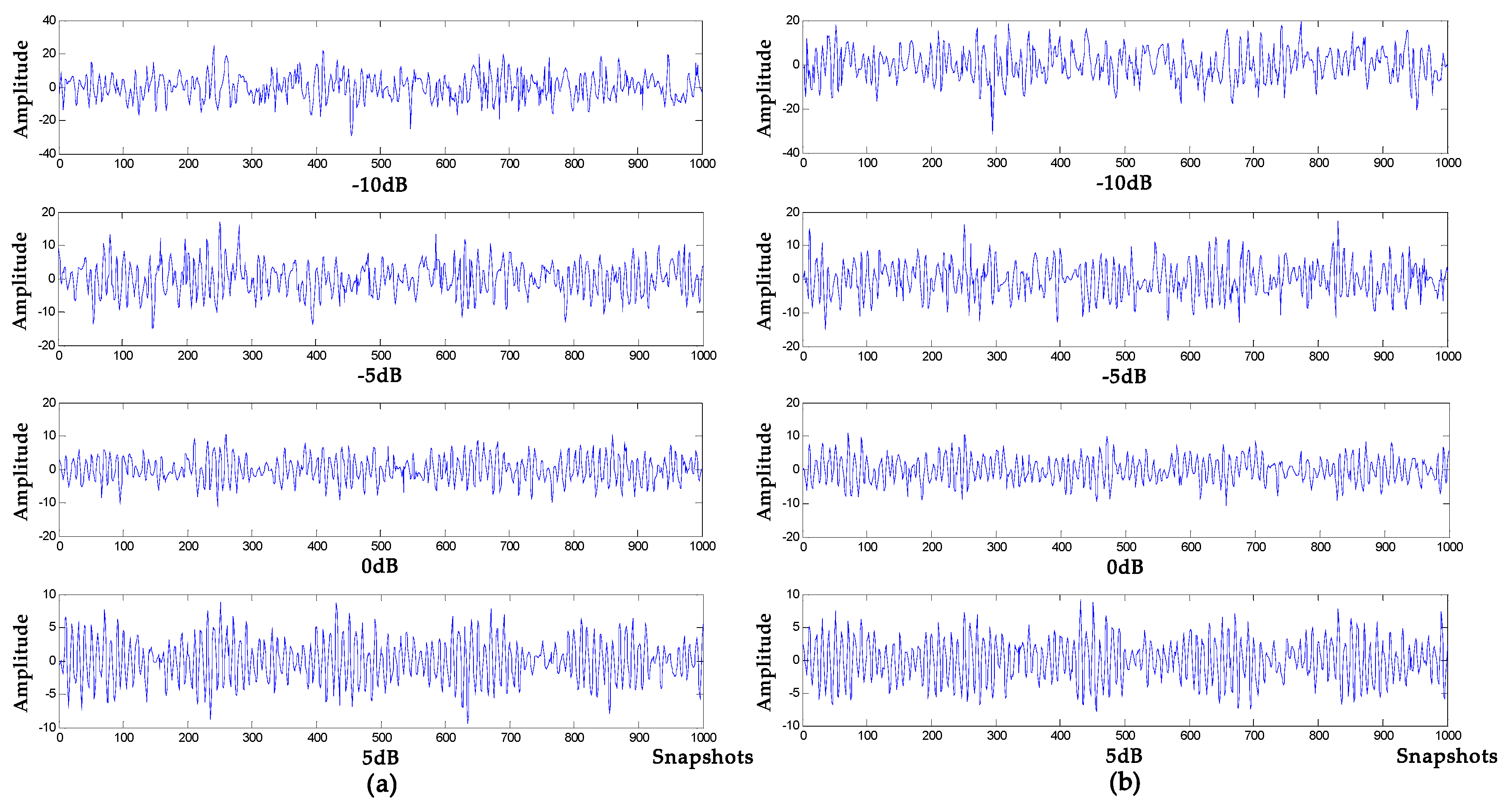
4.1. Simulation Experiment 1
4.2. Simulation Experiment 2
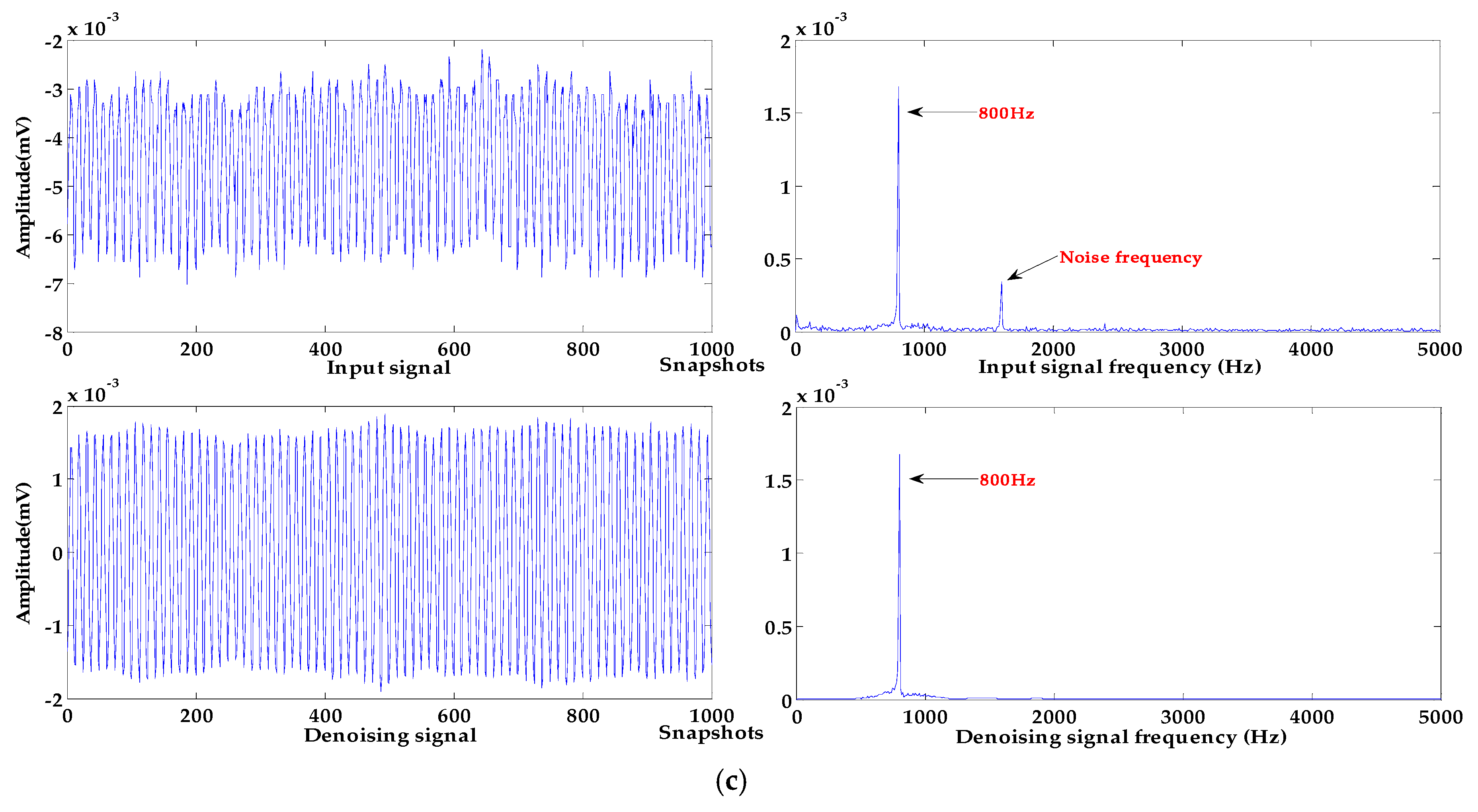
5. Application in the Experiments of MEMS Hydrophone
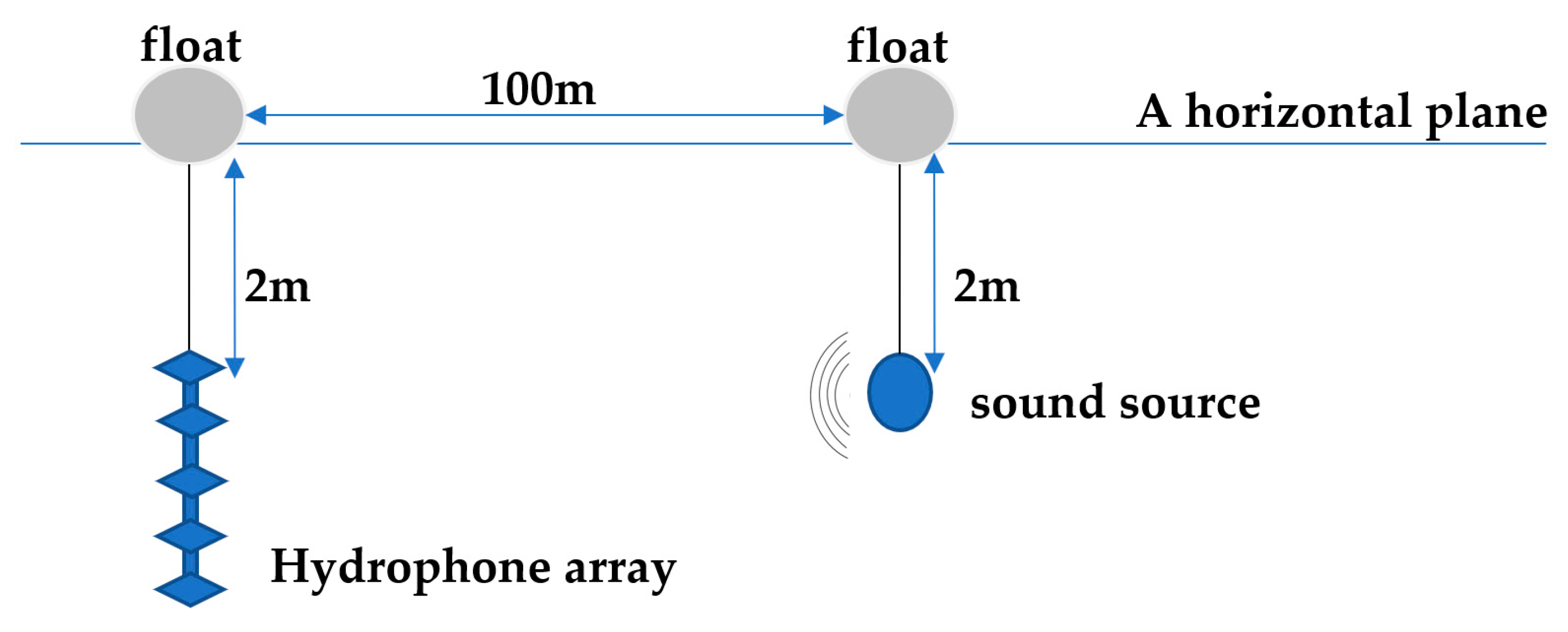
5.1. MEMS Vector Hydrophone and Signal Acquisition
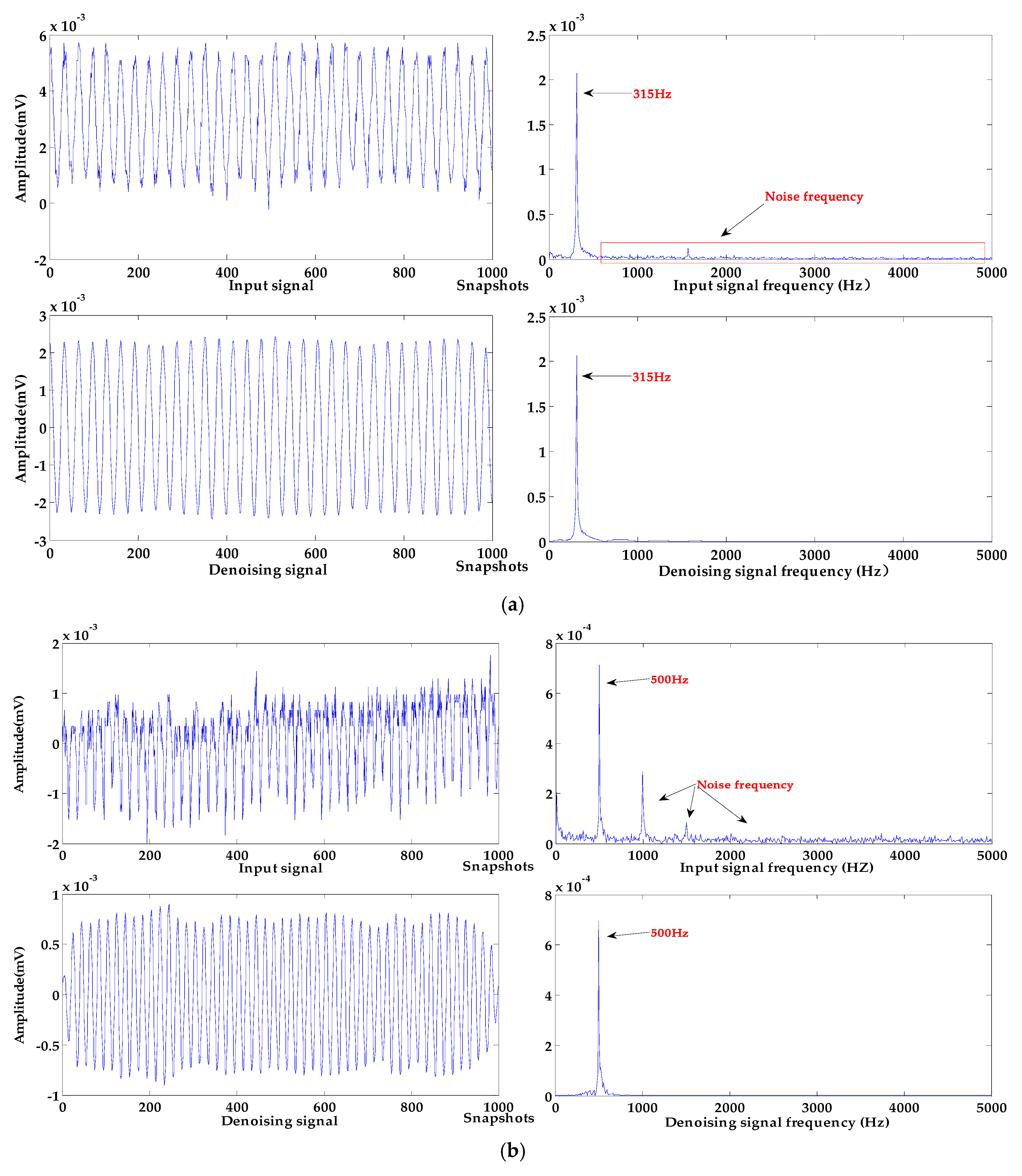
5.2. Denoising and Baseline Drift Removal Experiments for MEMS Vector Hydrophones
6. Conclusions
- (1)
- In many literatures, the parameters of VMD are selected by empirical method. In this paper, the whale-optimization algorithm is used to optimize the parameters of the VMD. While taking into account the mutual influence between the two parameters, it is easier to find the global optimal solution, which provides an idea for adaptively searching for the parameters of the VMD.
- (2)
- Power spectrum entropy (PSE) can reflect the variation characteristics of the frequency in the signal. In the whale-optimization algorithm, PSE is used as the fitness function, and it is easier to find the optimal parameters , which can improve the accuracy of signal decomposition. There is no modal aliasing when decomposing the signal using the algorithm proposed in this paper.
- (3)
- This paper calculates the CCs of the IMFs and the original signal, and denoises the signal by setting the CC threshold. The correlation between the denoised signal and the original signal is fully considered, so that the denoised signal retains more important information of the original signal.
- (4)
- Conventional digital signal-processing methods tend to lose useful information when removing baseline drift. The algorithm in this paper has a good performance for baseline drift removal of signals with different characteristics. At the same time, more useful information is retained.
- (5)
- Compared with conventional digital signal-processing methods and other related algorithms proposed recently, the denoising effect of this algorithm is better.
Author Contributions
Funding
Conflicts of Interest
References
- Halpern, B.S.; Frazier, M.; Afflerbach, J.; Lowndes, J.S.; Micheli, F.; O’Hara, C.; Scarborough, C.; Selkoe, K.A. Recent pace of change in human impact on the world’s ocean. Sci. Rep. 2019, 9, 11609. [Google Scholar] [CrossRef] [PubMed]
- Principe, P.P.; Fisher, W.S. Spatial Distribution of Collections Yielding Marine Natural Products. J. Nat. Prod. 2018, 81, 2307–2320. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, S.; Jin, C.; Zhang, Y.; Jiang, T. A Survey of Underwater Magnetic Induction Communications: Fundamental Issues, Recent Advances, and Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 2466–2487. [Google Scholar] [CrossRef]
- Flandrin, P.; Gonçalvès, P.; Rilling, G. Detrending and denoising with empirical mode decompositions. In Proceedings of the 12th European Signal Processing Conference (EUSIPCO’04), Vienna, Austria, 6–10 September 2004; IEEE: Washington, DC, USA, 2004; Volume 2, pp. 1581–1584. [Google Scholar]
- Tu, C.-K.; Jiang, Y.-Y. Development of noise reduction algorithm for underwater signals. In Proceedings of the 2004 International Symposium on Underwater Technology (IEEE Cat. No.04EX869), Taipei, Taiwan, 20–23 April 2004; IEEE: Washington, DC, USA, 2005; pp. 175–179. [Google Scholar] [CrossRef]
- Baskar, V.V.; Rajendran, V.; Logashanmugam, E. Study of different denoising methods for underwater acoustic signal. J. Mar. Sci. Technol. 2015, 23, 414–419. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, R.; Zhang, W. Improved local cepstrum and its applications for gearbox and rolling bearing fault detection. Meas. Sci. Technol. 2019, 30, 075007. [Google Scholar] [CrossRef]
- Bahaz, M.; Benzid, R. Efficient algorithm for baseline wander and powerline noise removal from ECG signals based on discrete Fourier series. Australas. Phys. Eng. Sci. Med. 2018, 41, 143–160. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Chen, X. Operational Safety Assessment of Turbo Generators with Wavelet Rényi Entropy from Sensor-Dependent Vibration Signals. Sensors 2015, 15, 8898–8918. [Google Scholar] [CrossRef]
- Xu, X.; Liang, Y.; Yang, J. Adaptive Motion Artifact Reduction Based on Empirical Wavelet Transform and Wavelet Thresholding for the Non-Contact ECG Monitoring Systems. Sensors 2019, 19, 2916. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, L.; Yan, H.; Bai, Y.; Wang, P. Denoising and Baseline Drift Removal Method of MEMS Hydrophone Signal Based on VMD and Wavelet Threshold Processing. IEEE Access 2019, 7, 59913–59922. [Google Scholar] [CrossRef]
- Di Biagio, V.; Cossarini, G.; Salon, S.; Lazzari, P.; Querin, S.; Sannino, G.; Solidoro, C. Temporal scales of variability in the Mediterranean Sea ecosystem: Insight from a coupled model. J. Mar. Syst. 2019, 197, 103176. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, S.S.P. Hilbert-Huang Transform and Its Applications; World Scientific Publishing: Singapore, 1998; pp. 1–202. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Research on Ship-Radiated Noise Denoising Using Secondary Variational Mode Decomposition and Correlation Coefficient. Sensors 2018, 18, 48. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Identification of mechanical compound-fault based on the improved parameter-adaptive variational mode decomposition. ISA Trans. 2019, 84, 82–95. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Du, W. Research on Fault Diagnosis of Gearbox with Improved Variational Mode Decomposition. Sensors 2018, 18, 3510. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Zi, Y.; Pan, J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive. Mech. Syst. Signal Process. 2017, 85, 512–529. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M.; Xiang, L. Compound fault diagnosis of rotating machinery based on OVMD and a 1.5-dimension envelope spectrum. Meas. Sci. Technol. 2016, 27, 075002. [Google Scholar] [CrossRef]
- Wang, Z.; He, G.; Du, W.; Zhou, J.; Han, X.; Wang, J.; He, H.; Guo, X.; Wang, J.; Kou, Y. Application of Parameter Optimized Variational Mode Decomposition Method in Fault Diagnosis of Gearbox. IEEE Access 2019, 7, 44871–44882. [Google Scholar] [CrossRef]
- Vargas, R.N.; Paschoarelli, V.; Antônio, C. Electrocardiogram signal denoising by clustering and soft thresholding. IET Signal Process. 2018, 12, 1165–1171. [Google Scholar] [CrossRef]
- Piazzo, L.; Panuzzo, P.; Pestalozzi, M. Drift removal by means of alternating least squares with application to Herschel data. Signal Process. 2015, 108, 430–439. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Verma, A.K.; Saini, I.; Saini, B.S. The baseline wandering noise removal from ECG signal using forward–backward Riemann Liouville fractional integral-based empirical wavelet transform approach. Int. J. Wavelets Multiresolut. Inf. Process. 2018, 16, 1850049. [Google Scholar] [CrossRef]
- Sanyal, A.; Baral, A.; Lahiri, A. Application of Framelet Transform in Filtering Baseline Drift from ECG Signals. Procedia Technol. 2012, 4, 862–866. [Google Scholar] [CrossRef]
- Anu, S.; Harjit, S.; Anureet, K. QRS detection of ECG signal using hybrid derivative and MaMeMi filter by effectively eliminating the baseline wander. Analog Integr. Circ. Signal Process. 2018, 98, 1–9. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, K.H.; Lee, J.W.; Kim, K.S. Semi-real-time removal of baseline fluctuations in electrocardiogram (ECG) signals by an infinite impulse response low-pass filter (IIR-LPF. J. Supercomp. 2018, 74, 6785–6793. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, L. Denoising of MEMS Vector Hydrophone Signal Based on Empirical Model Wavelet Method. Proceedings 2019, 15, 11. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Liu, Z.; Yan, Z.; Jiao, L.; Wang, D.; Wang, J. EEMD-based online milling chatter detection by fractal dimension and power spectral entropy. Int. J. Adv. Manuf. Technol. 2017, 92, 1185–1200. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Schevill, W.A.; Schevill, W.E. Aerial Observation of Feeding Behavior in Four Baleen Whales: Eubalaena glacialis, Balaenoptera borealis, Megaptera novaeangliae, and Balaenoptera physalus. J. Mammal. 1979, 60, 155–163. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simmulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Urick, R.; Kuperman, W.A. Ambient Noise in the Sea. J. Acoust. Soc. Am. 1998, 86, 19–47. [Google Scholar] [CrossRef]
- Huang, G.; Li, Z.; Wu, S.; Xue, C.; Yang, S.; Zhang, W. A Bionic Fish Cilia Median-Low Frequency Three-Dimensional Piezoresistive MEMS Vector Hydrophone. Nano-Micro Lett. 2014, 6, 136–142. [Google Scholar] [CrossRef]




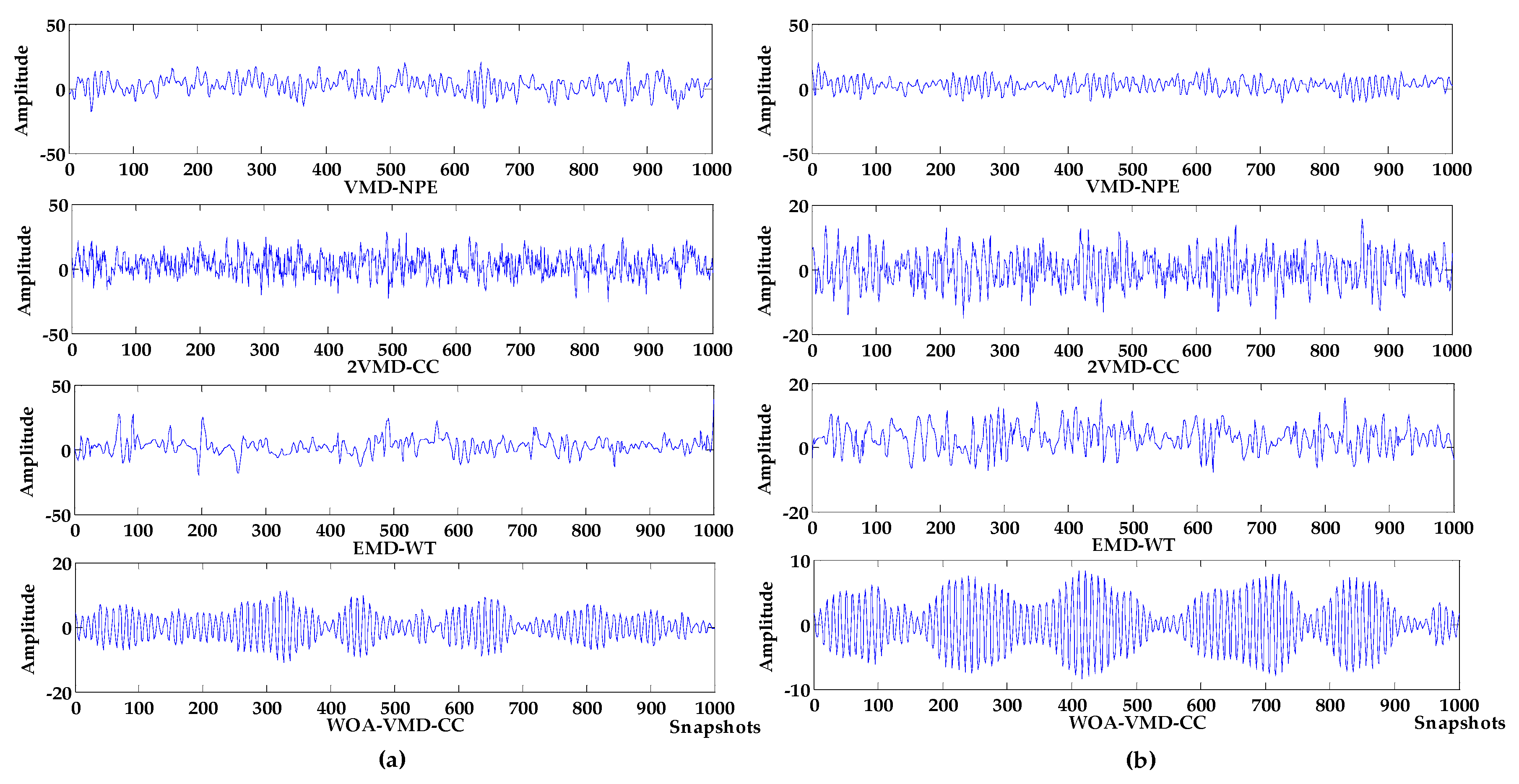
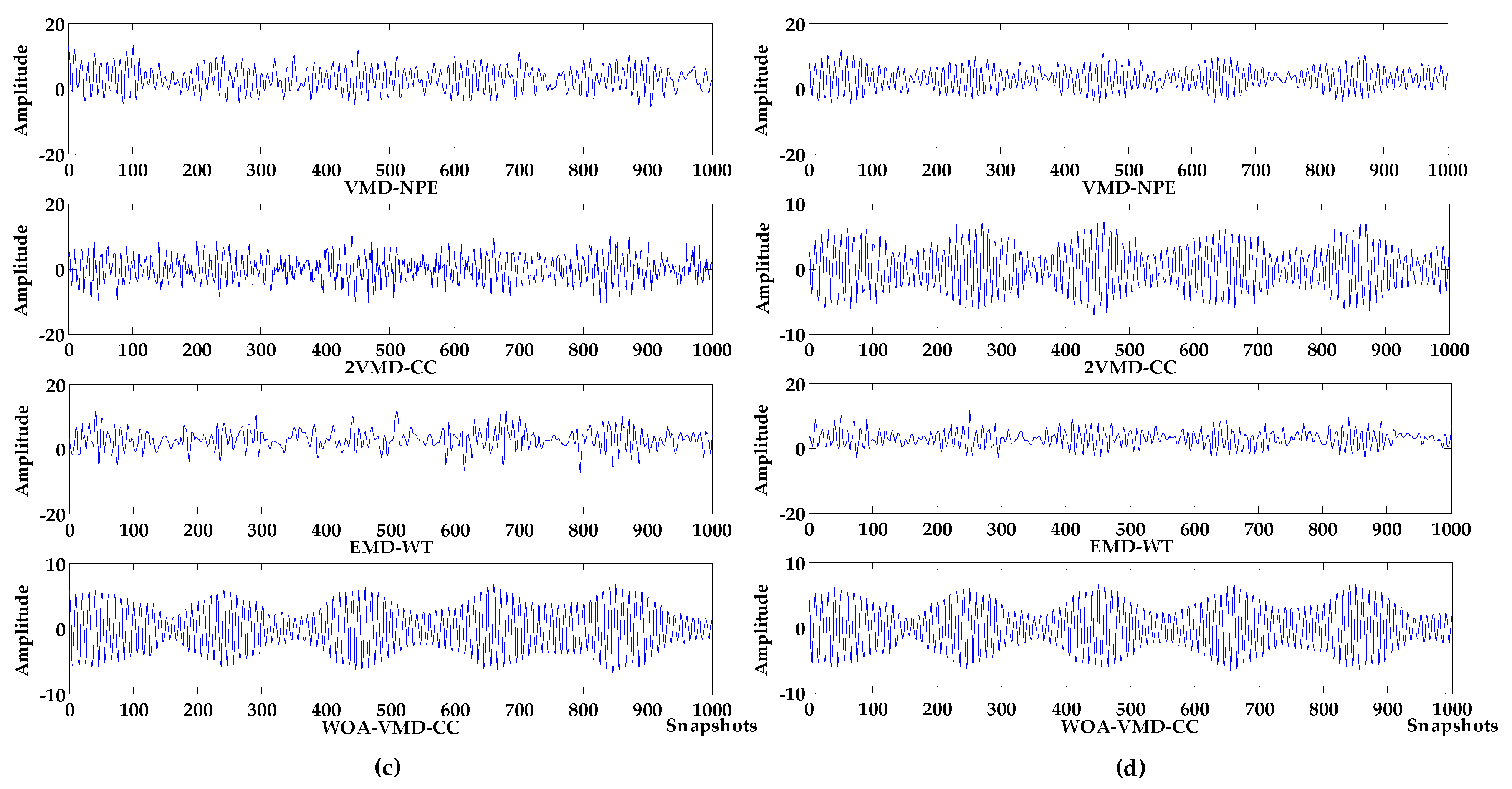

| Index | Input Signal | VMD-NPE | 2VMD-CC | EMD-WT | WOA-VMD-CC | LSF-WST | SGSF-WST |
|---|---|---|---|---|---|---|---|
| SNR | 5.8810 | 9.3281 | 9.4184 | 7.8212 | 18.5693 | 8.5445 | 8.5935 |
| RMSE | 1.6560 | 1.5796 | 0.4782 | 1.6382 | 0.1667 | 0.5288 | 0.5030 |
| Index | VMD-NPE | WOA-VMD-NPE | 2VMD-CC | WOA-2VMD-CC | WOA-VMD-CC |
|---|---|---|---|---|---|
| SNR | 9.3281 | 10.7579 | 9.4184 | 17.0467 | 18.5693 |
| RMSE | 1.5796 | 1.5480 | 0.4782 | 0.1987 | 0.1667 |
| Noise | Index | Input Signal | VMD-NPE | 2VMD-CC | EMD-WT | WOA-VMD-CC | LSF-WST | SGSF-WST |
|---|---|---|---|---|---|---|---|---|
| −10 db | SNR | −12.9540 | −5.4163 | −8.3212 | −6.1719 | 1.3264 | −7.1079 | −7.9754 |
| RMSE | 13.6503 | 6.0592 | 8.3504 | 6.7044 | 2.5752 | 6.8001 | 7.5148 | |
| −5 db | SNR | −7.9970 | −1.6381 | −2.5925 | −1.9593 | 5.8786 | −1.4992 | −2.6494 |
| RMSE | 8.0206 | 4.5489 | 4.0434 | 4.7587 | 1.5247 | 3.5635 | 4.0707 | |
| 0 db | SNR | −2.9637 | 3.2030 | 1.9962 | 1.6200 | 12.3969 | 2.0547 | 2.0923 |
| RMSE | 5.1673 | 3.6328 | 2.3840 | 3.8343 | 0.7199 | 2.3680 | 2.3585 | |
| 5 db | SNR | 2.0469 | 8.7231 | 11.0416 | 4.9440 | 15.1702 | 6.1727 | 6.4195 |
| RMSE | 3.8618 | 3.2409 | 0.8415 | 3.4430 | 0.5231 | 1.4740 | 1.4328 |
| Noise | Index | Input Signal | LSF-WOA-VMD-CC | SGSF-WOA-VMD-CC | WOA-VMD-CC |
|---|---|---|---|---|---|
| 5db | SNR | 2.0469 | 11.5326 | 13.3392 | 15.1702 |
| RMSE | 3.8618 | 0.7952 | 0.6459 | 0.5231 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Xu, T.; Wang, P.; Zhang, L.; Hu, H.; Bai, Y. MEMS Hydrophone Signal Denoising and Baseline Drift Removal Algorithm Based on Parameter-Optimized Variational Mode Decomposition and Correlation Coefficient. Sensors 2019, 19, 4622. https://doi.org/10.3390/s19214622
Yan H, Xu T, Wang P, Zhang L, Hu H, Bai Y. MEMS Hydrophone Signal Denoising and Baseline Drift Removal Algorithm Based on Parameter-Optimized Variational Mode Decomposition and Correlation Coefficient. Sensors. 2019; 19(21):4622. https://doi.org/10.3390/s19214622
Chicago/Turabian StyleYan, Huichao, Ting Xu, Peng Wang, Linmei Zhang, Hongping Hu, and Yanping Bai. 2019. "MEMS Hydrophone Signal Denoising and Baseline Drift Removal Algorithm Based on Parameter-Optimized Variational Mode Decomposition and Correlation Coefficient" Sensors 19, no. 21: 4622. https://doi.org/10.3390/s19214622
APA StyleYan, H., Xu, T., Wang, P., Zhang, L., Hu, H., & Bai, Y. (2019). MEMS Hydrophone Signal Denoising and Baseline Drift Removal Algorithm Based on Parameter-Optimized Variational Mode Decomposition and Correlation Coefficient. Sensors, 19(21), 4622. https://doi.org/10.3390/s19214622





