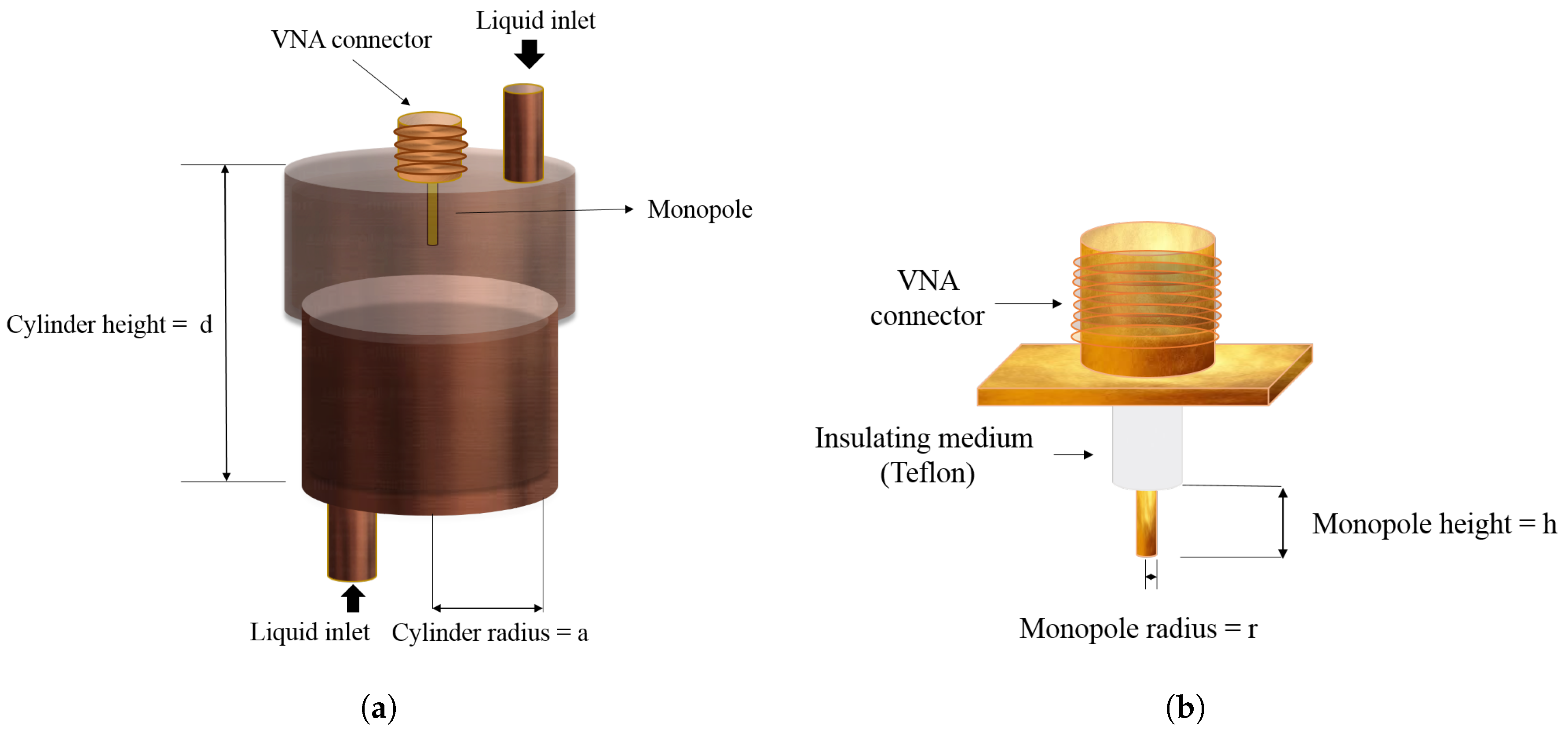
4.1. Sensor Fabrication and Experimental Setup
The proposed cylindrical cavity sensor is fabricated using conductive copper cylinder of inner radius (
a) 19.2 mm and height (
d) 35 mm. The height
h of the probe is set to 8 mm, which is equal to one-quarter of the wavelength of frequency 7.119 GHz, making the input impedance nearly equivalent to that of an open circuit. The dimensions of coupling probe are 0.5 mm × 8 mm, and it is wrapped with Teflon with radius size of 3 mm as shown in
Figure 7b. The manufactured sensor is shown in
Figure 7a. In this model, a coupling probe of height
h and radius
r is designed by extending the feeding coaxial cable, with a small distance, into the cylindrical cavity sensor and fixing at the bottom center.
The experimental set-up consists of a cylindrical cavity resonator with monopole, VNA, external pump, thermostatic bathing, cable, capillary tubes, and gasoline samples. The cylindrical cavity sensor is connected through a connector to supply microwave signals and to allow measurements to be taken using a calibrated series network analyzer VNA (100 KHz–8.5 GHz E5063A, KEYSIGHT) via a 50 Ω coaxial cable. The gasoline solutions are introduced in the cavity via a thermoplastic capillary. In particular, the capillary is connected to an external pump via tube fittings, so that a continuous gasoline flow is created and no air bubbles are formed in the capillary. A thermostatic bath and thermometer are used to control and monitor the temperature of gasoline samples as shown in
Figure 8b. The experimental setup described above is shown in
Figure 8a with gasoline bottles with different permittivities and microwave cavity sensor.
4.2. Results and Discussion
Two important properties of dielectric materials are complex permittivity
and loss tangent
. The real part,
, of
is the permittivity (i.e., product of the free space permittivity
and the relative real/absolute permittivity
) quantifying the stored energy within the medium and the imaginary part
represents dielectric loss factor related to the dissipation of energy within the medium. The ratio
quantifies the loss of power due to the propagation in a conductor. To analyze this loss of power, we performed experiments with the proposed sensor on gasoline samples with different permittivities as shown in
Figure 9 using
Table 5. The complex permittivity values were measured using N1501A permittivity measuring kit. The temperature of 20 °C was chosen as the proposed sensor is designed at the same temperature and also the N1501A kit can measure permittivity only from 0 to 120 degrees.
The permittivity of a solution changes with change in temperature, which in turn changes the resonant frequency. However, the effects are relatively small for hydrocarbon lubrication oils. The typical decrease in permittivity for hydrocarbon oils is about 0.0013 to 0.05 percent per degree Celsius [
27]. To verify this relationship and to analyze the ability of the proposed sensor for various gasoline samples in cold condition, we evaluated the sensor response as shown in
Figure 10. The temperature range of 0 °C to −35 °C was chosen for the cold condition, and the measurements were made with the help of thermostatic bath. In
Figure 10, small and linear change in resonant frequencies according to the temperature variation can be observed. The minimum frequency separation of 31 MHz lies between Euro4 and Cold CO at 0 °C temperature. The resonant frequency shifts towards a slightly higher value with the rise in temperature for Euro4, Cold CO, and Tier2. For Tier3 and LEV3, the resonant frequency shifts slightly to a lower value, as these two gasoline samples have higher percentages of ethanol and the ethanol tends to have low permittivity at higher temperatures [
28]. Nonetheless, the performance of the proposed sensor is almost the same which confirms the robustness of the sensor with temperature changes.
Using optimized parameters, we performed full wave analysis of the proposed sensor, using HFSS for the frequency range of 6.5 GHz to 7.5 GHz under different temperature conditions. By sweeping frequency from 6.5 GHz to 7.5 GHz, we achieved reflection coefficient for LEV3, Tier3, Euro4, Cold CO, and Tier2 at −35 °C to 0 °C temperatures, as shown in
Figure 11a,b, respectively. The proposed sensor fulfills the requirement of large frequency separations between different samples making it sensitive towards small changes in permittivity of a given sample. The gasoline sample, Tier2 shows minimum reflection coefficient at −35 °C with −63.64 dB dip at a resonant frequency of 7.15 GHz. In
Table 6, the frequency separations of close resonant peaks are listed. At higher temperatures, the resonant frequency increases. Higher temperatures increase the activity of electrons and reduce the relative permittivity of fuels; thus, resonant frequency as well as reflection coefficient increases. Here, note that the fuel with lower permittivity has higher resonant frequency and vice versa, i.e., Tier 2 as the fuel with the lower permittivity and LEV 3 as the fuel with higher permittivity. These results reveal that the proposed cylindrical cavity sensor is still very sensitive to distinguish normal and HiDI gasoline under different temperature conditions.
The relationship between permittivity of the different gasoline samples and resonant frequency is shown in
Figure 12a, where curve 1 shows theoretical values and curve 2 shows experimental values. The resonant frequencies of theoretical data are slightly higher than experimental values. The qualitative analysis of
Figure 12a suggests that resonant frequency decreases monotonically with increase in permittivity in both curves. The experimental results are in agreement with that of theoretical results. Now, to perform quantitative analysis of the given data, we define percentage error as follows; Percentage Error = |Experimental values − Theoretical|/Experimental values × 100.
Figure 12b represents the percentage error between the theoretical and experimental values of resonance frequencies for various gasoline samples with different permittivity. The overall error is below 1.7%, which confirms the accuracy of the proposed sensor.
All the measurements were repeated five times with the same sample, and their average value was considered. Samples with different dielectric constants in experimental measurements show various quality factors. However, as the repeated measurement error of all samples is 0.5 MHz, which is smaller than the minimum resonant frequency difference 29 MHz between samples, it is possible to distinguish between different samples even considering LEV3 with a lower quality factor.
Finally, we have performed a comparison of our proposed method with the capacitor method, which is one of the DI measurement method presented in [
5]. The results are summarized in
Table 7. The sensitivities of the proposed sensor are achieved by taking the ratio of difference in resonant frequencies (fr) of the samples to the difference in DI values and listed in
Table 7a. Similarly, sensitivities of the sensor in [
5] were calculated by taking the ratio of voltage difference of the samples to the difference in DI values, and they are listed in
Table 7b. It can be seen that the proposed sensor is better in terms of sensitivity to DI.