ACK-MSCKF: Tightly-Coupled Ackermann Multi-State Constraint Kalman Filter for Autonomous Vehicle Localization
Abstract
:1. Introduction
2. The Proposed Approach
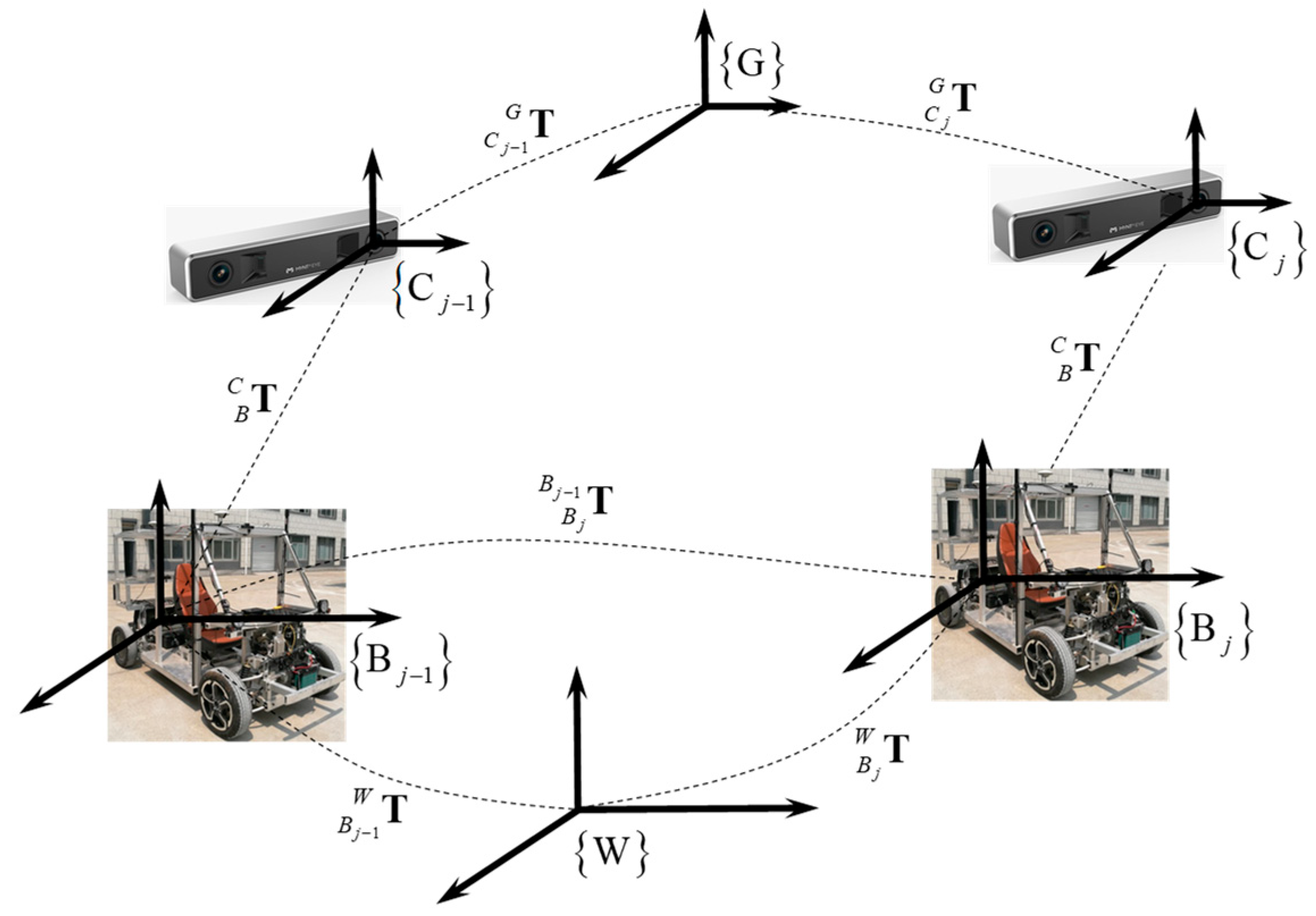
2.1. Coordinate Systems and Notations
2.2. Process Model and State Augmentation
2.3. Measurement Model
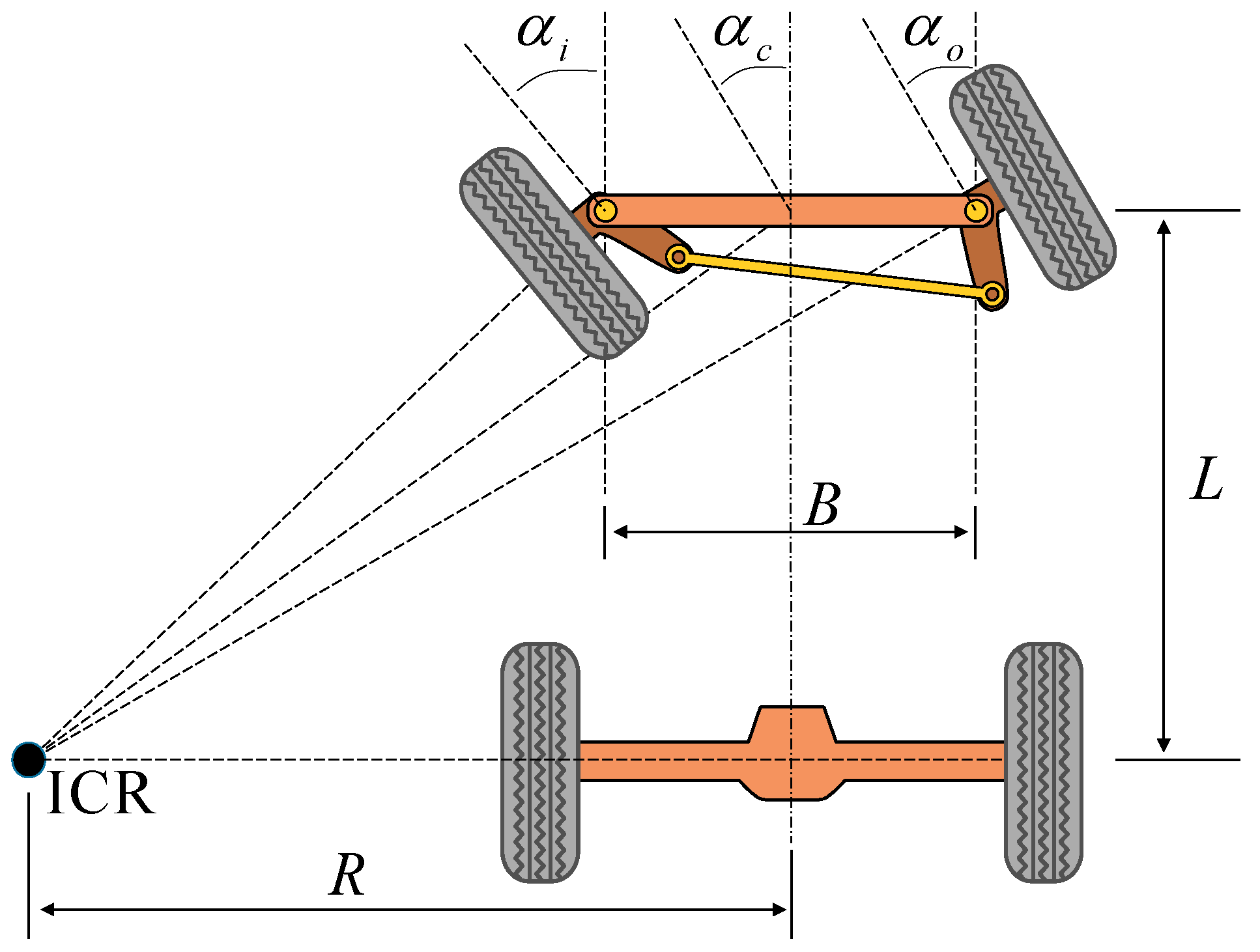
2.3.1. Vehicle Relative Rotation and Translation Estimation
2.3.2. Ackermann Error State Measurements
2.3.3. Visual Measurements
2.4. Extrinsic Parameters Calibration
3. Experiments and Results
3.1. Experimental Vehicle Setup
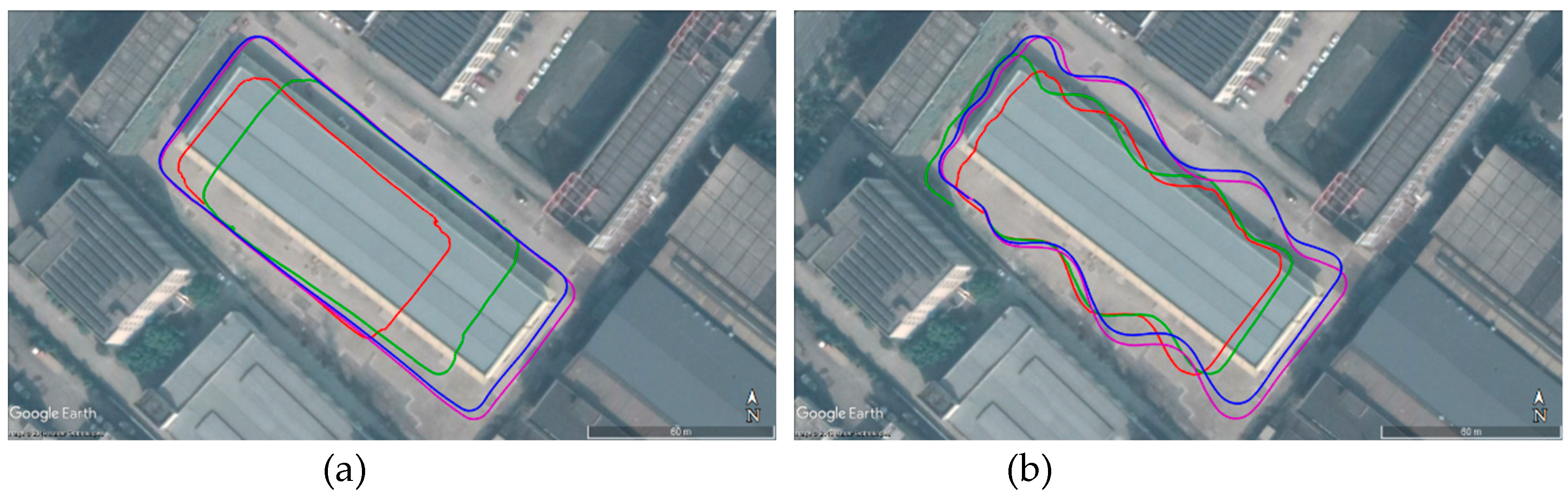
3.2. Experimental Results
3.2.1. Extrinsic Parameters Calibration Performance
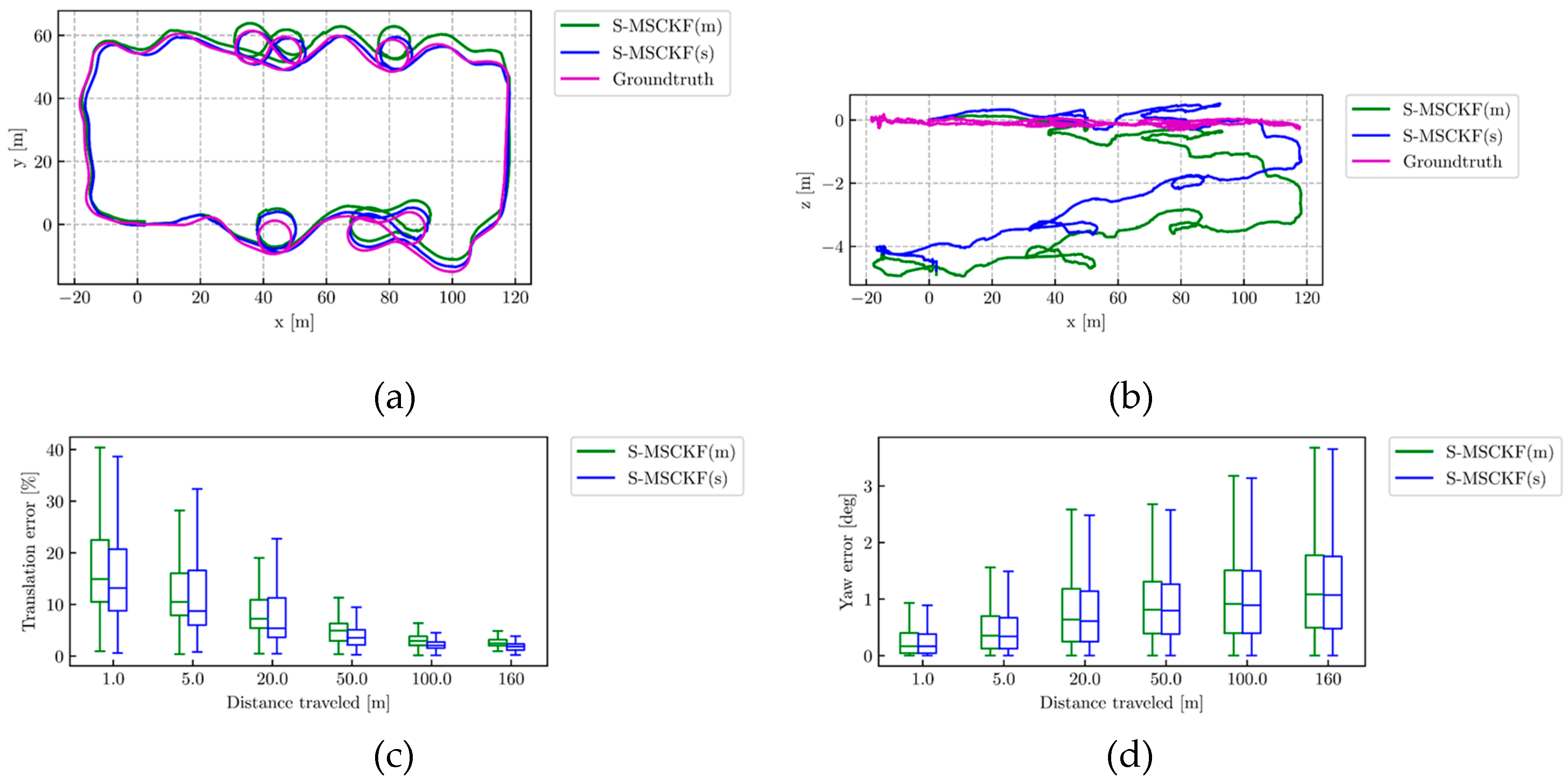
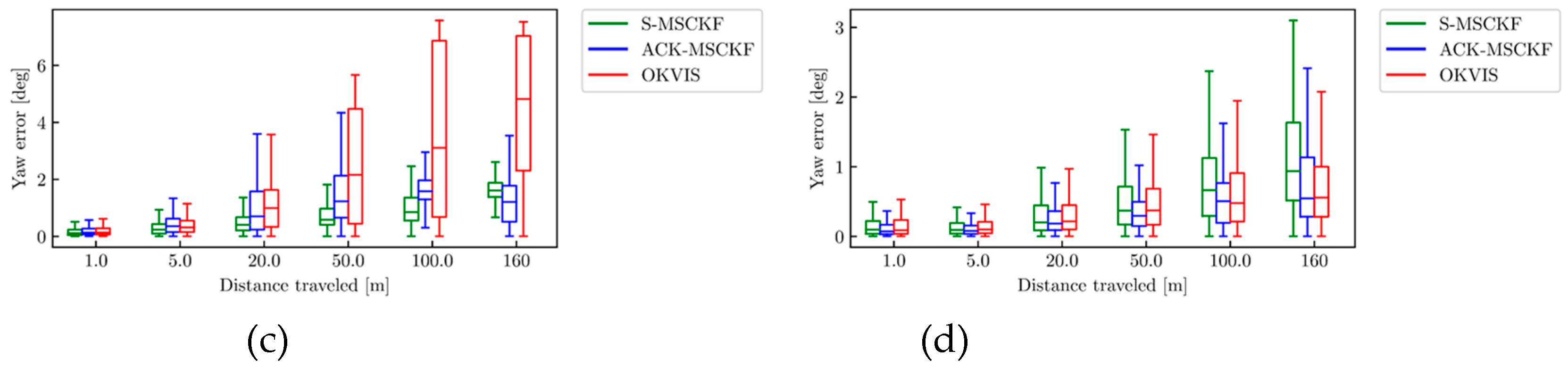
3.2.2. ACK-MSCKF Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, K.; Li, S.E.; Kum, D. Synthesis of Robust Lane Keeping Systems: Impact of Controller and Design Parameters on System Performance. IEEE Trans. Intell. Transport. Syst. 2018, 20, 3129–3141. [Google Scholar] [CrossRef]
- Lee, K.; Chung, W.; Yoo, K. Kinematic parameter calibration of a car-like mobile robot to improve odometry accuracy. Mechatronics 2010, 20, 582–595. [Google Scholar] [CrossRef]
- Toledo, J.; Piñeiro, J.; Arnay, R.; Acosta, D.; Acosta, L. Improving odometric accuracy for an autonomous electric cart. Sensors 2018, 18, 200. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Xue, H.; Fu, H.; Dai, B. IMU-Aided High-Frequency Lidar Odometry for Autonomous Driving. Appl. Sci. 2019, 9, 1506. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Visual-lidar odometry and mapping: Low-drift, robust, and fast. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2174–2181. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. SVO: Semidirect visual odometry for monocular and multicamera systems. IEEE Trans. Robot. 2017, 33, 249–265. [Google Scholar] [CrossRef]
- Younes, G.; Asmar, D.; Shammas, E.; Zelek, J. Keyframe-based monocular SLAM: Design, survey, and future directions. Robot. Auton. Syst. 2017, 98, 67–88. [Google Scholar] [CrossRef]
- Aqel, M.O.A.; Marhaban, M.H.; Saripan, M.I.; Ismail, N.B. Review of visual odometry: Types, approaches, challenges, and applications. Springerplus 2016, 5, 1897. [Google Scholar] [CrossRef]
- Saputra, M.R.U.; Markham, A.; Trigoni, N. Visual SLAM and Structure from Motion in Dynamic Environments: A Survey. ACM Comput. Surv. 2018, 51, 37. [Google Scholar] [CrossRef]
- Aladem, M.; Rawashdeh, S. Lightweight visual odometry for autonomous mobile robots. Sensors 2018, 18, 2837. [Google Scholar] [CrossRef] [PubMed]
- Huang, G. Visual-inertial navigation: A concise review. arXiv 2019, arXiv:1906.02650. [Google Scholar]
- Gui, J.; Gu, D.; Wang, S.; Hu, H. A review of visual inertial odometry from filtering and optimisation perspectives. Adv. Robot. 2015, 29, 1289–1301. [Google Scholar] [CrossRef]
- Mur-Artal, R.; TardÓs, J.D. Visual-Inertial Monocular SLAM with Map Reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Von Stumberg, L.; Usenko, V.; Cremers, D. Direct sparse visual-inertial odometry using dynamic marginalization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2510–2517. [Google Scholar]
- Ramezani, M.; Khoshelham, K. Vehicle Positioning in GNSS-Deprived Urban Areas by Stereo Visual-Inertial Odometry. IEEE Trans. Intell. Veh. 2018, 3, 208–217. [Google Scholar] [CrossRef]
- Mourikis, A.I.; Roumeliotis, S.I. A multi-state constraint Kalman filter for vision-aided inertial navigation. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar]
- Lynen, S.; Achtelik, M.W.; Weiss, S.; Chli, M.; Siegwart, R. A robust and modular multi-sensor fusion approach applied to MAV navigation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3923–3929. [Google Scholar]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust stereo visual inertial odometry for fast autonomous flight. IEEE Robot. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef]
- Huai, Z.; Huang, G. Robocentric visual-inertial odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6319–6326. [Google Scholar]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual–inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2014, 34, 314–334. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Zhao, J.; Guo, Y.; He, W.; Yuan, K. Pl-vio: Tightly-coupled monocular visual-inertial odometry using point and line features. Sensors 2018, 18, 1159. [Google Scholar] [CrossRef]
- Usenko, V.; Demmel, N.; Schubert, D.; Stückler, J.; Cremers, D. Visual-Inertial Mapping with Non-Linear Factor Recovery. arXiv 2019, arXiv:1904.06504. [Google Scholar]
- Delmerico, J.; Scaramuzza, D. A benchmark comparison of monocular visual-inertial odometry algorithms for flying robots. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2502–2509. [Google Scholar]
- Wu, M.; Lam, S.; Srikanthan, T. A Framework for Fast and Robust Visual Odometry. IEEE Trans. Intell. Transport. Syst. 2017, 18, 3433–3448. [Google Scholar] [CrossRef]
- Wu, K.J.; Roumeliotis, S.I. Unobservable Directions of VINS under Special Motions; Department of Computer Science & Engineering, University of Minnesota: Minneapolis, MN, USA, 2016. [Google Scholar]
- Shan, Z.; Li, R.; Schwertfeger, S. RGBD-Inertial Trajectory Estimation and Mapping for Ground Robots. Sensors 2019, 19, 2251. [Google Scholar] [CrossRef] [PubMed]
- Schmid, K.; Tomic, T.; Ruess, F.; Hirschmüller, H.; Suppa, M. Stereo vision based indoor/outdoor navigation for flying robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3955–3962. [Google Scholar]
- Zheng, F.; Liu, Y.H. SE(2)-Constrained Visual Inertial Fusion for Ground Vehicles. IEEE Sens. J. 2018, 18, 9699–9707. [Google Scholar] [CrossRef]
- Wu, K.J.; Guo, C.X.; Georgiou, G.; Roumeliotis, S.I. Vins on wheels. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5155–5162. [Google Scholar]
- Dang, Z.; Wang, T.; Pang, F. Tightly-coupled Data Fusion of VINS and Odometer Based on Wheel Slip Estimation. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1613–1619. [Google Scholar]
- Hong, E.; Lim, J. Visual-Inertial Odometry with Robust Initialization and Online Scale Estimation. Sensors 2018, 18, 4287. [Google Scholar] [CrossRef] [PubMed]
- Houseago, C.; Bloesch, M.; Leutenegger, S. KO-Fusion: Dense Visual SLAM with Tightly-Coupled Kinematic and Odometric Tracking. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Huskić, G.; Buck, S.; Zell, A. GeRoNa: Generic Robot Navigation. J. Intell. Robot. Syst. 2018, 95, 419–442. [Google Scholar] [CrossRef]
- ACK-MSCKF ROS Package. Available online: https://github.com/qdensh/ACK-MSCKF (accessed on 8 October 2019).
- Breckenridge, W.G. Quaternions proposed standard conventions. Jet Propuls. Lab. Pasadena CA Interoff. Memo. IOM 1999, 343–379. [Google Scholar]
- Trawny, N.; Roumeliotis, S.I. Indirect Kalman filter for 3D attitude estimation. Univ. Minn. Dept. Comp. Sci. Eng. Tech. Rep 2005, 2, 2005. [Google Scholar] [CrossRef]
- Sola, J. Quaternion kinematics for the error-state Kalman filter. arXiv 2017, arXiv:1711.02508. [Google Scholar]
- Scaramuzza, D.; Fraundorfer, F.; Pollefeys, M.; Siegwart, R. Absolute scale in structure from motion from a single vehicle mounted camera by exploiting nonholonomic constraints. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1413–1419. [Google Scholar] [Green Version]
- Kevin, M.L.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Marín, L.; Vallés, M.; Soriano, Á.; Valera, Á.; Albertos, P. Multi sensor fusion framework for indoor-outdoor localization of limited resource mobile robots. Sensors 2013, 13, 14133–14160. [Google Scholar] [CrossRef]
- Furgale, P.; Rehder, J.; Siegwart, R. Unified temporal and spatial calibration for multi-sensor systems. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1280–1286. [Google Scholar]
- Choi, S.; Park, J.; Yu, W. Simplified epipolar geometry for real-time monocular visual odometry on roads. Int. J. Control Autom. Syst. 2015, 13, 1454–1464. [Google Scholar] [CrossRef]
- Yang, Z.; Shen, S. Monocular visual-inertial state estimation with online initialization and camera-IMU extrinsic calibration. IEEE Trans. Autom. Sci. Eng. 2016, 14, 39–51. [Google Scholar] [CrossRef]
- Markley, F.L.; Cheng, Y.; Crassidis, J.L.; Oshman, Y. Averaging Quaternions. J. Guid. Control Dyn. 2007, 30, 1193–1197. [Google Scholar] [CrossRef]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.W.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 1157–1163. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Pfrommer, B.; Sanket, N.; Daniilidis, K.; Cleveland, J. Penncosyvio: A challenging visual inertial odometry benchmark. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3847–3854. [Google Scholar]
- Zhang, Z.; Scaramuzza, D. A tutorial on quantitative trajectory evaluation for visual (-inertial) odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7244–7251. [Google Scholar]
- Kaess, M.; Ranganathan, A.; Dellaert, F. ISAM: Incremental Smoothing and Mapping. IEEE Trans. Robot. 2008, 24, 1365–1378. [Google Scholar] [CrossRef]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.J.; Dellaert, F. ISAM2: Incremental smoothing and mapping using the Bayes tree. Int. J. Robot. Res. 2012, 31, 216–235. [Google Scholar] [CrossRef]
- Liu, H.; Chen, M.; Zhang, G.; Bao, H.; Bao, Y. Ice-ba: Incremental, consistent and efficient bundle adjustment for visual-inertial slam. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1974–1982. [Google Scholar]
- Li, X.; Wang, Y.; Khoshelham, K. Comparative analysis of robust extended Kalman filter and incremental smoothing for UWB/PDR fusion positioning in NLOS environments. Acta Geod. Geophys. 2019, 54, 157–179. [Google Scholar] [CrossRef]







| Dataset | Vehicle Driving Cycles | Environmental Condition | Duration (s) | Data Bulk | |||
|---|---|---|---|---|---|---|---|
| Vehicle CAN-Bus | Stereo Images | IMU | Ground Truth | ||||
| AM_01 | Straight | High-light | 151 | 24,171 | 4532 | 30,164 | 30,244 |
| AM_02 | Slalom | Motion blur | 170 | 27,135 | 5099 | 33,933 | 34,025 |
| AM_03 | Free | Low-light | 131 | 17,387 | 3930 | 26,258 | 13,111 |
| AM_04 | Free | Dynamic objects | 493 | 65,147 | 14,801 | 98,651 | 49,291 |
| AM_05 | Free | High-light | 238 | 38,020 | 7136 | 47,439 | 47,583 |
| Methods | RMSE (m) |
|---|---|
| S-MSCKF(s) | 3.05 |
| S-MSCKF(m) | 4.21 |
| Sub-trajectory Length (m) | Relative Translation Error (m) | Relative Yaw Error (deg) | ||
|---|---|---|---|---|
| S-MSCKF(s) | S-MSCKF(m) | S-MSCKF(s) | S-MSCKF(m) | |
| 1 | 0.17 | 0.19 | 0.25 | 0.27 |
| 5 | 0.61 | 0.67 | 0.46 | 0.48 |
| 20 | 1.56 | 1.76 | 0.76 | 0.79 |
| 50 | 1.94 | 2.39 | 0.91 | 0.93 |
| 100 | 2.20 | 2.96 | 1.00 | 1.02 |
| 160 | 2.97 | 4.14 | 1.18 | 1.20 |
| Methods | AM_01 (m) | AM_02 (m) | AM_03 (m) | AM_04 (m) |
|---|---|---|---|---|
| ACK-MSCKF | 2.25 | 3.43 | 1.57 | 5.13 |
| S-MSCKF | 15.24 | 12.26 | 5.23 | 21.66 |
| OKVIS | 24.62 | 13.01 | 9.68 | 13.63 |
| Sub-trajectory Length (m) | Relative Translation Error (m) | Relative Yaw Error (deg) | ||||
|---|---|---|---|---|---|---|
| ACK-MSCKF | S-MSCKF | OKVIS | ACK-MSCKF | S-MSCKF | OKVIS | |
| 1 | 0.25 | 0.41 | 0.46 | 0.14 | 0.15 | 0.36 |
| 5 | 0.34 | 0.75 | 0.80 | 0.21 | 0.20 | 0.41 |
| 20 | 0.97 | 2.48 | 2.65 | 0.43 | 0.39 | 0.68 |
| 50 | 1.85 | 4.99 | 5.88 | 0.59 | 0.55 | 0.87 |
| 100 | 2.99 | 7.70 | 9.99 | 0.74 | 0.78 | 1.11 |
| 160 | 4.18 | 10.41 | 12.94 | 0.80 | 1.04 | 1.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Shi, J.; Yang, Y.; Li, J.; Dai, K. ACK-MSCKF: Tightly-Coupled Ackermann Multi-State Constraint Kalman Filter for Autonomous Vehicle Localization. Sensors 2019, 19, 4816. https://doi.org/10.3390/s19214816
Ma F, Shi J, Yang Y, Li J, Dai K. ACK-MSCKF: Tightly-Coupled Ackermann Multi-State Constraint Kalman Filter for Autonomous Vehicle Localization. Sensors. 2019; 19(21):4816. https://doi.org/10.3390/s19214816
Chicago/Turabian StyleMa, Fangwu, Jinzhu Shi, Yu Yang, Jinhang Li, and Kai Dai. 2019. "ACK-MSCKF: Tightly-Coupled Ackermann Multi-State Constraint Kalman Filter for Autonomous Vehicle Localization" Sensors 19, no. 21: 4816. https://doi.org/10.3390/s19214816
APA StyleMa, F., Shi, J., Yang, Y., Li, J., & Dai, K. (2019). ACK-MSCKF: Tightly-Coupled Ackermann Multi-State Constraint Kalman Filter for Autonomous Vehicle Localization. Sensors, 19(21), 4816. https://doi.org/10.3390/s19214816





