Distorted Building Image Matching with Automatic Viewpoint Rectification and Fusion
Abstract
:1. Introduction
2. Materials and Methods
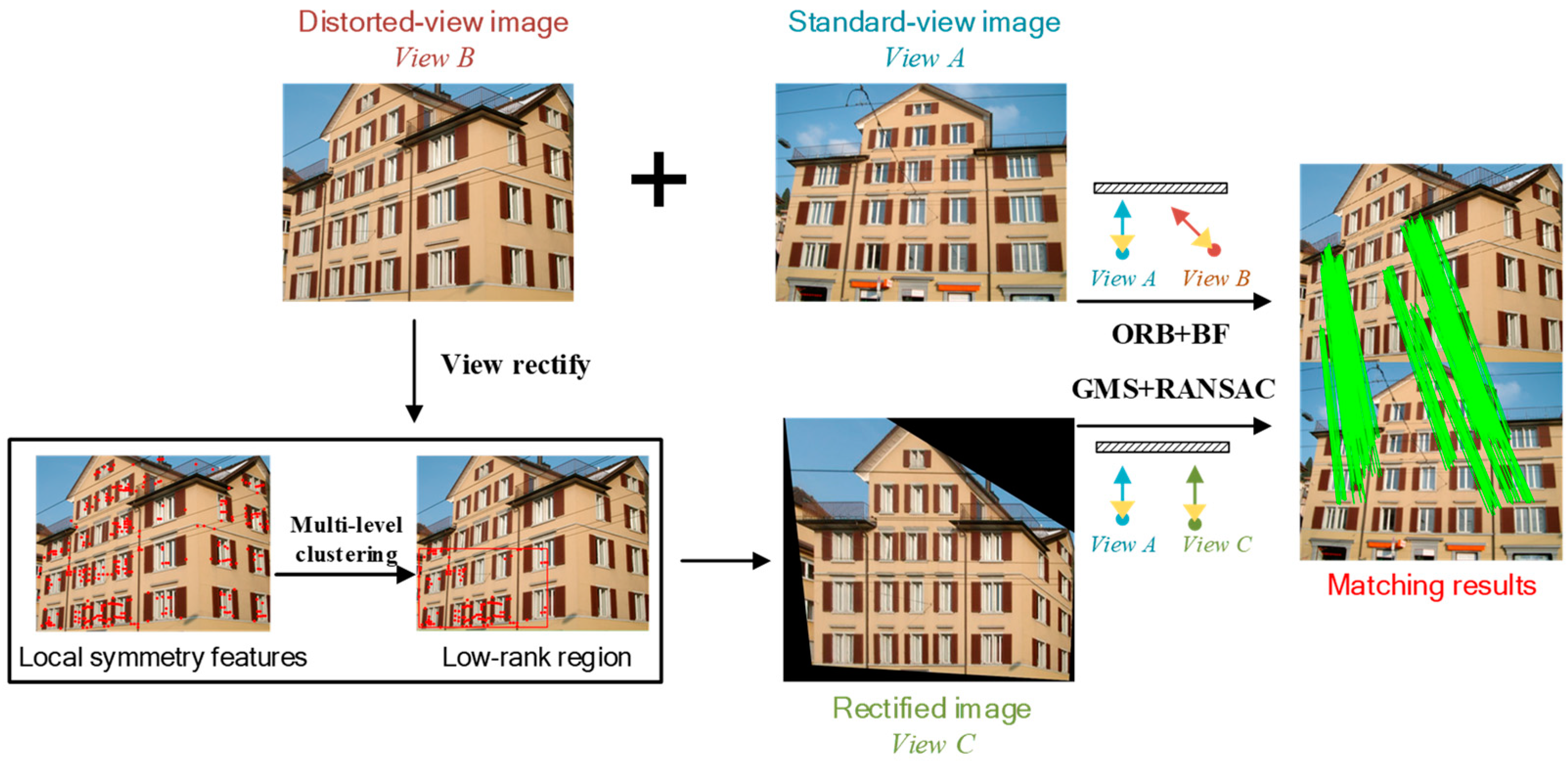
2.1. Viewpoint Rectification with Automatic Low-Rank Texture Recovery
2.1.1. Low-Rank Texture Recovery
2.1.2. Automatic Low-Rank Texture Extraction
- (i)
- Use mean shift to cluster the initial detected local symmetry feature points, and sort the clusters by the feature density.
- (ii)
- Select the feature cluster with the highest density as the primary cluster for the extraction of the low-rank texture regions, and the others are considered to be the candidates. The textural characteristics of the building facades determine the number of candidate clusters. In this paper, we classify the texture of the building facades into two categories, depending on whether there are dividing units between the windows, as shown in Figure 4. For the case where spaces exist between the windows (Figure 4a), is selected as the candidate cluster, which is because the dividing space would prevent the shift of the cluster centers. It is unnecessary to use candidate units for the latter (Figure 4b) case with no evident dividing units between the windows.
- (iii)
- For the selected feature points in the first-level clustering, there might be remaining discrete noise points. Thus, a mean shift is applied again to the obtained primary and subordinate clusters, respectively. In this step, threshold is set to constrain the second-level clustering procedure. As a result, only the top-two dense clusters with more than 10 feature points are counted, referring to , where and represent the serial number of the clusters in the first- and second-level clustering procedures.
- (iv)
- Furthermore, the candidate feature points are constrained with the bounding range of the primary cluster for the building facades with a non-rectangular 2D geometric shape, avoiding the candidate clusters of feature points located outside the range of the central low-rank texture region.
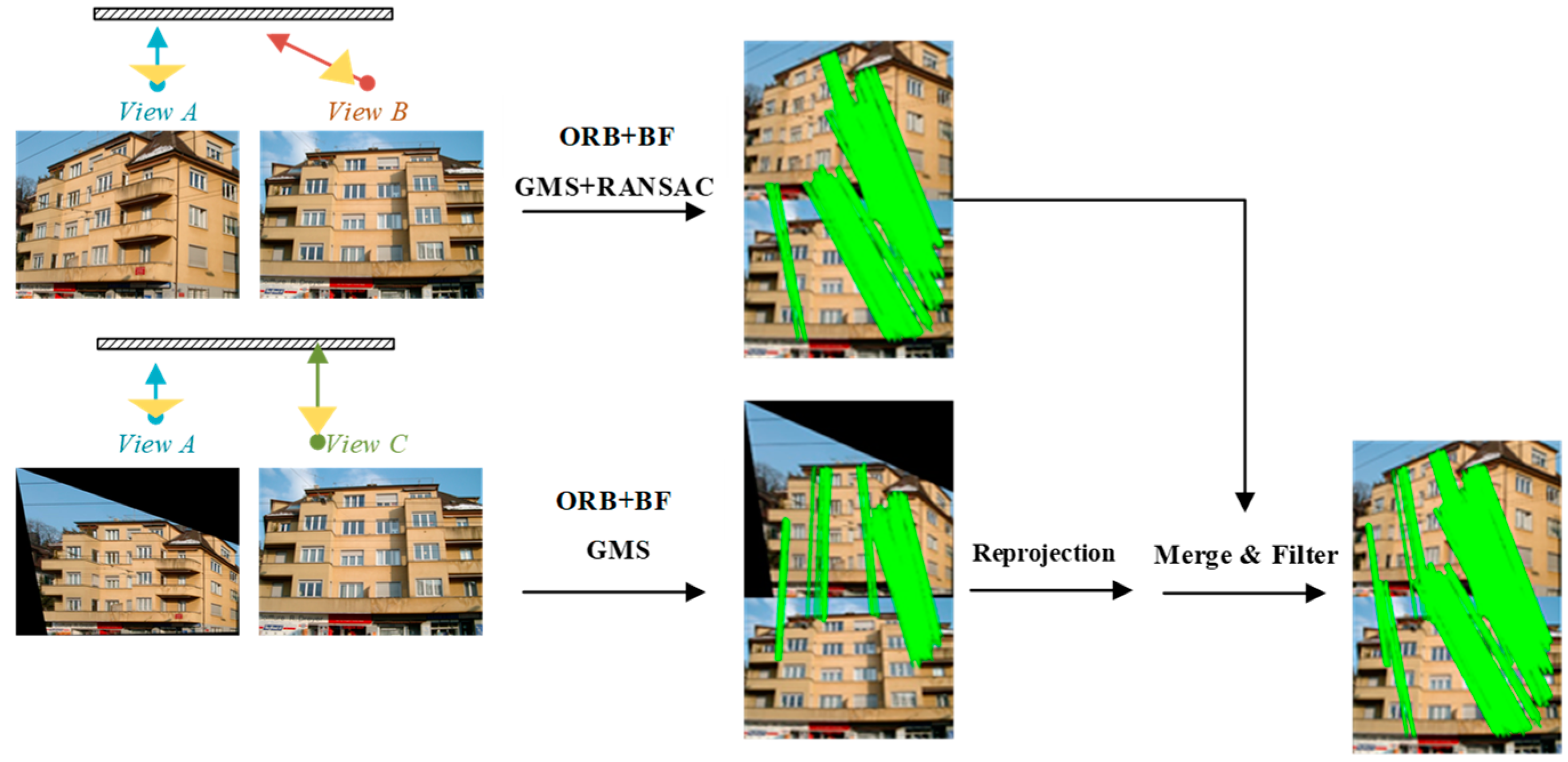
2.2. Image Matching and Viewpoint Fusion
2.2.1. Image Matching
2.2.2. Viewpoint Fusion for Image Dense Matching
3. Experiment Results
3.1. Data Preparation and Implementation
3.2. Results on ZuBud Dataset
3.2.1. Image Rectification
3.2.2. Matching Results
3.3. Results on Local Dataset
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Torii, A.; Sivic, J.; Pajdla, T. Visual localization by linear combination of image descriptors. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Xiang, T.; Xia, G.S.; Zhang, L. Image stitching with perspective-preserving warping. arXiv 2016, arXiv:1605.05019. [Google Scholar]
- Ma, W.; Xiong, H.; Dai, X.; Zheng, X.; Zhou, Y. An indoor scene recognition-based 3D registration mechanism for real-time AR-GIS visualization in mobile applications. ISPRS Int. J. Geo-Inf. 2018, 7, 112. [Google Scholar] [CrossRef]
- Verykokou, S.; Ioannidis, C. Automatic rough georeferencing of multiview oblique and vertical aerial image datasets of urban scenes. Photogr. Rec. 2016, 31, 281–303. [Google Scholar] [CrossRef]
- Sedaghat, A.; Ebadi, H. Remote sensing image matching based on adaptive binning SIFT descriptor. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5283–5293. [Google Scholar] [CrossRef]
- Baumberg, A. Reliable feature matching across widely separated views. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 15 June 2000. [Google Scholar]
- Tuytelaars, T.; Mikolajczyk, K. Local invariant feature detectors: A survey. Found. Trends Comput. Gr. Vis. 2008, 3, 177–280. [Google Scholar] [CrossRef]
- Ackermann, F. Digital image correlation: Performance and potential application in photogrammetry. Photogr. Rec. 1984, 11, 429–439. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogr. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Chen, M.; Qin, R.; He, H.; Zhu, Q.; Wang, X. A Local Distinctive Features Matching Method for Remote Sensing Images with Repetitive Patterns. Photogr. Eng. Remote Sens. 2018, 84, 513–524. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. An affine invariant interest point detector. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Mikolajczyk, K.; Schmid, C. Scale & affine invariant interest point detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar]
- Donoser, M.; Bischof, H. Efficient maximally stable extremal region (MSER) tracking. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the International Conference on Computer Vision Pattern Recognition, San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Chen, M.; Shao, Z.; Li, D.; Liu, J. Invariant matching method for different viewpoint angle images. Appl. Opt. 2013, 52, 96–104. [Google Scholar] [CrossRef] [PubMed]
- Morel, J.M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Cai, G.; Jodoin, P.; Li, S.; Wu, Y.; Su, S.; Huang, Z. Perspective-SIFT: An efficient tool for low-altitude remote sensing image registration. Signal Process. 2013, 93, 3088–3110. [Google Scholar] [CrossRef]
- Sicong, Y.; Qing, W.; Rongchun, Z. Robust wide baseline point matching based on scale invariant feature descriptor. Chin. J. Aeronaut. 2009, 22, 70–74. [Google Scholar] [CrossRef]
- Gao, X.; Hu, L.; Cui, H.; Shen, S.; Hu, Z. Accurate and efficient ground-to-aerial model alignment. Pattern Recogn. 2018, 76, 288–302. [Google Scholar] [CrossRef]
- Shan, Q.; Wu, C.; Curless, B.; Furukawa, Y.; Hernandez, C.; Seitz, S. Accurate geo-registration by ground-to-aerial image matching. In Proceedings of the 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014. [Google Scholar]
- Gao, X.; Shen, S.; Zhou, Y.; Cui, H.; Zhu, L.; Hu, Z. Ancient Chinese architecture 3D preservation by merging ground and aerial point clouds. ISPRS J. Photogr. Remote Sens. 2018, 143, 72–84. [Google Scholar] [CrossRef]
- Doubek, P.; Matas, J.; Perdoch, M.; Chum, O. Image matching and retrieval by repetitive patterns. In Proceedings of the 20th International Conference on Pattern Recognition, Washington, DC, USA, 23–26 August 2010. [Google Scholar]
- Bansal, M.; Daniilidis, K.; Sawhney, H. Ultrawide baseline facade matching for geo-localization. In Large-Scale Visual Geo-Localization; Springer: Berlin/Heidelberg, Germany, 2016; pp. 77–98. [Google Scholar]
- Wolff, M.; Collins, R.T.; Liu, Y. Regularity-driven facade matching between aerial and street views. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Simo-Serra, E.; Trulls, E.; Ferraz, L.; Kokkinos, I.; Fua, P.; Moreno-Noguer, F. Discriminative learning of deep convolutional feature point descriptors. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Yi, K.M.; Trulls, E.; Lepetit, V.; Fua, P. Lift: Learned invariant feature transform. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A. Matchnet: Unifying feature and metric learning for patch-based matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Moo Yi, K.; Verdie, Y.; Fua, P.; Lepetit, V. Learning to assign orientations to feature points. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Lenc, K.; Vedaldi, A. Learning covariant feature detectors. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Cao, Y.; McDonald, J. Improved feature extraction and matching in urban environments based on 3D viewpoint normalization. Comput. Vis. Image Underst. 2012, 116, 86–101. [Google Scholar] [CrossRef]
- Li, L.; Yang, F.; Zhu, H.; Li, D.; Li, Y.; Tang, L. An improved RANSAC for 3D point cloud plane segmentation based on normal distribution transformation cells. Remote Sens. 2017, 9, 433. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Blum, R.; Xiang, P. Matching of images with projective distortion using transform invariant low-rank textures. J. Vis. Commun. Image Represent. 2016, 38, 602–613. [Google Scholar] [CrossRef]
- Zhang, Z.; Ganesh, A.; Liang, X.; Ma, Y. TILT: Transform invariant low-rank textures. Int. J. Comput. Vis. 2012, 99, 1–24. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Chen, D.; Tsai, S.; Cheung, N.; Chen, H.; Takacs, G.; Reznik, Y.; Vedantham, R.; Grzeszczuk, R.; Bach, J. The stanford mobile visual search data set. In Proceedings of the 2nd Annual ACM Conference on Multimedia Systems, Santa Clara, CA, USA, 23–25 February 2011. [Google Scholar]
- Hauagge, D.C.; Snavely, N. Image matching using local symmetry features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Rublee, E.; Radbaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the ICCV 2011: The 13th International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Bian, J.; Lin, W.; Matsushita, Y.; Yeung, S.; Nguyen, T.; Cheng, M. GMS: Grid-based motion statistics for fast, ultra-robust feature correspondence. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Nistér, D. Preemptive RANSAC for live structure and motion estimation. Mach. Vis. Appl. 2005, 16, 321–329. [Google Scholar] [CrossRef]
- Fan, H.; Zipf, A.; Wu, H. Detecting repetitive structures on building footprints for the purposes of 3D modeling and reconstruction. Int. J. Digit. Earth 2017, 10, 785–797. [Google Scholar] [CrossRef]
- Zhang, Z.; Matsushita, Y.; Ma, Y. Camera calibration with lens distortion from low-rank textures. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Lindeberg, T. Scale-Space Theory in Computer Vision; Springer Science: Berlin/Heidelberg, Germany, 2013; p. 256. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 5, 603–619. [Google Scholar] [CrossRef]
- Zhou, H.; Yuan, Y.; Shi, C. Object tracking using SIFT features and mean shift. Comput. Vis. Image Underst. 2009, 113, 345–352. [Google Scholar] [CrossRef]
- Nistér, D. An efficient solution to the five-point relative pose problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–777. [Google Scholar] [CrossRef]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Alcantarilla, P.F.; Solutions, T. Fast explicit diffusion for accelerated features in nonlinear scale spaces. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 1281–1298. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]


















| Metrics | Multi-Level Clustering Threshold | Maximum Number of ORB Features | Number of GMS Grids | Rejection Distance for Viewpoint Fusion | |
|---|---|---|---|---|---|
| Parameters | |||||
| Value | 10 | 100,000 | 20 × 20 | 5 pixel | |
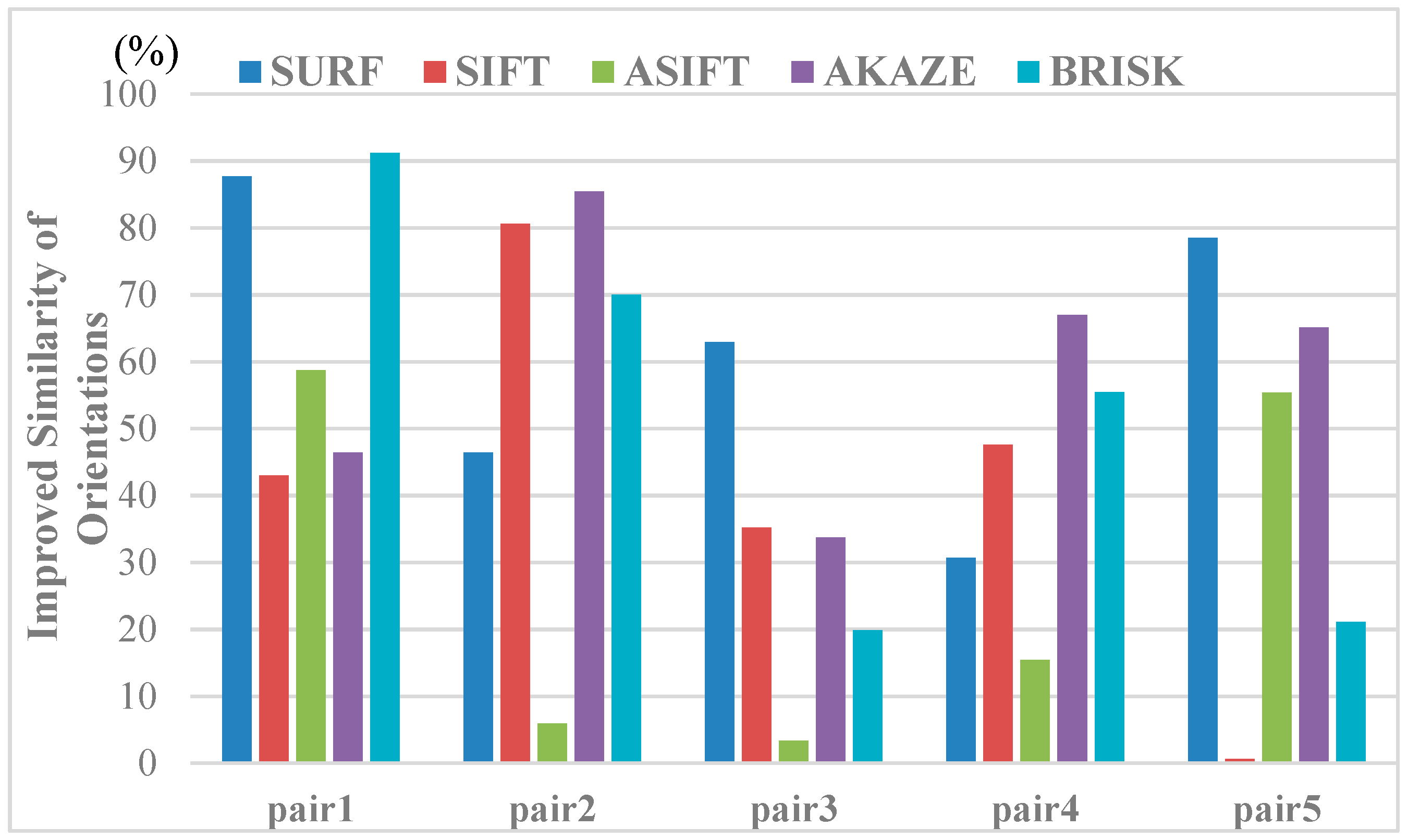
| Test Images | Metric | SIFT | SURF | AKAZE | BRISK | ASIFT | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Origin | Rectif | Origin | Rectif | Origin | Rectif | Origin | Rectif | Origin | Rectif | ||
| Pair 1 | 0/12/1102 | 5/16/1102 | 0/14/1937 | 40/43/1937 | 18/20/1090 | 37/58/1090 | 13/19/1430 | 35/35/1430 | 64/65/20694 | 91/93/20694 | |
| 0.00% | 31.25% | 0.00% | 93.02% | 90% | 63.79% | 68.42% | 100% | 98.46% | 97.85% | ||
| 0.00% | 0.45% | 0.05% | 2.07% | 1.65% | 3.39% | 0.91% | 2.45% | 0.31% | 0.44% | ||
| Pair 2 | 22/22/1416 | 41/44/1416 | 9/12/2210 | 47/48/2210 | 14/14/1150 | 56/56/1243 | 17/18/1466 | 38/38/1466 | 256/256/25545 | 264/264/25545 | |
| 100% | 93.18% | 75% | 97.92% | 100% | 100% | 94.44% | 100% | 100% | 100% | ||
| 1.55% | 2.90% | 0.41% | 2.13% | 1.22% | 4.51% | 1.16% | 2.59% | 1.00% | 1.03% | ||
| Pair 3 | 16/17/1607 | 22/23/1607 | 15/16/2355 | 28/28/2355 | 14/15/1055 | 27/33/1126 | 19/21/1585 | 38/39/1585 | 77/77/29824 | 82/83/29824 | |
| 94.12% | 95.65% | 93.75% | 100% | 93.33% | 81.82% | 90.48% | 97.44% | 100% | 98.80% | ||
| 1.00% | 1.37% | 0.64% | 1.19% | 1.33% | 2.40% | 1.20% | 2.40% | 0.26% | 0.28% | ||
| Pair 4 | 5/12/1799 | 53/53/1799 | 10/12/2168 | 49/49/2168 | 24/30/1358 | 108/108/1471 | 13/16/1902 | 109/109/1902 | 140/140/28142 | 148/148/28142 | |
| 41.67% | 100% | 83.33% | 100% | 80% | 100% | 81.25% | 100% | 100% | 100% | ||
| 0.28% | 2.94% | 0.46% | 2.26% | 1.77% | 7.34% | 0.68% | 5.73% | 0.50% | 0.53% | ||
| Pair 5 | 0/12/1081 | 6/14/979 | 2/14/2195 | 41/43/1733 | 1/10/792 | 24/25/893 | 0/14/965 | 0/22/1012 | 26/26/18987 | 31/31/16849 | |
| 0.00% | 42.90% | 14.29% | 95.35% | 10% | 96% | 0.00% | 0.00% | 100% | 100% | ||
| 0.00% | 0.61% | 0.09% | 2.37% | 0.13% | 2.69% | 0.00% | 0.00% | 0.14% | 0.18% | ||
| Test Images | Metric | Original | Rectified | Rectified + Fusion |
|---|---|---|---|---|
| Pair 1 | 186/257/22239 | 390/390/22239 | 527/527/22239 | |
| 72.37% | 100% | 100% | ||
| 0.84% | 1.75% | 2.37% | ||
| Pair 2 | 163/269/24353 | 290/290/24353 | 439/439/24353 | |
| 60.59% | 100% | 100% | ||
| 0.67% | 1.19% | 1.80% | ||
| Pair 3 | 752/752/25366 | 440/440/25366 | 1075/1075/25366 | |
| 100% | 100% | 100% | ||
| 2.96% | 1.73% | 4.24% | ||
| Pair 4 | 339/364/24915 | 628/663/24915 | 839/858/24915 | |
| 93.13% | 94.72% | 97.79% | ||
| 1.36% | 2.52%% | 3.37% | ||
| Pair 5 | 69/129/25034 | 452/573/20275 | 469/650/25034 | |
| 53.49% | 78.88%% | 72.15% | ||
| 0.26% | 2.23% | 1.87% |
| Image Pairs | Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||
|---|---|---|---|---|---|---|
| Metric | ||||||
| Number of matches | ASIFT | 170 | 273 | 33 | 92 | |
| GMS | 133 | 600 | 367 | 98 | ||
| Proposed | 413 | 1187 | 895 | 438 | ||
| Matching time (unit: s) | ASIFT | 21.05 | 14.12 | 59.02 | 11.9 | |
| GMS | 1.36 | 2.30 | 6.32 | 1.19 | ||
| Proposed | 11.07 | 11.25 | 18.12 | 7.53 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, L.; Li, H.; Zheng, X. Distorted Building Image Matching with Automatic Viewpoint Rectification and Fusion. Sensors 2019, 19, 5205. https://doi.org/10.3390/s19235205
Yue L, Li H, Zheng X. Distorted Building Image Matching with Automatic Viewpoint Rectification and Fusion. Sensors. 2019; 19(23):5205. https://doi.org/10.3390/s19235205
Chicago/Turabian StyleYue, Linwei, Hongjie Li, and Xianwei Zheng. 2019. "Distorted Building Image Matching with Automatic Viewpoint Rectification and Fusion" Sensors 19, no. 23: 5205. https://doi.org/10.3390/s19235205
APA StyleYue, L., Li, H., & Zheng, X. (2019). Distorted Building Image Matching with Automatic Viewpoint Rectification and Fusion. Sensors, 19(23), 5205. https://doi.org/10.3390/s19235205




