Optimization of Reconfigurable Satellite Constellations Using Simulated Annealing and Genetic Algorithm
Abstract
:1. Introduction
2. Methodology
2.1. Problem Formulation
2.2. Model Overview
2.2.1. Design Variables
- Altitude;
- Altitude difference;
- Number of orbit planes;
- Number of satellites per plane;
- Field of regard.
2.2.2. Internal Variables
2.2.3. Parameters
2.2.4. Constraints
2.2.5. Objectives
2.3. Simulation Model
2.3.1. Astrodynamics Module
2.3.2. Optics Module
2.3.3. Maneuvers Module
2.3.4. Propulsion and Constellation Modules
3. Preliminary Sampling and Analysis
- As the RGT ratio decreases, the mass of the entire constellation increases because more propellant is required (i) to raise the altitude of satellites from the parking orbit to higher altitudes at the beginning of life and (ii) to lower the altitude to the disposal orbit. Reconfiguration time also increases with the RGT ratio because there are fewer locations where reconfiguration can occur.
- High altitude difference increases both ROM revisit time and GOM revisit time because a satellite has to orbit along a longer trajectory with a lower orbit velocity, which leads to a longer orbit period. The constellation mass decreases as altitude difference increases, mainly, due to lower atmospheric drag and subsequent reduction in propellant mass. The reconfiguration time decreases as the absolute value of altitude difference increases because a greater deviation from the Walker altitude makes the orbit plane drift faster.
- Both ROM revisit time and GOM revisit time (to a lesser extent) decrease when the number of planes decreases and the number of satellites per plane increases.
- Increasing the FoR decreases the constellation mass.
- The number of revolutions per day should be large.
- The altitude difference from the Walker constellation should be large.
- The satellites should be distributed in a small number of orbit planes.
- The FoR should be large.
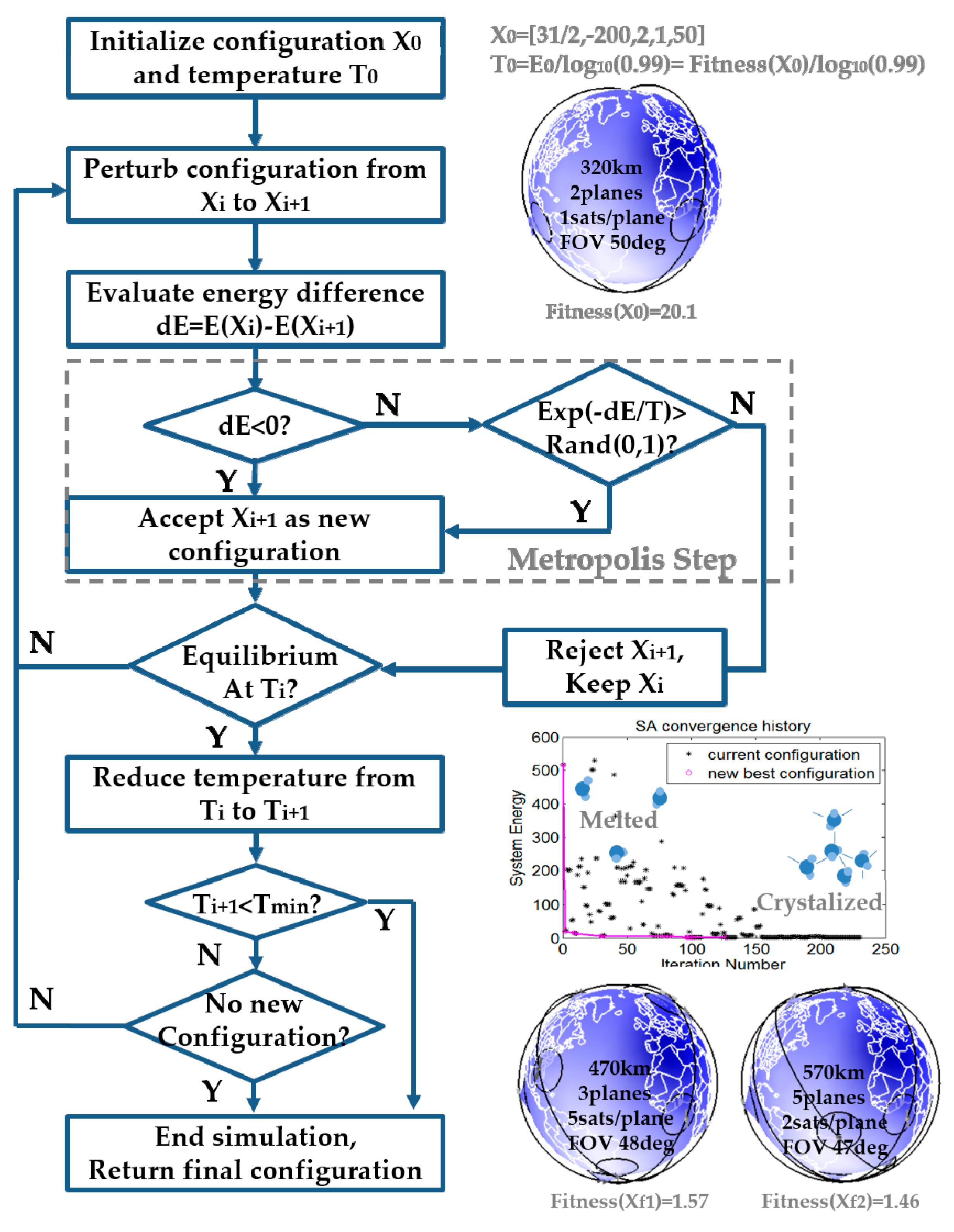
4. Simulated Annealing
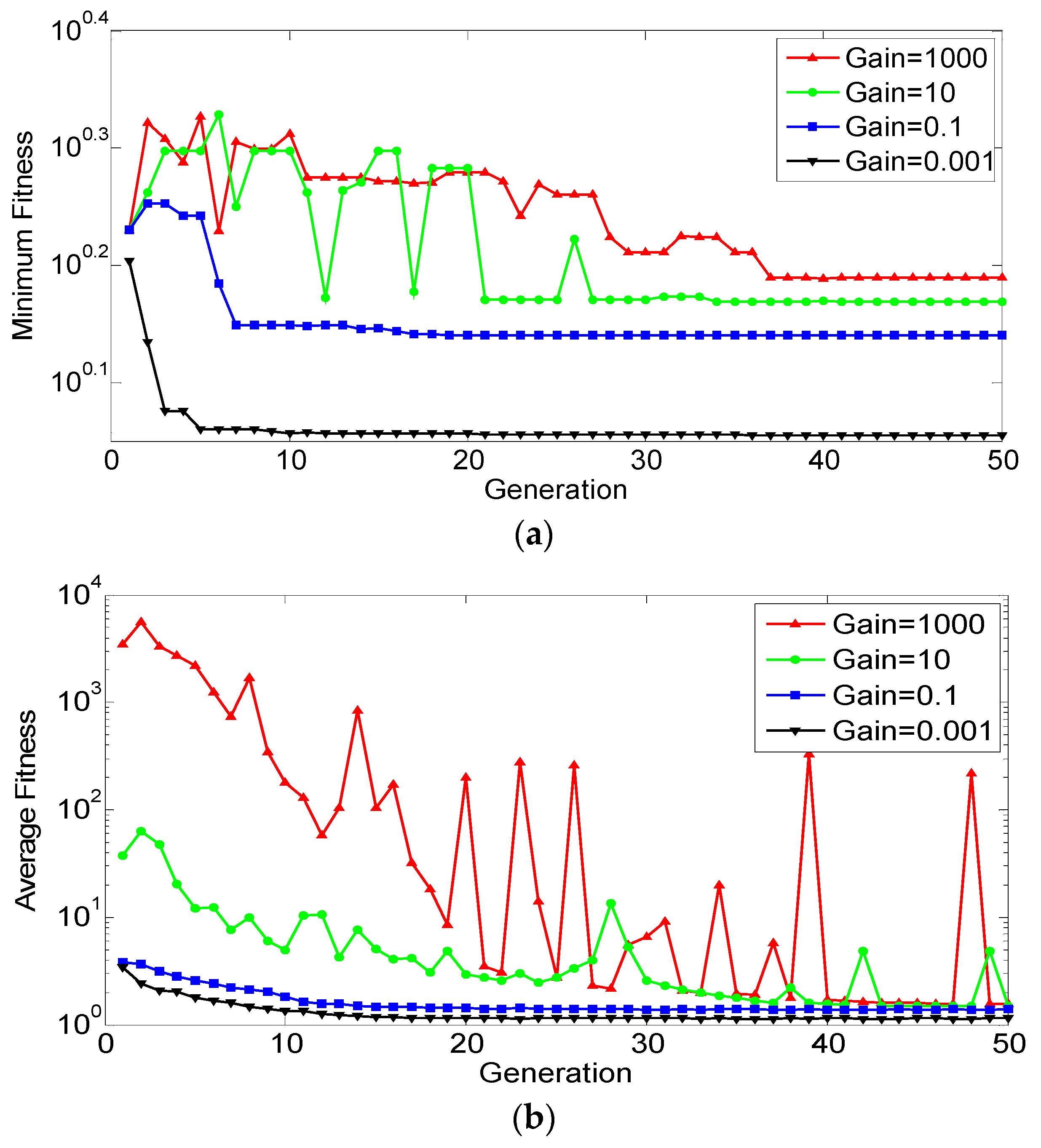
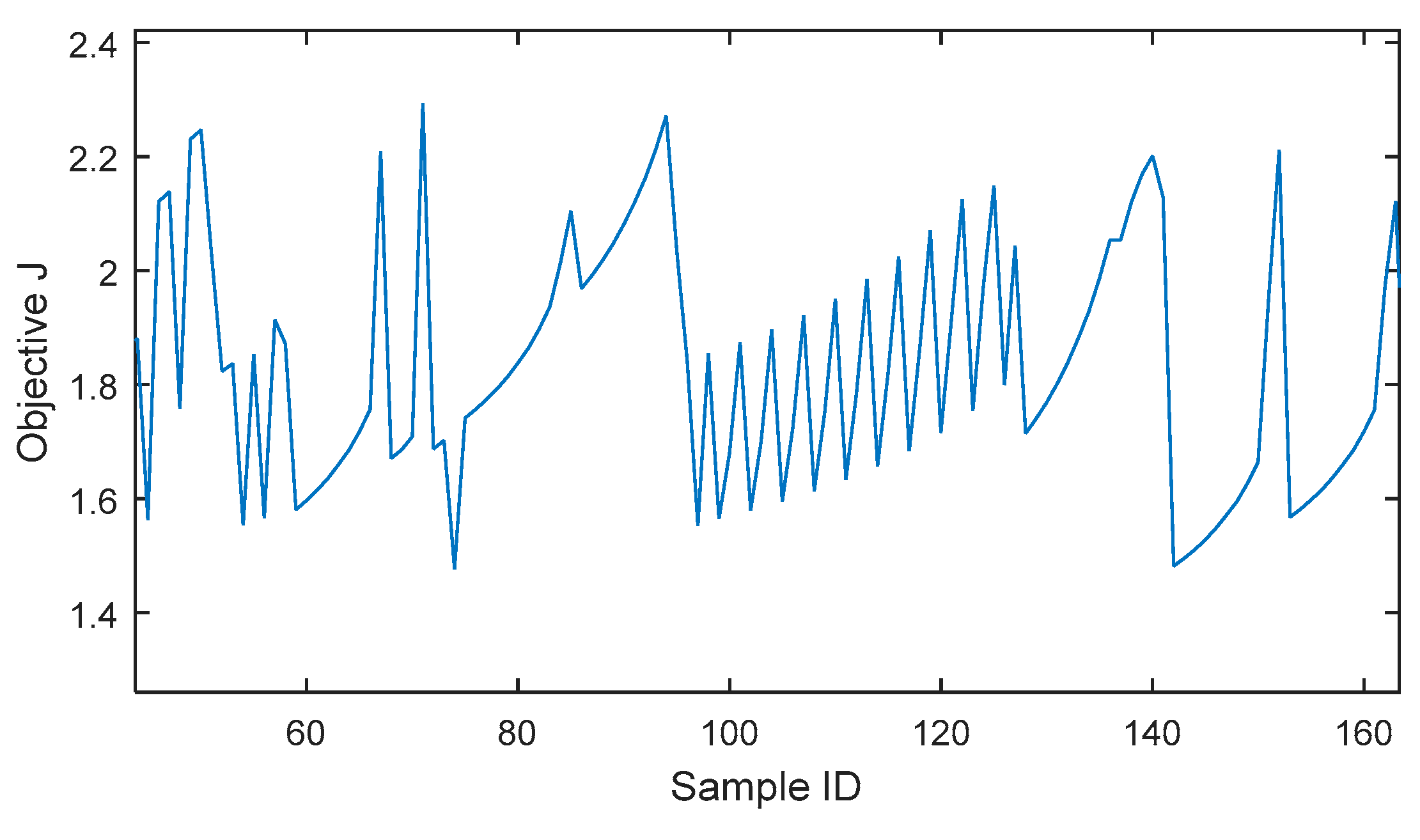
5. Genetic Algorithm
6. Discussion
6.1. Gradient-Based Optimization
6.2. Sensitivity Analysis
6.3. Sun-Synchronous Orbits
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Repeat Ground Tracks
Appendix B. Satellite Aperture and Tank Mass Data

| Mission | Payload | Vendor | Aperture (m) | Payload Mass (kg) |
|---|---|---|---|---|
| RapidEye TopSat OrbView-3 Quickbird WorldView-1 Ikonos GeoEye-1 | REIS RALCam 1 OHRIS BHRC 60 WV 60 OSA GIS | Jena-Optronik MDA Northrop Grumman ITT Exelis ITT Exelis Kodak ITT Exelis | 0.145 0.2 0.45 0.6 0.6 0.7 1.1 | 43 32 66 380 380 171 452 |
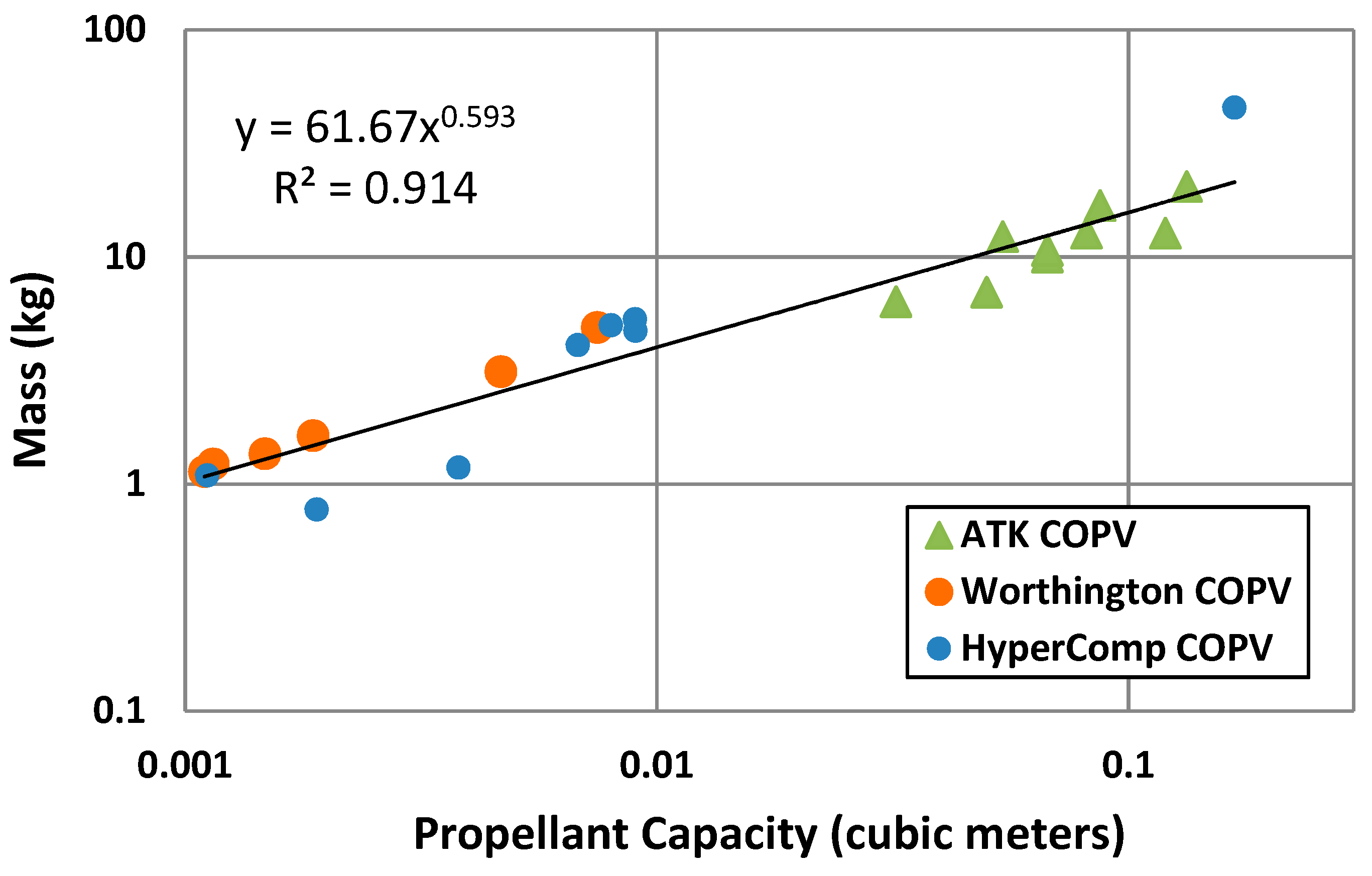
Appendix C. Fuel (“Delta-V”) Budget
References
- Paek, S.W.; Kim, S. Space-based Earth Remote Sensing: Part 1. Satellite Orbit Theory. Satell. Oceanogr. Meteorol. 2018, 18. [Google Scholar] [CrossRef]
- Paek, S.W.; Kim, S.; Kronig, L.; de Weck, O. Sun-synchronous repeat ground tracks and other useful orbits for future space missions. In Proceedings of the Australian International Aerospace Conference, Melbourne, Australia, 25–28 February 2019. [Google Scholar]
- He, Q.; Fok, H.S.; Chen, Q.; Chun, K.P. Water Level Reconstruction and Prediction Based on Space-Borne Sensors: A Case Study in the Mekong and Yangtze River Basins. Sensors 2018, 18, 3076. [Google Scholar] [CrossRef]
- Asakri, G.; Pour, A.B.; Pradhan, B.; Sarfi, M.; Nazemnejad, F. Band Ratios Matrix Transformation (BRMT): A Sedimentary Lithology Mapping Approach Using ASTER Satellite Sensor. Sensors 2018, 18, 3213. [Google Scholar] [CrossRef] [PubMed]
- Paek, S.W.; Kronig, L.G.; Ivanov, A.B.; de Weck, O.L. Satellite Constellation Design Algorithm for Remote Sensing of Diurnal Cycles Phenomena. Adv. Space. Res. 2018, 62, 2529–2550. [Google Scholar] [CrossRef]
- Chen, A.; Zhang, Y.; Chao, O.; Zhang, F.; Ma, J. Automated Landslides Detection for Mountain Cities Using Multi-Temporal Remote Sensing Imagery. Sensors 2018, 18, 821. [Google Scholar] [CrossRef] [PubMed]
- Blackwell, W.J.; Allen, G.; Galbraith, C.; Leslie, R.; Osaretin, I.; Scariton, M.; Shields, M.; Thompson, E.; Toher, D.; Townzen, D.; et al. MicroMAS: A First Step Towards a Nanosatellite Constellation for Global Storm. In Proceedings of the AIAA/USU Conference on Small Satellites, SSC13-XI-1, Logan, UT, USA, 14 August 2013. [Google Scholar]
- Paek, S.W.; de Weck, O. Delta-v map of useful orbits for Earth observation missions. In Proceedings of the International Astronautical Congress, IAC-14.B1.P.4.x24733, Toronto, ON, Canada, 29 September–3 October 2014. [Google Scholar]
- Paek, S.W. Reconfigurable Satellite Constellations (ReCon) for Geo-Spatially Adaptive Earth observation Missions. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2012. [Google Scholar]
- Paek, S.W.; de Weck, O.; Smith, M. Concurrent design optimization of Earth observation satellites and reconfigurable constellations. J. Brit. Interplanet. Soc. 2017, 70, 19–35. [Google Scholar]
- Ranjana, P.; Chandela, A.K.; Khot, L.R.; Bahlol, H.Y.; Zhou, J.; Boydston, R.A.; Miklas, P.N. Irrigated Pinto Bean Crop Stress and Yield Assessment using Ground based Low Altitude Remote Sensing Technology. Inf. Proc. Agric. 2019. [Google Scholar] [CrossRef]
- Gao, H.; Wang, C.; Wang, G.; Zhu, J.; Tang, Y.; Shen, P.; Zhu, Z. A Crop Classification Method Integrating GF-3 PolSAR and Sentinel-2A Optical Data in the Dongting Lake Basin. Sensors 2018, 18, 3139. [Google Scholar] [CrossRef]
- Bogosian, J.R. Image Collection Optimization in the Design and Operation of Lightweight, Low Areal-Density Space Telescopes. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
- Paek, S.W.; Legge, R.; Smith, M. Reconfigurable satellite constellations for geo-spatially adaptive Earth observation missions. In Proceedings of the International Workshop on Satellite Constellations and Formation Flying, Lisbon, Portugal, 13–15 March 2013. [Google Scholar]
- Paek, S.W.; de Weck, O.L.; Smith, M.W. Chapter 9. Concurrent Design Optimization of Satellites and Reconfigurable Constellations. In Horizons in Earth Science Research; Szigethy, J., Veress, B., Eds.; Nova Science Publishers, Inc.: New York, NY, USA, 2017; Volume 15, pp. 151–184. ISBN 978-1-6348-5696-6. [Google Scholar]
- European Space Agency. What is ERS? Available online: https://earth.esa.int/web/guest/missions/esa-operational-eo-missions/ers (accessed on 3 February 2019).
- Ducet, N.; Le Traon, P.Y.; Reverdin, G. Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and -2. J. Geophys. Res. Oceans 2000, 105, 19477–19498. [Google Scholar] [CrossRef] [Green Version]
- Langbroek, M. The Orbit of USA 245 and the Current KH-11 Constellation. Available online: https://sattrackcam.blogspot.com/2013/09/the-orbit-of-usa-245-and-current-kh-11.html (accessed on 3 February 2019).
- Nag, S.; Li, A.S.; Merrick, J.H. Scheduling algorithms for rapid imaging using agile Cubesat constellations. COSPAR Adv. Space Res. Astrodyn. 2018, 61, 891–913. [Google Scholar] [CrossRef]
- Yao, F.; Li, J.; Chen, Y.; Chu, X.; Zhang, B. Task Allocation Strategies for Cooperative Task Planning of Multi-autonomous Satellite Constellation. COSPAR Adv. Space Res. 2019, 63, 1073–1084. [Google Scholar] [CrossRef]
- The Aerospace Corporation. Constellation Reconfiguration. Available online: https://aerospace.org/article/constellation-reconfiguration (accessed on 3 February 2019).
- Selva, D.; Golkar, A.; Korobova, O.; i Cruz, I.L.; Collopy, P.; de Weck, O.L. Distributed Earth satellite systems: What is needed to move forward? J. Aerosp. Inform. Syst. 2017, 14, 412–438. [Google Scholar] [CrossRef]
- D’Errico. Distributed Space Missions for Earth System Monitoring; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Nag, S.; Hughes, S.P.; Le Moigne, J. Streamlining the design tradespace for Earth imaging constellations. In Proceedings of the AIAA SPACE 2016, Long Beach, CA, USA, 13–16 September 2016. [Google Scholar]
- Nag, S.; Gatebe, C.K.; Miller, D.W.; de Weck, O.L. Effect of satellite formations and imaging modes on global albedo estimation. Acta Astronaut. 2016, 126, 77–97. [Google Scholar] [CrossRef]
- Walker, J. Some circular orbit patterns providing continuous whole Earth coverage. J. Brit. Interplanet. Soc. 1971, 24, 369–384. [Google Scholar]
- Ballard, A.H. Rosette constellations of Earth satellites. IEEE Trans. Aeros. Electron. Syst. 1980, 16, 656–673. [Google Scholar] [CrossRef]
- Mortari, D.M.; Wilkins, M.P. Flower constellation set theory. Part I: Compatibility and phasing. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 953–962. [Google Scholar] [CrossRef]
- Kronig, L.; Paek, S.W.; Ivanov, A.; de Weck, O. Satellite constellation design for the SOLVE mission investigating diurnal cycles of vegetation phenomena. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Napa, CA, USA, 14–18 February 2016. [Google Scholar]
- Camps, A.; Milne, T.; Heron, M. Challenges and activity in the Polar Regions: Technology, measurement and information. In Proceedings of the IEEE Technical Activities Board 2017 Ad-hoc Committee, Phoenix, AZ, USA, 17–18 November 2017. [Google Scholar]
- Le Moigne, J.; Dabney, P.; de Weck, O.; Foreman, V.; Grogan, P.; Holland, M.; Hughes, S.; Nag, S. Tradespace analysis tool for designing constellations (TAT-C). In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Morris, G.M.; Goodsell, D.S.; Halliday, R.S.; Huey, R.; Hart, W.E.; Belew, R.K.; Olson, A.J. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1999, 19, 1640–1662. [Google Scholar] [CrossRef]
- Sexton, R.S.; Dorsey, R.E.; Johnson, J.D. Optimization of neural networks: A comparative analysis of the genetic algorithm and simulated annealing. Eur. J. Oper. Res. 1999, 114, 589–601. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.-T.; Kao, C.-Y.; Hsu, C.-C. Applying the genetic approach to simulated annealing in solving some NP-hard problems. IEEE Trans. Syst. Man Cybern. 1999, 23, 1752–1767. [Google Scholar]
- Leung, T.W.; Chan, C.K.; Troutt, M.D. Application of a mixed simulated annealing-genetic algorithm heuristic for the two-dimensional orthogonal packing problem. Eur. J. Oper. Res. 2003, 145, 530–542. [Google Scholar] [CrossRef]
- Hassan, R.; Cohanim, B.; de Weck, O. A Comparison of Particle Swarm Optimization and the Genetic Algorithm. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials (SDM) Conference, AIAA2005-1897, Austin, TX, USA, 18–21 April 2005. [Google Scholar]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Luo, X.; Wang, M.; Dai, G.; Chen, X. A Novel Technique to Compute the Revisit Time of Satellites and Its Application in Remote Sensing Satellite Optimization Design. Int. J. Aerosp. Eng. 2017, 6469439. [Google Scholar] [CrossRef]
- Capderou, M. Handbook of Satellite Orbits: From Kepler to GPS; Springer International Publishing: Cham, Switzerland, 2014; ISBN 978-3-3190-3415-7. [Google Scholar]
- Liu, X.; Baoyin, H.; Ma, X. Five Special Types of Orbits Around Mars. J. Guid. Control Dyn. 2010, 33, 1294–1301. [Google Scholar] [CrossRef]
- Turner, A.E. Constellation Design Using Walker Patterns, AIAA 2002-4904. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Guidance, Navigation, and Control and Co-located Conferences, Monterey, CA, USA, 5–8 August 2002. [Google Scholar]
- Kasischke, E.S.; French, N.H.S. Locating and estimating the areal extent of wildfires in Alaskan boreal forests using multiple-season AVHRR NDVI composite data. Remote Sens. Environ. 1995, 51, 263–275. [Google Scholar] [CrossRef]
- Fraser, R.H.; Hall, R.J.; Landry, R.; Lynham, T.; Raymond, D.; Lee, B.; Li, Z. Validation and Calibration of Canada-Wide Coarse-Resolution Satellite Burned-Area Maps. Photogram. Eng. Remote Sens. 2004, 4, 451–460. [Google Scholar] [CrossRef]
- Digital Globe. WorldView-3 Datasheet. Available online: https://www.spaceimagingme.com/downloads/sensors/datasheets/DG_WorldView3_DS_2014.pdf (accessed on 11 February 2019).
- Astrium. An EADS Company, SPOT 6|SPOT 7 Technical Sheet. Available online: http://www.intelligence-airbusds.com/files/pmedia/edited/r18072_9_spot_6_technical_sheet.pdf (accessed on 11 February 2019).
- Vallado, D.A. Fundamentals of Astrodynamics and Applications, 3rd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Driggers, R.G. Encyclopedia of Optical Engineering; CRC Press: Boca Raton, FL, USA, 2003; p. 1392. ISBN 978-0-8247-4251-5. [Google Scholar]
- Wertz, J.R.; Everett, D.F.; Puschell, J.J. Space Mission Engineering: The New SMAD; Microcosm Press: El Segundo, CA, USA, 2010; ISBN 978-1-8818-8315-9. [Google Scholar]
- Krueger, M.K.; Daniel, S.; Smith, M.W.; Keese, J. Spacecraft and Constellation Design for a Continuous Responsive Imaging System in Space. In Proceedings of the AIAA SPACE 2009 Conference & Exposition, Pasadena, CA, USA, 14–17 September 2009. [Google Scholar]
- Satellite Missions—eoPortal Directory. Available online: https://directory.eoportal.org/web/eo portal/sate llite-missions (accessed on 29 November 2018).
- Thomas, S.J.; Mueller, J.B.; Paluszek, M. Formations for Close-Orbiting Escort Vehicles, AIAA 2004-6289. In Proceedings of the AIAA 1st Intelligent Systems Technical Conference, Chicago, IL, USA, 20–22 September 2004. [Google Scholar]
- Cohanim, B.E.; Hewitt, J.N.; de Weck, O.L. The Design of Radio Telescope Array Configurations using Multiobjective Optimization: Imaging Performance versus Cable Length. Astrophys. J. 2004, 154, 705–719. [Google Scholar] [CrossRef] [Green Version]
- Wood, L. SaVi: Satellite constellation visualization. In CCSR Research Symposium (CRS 2011); University of Surrey: Guildford, UK, 30 June 2011. [Google Scholar]
- SaVi—Satellite Constellation Visualization Software. Available online: http://savi.sf.net/ (accessed on 11 February 2019).
- Vikhar, P.A. Evolutionary algorithms: A critical review and its future prospects. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, Maharashtra, India, 22–24 December 2016; pp. 261–265, ISBN 978-1-5090-0467-6. [Google Scholar]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Senthilnath, J.; Sindhu, S.; Omkar, S.N. GPU-based normalized cuts for road extraction using satellite imagery. Earth Syst. Sci. 2014, 123, 1759–1769. [Google Scholar] [CrossRef]
- Lembke, J. The Politics of Galileo. European Policy Papers #7. Available online: http://aei.pitt.edu/29/ (accessed on 11 February 2019).
- Ito, A. Legal Aspects of Satellite Remote Sensing; Brill Publishers: Leiden, The Netherlands, 2011; ISBN 9004190325. [Google Scholar]
- Wood, L.; Clerget, A.; Andrikopoulos, I.; Pavlou, G.; Dabbous, W. IP routing issues in satellite constellation networks. Int. J. Satell. Commun. Netw. 2001, 1, 69–92. [Google Scholar] [CrossRef]
- Holdaway, R. Is space global disaster warning and monitoring now nearing reality? Space Policy 2001, 17, 127–132. [Google Scholar] [CrossRef]
- Gonzalez, J.; Saccoccia, G. ESA Electric Propulsion Activities. In Proceedings of the 32nd International Electric Propulsion Conference, Wiesbaden, Germany, 11–15 September 2011. [Google Scholar]
- Japan Aerospace Exploration Agency, Super Low Altitude Test Satellite “TSUBAME” (SLATS, In Operation). Available online: http://global.jaxa.jp/projects/sat/slats/ (accessed on 7 February 2019).












| Figure of Merit | Definition | Constraint | Definition |
|---|---|---|---|
| F1 F2 F3 F4 | (−1) × GOM coverage (%) ROM revisit time (s) Constellation mass (kg) Reconfiguration time (day) | h1 h2 h3 h4 | Minimum altitude (km) Maximum altitude (km) Maximum aperture (m) Max propellant mass fraction |
| Design Variable | Description | Range | Unit |
|---|---|---|---|
| nk | Repeat ground track (RGT) ratio () | {31/2, 15/1, 29/2, 14/1} | - |
| delta_alt n_planes n_sats regard prop | Walker altitude difference from RGT altitude # of planes in Walker constellation # of satellites per orbit plane Field of regard Propulsion type | [−50, 50] {2, 3, 4, 5, 6, 7, 8, 9} {1, 2, 3, 4, 5} [5, 50] {cold gas, monoprop, biprop} 1 | km - - ° - |
| Internal Variable | Description | Unit |
|---|---|---|
| aperture | Optical telescope aperture diameter | m |
| fl prop_dry_mass propellant_mass optics_mass rgt_alt delta_v sat_dry_mass | Optical telescope focal length Propulsion system dry mass Propellant mass Optical subsystem mass Repeating groundtrack altitude Total lifetime fuel burn Satellite dry mass | m kg kg m km m/s kg |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| life | Orbit lifetime | 5 | Year |
| e walker_phase inc n_recons gsd regional_lat global_lat_band | Orbit eccentricity Walker phasing parameter Orbit inclination # of reconfigurations over lifetime Ground sample distance Regional latitude of interest Global latitude band of interest | 0 1 60 10 0.5 55 [0, 60] | - - ° - m ° ° |
| Constraint | Description | Value | Unit |
|---|---|---|---|
| min_alt | Minimum altitude | 350 | km |
| max_alt max_regard max_aperture max_prop_frac | Maximum altitude Maximum field of regard Maximum aperture diameter Maximum propellant mass fraction | 1200 50 1.8 0.3 | km ° m - |
| Objective | Description | Unit |
|---|---|---|
| rom_revisit | ROM revisit time | s |
| gom_coverage reconfg_time const_mass | GOM temporal coverage Reconfiguration time between GOM and ROM Constellation total mass | % days kg |
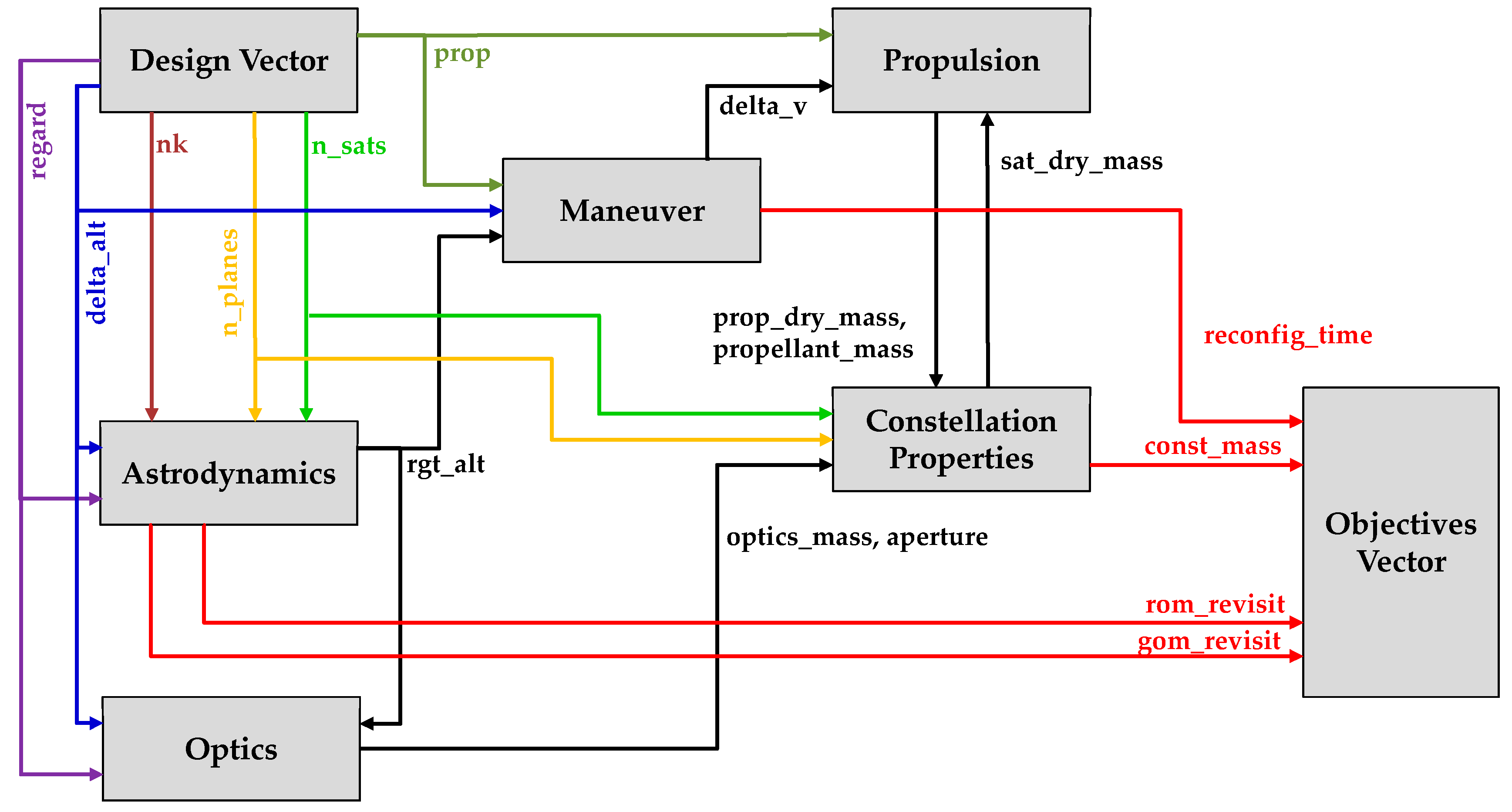
| Module | Input Variables | Output Variables |
|---|---|---|
| Astrodynamics | nk, delta_alt, n_planes, n_sats, regard, e, walker_phase, inc | rgt_alt, rom_revisit, gom_revisit |
| Optics Maneuvers Propulsion | regard, delta_alt, fov, gsd, rgt_alt prop, delta_alt, life, n_recons, rgt_alt, area prop, sat_dry_mass, delta_v | optics_mass, aperture delta_v, reconfig_time prop_dry_mass, propellant_mass |
| Constellation | n_planes, n_sats, optics_mass, aperture, prop_dry_mass, propellant_mass | sat_dry_mass, const_mass, area |
| Design Variable | Description | Factor | #Levels | Units |
|---|---|---|---|---|
| nk | RGT ratio | N | 4 | - |
| delta_alt n_planes n_sats regard | Altitude difference between Walker and RGT Number of orbit planes Number of satellites per plane Field of regard | A P S R | 8 4 4 8 | km - - ° |
| Factor/ Level | Value of Level [Unit] | △ROM Revisit [sec] | △GOM Revisit [sec] | △Constellation Mass [kg] | △Reconfig Time [day] |
|---|---|---|---|---|---|
| N1 N2 N3 N4 | 31/2 15/1 29/2 14/1 | −667 −1658 +2739 +317 | −7800 −479 +11,797 −1969 | −2444 −246 +1005 +2962 | −0.1 −3.4 +0.8 +2.1 |
| A1 A2 A3 A4 A5 A6 A7 A8 | −40 km −30 km −20 km −10 km 10 km 20 km 30 km 40 km | −3522 −3625 −858 +561 +1021 +565 +1080 +8243 | −22,931 −25,629 −332 +6831 +5863 +6457 +8794 +37,467 | +6775 +2482 −262 −424 −1462 −1953 −323 −4216 | −6.7 −5.2 −0.4 +10.9 +8.6 −1.5 −5.5 −7.0 |
| P1 P2 P3 P4 | 1 plane 2 planes 3 planes 4 planes | +428 −489 +1098 −598 | −5662 −7380 +7839 +6207 | −912 +479 +217 +162 | −0.2 −0.4 −1.4 +1.4 |
| S1 S2 S3 S4 | 2 sats 3 sats 4 sats 5 sats | +3956 −924 −1423 +1584 | +19,599 −3003 −6482 −10,062 | −4722 +448 +1052 +2239 | 3.2 −2.7 −1.6 +0.4 |
| R1 R2 R3 R4 R5 R6 R7 R8 | 5° 10° 15° 20° 25° 30° 35° 40° | +5072 +1798 −734 +1205 −1122 −1971 −1648 −2995 | +44,821 +7602 +368 +9709 −14,134 −17,839 −16,690 −20,366 | +491 +2281 +738 −2154 +1518 −681 −972 498 | +2.7 +6.2 +0.5 −2.4 −4.0 −2.3 +0.9 −1.1 |
| Design Variable | Description | Range | Initial Value | Type |
|---|---|---|---|---|
| nk | RGT ratio | [13/1, 31/2] | 31/2 | Discrete |
| delta_alt n_planes n_sats regard prop | Altitude difference Number of orbital planes Number of satellites per plane Field of regard (FoR) Propellant Type | [−200, 200] [2, 9] [1, 5] [5, 50] Monopropellant | −200 km 2 1 50° - | Continuous Integer Integer Continuous - |
| Figure of Merit | Definition | Typical Value | Scaling (si) | Weighting (wi) |
|---|---|---|---|---|
| F1 F2 F3 F4 | (−1) × GOM coverage (%) ROM revisit time (s) Constellation mass (kg) Reconfiguration time (day) | −5 1000 10,000 2 | 0.5 0.001 0.0001 1 | 0.25 0.25 0.30 0.20 |
| Constraint | Definition | Typical Value | Scaling (si) | Gain (wi) |
|---|---|---|---|---|
| h1 h2 h3 h4 | Minimum altitude (km) Maximum altitude (km) Maximum aperture (m) Max propellant mass fraction | 350 1200 1.8 0.3 | 0.5 0.001 0.0001 1 | 0.1 |
| Type | Symbol | Description | Optimum |
|---|---|---|---|
| Design variable | nk delta_alt n_planes n_sats regard | RGT ratio Altitude difference Number of orbital planes Number of satellites per plane Field of regard | 15/1 −42.9 km 3 5 47.8° |
| Performance metrics | F1 F2 F3 F4 J | GOM area coverage ROM revisit time Constellation mass Reconfiguration time Objective function | 3.32 % 1018 sec 32,796 kg 3.13 day 1.570 |
| Type | Symbol | Description | Optimum |
|---|---|---|---|
| Design variable | nk delta_alt n_planes n_sats regard | RGT ratio Altitude difference Number of orbital planes Number of satellites per plane Field of regard | 15/1 49.6 km 5 2 46.8° |
| Performance metrics | F1 F2 F3 F4 J | GOM area coverage ROM revisit time Constellation mass Reconfiguration time Objective function | 2.89 % 1609 sec 26,276 kg 3.17 days 1.463 |
| Design Variable | Range | Bits | Type |
|---|---|---|---|
| RGT ratio | [13/2, 14/1] | 4 | Discrete |
| Altitude difference Number of orbital planes Number of satellites per plane Field of regard (FoR) Propellant Type | [−100, 100] [2, 7] [1, 7] [5, 60] - | 12 4 4 12 - | Continuous Integer Integer Continuous Fixed |
| Type | Symbol | Description | Optimum |
|---|---|---|---|
| Design variable | nk delta_alt n_planes n_sats regard | RGT ratio Altitude difference Number of orbital planes Number of satellites per plane Field of regard | 15/1 −53.9 km 3 4 46.8° |
| Performance metrics | F1 F2 F3 F4 J | GOM area coverage ROM revisit time Constellation mass Reconfiguration time Objective function | 1.95 % 1346 sec 25,187 kg 2.92 days 1.385 |
| Type | Symbol | Description | Optimum |
|---|---|---|---|
| Design variable | nk delta_alt n_planes n_sats regard | RGT ratio Altitude difference Number of orbital planes Number of satellites per plane Field of regard | 15/1 −54.7 km 5 2 47.1° |
| Performance metrics | F1 F2 F3 F4 J | GOM area coverage ROM revisit time Constellation mass Reconfiguration time Objective function | 1.95 % 1602 sec 21,318 kg 2.93 days 1.382 |
| Type | Symbol | Description | Optimum |
|---|---|---|---|
| Design variable | nk delta_alt n_planes n_sats regard | RGT ratio Altitude difference Number of orbital planes Number of satellites per plane Field of regard | 15/1 −100 km 3 4 30° |
| Performance | J | Objective function | 1.565 |
| Type | Symbol | Description | Optimum |
|---|---|---|---|
| Design variable | nk delta_alt n_planes n_sats regard | RGT ratio Altitude difference Number of orbital planes Number of satellites per plane Field of regard | 15/1 −90 km 2 5 37° |
| Performance | J | Objective function | 1.570 |
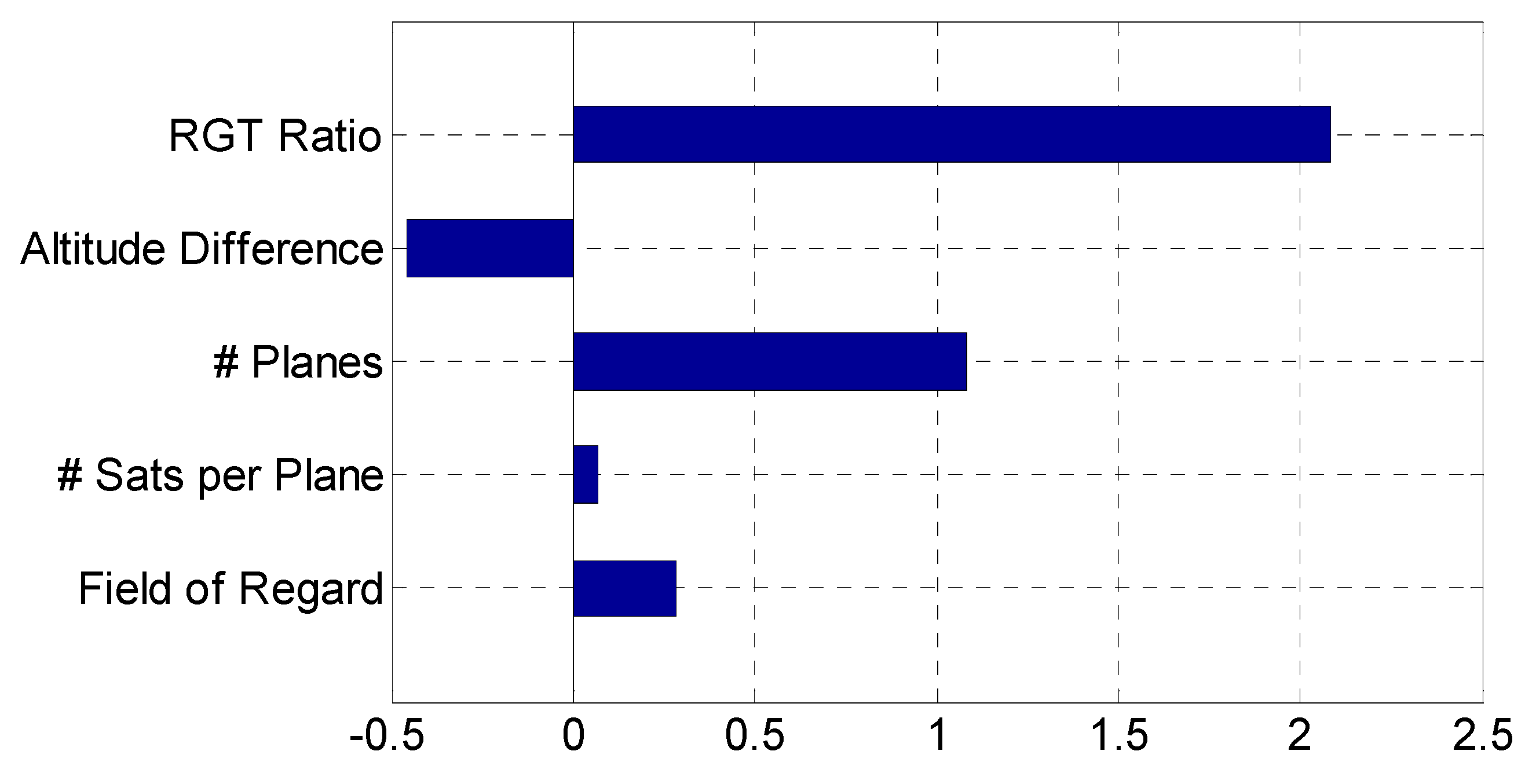
| Design Variable x | Step Size △x | Optimal Fitness J(x*) | Perturbed Fitness J(x* + △x) | Partial Derivative ∂J/∂x | Normalized Sensitivity ▽J(x*)x*/J(x*) |
|---|---|---|---|---|---|
| RGT ratio | 0.5 | 1.382 | 2.343 | 1.922 | 20.87 |
| Altitude difference Number of orbital planes Number of satellites per plane Field of regard (FoR) | 10 km 1 1 5° | 1.498 1.681 1.428 1.423 | 0.012 0.299 0.046 0.008 | −0.458 1.083 0.067 0.284 |
| Symbol | Description | ||
|---|---|---|---|
| Design variable | nk delta_alt n_planes n_sats regard | RGT ratio Altitude difference Number of orbital planes Number of satellites per plane Field of regard | 29/2 −19.9 km 5 3 41.4° |
| Performance metrics | J1 J2 J3 J4 | GOM area coverage ROM revisit time Constellation mass Reconfiguration time | 4.71 % 1173 sec 41796 kg 13.6 days |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paek, S.W.; Kim, S.; de Weck, O. Optimization of Reconfigurable Satellite Constellations Using Simulated Annealing and Genetic Algorithm. Sensors 2019, 19, 765. https://doi.org/10.3390/s19040765
Paek SW, Kim S, de Weck O. Optimization of Reconfigurable Satellite Constellations Using Simulated Annealing and Genetic Algorithm. Sensors. 2019; 19(4):765. https://doi.org/10.3390/s19040765
Chicago/Turabian StylePaek, Sung Wook, Sangtae Kim, and Olivier de Weck. 2019. "Optimization of Reconfigurable Satellite Constellations Using Simulated Annealing and Genetic Algorithm" Sensors 19, no. 4: 765. https://doi.org/10.3390/s19040765
APA StylePaek, S. W., Kim, S., & de Weck, O. (2019). Optimization of Reconfigurable Satellite Constellations Using Simulated Annealing and Genetic Algorithm. Sensors, 19(4), 765. https://doi.org/10.3390/s19040765






