ID Insertion and Data Tracking with Frequency Offset for Physical Wireless Parameter Conversion Sensor Networks †
Abstract
:1. Introduction
- This paper proposes the fractional CFO used as the ID for specifying the sensor node from the received signal.
- For the ICI caused via CFO, the construction of the ICI replica from the narrow band wireless communication is proposed.
- The multiple dimensional tracking based on sensing result, CSI, and CFO is proposed. In addition, if the duplication of sensing results occurs, instead of it, the tracking based on sensing results and the spectrum is proposed.
2. Related Works
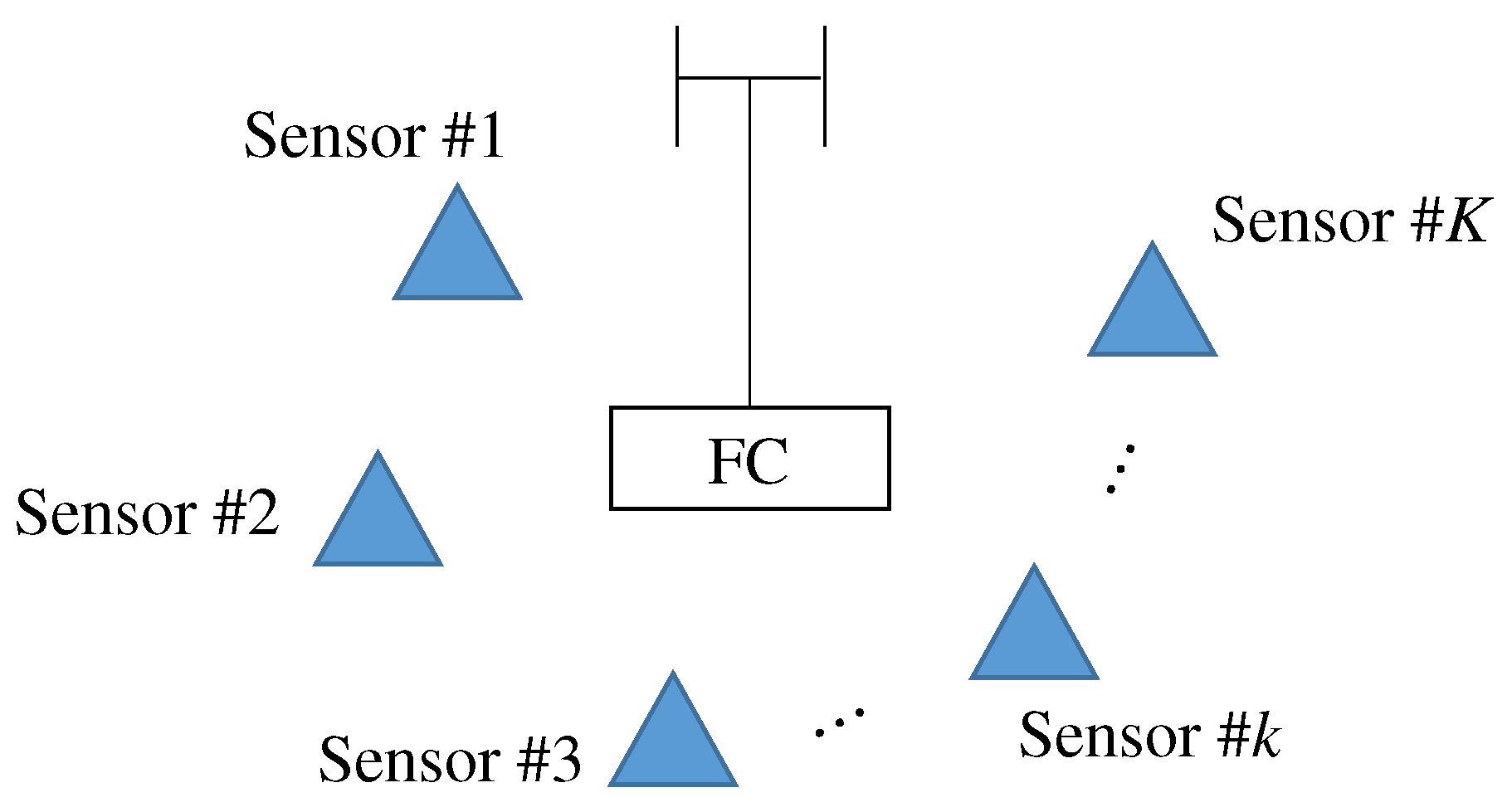
3. Overview of PhyC-SN
3.1. Data Transmission and Collection in PhyC-SN
3.2. Sensing Results Separation
4. Proposed Sensing Results Separation
4.1. Sensor Track based on Fractional CFO
4.2. Sensing Results Separation without Duplication of Sensing Results
4.2.1. Spectrum Detection and Estimating CSI and CFO
4.2.2. Construction of ICI Replica and Process of Interference Cancellation
4.2.3. Data Tracking for Sensing Result Separation
4.3. Sensing Results Separation with Duplication of Sensing Results
4.3.1. Detecting Duplication of Sensing Results
4.3.2. Data Tracking Based on Vector of Detected Subcarrier
5. Numerical Results
5.1. Simulation Results
5.2. Performance Evaluation Based on Actual Sensing Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A Survey on Enabling Technologies, Protocols, and Applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Verma, S.; Kawamoto, Y.; Fadlullah, Z.M.; Nishiyama, H.; Kato, N. A Survey on Network Methodologies for Real-Time Analytics of Massive IoT Data and Open Research Issues. IEEE Commun. Surv. Tutor. 2017, 19, 1457–1477. [Google Scholar] [CrossRef]
- Lu, C.; Saifullah, A.; Li, B.; Sha, M.; Gonzalez, H.; Gunatilaka, D.; Wu, C.; Nie, L.; Chen, Y. Real-Time Wireless Sensor-Actuator Networks for Industrial Cyber-Physical Systems. Proc. IEEE 2016, 104, 1013–1024. [Google Scholar] [CrossRef]
- Jiang, N.; Deng, Y.; Nallanathan, A.; Kang, X.; Quek, T.Q.S. Analyzing Random Access Collisions in Massive IoT Networks. IEEE Trans. Wire. Commun. 2018, 17, 6853–6870. [Google Scholar] [CrossRef]
- Endou, T.; Sakai, S.; Fujii, T. Information gathering for wireless sensor networks with information converting to wireless physical parameters. IEICE Trans. Commun. 2015, E98-B, 984–995. [Google Scholar] [CrossRef]
- Myoenzono, R.; Takyu, O.; Shirai, K.; Fujii, T.; Ohta, M.; Sasamori, F.; Handa, S. Data tracking and effect of frequency offset to simultaneous collecting method for wireless sensor networks. In Proceedings of the 2014 International Conference on Information and Communication Technology Convergence (ICTC), Busan, Korea, 22–24 October 2014. [Google Scholar]
- Oriuchi, M.; Takyu, O.; Shirai, K.; Sasamori, F.; Handa, S.; Fujii, T.; Ohta, M. Performance evaluation of multi-target tracking for PhyC-SN. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference (WCNCW), Doha, Qatar, 3–6 April 2016; pp. 351–354. [Google Scholar]
- Proakis, J.G. Digital Communications, 4th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Razavi, B. RF Microelectronics, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Zeng, Z.; Chang, J. Research and improvement of LTE uplink frequency offset estimation and compensation. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 19–22 September 2015. [Google Scholar]
- Fa, R.; Zhang, L.; Ramirez-Gutierrez, R. Blind carrier frequency offset tracking based on multiuser interference cancellation in OFDMA uplink systems. In Proceedings of the European Wireless 2012, 18th European Wireless Conference 2012, Poznan, Poland, 18–20 April 2012; pp. 1–5. [Google Scholar]
- Feng, Y.; Zhang, W.; Gao, F.; Sun, Q. Computationally Efficient Blind CFO Estimation for Massive MIMO Uplink. IEEE Trans. Veh. Technol. 2018, 67, 7795–7799. [Google Scholar] [CrossRef]
- Santra, A.; Hari, K.V.S. A Novel Subspace Based Method for Compensation of Multiple CFOs in Uplink MIMO OFDM Systems. IEEE Commun. Lett. 2017, 21, 1993–1996. [Google Scholar] [CrossRef]
- Choi, J.; Lee, C.; Jung, H.W.; Lee, Y.H. Carrier frequency offset compensation for uplink of OFDM-FDMA systems. IEEE Commun. Lett. 2000, 4, 414–416. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.C.; Carvalho, E.D.; Prasad, R. Multi-User Interference Cancellation Schemes for Carrier Frequency Offset Compensation in Uplink OFDMA. IEEE Trans. Wire. Commun. 2014, 13, 1164–1171. [Google Scholar] [CrossRef] [Green Version]
- Aziz, B.; Fijalkow, I.; Ariaudo, M. Joint estimation of channel and carrier frequency offset from the emitter, in an uplink OFDMA system. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 3492–3495. [Google Scholar]
- Pareyani, S.; Patel, P. An Improved ICI Cancellation Method to Reduce the Impact of Frequency Offset in OFDM Systems. In Proceedings of the 2015 International Conference on Computational Intelligence and Communication Networks (CICN), Jabalpur, India, 12–14 December 2015; pp. 496–501. [Google Scholar]
- Yeh, H. Space-time ICI conjugate cancellation techniques for OFDMA downlink in mobile fading channels. In Proceedings of the 2018 Annual IEEE International Systems Conference (SysCon), Vancouver, BC, Canada, 23–26 April 2018; pp. 1–6. [Google Scholar]
- Hwang, J.; Li, C.; Ma, C. Efficient Detection and Synchronization of Superimposed NB-IoT NPRACH Preambles. IEEE Int. Things J. 2018. [Google Scholar] [CrossRef]
- Lin, X.; Adhikary, A.; Wang, Y.E. Random Access Preamble Design and Detection for 3GPP Narrowband IoT Systems. IEEE Wire. Commun. Lett. 2016, 5, 640–643. [Google Scholar] [CrossRef]
- Martinez, B.; Vilajosana, X.; Dujovne, D. Accurate Clock Discipline For Long-Term Synchronization Intervals. IEEE Sens. J. 2017, 17, 2249–2258. [Google Scholar] [CrossRef]
- Wuerll, R.; Robert, J.; Kilian, G.; Heuberger, A. A comparison of methods for detecting preambles with frequency offset at low SNR. In Proceedings of the 2017 2nd International Conference on Computer and Communication Systems (ICCCS), Krakow, Poland, 11–14 July 2017; pp. 96–100. [Google Scholar]
- Wolf, F.; Villien, C.; Rivaz, S.D.; Dehmas, F.; Cances, J. Improved multi-channel ranging precision bound for narrowband LPWAN in multipath scenarios. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Sakai, S.; Fujii, T. Performance of physical wireless parameter conversion sensor network (PHY-C SN) using frequency hopping. In Proceedings of the 2014 4th IEEE International Conference on Network Infrastructure and Digital Content, Beijing, China, 19–21 September 2014; pp. 293–296. [Google Scholar]
- Prasad, R.; Van Nee, R.D.J. OFDM Wireless Multimedia Communications; Artech House: Norwood, MA, USA, 1999; Available online: http://uk.artechhouse.com/OFDM-for-Wireless-Multimedia-Communications-P1058.aspx (accessed on 13 February 2019).
- Zheng, C.; Chu, X.; McAllister, J.; Woods, R. Real-Valued Fixed-Complexity Sphere Decoder for High Dimensional QAM-MIMO Systems. IEEE Trans. Sig. Proc. 2011, 59, 4493–4499. [Google Scholar] [CrossRef]
- Sakai, T.; Takyu, O.; Shirai, K.; Ohta, M.; Fujii, T.; Sasamori, F.; Handa, S. Data Tracking Using Frequency Offset and SIC for Physical Wireless Conversion Sensor Networks. In Proceedings of the IEEE Wireless Communications and Networking Conference Workshops (WCNCW), San Francisco, CA, USA, 19–22 March 2017. [Google Scholar]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takyu, O.; Shirai, K.; Ohta, M.; Fujii, T. ID Insertion and Data Tracking with Frequency Offset for Physical Wireless Parameter Conversion Sensor Networks. Sensors 2019, 19, 767. https://doi.org/10.3390/s19040767
Takyu O, Shirai K, Ohta M, Fujii T. ID Insertion and Data Tracking with Frequency Offset for Physical Wireless Parameter Conversion Sensor Networks. Sensors. 2019; 19(4):767. https://doi.org/10.3390/s19040767
Chicago/Turabian StyleTakyu, Osamu, Keiichiro Shirai, Mai Ohta, and Takeo Fujii. 2019. "ID Insertion and Data Tracking with Frequency Offset for Physical Wireless Parameter Conversion Sensor Networks" Sensors 19, no. 4: 767. https://doi.org/10.3390/s19040767
APA StyleTakyu, O., Shirai, K., Ohta, M., & Fujii, T. (2019). ID Insertion and Data Tracking with Frequency Offset for Physical Wireless Parameter Conversion Sensor Networks. Sensors, 19(4), 767. https://doi.org/10.3390/s19040767





