Fast Optical Humidity Sensor Based on Hydrogel Thin Film Expansion for Harsh Environment †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Flory–Huggins Theory
2.2. Hydrogel Thin Film
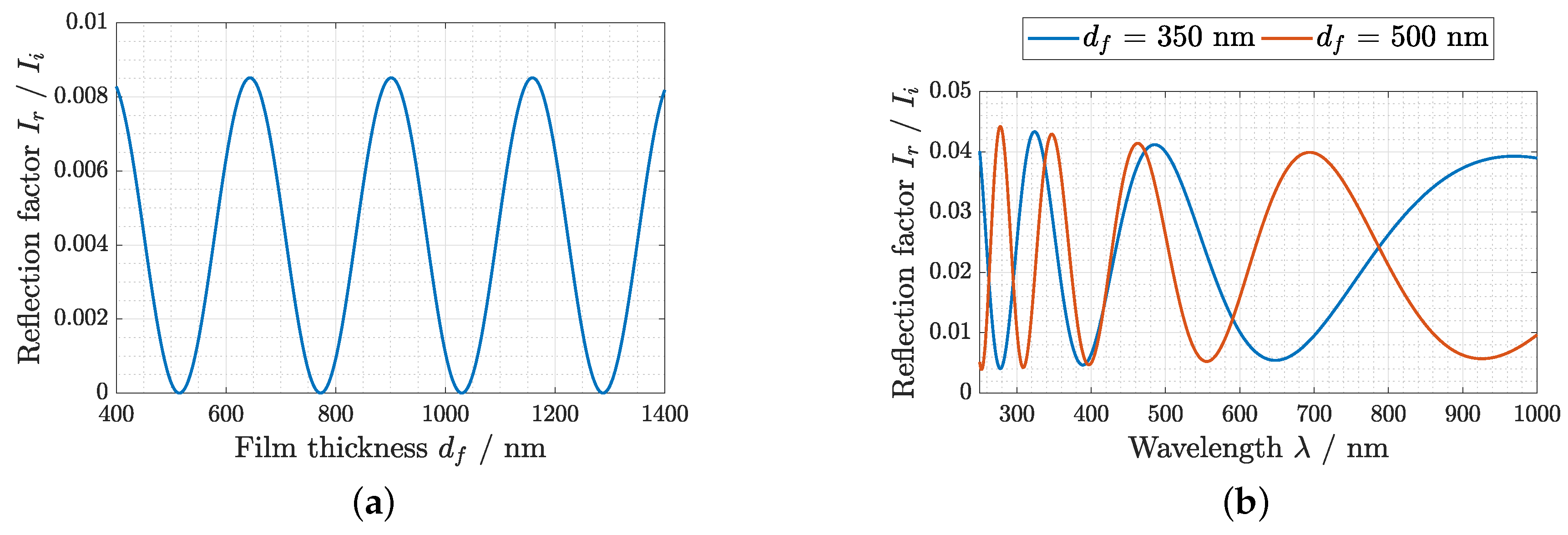
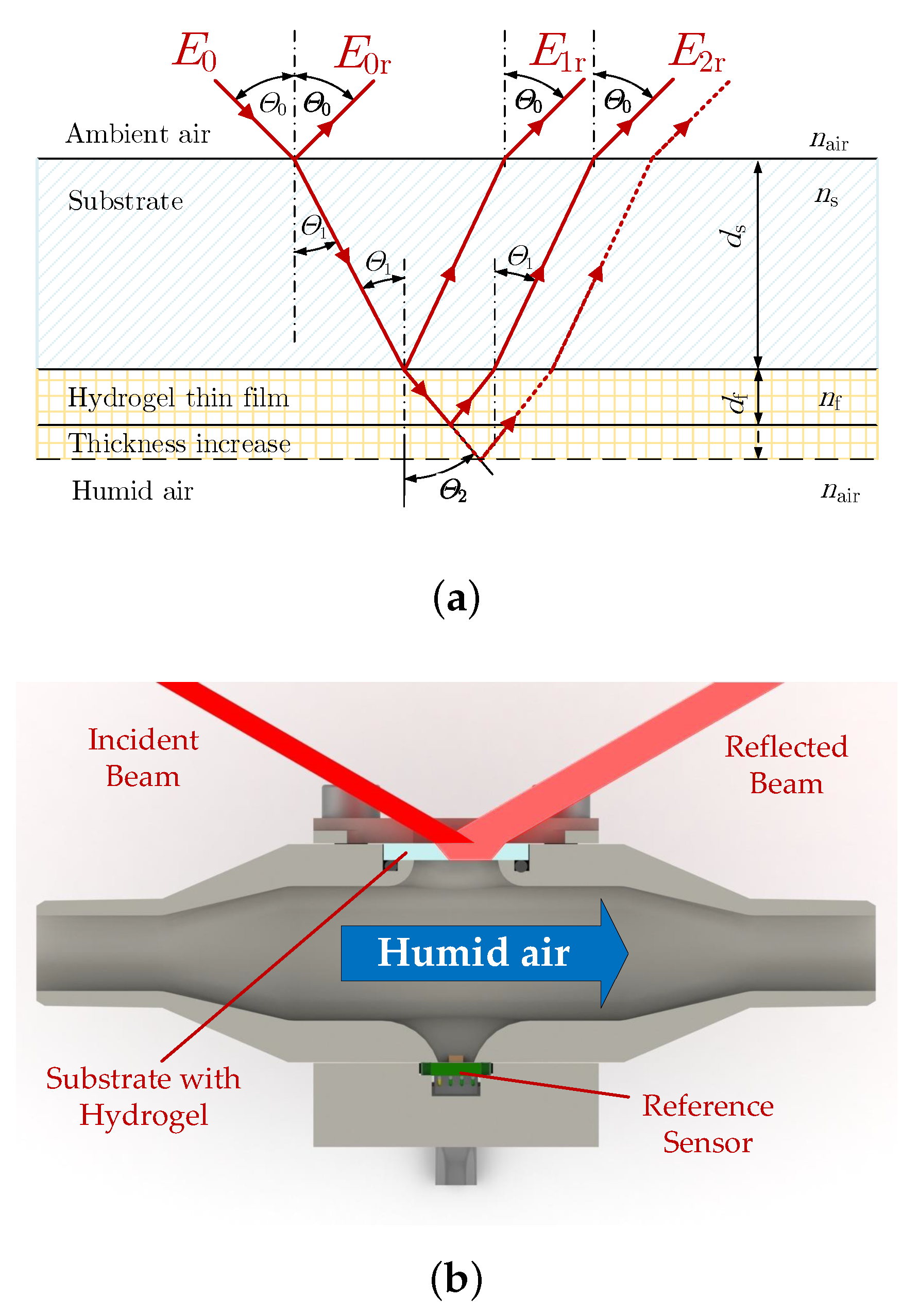
2.3. Optical Setup
3. Results and Discussion
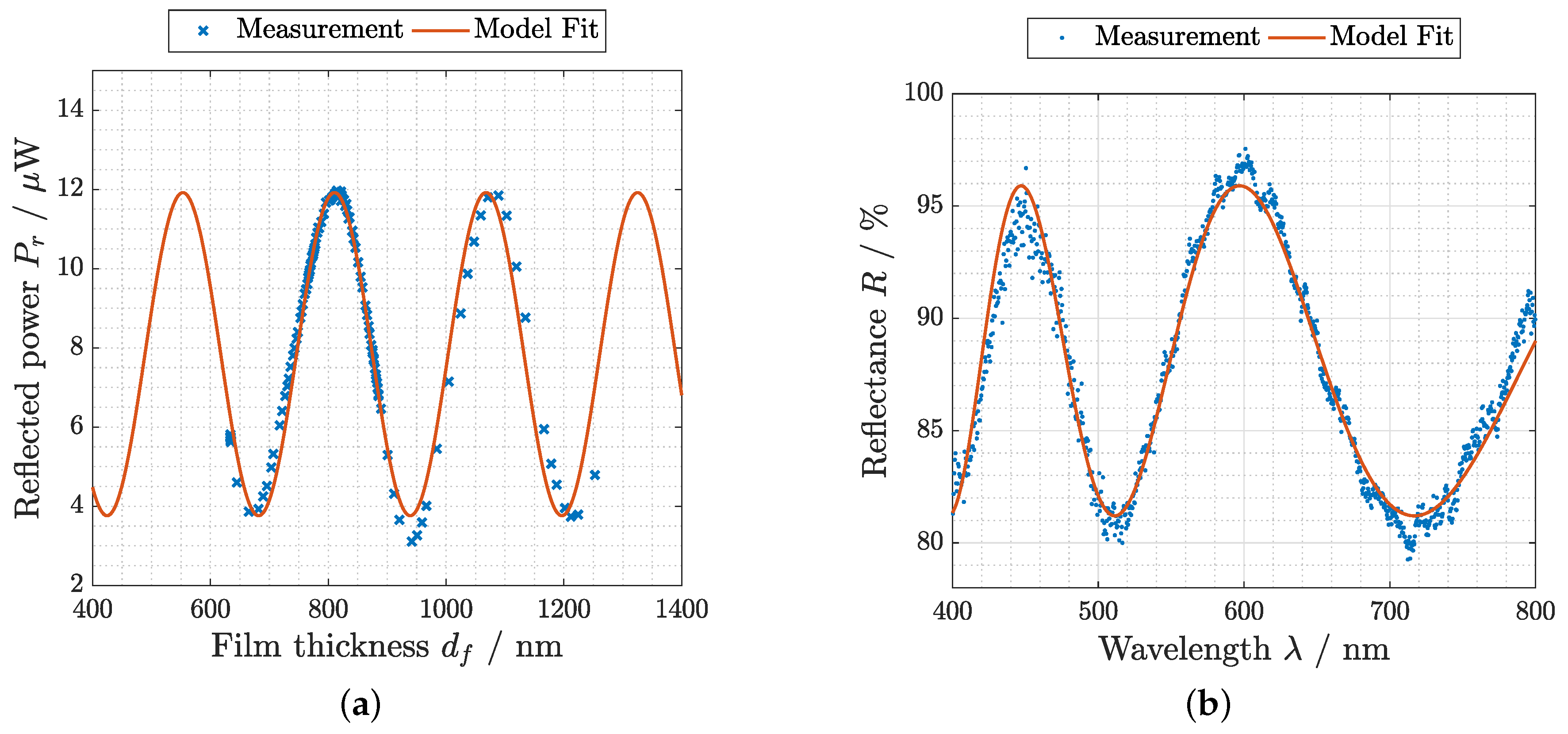
3.1. Thickness Measurement
3.2. Evaluation Flory–Huggins Theory
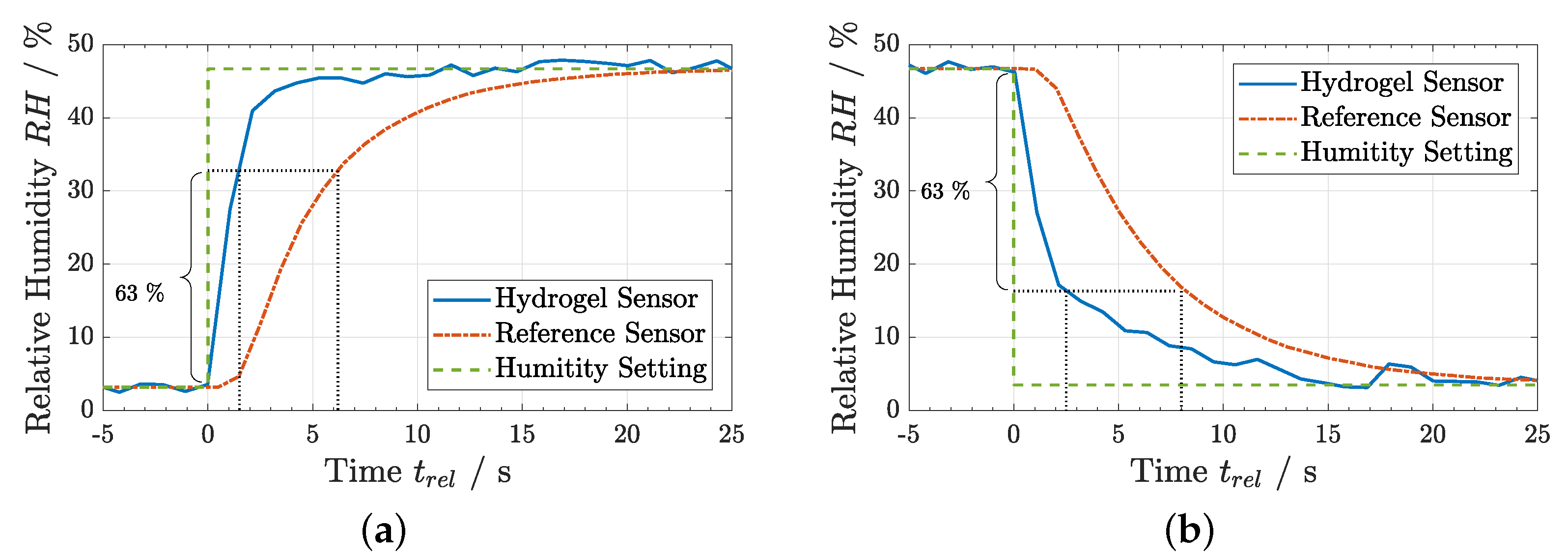
3.3. Humidity Measurements
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lozán, J.L.; Karbe, L.; Neukirch, U. GLOBAL CHANGE: Enough Water for All? Warnsignal Klima: Hamburg, Germany, 2007; p. 21. [Google Scholar]
- Kolpakov, S.A.; Gordon, N.T.; Mou, C.; Zhou, K. Toward a new generation of photonic humidity sensors. Sensors 2014, 14, 3986–4013. [Google Scholar] [CrossRef] [PubMed]
- Wernecke, R.; Wernecke, J. Industrial Moisture and Humidity Measurement; Wiley-VCH: Weinheim, Germany, 2014. [Google Scholar]
- Laville, C.; Pellet, C.; N’Kaoua, G. Interdigitated humidity sensors for a portable clinical microsystem. IEEE-EMBS Lyon Proc. 2000, 49, 572–577. [Google Scholar] [CrossRef]
- Draper, J.W. A Text-Book on Chemistry; Harper & Brothers: New York, NY, USA, 1861. [Google Scholar]
- Narayanaswamy, R.; Wofbeis, O.S. Optical Sensors—Industrial Environmental and Diagnostic Applications; Springer: Berlin, Germany, 2004; p. 253. [Google Scholar]
- Wexler, A.; Hyland, R.W. The NBS Standard Hygrometer; National Bureau of Standards: Washington, DC, USA, 1964.
- Sakai, Y.; Sadaoka, Y.; Matsuguchi, M. Humidity sensors based on polymer thin films. Sens. Actuators B Chem. 1996, 35, 85–90. [Google Scholar] [CrossRef]
- Farahani, H.; Wagiran, R.; Hamidon, M.N. Humidity sensors principle, mechanism, and fabrication technologies: A comprehensive review. Sensors 2014, 14, 7881–7939. [Google Scholar] [CrossRef] [PubMed]
- Løkken, T.V. Comparison of hygrometers for monitoring of water vapour in natural gas. J. Nat. Gas Sci. Eng. 2012, 6, 24–36. [Google Scholar] [CrossRef] [Green Version]
- Perry, R.H.; Green, D.W.; Maloney, J.O. Chemical Engineers’ Handbook, 7th ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Unger, K.; Resel, R.; Coclite, A.M. Dynamic studies on the response to humidity of poly(2-hydroxyethylmethacrylate) hydrogels produced by initiated chemical vapor deposition. Macromol. Chem. Phys. 2016, 217, 2372–2379. [Google Scholar] [CrossRef]
- Stuart, M.A.C.; Huck, W.T.S.; Genzer, J.; Müller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.V.; Urban, M.; et al. Emerging applications of stimuli-responsive polymer materials. Nat. Mater. 2010, 9, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Teraoka, I. Polymer Solutions; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Reeja-Jayan, B.; Kovacik, P.; Yang, R.; Sojoudi, H.; Ugur, A.; Kim, D.H.; Petruczok, C.D.; Wang, X.; Liu, A.; Gleason, K.K. A route towards sustainability through engineered polymeric interfaces. Adv. Mater. Interfaces 2014, 1, 1–30. [Google Scholar] [CrossRef]
- Petruczok, C.D.; Armagan, E.; Ince, G.O.; Gleason, K.K. Initiated chemical vapor deposition and light-responsive cross-linking of poly(vinyl cinnamate) thin films. Macromol. Rapid Commun. 2014, 35, 1345–1350. [Google Scholar] [CrossRef] [PubMed]
- Coclite, A.M.; Howden, R.M.; Borrelli, D.C.; Petruczok, C.D.; Yang, R.; Yagüe, J.L.; Ugur, A.; Chen, N.; Lee, S.; Jo, W.J.; et al. 25th anniversary article: CVD polymers: A new paradigm for surface modification and device fabrication. Adv. Mater. 2013, 25, 5392–5423. [Google Scholar] [CrossRef] [PubMed]
- Christian, P.; Ehmann, H.M.; Werzer, O.; Coclite, A.M. Wrinkle formation in a polymeric drug coating deposited via initiated chemical vapor deposition. Soft Matter 2016, 12, 9501–9508. [Google Scholar] [CrossRef] [PubMed]
- Ranacher, C.; Resel, R.; Moni, P.; Cermenek, B.; Hacker, V.; Coclite, A.M. Layered nanostructures in proton conductive polymers obtained by initiated chemical vapor deposition. Macromolecules 2015, 48, 6177–6185. [Google Scholar] [CrossRef]
- Reinhardt, H.M.; Recktenwald, D.; Kim, H.C.; Hampp, N.A. High refractive index TiO2-PHEMA hydrogel for ophthalmological applications. J. Mater. Sci. 2016, 51, 9971–9978. [Google Scholar] [CrossRef]
- Sperling, L.H. Introduction to Physical Polymer Science, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; p. 84. [Google Scholar]
- Mark, J. Physical Properties of Polymers Handbook, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Rodríguez, O.; Fomasiero, F.; Arcea, A.; Radkea, C.J.; Prausnitz, J.M. Solubilities and diffusivities of water vapor in poly(methylmethacrylate), poly(2-hydroxyethylmethacrylate), poly(N-vinyl-2-pyrrolidone) and poly(acrylonitrile). Polymer 2003, 44, 6323–6333. [Google Scholar] [CrossRef]
- Salzmann, P.; Perrotta, A.; Coclite, A.M. Different response kinetics to temperature and water vapor of acrylamide polymers obtained by initiated chemical vapor deposition. ACS Appl. Mater. Interfaces 2018, 10, 6636–6645. [Google Scholar] [CrossRef] [PubMed]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buchberger, A.; Peterka, S.; Coclite, A.M.; Bergmann, A. Fast Optical Humidity Sensor Based on Hydrogel Thin Film Expansion for Harsh Environment. Sensors 2019, 19, 999. https://doi.org/10.3390/s19050999
Buchberger A, Peterka S, Coclite AM, Bergmann A. Fast Optical Humidity Sensor Based on Hydrogel Thin Film Expansion for Harsh Environment. Sensors. 2019; 19(5):999. https://doi.org/10.3390/s19050999
Chicago/Turabian StyleBuchberger, Anton, Sebastian Peterka, Anna Maria Coclite, and Alexander Bergmann. 2019. "Fast Optical Humidity Sensor Based on Hydrogel Thin Film Expansion for Harsh Environment" Sensors 19, no. 5: 999. https://doi.org/10.3390/s19050999
APA StyleBuchberger, A., Peterka, S., Coclite, A. M., & Bergmann, A. (2019). Fast Optical Humidity Sensor Based on Hydrogel Thin Film Expansion for Harsh Environment. Sensors, 19(5), 999. https://doi.org/10.3390/s19050999




