Mapping the Dielectric Properties of Unknown Targets by Using a Network of Microwave Sensors: A Proof-of-Concept †
Abstract
1. Introduction
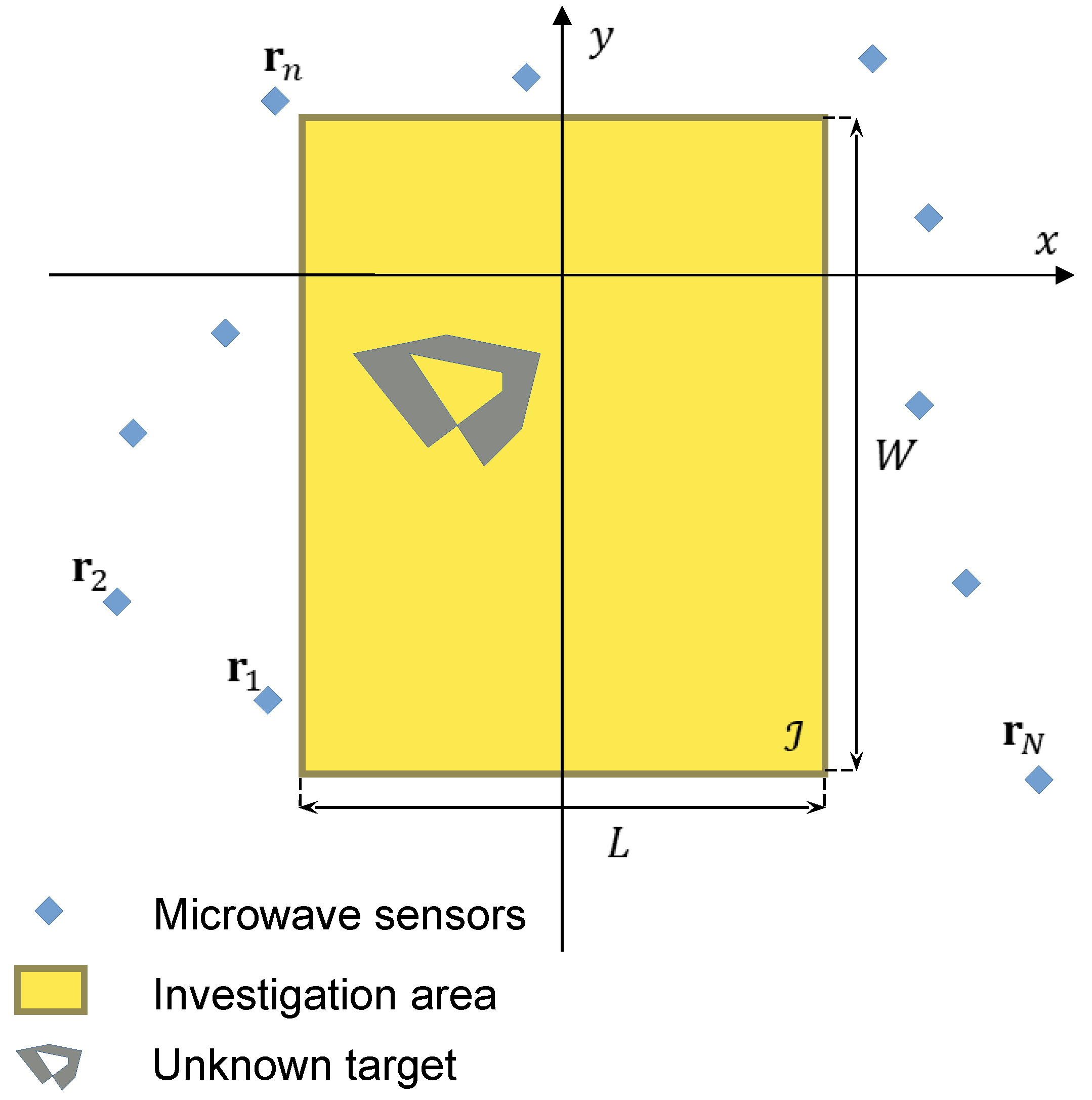
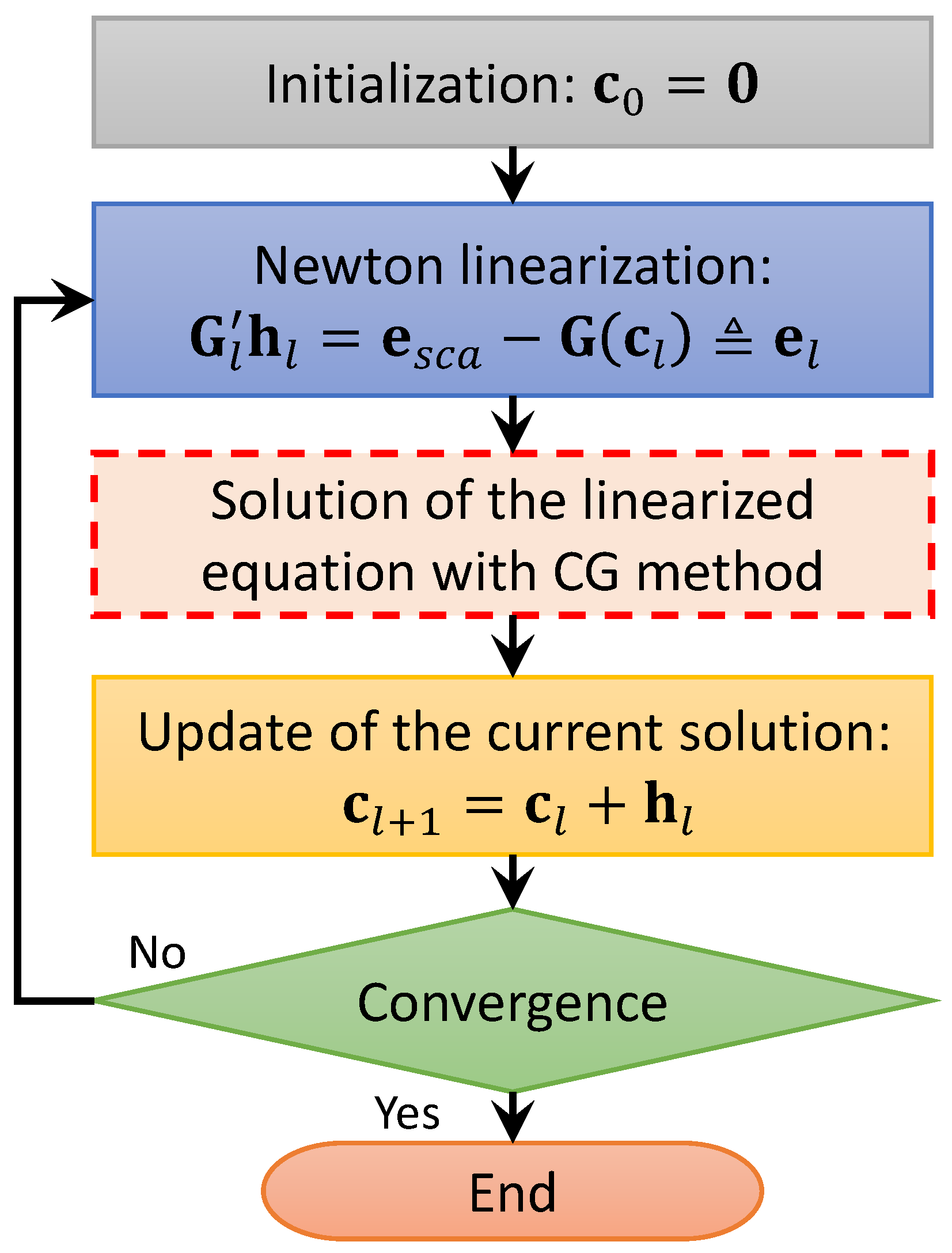
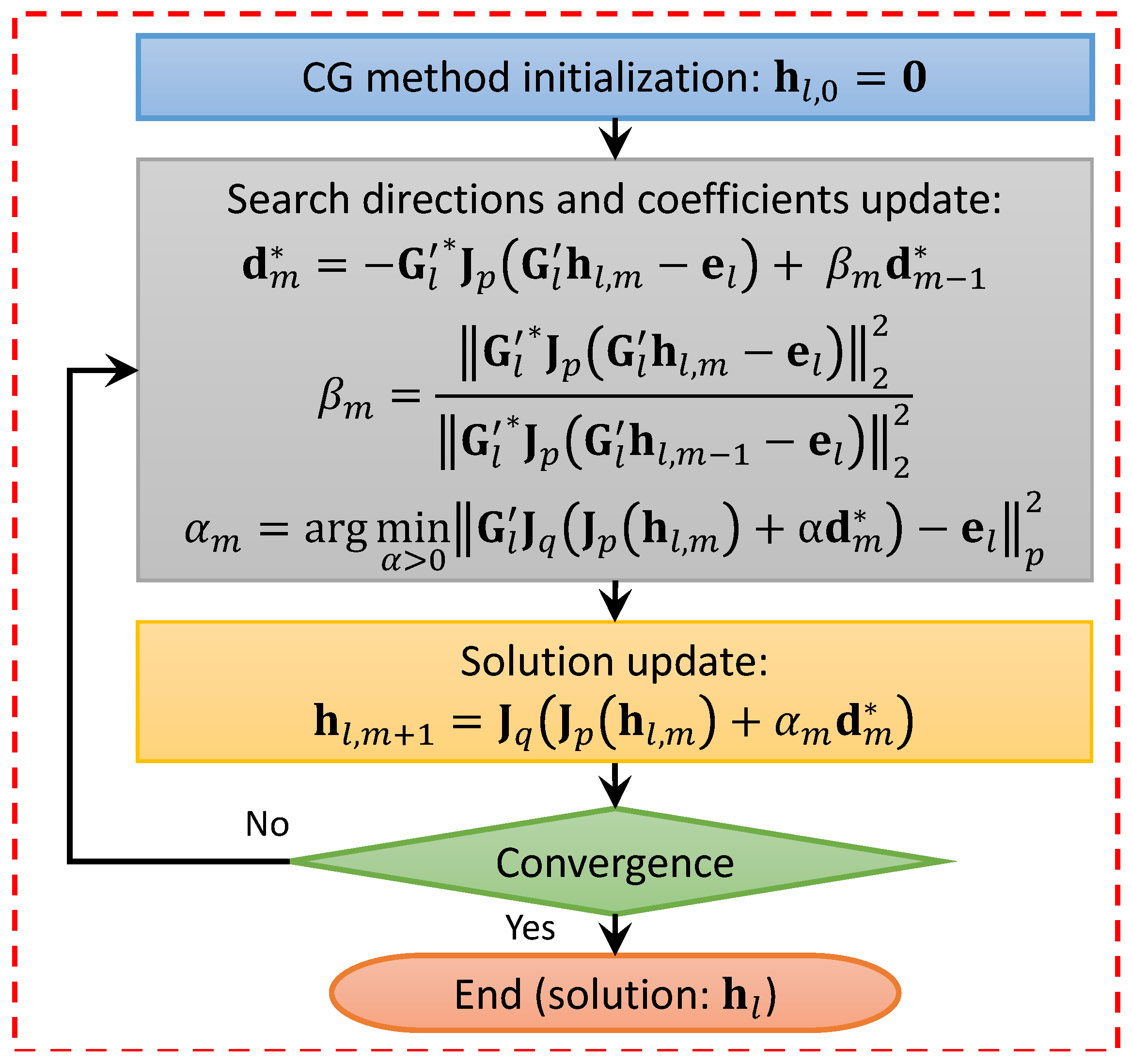
2. Problem Description and Solution Strategy
3. Preliminary Results
3.1. Simulated Environment
- center at the point ;
- side lengths and ;
- relative dielectric permittivity ;
- electric conductivity S/m.
3.1.1. Aligned Sensors
3.1.2. Non-Aligned Sensors
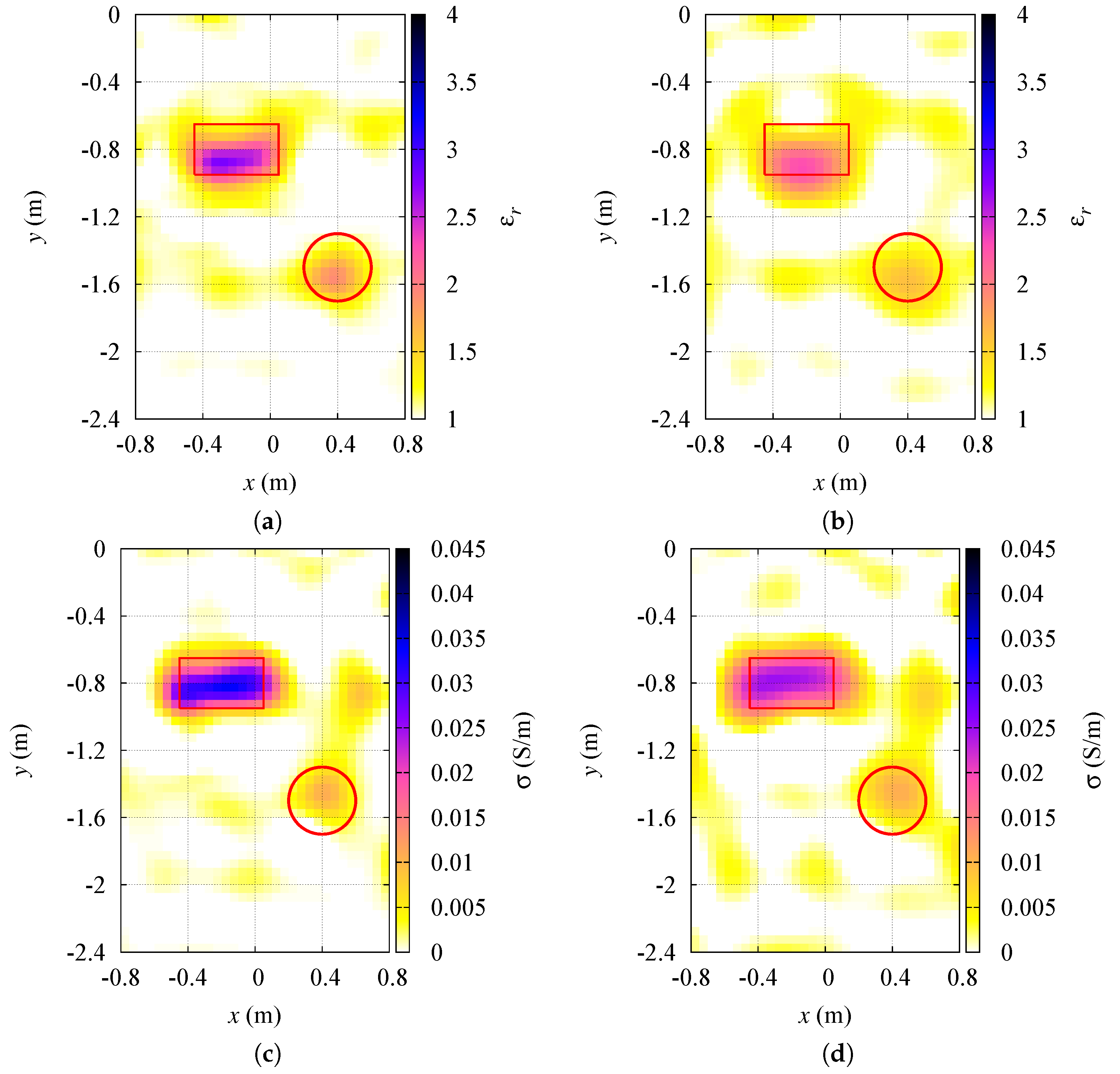
3.1.3. Multiple Targets in the Investigation Area
- radius m;
- relative dielectric permittivity ;
- electric conductivity S/m.
3.1.4. Variation of the Number of Sensors
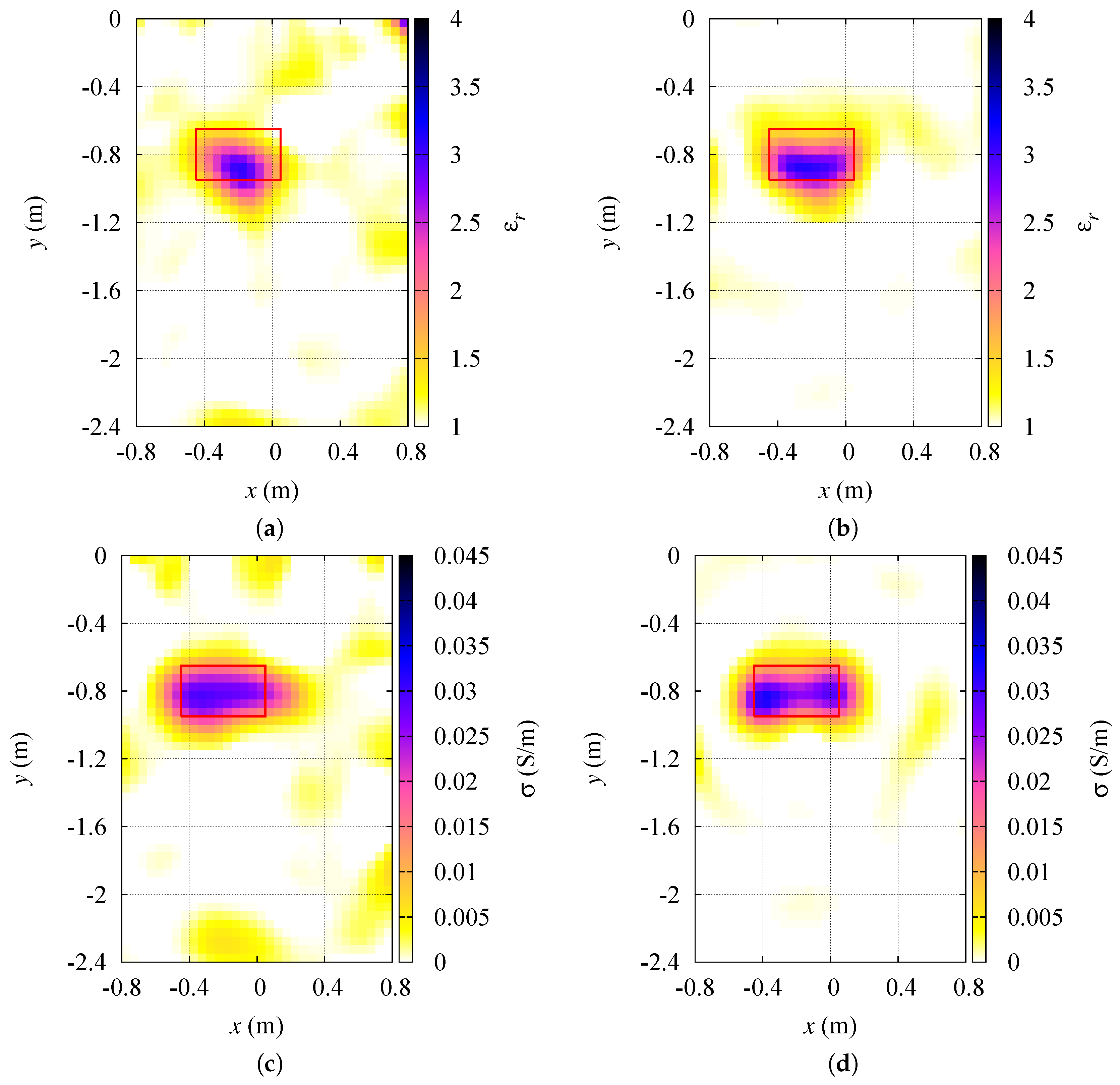
3.1.5. Effect of Uncertainties in Sensor Positions
- side lengths and ;
- relative dielectric permittivity ;
- electric conductivity S/m.
3.1.6. Variation of the Dielectric Properties
- radius m;
- relative dielectric permittivity varied in the interval ;
- electric conductivity S/m.
3.1.7. Spatial Resolution
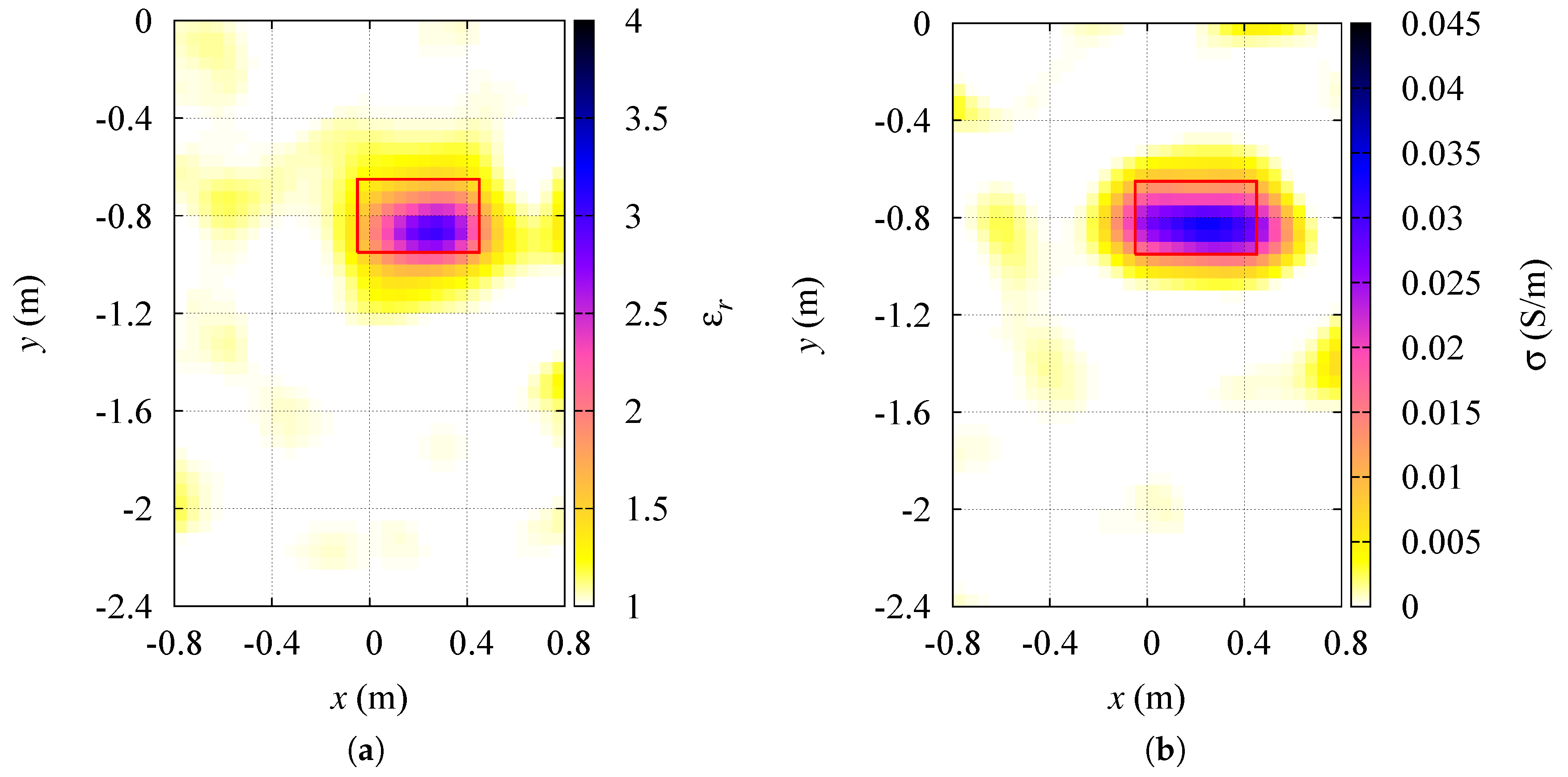
3.2. Mapping from Experimental Data
- radius m;
- relative dielectric permittivity ;
- electric conductivity S/m.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xia, F. Wireless Sensor Technologies and Applications. Sensors 2009, 9, 8824–8830. [Google Scholar] [CrossRef] [PubMed]
- Skiani, E.D.; Mitilineos, S.A.; Thomopoulos, S.C.A. A study of the performance of wireless sensor networks operating with smart antennas. IEEE Antennas Propag. Mag. 2012, 54, 50–67. [Google Scholar] [CrossRef]
- Tan, X.; Sun, Z.; Akyildiz, I.F. Wireless underground sensor networks: MI-based communication systems for underground applications. IEEE Antennas Propag. Mag. 2015, 57, 74–87. [Google Scholar] [CrossRef]
- Ali, S.; Ashraf, A.; Qaisar, S.B.; Afridi, M.K.; Saeed, H.; Rashid, S.; Felemban, E.A.; Sheikh, A.A. SimpliMote: A wireless sensor network monitoring platform for oil and gas pipelines. IEEE Syst. J. 2018, 12, 778–789. [Google Scholar] [CrossRef]
- Zhang, Q.; Wan, J.W.; Wang, D.D.; Chen, J.Y.; Wang, D.H. Sparsity-incorporated secure localisation for wireless sensor networks. Electron. Lett. 2017, 53, 629–631. [Google Scholar] [CrossRef]
- Oteafy, S.M.A.; Hassanein, H.S. Big sensed data: Evolution, challenges, and a progressive framework. IEEE Commun. Mag. 2018, 56, 108–114. [Google Scholar] [CrossRef]
- Sheng, Z.; Tian, D.; Leung, V.C.M. Toward an energy and resource efficient internet of things: A design principle combining computation, communications, and protocols. IEEE Commun. Mag. 2018, 56, 89–95. [Google Scholar] [CrossRef]
- Buratti, C.; Conti, A.; Dardari, D.; Verdone, R. An Overview on Wireless Sensor Networks Technology and Evolution. Sensors 2009, 9, 6869–6896. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Zhang, Z.; Liu, C.; Luo, H. Reliable and cooperative target tracking based on wsn and WiFi in indoor wireless networks. IEEE Access 2018, 6, 24846–24855. [Google Scholar] [CrossRef]
- Fang, X.; Nan, L.; Jiang, Z.; Chen, L. Multi-channel fingerprint localisation algorithm for wireless sensor network in multipath environment. IET Commun. 2017, 11, 2253–2260. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Q.; Wang, H.; Yu, Y.; Jin, M. Time-of-Flight-Based Radio Tomography for Device Free Localization. IEEE Trans. Wirel. Commun. 2013, 12, 2355–2365. [Google Scholar] [CrossRef]
- Lanzisera, S.; Zats, D.; Pister, K.S.J. Radio Frequency Time-of-Flight Distance Measurement for Low-Cost Wireless Sensor Localization. IEEE Sens. J. 2011, 11, 837–845. [Google Scholar] [CrossRef]
- Werner, J.; Wang, J.; Hakkarainen, A.; Gulati, N.; Patron, D.; Pfeil, D.; Dandekar, K.; Cabric, D.; Valkama, M. Sectorized Antenna-based DoA Estimation and Localization: Advanced Algorithms and Measurements. IEEE J. Sel. Areas Commun. 2015, 33, 2272–2286. [Google Scholar] [CrossRef]
- Pastorino, M.; Randazzo, A. The SVM-based smart antenna for estimation of the directions of arrival of electromagnetic waves. IEEE Trans. Instrum. Meas. 2006, 55, 1918–1925. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. TDOA Positioning Irrespective of Source Range. IEEE Trans. Signal Process. 2017, 65, 1447–1460. [Google Scholar] [CrossRef]
- Sahu, P.K.; Wu, E.H.; Sahoo, J. DuRT: Dual RSSI trend based localization for wireless sensor networks. IEEE Sens. J. 2013, 13, 3115–3123. [Google Scholar] [CrossRef]
- Bisio, I.; Cerruti, M.; Lavagetto, F.; Marchese, M.; Pastorino, M.; Randazzo, A.; Sciarrone, A. A trainingless WiFi fingerprint positioning approach over mobile devices. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 832–835. [Google Scholar] [CrossRef]
- Niu, R.; Vempaty, A.; Varshney, P.K. Received-signal-strength-based localization in wireless sensor networks. Proc. IEEE 2018, 106, 1166–1182. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.G.; Ding, J.; Liu, P.K.; Xia, M.Y.; Cui, T.J. A probabilistic model for the nonlinear electromagnetic inverse scattering: TM case. IEEE Trans. Antennas Propag. 2017, 65, 5984–5991. [Google Scholar] [CrossRef]
- Desmal, A.; Bağcı, H. Sparse nonlinear electromagnetic imaging accelerated with projected steepest descent algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3810–3822. [Google Scholar] [CrossRef]
- Boero, F.; Fedeli, A.; Lanini, M.; Maffongelli, M.; Monleone, R.; Pastorino, M.; Randazzo, A.; Salvadè, A.; Sansalone, A. Microwave tomography for the inspection of wood materials: imaging system and experimental results. IEEE Trans. Microw. Theory Tech. 2018, 66, 3497–3510. [Google Scholar] [CrossRef]
- Zhong, Y.; Lambert, M.; Lesselier, D.; Chen, X. A new integral equation method to solve highly nonlinear inverse scattering problems. IEEE Trans. Antennas Propag. 2016, 64, 1788–1799. [Google Scholar] [CrossRef]
- Salucci, M.; Oliveri, G.; Anselmi, N.; Viani, F.; Fedeli, A.; Pastorino, M.; Randazzo, A. Three-dimensional electromagnetic imaging of dielectric targets by means of the multiscaling inexact-Newton method. J. Opt. Soc. Am. A 2017, 34, 1119. [Google Scholar] [CrossRef] [PubMed]
- Bisio, I.; Fedeli, A.; Lavagetto, F.; Pastorino, M.; Randazzo, A.; Sciarrone, A.; Tavanti, E. A numerical study concerning brain stroke detection by microwave imaging systems. Multimed. Tools Appl. 2018, 77, 9341–9363. [Google Scholar] [CrossRef]
- Randazzo, A. Swarm optimization methods in microwave imaging. Int. J. Microw. Sci. Technol. 2012, 2012, 491713. [Google Scholar] [CrossRef]
- Abubakar, A.; Habashy, T.M.; Pan, G. Microwave data inversions using the source-receiver compression scheme. IEEE Trans. Antennas Propag. 2012, 60, 2853–2864. [Google Scholar] [CrossRef]
- Pastorino, M. Short-range microwave inverse scattering techniques for image reconstruction and applications. IEEE Trans. Instrum. Meas. 1998, 47, 1419–1427. [Google Scholar] [CrossRef]
- Shumakov, D.S.; Nikolova, N.K. Fast quantitative microwave imaging with scattered-power maps. IEEE Trans. Microw. Theory Tech. 2018, 66, 439–449. [Google Scholar] [CrossRef]
- Caorsi, S.; Massa, A.; Pastorino, M.; Randazzo, A. Electromagnetic detection of dielectric scatterers using phaseless synthetic and real data and the memetic algorithm. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2745–2753. [Google Scholar] [CrossRef]
- Eskandari, A.R.; Naser-Moghaddasi, M.; Virdee, B.S. Target identification enhancement using a combination of linear sampling method and adjoint sensitivity analysis. Antennas Propag. IET Microw. 2012, 6, 461–469. [Google Scholar] [CrossRef]
- Shah, P.; Chen, G.; Stang, J.; Moghaddam, M. 3-D Level Set Method for Joint Contrast and Shape Recovery in Microwave Imaging. IEEE Trans. Comput. Imaging 2019, 5, 97–108. [Google Scholar] [CrossRef]
- Solimene, R.; Leone, G. MUSIC Algorithms for Grid Diagnostics. IEEE Geosci. Remote Sens. Lett. 2013, 10, 226–230. [Google Scholar] [CrossRef]
- Abubakar, A.; Hu, W.; van den Berg, P.M.; Habashy, T.M. A finite-difference contrast source inversion method. Inverse Probl. 2008, 24, 065004. [Google Scholar] [CrossRef]
- Randazzo, A.; Oliveri, G.; Massa, A.; Pastorino, M. Electromagnetic inversion with the multiscaling inexact Newton method-experimental validation. Microw. Opt. Technol. Lett. 2011, 53, 2834–2838. [Google Scholar] [CrossRef]
- Desmal, A.; Bağcı, H. A Preconditioned Inexact Newton Method for Nonlinear Sparse Electromagnetic Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 532–536. [Google Scholar] [CrossRef]
- Mojabi, P.; LoVetri, J.; Shafai, L. A multiplicative regularized Gauss-Newton inversion for shape and location reconstruction. IEEE Trans. Antennas Propag. 2011, 59, 4790–4802. [Google Scholar] [CrossRef]
- Fedeli, A.; Gragnani, G.L.; Pastorino, M.; Randazzo, A. Microwave Sensor Network for Quantitative Characterization of Targets: A Proof-of-Concept. In Proceedings of the 2018 Advances in Wireless and Optical Communications (RTUWO), Riga, Latvia, 15–16 November 2018; pp. 246–250. [Google Scholar] [CrossRef]
- Belkebir, K.; Saillard, M. Special section: Testing inversion algorithms against experimental data. Inverse Probl. 2001, 17, 1565–1571. [Google Scholar] [CrossRef]
- Estatico, C.; Fedeli, A.; Pastorino, M.; Randazzo, A. Microwave imaging of elliptically shaped dielectric cylinders by means of an Lp Banach-space inversion algorithm. Meas. Sci. Technol. 2013, 24, 074017. [Google Scholar] [CrossRef]
- Estatico, C.; Fedeli, A.; Pastorino, M.; Randazzo, A. A multifrequency inexact-Newton method in Lp Banach spaces for buried objects detection. IEEE Trans. Antennas Propag. 2015, 63, 4198–4204. [Google Scholar] [CrossRef]
- Estatico, C.; Fedeli, A.; Pastorino, M.; Randazzo, A. A Banach space regularization approach for multifrequency microwave imaging. Int. J. Antennas Propag. 2016, 2016, 9304371. [Google Scholar] [CrossRef]
- Bisio, I.; Estatico, C.; Fedeli, A.; Lavagetto, F.; Pastorino, M.; Randazzo, A.; Sciarrone, A. Brain stroke microwave imaging by means of a Newton-conjugate-gradient method in Lp Banach spaces. IEEE Trans. Microw. Theory Tech. 2018, 66, 3668–3682. [Google Scholar] [CrossRef]
- Estatico, C.; Gratton, S.; Lenti, F.; Titley-Peloquin, D. A conjugate gradient like method for p-norm minimization in functional spaces. Numer. Math. 2017, 137, 895–922. [Google Scholar] [CrossRef]
- Pastorino, M.; Randazzo, A. Microwave Imaging Methods and Applications; Artech House: Boston, MA, USA, 2018. [Google Scholar]
- Harrington, R.F. Field Computation by Moment Methods; IEEE: Piscataway, NJ, USA, 1993. [Google Scholar]
- Estatico, C.; Fedeli, A.; Pastorino, M.; Randazzo, A. Quantitative microwave imaging method in Lebesgue spaces with nonconstant exponents. IEEE Trans. Antennas Propag. 2018, 66, 7282–7294. [Google Scholar] [CrossRef]





| Sensor ID | x (m) | y (m) | Sensor ID | x (m) | y (m) | Sensor ID | x (m) | y (m) |
|---|---|---|---|---|---|---|---|---|
| 1 | −1.00 | 0.50 | 6 | −1.00 | −2.00 | 11 | 1.00 | −2.00 |
| 2 | −0.50 | 0.50 | 7 | −1.00 | −1.50 | 12 | 1.00 | −1.50 |
| 3 | 0 | 0.50 | 8 | −1.00 | −1.00 | 13 | 1.00 | −1.00 |
| 4 | 0.50 | 0.50 | 9 | −1.00 | −0.50 | 14 | 1.00 | −0.50 |
| 5 | 1.00 | 0.50 | 10 | −1.00 | 0 | 15 | 1.00 | 0 |
| Test Case | Value of p | Relative Characterization Errors | ||
|---|---|---|---|---|
| Background Area, | Target Area, | Whole Inspection Domain, | ||
| Aligned sensors | 1.4 | 0.122 | 0.456 | 0.135 |
| 2.0 | 0.205 | 0.453 | 0.215 | |
| Non-aligned sensors | 1.4 | 0.107 | 0.431 | 0.120 |
| 2.0 | 0.182 | 0.439 | 0.192 | |
| Multiple targets | 1.4 | 0.142 | 0.369 | 0.158 |
| 2.0 | 0.216 | 0.394 | 0.229 | |
| Sensor ID | x (m) | y (m) | Sensor ID | x (m) | y (m) | Sensor ID | x (m) | y (m) |
|---|---|---|---|---|---|---|---|---|
| 1 | −1.05 | 0.40 | 6 | −0.90 | −2.10 | 11 | 0.90 | −2.00 |
| 2 | −0.50 | 0.50 | 7 | −1.00 | −1.40 | 12 | 1.00 | −1.60 |
| 3 | 0.10 | 0.45 | 8 | −0.95 | −1.10 | 13 | 1.10 | −1.20 |
| 4 | 0.50 | 0.55 | 9 | −0.85 | −0.50 | 14 | 0.85 | −0.60 |
| 5 | 1.10 | 0.45 | 10 | −1.00 | 0.10 | 15 | 0.95 | 0.20 |
| Number of Sensors | Relative Characterization Errors | ||
|---|---|---|---|
| Background Area, | Target Area, | Whole Inspection Domain, | |
| 9 | 0.177 | 0.448 | 0.166 |
| 18 | 0.115 | 0.445 | 0.101 |
| 27 | 0.120 | 0.418 | 0.108 |
| 36 | 0.112 | 0.391 | 0.101 |
| 45 | 0.115 | 0.390 | 0.104 |
| 54 | 0.110 | 0.380 | 0.099 |
| Displacement width, d (m) | Relative Characterization Errors | ||
|---|---|---|---|
| Background Area, | Target Area, | Whole Inspection Domain, | |
| 0.025 | 0.145 | 0.347 | 0.153 |
| 0.075 | 0.172 | 0.524 | 0.186 |
| 0.125 | 0.175 | 0.626 | 0.192 |
| 0.175 | 0.161 | 1.060 | 0.196 |
| Relative Characterization Errors | ||
|---|---|---|
| Background area, | Target area, | Whole inspection domain, |
| 0.0297 | 0.255 | 0.0276 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estatico, C.; Fedeli, A.; Gragnani, G.L.; Pastorino, M.; Randazzo, A. Mapping the Dielectric Properties of Unknown Targets by Using a Network of Microwave Sensors: A Proof-of-Concept. Sensors 2019, 19, 1270. https://doi.org/10.3390/s19061270
Estatico C, Fedeli A, Gragnani GL, Pastorino M, Randazzo A. Mapping the Dielectric Properties of Unknown Targets by Using a Network of Microwave Sensors: A Proof-of-Concept. Sensors. 2019; 19(6):1270. https://doi.org/10.3390/s19061270
Chicago/Turabian StyleEstatico, Claudio, Alessandro Fedeli, Gian Luigi Gragnani, Matteo Pastorino, and Andrea Randazzo. 2019. "Mapping the Dielectric Properties of Unknown Targets by Using a Network of Microwave Sensors: A Proof-of-Concept" Sensors 19, no. 6: 1270. https://doi.org/10.3390/s19061270
APA StyleEstatico, C., Fedeli, A., Gragnani, G. L., Pastorino, M., & Randazzo, A. (2019). Mapping the Dielectric Properties of Unknown Targets by Using a Network of Microwave Sensors: A Proof-of-Concept. Sensors, 19(6), 1270. https://doi.org/10.3390/s19061270








