Adaptive Unscented Kalman Filter for Target Tracking with Unknown Time-Varying Noise Covariance
Abstract
:1. Introduction
2. The UKF Algorithm for Nonlinear State Estimation
2.1. Standard UKF
2.2. Problem Description of UKF for Time-Varying Noise Covariance
3. An Innovative Adaptive UKF Scheme
3.1. Adaptive Q Estimation
3.2. Adaptive R Estimation
3.3. Adaptive UKF Scheme
4. Simulation Results and Discussion
4.1. Simulation Parameter and Cases
4.2. Simulation Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix
References
- Zhou, H.; Huang, H.; Zhao, H.; Zhao, X.; Yin, X. Adaptive Unscented Kalman Filter for Target Tracking in the Presence of Nonlinear Systems Involving Model Mismatches. Remote Sens. 2017, 9, 657. [Google Scholar] [CrossRef]
- Chatterjee, S.; Sardar, S.; Biswas, S.; Roy, S. WSN based robust ground target tracking for precision guided missiles. Int. J. Res. Comput. Appl. Manag. 2013, 3, 4. [Google Scholar]
- Sreeja, S.; Hablani, H. Precision munition guidance and estimation of target position in 2-D. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Cao, Y.; Wang, G.; Yan, D.; Zhao, Z. Two Algorithms for the Detection and Tracking of Moving Vehicle Targets in Aerial Infrared Image Sequences. Remote Sens. 2016, 8, 28. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, X.; Yang, Q. Modified Multi-Mode Target Tracker for High-Frequency Surface Wave Radar. Remote Sens. 2016, 8, 28. [Google Scholar] [CrossRef]
- Benfold, B.; Reid, I. Stable multi-target tracking in real-time surveillance video. In Proceedings of the Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3457–3464. [Google Scholar]
- Duh, F.B.; Lin, C.T. Tracking a maneuvering target using neural fuzzy network. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 16–33. [Google Scholar] [CrossRef]
- Shi, Y.; Han, C.Z. Adaptive UKF Method with Applications to Target Tracking. Acta Autom. Sin. 2011, 37, 755–759. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problem. J. Basic Eng. 1960, 82, 95–108. [Google Scholar] [CrossRef]
- Van der Merwe, R.; Doucet, A.; De Freitas, N.; Wan, E. The unscented particle filter. Adv. Neural Inf. Process. Syst. 2001, 96, 584–590. [Google Scholar]
- Aditya, P.; Apriliani, E.; Khusnul Arif, D.; Baihaqi, K. Estimation of three-dimensional radar tracking using modified extended kalman filter. J. Phys. Conf. Ser. 2018, 897, 012071. [Google Scholar] [CrossRef]
- Kumar, G.; Prasad, D.; Singh, R.P. Target tracking using adaptive Kalman Filter. In Proceedings of the 2017 International Conference on Smart grids, Power and Advanced Control Engineering, Bangalore, India, 17–19 August 2017; pp. 376–380. [Google Scholar]
- Lippiello, V.; Siciliano, B.; Villani, L. Visual motion tracking with full adaptive extended Kalman filter: An experimental study. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005; pp. 283–288. [Google Scholar]
- Wang, X.; Wang, S.; Ma, J.J. An Improved Particle Filter for Target Tracking in Sensor Systems. Sensors 2007, 7, 144–156. [Google Scholar] [CrossRef] [Green Version]
- Okuma, K.; Taleghani, A.; De Freitas, N.; Little, J.; Lowe, D. A Boosted Particle Filter: Multitarget Detection and Tracking. In Proceedings of the 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 28–39. [Google Scholar]
- Julier, S.; Uhlmann, J.K. A General Method for Approximating Nonlinear Transformations of Probability Distributions. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.46.6718 (accessed on 26 September 2018).
- Konatowski, S.; Pieniężny, A.T. A comparison of estimation accuracy by the use of KF, EKF & UKF filters. Wit Trans. Model. Simul. 2007, 46, 779–789. [Google Scholar]
- Tang, X.; Xie, J.; Wang, X.; Jiang, W. High-Precision Attitude Post-Processing and Initial Verification for the ZY-3 Satellite. Remote Sens. 2014, 7, 111–134. [Google Scholar] [CrossRef] [Green Version]
- Wan, E.A.; Van der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Blair, W.D.; Watson, G.A.; Rice, T.R. Tracking maneuvering targets with an interacting multiple model filter containing exponentially-correlated acceleration models. In Proceedings of the Twenty-Third Southeastern Symposium on System Theory, Columbia, SC, USA, 10–12 March 1991. [Google Scholar]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part V. Multiple-model methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar]
- Farina, A.; Immediata, S.; Timmoneri, L. Impact of ballistic target model uncertainty on IMM-UKF and IMM-EKF tracking accuracies. In Proceedings of the 2006 14th European Signal Processing Conference, Florence, Italy, 4–6 September 2006. [Google Scholar]
- Xu, Q.; Li, X.; Chan, C.Y. A Cost-Effective Vehicle Localization Solution Using an Interacting Multiple Model-Unscented Kalman Filters (IMM-UKF) Algorithm and Grey Neural Network. Sensors 2017, 17, 1431. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S. An Adaptive Unscented Kalman Filter for Dead Reckoning Systems. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009. [Google Scholar]
- Soken, H.E.; Hajiyev, C. Adaptive Fading UKF with Q-Adaptation: Application to Picosatellite Attitude Estimation. J. Aerosp. Eng. 2013, 26, 628–636. [Google Scholar] [CrossRef]
- Li, L.; Hua, C.; Yang, H. A new adaptive unscented Kalman filter based on covariance matching technique. In Proceedings of the 2014 International Conference on Mechatronics and Control, Jinzhou, China, 3–5 July 2014; pp. 1308–1313. [Google Scholar]
- Meng, Y.; Gao, S.; Zhong, Y.; Hu, G.; Subic, A. Covariance matching based adaptive unscented Kalman filter for direct filtering in INS/GNSS integration. Acta Astronaut. 2016, 120, 171–181. [Google Scholar] [CrossRef]
- Akhlaghi, S.; Zhou, N.; Huang, Z. Adaptive adjustment of noise covariance in Kalman filter for dynamic state estimation. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Partovibakhsh, M.; Liu, G. An adaptive unscented Kalman filtering approach for online estimation of model parameters and state-of-charge of lithium-ion batteries for autonomous mobile robots. IEEE Trans. Control Syst. Technol. 2015, 23, 357–363. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, M.; Wang, C.; Cheng, G.; Niu, S. Adaptive Filtering Algorithm of Multi-Sensor Information Fusion for Individual Navigation. Navig. Position. Timing 2018, 5, 35–41. [Google Scholar]
- Zhang, H.; Chang, Y.H.; Che, H. Measurement-based adaptive Kalman filtering algorithm for GPS/INS integrated navigation system. J. Chin. Inert. Technol. 2010, 18, 696–701. [Google Scholar]
- Zhou, Q.; Zhang, H.; Li, Y.; Li, Z. An Adaptive Low-Cost GNSS/MEMS-IMU Tightly-Coupled Integration System with Aiding Measurement in a GNSS Signal-Challenged Environment. Sensors 2015, 15, 23953–23982. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Zhang, H.; Wang, Y. A Redundant measurement Adaptive Kalman Filter Algorithm. Acta Aeronaut. Astronaut. Sin. 2015, 36, 1596–1605. [Google Scholar]
- Li, Z.; Zhang, H.; Zhou, Q.; Che, H. An Adaptive Low-Cost INS/GNSS Tightly-Coupled Integration Architecture Based on Redundant Measurement Noise Covariance Estimation. Sensors 2017, 17, 2032. [Google Scholar] [CrossRef] [PubMed]
- Kandepu, R.; Foss, B.; Imsland, L. Applying the unscented Kalman filter for nonlinear state estimation. J. Process Control 2008, 18, 753–768. [Google Scholar] [CrossRef]
- Julier, S.J. The Scaled Unscented Transformation. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 4555–4559. [Google Scholar]
- Salahshoor, K.; Mosallaei, M.; Bayat, M. Centralized and decentralized process and sensor fault monitoring using data fusion based on adaptive extended Kalman filter algorithm. Measurement 2008, 41, 1059–1076. [Google Scholar] [CrossRef]
- Hajiyev, C. Robust adaptive unscented Kalman filter for attitude estimation of pico satellites. Int. J. Adapt. Control Signal Process. 2014, 28, 107–120. [Google Scholar] [CrossRef]
- Myers, K.; Tapley, B. Adaptive sequential estimation with unknown noise statistics. IEEE Trans. Autom. Control 1976, 21, 520–523. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, H. Redundant measurement-based second order mutual difference adaptive Kalman filter. Automatica 2019, 100, 396–402. [Google Scholar] [CrossRef]

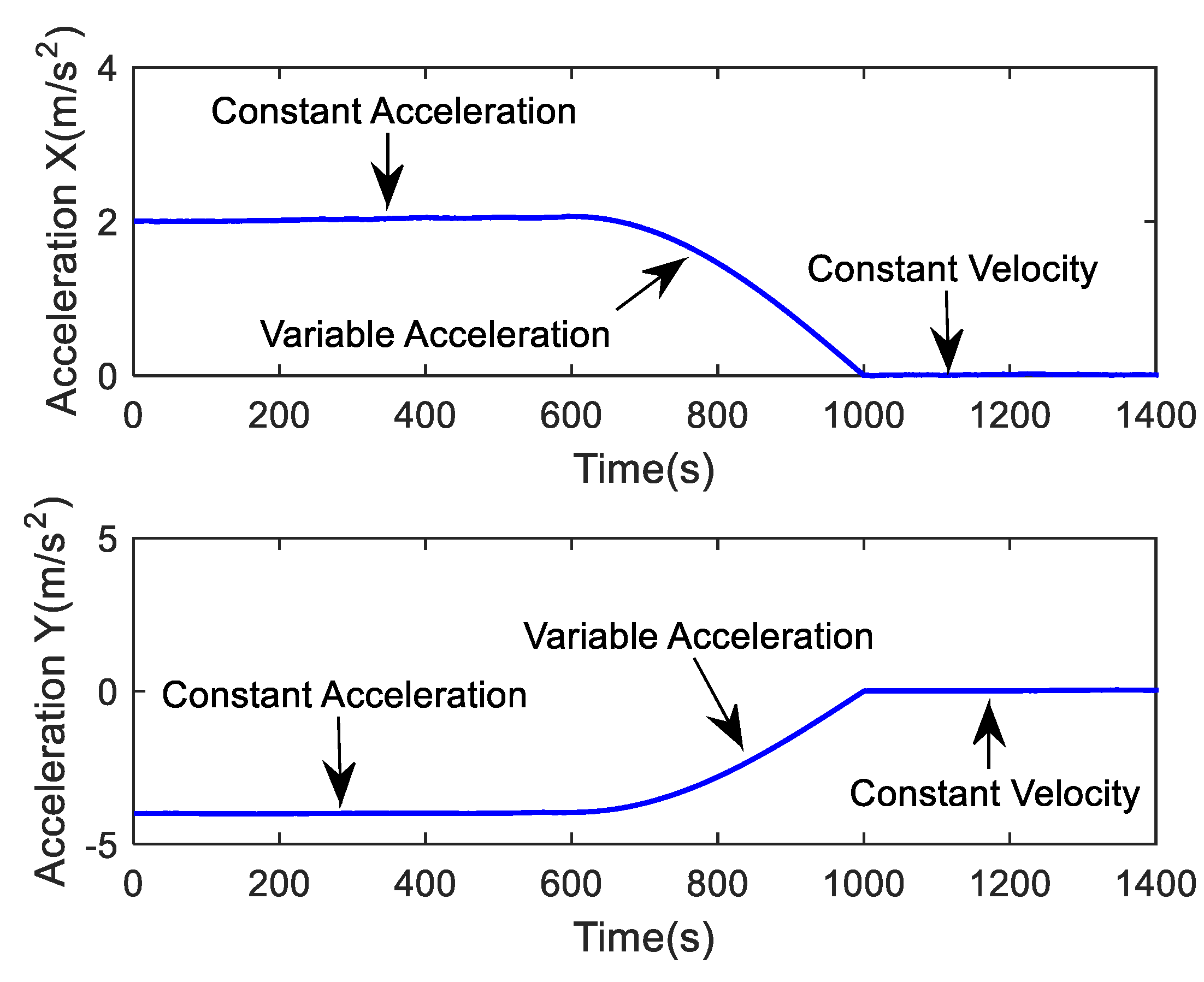

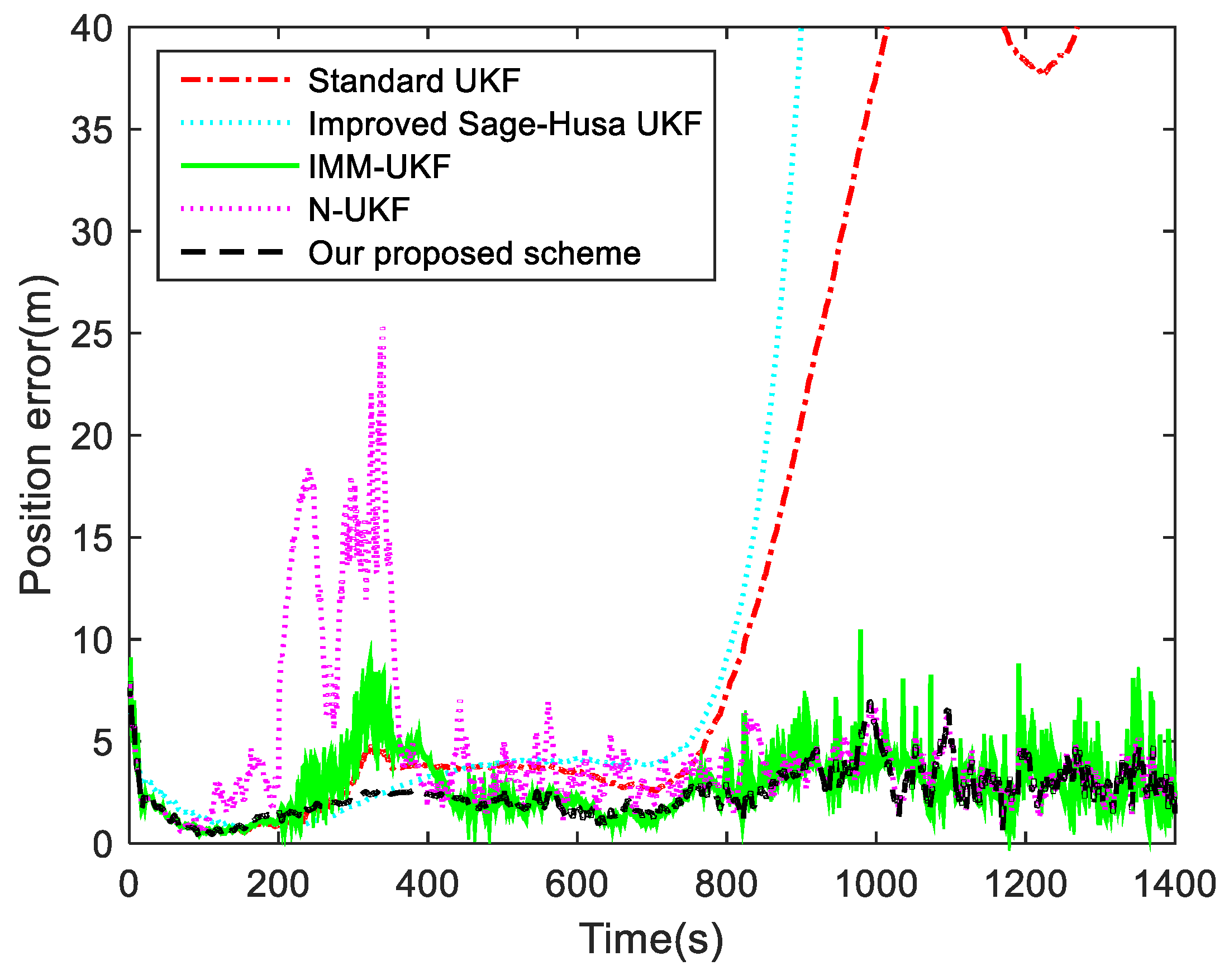



| Algorithm | 200–550 s | 550–1400 s | ||
|---|---|---|---|---|
| Mean (m) | Variance (m2) | Mean (m) | Variance (m2) | |
| Standard UKF | 1.4549 | 0.3783 | 25.7565 | 341.6688 |
| Adaptive fading UKF | 2.1264 | 0.2519 | 2.8608 | 0.2411 |
| IMM-UKF | 1.3258 | 0.1141 | 2.7311 | 0.5510 |
| N-UKF | 3.7332 | 0.4344 | 4.5229 | 0.6996 |
| Our proposed scheme | 1.3398 | 0.1080 | 2.7165 | 0.5497 |
| Algorithm | 200–350 s | 600–1400 s | ||
|---|---|---|---|---|
| Mean (m) | Variance (m2) | Mean (m) | Variance (m2) | |
| Standard UKF | 2.9130 | 0.7260 | 26.7439 | 337.3589 |
| Improved Sage-Husa UKF | 2.4260 | 0.8123 | 359.2692 | 2.1492 × 105 |
| IMM-UKF | 3.0745 | 2.2106 | 2.8958 | 1.3549 |
| N-UKF | 7.9900 | 27.0631 | 3.5731 | 0.9831 |
| Our proposed scheme | 1.9730 | 0.1264 | 2.9107 | 1.0564 |
| Algorithm | 200–550 s | 550–1400 s | ||
|---|---|---|---|---|
| Mean (m) | Variance (m2) | Mean (m) | Variance (m2) | |
| Standard UKF | 4.8845 | 4.0442 | 26.8136 | 316.1329 |
| Robust adaptive UKF | 4.6399 | 5.0780 | 3.0834 | 0.2204 |
| IMM-UKF | 3.9900 | 1.3483 | 4.6487 | 2.3042 |
| N-UKF | 4.7748 | 5.6900 | 3.3517 | 0.3042 |
| Our proposed scheme | 3.0623 | 1.0426 | 3.7313 | 0.7709 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, B.; Zhang, H.; Jiang, L.; Li, Z.; Butt, M.M. Adaptive Unscented Kalman Filter for Target Tracking with Unknown Time-Varying Noise Covariance. Sensors 2019, 19, 1371. https://doi.org/10.3390/s19061371
Ge B, Zhang H, Jiang L, Li Z, Butt MM. Adaptive Unscented Kalman Filter for Target Tracking with Unknown Time-Varying Noise Covariance. Sensors. 2019; 19(6):1371. https://doi.org/10.3390/s19061371
Chicago/Turabian StyleGe, Baoshuang, Hai Zhang, Liuyang Jiang, Zheng Li, and Maaz Mohammed Butt. 2019. "Adaptive Unscented Kalman Filter for Target Tracking with Unknown Time-Varying Noise Covariance" Sensors 19, no. 6: 1371. https://doi.org/10.3390/s19061371
APA StyleGe, B., Zhang, H., Jiang, L., Li, Z., & Butt, M. M. (2019). Adaptive Unscented Kalman Filter for Target Tracking with Unknown Time-Varying Noise Covariance. Sensors, 19(6), 1371. https://doi.org/10.3390/s19061371






