Electromechanical Dynamics Model of Ultrasonic Transducer in Ultrasonic Machining Based on Equivalent Circuit Approach
Abstract
:1. Introduction
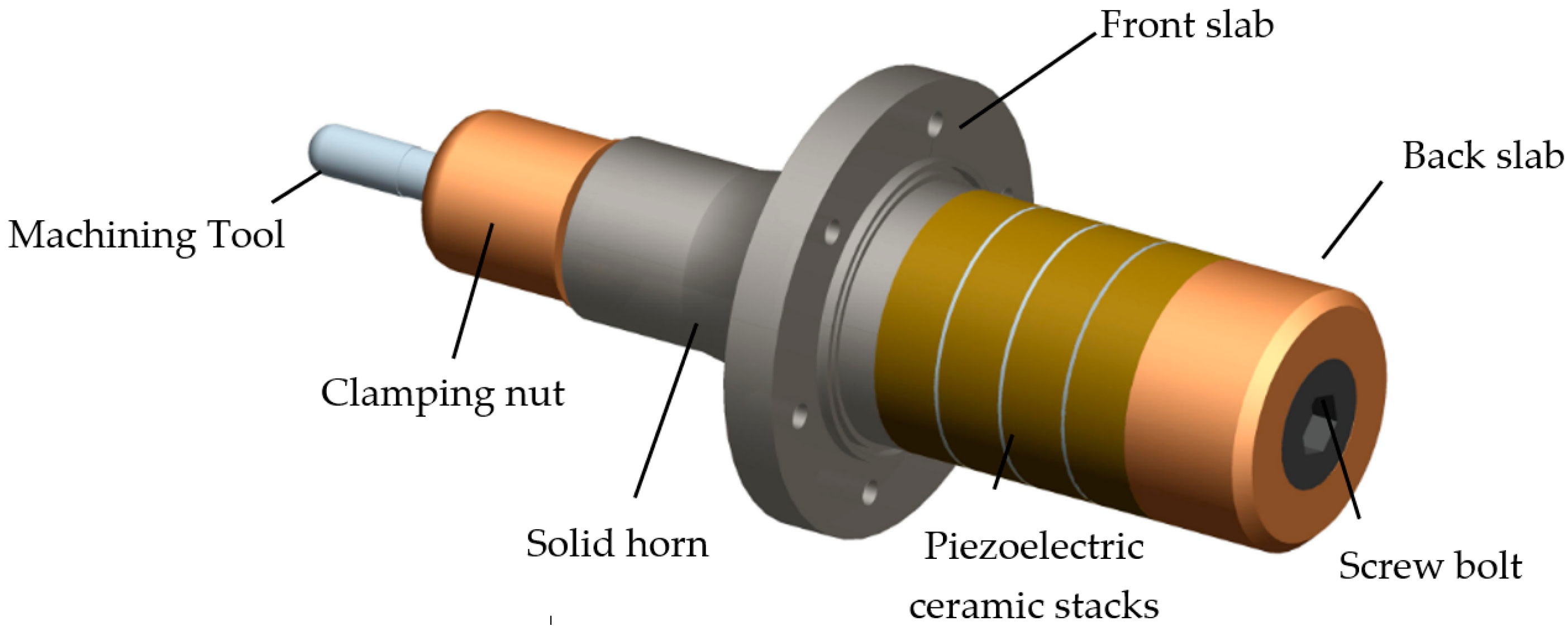
2. Mechanical Structure of Ultrasonic Transducer
3. Impedance Modeling
3.1. The piezoelectric Ceramic Stacks and Screw Bolt
3.2. The Solid Horn Structures
3.3. The Tightening Torque of Clamping Nut
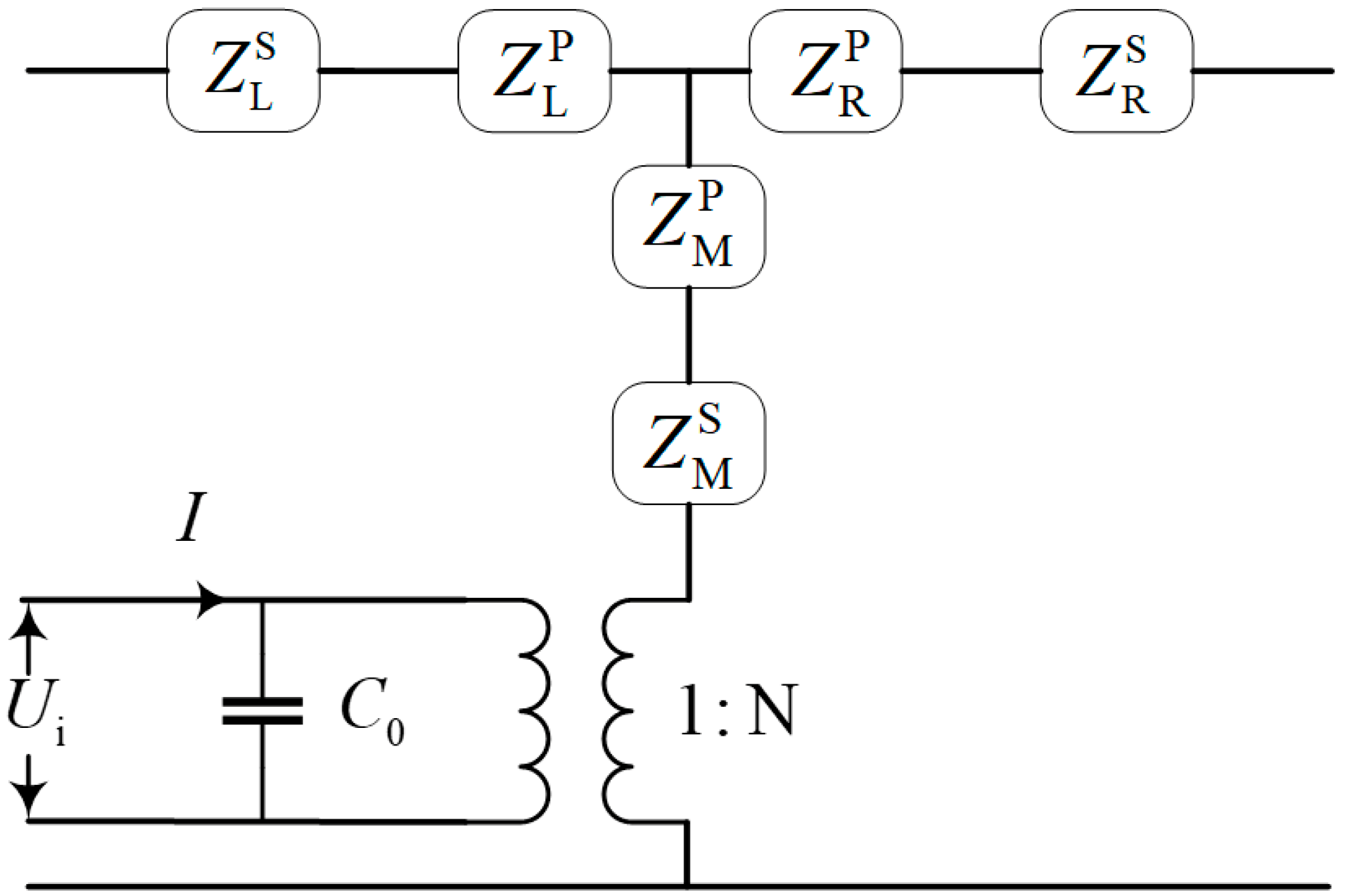
3.4. Impedance Equivalent Modeling
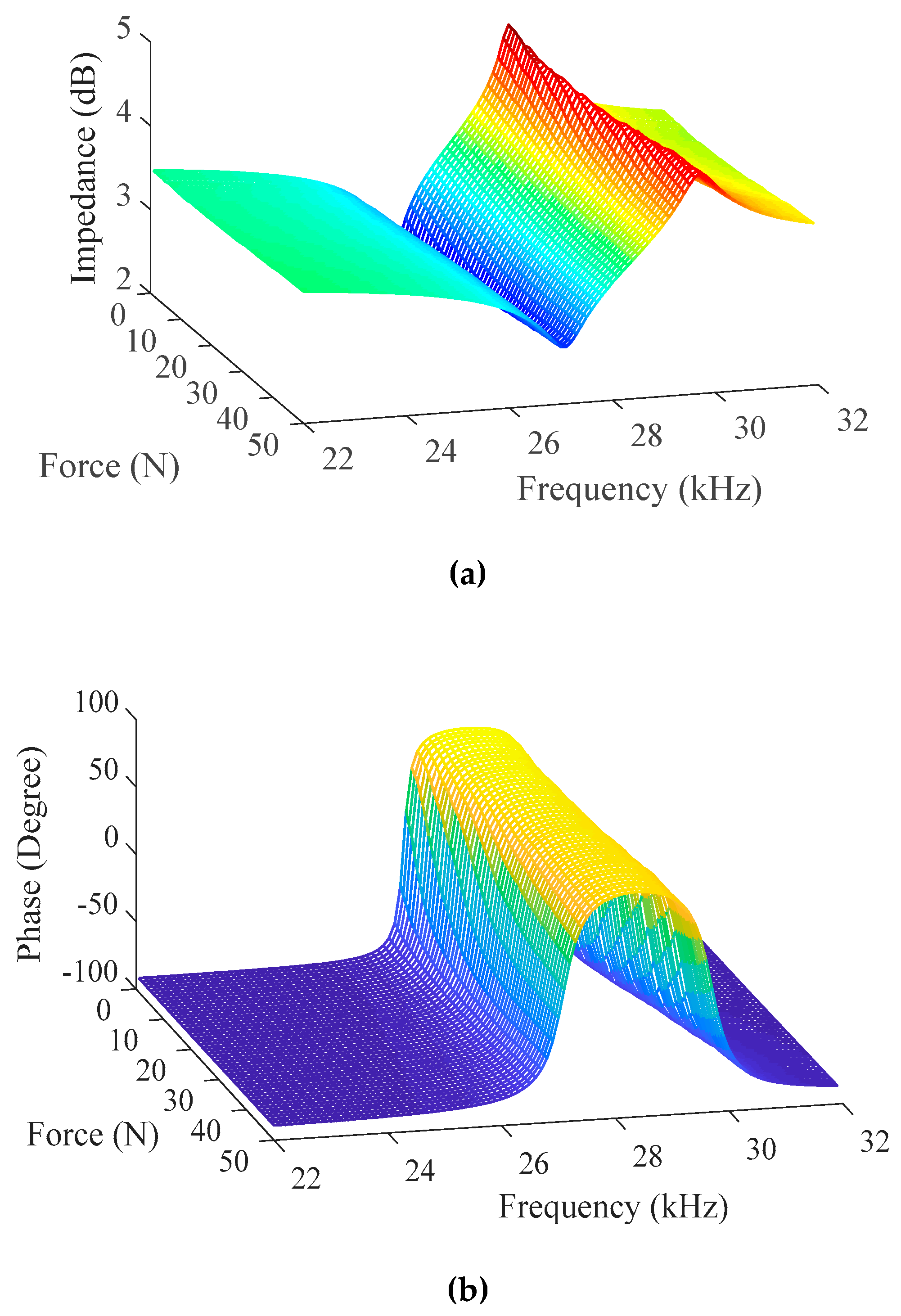
4. Numeral Calculation and Discussion
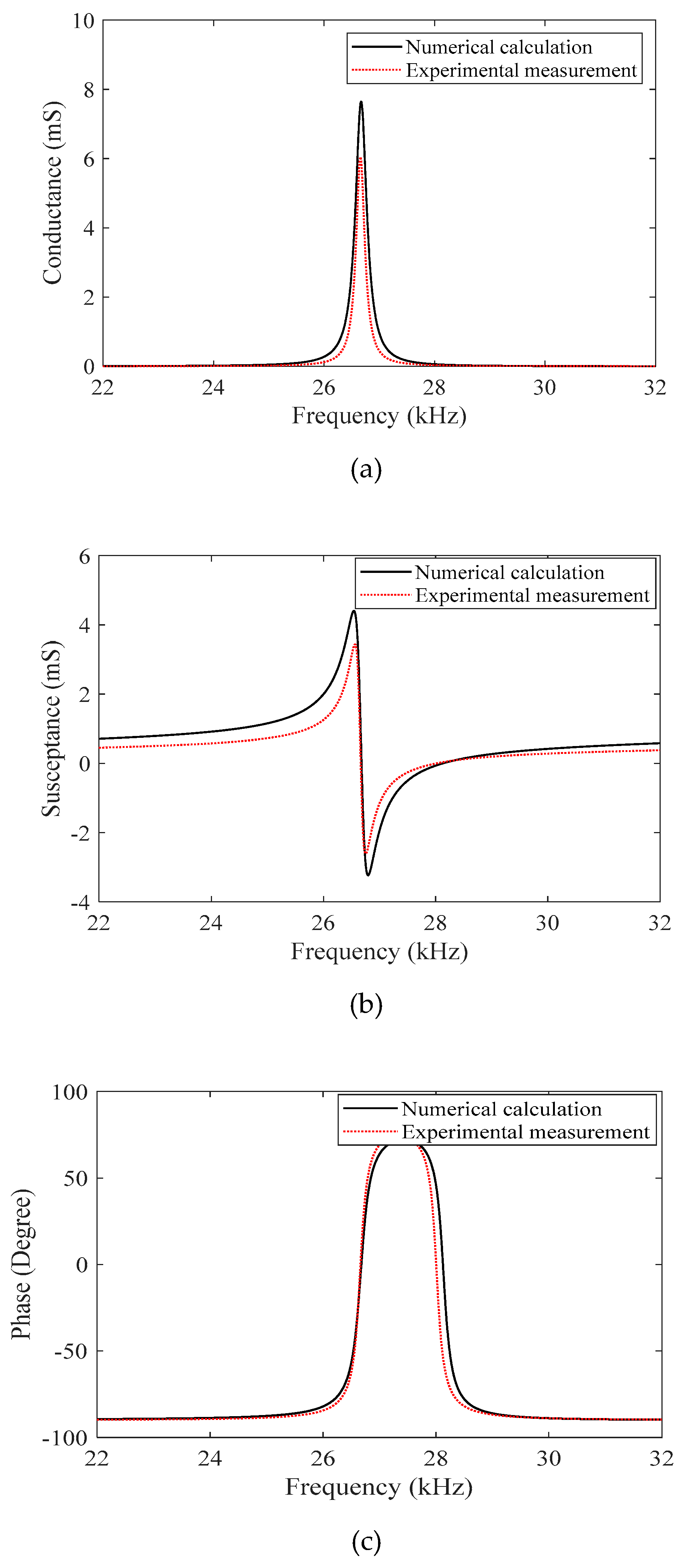
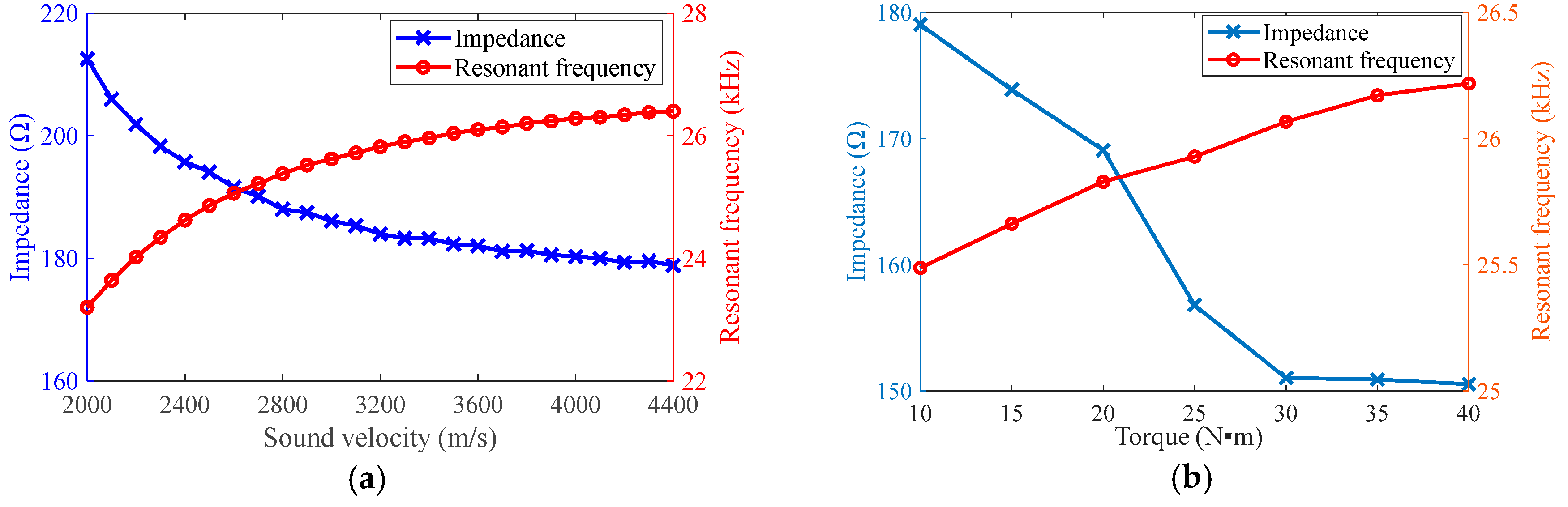
4.1. Load of Ultrasonic Transducer
4.2. Load with Different Torques of Clamping Nut
4.3. Load with Different Extension Lengths of Tool
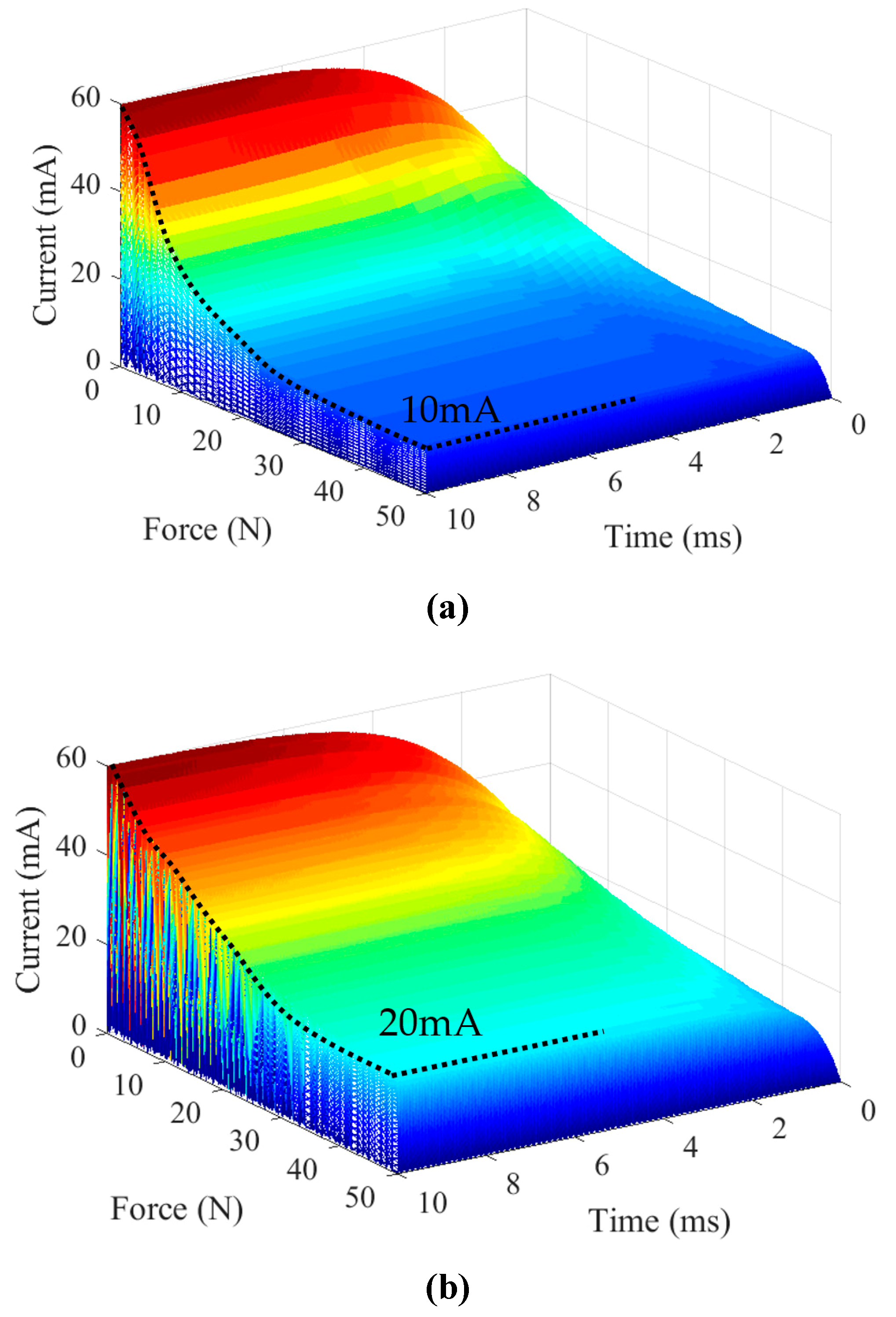
5. Dynamic Modeling of Ultrasonic Transducer
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, J.; Khamba, J.S.; Mohapatra, S.K. An investigation into the machining characteristics of titanium using ultrasonic machining. Int. J. Mach. Mach. Mater. 2008, 3, 143–161. [Google Scholar] [CrossRef]
- Singh, R.P.; Singhal, S. Rotary ultrasonic machining: A review. Adv. Manuf. Process. 2016, 31, 1795–1824. [Google Scholar] [CrossRef]
- Wang, J.J.; Zhang, J.F.; Feng, P.F.; Ping, G. Damage formation and suppression in rotary ultrasonic machining of hard and brittle materials: A critical review. Ceram. Int. 2018, 44, 1227–1239. [Google Scholar] [CrossRef]
- Wang, H.; Ning, F.D.; Hu, Y.B.; Cong, W.L. Surface grinding of CFRP composites using rotary ultrasonic machining: A comparison of workpiece machining orientations. Int. J. Adv. Manuf. Technol. 2018, 95, 2917–2930. [Google Scholar] [CrossRef]
- Singh, R.P.; Singhal, S. Investigation of machining characteristics in rotary ultrasonic machining of alumina ceramic. Adv. Manuf. Process. 2016, 32, 309–326. [Google Scholar] [CrossRef]
- Gao, C.Y.; Xiao, D.G.; Pan, Q.X.; Xu, C.G. Ultrasonic transducers frequency response study with equivalent circuit and finite element method. In Proceedings of the IEEE International Conference Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 1746–1750. [Google Scholar]
- Roh, Y.; Khuri-Yakub, B.T. Finite element modeling of capacitor micromachined ultrasonic transducers. In Proceedings of the IEEE Ultrasonics Symposium, San Juan, Puerto Rico, 22 October 2000; pp. 905–908. [Google Scholar]
- Kuo, K.L. Design of rotary ultrasonic milling tool using FEM simulation. J. Mater. Process. Tech 2008, 201, 48–52. [Google Scholar] [CrossRef]
- Abboud, N.N.; Wojcik, G.L.; Vaughan, D.K.; Mould, J.; Powell, D.J.; Nikodym, L. Finite element modeling for ultrasonic transducers. In Proceedings of the SPIE International Sumposium Medical Imaging 1998: Ultrasonic Transducer Engineering, San Diego, CA, USA, 16–21 February 1998; pp. 19–43. [Google Scholar]
- Amir, A.; Abbas, P. Correct Prediction of the vibration behavior of a high power ultrasonic transducer by FEM simulation. Int. J. Adv. Manuf. Technol. 2008, 39, 21–28. [Google Scholar]
- Long, Z.L.; Wu, Y.X.; Han, L.; Zhong, J. Dynamics of ultrasonic transducer system for thermosonic flip chip bonding. IEEE Trans. Compon. Packag. Technol. 2009, 32, 261–267. [Google Scholar] [CrossRef]
- Chen, X.Z.; Yin, Y.X.; Hou, Q.W.; Jin, L.W.; Li, X.L. The simulation and structural optimization of ultrasonic transducer. In Proceedings of the International Conference on Industrial and Information Systems, Dalian, China, 10 July 2010; pp. 330–333. [Google Scholar]
- Saleem, A.; Salah, M.; Ahmad, N.; Siberschmidt, V. Control of ultrasonic transducers for machining applications. In Proceedings of the International Symposium on Mechatronics and Its Applications, Amman, Jordan, 11 April 2013. [Google Scholar]
- Voronina, S.; Babitsky, V. Autoresonant control strategies of loaded ultrasonic transducer for machining applications. J. Sound Vib. 2018, 313, 395–417. [Google Scholar] [CrossRef]
- Babitsky, V.I.; Astashev, V.K.; Kalashnikov, A.N. Autoresonant control of nonlinear mode in ultrasonic transducer for machining applications. Ultraosnics 2004, 42, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.H.; Tsai, M.C. Dynamic modeling of thickness-mode piezoelectric transducer using the block diagram approach. Ultrasonics 2011, 51, 617–624. [Google Scholar] [CrossRef] [PubMed]
- Sherrit, S.; Leary, S.P.; Dolgin, B.P.; Bar-Cohen, Y. Comparison of the Mason and KLM equivalent circuits for piezoelectric resonators in the thickness mode. In Proceedings of the IEEE Ultrasonics Symposium, Caesars Tahoe, NV, USA, 17 October 1999; pp. 921–926. [Google Scholar]
- Smyth, K.; Kim, S.G. Experiment and simulation validated analytical equivalent circuit model for piezoelectric micromachined ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2015, 62, 744–765. [Google Scholar] [CrossRef] [PubMed]
- Je, Y.; Ahn, H.; Been, K.; Moon, W.; Lee, H. An advanced equivalent circuit for a piezoelectric micromachined ultrasonic transducer and its lumped parameter measurement. In Proceedings of the IEEE Ultrasonics Symposium, Prague, Czech Republic, 21–25 July 2013; pp. 279–282. [Google Scholar]
- Caronti, A.; Caliano, G.; Iula, A.; Pappalardo, M. An accurate model for capacitive micromachined ultrasonic transducers. IEEE Ultrason. Ferroelectr. Freq. Control Soc. 2002, 49, 159–168. [Google Scholar] [CrossRef]
- Wang, F.J.; Zhang, H.J.; Liang, C.M.; Tian, Y.L.; Zhao, X.Y.; Zhang, D.W. Design of high-frequency ultrasonic transducers with flexure decoupling flanges for thermosonic bonding. IEEE Trans. Ind. Electron. 2016, 63, 2304–2312. [Google Scholar] [CrossRef]
- Lin, S.Y.; Guo, H.; Xu, J. Actively adjustable step-type ultrasonic horns in longitudinal vibration. J. Sound Vib. 2018, 419, 367–379. [Google Scholar] [CrossRef]
- Lin, S.Y. Radiation impedance and equivalent circuit for piezoelectric ultrasonic composite transducers of vibrational mode-conversion. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 139–149. [Google Scholar]
- Sammoura, F.; Kim, S.G. Theoretical modeling and equivalent electric circuit of a bimorph piezoelectric micromachined ultrasonic transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 990–998. [Google Scholar] [CrossRef]
- Dang, C.; Schmerr, W.; Sedov, A. Ultrasonic transducer sensitivity and model-based transducer characterization. Res. Nondestr. Eval. 2003, 14, 203–228. [Google Scholar] [CrossRef]
- Milan, N.; Lenka, C. The effect of the shape parameters on modal properties of ultrasonic horn design for ultrasonic assisted machining. In Proceedings of the International DAAAM Baltic Conference, Tallinn, Estonia, 19–21 April 2012. [Google Scholar]
- Nassar, S.; Veeram, A.B. Ultrasonic control of fastener tightening using varying wave speed. J. Press. Vessel Technol. 2006, 128, 189–198. [Google Scholar] [CrossRef]
- Schomburg, W.K. Piezoelectric Effect; Springer: Berlin, Germany, 2011. [Google Scholar]
- McBrearty, M.; Kim, L.H.; Bilgutay, N.M. Analysis of impedance loading in ultrasonic transducer systems. In Proceedings of the IEEE Ultrasonics Symposium, Chicago, IL, USA, 5 October 1998; pp. 497–502. [Google Scholar]
- Salama, K.; Barber, G.C.; Chandrasekaran, N. Measurement of residual stress using the temperature dependence of ultrasonic velocity. In Proceedings of the IEEE Ultrasonics Symposium, San Diego, CA, USA, 27 October 1982; pp. 877–894. [Google Scholar]
- Long, Z.L.; Zhang, J.G.; Wu, X.J.; Liu, Y.C.; Zhou, X.; Li, Z.H. Impedance modeling of ultrasonic transducers used in heavy aluminum wire bonding. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1107–1115. [Google Scholar] [CrossRef]
- Mason, W.P. Electromechanical Transducers and Wave Filters; Van Nostrand: Princeton, NJ, USA, 1948. [Google Scholar]




| Type | Shape | Parameters | Equations |
|---|---|---|---|
| Constant horn | 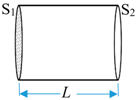 | S = S1 = S2 S1 and S2 are the area of front and back section. L is the horn length. | |
| Exponential horn |  | Se = S1e−2βL S1 and Se are the area of front and back section. |
| Type | Density (kg. m−3) | Poisson Ratio | Dimensions | Other Parameters | ||
|---|---|---|---|---|---|---|
| Diameter (mm) | Length (mm) | |||||
| Piezoelectric Ring | PZT-4 | 7700 | 0.25 | Outer:32.0 Inner:13.9 | 6 | d33 = 270(1 − 0.0003i) pC/N = 2 × 1011(1 − 0.0012i) m2/N |
| Screw bolt | Stainless steel | 7930 | 0.28 | 13.5 | 36.5 | E = 2.15 × 1011(1 + 0.001i) N/m2 |
| Back slab | 32.0 | 10.8 | ||||
| Front slab (1) | 32.0 | 3.5 | ||||
| Front slab (2) | 43.2 | 5.1 | ||||
| Exponential horn | S1:28.2 Se:22.1 | 27.8 | ||||
| Clamping nut | 17.1 | 15.2 | ||||
| Machining tool | 6.0 | (15*) 38.7 | ||||
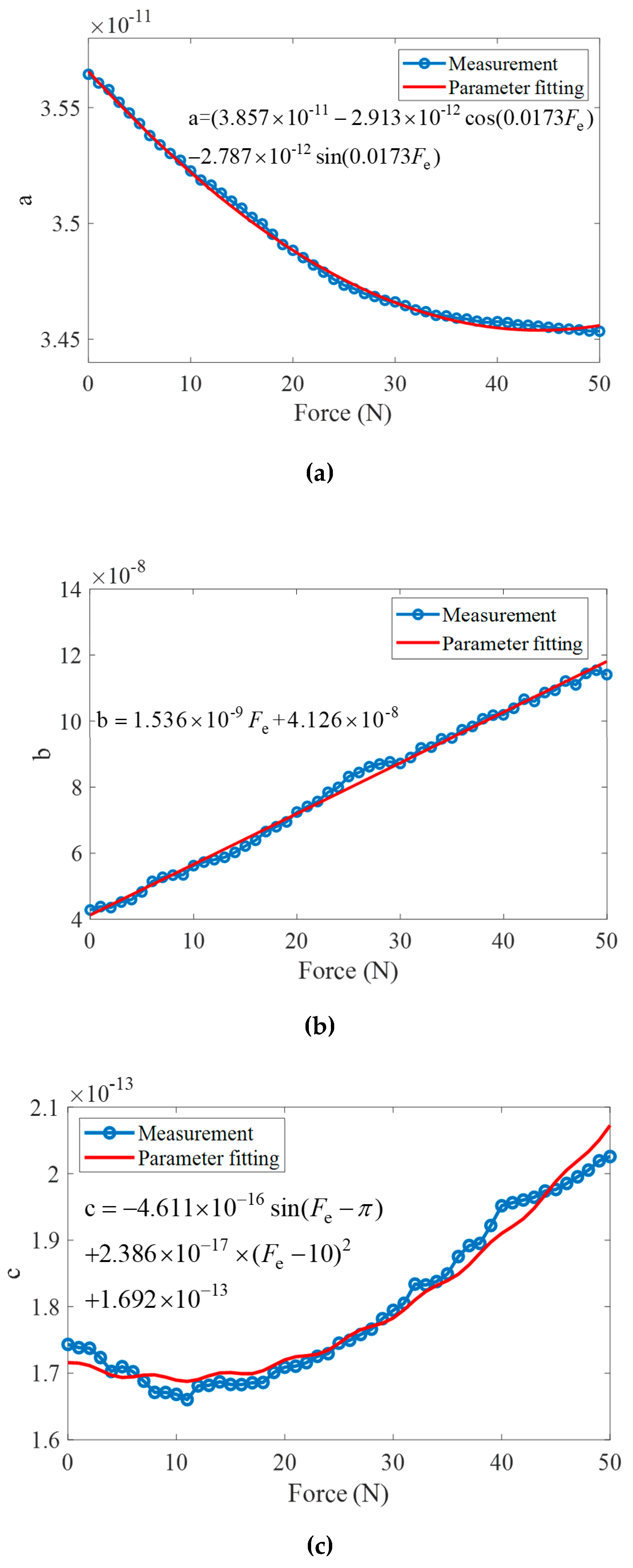
| Parameters | Type | Function | R2 |
|---|---|---|---|
| a | Fourier | 0.9983 | |
| b | Polynomial | 0.9952 | |
| c | Linear Fitting | 0.971 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.-G.; Long, Z.-L.; Ma, W.-J.; Hu, G.-H.; Li, Y.-M. Electromechanical Dynamics Model of Ultrasonic Transducer in Ultrasonic Machining Based on Equivalent Circuit Approach. Sensors 2019, 19, 1405. https://doi.org/10.3390/s19061405
Zhang J-G, Long Z-L, Ma W-J, Hu G-H, Li Y-M. Electromechanical Dynamics Model of Ultrasonic Transducer in Ultrasonic Machining Based on Equivalent Circuit Approach. Sensors. 2019; 19(6):1405. https://doi.org/10.3390/s19061405
Chicago/Turabian StyleZhang, Jian-Guo, Zhi-Li Long, Wen-Ju Ma, Guang-Hao Hu, and Yang-Min Li. 2019. "Electromechanical Dynamics Model of Ultrasonic Transducer in Ultrasonic Machining Based on Equivalent Circuit Approach" Sensors 19, no. 6: 1405. https://doi.org/10.3390/s19061405
APA StyleZhang, J.-G., Long, Z.-L., Ma, W.-J., Hu, G.-H., & Li, Y.-M. (2019). Electromechanical Dynamics Model of Ultrasonic Transducer in Ultrasonic Machining Based on Equivalent Circuit Approach. Sensors, 19(6), 1405. https://doi.org/10.3390/s19061405






