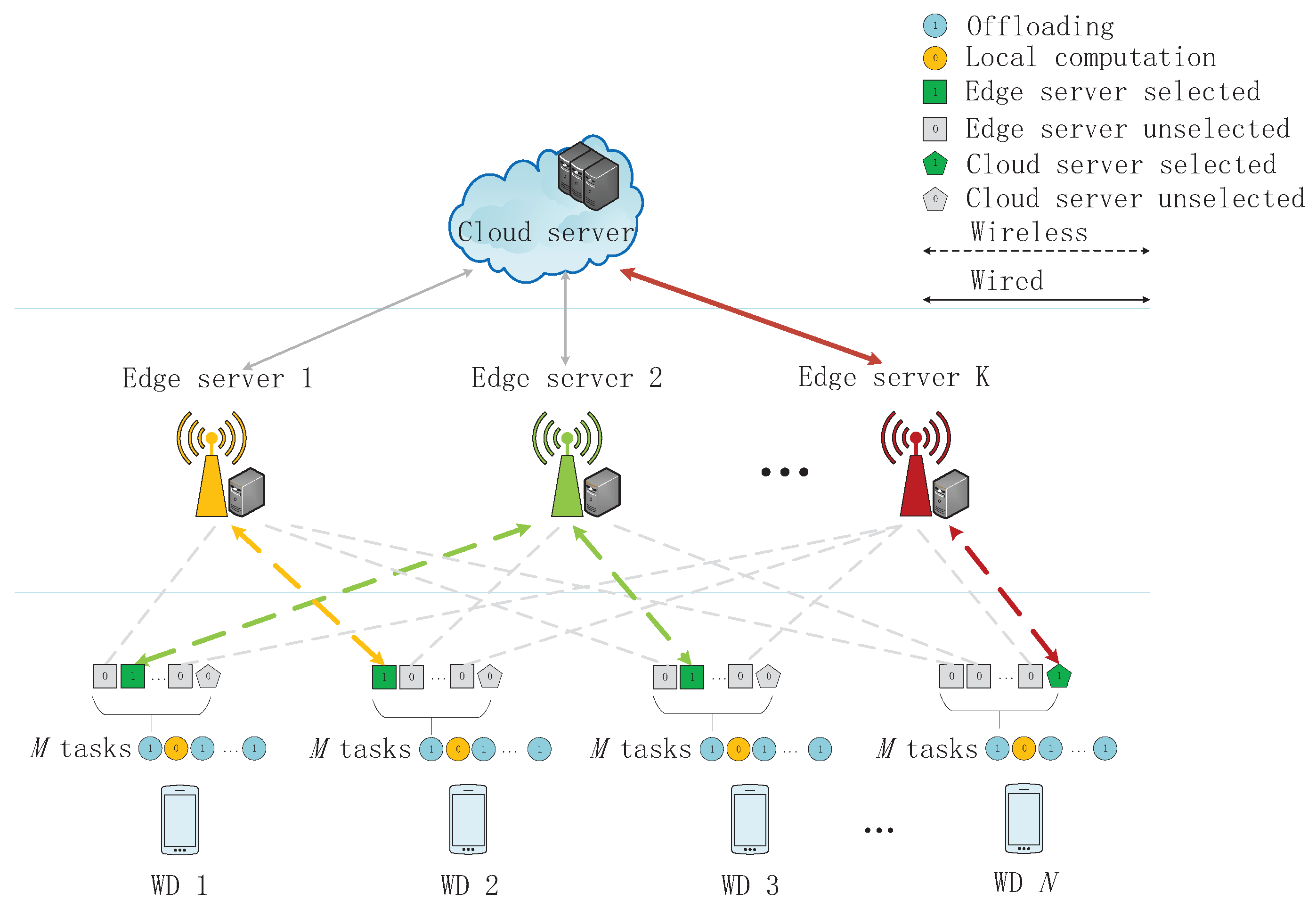
The last decade has witnessed how mobile devices and mobile applications have become an indispensable part of peoples’ lives. Mobile devices provide a wide range of digital services, such as map navigation, language recognition, web browsing, and so on. Besides being a means of phone calls and content consumption, mobile devices tend to be platforms that assist people to accomplish more online tasks as a complement to desktop computers and laptops. These tasks require a large amount of computing resources and stringent quality of service (QoS), e.g., Augmented Reality (AR) applications [
1], Vehicular ad-hoc networks (VANETs) [
2], and cloud gaming [
3]. Due to limited computation resources and the size-constrained batteries of mobile devices, computationally intensive tasks are offloaded to remote computational servers, which then transfer computing results back to the mobile devices, known as cloud computing [
4]. However, this approach suffers high latency and unstable QoS due to data propagation and routing between mobile devices and remote cloud servers. Although different wireless communication technologies [
5,
6,
7] and data transmission scheduling schemes [
8,
9,
10,
11] have been developed in the past decades, the QoS is slightly improved due to the long-distance transmissions between mobile devices and remote cloud servers. Recently, mobile edge computing (MEC) network is proposed to deploy multiple edge servers close to mobile devices. Mobile devices in MEC networks can efficiently offload their tasks to nearby edge servers and receive immediate feedback after processing, so as to improve the QoS. For example, after the emergence of Internet of Things (IoT), more and more sensors are connected to MEC networks. The massive measured data can be offloaded to edge servers with low processing latency, which can also extend the computation power of IoT sensors [
12]. In the coming fifth-generation (5G) mobile network, the deployment of ultra-dense small cell networks (UDNs) is envisaged [
13]. There are going to be multiple edge servers within the wireless communication range of each mobile device, so as to provide sufficient edge servers and communication capacity for MEC networks. However, it is challenging to make computation offloading decisions when multiple edge servers and mobile devices are available in MEC networks. For example,
whether a computing task should be offloaded to edge servers? Which edge server should it be offloaded to? Different offloading decisions result in different QoS of the MEC networks. Thus, it is important to carefully design computation offloading mechanism for MEC networks.
In MEC networks, computation offloading is challenged by limited computing resources and real-time delay constraint. Different from large-scale cloud computing centers, edge servers are small-scale with limited processing capacity. When lots of tasks being offloaded to the same edge server it causes congestion, resulting in longer processing time delay for all tasks. Therefore, simply offloading a task to its closest edge server may not be a good choice. An offloading decision depends on available computing capacities at local mobile device, edge servers, and cloud servers, along with communication capacity. Computation offloading in MEC networks is widely studied by using convex optimization [
14] and linear relaxation approximation [
15,
16], which takes too long time to be employed in MEC networks with dynamic computation tasks and time-varying wireless channels. An efficient and effective computation offloading policy for multi-server multi-use MEC networks is still absent.
In this paper, we consider a MEC network with multiple edge servers and one remote cloud server, where multiple wireless devices (WDs) offload their tasks to edge/cloud servers. We investigate both a linear programing relaxation-based (LR-based) algorithm and a heterogeneous distributed deep learning-based offloading (DDLO) algorithm to guarantee QoS of the MEC network and to minimize WDs’ energy consumption. The heterogeneous DDLO algorithm takes advantage of deep reinforcement learning and is insensitive to the number of WDs. It outperforms the LR-based algorithm in terms of both system utility and computing delay.
Deep reinforcement learning has been applied in many aspects, e.g., natural language process [
17], gaming [
18], and robot control [
19]. It uses a deep neural network (DNN) to empirically solve large-scale complex problems. There exist few recent works on deep reinforcement learning-based computation offloading for MEC networks [
20,
21,
22,
23]. Huang et al. proposed a distributed computation offloading algorithm based on deep reinforcement learning, DDLO [
23], for MEC networks with one edge server and multiple WDs. They take advantage of multiple DNNs with identical network structure and show that the computation delay is independent of the number of DNNs. In this paper, we apply DDLO to MEC networks with multiple servers and multiple WDs and further improve the performance of DDLO by using heterogeneous DNN structures.
1.1. Previous Work on Computation Offloading in MEC Networks
Considering a MEC network single edge server, Wei et al. [
24] presented an architecture, MVR, to enable the use of virtual resources in edge server to alleviate the resource burden and reduce energy consumption of the WDs. You et al. [
25] proposed a framework where a WD can harvest energy from a base station or offload task to it. Muñoz et al. [
26] jointly optimized the allocation of radio and computational resource to minimize the WD’s energy consumption. For MEC networks with multiple WDs, Huang et al. [
23] proposed a distributed deep learning-based offloading algorithm, which can effectively provide almost optimal offloading decisions for a MEC nework with multiple WDs and single edge server. To get avoid of the curse of dimensionality problem, Huang et al. [
27] proposed a deep reinforcement learning-based online offloading (DROO) framework to instantly generate offloading decisions. Chen et al. [
28] proposed an efficient distributed computation offloading algorithm which can be used to achieve a Nash equilibrium in multiple WDs scenario.
Considering a MEC network with multiple edge servers, Dinh et al. [
16] considered a MEC with multiple edges servers, and proposed two approach, linear relaxation-based approach, and a semidefinite relaxation (SDR)-based approach to minimize both total tasks’ execution latency and WDs’ energy consumption. Authors [
29] also considered the case of multiple edge servers and obtain the optimal computation distribution among servers. For multiple-server multiple-user MEC networks, authors [
30] proposed a model free reinforcement learning offloading mechanism (Q-learning) to achieve the long-term utilities.
Considering a MEC network with both edge servers and a remote cloud server. Chen et al. [
31] studied a general multi-user mobile cloud computing system with a computing access point (CAP), where each mobile user has multiple independent tasks that may be processed locally, at the CAP, or at a remote cloud server. Liu et al. [
12] studied an edge server and cloud server to reduce energy consumption and enhance computation capability for resource-constrained IoT devices. Li et al. [
32] also studied a computation offloading management policy by jointly processing the heterogeneous computation resources, latency requirements, power consumption at end devices, and channel states. We further categorize all these related works with respect to the number of tasks, WDs, and servers in
Table 1.
1.2. Our Approach and Contributions in This Paper
In this paper, we consider a network with multiple WDs, multiple edge servers, and one cloud server. Each WD has multiple tasks, which can be offloaded to and processed at edge and cloud servers. To guarantee the QoS of the network and minimize WDs’ energy consumption, we obtain the following results:
We model the system utility as the weighted sum of task completion latency and WDs’ energy consumption. To minimize the system utility, we investigate a linear programming relaxation-based (LR-based) algorithm to approximately optimize the offloading decisions for each task of a WD.
We extend the DDLO algorithm to multiple-server MEC network. We further propose a heterogeneous DDLO algorithm by generating offloading decisions through multiple DNNs with heterogeneous network structure, which has better convergence performance than DDLO.
We provide extensive simulation results to evaluate LR-based algorithm, DDLO algorithm, and heterogeneous DDLO algorithm. Extensive numerical results show that the DDLO algorithms guarantee better performance than the LR-based algorithms.
The rest of the paper is organized as follows. In
Section 2, we present the system model and problem formulation. We present an LR-based algorithm in
Section 3 and an heterogeneous DDLO algorithm in
Section 4. Numerical results are presented in
Section 5, and a conclusion is provided in
Section 6.