Tuning Multiple Fano Resonances for On-Chip Sensors in a Plasmonic System
Abstract
:1. Introduction
2. Basic Model and Theoretical Analysis
3. A Way to Induce Multiple Fano Resonances
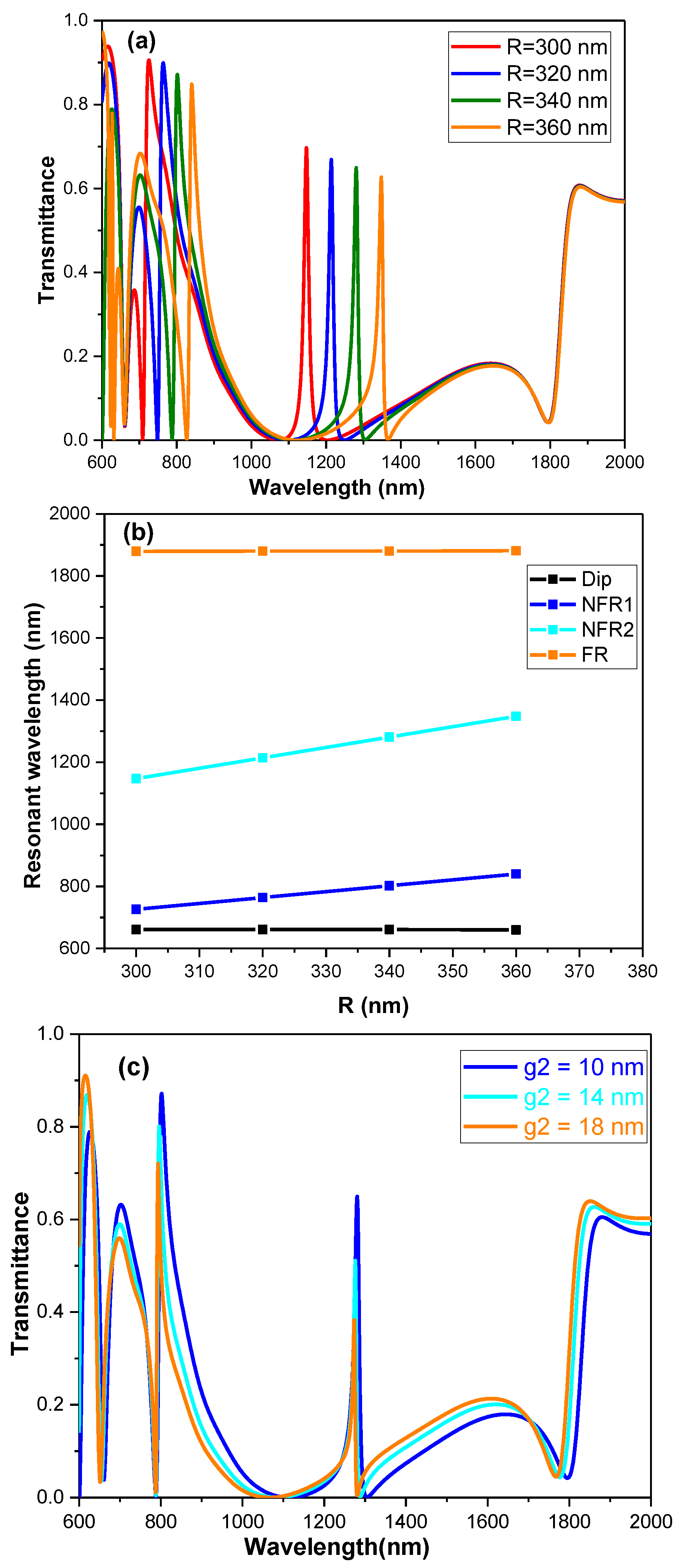
3.1. Adding a Circle Cavity to Induce Triple Fano Resonances.
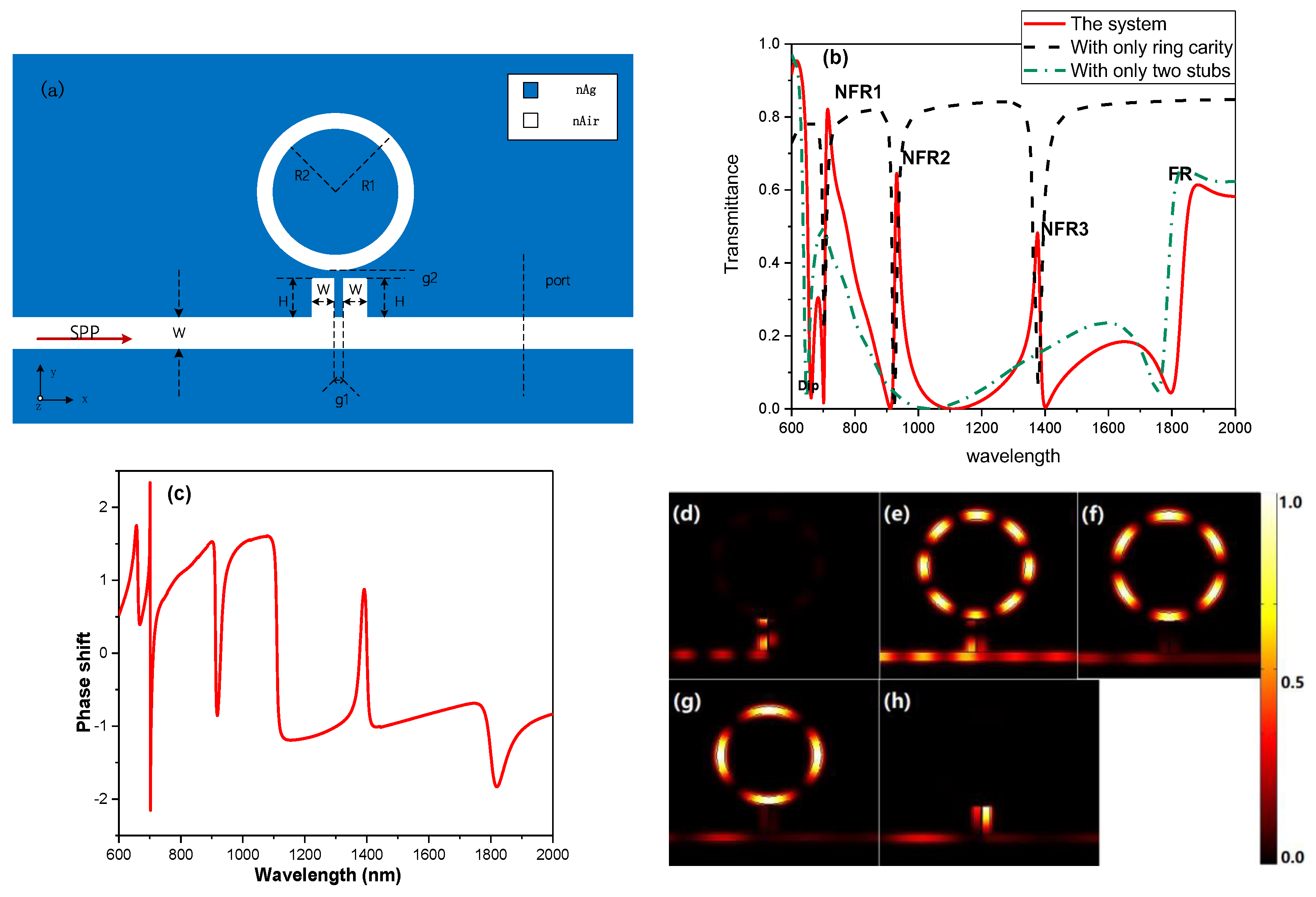
3.2. Adding a Ring Cavity to Induce Quadruple Fano Resonances.
4. Potential Applications of the Proposed Multiple Fano Resonances Structures
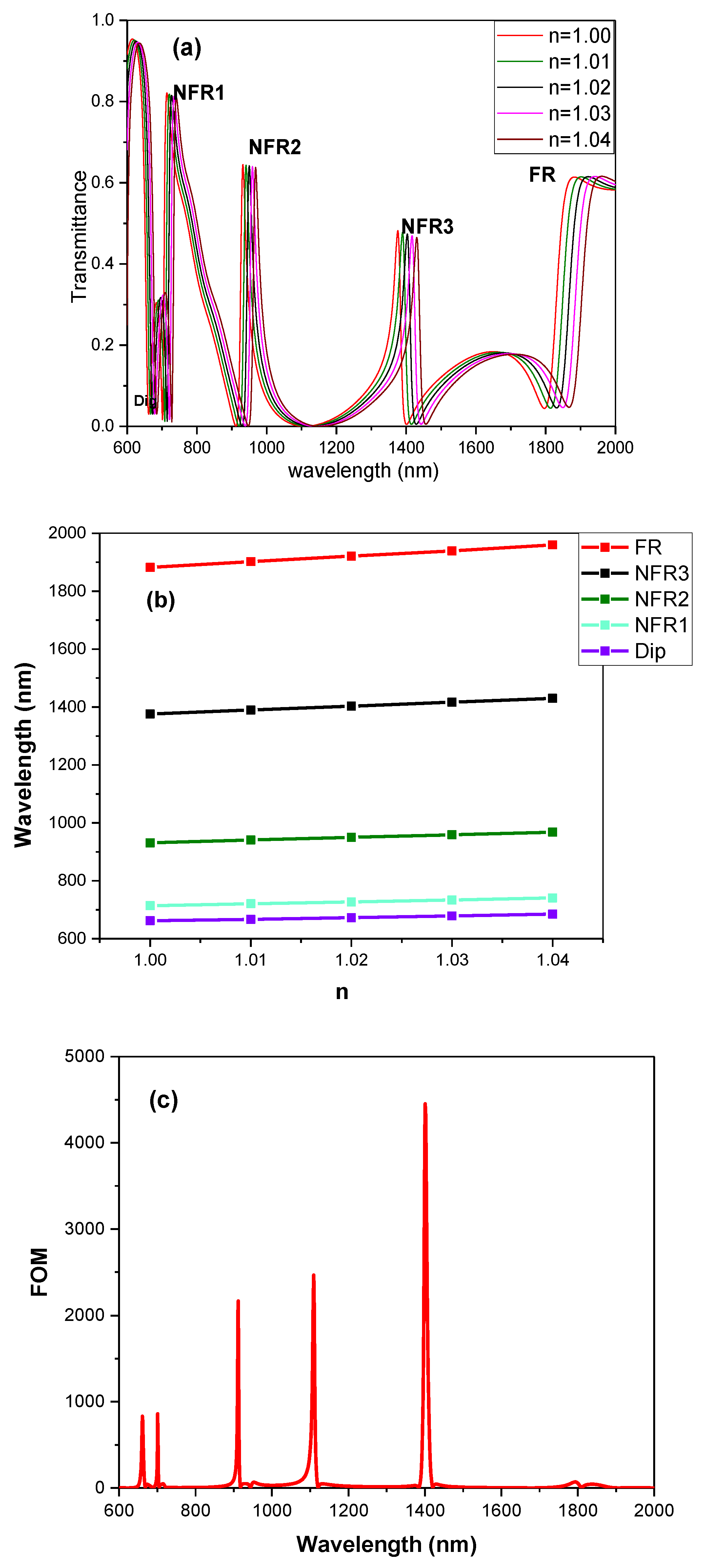
4.1. Refractive Index Sensing Based on the Multiple Fano Resonances
4.2. Slow Light Effects of the Multiple Fano Resonances
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 1961, 124, 1866. [Google Scholar] [CrossRef]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano resonances in photonics. Nat. Photonics 2017, 11, 543. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, L. Multiple fano resonances based on different waveguide modes in a symmetry breaking plasmonic system. IEEE Photonics J 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, X.Y.; Song, X.K.; Wang, L.L.; Yu, L. Side-Coupled Cavity-Induced Fano Resonance and Its Application in Nanosensor. Plasmonics 2015, 11, 307–313. [Google Scholar] [CrossRef]
- Krasnok, A.; Caldarola, M.; Bonod, N.; Alú, A. Spectroscopy and Biosensing with Optically Resonant Dielectric Nanostructures. Adv. Opt. Mater. 2018, 6, 1701094. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.S.; Lee, C.K. Optical nano filters based on meta-atom sidecoupled plasmonics metalinsulator-metal waveguides. J. Lightw. Technol. 2013, 31, 2876–2880. [Google Scholar] [CrossRef]
- Nan, F.; Zhang, Y.F.; Li, X.; Zhang, X.T.; Li, H.; Zhang, X.; Jiang, R.; Wang, J.; Zhang, W.; Zhou, L.; et al. Unusual and tunable one-photon nonlinearity in gold-dye plexcitonic Fano systems. Nano Lett. 2015, 15, 2705–2710. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Zhang, X.; Chen, Y.; Wang, L.; Zhang, Y.; Yu, L. Evolution of Fano resonance based on symmetric/asymmetric plasmonic waveguide system and its application in nanosensor. Opt. Commum. 2016, 370, 203–280. [Google Scholar] [CrossRef]
- Fan, J.A.; Wu, C.; Bao, K.; Bao, J.; Bardhan, R.; Halas, N.J.; Manoharan, V.N.; Nordlander, P.; Shvets, G.; Capasso, F. Self-assembled plasmonic nanoparticle clusters. Science 2010, 328, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Saliba, M.; Vogelgesang, R.; Giessen, H.; Alivisatos, A.P.; Liu, N. Transition from isolated to collective modes in plasmonic oligomers. Nano Lett. 2010, 10, 2721–2726. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, X.; Huang, Y.; Yang, H.; Gong, Q. Fast and low-power all-optical tunable Fano resonance in plasmonic microstructures. Adv. Opt. Mater. 2013, 1, 61–67. [Google Scholar] [CrossRef]
- Lu, H.; Liu, X.; Wang, L.; Gong, Y.; Mao, D. Ultrafast all-optical switching in nanoplasmonic waveguide with Kerr nonlinear resonator. Opt. Express 2011, 19, 2910–2915. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.G.; Yu, S.L. Ultra-High Sensitivity Nanosensor Based on Multiple Fano Resonance in the MIM Coupled Plasmonic Resonator. Plasmonics 2018, 13, 1115–1120. [Google Scholar] [CrossRef]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Sun, Q. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688–14695. [Google Scholar] [CrossRef] [PubMed]
- Piao, X.; Yu, S.; Koo, S.; Lee, K.; Park, N. Fano-type spectral asymmetry and its control for plasmonic metal-insulator-metal stub structures. Opt. Express 2011, 19, 10907–10912. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, J.; Zhao, Y.; Lu, D.; Xiong, Z. Numerical Investigation of a Branch-Shaped Filter Based on Metal-Insulator-Metal Waveguide. Plasmonics 2011, 6, 773. [Google Scholar] [CrossRef]
- Kou, Y.; Chen, F.X. Multimode interference demultiplexers and splitters in metal-insulator-metal waveguides. Opt. Express 2011, 19, 6042–6047. [Google Scholar] [CrossRef]
- Zhou, Z.; Hu, F.; Yi, H. Wavelength demultiplexing structure based on arrayed plasmonic slot cavities. Opt. Lett. 2011, 36, 1500–1502. [Google Scholar]
- Wu, C.; Khanikaev, A.B.; Shvets, G. Broadband slow light metamaterial based on a double-continuum Fano resonance. Phys. Rev. Lett. 2011, 106, 107403. [Google Scholar] [CrossRef]
- Artar, A.; Yanik, A.A.; Altug, H. Directional double Fano resonances in plasmonic hetero-oligomers. Nano Lett. 2011, 11, 3694–3700. [Google Scholar] [CrossRef]
- Wang, D.; Yu, X.; Yu, Q. Tuning multiple Fano and plasmon resonances in rectangle grid quasi-3D plasmonic photonic nanostructures. Appl. Phys. Lett. 2013, 103, 053117. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Wang, Y.; Jiao, R.; Wang, L.; Yu, L. Multiple Fano Resonances Based on Plasmonic Resonator System With End-Coupled Cavities for High-Performance Nanosensor. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, L.; Wang, L.L.; Duan, G.Y.; Zhao, F.Y.; Xiao, J.H. A refractive index nanosensor based on Fano resonance in the plasmonic waveguide system. IEEE Photonics Technol. Lett. 2015, 27, 1695–1698. [Google Scholar] [CrossRef]
- Wang, Y.L.; Li, S.L.; Zhang, Y.Y.; Yu, L. Ultrasharp Fano Resonances Based on the Circular Cavity Optimized by a Metallic Nanodisk. IEEE Photonics J. 2016, 8, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Cui, L.N.; Song, X.K.; Yu, L.; Xiao, J.H. High sensitivity plasmonic sensing based on Fano interference in a rectangular ring waveguide. Opt. Commun. 2015, 340, 1–4. [Google Scholar] [CrossRef]
- Wen, K.; Chen, L.; Zhou, J.; Lei, L.; Fang, Y. A Plasmonic Chip-Scale Refractive Index Sensor Design Based on Multiple Fano Resonances. Sensors 2018, 18, 3181. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, Y.; Song, X.; Wang, Y.; Yu, L. Tunable triple Fano resonances based on multimode interference in coupled plasmonic resonator system. Opt. Express 2016, 24, 15351–15361. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Zhang, Y.; Yu, L. Independently Formed Multiple Fano Resonances for Ultra-High Sensitivity Plasmonic Nanosensor. Plasmonics 2016, 11, 107–113. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Chen, Z.; Jiang, P.; Jiao, R.; Zhang, Y.; Wang, L.; Yu, L. Ultra-high Sensitivity Plasmonic Nanosensor Based on Multiple Fano Resonance in the MDM Side-Coupled Cavities. Plasmonics 2017, 12, 1099–1105. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Jiao, R.; Wang, L.; Duan, G.; Yu, L. Fano resonances based on multimode and degenerate mode interference in plasmonic resonator system. Opt. Express 2017, 25, 3525–3533. [Google Scholar] [CrossRef]
- Piao, X.; Yu, S.; Park, N. Control of Fano asymmetry in plasmon induced transparency and its application to plasmonic waveguide modulator. Opt. Express 2012, 20, 18994–18999. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.G.; Yu, S.L. Fano resonance induced by stub and applied in nanosensor. Optik 2018, 157, 1381–1390. [Google Scholar]
- Lin, X.S.; Huang, X.G. Tooth-shaped plasmonic waveguide filters with nanometeric sizes. Opt. Lett. 2008, 33, 2874–2876. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Huang, X.G.; Lin, X.S.; Tao, J.; Jin, X.P. A subwavelength coupler-type MIM optical filter. Opt. Express 2009, 17, 7549–7554. [Google Scholar] [CrossRef]
- Hu, F.; Yi, H.; Zhou, Z. Band-pass plasmonic slot filter with band selection and spectrally splitting capabilities. Opt. Express 2011, 19, 4848–4855. [Google Scholar] [CrossRef]
- Dionne, J.A.; Sweatlock, L.A.; Atwater, H.A. Plasmon slot waveguides: Towards chip-scale propagation with subwavelength-scale localization. Phys. Rev. B 2006, 73, 035407. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Na. Mater. 2010, 9, 707. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Becker, J.; Trügler, A.; Jakab, A.; Hohenester, U.; Sönnichsen, C. The optimal aspect ratio of gold nanorods for plasmonic bio-sensing. Plasmonics 2010, 5, 161–167. [Google Scholar] [CrossRef]
- Ameling, R.; Langguth, L.; Hentschel, M.; Mesch, M. Cavity-enhanced localized plasmon resonance sensing. Appl. Phys. Lett. 2010, 97, 253116. [Google Scholar] [CrossRef]






| Reference | Type | Sensitivity (nm/RIU) | FOM |
|---|---|---|---|
| [3] | single | 820 | |
| [4] | dual | 760/1320 | 815/760 |
| [7] | triple | 800/800/800 | |
| [13] | quad | 200/600/600/2000 | 3000/500/1500/200 |
| [22] | triple | 650/750/1000 | Max 8984 |
| quad | 650/750/950/1100 | ||
| [23] | single | 1260 | |
| [24] | dual | 800/1450 | |
| [25] | single | 1300 | 6838 |
| [26] | dual | 640/950 | |
| [27] | triple | 600/500/500 | 3803/816/2947 |
| [28] | triple | 1700/2000/1000 | 7100/8600/7500 |
| [29] | quad | 700/800/1900/1600 | Max 38000 |
| [30] | triple | 850/750/950 | 100/100/100 |
| This work | triple | 800/1300/2000 | |
| quad | 650/900/1350/2000 | 860/2169/4452/70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Zhao, T.; Yu, J.; Pan, D. Tuning Multiple Fano Resonances for On-Chip Sensors in a Plasmonic System. Sensors 2019, 19, 1559. https://doi.org/10.3390/s19071559
Yu S, Zhao T, Yu J, Pan D. Tuning Multiple Fano Resonances for On-Chip Sensors in a Plasmonic System. Sensors. 2019; 19(7):1559. https://doi.org/10.3390/s19071559
Chicago/Turabian StyleYu, Shilin, Tonggang Zhao, Jianguo Yu, and Dafa Pan. 2019. "Tuning Multiple Fano Resonances for On-Chip Sensors in a Plasmonic System" Sensors 19, no. 7: 1559. https://doi.org/10.3390/s19071559




