Frequency-Dependent Streaming Potential in a Porous Transducer-Based Angular Accelerometer
Abstract
:1. Introduction
2. System Structure and Principle of LCAA
3. Theoretical Analysis of the Transient Model of the Electrokinetic Effect
3.1. Modifying the Transient Model in the Circular Tube
3.2. Establishing the Transient Model of the Molecular Electronic System
3.2.1. Capillary Bundle Model of the Porous Transducer
3.2.2. Transient Model of the Electrokinetic Effect for the Capillary Bundle
3.3. Analyzing the Influence Factors of the Electrokinetic Effect
3.3.1. Effect of the Structure Parameters of the Porous Transducer
3.3.2. Effect of the Properties of the Solution
4. Experiments
- Pressure transducers and electrodes;
- Porous sample;
- Three-way valves;
- Syringes for electrolyte transport;
- Conductivity probe and pH electrode;
- Cylindrical measuring slot;
- Reservoir cup.
5. Results and Discussion
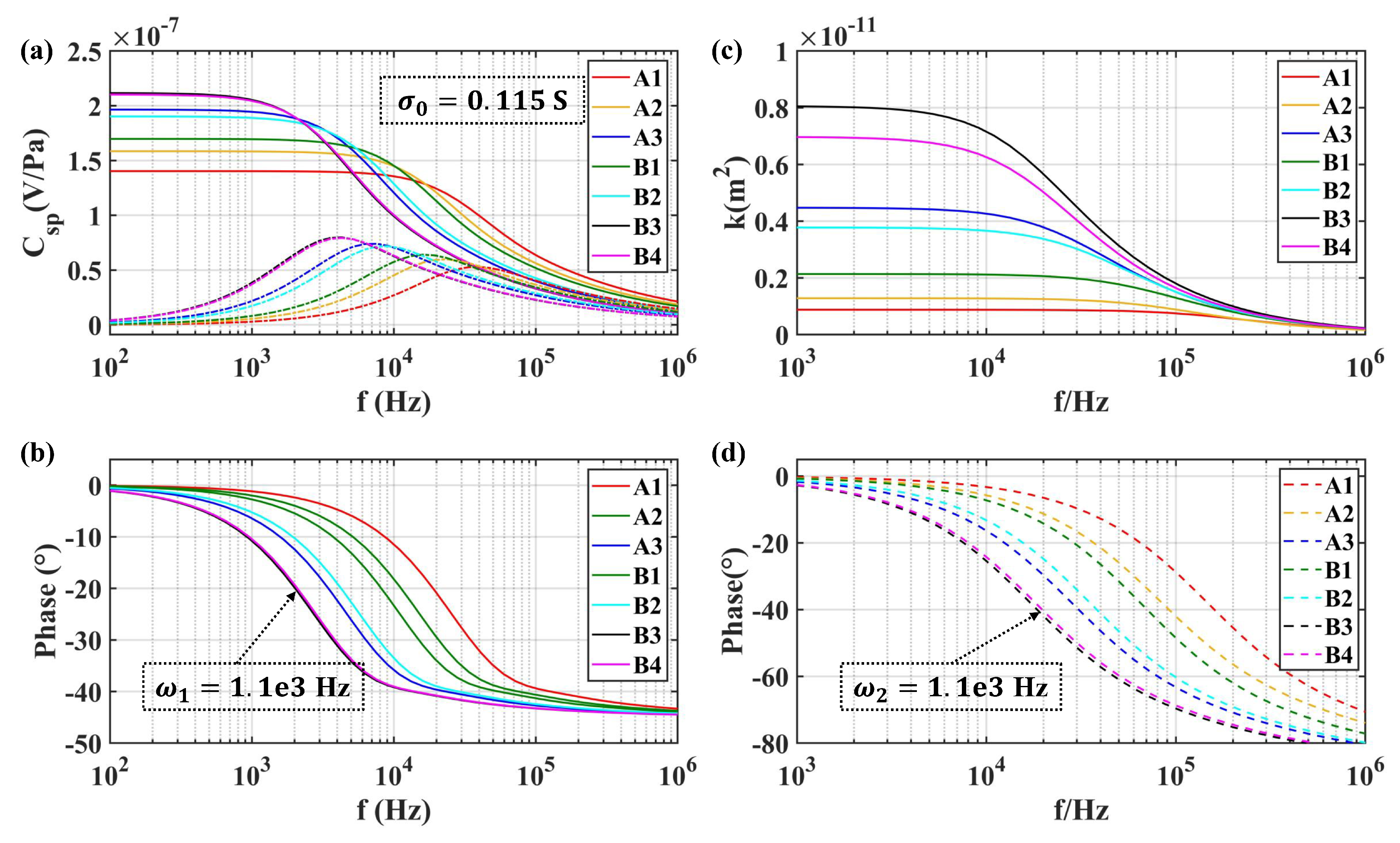
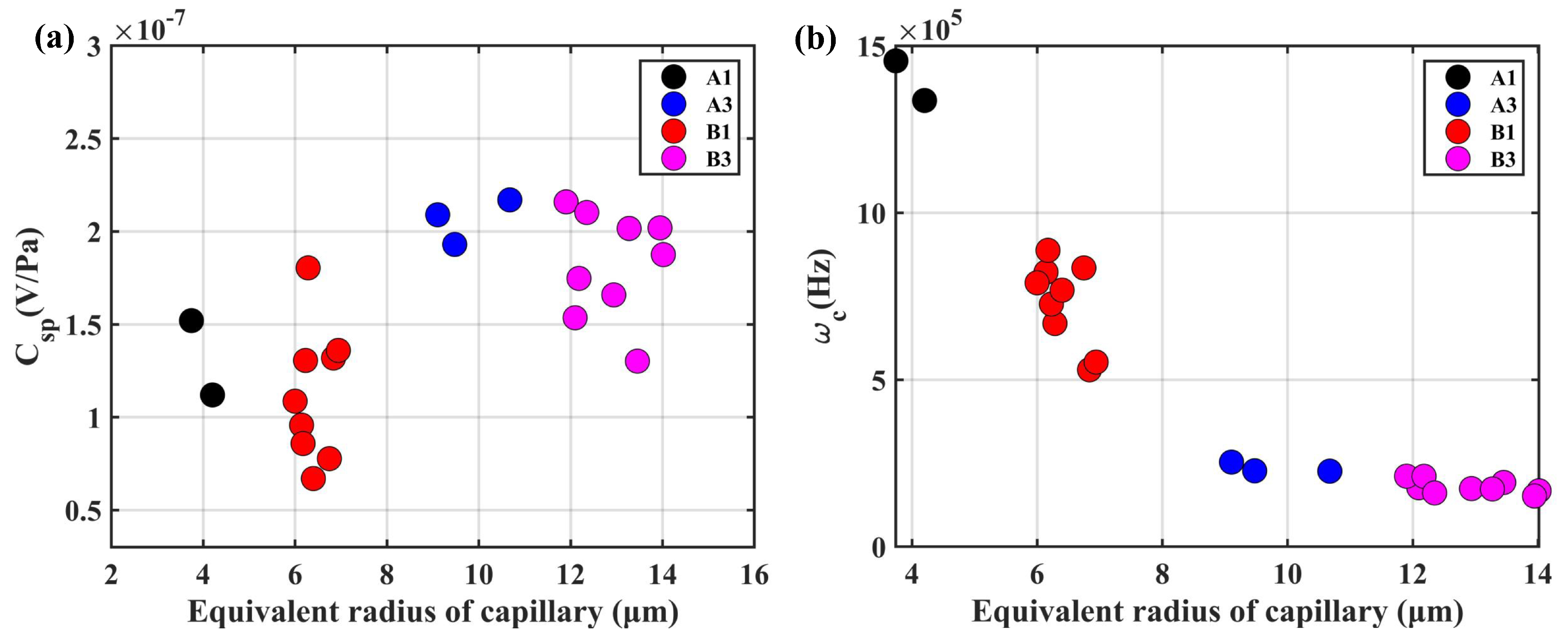
5.1. Variation from Porous Transducer
5.2. Variation from the Electrolyte Solution
- Since wave speed is the most important parameter in a fluidic system, improving the wave speed can extend the bandwidth and optimize the dynamic response, while the low-frequency gain remains the same. At present, it can be achieved only by reducing the gas percentage in fluid and increasing the thickness of the circular tube wall, which both have high technical difficulty.
- In engineering, we can change the radius of a circular tube to improve the bandwidth. However, there is a “trade-off” between low-frequency gain and the performance of transient response. We need to select a suitable value according the requirement of the application.
- Adjusting the PSD of the porous transducer, the transient response of the molecular electronic system and fluidic system both can be optimized, while the low-frequency gain of the molecular electronic system is deduced.
- Reducing the inner radius of the circular tube can improve transient performance.
- The zeta potential is the key property that can effectively increase the low-frequency gain for the molecular electronic system, which can be adjusted by changing the types of solvent or the conductivity of the electrolyte solution.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, J.D.; Wang, Y.C.; Tan, D.L.; Xu, W.L. Acceleration Feedback Control for Direct-drive Motor System. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 31 October–5 November 2000; pp. 1068–1074. [Google Scholar]
- Cheng, S.; Wang, M.; Xiang, L.; Xiao, M.; Fu, M.; Xin, Z. Transfer function of fluidic system in liquid-circular angular accelerometer. In Proceedings of the Instrumentation & Measurement Technology Conference, Taipei, Taiwan, 23–26 May 2016. [Google Scholar]
- Cheng, S.; Fu, M.; Wang, M.; Xiang, L.; Xiao, M.; Wang, T. Modeling for Fluid Transients in Liquid-Circular Angular Accelerometer. IEEE Sens. J. 2017, 17, 267–273. [Google Scholar]
- Cheng, S.; Fu, M.; Wang, M.; Ming, L.; Fu, H.; Wang, T. Dynamic Fluid in a Porous Transducer-Based Angular Accelerometer. Sensors 2017, 17, 416. [Google Scholar] [CrossRef] [PubMed]
- Fu, M.; Cheng, S.; Wang, M.; Li, M.; Wang, T. Permeability modeling for porous transducer of liquid-circular angular accelerometer. Sens. Actuators A Phys. 2017, 257, 145–153. [Google Scholar]
- Cheng, S.; Fu, M.; Wang, M.; Kulacki, F.A. The influence of tube wall on fluid flow, permeability and streaming potential in porous transducer for liquid circular angular accelerometers. Sens. Actuators A Phys. 2018, 276, 176–185. [Google Scholar] [CrossRef]
- Huang, H.; Agafonov, V.M.; Yu, H. Molecular electric transducers as motion sensors: A review. Sensors 2013, 13, 4581–4597. [Google Scholar] [CrossRef]
- Sun, Z.; Agafonov, V.M. 3D numerical simulation of the pressure-driven flow in a four-electrode rectangular micro-electrochemical accelerometer. Sens. Actuators B Chem. 2010, 146, 231–238. [Google Scholar] [CrossRef]
- Agafonov, V.M.; Zaitsev, D.L. Convective noise in molecular electronic transducers of diffusion type. Tech. Phys. 2010, 55, 130–136. [Google Scholar] [CrossRef]
- Krishtop, V.G.; Agafonov, V.M. Technological principles of motion parameter transducers based on mass and charge transport in electrochemical microsystems. Russ. J. Electrochem. 2012, 48, 746–755. [Google Scholar] [CrossRef]
- Gola, A.; Chiesa, E.; Lasalandra, E.; Pasolini, F.; Tronconi, M.; Ungaretti, T.; Baschirotto, A. Interface for MEMS-based Rotational Accelerometer for HDD Applications with 2.5 rad/s2 Resolution and Digital Output. IEEE Sens. J. 2003, 3, 383–392. [Google Scholar] [CrossRef]
- Lin, J.M.; Cho, K.H.; Lin, C.H.; Lu, H.H. A Novel Wireless Thermal Convection Type Angular Accelerometer Integrated with an Active RFID-Tag. Appl. Mech. Mater. 2013, 284–287, 2005–2008. [Google Scholar] [CrossRef]
- Alrowais, H.; Getz, P.; Kim, M.G.; Su, J.J.; Brand, O. Bio-inspired fluidic thermal angular accelerometer. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems, Shanghai, China, 24–28 January 2016. [Google Scholar]
- Zhao, H.; Feng, H. A novel angular acceleration sensor based on the electromagnetic induction principle and investigation of its calibration tests. Sensors 2013, 13, 10370–10385. [Google Scholar] [CrossRef] [PubMed]
- Delgado, A.V.; González-Caballero, F.; Hunter, R.J.; Koopal, L.K.; Lyklema, J. Measurement and Interpretation of Electrokinetic Phenomena. Pure Appl. Chem. 2005, 77, 1753–1805. [Google Scholar] [CrossRef]
- Revil, A.; Pezard, P.A.; Glover, P.W.J. Streaming Potential in Porous Media: 1. Theory of the Zeta Potential. J. Geophys. Res. Solid Earth 1999, 104, 20021–20031. [Google Scholar] [CrossRef]
- Wang, J.; Hu, H.; Guan, W.; Li, H. Electrokinetic Experimental Study on Saturated Rock Samples: Zeta Potential and Surface Conductance. Geophys. J. Int. 2015, 201, 869–877. [Google Scholar] [CrossRef]
- Revil, A.; Schwaeger, H.; Cathles, L.M., III; Manhardt, P.D. Streaming potential in porous media: 2. Theory and application to geothermal systems. J. Geophys. Res. 1999, 104, 20033–20048. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Toksöz, M.N. Experimental measurements of the streaming potential and seismoelectric conversion in Berea sandstone. Geophys. Prospect. 2013, 61, 688–700. [Google Scholar] [CrossRef]
- Jackson, M.D. Characterization of Multiphase Electrokinetic Coupling using a Bundle of Capillary Tubes Model. J. Geophys. Res. Solid Earth 2008, 113, B04201. [Google Scholar] [CrossRef]
- Jackson, M.D. Multiphase Electrokinetic Coupling: Insights into the Impact of Fluid and Charge Distribution at the Pore Scale from a Bundle of Capillary Tubes Model. J. Geophys. Res. Solid Earth 2010, 115, B07206. [Google Scholar] [CrossRef]
- Khaddour, F.; Greggoire, D.; Pijaudier-Cabot, G. Capillary Bundle Model for the Computation of the Apparent Permeability from Pore Size Distributions. Eur. J. Environ. Civ. Eng. 2015, 19, 168–183. [Google Scholar] [CrossRef]
- Xiong, Q.; Baychev, T.G.; Jivkov, A.P. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport. J. Contam. Hydrol. 2016, 192, 101–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, B.; Kim, S.J. The Effect of the Particle Size Distribution and Packing Structure on the Permeability of Sintered Porous Wicks. Int. J. Heat Mass Transf. 2013, 61, 499–504. [Google Scholar]
- Zhang, W.; Yao, J.; Ying, G.; Qi, Z.; Hai, S. Analysis of electrokinetic coupling of fluid flow in porous media using a 3-D pore network. J. Pet. Sci. Eng. 2015, 134, 150–157. [Google Scholar] [CrossRef]
- Glover, P.W.J.; Ruel, J.; Tardif, E.; Walker, E. Frequency-dependent Streaming Potential of Porous Media—Part 1: Experimental Approaches and Apparatus Design. Int. J. Geophys. 2012, 2012, 846204. [Google Scholar] [CrossRef]
- Zhu, Z.; Toksoz, M.N.; Zhan, X. Experimental Studies of Streaming Potential and High Frequency Seismoelectric Conversion in Porous Samples; Technical Report; Massachusetts Institute of Technology, Earth Resources Laboratory: Cambridge, MA, USA, 2009. [Google Scholar]
- Tardif, E.; Glover, P.W.J.; Ruel, J. Frequency-dependent Streaming Potential of Ottawa Sand. J. Geophys. Res. Solid Earth 2011, 116, B04206. [Google Scholar] [CrossRef]
- Glover, P.W.J.; Walker, E.; Ruel, J.; Tardif, E. Frequency-Dependent Streaming Potential of Porous Media—Part 2: Experimental Measurement of Unconsolidated Materials. Int. J. Geophys. 2012, 2012, 728495. [Google Scholar] [CrossRef]
- Packard, R.G. Streaming Potentials across Glass Capillaries for Sinusoidal Pressure. J. Chem. Phys. 1953, 21, 303–307. [Google Scholar] [CrossRef]
- Reppert, P.M.; Morgan, F.D. Streaming Potential Collection and Data Processing Techniques. J. Colloid Interface Sci. 2001, 233, 348–355. [Google Scholar] [CrossRef] [PubMed]
- Pride, S. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B 1994, 50, 15678. [Google Scholar] [CrossRef]
- Jouniaux, L.; Bordes, C. Frequency-Dependent Streaming Potentials: A Review. Int. J. Geophys. 2012, 2012, 194–203. [Google Scholar] [CrossRef]
- Cheng, S.; Fu, M.; Kulacki, F. Characterization of a porous transducer using a capillary bundle model: Permeability and streaming potential prediction. Int. J. Heat Mass Transf. 2018, 118, 349–354. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1937, 75, S32–S48. [Google Scholar] [CrossRef]
- Carman, P.C. Permeability of saturated sands, soils and clays. J. Agric. Sci. 1939, 29, 262–273. [Google Scholar] [CrossRef]
- Worthington, A. SCA guidelines for sample preparation and porosity measurement of electrical resistivity samples, Part I—Guidelines for preparation of brine and determination of brine resistivity for use in electrical resistivity measurements. Log Anal. 1990, 31, 20–28. [Google Scholar]
- Esmaeili, S.; Rahbar, M.; Pahlavanzadeh, H.; Ayatollahi, S. Investigation of streaming potential coupling coefficients and zeta potential at low and high salinity conditions: Experimental and modeling approaches. J. Pet. Sci. Eng. 2016, 145, 137–147. [Google Scholar] [CrossRef]
- Boleve, A.; Crespy, A.; Revil, A.; Janod, F.; Mattiuzzo, J.L. Streaming potentials of granular media: Influence of the Dukhin and Reynolds numbers. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Glover, P.W.J. Modelling pH-Dependent and Microstructure-Dependent Streaming Potential Coefficient and Zeta Potential of Porous Sandstones. Transp. Porous Media 2018, 124, 31–56. [Google Scholar] [CrossRef] [Green Version]



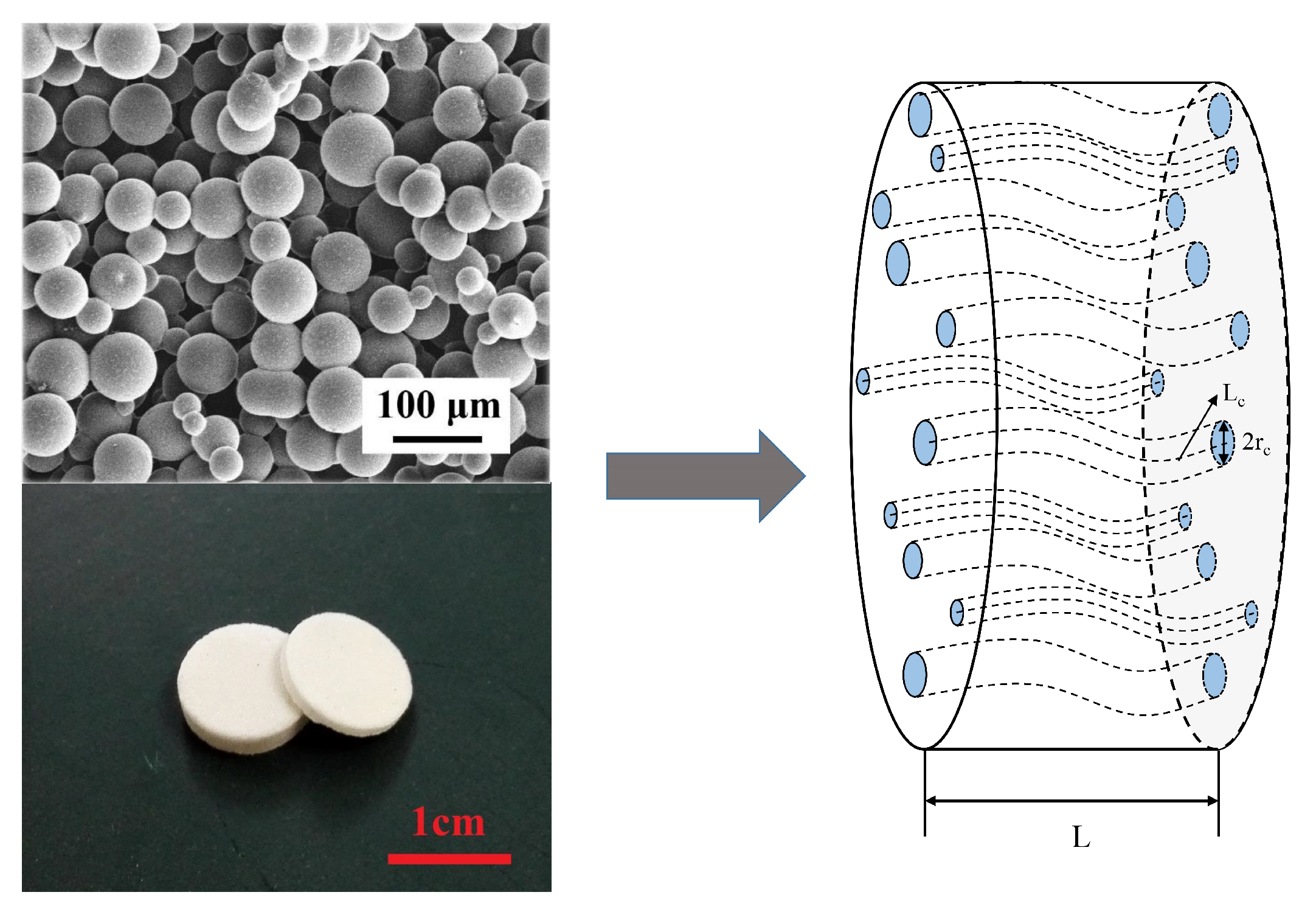

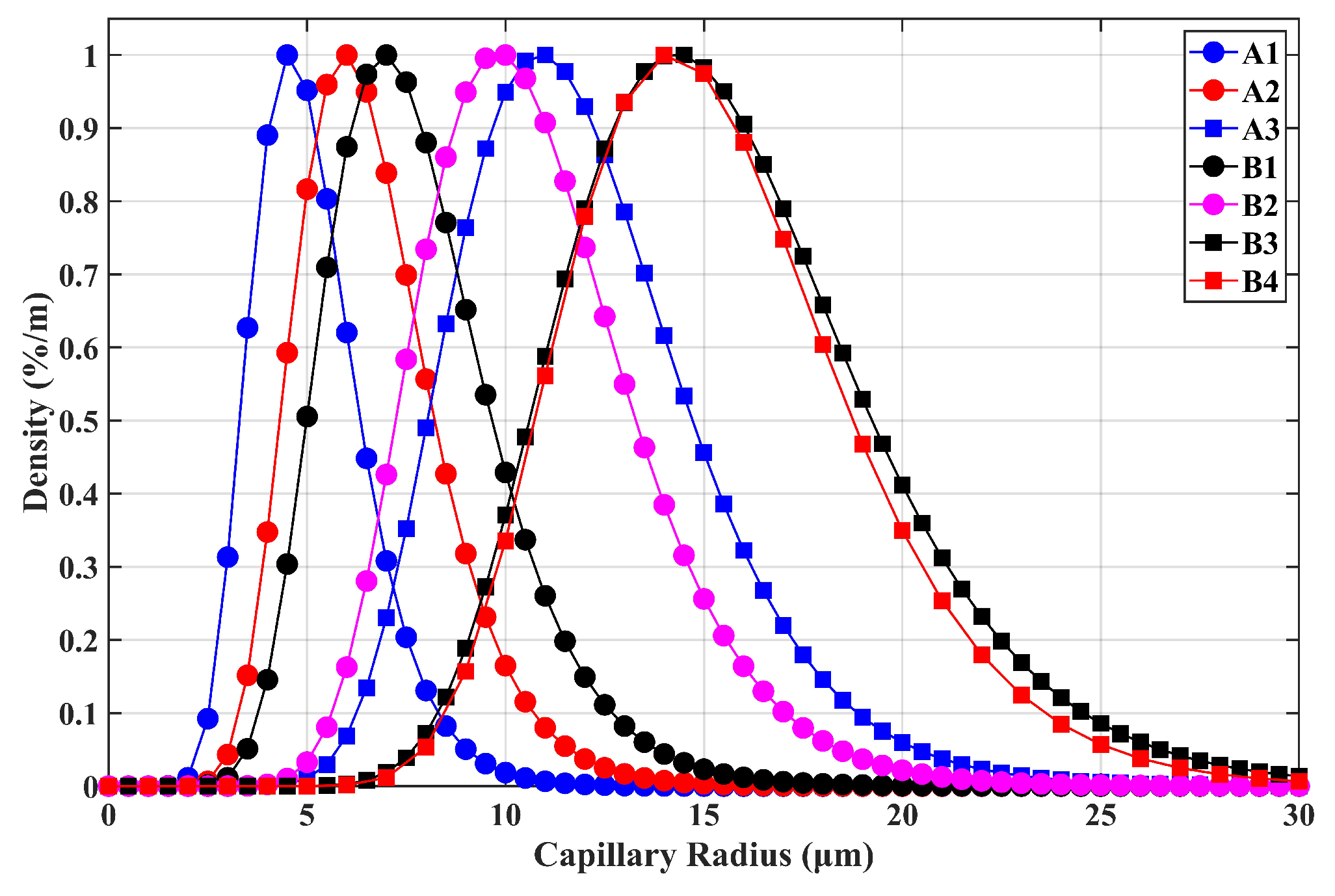



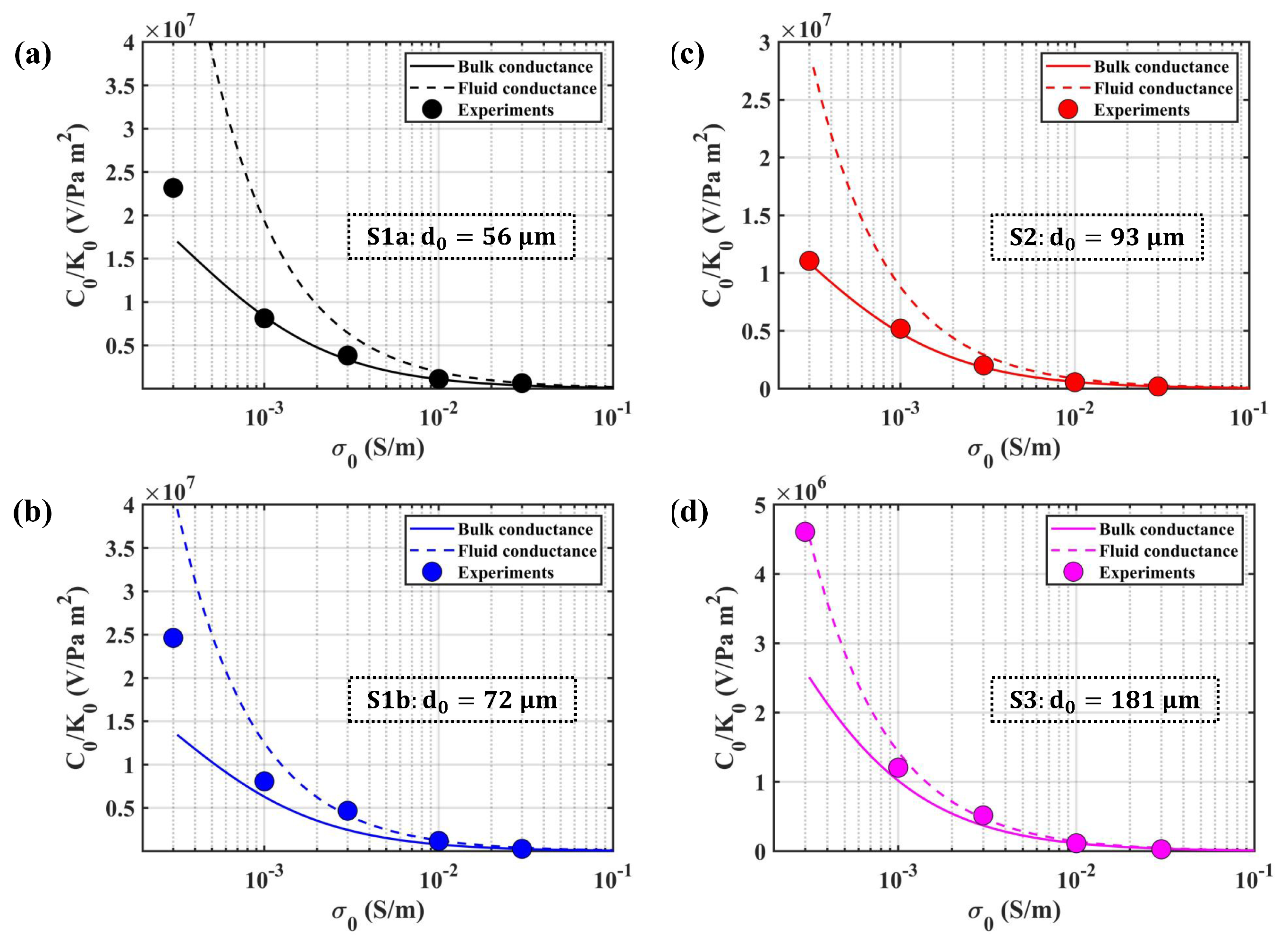

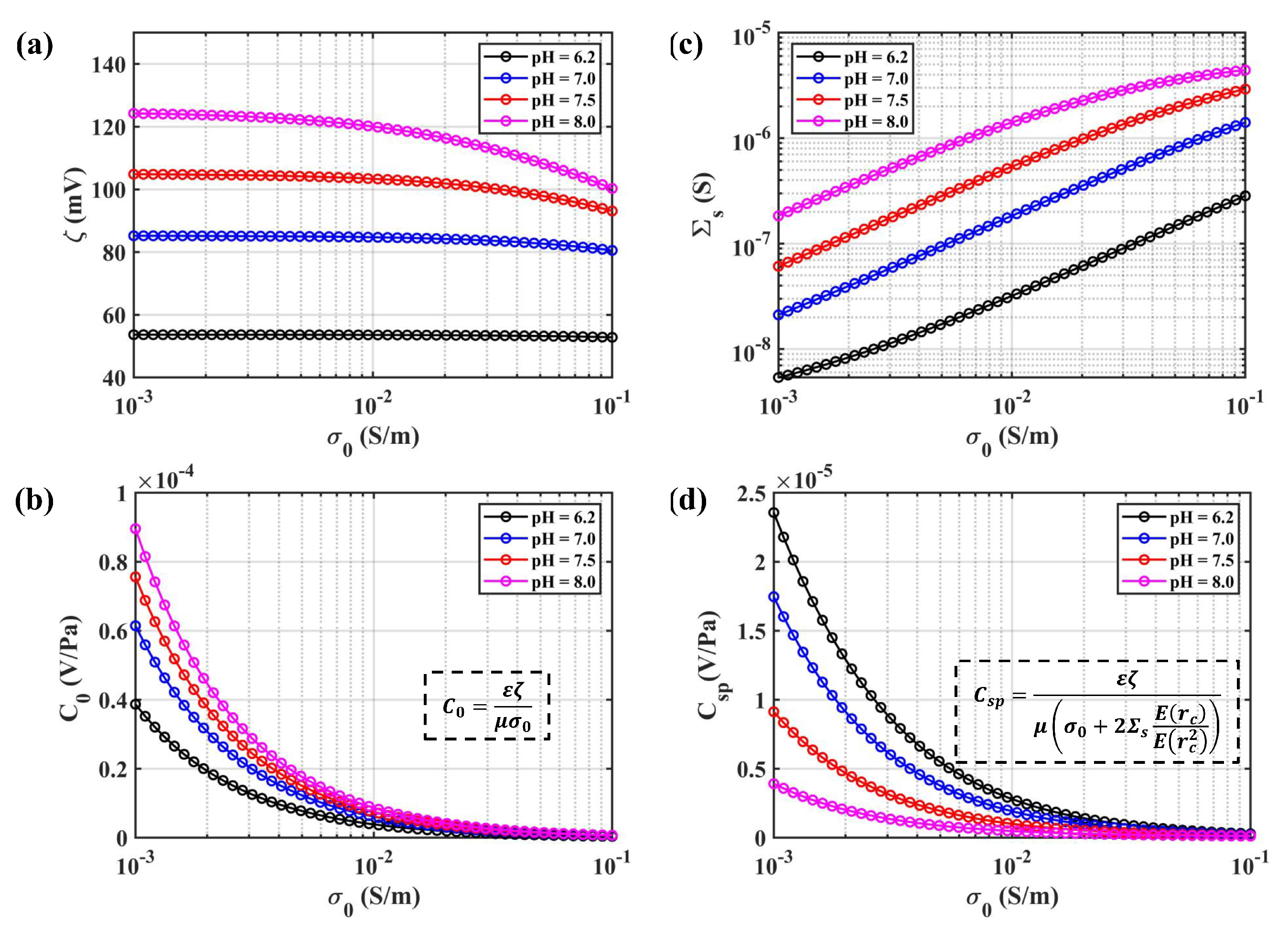


| Type | ||||||
|---|---|---|---|---|---|---|
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| B1 | ||||||
| B2 | ||||||
| B3 | ||||||
| B4 |
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| 0.0115 | 9.3 | ||
| 0 | |||
| 115 | |||
| pH |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | |||
| T | 300 | m | |
| 70 m | |||
| 20 | |||
| Parameter | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| R (m) | 70 | 7 | ||
| () |
| Index | Value | Unit |
|---|---|---|
| Bandwidth | 0.5∼120 | Hz |
| Measurement Range | −25,000∼+25,000 | |
| Scale Factor | 0.5 | |
| Power Supply | ±15 | |
| External Size | 75 × 41 | mm |
| Temperature Range | −40∼+60 | °C |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, L.; Wang, M.; Ning, K. Frequency-Dependent Streaming Potential in a Porous Transducer-Based Angular Accelerometer. Sensors 2019, 19, 1780. https://doi.org/10.3390/s19081780
Ming L, Wang M, Ning K. Frequency-Dependent Streaming Potential in a Porous Transducer-Based Angular Accelerometer. Sensors. 2019; 19(8):1780. https://doi.org/10.3390/s19081780
Chicago/Turabian StyleMing, Li, Meiling Wang, and Ke Ning. 2019. "Frequency-Dependent Streaming Potential in a Porous Transducer-Based Angular Accelerometer" Sensors 19, no. 8: 1780. https://doi.org/10.3390/s19081780
APA StyleMing, L., Wang, M., & Ning, K. (2019). Frequency-Dependent Streaming Potential in a Porous Transducer-Based Angular Accelerometer. Sensors, 19(8), 1780. https://doi.org/10.3390/s19081780





